I. 서 론

정합장 처리(Matched-Field Processing, MFP)^[1]는 수중 음원의 위치(거리 및 심도)를 추정하기 위한 방법으로, 1970년대 Bucker^[2]에 의해 처음 제안되어 현재까지도 많은 연구가 이루어지고 있다. 정합장 처리는 평면파를 가정하는 기존의 빔형성 기법과는 달리, 복잡한 해양 음향 환경을 정밀하게 모사할 수 있는 파동 방정식의 해를 이용한다. 따라서, 정합장 처리는 평면파 빔형성 기법을 일반화한 배열 처리 알고리즘으로 분류된다.

정합장 처리는 수직 또는 수평 배열을 통해 수신된 데이터 벡터와 수중 음원이 존재할 가능성이 있는 모든 위치에서 계산된 파동 방정식의 해인 레플리카 벡터 사이의 상관성을 분석하여 수중 음원의 위치 정보를 제공한다. 이 과정에서 음속 구조, 수심, 해저 지형, 지음향 인자, 배열 기울기 등의 해양 음향 환경 변수들에 대한 정확한 정보가 필수적으로 요구된다. 이러한 환경 변수들에 대한 부정확성은 모델 오정합으로 이어질 수 있으며, 이는 정합장 처리의 성능에 큰 영향을 미칠 수 있다. 이에 따라, 모델 오정합 문제를 극복하기 위해 적응형 정합장 처리 방법^[3,4,5]에 관한 많은 연구가 활발히 이루어지고 있다.

최근 연구에서는 모델 오정합 문제를 최소화하기 위해 도파관 불변성(Waveguide Invariant, WI)^[6,7,8] 이론에 기반한 수중 음원 거리 추정 방법이 제안되었다.^[9,10] 도파관 불변성 이론은 도파관에서 전파되는 모드들의 군속도와 위상속도의 관계를 통해 모드 분산 특성을 설명한다. 거리 독립적인 이상적인 도파관에서의 도파관 불변성 파라미터는 β=cos2θ와 같은 해석적인 표현으로 정의되며,^[11] 이는 접지각 𝜃의 함수임을 알 수 있다. 또한, 거리 종속적인 이상적인 도파관에서의 도파관 불변성 파라미터 𝛽는 수신기와 음원 사이의 해저지형 및 접지각에 대한 복잡한 함수로 정의된다.^[12]

이와 같이 도파관 불변성 파라미터 𝛽는 이상적인 도파관에서 정의되지만, 실제 해역과 같은 일반적인 도파관에서의 도파관 불변성 파라미터 𝛽의 적용 가능성이 다양한 연구를 통해 확인되었다.^[13,14] 이는 일반적인 도파관에서 해수면과 해저면 경계면 반사에 의해 전파되는 모드들의 분산 특성이 이상적인 도파관에서의 모드 분산 특성과 매우 유사하기 때문이다. 따라서, 일반적인 도파관에서의 경계면 반사에 의해 전파되는 모드들을 활용하면, 주파수, 음속 구조, 지음향 인자 등과 같은 해양 음향 환경 변수와 관계없이 이상적인 도파관에서 정의된 𝛽를 활용한 수중 음원 거리 추정이 가능함을 알 수 있다.

하지만, 심해 환경과 같이 굴절파가 우세한 조건에서는 도파관 불변성 파라미터 𝛽의 값이 음원과 수신기의 상대적인 거리 및 심도에 따라 크게 변동^[15]하기 때문에, 도파관 불변성 파라미터 𝛽를 활용한 수중 음원 거리 추정 방법은 경계면 반사가 존재하는 천해 환경에 제한적으로 적용 가능함을 알 수 있다.

본 논문에서는 Fig. 1과 같이 얕은 웅덩이가 존재하는 천해 환경에서 도파관 불변성 이론을 기반으로 한 수중 음원 거리 추정 연구에 대해 논의한다. Fig. 1과 같은 거리 종속적인 환경에서의 도파관 불변성 파라미터 𝛽를 정의하기 어렵기 때문에, 거리 독립적인 이상적인 도파관 환경에서 정의된 도파관 불변성 파라미터 β=cos2θ를 활용하였다. 이에 따라 발생하는 음원 거리 추정 오차 및 오차 원인을 해상실험 데이터와 수치 시뮬레이션을 통해 자세히 분석하였다. 즉, 본 논문의 목적은 천해 환경에서 관찰될 수 있는 얕은 웅덩이 형태의 해저지형에 대한 음원 거리 추정 성능을 분석하는 것이다.

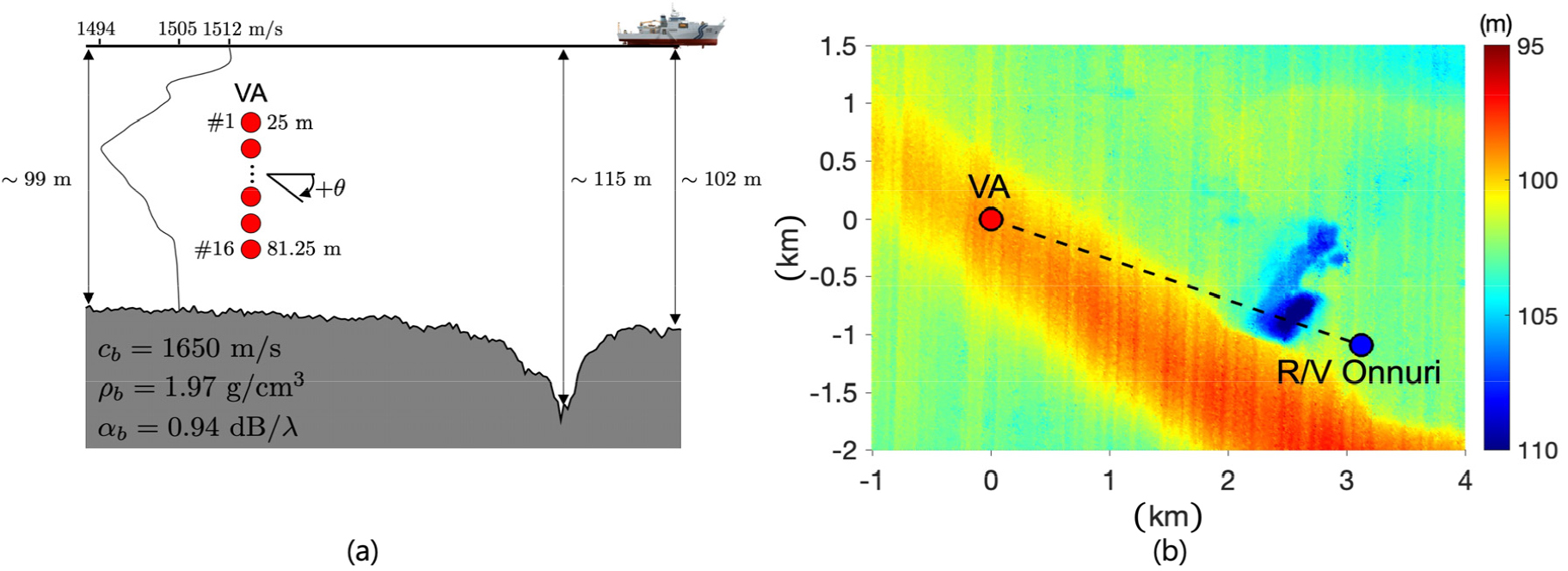
Fig. 1.

(Color available online) (a) Schematic of a source-tow run on JD 145 (May 25) using the R/V Onnuri during the SAVEX15. A positive grazing angle of 𝜃 is assigned to an up-going ray path. (b) Bathymetry of the experimental site with the Vertical Array (VA) at the origin (red dot). The blue dot denotes the Onnuri at a range of 3.3 km (JD15145155300). Note that the bathymetry shows a diagonal strip of sand dune (reddish) and pits (bluish) east of the VA.

본 논문의 구성은 다음과 같다. II장에서는 도파관 불변성 이론을 기반으로 한 음원 거리 추정 방법을 설명한다. III장에서는 SAVEX15 환경을 설명하고, 실험 데이터를 이용한 거리 추정 결과를 논의한다. IV장에서는 수치 시뮬레이션을 통해 III장에서의 실험데이터 분석 결과를 해석하고, 단순화된 웅덩이가 포함된 해저지형서의 음원 거리 추정 결과를 추가적으로 분석한다. V장에서는 최종적으로 결론을 제시한다.

II. 도파관 불변성 기반의 음원 거리 추정

거리 독립적인 환경에서의 도파관 불변성 파라미터 𝛽는 다음과 같이 정의된다.^[11]

여기서 vg는 군속도를, vp는 위상속도를 나타낸다. 또한, Sg와 Sp는 각각 군속도와 위상속도의 역수를 나타낸다. Eq. (1)에 Sg=t/r0와 Sp=cosθ/c를 각각 대입한 후 정리하면, 아래와 같이 음원의 거리 r0에 관한 식을 얻는다.

여기서 c는 수신기 위치에서의 명목상의 음속 값을 나타내며, 일반적으로 c=1500m/s를 가정한다. 명목상의 음속 c=1500m/s에서 편차 ∆c=15m/s가 발생하더라도 추정 거리 오차율은 단지 1 %에 불과하므로, 실용적인 관점에서 c=1500m/s의 가정이 합리적임을 알 수 있다.

본 논문에서는 접지각 𝜃를 얻기 위해 수직 배열(Vertical Array, VA)을 가정한다. 따라서, 접지각 𝜃는 빔형성을 통해 계산된 다중경로 신호들의 빔각도를 의미하며, t는 해당 다중경로 신호들의 도달 시간을 나타낸다. 또한, 도파관 불변성 파라미터는 β=cos2θ로 정의되며, 이는 거리 독립적인 이상적인 도파관에서의 군속도 vg=ccosθ와 위상속도 vp=c/cosθ를 이용하여 Eq. (1)로부터 얻을 수 있다.^[11]

최종적으로 음원 거리 추정에 관한 식을 아래와 같이 나타낼 수 있다.^[10]

여기서 χβ는 배열 불변성 파라미터로 다음과 같이 정의되며,

편의상 수직 배열을 이용한 빔형성의 출력 값인 sinθ로 표현한다. Eq. (4)의 양변을 적분하면 아래의 식을 얻을 수 있다.

여기서 t0와 θ0는 임의의 상수를 나타내며, Eq. (5)를 정리하면 아래 Eq. (6)과 같이 나타낼 수 있다.

여기서 tc는 아래와 같다.

위 식들을 이용하여 최종적으로 Fig. 2(b)의 검은색 실선에 해당하는 빔-시간 이주선을 Eq. (8)과 같이 정의할 수 있다.

배열 불변성 파라미터 χβ는 빔-시간 영역[refer to Fig. 2(b)]에서의 다중경로 신호들의 빔각도와 도달 시간 정보를 이용하여 Eq. (9)로부터 계산될 수 있다.

여기서 dβ는 절편 값을 나타낸다. 실제 거리 추정 및 빔-시간 이주선은 최소제곱법을 통해 계산된 χ^β와 d^β를 이용한다.^[10,12]

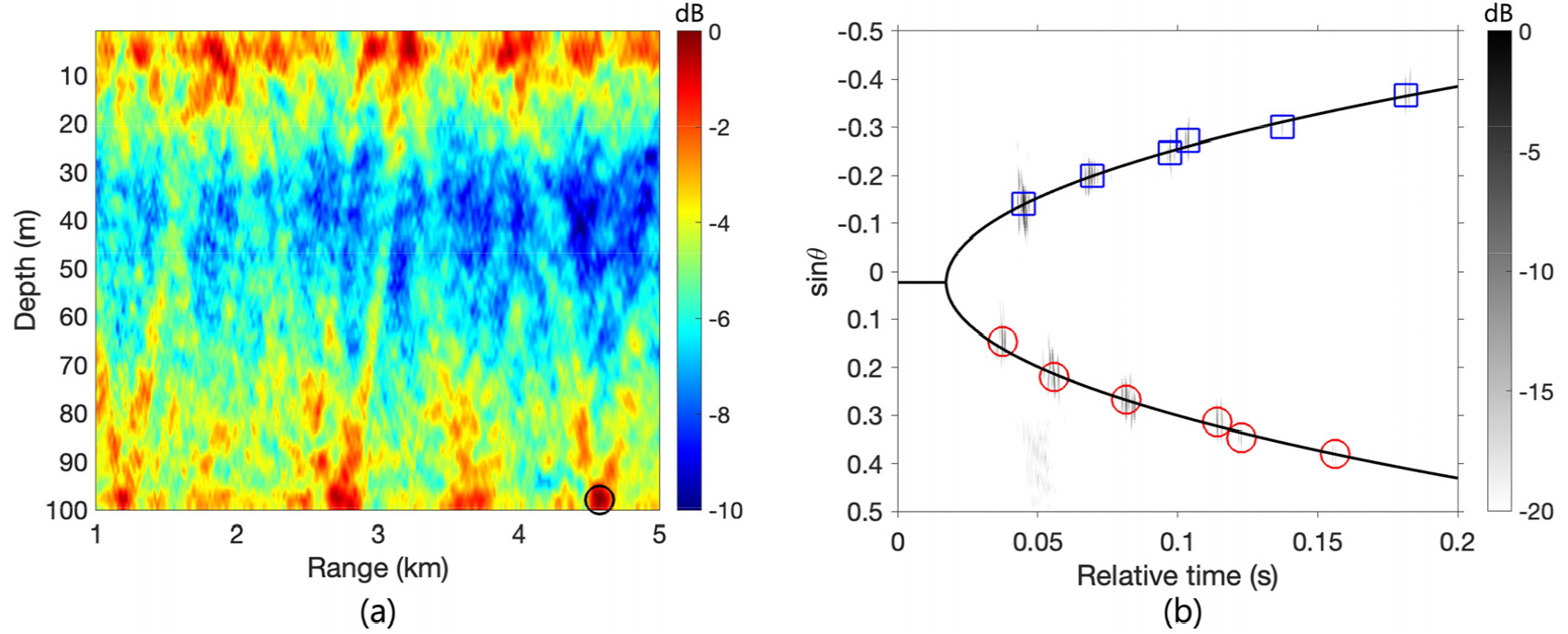
Fig. 2.

(Color available online) MFP versus WI for a shallow pit (refer to Fig. 1). (a) Ambiguity surface of MFP. (b) Beam-time domain of WI.

III. SAVEX15 실험

3.1 해상 실험 환경

Shallow-water Acoustic Variability EXperiment 2015 (SAVEX15)^[16] 해상 실험은 2015년 5월 동중국해 북동부에서 연구선 온누리호(R/V Onnuri)를 이용하여 수행되었다. 실험 해역의 평균 수심은 약 100 m이며, 3.75 m 간격의 16개 센서로 구성된 56.25 m 길이의 수직 배열이 음향 데이터 수신을 위해 사용되었다. Fig. 1(a)에 보여지는 음속 구조는 JD145(5월 25일) 전후 두 개의 Conductivity, Temperature, and Depth(CTD) 자료 평균을 나타내며, 약 40 m 수심에서 음향 축이 형성되었음을 알 수 있다. Fig. 1(b)는 실험 해역의 일부 해저지형 정보를 나타낸다. 수직 배열(빨간색 점) 주변으로 대각선 형태의 수중 사구와 약 115 m 깊이의 얕은 웅덩이 형태의 지형이 관찰됨을 알 수 있다.

3.2 데이터 분석 결과

본 절에서는 Fig. 1에서 보여지는 해양 음향 환경 조건에서의 음원 거리 추정 결과에 대해 논의한다. 약 1.5 m/s 속도로 이동하며 1 kHz 미만의 광대역 소음을 방사하는 온누리호를 음원으로 가정하였다. 약 115 m 깊이의 얕은 웅덩이가 음원 거리 추정에 미치는 영향을 분석하기 위해, 수직 배열과 음원 사이에 해당 웅덩이가 관찰되는 시간대(JD15145155300)의 2 s(25 s ~ 27 s) 선박 소음 데이터(200 Hz ~ 900 Hz)를 분석하였다. 이때, 수직 배열과 음원 사이의 거리는 r0=3308m이며, 수직 배열과 음원 위치에서의 수심은 각각 약 99 m 및 102 m로, 약간의 경사를 가지는 해저지형이다.

Fig. 2(a)는 Fig. 1(a)에서 보여지는 해양 음향 환경을 가정한 정합장 처리 결과를 보여준다. 거리(x축) 및 수심(y축)에 따른 상관성을 데시벨(dB) 단위로 나타내었으며, 빨간색은 높은 상관성을, 파란색은 낮은 상관성을 의미한다. 레플리카 계산을 위해 노말 모드 기반의 KRAKEN 모델^[17]을 이용하였으며, 얕은 웅덩이의 영향을 파악하기 위해 수심 100 m의 거리 독립적인 평탄한 해저지형을 가정하였다. 세부적인 정합장 처리 방법은 Reference [18]을 참고하였다. 해수면 근처의 온누리호가 음원으로 이용되었음에도 불구하고, 4.5 km 부근 해저면 근처에서 가장 높은 상관성(검은색 원) 값을 확인할 수 있다. 이 결과는 레플리카 벡터 계산 시 실제 해저 지형을 고려하지 않고 수심 100 m의 평탄한 해저지형을 가정함으로써 발생하는 해저지형 오정합 문제를 나타낸다. 이를 통해, 정합장 처리는 해저지형에 대해 매우 민감한 음원 위치 추정 성능을 보이는 것을 확인할 수 있다.

Fig. 2(b)는 도파관 불변성을 기반으로 한 빔-시간 영역을 보여준다. x축과 y축은 빔형성을 통해 분리된 다중경로 신호들의 빔각도 및 도달 시간 정보를 나타내며, 빨간색 원과 파란색 사각형은 각각 상향 도 착 및 하향 도착을 의미한다. 분리된 다중경로 신호들의 빔각도 및 도달 시간 정보를 활용하여 Eq. (8)을 통해 검은색 실선에 해당하는 빔-시간 이주선을 그릴 수 있으며, 선택된 모든 다중경로 신호들을 크게 벗어나지 않는 것을 확인할 수 있다.

최종적으로, 선택된 모든 다중경로 신호들을 이용한 음원의 추정 거리는 약 2.9 km이며, –12 %의 거리 오차를 갖는다. 만약 도파관 불변성 파라미터를 선형 기울기를 가지는 해저지형에서의 도파관 불변성 파라미터 β=Ds/Dr≈1.03으로 가정하면,^[12] 추정된 음원의 거리는 약 3.2 km이며, 실제 음원의 거리와 매우 유사함을 확인할 수 있다. 여기서 Ds와 Dr은 각각 음원과 수신 배열 위치에서의 수심을 의미한다. 따라서, 이러한 오차의 원인은 얕은 웅덩이의 영향보다는 약간의 기울기를 가진 실제 해저지형 형상의 영향이 큰 것으로 판단된다. 다음 장에서는 웅덩이에 대한 거리 추정 성능을 시뮬레이션을 통해 자세히 분석하였다.

IV. 수치 시뮬레이션

4.1 실제 해저지형에서의 거리 추정

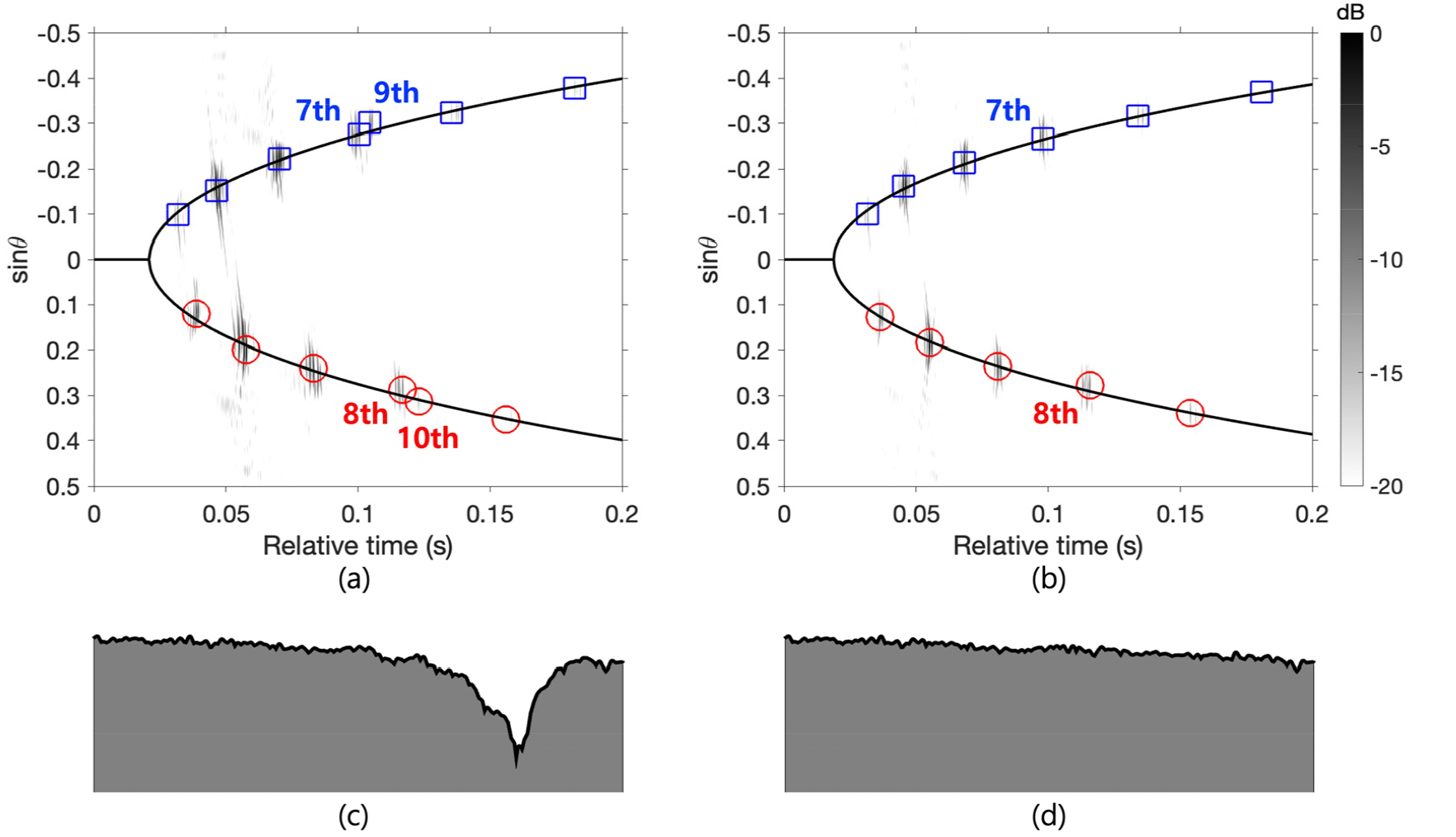
본 절에서는 Fig. 1(a)와 동일한 해양 음향 환경 조건에서의 수치 시뮬레이션 결과를 분석한다. Fig. 3은 얕은 웅덩이의 유무에 따른 도파관 불변성 기반의 음원 거리 추정 결과를 보여준다. Fig. 3(a)와 (b)는 각각 아래에 위치한 Fig. 3(c)와 (d)의 해저지형을 가정한 빔-시간 영역을 나타낸다. 해상실험 데이터[refer to Fig. 2(b)]와의 비교를 위해, 음원의 거리 r0=3308m와 심도 z0=5m를 가정하였다.

Fig. 3.

(Color available online) (a) Beam-time domain for the bathymetry shown in (c). (b) Beam-time domain for the bathymetry shown in (d). The 9th and 10th multipath arrivals in panel (a) indicate those caused by the shallow pit shown in (c).

얕은 웅덩이가 관찰되는 해저지형의 경우[Fig. 3(a)], 총 13개의 분리된 다중경로 신호가 확인되며, 이는 해상실험 데이터를 활용한 빔-시간 영역 결과와 매우 유사함을 확인할 수 있다. 모든 다중경로 신호들을 이용하여 추정된 음원의 거리는 약 3.0 km이며, 거리 오차는 –10 %이다. 반면, 얕은 웅덩이가 관찰되지 않는 해저지형의 경우[Fig. 3(b)], 총 11개의 분리된 다중경로 신호가 확인되며, Fig. 3(a)와 비교했을 때 9th와 10th 다중경로 신호가 관찰되지 않음을 알 수 있다. 이로부터, 9th와 10th 다중경로 신호는 얕은 웅덩이의 영향에 의해 발생된 것임을 추론할 수 있다.

Fig. 4는 보다 상세한 분석을 위한 음선 추정 결과를 보여준다. 이 그림에서 파란색 점은 음원의 위치를, 빨간색 점은 수신 배열의 중앙 위치(z=53.125m)를 나타낸다. Fig. 4(a)와 (b)는 각각 7th와 8th 다중경로 신호들의 음선 경로를 나타내며, 이들 음선은 웅덩이의 영향을 받지 않는 것으로 나타난다. 반면, Fig. 4(c)와 (d)는 각각 9th와 10th 다중경로 신호들의 음선 경로를 보여주며, 확대된 그림을 통해 이들 음선이 웅덩이의 영향을 받는 것으로 확인할 수 있다.

Fig. 4.

(Color available online) Ray diagram for the (a) 7th, (b) 8th, (c) 9th, and (d) 10th multipath arrivals separated in Fig. 3(a). The red dot denotes a receiver located at the center of the VA, while the blue dot denotes the source location. As seen in the enlarged panel in (c) and (d), the 9th and 10th multipath arrivals are affected by the shallow pit.

만약 Fig. 3(a)에서 9th와 10th 다중경로 신호를 제외하더라도, 추정된 음원의 거리는 약 3.0 km로, 모든 다중경로 신호를 활용한 추정 값과 큰 차이가 없는 것을 확인할 수 있다. 이는 얕은 웅덩이의 영향을 받는 9th와 10th 다중경로 신호들이 웅덩이의 영향을 받지 않는 7th와 8th 다중경로 신호들과 유사한 경로로 수신되었기 때문인 것으로 판단된다. 따라서, 빔-시간 이주선이 모든 다중경로 신호들을 크게 벗어나지 않는 것을 확인할 수 있다. 마찬가지로, 도파관 불변성 파라미터 β=Ds/Dr≈1.03을 가정하면 추정된 음원의 거리는 약 3.3 km로 실제 음원의 거리와 매우 유사하게 추정됨을 확인할 수 있다.

4.2 단순화된 해저지형에서의 거리 추정

본 절에서는 얕은 웅덩이의 영향을 받는 다중경로 신호들로 인해 도파관 불변성 기반 음원 거리 추정 성능이 저하되는 경우에 대해 논의한다. 이를 위해 음원의 거리 및 심도를 각각 2 km와 5 m로 가정하였으며, 단순화된 웅덩이가 존재하는 수심 100 m의 평탄한 해저지형을 가정하였다. 그 외의 수신 배열, 음속 구조, 및 지음향 인자는 Fig. 1(a)에서 보여지는 동일한 조건을 가정하였다.

Fig. 5는 위에서 언급한 해양 음향 환경에서의 빔-시간 영역을 나타낸다. Fig. 5(a)는 (c)에서와 같이, 거리 500 m를 중심으로 폭 300 m와 깊이 115 m의 단순화된 웅덩이가 존재하는 해저지형에서 분리된 다중 경로 신호들을 보여준다. 총 3개의 하향 도착과 5개의 상향 도착 다중경로 신호들을 모두 이용하여 추정한 음원의 거리는 약 1.8 km로, –10 %의 거리 오차를 가진다. 여기서 해당 빔-시간 이주선은 검은 실선으로 나타내었다. 만약 웅덩이의 영향을 받는 4th 와 6th 다중경로 신호들을 제외하면, 추정된 음원의 거리 오차는 약 –2 %로 우수한 거리 추정 성능을 확인할 수 있다.

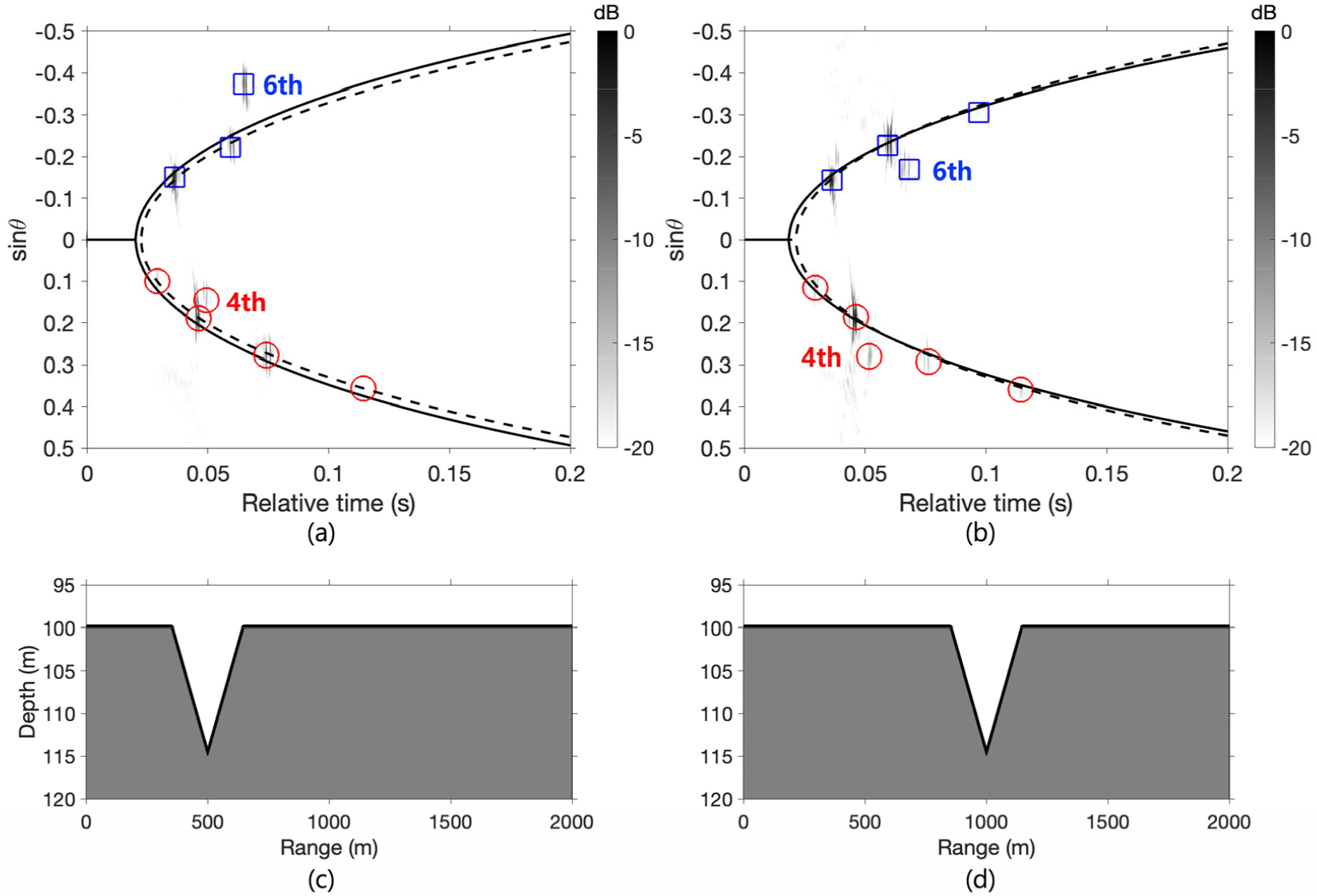
Fig. 5.

(Color available online) (a) Beam-time domain for the bathymetry shown in (c). (b) Beam-time domain for the bathymetry shown in (d). Simplified pits with a width of 300 m and a depth of 115 m were assumed in a flat bottom with a depth of 100 m. The solid line indicates the beam-time migration using all multiple signals, while the dashed line represents the beam-time migration excluding the arrivals affected by the pit.

Fig. 5(b)는 (d)에서의 거리 1 km를 중심으로 동일한 웅덩이가 존재하는 해저지형에서 분리된 다중경로 신호들을 나타낸다. 모든 다중경로 신호들을 이용하여 추정된 음원의 거리는 약 2.2 km로, 8 %의 거리 오차를 가진다. 마찬가지로 웅덩이의 영향을 받는 4th와 6th 다중경로 신호들을 제외하면, 추정된 거리 오차는 약 0.5 %로 매우 우수한 거리 추정 성능을 보여준다. 모든 다중경로 신호를 포함한 거리 추정 결과의 오차가 상대적으로 큰 이유는 웅덩이의 영향에 의한 다중경로 신호들이 배열 불변성 파라미터 χβ의 계산에 포함되었기 때문이라 판단된다. 여기서 검은 점선은 웅덩이의 영향을 받는 다중경로 신호들을 제외한 빔-시간 이주선을 나타내며, 검은 실선에 비해 웅덩이의 영향이 없는 다중경로 신호들과 잘 겹치는 것을 확인할 수 있다.

4.3 최적의 다중경로 신호 개수

Fig. 6은 Fig. 5에서 분리된 다중경로 신호들의 선택된 개수에 따른 거리 추정 결과를 보여준다. 선택된 다중경로 신호 개수(x축)와 추정 거리(y축)에 대한 히스토그램 도수를 나타내며, 각 구간의 간격은 50 m로 설정하였다. 또한, 선택할 수 있는 다중경로 신호의 개수(n)를 최소 2개 최대 N-1개를 설정하였다. 여기서 N은 분리된 총 다중경로 개수를 의미한다. 예를 들면, Fig. 6(a)에서 n=2인 경우는 C(8,2)=28개의 조합에 대한 거리 추정을 히스토그램 도수로 나타낸 것을 의미한다.

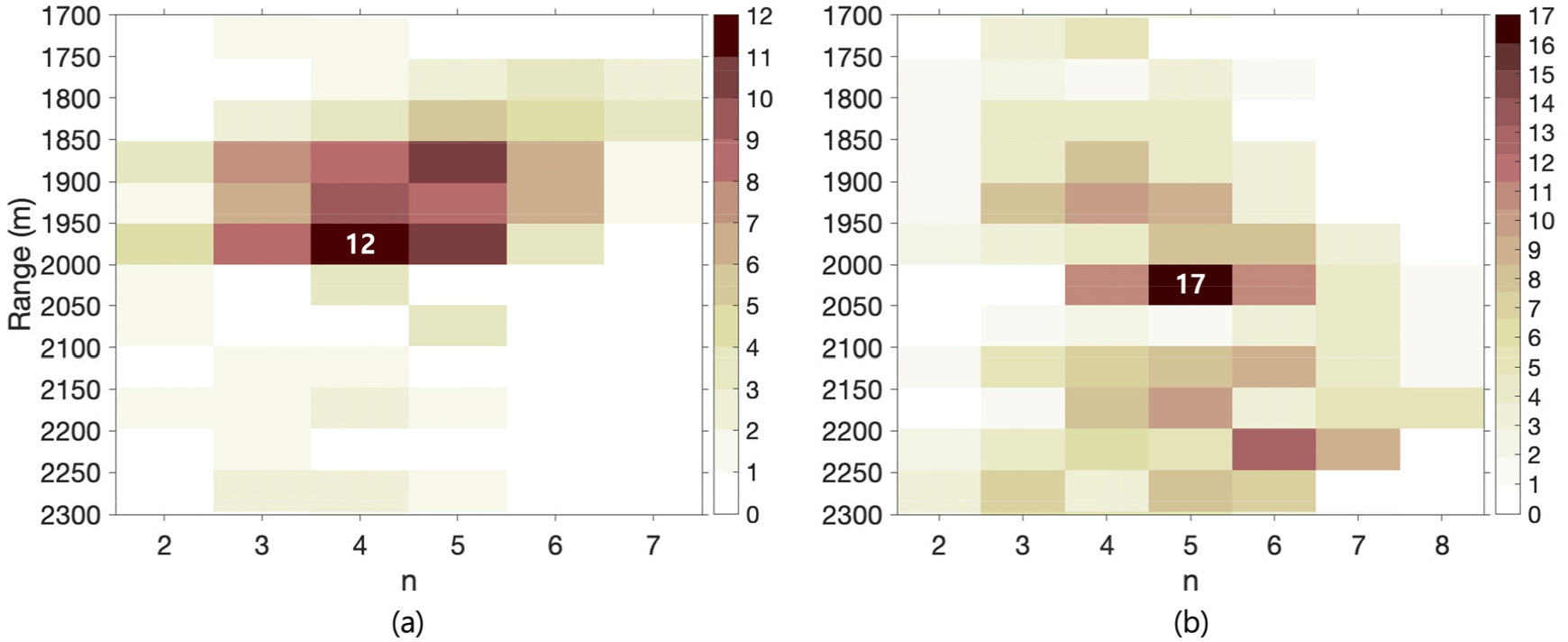
Fig. 6.

(Color available online) Relationship between the number of multiple arrivals used for the range estimation (x-axis), the estimated range (y-axis), and the histogram bin count (color) for Fig. 5(a) and (b), respectively. The bin size is set to 50 m.

Fig. 6(a)는 Fig. 5(a)의 빔-시간 영역에 대한 결과로, C(8,2)=28개의 조합부터 C(8,7)=8개의 조합에 대한 결과를 나타낸다. 이 중, C(8,4)=70개의 조합, 즉 총 8개의 다중경로 신호 중에 4개를 선택했을 때 모든 조합 중에서 12개에 해당하는 가장 큰 도수 값을 가지는 것을 확인할 수 있다. 이때의 해당 추정 거리 구간 1,950 m ~ 2,000 m는 실제 가정한 음원의 거리 2,000 m와 가장 유사함을 알 수 있다. 마찬가지로 Fig. 6(b)는 Fig. 5(b)의 빔-시간 영역에 대한 결과를 보여주며, C(9,2)=36개의 조합부터 C(9,8)=9개의 조합에 대한 결과를 나타낸다. 그 결과, C(9,5)=126개의 조합 중에 추정 거리 2,000 m ~ 2,050 m 구간에서 17개에 해당하는 가장 큰 도수 값을 가지는 것을 확인할 수 있다. 이를 통해, 웅덩이가 존재하는 해저지형에서도 임의로 선택된 다중경로 신호들의 개수 조합을 이용하여 효율적인 음원의 거리 추정 가능성을 확인할 수 있다. 하지만, 본 방법은 웅덩이에 영향을 받지 않는 다중경로 신호들의 개수가 우세한 경우에 제한적으로 적용 가능한 방법이라 판단된다.

Ⅴ. 결 론

거리 독립적인 이상적인 도파관에서의 모드 분산 특성을 바탕으로 도파관 불변성 파라미터 β=cos2θ가 정의된다. 경계면에서의 반사가 우세한 천해 환경에서는 음속 구조, 주파수, 그리고 지음향 인자 등과 같은 해양 음향 환경 변수에 영향을 받지 않고 β=cos2θ을 활용할 수 있음이 많은 연구를 통해 검증되었다.

본 논문에서는 얕은 웅덩이가 관찰되는 해저지형에서 β=cos2θ을 이용한 음원 거리 추정 성능에 대해 논의하였다. 실험 데이터 분석 결과, 음장을 비교하는 정합장 처리와 달리, 분리된 다중경로 신호들의 정보를 이용하는 도관 불변성 기반의 음원 거리 추정 방법이 웅덩이가 있는 해저지형에서 더욱 강인한 거리 추정 성능을 제시함을 확인하였다.

수치 시뮬레이션을 통해, 얕은 웅덩이의 영향을 받는 다중경로 신호들이 웅덩이의 영향을 받지 않는 다중경로 신호들로 구성된 빔-시간 이주선을 벗어날수록 거리 오차가 커지는 것을 확인하였다. 또한, 선택 가능한 다중경로 신호들의 개수 조합을 이용하여 웅덩이가 존재하는 해저지형에서의 효율적인 음원 거리 추정 가능성을 제시하였다.