I. 서 론
최근 해군의 작전 수행에서 스텔스 성능이 중요한 요소로 부각되며, 잠수함의 저소음 설계에 대한 연구가 활발히 진행되고 있다. 특히, 잠수함의 소음 성능은 작전 지역에서의 탐지 가능성을 최소화하고 효과적인 작전 수행을 가능하게 하는 핵심 요소로 작용한다. 이러한 소음은 기계적 소음과 유동소음으로 구분되며, 기존 연구는 주로 기계적 소음 저감을 위한 방진 및 방음 기술에 집중해 왔다. 그러나 현대의 저소음 추진 시스템이 발전함에 따라 유동소음 성능 개선에 대한 관심이 증가하고 있다.
유동소음은 잠수함이 수중에서 운항할 때 선체 주변 유체의 난류, 와류, 공동현상 등으로 인해 발생하는 소음으로, 항속 성능과 작전 지속력에 영향을 미친다. 특히 고속 운항 조건에서는 선체와 선미부에서 유동 박리, 와류 형성, 공동현상이 두드러지게 나타나 이에 따라 소음이 증가한다. 그 결과 수중에서 적함에 탐지될 가능성이 커지며, 이는 작전 수행에 치명적인 영향을 미친다.
따라서 잠수함의 유동소음 저감을 위해서는 유동 해석 및 소음 예측 기술의 개발이 필수적이다. 모형 실험은 비용이 크고, 실험 환경의 제약으로 인해 실선의 유체역학적 무차원수를 재현하기 어렵다는 한계가 있다. 따라서, 수치해석 기법을 활용한 정량적 예측이 중요한 대안으로 떠오르고 있다. 전통적으로 유동소음 해석에는 유한차분법, 유한요소법, 유한체적법 등이 사용되었으나, 최근에는 수치 감쇄가 적고 이산 보존성이 우수한 격자 볼츠만 기법(Lattice Boltzmann Method, LBM)이 대안으로 주목받고 있다.
LBM은 난류 해석에 강점을 가지며, 기존 연속체 기반 방법과 달리 분자동역학적 접근을 통해 유동을 모델링함으로써 난류 유동장에서 발생하는 유동소음의 미세한 특징을 정밀하게 포착할 수 있다. 이는 LBM이 유체 입자의 충돌과 이동을 모델링하여 소음원을 직접 모사할 수 있기 때문이다. 이는 LBM을 공력 소음 해석에 적용하여 분산과 소산 오류를 최소화하는 최적화 기법을 제안하고, 약한 음향 섭동을 포착하는 데 있어 LBM의 우수성을 입증한 Xu와 Sagaut[1]의 연구에서 확인할 수 있다. 또한, LBM은 병렬 연산에 적합하여 고해상도 격자를 활용한 대규모 해석이 용이한 장점이 있다. Bocanegra et al.[2]은 LBM이 평균 유동과 음향장을 동시에 해석할 수 있는 강점을 바탕으로 유동소음 예측에서의 활용 가능성을 체계적으로 검토했다. 이러한 특성으로 인해 LBM을 활용한 유동소음 해석 연구가 점차 확대되고 있다.
Ha et al.[3]은 날개 끝 와류 공동에 대해 압축성 및 비압축성 해석을 수행하고, Ffowcs Williams-Hawkings(FW-H) 음향상사법을 적용해 유동소음을 예측한 뒤 실험 결과와 비교했다. 그 결과, 압축성 해석을 통해 예측한 유동소음이 실험 결과와 더 유사함을 확인했다.
Ku et al.[4]은 SUBOFF 함형과 펌프젯 추진기를 대상으로 추진기 덕트, 스테이터, 로터의 소음 기여도를 평가했다. 이를 통해 스테이터가 덕트와 로터에서 발생하는 유동 박리로 인한 소음원 형성에 영향을 미침을 밝혔다.
Fureby et al.[5]은 DSTO 제너릭 잠수함 모델을 대상으로 수치해석과 실험 기법을 결합해 복잡한 유동장을 분석하는 방법을 제안했다. 이를 통해 잠수함 함형 주변에서 발생하는 주요 와류 성분을 정의하고, 그 발생 메커니즘을 분석했다.
Wang et al.[6]은 수중 운송체 모델의 유동소음을 예측하기 위해 Large Eddy Simulation 모델과 FW-H 음향상사법을 기반으로 한 예측 모델을 개발했다. 또한 세일과 같은 부가물이 유동소음에 미치는 영향을 분석한 결과, 세일 부착 시 유동소음이 증가함을 확인했다.
Chu et al.[7]은 SUBOFF 모델의 유동 특성을 분석하기 위해 LBM을 활용해 고해상도 수치해석을 수행했다. LBM을 통해 모델 주변의 난류 유동 구조와 압력 분포를 분석하고, 선체 후류에서 형성되는 Q-criterion 기반 와류 구조를 확인했다. 그 결과, LBM 기반 해석이 기존 유한체적법이나 유한요소법에 비해 장시간 시뮬레이션에서도 난류 구조를 더 정확하게 유지할 수 있음을 밝혔다.
본 연구에서는 LBM을 활용해 잠수함 운항 시 발생하는 유동소음을 수치적으로 예측하는 해석 기법을 개발하고, 이를 기반으로 함형 및 부가물이 유동장과 소음원에 미치는 영향을 분석했다. 이를 위해 LBM 기반 오픈 소스 코드를 사용해 잠수함 형상 주변의 난류 유동 특성을 해석하고, 외부 유동장을 정밀하게 예측할 수 있는 알고리즘을 구축했다. 특히 개발한 기법을 적용해 Defense Advanced Research Projects Agency(DARPA) SUBOFF AFF1 모델(함형)과 AFF8 모델(부가물 포함)에 대한 유동 해석을 수행하고, 두 모델 간 표면 압력 차이를 분석함으로써 자체소음 관점에서 부가물의 영향을 평가했다. 또한 FW-H 방정식을 활용해 원방으로 전파되는 음향파를 예측 및 비교함으로써 수중방사소음 관점에서 부가물의 영향을 분석했다. 수중방사소음 분석은 부가물이 잠수함의 탐지 가능성에 미치는 영향을 정량적으로 평가하는 데에 중점을 둔다. 이를 통해 부가물 주변에서 형성되는 난류 구조와 유동소음의 주요 원인을 규명했으며, 이를 바탕으로 향후 저소음 함형 설계에 필요한 기초 데이터를 제공할 수 있을 것으로 기대된다.
II. 유동 수치해석 기법
본 연구에서는 잠수함 함형과 부가물 주변 유동을 예측하기 위해 LBM을 이용하여 유동 해석 알고리즘을 개발하였다. LBM은 유체를 다수의 가상 입자 집합으로 근사하고, 입자의 충돌과 이동을 속도 분포 함수를 통해 순차적으로 계산하며, 이를 통해 모멘트를 도출하여 유체 거동을 설명하는 해석 기법이다. LBM은 본질적으로 압축성 유체 해석이며, Macro 기반 전산유체역학 기법에 비해 수치적 점성이 낮고, 낮은 차수의 차분식에서도 이산 보존성을 유지하여 유동소음 해석에 유리하다. 유동 해석을 위한 지배 방정식은 Bhatnagar-Gross-Krook(BGK) 충돌 모델을 통해 단순화한 볼츠만 방정식을 속도 이산화를 통해 유한개의 분포 함수로 나타내고, 공간과 시간에 대해 이산화하여 도출한 격자 볼츠만 방정식을 사용하였다. 이 과정은 다음과 같은 식으로 표현된다.
Eq. (1)은 볼츠만 방정식이며, Eq. (2)는 BGK 충돌 모델과 속도 이산화를 적용해 연속된 속도 대신 유한개의 이산 속도 로 분포 함수를 정의한 식이다. Eq. (3)에서는 공간과 시간에 대한 이산화를 통해 수송과 충돌 과정을 분리하였고, 의 관계를 활용해 지배 방정식인 격자 볼츠만 방정식을 Eq. (4)와 같이 유도하였다.
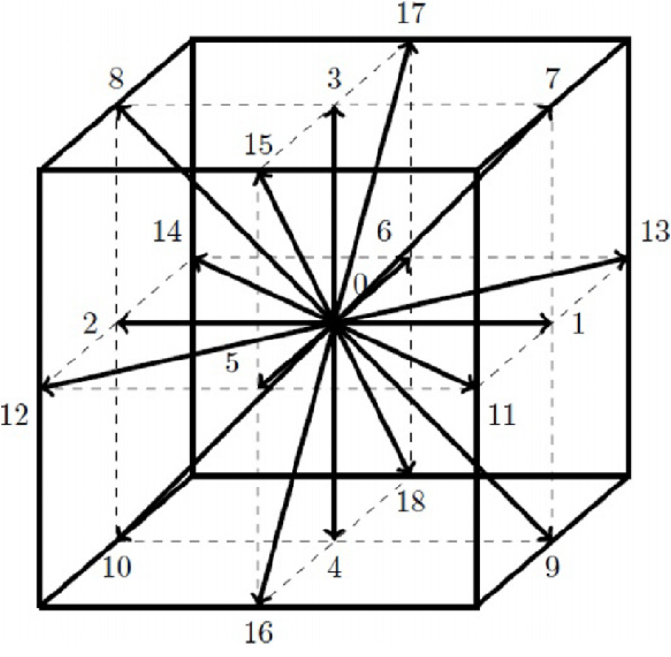
LBM을 활용한 3차원 해석을 수행하기 위해 아래 Fig. 1과 같이 D3Q19 격자 볼츠만 모델을 사용하였다. D3Q19 모델은 3차원 공간을 19개의 이산 속도 벡터로 표현하며, 3차원 LBM 해석에 주로 활용된다.
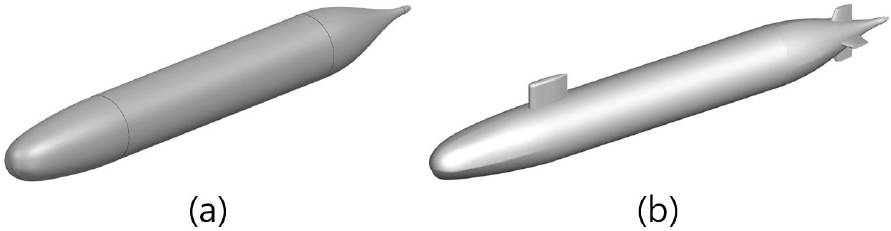
앞서 설명한 바와 같이, 본 연구는 함형과 부가물 주변 유동을 예측하고 부가물로 인한 유동 소음원을 모사하는 데 목적이 있다. 이를 위해 DARPA에서 개발한 공개된 표준 잠수함 형상인 SUBOFF 모델 중 함형만으로 구성되어 대칭적인 형상인 AFF1 모델과 함형에 세일과 핀 부가물이 부착된 AFF8 모델을 대상으로 선정하였다. 대상 형상은 Fig. 2에 나타낸다.
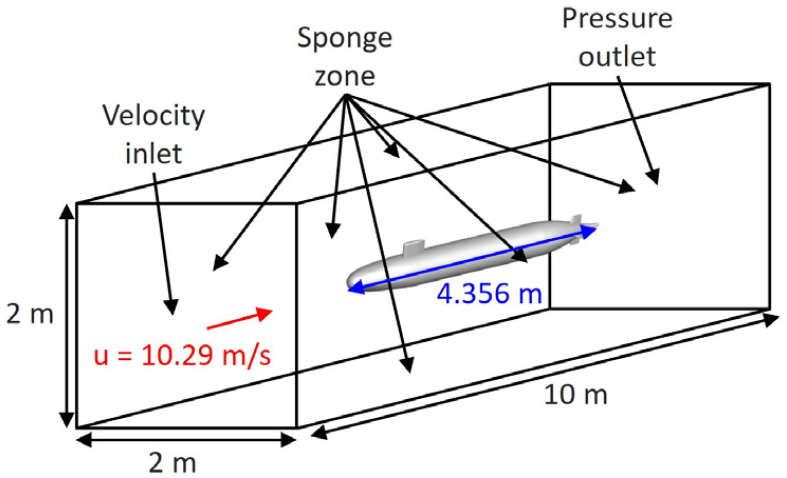
잠수함 형상 주변 해석을 위한 해석 영역은 Fig. 3과 같이 2 m × 2 m × 10 m 크기로 구성하였다. 잠수함 형상 길이는 4.356 m이며, 입구 면에서 2.5 m 떨어진 지점에 위치한다. 수중 운항 조건을 모사하기 위해 입구 경계에 속도 경계조건을 적용하였으며, 유속은 10.29 m/s로 설정하였다. 출구에는 압력 경계조건을 적용하였으며, 측면 및 상하 벽면에는 수중 환경을 모사하기 위해 대칭(symmetry) 조건을 설정하였다. 또한, 소음 해석을 고려하여 전체 경계에 스펀지 영역을 적용함으로써 비반사 경계조건을 구현하였다.
작동 유체는 잠수함 운항 조건을 고려하여 해수를 선정하였으며, Table 1에 물성치를 표기하였다.
Table 1.
Property of working fluid.
| Property | Value |
| Density [] | 1,023 |
| Temperature [℃] | 25 |
| Kinematic viscosity [] | 9.0×10-7 |
| Sound speed [] | 1,500 |
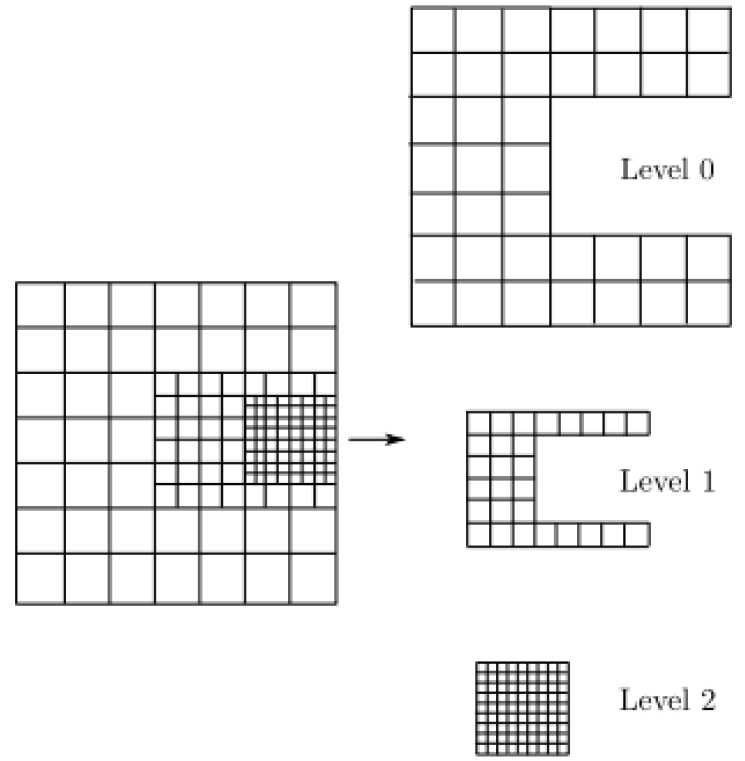
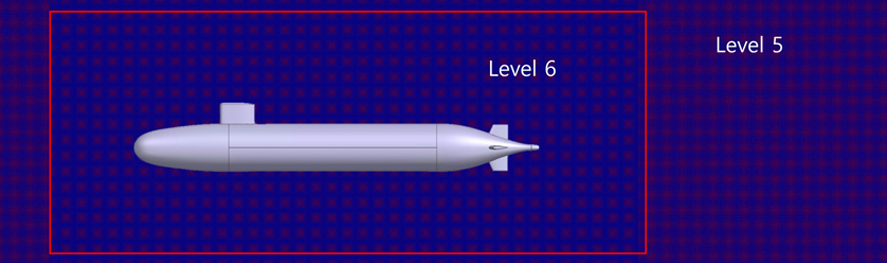
다음으로, 잠수함 함형과 부가물에서 발생하는 와류를 정밀히 모사하면서 CPU 성능과 메모리 사용 효율을 높이기 위해 다중 영역 접근법을 활용하여 격자 최적화를 수행하였다. 다중 영역 접근법은 Fig. 4와 같이 전체 해석 영역을 여러 하위 영역으로 분할하고, 각 하위 영역을 서로 다른 해상도의 격자로 구성하는 기법이다. 이를 통해 전체 해석 영역을 Fig. 5와 같이 2개 레벨의 하위 영역으로 분할하여 약 1억 7,800만 개(1.078 × 108) 격자를 구성하였다. 이때, Level 5와 Level 6의 격자 크기에 대한 자세한 정보는 Table 2에 제시하였다. 유동 해석을 위해 오픈 소스 코드인 Parallel Lattice Boltzmann Solver(Palabos)[8]를 사용하였고, 추후 진행할 소음 해석을 고려하여 해석 시간 간격은 0.00005 s(1/20,000)로 설정하였다.
III. 유동 수치해석 결과 및 분석
본 연구에서는 LBM을 활용하여 잠수함 함형과 부가물에 대한 유동 해석을 수행하기에 앞서 해석의 유효성 검증을 위해 AFF8 모델에 대한 실험 결과와 유동 해석 결과를 비교하였다. 세일이 포함된 단면의 압력 계수를 분석하여 기존 연구와 일치성을 확인하였다. 압력 계수 계산에 사용된 식은 다음과 같다.
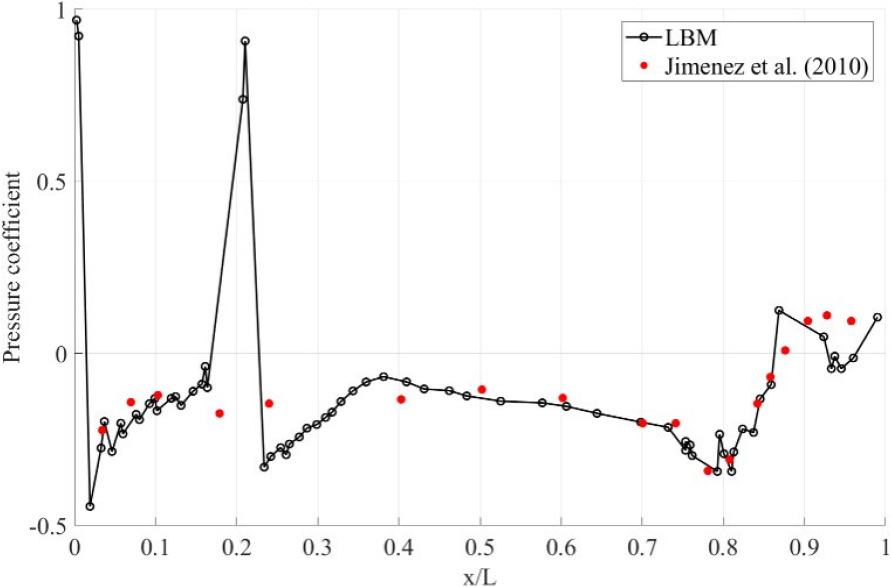
Jiménez et al.[9]의 실험은 프린스턴 대학교 High Reynolds Number Test Facility(HRTF) 폐쇄 루프 풍동에서 DARPA SUBOFF 모델을 대상으로 수행되었다. 압력 계수는 모델 표면에 설치된 45개의 압력 탭을 통해 측정되었으며, 30 kHz에서 10초간 샘플링되었다. 본 연구에서는 모델 길이를 기준으로 한 레이놀즈수()가 1.2 × 107인 조건에서의 실험 데이터를 활용하였다. 해당 실험 결과, 잠수함 표면 압력 계수는 선두의 정체점(stagnation point) 주변에서 높은 값을 나타내며, 선미의 단면적이 줄어드는 영역 ()에서 점차 증가하는 경향을 보였다. LBM을 통해 얻은 압력 계수는 선두와 세일, 핀의 전면에서 높은 값을 나타내며 선미에서 점진적으로 증가하는 경향을 보였으며, 이는 실험에서 관찰된 경향과 유사하다. 이러한 실험과 LBM 해석 결과의 압력 계수 분포는 선체 벽면을 따라 계산한 그래프인 Fig. 6에 제시하였으며, 이를 통해 LBM 기반 유동 해석이 실제 물리 현상을 정확히 반영함을 확인하였다.
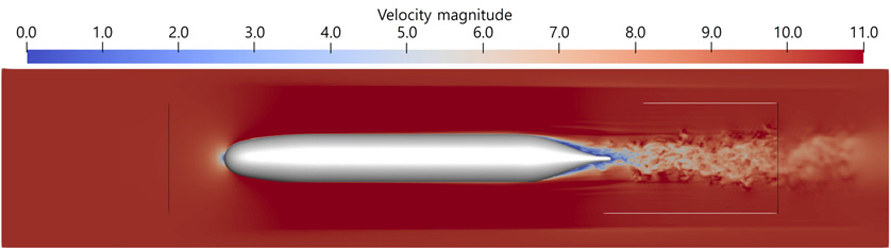
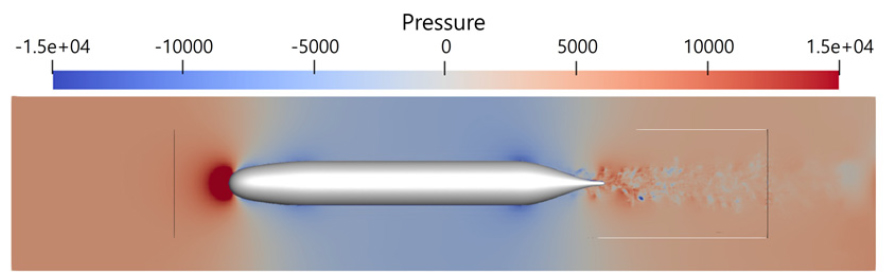
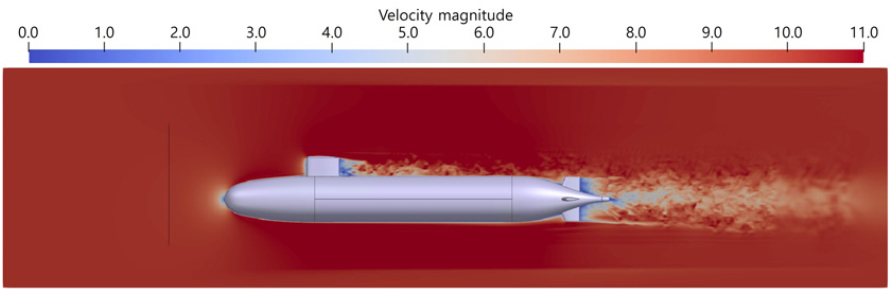
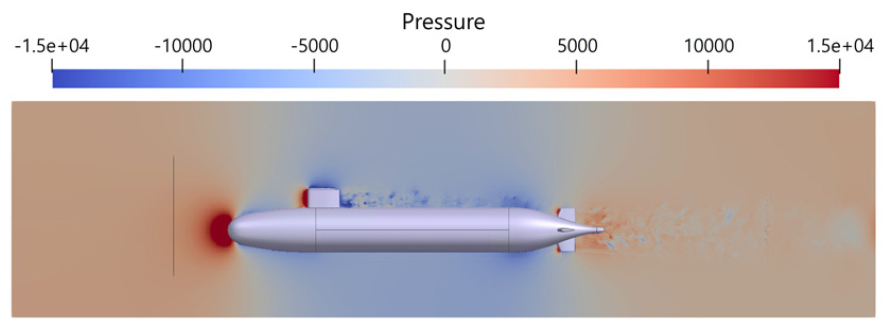
유효성을 검증한 유동 해석 모델을 활용해 잠수함 함형만으로 구성된 AFF1 모델을 대상으로 함형 주변 유동장을 예측하였다. Fig. 7에 나타난 속도장 분포에서 함형에 의해 발생하는 와류를 관찰할 수 있다. 중앙 선체에서 유동 박리로 인해 와류가 발생하여 후류 방향으로 성장 및 전파된다. 이 현상은 선미에서도 발생하지만, 더 큰 규모로 나타난다. 또한 Fig. 8에 함형으로 인한 압력장을 나타냈다. 선두의 정체점에서 고압 영역이 발생하며, 중앙 선체에서 발생하는 와류로 인해 압력 섭동이 발생함을 확인하였다. 이러한 압력 섭동은 후류 방향으로 성장하며 속도장에서와 동일하게 선미에서 더 큰 규모로 발생한다.
AFF1 모델에 세일과 핀을 추가한 AFF8 모델을 분석하여 부가물이 유동장에 미치는 영향을 파악하였다. AFF8의 유동 해석 결과에서, 중앙 선체에서 유동 박리로 인해 발생하는 와류 성분은 AFF1과 유사하지만, 세일과 핀에 의해 후류로 전파되는 추가적인 와류 성분이 발생함을 Fig. 9의 속도장 분포에서 확인하였다. Fig. 10에 AFF8 모델의 압력 분포를 나타냈다. 선두에서 정체가 발생하는 현상은 AFF1과 동일하지만, AFF8에서는 세일과 핀의 전방에서도 정체로 인한 고압 영역이 발생한다. 또한 속도 분포에서 확인한 와류 성분으로 인해 압력 섭동이 세일과 핀의 후류에서 발생하며, 이로 인해 AFF1보다 큰 유동소음이 발생할 가능성을 확인하였다.
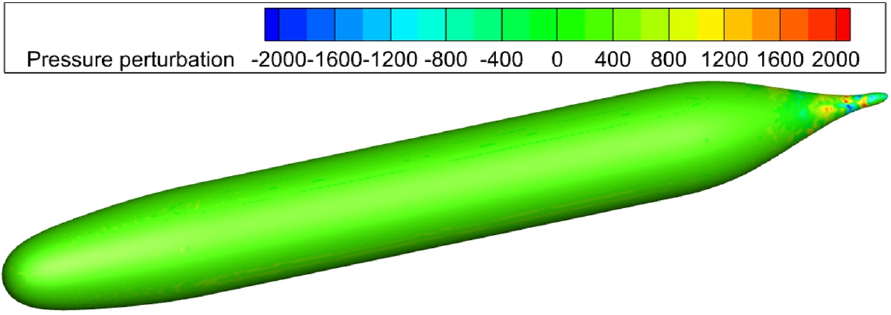
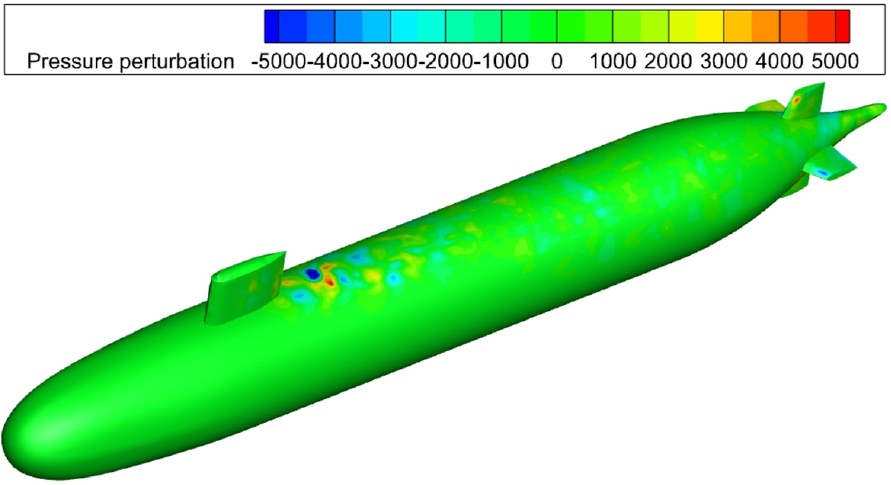
유동장 분석 결과를 바탕으로, AFF1 및 AFF8 모델의 표면 압력 섭동을 추가로 분석하였다. Fig. 11은 AFF1 모델의 표면 압력 섭동 분포를 나타내며, 선미에서 발생하는 와류로 인해 주로 압력 섭동이 발생하는 것을 확인하였다. 이때 압력 섭동의 크기는 약 –2,000 Pa에서 2,000 Pa로 관찰되었다. Fig. 12는 AFF8 모델의 표면 압력 섭동 분포를 보여주며, AFF1과 달리 세일의 후류에서 큰 압력 섭동이 발생하며, 핀에서는 상대적으로 작은 압력 섭동이 관찰되었다. AFF8의 압력 섭동은 약 –5,000 Pa에서 5,000 Pa로, AFF1보다 약 2.5배 큰 진폭을 보였다. 이는 부가물이 주요한 유동 소음원으로 작용할 가능성을 뒷받침한다. 두 모델의 압력 섭동을 비교한 결과, AFF8의 세일과 핀은 압력 섭동을 증가시키는 요인으로 확인되었으며, 이러한 차이는 후속 음향 해석에서 유동소음의 강도에 중요한 영향을 미칠 것으로 보인다.
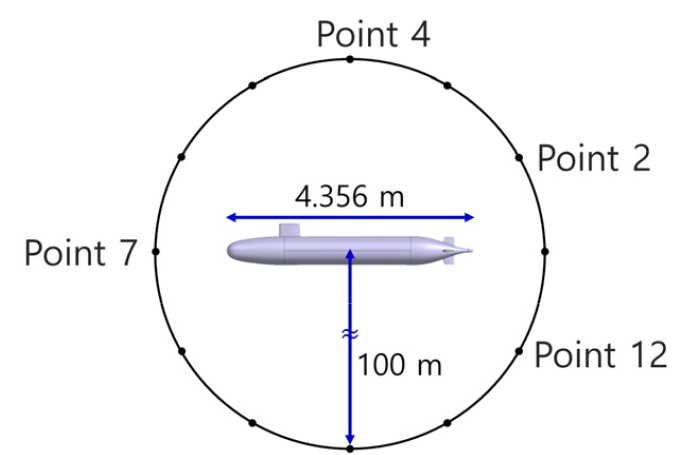
LBM을 통해 예측한 잠수함 표면 압력장을 입력값으로 활용하여 FW-H 방정식을 이용해 원방으로 전파되는 음압 스펙트럼을 예측하였다. FW-H 방정식을 적용하기 위해 잠수함 외부 표면을 따라 밀폐된 비투과성 적분면을 적용하였다. 이는 LBM으로 계산된 표면 압력 변동에 기인한 단극 및 쌍극 소음을 반영하기 위함이다. 적분면 외부는 자유장 조건을 가정하였으며 수면과 해저의 반사 효과는 고려하지 않았다. 또한 매질은 Table 1에 제시된 물성치(밀도 1,023 kg/m 3, 음속 1,500 m/s)를 가진 해수로 설정되었다. 측정 지점은 Fig. 13과 같이 잠수함 함형에서 100 m 떨어진 위치에 30도 간격으로 12개의 점을 설정하였다.
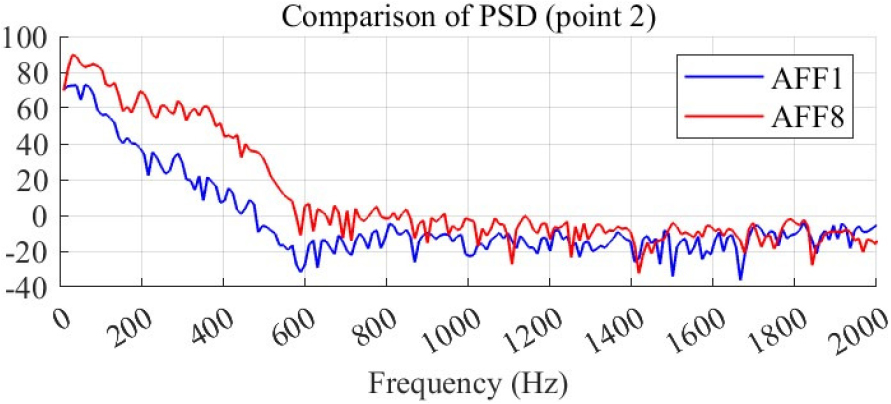
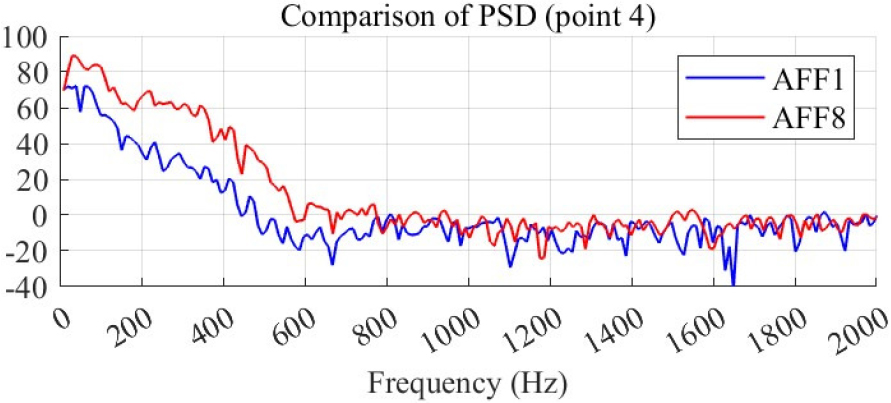
Figs. 14와 15에서 12개의 측정 지점 중 핀에서 발생하는 압력 섭동이 영향을 미칠 것으로 예상되는 point 2(후방 30°)와 세일 후류의 압력 섭동이 지배적일 것으로 예상되는 point 4(세일 위)에서의 함형별 음압 스펙트럼 예측 결과를 비교하였다. 비교 결과, AFF8의 경우 point 2와 point 4 모두에서 0 Hz ~ 600 Hz 주파수 대역에서 AFF1보다 더 큰 소음 스펙트럼이 관찰되었으며, 특히 70 Hz에서 두드러진 피크가 나타났다. 이는 이전 유동장 분석에서 AFF8의 세일 후류와 핀에서 큰 압력 섭동이 관찰된 결과와 일치한다. 그러나 point 2와 point 4 간의 소음 스펙트럼은 유사한 경향을 보였으며, 핀과 세일의 개별 소음원 기여를 명확히 구분하기 어려운 결과를 보였다. 이러한 결과는 세일과 핀의 소음 기여를 입증하기 위한 추가적인 유동장 분석이 필요함을 시사한다.
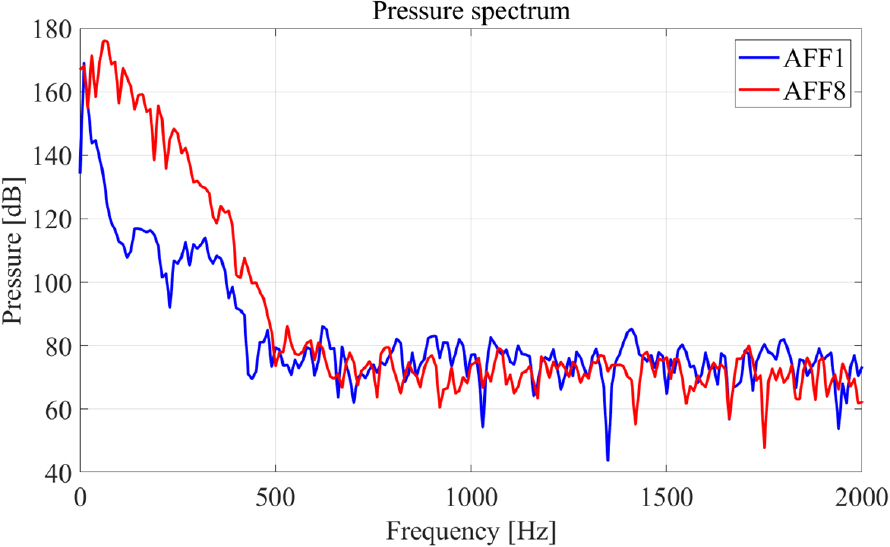
세일과 핀의 소음 기여를 규명하기 위해, AFF1과 AFF8 모델의 세일 후방에 위치한 동일한 지점에서 압력 데이터를 추출하여 주파수 스펙트럼을 분석하였다. Fig. 16은 세일 후방 지점에서의 압력 스펙트럼 결과를 나타내며, FW-H 음향 해석 결과와 유사한 경향을 보였다. AFF8의 경우 0 Hz ~ 600 Hz 주파수 대역에서 AFF1보다 큰 압력 스펙트럼이 관찰되었으며, 특히 70 Hz에서 두드러진 피크가 나타났다. 이는 point 2와 point 4에서의 PSD 결과와 일치하며, AFF8의 세일 후류에서 발생하는 압력 섭동이 70 Hz 피크의 주요 원인일 가능성을 시사한다. 이러한 결과는 세일 후방에서의 유동 불안정성이 저주파 소음을 증폭시키는 요인임을 보여준다.
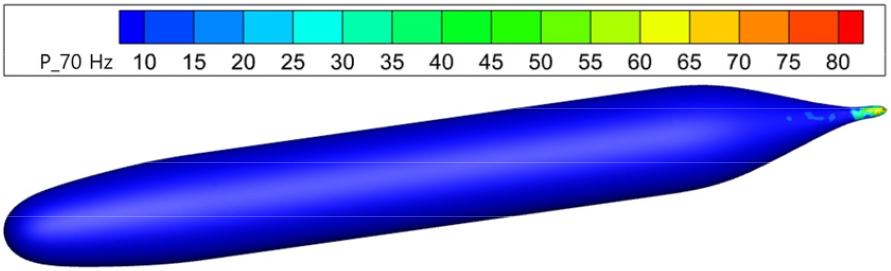
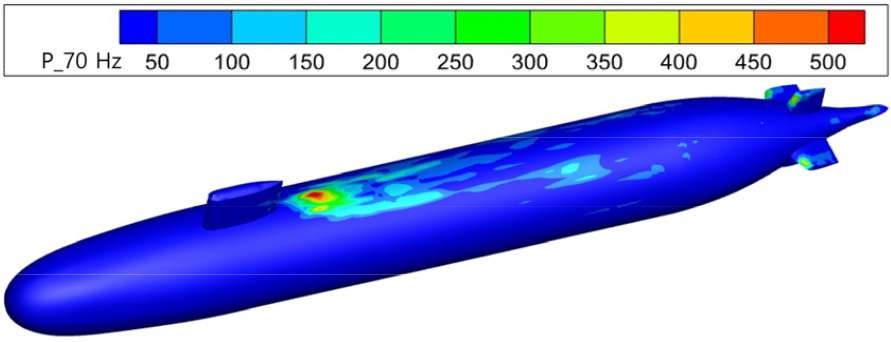
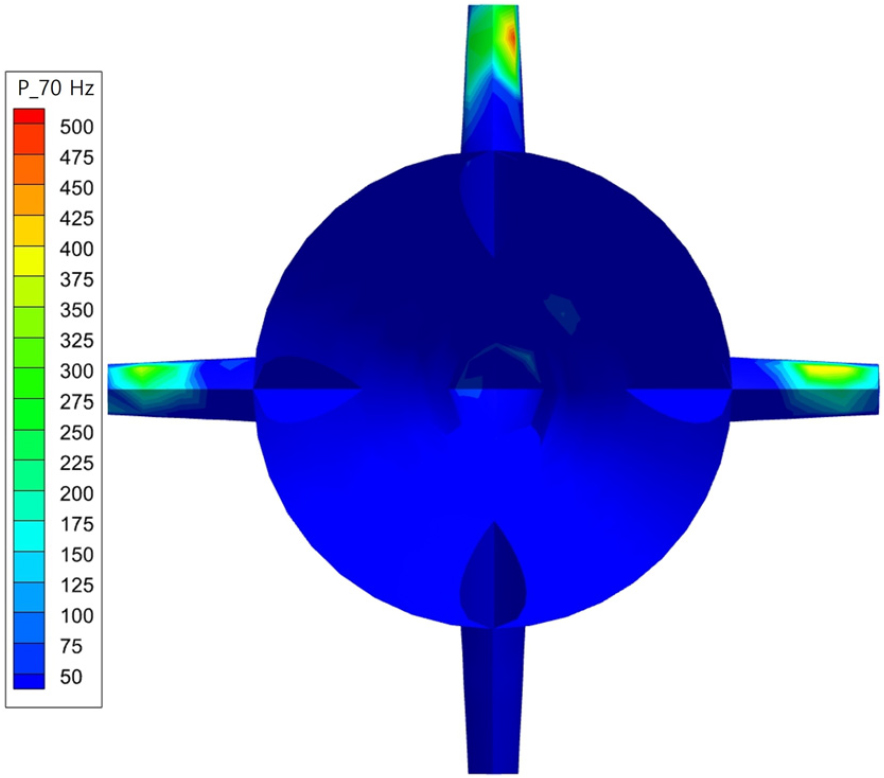
FW-H 음향 해석 결과와 세일 후방 압력 스펙트럼에서 관찰된 70 Hz 피크의 원인을 규명하기 위해 유동장을 추가 분석하였다. 잠수함 표면 압력 데이터를 전체 시간 영역에 대해 FFT를 수행하여 70 Hz 성분만 추출하였다. Fig. 17에 나타난 AFF1의 경우 선미에서 약 80 Pa의 압력 성분이 관찰되었으나, Fig. 18에 나타난 AFF8에서는 세일 후류에서 약 500 Pa의 압력 성분이 나타났다. 핀의 경우 상하좌우 4개로 구성되어 있으며, Fig. 19에서 확인된 바와 같이 세일 뒤에 위치한 상단 핀에서 약 500 Pa, 좌우 핀에서 약 400 Pa의 압력 성분이 관찰되었으나, 하단 핀에서는 70 Hz 성분이 거의 나타나지 않았다. 이는 70 Hz 성분이 세일 후류와 상단 핀에서의 압력 섭동에 의해 주로 기인함을 시사한다. 특히 세일 후류와 상단 핀의 압력 성분(500 Pa)이 좌우 핀(400 Pa)보다 약 25 % 더 크며, 하단 핀에서 70 Hz 성분이 관찰되지 않은 점을 고려할 때, 세일 후류와 상단 핀이 AFF8의 70 Hz 피크에 주요 기여를 한다고 판단된다. 또한, 유속 10.29 m/s와 70 Hz 주파수를 기반으로 스트로할수()를 활용하여 특성 길이를 분석하였다. 핀의 두께인 3.1 cm를 사용해 스트로할수 를 계산하면 로, 이는 유선형 구조물의 일반적인 스트로할수 범위(0.15 ~ 0.25)와 일치한다. 이는 핀에서 발생하는 vortex shedding이 70 Hz 소음을 유발하는 주요 메커니즘임을 뒷받침한다. 이러한 결과는 세일 후류와 상단 핀에서 발생하는 와류 구조가 70 Hz 대역의 소음을 증폭시키는 주요 요인임을 입증한다.
IV. 결 론
본 연구에서는 LBM을 활용하여 잠수함 함형과 부가물로 인해 발생하는 유동소음을 수치적으로 해석하고, 그 영향을 평가하였다. 이를 위해 오픈 소스 코드 Palabos를 기반으로 유동 수치해석 알고리즘을 개발하였으며, DARPA SUBOFF의 AFF1(함형 단독)과 AFF8(세일 및 핀 포함) 모델을 대상으로 수치해석을 수행하였다.
LBM 기반 유동 해석을 통해 계산된 압력 계수를 Jiménez et al.[9]의 실험 결과와 비교하여, 본 연구에서 개발한 알고리즘의 유효성을 검증하였다. AFF1과 AFF8 모델의 유동장을 비교한 결과, AFF8에서 세일과 핀 후류에서 –5,000 Pa에서 5,000 Pa의 큰 압력 섭동이 관찰되었으며, 이는 AFF1(선미 중심의 압력 섭동)보다 약 2.5배 큰 진폭이다. 이를 바탕으로 부가물이 후류로 전파되는 추가적인 와류를 형성하며 유동소음을 증가시킴을 확인하였다.
또한, FW-H 방정식을 적용하여 함형에서 100 m 떨어진 12개 측정 지점(point 2 및 point 4 포함)의 음압 스펙트럼을 비교한 결과, AFF8 모델이 AFF1에 비해 0 Hz ~ 600 Hz 주파수 대역에서 더 높은 PSD를 보였으며, 특히 70 Hz에서 두드러진 피크가 나타났다. 추가 분석을 통해 세일 후류에서 500 Pa, 상단 핀에서 500 Pa, 좌우 핀에서 400 Pa의 70 Hz 압력 성분이 확인되었고, 하단 핀에서는 70 Hz 성분이 관찰되지 않았다. 이는 세일과 상단 핀이 70 Hz 피크에 주요 기여를 한다는 것을 시사하며, 부가물로 인한 복잡한 난류 구조가 소음 발생에 지배적인 영향을 미친다는 점을 뒷받침한다. 스트로할수 분석에서는 핀 두께(3.1 cm), 유속(10.29 m/s), 및 70 Hz 주파수를 기반으로 가 계산되어, 핀에서 발생하는 vortex shedding이 70 Hz 소음을 유발하는 주요 메커니즘임을 입증하였다.
결론적으로, 잠수함 부가물이 유동소음 발생에 크게 기여하며, 특히 세일 및 상단 핀 주변의 난류 구조와 압력 섭동을 정밀히 분석함으로써 부가물 설계를 최적화하면 소음 성능을 개선할 수 있음을 확인하였다. 이러한 결과는 향후 저소음 잠수함 설계에 필요한 기초 자료로 활용될 것으로 기대된다.