I. 서 론
II. 수치해석 기법
2.1 압축기 배관계 내부 냉매 유동 해석 기법
2.2 파수-주파수 분리 기법
2.3 진동-소음 연성 해석 기법
III. 수치해석 결과
3.1 수치해석 결과 및 유효성 검증
3.2 주파수 대역별 냉매 유발 진동-소음 기여도 분석
3.3 냉매 유발 소음원 정량적 분석
IV. 결 론
I. 서 론
최근 계절별 냉방/난방을 위해 사용할 수 있는 인버터형 에어컨이 출시되며 보급량이 꾸준히 증가하고 있다. 또한, 에어컨의 고효율/고성능 운전을 위해 실외기 압축기의 작동속도와 비례하여 압축기 내부 냉매의 유동 속도 또한 증가하였다. 이러한 높은 속도의 냉매 유동은 실외기 전체 소음에 대한 압축기 배관계의 내부 냉매 유동 소음의 상대적 기여도를 증가시켜왔다.
특히, 인버터형 에어컨은 효율적인 냉/난방을 위해 압축기의 작동 속도를 끊임없이 변화시키며, 이로인해 소비자들에게 인지되기 쉬운 변동 소음을 유발하기에 이를 저감할 수 있는 저소음 설계기술 개발의 중요성이 부각 되고 있다.
압축기 배관계 내부 냉매 유동에 의한 소음은 복잡한 유로로 인해 소음 발생 메커니즘의 실험적 분석이 까다롭기에, 본 논문에서는 수치적 기법을 이용하여 압축기 배관계 소음의 발생 메커니즘을 분석하였다.
배관 내부에서 유로를 따라 흐르는 유체에 의한 소음의 물리적인 메커니즘은 다음과 같다. 먼저, 유체의 흐름으로 발생한 난류에 의해 배관 내 압력 섭동이 형성된다. 이러한 압력장은 두 종류의 성분으로 구분할 수 있는데, 유체가 곡관, 오리피스 등의 불연속적인 구조물을 만나며 생성되는 난류 유동 구조가 유속 수준으로 전파하는 비압축성 압력 성분과, 이러한 난류 구조로부터 발생한 음향파가 음속으로 전파하는 압축성 압력 성분이 있다. 이러한 비압축성, 압축성 압력장은 합성되어 배관 벽면을 가진하여 배관의 진동을 유발한다. 이러한 배관 진동은 외부 매질인 공기를 가진하여 외부 방사 소음을 발생시킨다. 이와 같이 배관 내부 유동 기인 소음을 예측하기 위해서는 물리적인 메커니즘을 구현할 수 있는 고정밀한 예측 전략이 필요하다.
배관 내부의 유동에 의해서 발생하는 소음에 대해 수치적으로 예측하는 연구가 여러 분야에서 활발하게 진행되고 있다. Kottapalli[1,2]는 원자로 내의 난류에 의해 노심의 벽면에 발생하는 압력 섭동에 대해 Reynolds Averaged Navier-Stokes(RANS) 방정식 기반의 및 난류 모델을 이용하여 수치적으로 예측하였고, 해당 모델이 압력 섭동에 대해 실험보다 낮게 예측하는 경향이 나타남을 확인하였다. 이후 동일한 오리피스 배관에 대해 비압축성 대와류모사(Large Eddy Simulation, LES) 기법을 이용하여 벽면 압력 섭동을 예측하였고, 실험과 비교하여 유효성을 확인하였다. 해석 결과, 비압축성 압력의 영향이 지배적인 저주파수 대역에서 수치해석의 정확도가 높으나 압축성 압력장의 영향이 큰 고주파 대역에서 정확도가 낮은 경향을 확인하였다. Maurerlehner et al.[3]은 비압축성 LES 기법으로 오리피스 배관의 유동장을 예측하고, 이후 Lighthill이 유도한 와류 소음원과 그에 기초하여 변형된 식을 이용해 각각 배관 내부 음장을 예측하여 실험과 비교하였고, 정확도가 높은 모델을 도출하였다. Kim et al.[4]은 고압 가스 배관의 밸브 유동 소음에 대해 압축성 및 비압축성 성분을 모두 고려할 수 있는 압축성 LES 기법을 적용하였고, Howe[5]의 와류 소음원을 이용하여 다공판의 소음 저감 효과를 간접적으로 비교 분석하였다. Lee et al.[6,7]은 실외기 압축기의 배기 배관계에 대하여 내부 유동에 기인하여 외부로 방사하는 소음을 예측할 수 있는 수치해석 기법을 정립하였고 실험 측정결과와 높은 상관성을 보였다. 또한 배기 배관계에서 다양한 가진력으로 작용하는 기기 기인 진동과 유동 기인 진동의 방사소음에 대한 상대적 기여도를 분석하였고, 주파수 대역별 영향도를 확인하였다. 많은 연구들로 인해 배관 내부의 압력 섭동, 내부 음장과 외부 방사 소음을 예측하는 수치 기법이 발달해왔지만, 유체기인소음의 발생 메커니즘을 분석한 연구가 미비하다. 배관에서의 내부 유체의 거동에 의한 진동 및 소음 발생의 소음원 분석을 위해선 비압축성 및 압축성 압력 섭동 각각을 분리하여 소음원을 분석할 필요가 있다.
앞서 설명한 바와 같이 배관에서 발생하는 소음의 원인은 비압축성 압력에 기인한 배관의 진동과 압축성 압력에 기인한 배관의 진동으로 구분할 수 있다. 먼저, 유동 기인 소음의 발생 메커니즘을 규명하기 위해선 두 가지의 압력성분을 분리하여 원인을 분석 해야 한다. 이를 위해 배관의 소음 메커니즘 분석에 활발하게 적용되고 있는 파수-주파수 기법(Wavenumber - Frequency Analysis, WFA)을 적용하였다.[8,9,10] 파수- 주파수 기법은 시간 및 공간 대역에서의 신호를 파수와 주파수 영역의 신호로 변환하여 압력장을 분석하는 기법이다. 여기서 압력 섭동의 신호에 대해 압축성/비압축성 성분의 전파 속도 차이를 이용하여 두 성분을 분리할 수 있다.
본 논문에서는 실외기 압축기의 흡배기 배관계에 대해 압축성 LES 기법을 적용하여 내부 냉매의 유동을 모사하였다. 이후, 유한요소법을 이용하여 배관의 진동 응답과 외부 방사소음에 대한 연성 수치해석을 진행하였다. 이 단계에서 유동해석을 통해 추출한 벽면 압력장을 유한요소법 해석 단계의 가진력으로 활용하였다. 또한, 소음 방사 메커니즘 분석을 위해 소음에 지배적으로 기여할 것으로 판단되는 배관 및 배관 요소를 선정하여 배관 내부 벽면에 대해 WFA를 적용하였고, 그 결과를 진동 응답과 방사소음과의 비교를 통해 각 주파수 대역별 소음원을 정량적으로 분석하였다.
II. 수치해석 기법
2.1 압축기 배관계 내부 냉매 유동 해석 기법
압축기 작동 시, 작동 냉매 유동에 의해 형성되는 배관 내부의 압력장을 예측하기 위해서는 전산 유체 역학(Computational Fluid Dynamics, CFD) 기반의 고정밀 수치해석 기법이 필요하다. 본 논문에서는 난류 유동을 정밀하게 모사하고, 작동 유체의 압력 섭동에 의한 압축성 압력장을 모사하기 위해 3차원 압축성 비정상 LES 기법을 사용하였으며, 지배방정식은 아래와 같다.
Eqs. (1), (2), (3)은 각각 질량, 운동량, 그리고 에너지 보존 방정식이다. Eq. (2)의 와 는 전단 응력 텐서와 아격자 응력 텐서이며 아래와 같다.
Eq. (5)에서 는 변형률 텐서이며, 다음과 같다.
LES 기법은 수치 격자보다 큰 와류에 대해서는 난류 모델링 없이 직접 계산하고, 수치 격자보다 작은 와류에 대해 아격자 모델을 이용하여 고정밀한 계산을 수행한다. Eq. (5)의 난류 점성을 계산하는 아격자 모델로써 Smagorinsky-Lilly 모델을 사용하였고, 식은 아래와 같다.
Eq. (7)의 는 Smagorinsky 상수이며, Eq. (9)의 는 격자의 부피를 나타낸다.
작동 냉매는 R-410a로써, 고온 및 고압의 과열 기체 상태로 압축기 배관계를 순환하기 때문에 냉매의 거동을 결정할 필요가 있다. 따라서 이상기체로부터의 이탈 정도를 나타내는 압축성 인자를 냉매 거동의 평가 지표로 선정하였고, 식은 다음과 같다.
압축기의 토출부와 흡입부에서 각각 0.8과 0.88의값을 가지게 되며 이는 이상기체 거동을 하지 않음을 의미한다. 따라서 실제 기체의 거동을 모사하기 위해 Aungier-Redlich-Kwong(ARK) 실제 기체 모델을 적용했으며 아래와 같이 정의된다.
여기서 아래 첨자 는 임계점을 의미하며, 는 각각 가스 상수, 온도, 압력, 부피, acentric 수를 의미한다. 작동 냉매의 비열과 열전도계수는 실험 결과를 기반으로 하여 적용하였다.
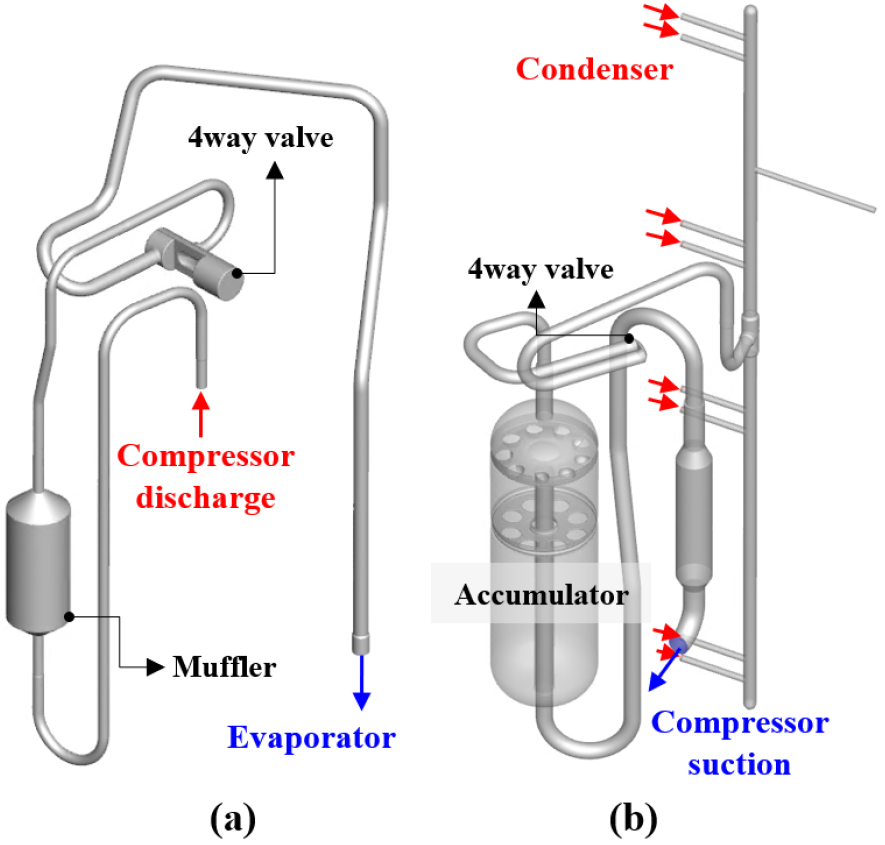
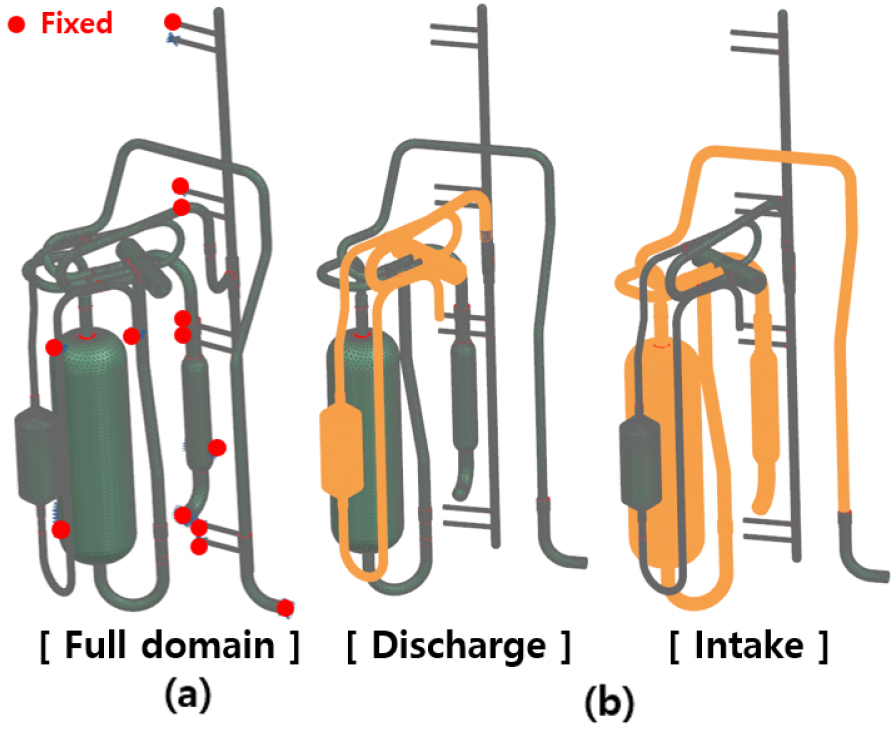
해석 대상인 실외기 압축기 배관계 영역은 Fig. 1과 같으며 작동 모드에 따라 사방변 밸브가 유로를 조절한다. 압축기에서 실내기와 열교환기로 연결되는 배관을 해석 영역으로 구분하여 구성하였으며, 압축기에서의 유로 방향을 고려하여 배기 배관계와 흡기 배관계로 명명하였다. Fig. 2에 난방 모드에서의 배기/흡기 배관계 해석 영역을 나타내었고, 본 논문에서는 난방 모드에 대해서만 분석하였다. 배기 배관계의 유로는 압축기 토출부에서 머플러, 사방변 밸브를 거쳐 증발기 입구부까지로 선정하였으며, 흡기 배관계의 유로는 응축기 입구부에서 여과기, 사방변밸브를 거쳐 압축기 흡입부까지로 선정하였다. 흡기 배관계의 경우 경계조건으로써 실험 측정치를 사용하여 입구단에는 질량 유량과 온도 조건을 적용하였으며, 출구단에는 압력과 온도 조건을 적용하였다.
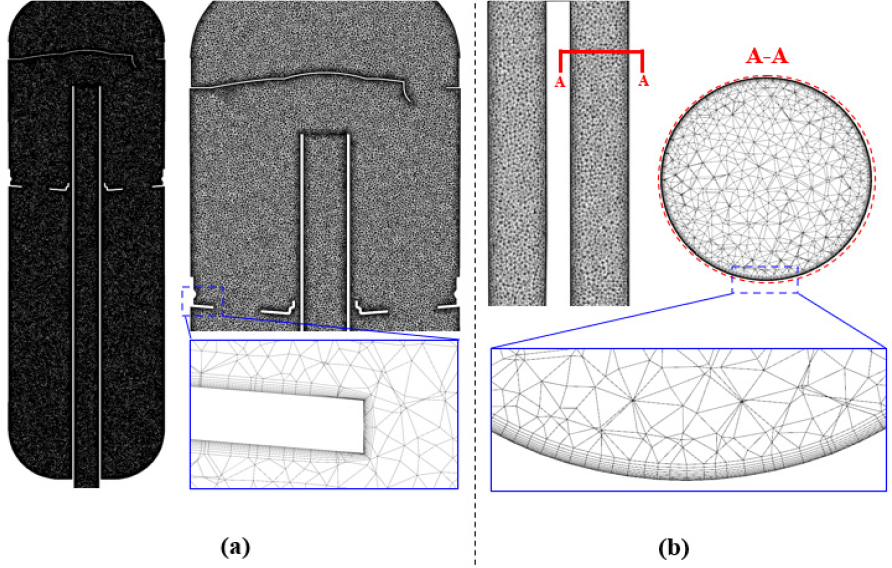
Fig. 3에 해석에 사용된 배관 내부 격자 구성을 나타내었다. 직경이 작고 유로가 긴 배관 특성뿐만 아니라 해석을 위한 시간을 고려하여 적절한 격자를 구성할 필요가 있다. 따라서 반지름 방향으로 전파하는 성분 중 가장 큰 파장을 갖는 성분에 대해 최소 20개의 격자가 구성되도록 0.5 mm 크기의 사면체 체적격자를 구성하였다. 또한 배관 벽면의 경계층에서의 유동 현상을 정밀하게 모사하기 위하여 을 만족하는 10개 층의 프리즘 격자를 구성하였다. 해석에 사용된 격자의 수는 약 5천만개이다.
압력과 속도의 연성 기법으로 Coupled를 사용했으며, 압력, 운동량과 에너지 차분 기법으로는 2차 풍향 차분 기법을 사용하였다. 해석 시간 간격은 관심 주파수가 5,000 Hz임을 고려하여 그 20배인 1e-5 s(1/100,000 s)로 설정하였다. 유동 해석은 상용 소프트웨어인 ANSYS Fluent 2023 R1을 이용하여 계산하였다.
2.2 파수-주파수 분리 기법
원통형 좌표계에서 파동 방정식의 이론해는 다음과 같다.
여기서 는 각각 반지름, 원주, 축 방향 좌표를 의미하고 는 시간을, 는 차수의 제1종 베셀 함수를 의미한다. 는 각주파수를, 는 원주 방향으로 차수의 모드와, 반지름 방향으로 차수의 모드를 갖는 축 방향 파수를 의미하며 는 미정계수이다. 상첨자 +, -는 각각 상류, 하류 방향으로의 전파하는 성분임을 의미한다. 압력신호에 대해 푸리에 변환(Fourier transform)을 적용하여 압력 스펙트럼을 다음과 같이 유도할 수 있다.
또한, Eq. (19)에 대해 이산화한 압력 스펙트럼 밀도(Power Spectral Density, PSD)는 다음과 같이 정리되며, 신호 처리 과정에서 변형된 형태의 3차원 Hanning window를 적용하였고 로 표기하였다.
특정 배관 벽면의 원주 방향, 축 방향, 시간 영역의 3차원 압력장에 대해 Eq. (20)를 적용하여 3차원의 파수-주파수 스펙트럼 밀도를 계산하였다. 또한, 내부 유동에서 전파하는 압축성 파동은 다음의 이산 보존 관계를 따르게 된다.
여기서 은 계산 영역의 평균 속도에 대한 마하수를 의미하고, 는 시간 영역에서의 평균 음속에 대한 파수를 의미한다. 축 방향으로 전파하는 파수에 대해 정리하면, 다음과 같이 양과 음의 방향으로 전파하는 성분을 얻을 수 있다.
여기서 파수가 실수값을 가지기 위한 조건으로써 아래와 같이 Eq. (23)의 제곱근 내 부호가 양수를 만족해야 한다.
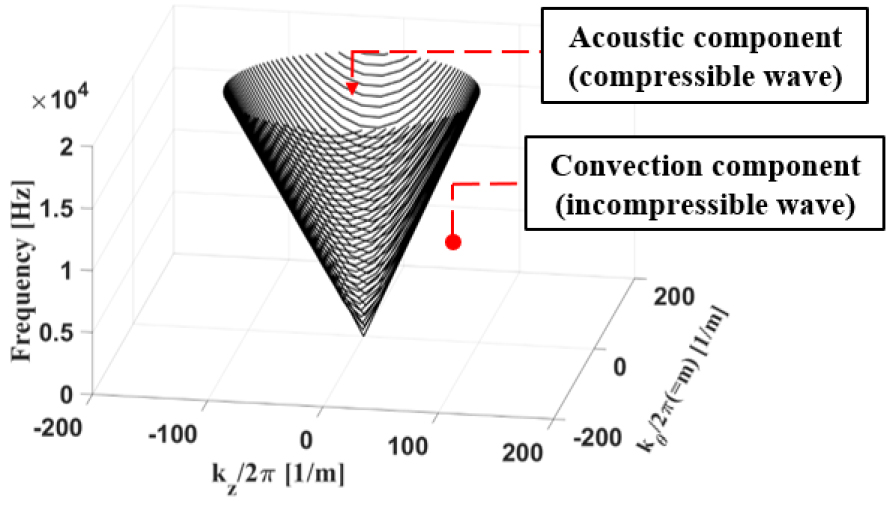
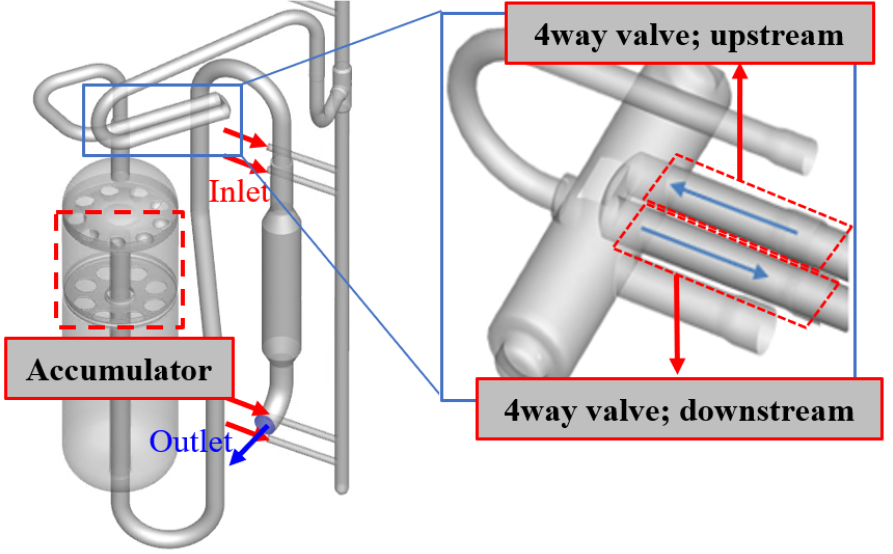
이를 기준으로 압축성 압력 섭동의 cut-on higher mode가 결정되며, Fig. 4의 dirac cone 형상 내의 스펙트럼 영역이 압축성 압력 섭동에 해당하며 비압축성 압력 섭동과 구분 지을 수 있다. 유동 해석을 통해 얻은 배관 내부의 벽면 압력장에서 큰 소음을 유발할 것으로 예상되는 배관 요소인 여과기와 사방변밸브에 대하여 WFA 계산을 진행하였으며, Fig. 5에 대상 영역을 도시하였다. 흡기 배관계의 사방변밸브 유로의 경우 오리피스 형태의 유로를 기준으로 상류, 하류를 구분해 분석하였다. 각 계산 영역의 평균 유동 속도와 평균 음속을 기준으로 압축성/비압축성 성분을 분리하였고 Table 1에 세부 정보를 표기하였다.
Table 1.
The properties for three-dimensional wavenumber-frequency spectrum.
| Time domain | Axial domain | Radial domain |
| =1/20,000 s | =0.5 mm | =2.9° |
| =1,000 ea | =542 ea | =124 ea |
| =20 Hz | =3.7 (1/m) | =16.1 (1/m) |
2.3 진동-소음 연성 해석 기법
유동 해석을 통하여 계산된 배관 내부 벽면 압력장을 가진력으로 하여 배관계의 진동 및 방사소음을 예측하였다. 운동방정식은 행렬의 형태로 유도되며 다음과 같다.
Eqs. (25), (26), (27), (28), (29)에서 는 각각 질량, 감쇠, 강성 행렬을 나타낸다. 그리고, 와 는 각각 유한요소 격자에서의 응답과 가진력 행렬을 의미한다. 또한, 하첨자 와 는 각각 구조 및 소음 해석 영역을 나타낸다. 행렬 의 요소 는 연성 계수를 의미하며 구조와 소음 해석 영역 간의 데이터 전달 방식이 양방향으로 연성될 때는 가 값을 가지며, 단방향일 경우 0이다. 여기서 의 와 는 각각 구조와 소음 격자를 정의하는 함수를 의미한다. 해당 해석에서는 외부 공기의 밀도가 구조 밀도보다 작기 때문에 소음에 의해 발생하는 압력 섭동이 구조의 응답에 영향이 없을 것으로 판단되어 단방향의 연성 해석 기법을 적용하였다.
본 논문에서는 주파수 대역에서 Eq. (25)의 좌변의 역행렬을 이용하여 응답을 계산하는 직접법을 적용하였다. 시간영역이 아닌 주파수 영역에서의 계산을 위해 가진력을 주파수 영역으로 변환하였으며, 위상을 고려하기 위해 실수항 및 허수항으로 가진력을 구분하였다. 최종적으로 Eq. (25)의 항과 응답을 아래의 수식을 이용하여 도출하였다.
유동해석 단계에서는 흡기와 배기의 유로가 분리되어 있으므로 독립적으로 해석이 가능하였지만, 배관의 진동에 의해 방사되는 소음은 각 유로의 구조물에서 반사가 일어날 수 있다. 따라서, 흡배기 배관계 전체를 해석 영역으로 구성하였다. Fig. 6(a)는 압축기를 제외한 흡배기 배관계 벽면의 격자와 구속 조건 적용 위치를 나타내었다. 배관계만의 응답을 고려하기 위해 실외기 타 요소와의 연결부에 구속을 적용하였다. Fig. 6(b)는 가진력을 적용한 부분을 나타내었다. 구조물의 물성치는 각각 배관 요소를 구성하는 재료를 고려하여 적용하였다. 구조 해석 영역은 배관 길이에 비해 두께가 매우 작으므로 반경 방향의 응력을 무시할 수 있다. 따라서, 두께를 갖는 2D Shell mesh 기능을 이용하여 계산 효율을 증가시켰다. 해석에 사용된 구조 격자의 총 개수는 약 43,000개이다.
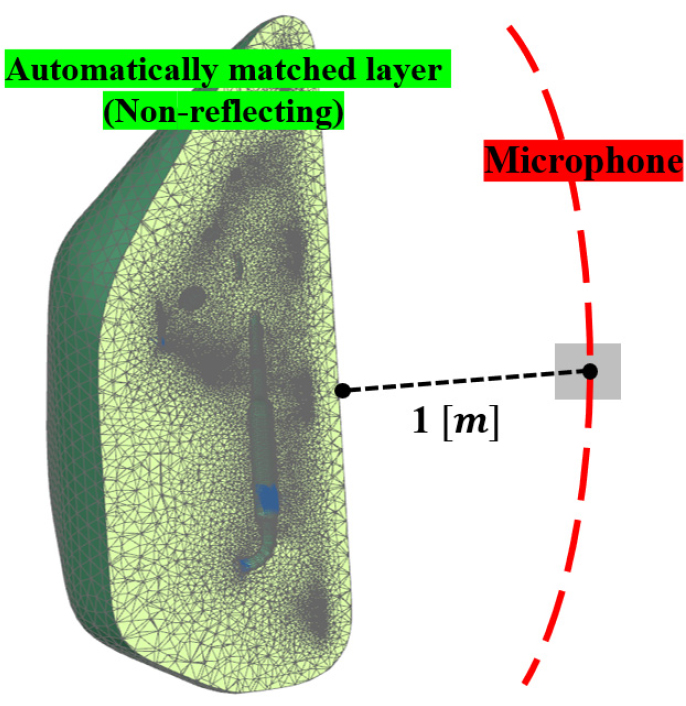
진동 해석으로 계산된 배관 외부 벽면의 속도 응답을 소음원으로 하여 소음 해석을 진행하였다. Fig. 7에는 소음 해석 격자를 나타내었다. 근접장 예측을 위해 유한요소법을 사용하였으며, 근접장의 경계면에 비반사 경계조건인 Auto-matically Matched Layer(AML)를 적용하였다. 실험과의 비교를 위해 수음점을 실험과 동일한 위치인 배관계로부터 1 m 떨어진 거리로 설정하였다. 근접장 예측을 위한 격자 수는 약 29만개로 구성하였다.
유동 해석을 통하여 추출한 2,500개의 데이터에 대해 해석 시간을 고려하여 5개 간격으로 추출하였고, 500개의 입력하중에 대해 고속 푸리에 변환을 하여 주파수 대역에서의 압력값을 계산하였다. 샘플링 주파수는 20,000 Hz가, 주파수 간격은 40 Hz가 되도록 구성하였고 관심 주파수 대역을 5,000 Hz로 고려하였다. 상용 소프트웨어인 Simcenter 3D 2020.1을 사용하여 Vibro-acoustics 연성 해석을 기반으로 하여 진동과 소음을 동시에 해석하였다.
III. 수치해석 결과
3.1 수치해석 결과 및 유효성 검증
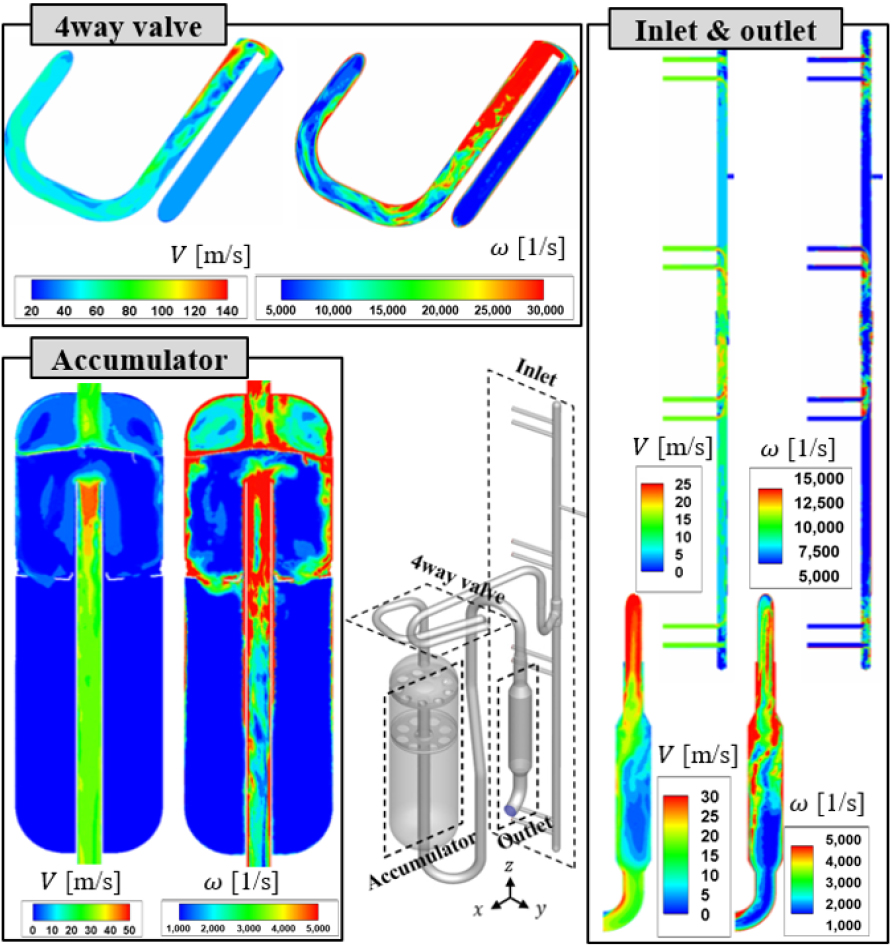
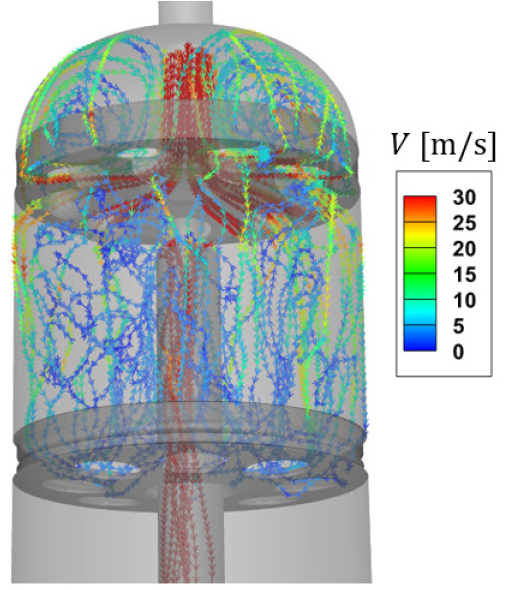
흡기 배관계 내부의 사방변밸브, 여과기와 입출구 영역에 대한 속도장과 와류장 단면을 Fig. 8에 제시하였다. 사방변밸브에서는 유로의 급격한 변화로 인해 냉매 유속이 가장 빠르고 강한 와류가 발생하게 됨을 확인할 수 있다. 또한 여과기에서는 유로의 단면적이 증가함에 따라 냉매의 유속이 감소하며, 회전 유동이 발생한다. Fig. 9에 제시한 여과기 내부 유선 흐름을 참고하면, 냉매가 액상과 기상을 분리하는 분리망을 만나며 일부의 유동은 회전하고, 일부는 분리되어 상부 분리망을 거쳐 여과기의 벽면을 규칙적으로 강타한다. 이후 분리된 유동은 다시 결합하며 여과기 내부의 배관으로 유입되는 것을 확인할 수 있다.
다음으로 유동해석의 유효성 검증을 위하여 난류 운동 에너지(Turbulent Kinetic Energy, TKE)를 평가 지표로 이용하였다. TKE는 단위 질량당 난류 운동에너지를 나타내며, 아래와 같이 정의된다.
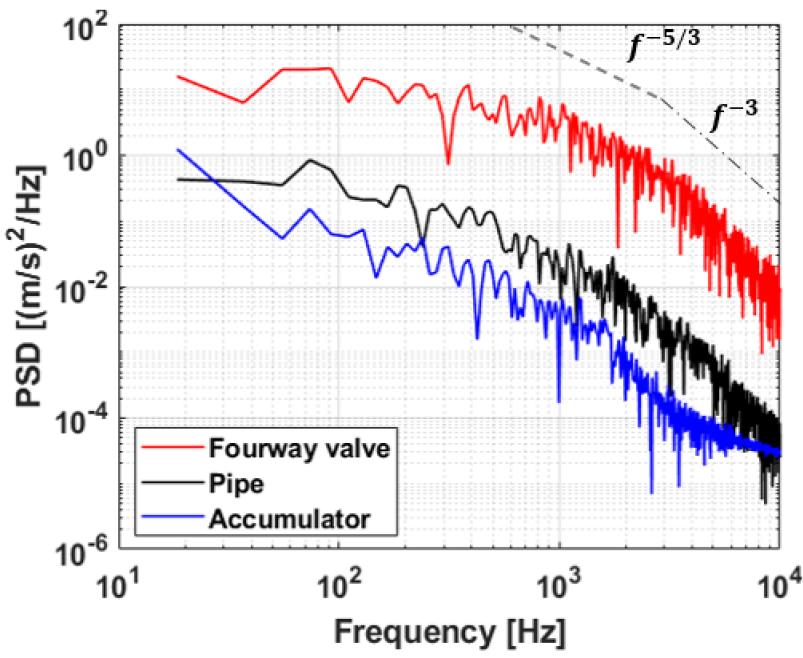
TKE 값은 비압축성 압력성분에 대한 배관 요소별 상대적 기여도를 비교할 수 있는 하나의 지표로서 이용할 수 있다. 소음에 크게 기여할 것으로 판단되는 요소인 사방변밸브, 여과기 영역 그리고 나머지 흡기 배관계 영역으로 분리하여 TKE를 계산하였다. Fig. 10에 흡기 배관계의 세 영역에 대한 TKE의 파워 스펙트럼 밀도를 나타내었다. Fig. 8을 참고하면 사방변밸브의 강한 와류가 높은 TKE값을 발생키는 것으로 확인된다. 여과기에서는 유로의 단면적이 증가하고 하부 영역의 유속이 낮기 때문에, 이에 따라 TKE의 값이 낮게 계산되었다.
Energy cascade 이론에 따르면 TKE는 와류가 소산하는 과정에서 inertial subrange와 dissipative range로 구분된다.[11]Kolmogorov는 이론적으로 TKE의 파워 스펙트럼 밀도가 inertial subrange에서 파수의 –5/3승에 비례하여 감소하는 것을 제시하였다. Fig. 10의 inertial subrange에서 주파수에 따른 TKE의 기울기가 –5/3승을 잘 따라가는 분포를 확인하여 유동해석의 유효성을 검증하였고, 냉매의 유속이 증가함에 따라 inertial subrange에서 dissipative range로 전이되는 주파수가 증가하는 것을 확인하였다.
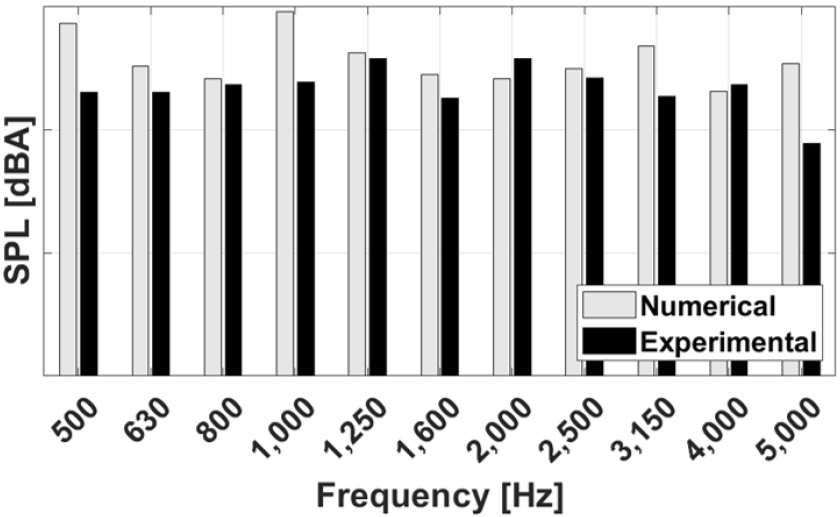
Fig. 11에 압축기 내부의 냉매에 기인하여 흡배기 배관계에서 방사되는 소음의 예측 결과와 실제 작동 시 실외기 전체에서 발생하는 소음의 측정값을 비교하여 나타내었다. 두 값 모두 A-청감보정을 적용한 음압 레벨(Sound Pressure Level, SPL)로 계산하였으며, 1/3 octave band spectrum으로 나타내었다. 비교 주파수 대역은 500 Hz 대역부터 관심 주파수인 5,000 Hz 대역까지로 선정하였다. 수치해석의 결과가 대부분의 주파수 대역에서 실험과 비슷한 경향을 나타냈지만, 특정 밴드에서 수치해석의 결과가 과도하게 예측되었다. 이는 특정 주파수 대역에서 구조적 모드가 발생하였는데, 해당 대역에서 적절한 감쇠 상수를 고려하지 못했기 때문에 진동 및 방사 소음의 가진력이 증가했다고 판단된다. 따라서 이를 보완하면 수치해석이 과도 예측하는 경향을 개선할 수 있을 것으로 판단하고, 실외기의 실제 전체 소음에서 주파수에 따른 냉매유체유기 방사소음의 경향성을 정확히 파악할 것이다.
3.2 주파수 대역별 냉매 유발 진동-소음 기여도 분석
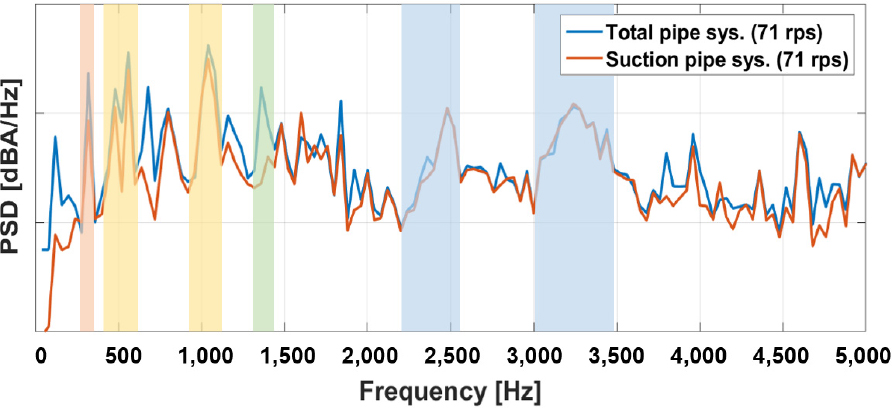
Fig. 12은 수치해석 결과에 대해 흡기 배관계만의 소음과 흡배기 전체 배관계에서의 소음을 narrow band로 나타낸 결과이다. Fig. 11에서 소음에 지배적인 5개의 대역을 선정하여 Fig. 12에 컬러바로 그 영역을 나타냈으며, 각 대역에서 소음이 크게 발생하는 주파수에 대한 흡배기 배관계의 진동 응답과 방사하는 음향장 결과를 Fig. 13에 나타내었다. 먼저, 500 Hz와 1,000 Hz 대역은 여과기에서 음압이 강하게 형성됨을 확인할 수 있다. 여과기는 배관계 요소 중 가장 크기가 크기 때문에 저주파수 대역에서 진동에 의한 소음이 크게 발생한다고 판단된다. 1,250 Hz는 압축기에서 토출되어 실내기까지 이어지는 배기 배관계 영역의 진동이 강하고, 이로 인해 소음이 크게 발생하는 것을 음향장에서 확인할 수 있다. 다음으로 2,500 Hz 및 3,150 Hz는 사방변밸브에서 여과기로 흐르는 흡기 배관계의 유로에 의한 진동 및 소음이 지배적이다.
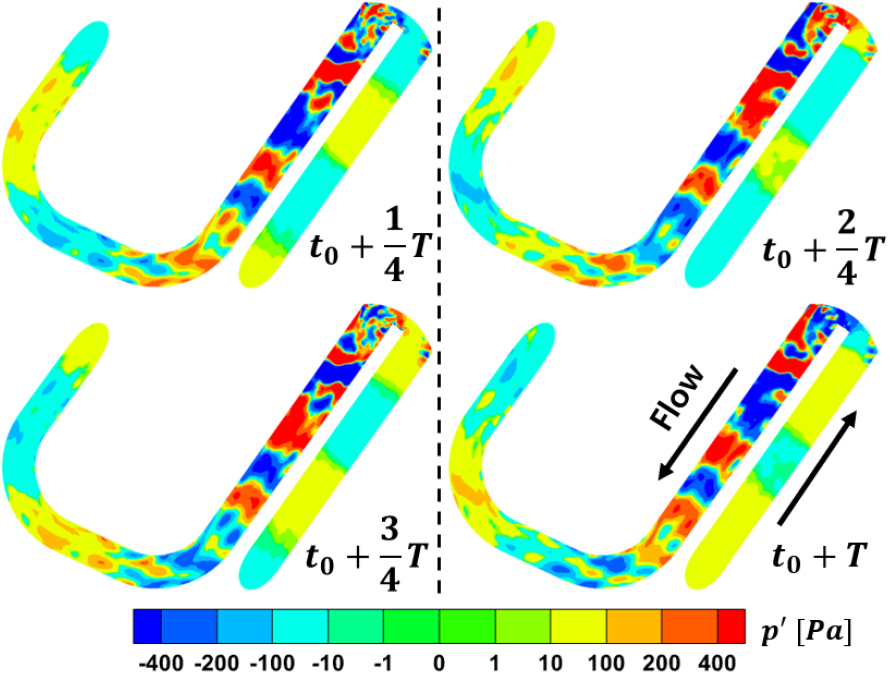
Fig. 14에 2,480 Hz 성분에 대한 사방변밸브의 압력 섭동을 1/4주기로 나누어 제시하였다. 오리피스 형태를 기준으로 하류에서는 파장이 짧고 섭동량이 큰 성분이 존재하다 소산하고, 파장이 길고 섭동량이 작은 성분은 양방향으로 전파되는 것이 확인됐다. 따라서 하류 영역에서의 파장이 짧고 강한 와류가 소산하는 과정에서 광대역의 2,500 Hz 및 3,150 Hz 대역의 진동과 소음을 유발했다고 판단된다.
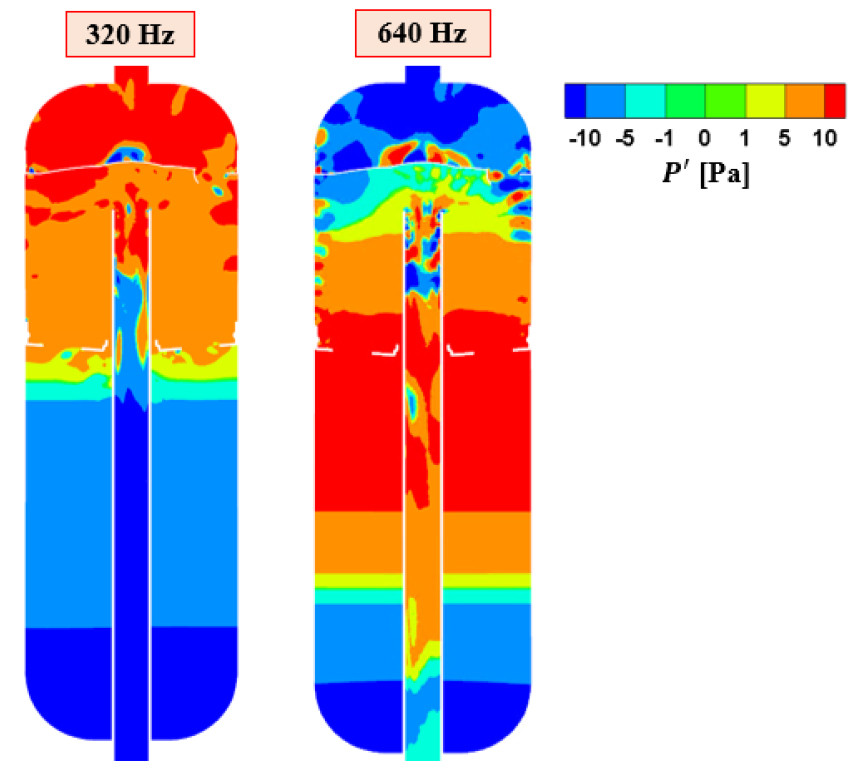
추가로, Fig. 12의 320 Hz에서 협소하게 강한 주파수 성분이 존재한다. 이는 Fig. 15의 여과기 내부에서의 320 Hz 및 640 Hz 성분의 압력 섭동 분포를 참고하면 조화력을 이루었음을 확인할 수 있고, 그 주파수는 양 끝단이 열린 실린더형 resonator에서의 공진 주파수와 일치하며 그 식은 다음과 같다.
여기서 은 자연수이며 는 냉매의 음속을, 은 실린더의 축 방향 길이를 의미한다. 따라서 320 Hz 성분은 여과기의 구조상 발생하는 음향공진에 의한 소음임을 확인했다.
3.3 냉매 유발 소음원 정량적 분석
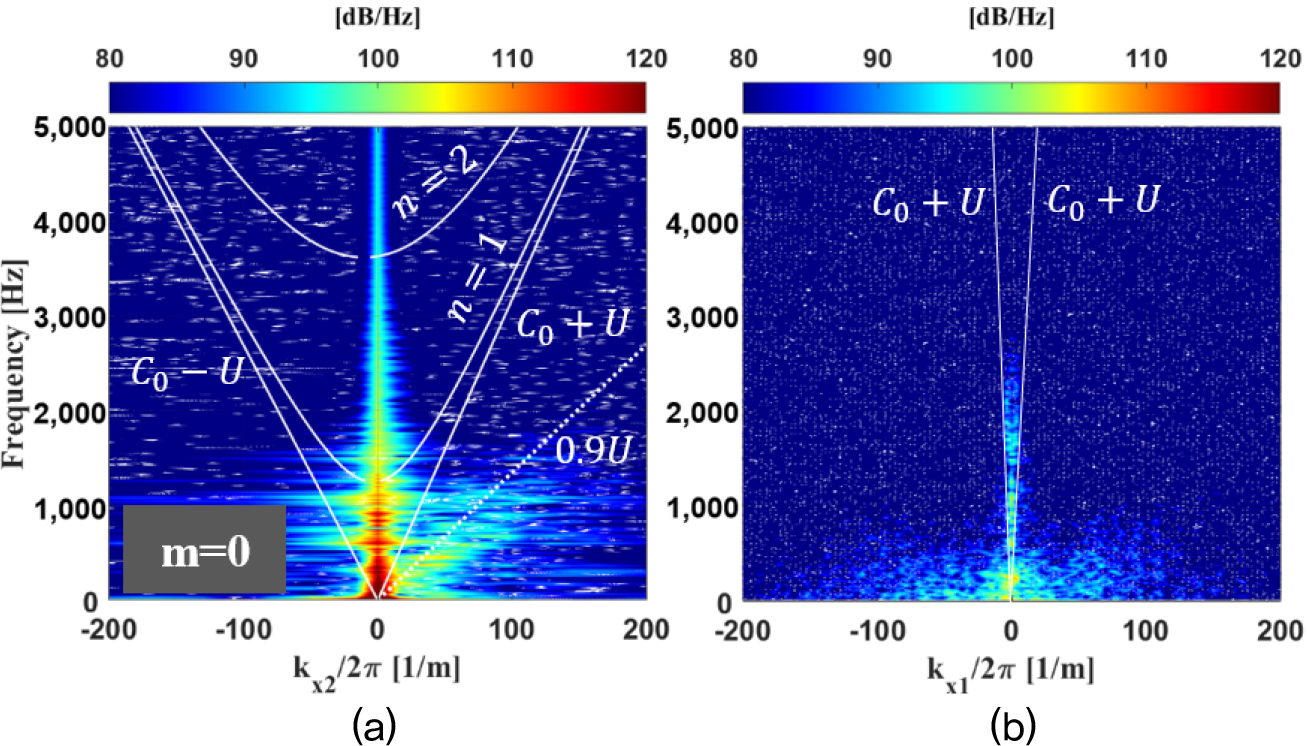
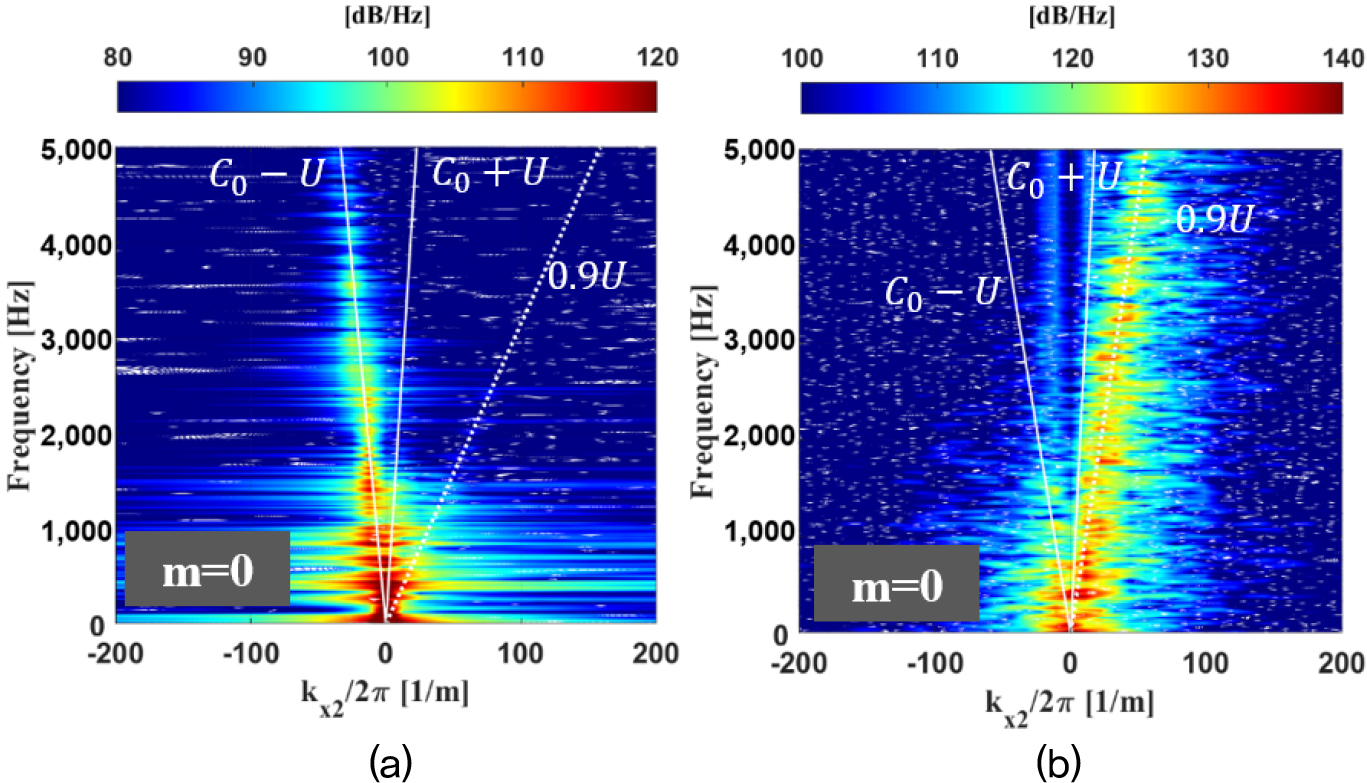
소음의 기여도가 큰 배관 영역에서 비압축성/압축성 압력 섭동 각각의 소음원 분석을 위해 Fig. 5와 같이 원통형 형상의 배관 벽면에 Eq. (20)을 이용해 파수-주파수 분석을 수행하였다. Fig. 16(a)는 여과기의 3차원 파수-주파수 선도 중 =0일 때의 평면인, 즉 배관의 축 방향으로 전파하는 성분의 =0모드 결과이다. 또한 Fig. 16(b)는 여과기의 원주 방향으로 전파하는 성분을 나타내었다. 평균 음속 성분인 와, 평균 유속 성분인 는 모두 계산한 해당 영역 내의 평균값을 의미한다. Fig. 16(a)에서 원통형 배관에서의 압축성 모드는 구분되지 않으나 1,000 Hz 이하에서 강한 압축성 성분이 확인되었다. 또한 0.9에 해당하는 비압축성 성분의 전파가 구분됐다. Fig. 16(b)에서는 원주 방향으로 압축성 성분과 비압축성 성분이 양방향으로 전파함을 확인하였다.
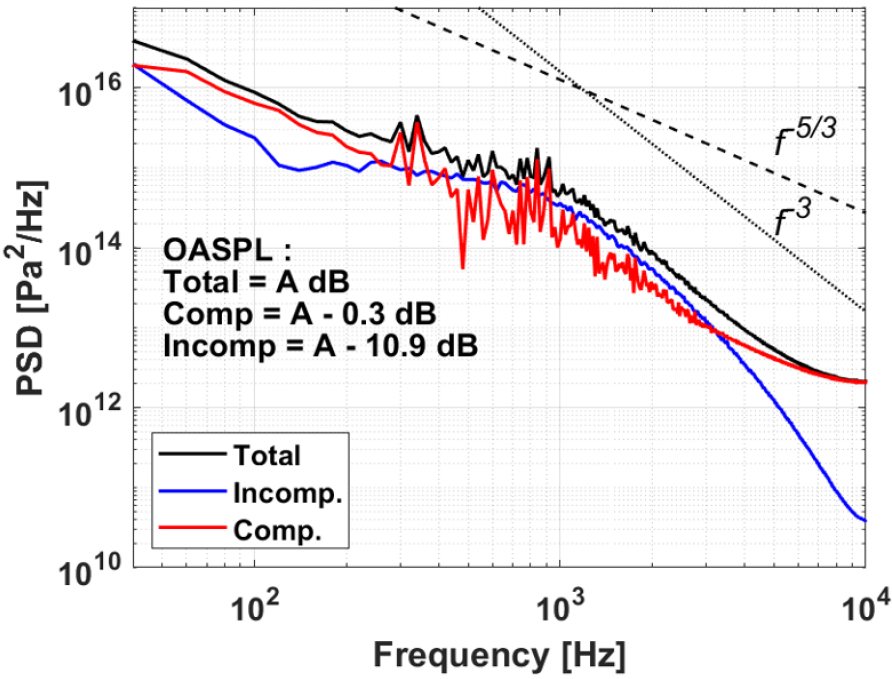
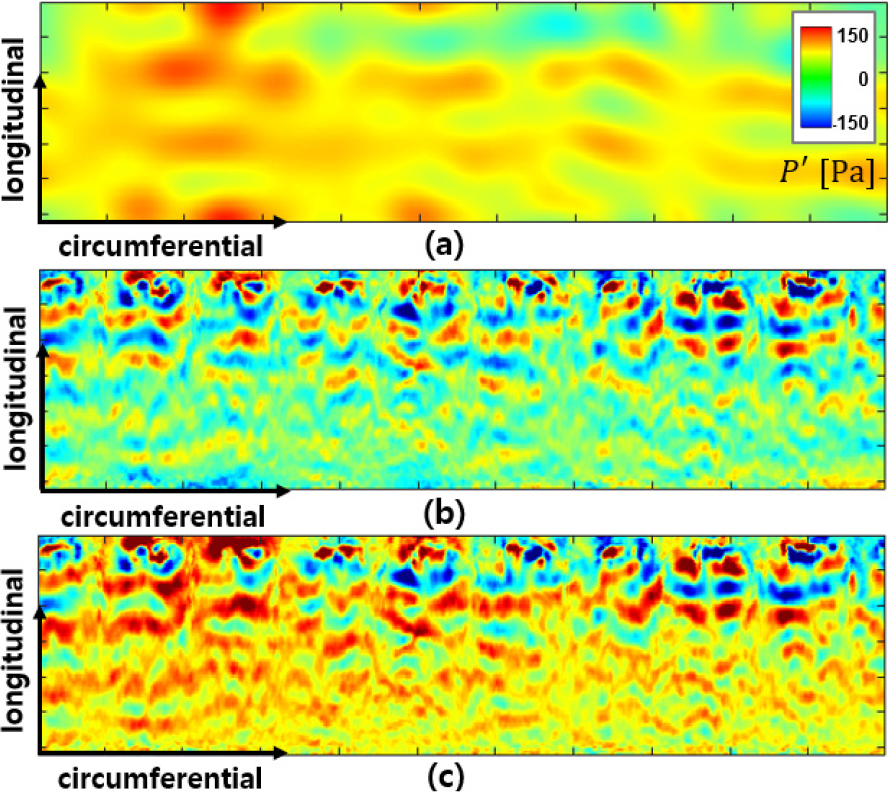
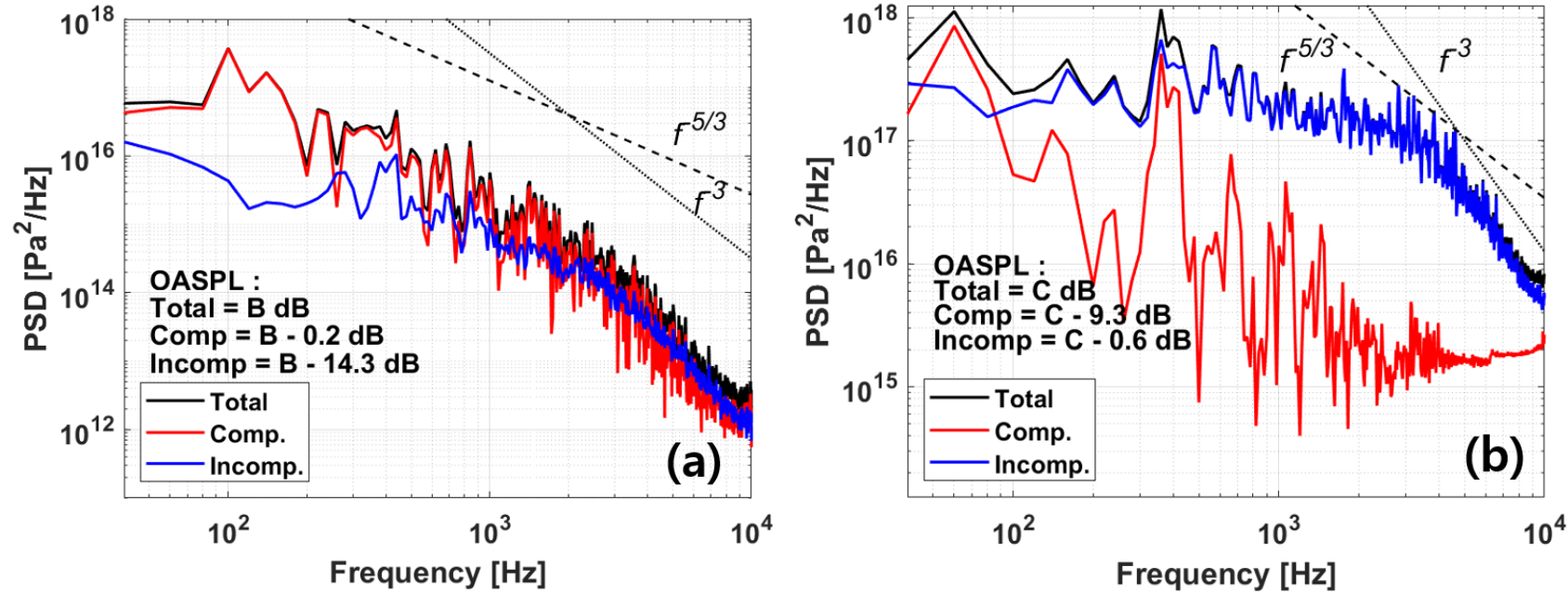
Dirac cone()을 기준으로 여과기의 압축성/비압축성 압력 섭동을 분리한 결과를 Fig. 17에 나타냈고, 1,000 Hz 이하에서는 압축성 압력 섭동 성분이 지배적임을 확인했다. 또한, 난류의 직접적인 가진에 의해 발생하는 비압축성 압력 섭동은 inertial subrange에서 –5/3승의 기울기로 소산하는 것이 TKE와 그 경향이 유사하였다. Fig. 18에는 1,000 Hz 이하의 주파수 중 압축성 성분이 강한 임의의 주파수인 840 Hz에 대한 분리된 섭동 분포와 전체 압력 섭동 분포를 도시하였다. 비압축성 분포의 경우 분리망을 지난 유동이 벽면에 규칙적인 와류를 발생하나 하부 방향으로 소산하고, 압축성 분포의 경우 원주 방향과 축 방향 성분이 혼재되어 전파된다. 특히 Fig. 16(a)에서 알 수 있듯 축 방향의 압축성 성분은 계산 영역보다 긴 파장의 성분들이 강하게 전파됐기에, 전반적 영역에서의 전체 압력 섭동 분포에 강한 영향을 끼쳤다. 따라서 이러한 축 방향의 압축성 성분에 의해 여과기에서 1,000 Hz 미만 대역의 진동과 소음이 유발되었다고 판단된다.
다음으로 사방변밸브의 상류와 하류 영역에 대한 원주 방향 성분의 =0모드를 Fig. 19에 나타냈고 분리된 압축성/비압축성 성분을 Fig. 20에 나타냈다. 상류에서는 압축성 성분이 유동 반대 방항으로 전파하고, 하류에서는 비압축성 성분이 유동 방향으로 강하게 전파되었다. 하류 영역의 유속이 크기 때문에 압축성 성분과 구분되지 않았지만, Fig. 14를 참고하면 파장이 짧고 섭동량이 큰 비압축성 성분이 하류에서 지배적으로 발생했고 이에 따라 진동과 소음이 발생했다. 따라서 2,500 Hz와 3,150 Hz의 고주파 대역에서는 사방변밸브 하류의 비압축성 광대역 성분에 의해 소음이 유발된다고 평가했다.
IV. 결 론
본 논문에서는 에어컨 실외기의 압축기 배관계에 대해서 냉매의 유동에 기인하여 발생하는진동 및 소음에 대해 수치적으로 예측하였고, 그 소음원을 분석하였다. 먼저 압축기 배관계 내부 냉매의 유동에 대해 압축성 고정밀 대와류모사(Large Eddy Simulation, LES) 기법을 이용하여 예측하였고, 난류운동에너지(Turbulent Kinetic Energy, TKE)를 지표로써 해석 유효성을 확인하였다. 예측 결과로 얻어낸 내부 벽면 압력장을 가진력으로 하여 배관의 진동과 방사소음에 대해 연성 수치해석(Vibro-acoustic)을 적용하여 예측하였고, 실험 소음과 비교하였다. 이후, 압축성/비압축성 압력 섭동이 혼재된 내부 멱면 압력장에 대해 파수-주파수 분리 기법(Wavenumber-Frequency Analysis, WFA)을 적용하여 소음에 주요하게 기여하는 배관 요소들의 벽면 압력장을 분리하여 정량적으로 분석하였다.
여과기의 경우 저주파수 대역인 500 Hz와 1,000 Hz에서 압축성 압력 섭동 성분의 축 방향으로의 전파에 의해 진동과 소음이 주요하게 유발되었고, 특히 320 Hz는 음향 공진에 의한 소음임을 확인했다. 다음으로 압축기의 냉매 토출에 의한 배기 배관계의 유동이 1,250 Hz 대역을 가진하여 소음을 유발하였고, 사방변밸브의 하류 영역에서 생성되는 강한 와류에 의한 비압축성 압력 섭동이 여과기까지 연결되는 배관을 진동하여 고주파수 대역인 2,500 Hz와 3,150 Hz의 소음에 기여한 것을 확인하였다. 본 연구의 분석을 통해 압축기 배관계의 냉매 유체에 의한 소음의 발생 과정을 확인하였고, 추후 소음 발생 메커니즘 분석 방법론을 적용하여 유동 단계에서의 형상 변경에 의한 소음 저감 평가를 통해 설계 단계에서의 저소음 기술 개발에 기여할 수 있을 것이다.