I. 서 론
수중에서 이동체의 위치를 추정하는 것은 일반적인 소나 시스템에서 중요한 문제 가운데 하나이며, 이에 대한 많은 연구가 이루어져 왔다.[1,2,3] 이는 수중 이동체의 탐지, 식별 및 추적 등의 분야뿐만 아니라 함정이 건조되는 과정에서도 필요로 한다. 즉, 기동하는 함정에서 방사되는 수중 방사 소음은 함정의 생존성과도 연계되어 있어 함정이 만들어지고 이를 측정하는 시험평가를 진행하면서 정해진 수중 방사 소음 기준을 만족하는지 판단하게 된다. 이 때 수중 방사 소음 측정 기준에는 대상 수중 이동체와 신호를 수집하는 수중 청음기까지의 거리가 함께 정의되어 있어서 정밀한 거리 정보를 필요로 한다. 주로 민간 선박을 담당하는 국내 선급에서도 수중 방사 소음 지침을 두고 있다.[4] 이 지침에서는 수중 청음기 위의 해수면 위치에서 시험 중인 선박의 기준점까지의 수평 거리를 측정하여야 하며, 거리 측정 장치는 10 m 이내로 정확해야 한다고 명시하고 있다. 수상 선박의 경우 레이더나 Global Positioning System(GPS)를 활용하여 비교적 정밀한 거리 측정이 가능하지만 수중 이동체의 경우에는 매질의 특성으로 인하여 Radio Frequency(RF) 신호의 사용이 불가능하므로 대체 수단으로써 별도의 음향 신호를 사용해야 한다.
이동체까지의 거리를 추정하기 위해 이동체에 트랜스듀서를 부착하여 미리 설계된 능동신호를 방출하도록 하고, 이를 수신하여 이들 사이의 상관도를 구하여 도달 시간을 측정하는 방법이 있다.[5] 트랜스듀서와 청음기가 미리 시간 동기화가 되어 있어야 한다는 제약이 있기는 하나 비교적 정확한 거리 추정이 가능한 것으로 알려져 있다. 도달 시간을 측정하는 방법 이외에 도플러 주파수 차를 추정하거나 도플러 주파수 맵을 이용하는 방법 등 다양한 방법들이 있다.[6,7] 이러한 거리 추정 방법들은 적용하는 송신 신호의 특성에 영향을 받지만 이와 함께 다중경로 전달, 도플러 천이 및 잡음을 포함한 불규칙한 해양 환경으로부터도 영향을 받게 되어 거리 측정값에 오류를 유발하게 된다.[8,9] 특히, 측정 오류에는 비교적 작은 크기의 오류도 있지만 순간적인 임펄스 형태의 오류인 특이값도 포함된다. 이러한 특이값에 의해 손상된 측정값은 추정된 수중 이동체까지의 거리에 대한 모델링을 어렵게 만든다.[10]
Ultra Short Base Line(USBL) 시스템을 이용한 특이값 제거와 관련한 몇몇 기존의 연구들이 있다.[11,12] Hassan et al.[13]은 반복 평활화 및 특이값 탐지 방법을 제시하였다. 또한 추적 분야에서 많이 적용되는 칼만 필터는 항법에서 유용한 도구이지만 특이값이 발생하면 이로 인해 성능이 저하된다. 특이값이 있는 경우에 칼만 필터의 성능을 향상시키기 위한 접근 방식도 연구되었다.[9]
본 논문에서는 직선 궤적으로 최근접점인 Closest Point of Approach(CPA)를 지나는 수중 이동체까지의 거리를 추정함에 있어서 추정된 거리 정보에 포함된 특이값을 제거하면서 시간에 따라 변화하는 거리 값을 하나의 특정한 함수로 적합하는 방법을 제안하였다. 제안한 방법의 성능을 고찰하기 위하여 모의실험과 함께 실제 호수 및 해상실험에서 획득한 데이터를 이용하여 타당성을 검증하였다.
본 논문의 구성은 다음과 같다. 제II장에서는 다루고자 하는 문제인 수중 이동체의 거리 추정 과정에서 발생할 수 있는 특이값 문제를 서술한 뒤 이러한 특이값 제거를 위하여 제안하는 방법인 비선형 최소 제곱 적합을 통해 특정 함수로의 모델링을 통한 매개변수를 찾는 방법에 대해 설명하고, 제III장에서는 모의실험, 호수실험 및 해상실험 결과를 제시한다. 마지막으로 제IV장에서는 결론을 서술한다.
II. 제안한 방법
2.1 문제의 정의
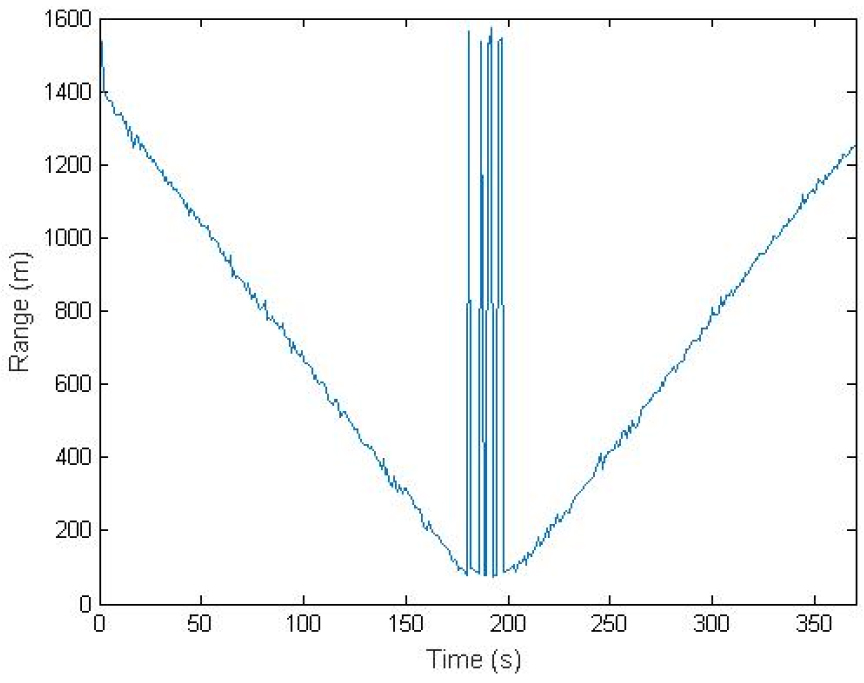
수중 이동체까지의 거리를 측정하는 문제에서 어떠한 신호를 송신하고, 도달 시간 추정이나 도플러 주파수 추정 등과 같이 어떤 방법으로 거리를 측정할지는 이 논문의 관심 대상은 아니며, 이 논문에서는 임의의 방법을 사용하여 시간에 따라 측정된 거리 정보가 있으며, 이에는 특이값들이 포함되어 있다고 가정한다. Fig. 1은 실제 해상실험을 통하여 측정된 거리 정보의 예를 보여준다. 그림의 결과는 거리 측정을 위하여 도달 시간 측정 방식을 적용한 것으로써 송신기와 수신기는 초기에 서로 시간 동기화 되었으며, 이동하는 송신기에서 주기적으로 송신하는 신호는 알고 있는 상황이다. 송신 신호와 수신 신호 사이에 상호상관도를 구하여 위치가 고정된 수신기에 수신된 신호가 도달한 시점을 추정하고, 송신 시점과의 시간차를 구함으로써 신호가 전달되는데 걸린 시간을 추정하여 거리로 나타낸 것이다.
Fig. 1에서 측정 대상 이동체가 원거리에서 시간에 따라 직선 궤적으로 이동하면서 점점 다가오고 있으며, 가장 근접하였을 때 약 75 m 정도의 거리를 지나서 다시 점점 멀어지는 형태임을 볼 수 있다.다만 CPA를 지나는 시점에서 측정 오류가 발생한 것을 볼 수 있으며, 이들은 임펄스 형태의 특이값으로 간주된다. 특이값 발생은 해양 환경의 불규칙성으로 인하여 CPA 인근에만 국한되는 것이 아니라 어느 위치에서든지 가능하지만 CPA 전후로는 도플러 주파수의 변화가 상대적으로 크고, 송신기가 부착되어 이동하는 함정과 케이블에 매달린 수신기 사이의 거리가 근접하여 물리적인 변동성이 증가하면서 오류가 발생할 수 있다. 이 특이값들은 주변 데이터의 분포에서 현저하게 벗어나 있다. 이외의 구간에서도 잡음 형태의 거리 측정 오류가 포함되어 변동성이 있음을 볼 수 있다. 이 논문에서는 이렇게 측정된 거리 정보에 오류가 포함된 경우 이러한 특이값들의 영향을 줄이고 가장 근사하는 함수 모델을 찾아 거리 정보를 보정한다.
2.2 제안한 방법
이 논문의 주요 내용은 특이값을 포함하고 있는 측정 데이터를 이용하여 특이값을 제거하면서 동시에 미리 정해진 모델링 함수의 계수 값들을 찾는 것이다. 이러한 과정으로부터 산출된 모델링 함수를 이용하여 거리 정보를 보정하는 것이다. 여기서 특이값 제거를 위해 RANdom SAmple Consensus(RANSAC) 방법을 사용하였으며, 모델링 함수로는 V-곡선 함수를 적용하였다. 또한 모델링 함수로의 곡선 적합을 위해 모델의 관측값과 예측값의 차의 제곱의 합을 최소화하여 매개변수를 추정하는 비선형 최소 제곱 적합 방법을 적용하였다.
RANSAC 방법은 영상 처리 분야에서 소개된 방법으로써 특이값을 제거하는데 효과적인 것으로 알려져 있다.[14] 개선된 형태의 RANSAC 방법인 Maximum Likelihood SAC(MLESAC), 적응형 RANSAC 방법[15]도 있으나 이 논문에서는 RANSAC 방법 자체가 관심 대상은 아니므로 기본적인 RANSAC 방법을 적용하였다. 기본적인 RANSAC 방법은 우선 어떤 모델 함수를 적용할지 정한 뒤 무작위로 데이터 몇 개를 뽑아서 이 샘플들을 만족하는 모델의 매개변수를 구한다. 이렇게 구한 모델과 일정 범위 내의 가까이에 있는 데이터들의 개수를 세어서 그 개수가 크다면 이 모델의 매개변수를 저장한다. 이러한 과정을 여러 번 반복한 후 근접하는 데이터의 개수가 가장 많은 모델을 최종 결과로 결정한다.
제안하는 방법의 전체적인 구성은 기본적으로 RANSAC 방법을 따르지만 응용 분야의 특성에 맞추어 아래에서 언급할 V-곡선이라는 모델링 함수와 비선형 최소 제곱 적합 방식을 적용하였다. 이러한 과정을 Table 1에 나타내었다.
Table 1.
Flow of the proposed method.
일반적으로 데이터들을 근사하기 위한 모델 함수로는 임의의 차수를 갖는 다항식을 많이 사용하지만 경우에 따라서는 고차 다항식이 필요한 경우도 있어서 이러한 경우에는 로그 또는 지수함수 형태의 비선형 함수를 사용하기도 한다. 이 논문에서는 적용 분야의 특징을 고려하여 V-곡선 함수를 적용하였는데 V-곡선은 일종의 변형된 쌍곡선 함수로 볼 수 있다. Fig. 1에서 CPA 인근의 특이값들이 없는 이상적인 경우를 가정하면 그림은 3개의 영역으로 구분될 수 있다. CPA 지점으로 접근하는 직선 구간, CPA 지점을 지나 멀어지는 직선 궤적 및 이들 사이의 CPA 지점 근처 영역의 곡선 영역으로 나눌 수 있다. 기존에는 이와 같은 3개의 영역을 별도로 구분한 뒤 각 영역별로 다른 함수로 모델링한 경우도 있지만 이 논문에서는 V-곡선이라는 하나의 모델 함수를 사용하였다. V-곡선으로 모델링한 이유는 비교적 적은 수의 매개변수를 구하면 되고, 일반적인 고차 다항식으로 모델링하는 경우에는 먼저 적절한 차수가 결정되어야 하는 문제가 있기 때문이다. 동시에 V-곡선은 영역을 구분하지 않고 하나의 함수로 모델링될 수 있기 때문이기도 하다. V-곡선 함수의 일반식은 아래와 같다.[16]
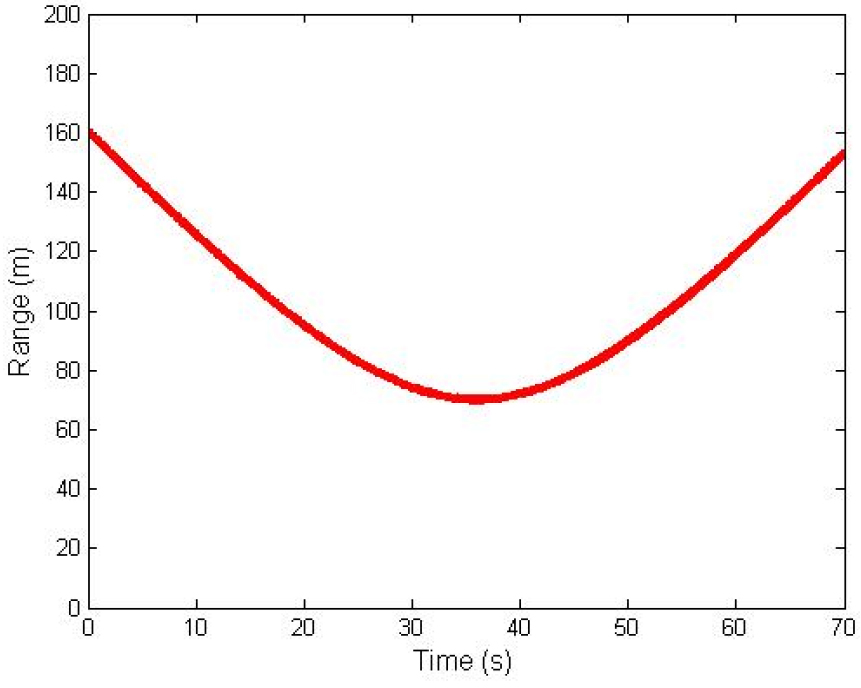
Eq. (1)에서 는 가로축에 해당하는 시간 인덱스이며, 은 세로축 값인 거리에 해당한다. 이는 쌍곡선 함수에 기반한 함수이며, ,, , 는 곡선의 위치와 모양을 결정하는 매개변수들이다. 매개변수들 가운데 와 는 V-곡선에서 “V” 형태의 벌어진 정도를 정하는데 이는 물리적으로는 이동체의 이동속도와 관련된다. 는 최소값을 갖는 지점의 가로축에서의 위치를 결정하고, 는 함수의 최소값을 갖는 지점에서 세로축 값과 관련이 있다. Fig. 2는 =-17.5, =70, =36, =0.13인 경우에 V-곡선 함수의 예를 보여준다.
선택된 거리 값들을 이용하여 V-곡선 함수로 적합하기 위하여 비선형 최소 제곱 적합 방법을 활용하였다. 비선형 최소 제곱 적합 방법이란 일반적으로 min() 을 푸는 것을 의미하는데 여기서 는 비선형 모델 함수이고, 는 주어진 데이터들이다. 비선형 최소 제곱 적합 방법은 일반적인 함수에 사용할 수 있도록 선형 최소 제곱 적합 방법을 확장한 것으로 변수 사이의 관계를 선형 방정식으로 표현할 수 없는 모델에 주로 사용한다. 즉, 주어진 데이터들을 이용하여 비선형 함수로 적합할 때 적용되는데 V-곡선이 비선형 함수이기에 이 방법을 적용하였다. 선형 최소 제곱 적합 방법과 다르게 비선형 최소 제곱 적합 방법에서 매개변수를 사용할 수 있는 방식에는 제한이 거의 없다. 이에 따라 비선형 최소 제곱 적합 방법의 가장 큰 장점은 적합할 수 있는 함수의 범위가 넓다는 것이다. 많은 형태가 선형 모델이나 상대적으로 간단한 유형의 모델을 사용해도 되지만 비선형 모델도 있기 때문에 이러한 경우에 적합하다.
III. 실험 및 결과
이번 장에서는 모의실험과 함께 실제 호수 및 해상실험을 통해 획득한 데이터를 이용하여 제안한 방법의 성능을 분석한다.
3.1 모의실험
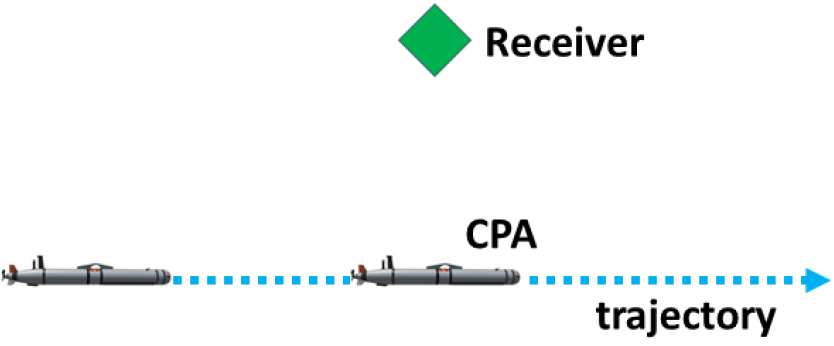
모의실험에서는 수중 이동체와 수신기 사이의 거리를 측정하기 위하여 펄스 형태의 신호를 주기적으로 송신하는 송신기가 부착된 수중 이동체가 Fig. 3과 같이 일정한 속도를 갖고 직선으로 이동하는 환경을 가정하였다. 편의를 위하여 이동체의 수심은 변하지 않고 수신기와 같은 수심인 2차원 평면에서 이동한다고 하였다. 주기적인 송신 신호는 선형 주파수 변조된 펄스 형태의 신호를 적용하였다. 적용된 신호는 0.1 s의 길이를 가지며 중심주파수는 30 kHz이면서 대역폭은 2 kHz로 하였다. 또한 이와 같은 신호가 1 s 간격으로 반복되는 상황을 가정하였다. 모의실험을 위해 적용한 파라메타들은 Table 2와 같다.
Table 2.
Simulation parameters.
| Parameter | Value |
| Sampling frequency | 100 kHz |
| Center frequency | 30 kHz |
| Bandwidth | 2 kHz |
| Moving speed | 4 m/s |
| CPA range | 70 m |
| Pulse length | 0.1 s |
| Pulse repetition interval | 1 s |
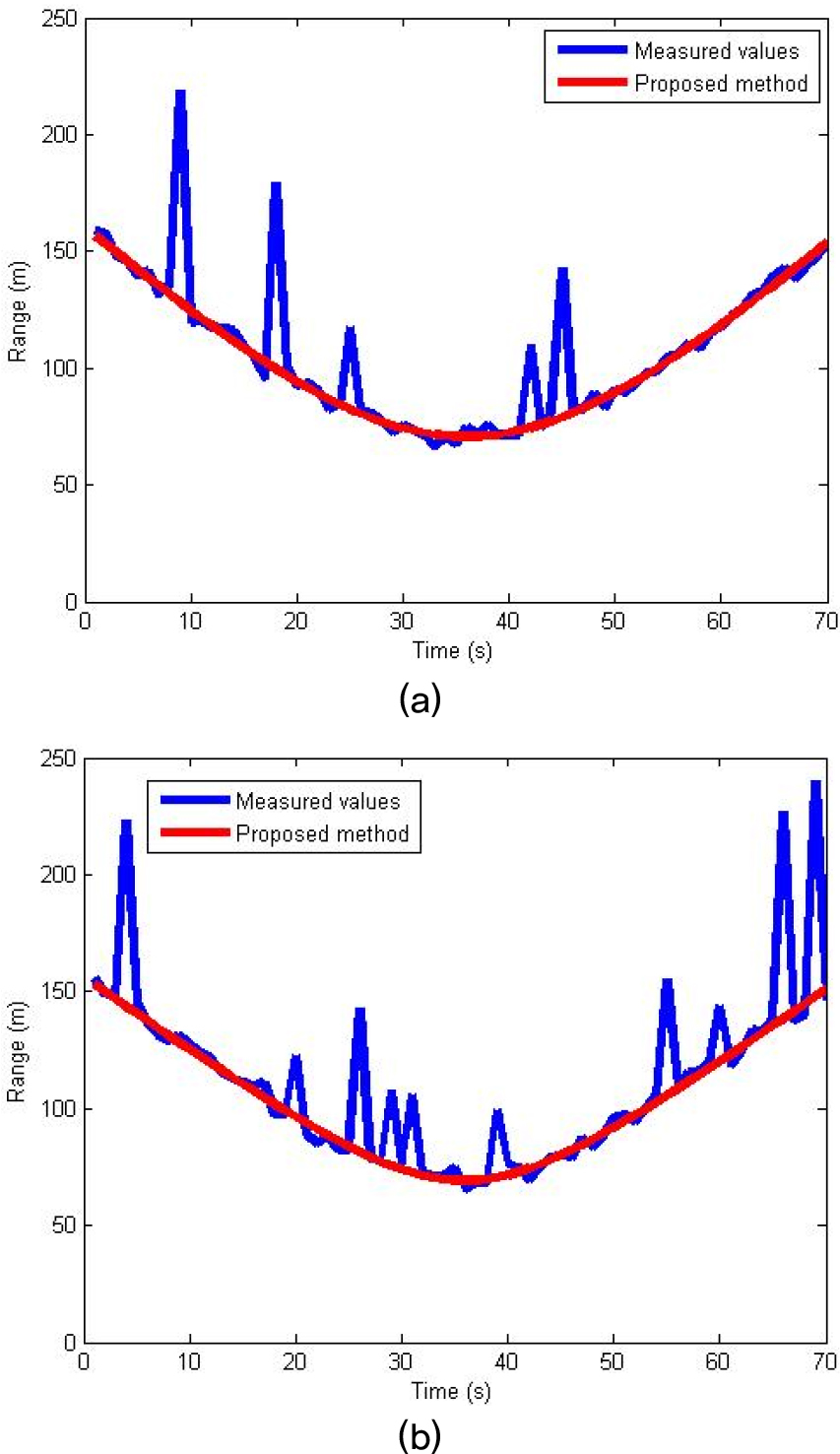
모의실험에서 특이값은 전체 구간에서 최대로 발생 가능한 비율만 설정하고, 발생 횟수, 위치 및 크기는 랜덤한 방법으로 설정되도록 하였다. 다만 발생되는 특이값의 크기가 너무 터무니없는 값을 갖지 않도록 미리 정한 최대값을 벗어나면 반영하지 않도록 하였는데 Fig. 4에서는 최대값을 250 m로 설정한 것이다. Fig. 4는 2가지 경우에 대한 결과를 나타낸 것으로써 이들의 차이는 전체 구간에서 특이값이 차지하는 비율이다. Case 1은 전체 구간 가운데 특이값이 발생한 비율을 10 % 이하로 설정한 것이며, Case 2는 Case 1에 비해 특이값이 보다 많이 발생한 경우로써 특이값이 15 % 이하인 경우이다. 제안한 방법에서 특이값 제거를 위한 처리 과정에 문턱치는 10 m로 설정하였는데 이는 경험에 의하여 정한 것이다. 모든 경우에서 제안한 방법으로 특이값 제거와 비선형 함수 모델링이 수행된 경우 오차가 감소하는 것을 볼 수 있는데 이는 Table 3에서 수치적으로 확인할 수 있다. Table 3은 Root Mean Square Error(RMSE) 값을 나타낸 것으로 다음과 같은 식으로 산출하였다.
Eq. (2)에서 는 설정된 정답 또는 기준 거리 값이며, 는 측정되었거나 제안한 방법으로 보정된 거리 값이다. 또한 은 측정된 이벤트 횟수이다. Table 3의 결과에서 특이값 제거 전에는 17.9 m와 26.7 m의 오차를 보였으나 제안한 방법을 적용한 경우 모두 1 m 이내의 오차를 나타내었다.
Table 3.
RMSE in simulation results.
| Case 1 | Case 2 | |
| Measured | 17.9 m | 26.7 m |
| Proposed method | 0.6 m | 0.6 m |
3.2 호수실험
모의실험에 이어 호수실험을 통해 획득한 데이터를 활용하여 제안한 방법의 성능을 확인하였다. 호수실험은 경상북도에 위치한 호수에서 2017년 8월에 수행되었는데 GPS가 장착된 보트에 로프를 이용하여 별도로 제작된 송신기를 연결하였으며 CPA가 약 30 m ~ 40 m 정도 되면서 보트가 지나가도록 주행하였다. 보트는 약 2 knots 내외의 등속으로 직선 이동하였으며, 로프에 달린 송신기는 약 10 m의 수심을 유지하려고 하였으나 실제로는 이동 과정에서 부력으로 인하여 일정한 수심을 유지하기는 어려웠다. 수신을 위한 하이드로폰으로는 B&K사의 8106 모델을 사용하였으며, 수심 18 m에 설치하였다. 거리 추정을 위하여 송수신단이 서로 시간적으로 동기화된 시스템을 사용하였다. 주기적으로 송신되는 신호가 수신기에 도달하기까지의 시간을 추정하는 방법을 사용하였는데 이를 위해 수신단에서는 송신된 신호의 리플리카와의 상호 상관함수를 구하였다. 일정 시간 구간 안에서 상호 상관함수가 최대값을 나타내는 시점까지의 시간을 도출하였다.
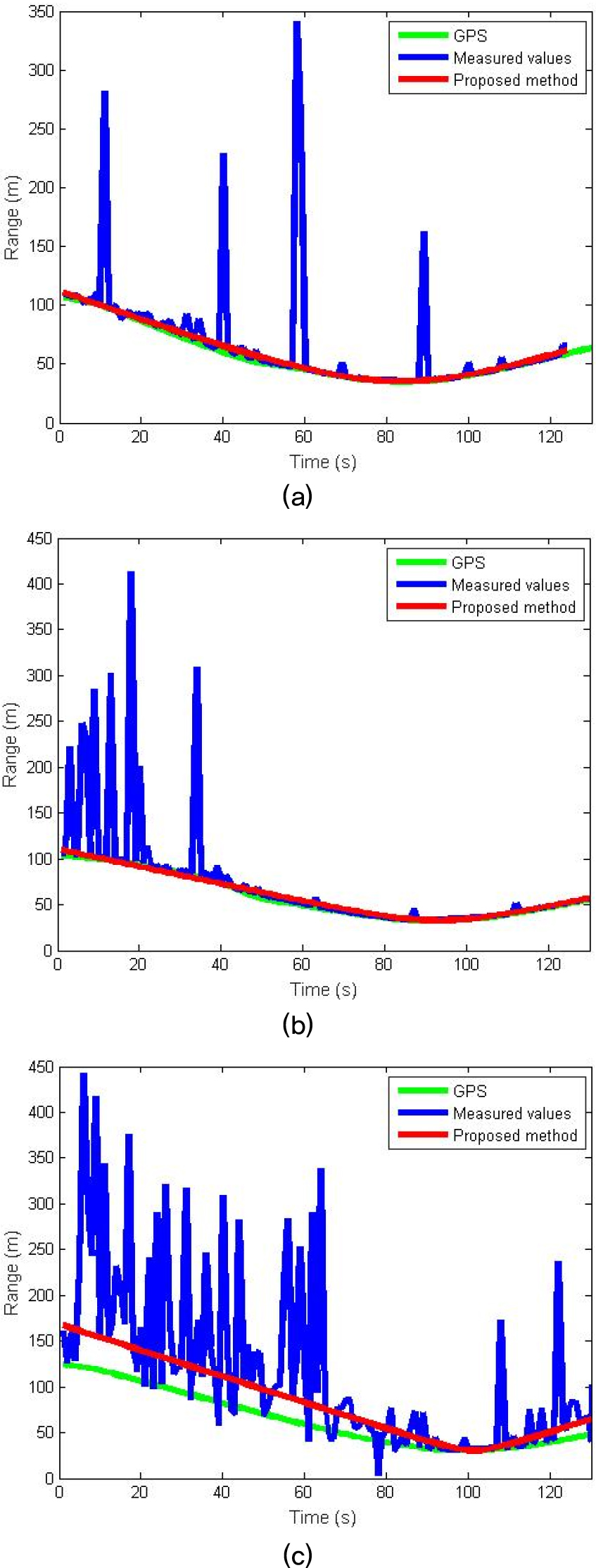
Fig. 5는 3가지 경우에 대한 호수실험 결과를 보여준다. Case 3은 특이값들이 전체 관심 영역에 넓게 퍼져 있는 형태이며, Case 4는 일부 시간 영역에 집중된 경우이다. 이에 비해 Case 5는 특이값이 많이 발생한 경우이다.
Fig. 5의 결과에서 제안한 방법을 적용한 경우 모두 특이값 제거와 동시에 이동체의 궤적을 유사하게 따르는 것을 볼 수 있는데 RMSE 결과는 Table 4에서 확인할 수 있다. 모든 경우 제안한 방법의 적용을 통해 RMSE 값이 감소한 것을 확인할 수 있다. RMSE 값을 산출할 때 기준값 는 GPS에 의해 측정된 보트의 위치를 이용하여 계산된 거리 값으로 하였다. 하지만 실제 GPS 값에는 오류가 있는데다 실험에서 GPS는 보트 본체에 장착되었고, 송신기는 로프로 연결된 길이만큼 떨어져 있는 동시에 송신기가 위치한 수심과 수신기의 수심에 차이가 있었기 때문에 약 7 m 내외의 거리 오차가 나타났다. Case 5의 경우 너무 많은 특이값들이 절반 이상의 영역에서 발생하였기 때문에 상대적으로 오차가 크게 나타난 것을 볼 수 있으며, 특히 특이값이 집중적으로 발생한 지점에서의 오차가 크게 나타났다. 하지만 이러한 호수실험 결과를 보면 RMSE 관점에서 약 85 % 정도의 거리 추정 오차가 감소하였다.
Table 4.
RMSE in lake trial results.
| Case 3 | Case 4 | Case 5 | |
| Measured | 47.3 m | 47.8 m | 93.6 m |
| Proposed method | 7.3 m | 7.7 m | 28.4 m |
3.3 해상실험
마지막으로 실제 해상실험에서 얻어진 데이터를 활용하여 성능을 분석하였다. 실험은 동해 포항 인근 해역에서 진행되었으며, 송신기는 약 10 knots 이상의 속도로 이동하였다. 송신기와 수신기는 모두 수심 약 50 m에 설치되었다. 해상실험에서도 거리 추정을 위해서 앞서 호수실험 과정에서 설명한 TOA 값을 추정하는 방법을 동일하게 적용하였다. 다만 해상실험에서는 앞선 호수실험과는 다르게 수중 이동체를 대상으로 하였기에 기준값이 되는 GPS 정보를 사용할 수 없어서 RMSE 값을 구할 수 없었다.
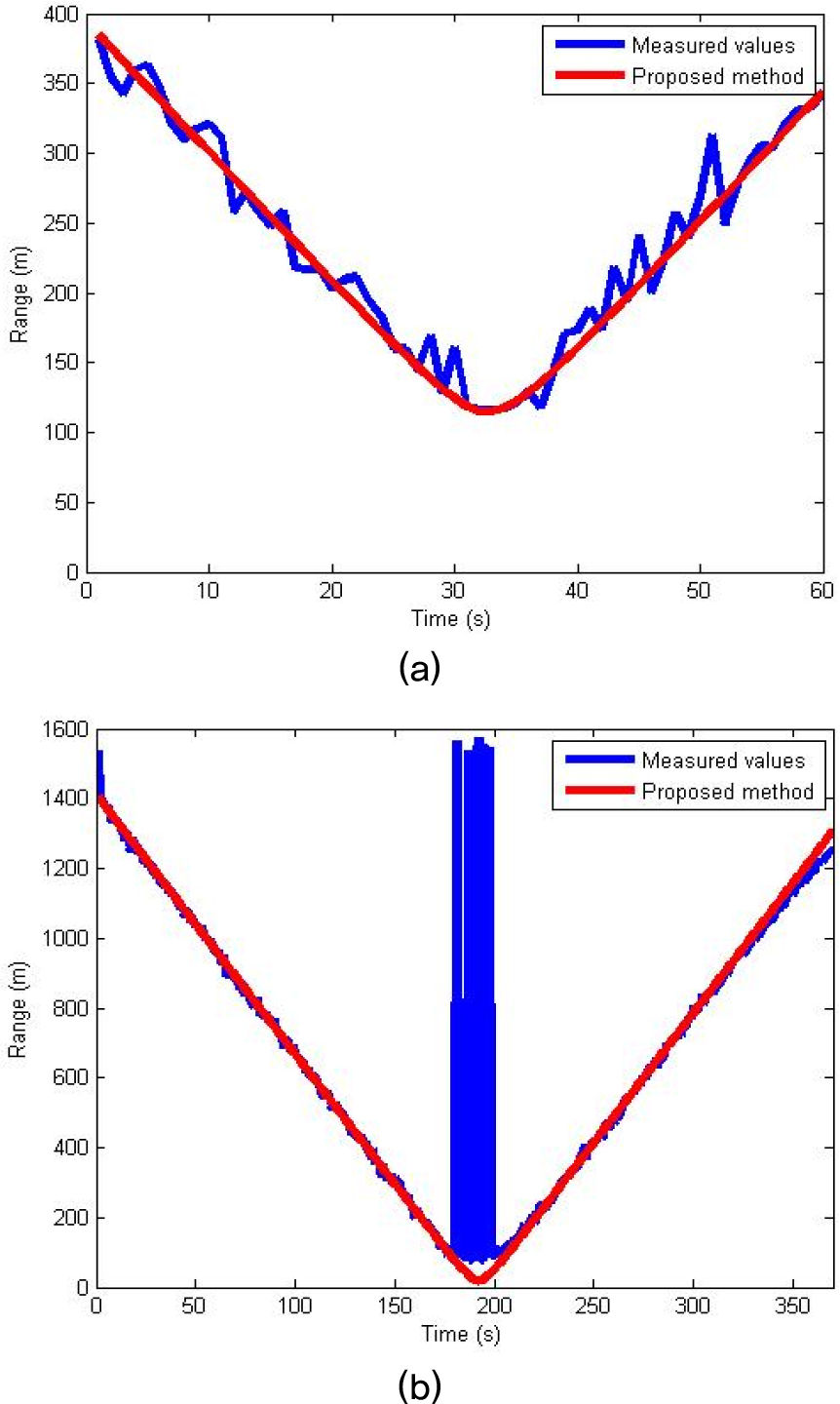
Fig. 6은 2가지 경우에 대한 결과를 나타낸 것으로 이동체 모두 직선 경로를 따라 일정한 속도로 이동하였다. 첫 번째는 CPA 지점에서의 거리가 약 110 m 정도이면서 큰 특이값 보다는 전 구간에 걸쳐 추정된 거리 값의 변동성이 있는 경우이며, 두 번째는 CPA 지점에서의 거리가 약 80 m 정도이면서 동시에 CPA 인근 영역에서 집중적으로 큰 특이값들이 발생한 경우이다. 2가지 경우 모두 제안한 방법을 적용하여 거리 값의 변화를 잘 추적하는 것을 볼 수 있으며, 특히 두 번째 경우에는 CPA 인근 지점에서 집중적으로 발생한 특이값들을 효율적으로 모두 제거한 것을 볼 수 있다.
IV. 결 론
이 논문에서는 수중 이동체와의 거리 측정에서 특이값 탐지 및 제거를 위한 방법을 다루었다. 이를 위해 RANSAC 방법을 이용하여 특이값을 제거하면서 동시에 비선형 최소 제곱 적합을 통해 V-곡선 모델링을 위한 매개변수를 찾도록 하였다. 모의 및 호수실험을 통하여 제안한 방법으로 추정한 거리 값과 기준값 사이를 비교하여 성능을 입증하였고, 해상실험에서 획득한 데이터를 활용한 결과를 보였다. 제안한 방법은 실시간 처리보다는 데이터 획득 후 사후 분석을 위해 적용가능하다.
이 연구에서는 정해진 직선 이동 궤적에 한정되어 있는 경우만을 대상으로 하였으나 향후 연구에서는 임의의 곡선 형태로 기동하는 경우에 특이값 탐지 및 제거에 대한 연구가 필요할 것으로 보인다.