I. 서 론

수상함에 탑재되는 선체고정형소나는 적 어뢰, 적 수상함 및 잠수함 등의 신호를 탐지하고 추적하는 데 중요한 역할을 한다.^[1] 수상함은 관련 규정에 따라 해군으로 함정을 인도하기 전, 건조 과정에서 시뮬레이션 데이터를 활용한 기능 확인 등을 포함한 정박 시운전(Harbor Acceptance Test, HAT)을 수행하고, 항해 시운전 평가(Sea Acceptance Testm, SAT) 과정을 거치는데, 선체고정형소나는 수립된 절차를 통하여 방위정확도, 탐지거리 등 해상에서의 탐지성능을 검증한다. 그러나, 현재 함 건조 과정 중 선체고정형소나의 해상 시운전 절차는 계절적 요인, 해저 지형 등에 따른 탐지 성능의 변동성을 충분히 반영하지 못하고 있다. Reference [2]에서는 계절별 음파 전달 특성이 반영된 선체고정형소나 해상 시운전 절차의 필요성을 제기하였으나, 특정 년도 및 시점을 지정하여 한가지 특정 음속 구조에 한정하여 거리 예측 등 분석 결과를 제시하였고, 함정 배치, 해상 시운전 구역 선정 등 세부적인 수행 방안을 제시하지 않았으며 하계절과 동계절에 대해서만 음파 전달 특성을 분석하여 그 결과를 제시하였다는 한계점이 있다.

본 논문에서는 이러한 한계점을 해소하고, 선체고정형소나 해상 시운전의 효율적 수행을 위한 방안을 제시하고자 한다. 해저 지형에 의한 음파 전달 특성의 영향을 최소화하기 위해 해저면이 비교적 평평한 동해 울릉 분지의 일부 구역을 해상 시운전 수행 구역으로 선정하고, 국립기상과학원(National Institute of Meteorological Sciences, NIMS)의 Array for Real time Geostrophic Oceanography(ARGO) 플로트 및 국립수산과학원(National Institute of Fisheries Science, NIFS)의 정선 해양관측 정점으로부터 데이터를 획득하여 선정 구역에서의 월별 평균 음속 구조를 산출하고 분석하였다. 수집된 데이터를 이용하여 기계학습 기반의 특정 년, 월, 그리고 선정 구역 내 특정 지점에서의 예측 음속 구조를 산출하고, Bellhop 모델링을 통해 계절적 요인에 따른 탐지 성능 변동성이 반영된 해상 시운전 활용 방안을 제시하였다. 또한, 기존의 절차에는 세부적으로 제시되지 않았던 해저 지형의 경사, 선체고정형소나와 표적함의 배치, 소나 음파 전송 방향 및 빔 조향각 측면에서 살펴보았으며, Bellhop 모델링 결과를 이용하여 상기 제시한 내용에 대한 세부 수행 방안을 제안하였다.

II. 동해 음속 구조 분석

해상에서의 음파는 해수면과 해저면의 반사를 거치면서 전달되고, 해상 상태와 해저면의 형태에 따라 다양한 음파전달 경로가 생성된다. 해상 상태에 따른 해수면 상태, 그리고 계절적인 변화에 의한 수온 변화 및 저염수 현상 등은 음파 전달 특성에 영향을 미치는 불가피한 변수들이나, 해저면과 같은 지형적 요소는 해상 시운전 수행 구역 선정을 통해 통제 가능한 변수로 간주할 수 있다.

울릉분지 내 위도 36.0°N에서 37.5°N, 경도 129.7°E에서 132.0°E에 해당하는 해역을 해상 시운전 수행 구역으로 선정함으로써 음파 전달에 영향을 미칠 수 있는 다양한 해저면 경로의 영향을 최소화하였다. 해저 지형 데이터를 활용하여 위도 36.8°N에서 동서 방향으로의 단면을 분석한 결과, 약 180 km에 걸쳐 수심이 대체로 일정하게 1,900 m에서 2,200 m 사이를 유지하는 것으로 확인되었다.^[3,4]

선정된 구역 내에서 유효한 음속 구조 예측 모델을 산출하기 위해 필요한 학습 데이터를 수집하였으며, 해당 구역에서의 실제 음속 구조는 국립기상과학원의 ARGO 플로트 데이터와 국립수산과학원의 정선 해양관측 정점 데이터를 통해 획득하였다.

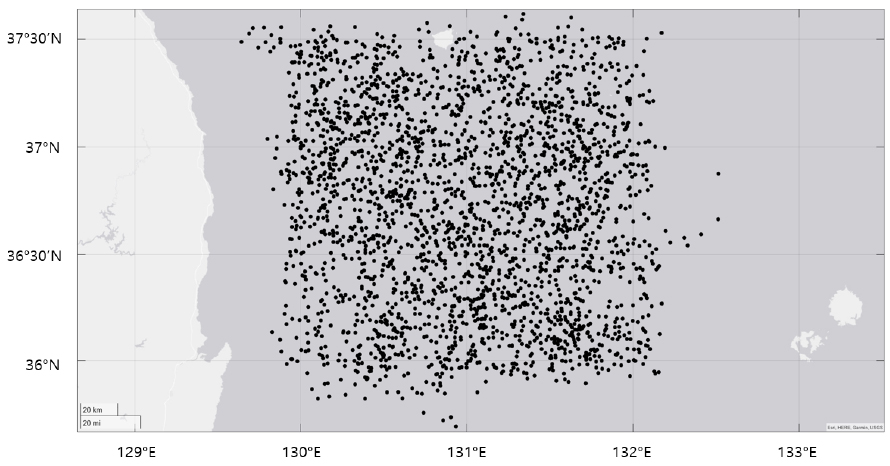
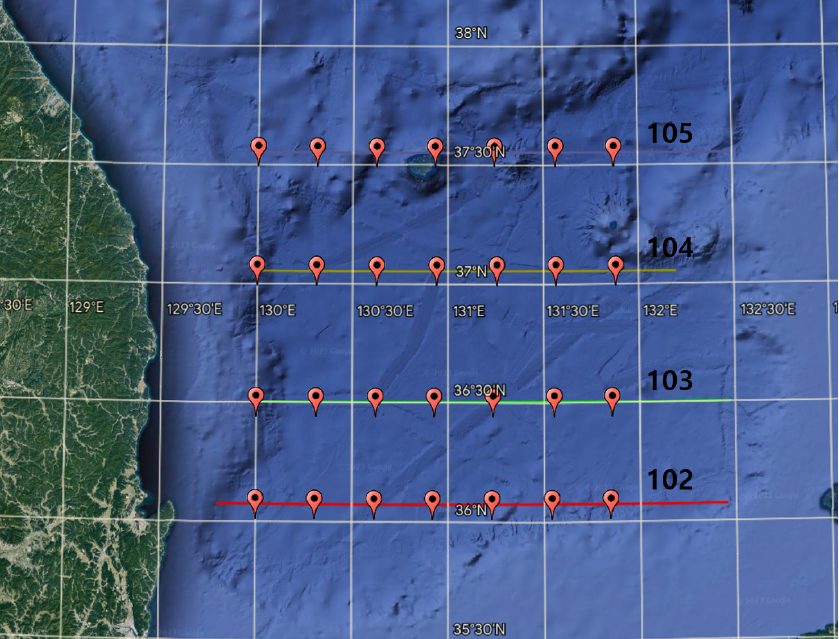
ARGO 플로트 데이터의 경우, 플로트 총 70개로부터 2002년부터 2022년까지 수온과 염도의 수직 프로파일을 2,837개 수집하였으며,^[5] 정선 해양관측 정점 데이터의 경우, 정선 관측 지점 총 28개로부터 1967년부터 2022년까지 수온과 염도의 수직 프로파일을 7,602개 수집하였다.^[6] Fig. 1은 ARGO 플로트를 통한 데이터 획득 지점을 나타내며, Fig. 2는 정선 해양관측 정점을 통한 데이터 획득 지점을 나타낸다.

Fig. 1.

ARGO floats data acquisition points in the sea trial area.

Fig. 2.

(Color available online) Ocean observers data acquisition points in the sea trial area.

수집한 데이터를 1월부터 12월까지 월별로 구분하고, Eq. (1)에 나타낸 Medwin의 경험식을 이용하여 월별 평균 음속 구조를 계산하였다.^[7]

Fig. 3은 선정된 구역에서 2002년부터 2022년까지 ARGO 플로트틀 통해 관측된 월별 평균 음속 구조를 약 450 m 수심까지 분석한 것이다. 이 결과는 음속 구조가 매월 다양하게 변화하지만, 이 수심을 넘어서면 년도와 관계 없이 거의 유사하게 나타남을 보여준다.

Fig. 3.

(Color available online) Monthly average sound speed profile of ARGO floats.

Bellhop 모델을 이용한 시뮬레이션을 위해 약 450 m 이상 수심에서의 음속 구조 유사성과 해상 시운전 수행 구역의 해저면이 거의 평평한 형태를 나타냄을 고려하여 2,200 m 수심까지의 값을 1 m 단위로 보간하여 나타냈다. 정선 해양관측 정점 데이터의 경우 장기간에 걸쳐 계측은 이루어졌으나, 수심별 수온, 염도가 세밀하게 계측되어 있지 않다. 다만, 측정된 값이 선체고정형소나가 운용되는 표층에 주로 분포되어 있고, 장기간에 걸쳐 계측된 점을 고려하여 기계학습 데이터로 활용하였다. 계절적 요인 등으로 인한 탐지 성능의 변화를 반영하는 해상 시운전 방안 제시를 위해서 음파 전달 특성에 직접적인 영향을 미치는 음속 구조와 음향층심도에 대하여 분석하였다.

Fig. 4는 표층 음향 채널을 형성하는 수심에 해당하는 음향층심도의 월별 변화를 나타낸다. 2월은 음향층심도의 분산이 가장 크며, 최소 0 m에서 최대 95 m에 이르는 넓은 범위를 보이고, 평균 깊이는 35.4 m이다. 반대로, 8월은 분산이 가장 적으며, 최대 음향층심도가 3 m에 불과하고 평균 깊이는 1.7 m로 거의 나타나지 않는다. 표면에서의 음향층심도 형성은 10월에 시작되어 2월까지 중앙값과 평균값이 점진적으로 증가하는 형태를 나타내며, 평균 깊이는 19.7 m에서 35.4 m사이가 된다. 이 기간 이후 3월부터는 중앙값과 평균값이 급격히 감소하고, 분산도 줄어들며, 9월까지는 음향층심도가 거의 나타나지 않는다.

Fig. 4.

(Color available online) Monthly variations of the sonic layer depth.

III. 기계학습 모델

ARGO 플로트 데이터와 정선 해양관측 정점 데이터를 학습 데이터로 이용하여 기계학습을 통해 해상 시운전 수행 구역의 음속 구조를 예측하였다. 기존 인공지능 분야의 순수 데이터 기반 학습 모델의 한계인 물리적 정합성 위배, 학습 데이터 부족 등의 문제 해결을 위하여 해석하고자 하는 계에 대한 지배방정식인 물리정보를 학습 모델에 부여함으로써 예측 성능을 향상시키고 물리적 정합성을 확보하기 위한 물리정보신경망(Physics-Informed Neural Networks, PINNs)을 구현하였다.^[8] 물리정보신경망이란 일반적인 Multi Layer Perceptron(MLP)의 매개변수 도출 프로세스인 참값과 예측값의 차이를 손실 함수로 구성하고, 해당 손실 함수에서 정의된 오차를 최소화하며 학습시켜나가는 구조이며, 문제 해결 대상 계를 지배하는 방정식을 손실 함수에 정의하는 것이다. 또한 물리정보신경망은 데이터 획득 비용, 학습 데이터 부족이라는 해결책으로 제시될 수 있으며,^[9] 분석 대상 구역의 영역 크기 대비 확보된 음속 구조 데이터가 충분하지 않은 본 연구 관련 데이터 확보 한계를 해소할 수 있는 방안으로 제시한다.

계의 지배 방정식은 편미분 방정식(Partial Differential Equations, PDE)이 될 수 있으며, 손실 함수에 정의된 편미분 방정식을 통하여 모델의 최적 매개변수를 학습한다. 계측값 기록 과정 중 발생 가능한 계측기기의 오차, 모델의 학습 과정에서 매개변수의 누적된 오차 등으로 발생한 오차는 각 뉴런의 레이어에 누적되어 모델 예측 성능을 저하시켜 물리적 정합성을 위배하는 예측 결과를 제시할 가능성이 있는데 정의된 공학 문제의 분석 영역에서 물리정보가 존재할 경우, 물리정보신경망을 통해 이러한 한계를 해소할 수 있다.^[8,9]

손실 함수는 Eqs. (2), (3), (4)로 나타낼 수 있다.

여기서 Nu는 학습 데이터 개수, 인공신경망 모델 u(t,x)는 (tui,xui)를 입력으로 받았을 때 ui를 출력, MSEu는 초기조건과 경계조건을 충족해야 한다. 또한 f(t,x;u)는 콜로케이션(collocation) 포인트 (tfi,xfi)에서 Eq. (4)를 만족해야 하며, Nf는 콜로케이션 포인트 개수를 나타낸다.

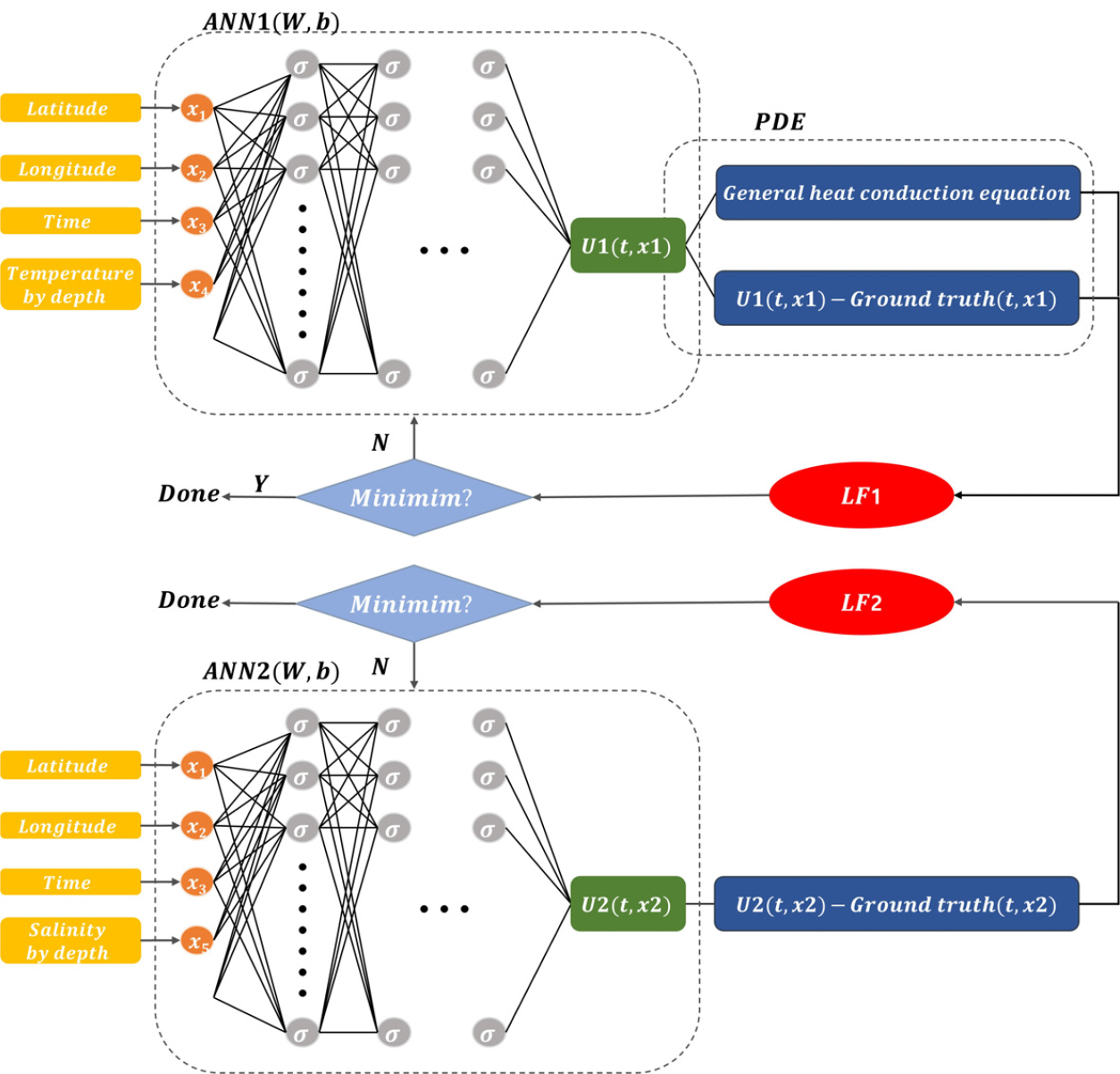
Fig. 5는 물리정보신경망이 적용된 학습 모델 구조이다. 학습 모델의 입력값으로는 ARGO 플로트 및 정선 해양관측 정점으로부터 획득한 수심별 수온 및 염도 관련 데이터, 데이터 취득 시점에 해당하는 연도 및 월과 같은 시간 정보, 데이터가 획득된 위도 및 경도와 같은 공간 정보가 있다. U1(t,x1)은 온도 예측 모델, U2(t,x2)는 염도 예측 모델이다.

Fig. 5.

(Color available online) PINNs machine learning model structure for temperature & salinity profile prediction.

이를 통해 해상 시운전 수행 구역에서 시공간적 변동성이 반영된 음속 구조를 예측한다. 음속 구조의 변화에 영향을 미치는 요인은 다양하나, 수온 변화가 주요인이므로^[10] 수온 학습 모델의 손실 함수에 직각 좌표계에서의 열전도 방정식을 적용하였으며, 열전도 방정식은 Eq. (5)와 같다.

여기서 T는 온도, k는 열전도도, q˙는 단위시간 당 단위부피에서 생성되는 열에너지, 𝜌는 밀도, Cp는 정압 비열을 나타낸다. 수심에 따른 음속 구조를 예측하고 그 결과를 바탕으로 전달 손실을 계산하므로, Z축 방향의 예측값만을 활용한다. 염도 학습 모델의 경우, 염도 데이터의 분산이 수온에 비해 상대적으로 작은 점을 고려하여 손실 함수에 별도의 물리정보를 적용하지 않고 계측값과의 잔차를 오차로 정의한 후, 이를 최소화하는 방식으로 모델을 최적화하였다.

분석 대상 구역의 영역 크기 대비 확보된 음속 구조 데이터가 충분하지 않은 점을 감안하여, 수심 0 m지점에서의 월별 평균 수온 및 염도값을 예측 구조의 초기값으로 설정하고, 실험적으로 Epoch를 100으로 설정, 트레이닝 데이터 셋은 80 %, 테스트 데이터 셋은 20 %로 구성하여 학습을 수행하였다. Fig. 6은 테스트 데이터 셋 중 임의의 위치 및 시점에 대한 학습 모델을 통한 예측 결과를 나타내며, 수온 및 염도 구조가 두드러지게 차이가 나는 2월과 8월을 대상으로 나타내었다. 예측값이 실측값과 유사한 형태를 나타내는 것을 확인할 수 있으며, Root Mean Squared Error(RMSE)는 Table 1과 같다.

Fig. 6.

(Color available online) Compare of ARGO & ocean observers observed/predicted temperature & salinity profile.

IV. 해상 시운전 수행 방안 제안

천해에서는 심해에 비해 다중 경계면에 따른 잔향음 제한 환경이 우세하나, 본 논문에서 제시한 해상 시운전 수행 구역은 심해인 점을 고려하여 소음 제한 환경으로 한정하였다.^[11,12] 소음 제한 환경에서의 소나 방정식은 Eq. (6)과 같으며, 신호 초과량을 통해 탐지 성능을 예측할 수 있다. 이 절에서는 소나 방정식과 더불어 Bellhop 모델링 결과를 이용하여 해저 지형의 경사, 선체고정형소나와 표적함의 배치, 소나 음파 전송 방향 및 빔 조향각 측면에서 세부 절차를 제시한다.

여기서 SE는 신호 초과량, SL은 음원 준위, TL은 전달 손실, TS는 표적 강도, NL은 잡음 준위, DI는 방향성 이득, DT는 탐지 문턱값을 나타낸다.^[13,14]

음원 준위, 음원 주파수, 음원 깊이, 방향성 이득, 탐지 문턱값 등의 변수들은 현재 운용 중인 선체고정형소나 관련 이전 연구에서 적용된 값들을 참고하여 설정하였다.^[1,13,14,15] 군사적 기밀성, 과거 분석 사례와 기술 발전을 반영하여 표적 강도를 10 dB로 설정^[16]하고, 분석 대상 구역의 거리는 30 km로 설정하여 해석하였다.

해저 지형 및 해저면 지질은 실질적으로는 복잡한 양상을 띄나, 수치실험을 위해 해상 시운전 구역에 대한 기존 연구 결과를 바탕으로 주로 나타나는 지질의 특성을 반영하였다.^[17,18]

계절별 음파 전달 특성을 확인하기 위해 춘계, 하계, 추계, 동계를 대표하는 각각의 월을 선정하였고, 춘계는 5월, 하계는 8월, 추계는 11월, 동계는 2월이다. 사용된 음속 구조는 월별 평균 음속 구조와 기계학습을 이용하여 예측된 음속 구조이며, 세부적인 수치 실험 입력 변수들은 Table 2에 나타내었다.

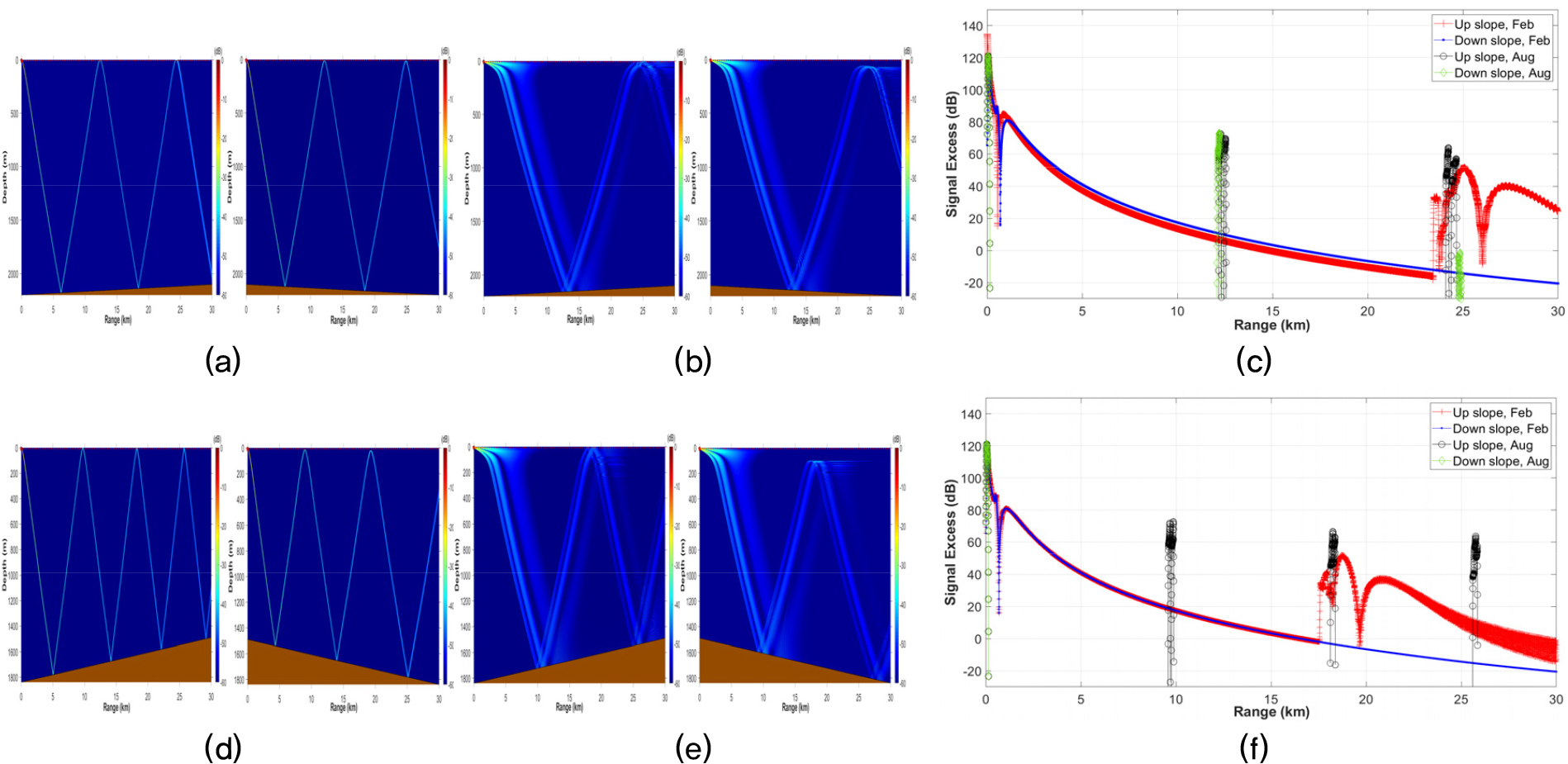
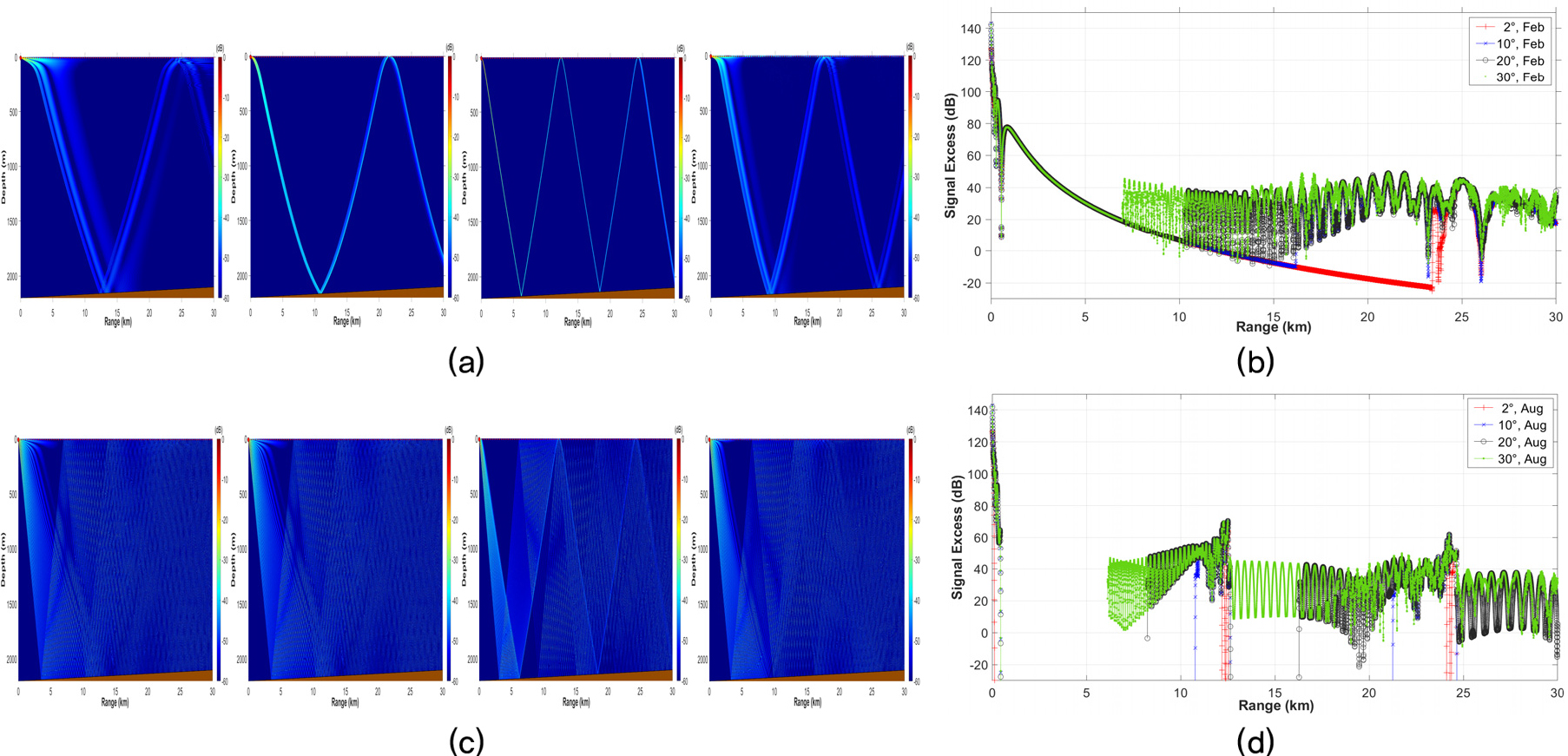
첫째, 해저면 기울기 및 음파 전송 방향 측면에서 살펴보았다. Fig. 7을 통해 계절, 완만/가파른 기울기와 관계 없이 오르막 경사로 음파가 전달되는 경우, 내리막 경사로 전달되는 상황에 비해 더 높은 신호 초과량을 나타내는 구간이 발생하는 것을 확인할 수 있다. 이는 음파 전달 시 거치는 수중 경로가 오르막 경사가 더 짧기 때문으로 판단된다. 선체고정형소나 성능 확인은 외부 환경 요인으로 인한 성능 저하 최소화가 필요하고, 외부 환경 요인으로 인한 성능 향상 통제도 이루어져야 한다. 음수렴구역에 따라 장거리 탐지 시 내리막 경사가 유리한 경우도 많다. 즉, 목적에 따라 음파 전송 방향은 다양할 수 있으나, 본 논문에서는 분석 대상 구역의 거리가 30 km인 점과 신호 초과량 관점에서 음파 전송은 완만한 경사가 있는 구역에서 오르막 경사로 이루어질 수 있도록 시험함과 표적함을 배치하는 것으로 제안한다.

Fig. 7.

(Color available online) Transmission loss. (a) Gentle up/down slope on Aug. (b) Gentle up/down slope on Feb. (c) SE for gentle up/down slope (d) Steep up/down slope on Aug. (e) Steep up/down slope on Feb. (f) SE for steep up/down slope.

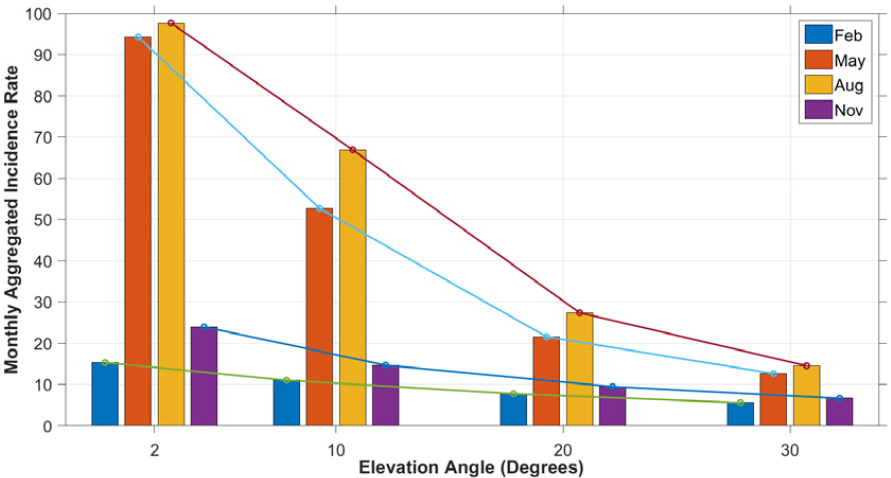
둘째, 선체고정형소나 빔 조향각 측면에서 살펴보았다. Fig. 8을 통해 계절에 관계없이 빔 조향각을 증가시킬 때 수상함 표적에 대한 신호 초과량이 0 이상인 영역이 점차 넓어지는 것이 관찰되었다. 춘계절 및 하계절은 음파의 하향 굴절로 인해 음영구역이 넓게 발생하고, 음파의 장거리 전달이 제한되나, 빔 조향각을 증가시키면 음파가 표층으로 전달되는 영역이 점차 증가한다. Fig. 9는 빔 조향각 변경에 따른 계절별 음영구역 발생 비율을 분석한 결과이다. 일반적으로 빔 조향각이 증가함에 따라 음영구역 발생 비율은 계절에 관계 없이 감소하는 경향이 있으며, 이 경향은 특히 춘계절과 하계절에 두드러지며, 춘계절과 하계절에서는 빔 조향각이 10°에서 20°로 변경될 때 음영구역 발생 비율 감소폭이 가장 크다. 반면, 추계절과 동계절에서는 빔 조향각 증가에 따른 음영구역 발생 비율 감소가 비교적 균일하게 나타난다.

Fig. 8.

(Color available online) Transmission loss. (a) Beam elevation 2° for each seasons (b) SE (Feb.) for each elevation (c) beam elevation 30° for each seasons (d) SE (Aug.) for each elevation.

Fig. 9.

(Color available online) Ratio of shadow zones by seasons according to beam elevation.

현재의 건조 중 함정의 선체고정형소나 해상 시운전 수행 절차는 빔 조향각은 일반적으로 5° 이내로 제한적으로 운용하도록 되어 있는데, 해상 시운전은 추계절 및 동계절에만 한정되어 수행하지 않고, 춘계절 및 하계절과 같은 음영구역 발생 비율이 높은 시점에도 수행하는 소요가 발생하므로 해상 시운전 수행 시 계절별 음파 전달 특성을 고려한 빔 조향각 변경 설정이 가능하도록 절차에 반영하는 것이 필요하다.

셋째, 기계학습을 통한 음파 전달 특성을 모델링하고 그 결과를 이용하여 계절적 요인에 의한 탐지 성능 변동성이 반영된 해상 시운전 절차를 제시하였다. eXpandable Bathy Thermograph(XBT)를 사용하여 음속 구조를 거리별로 측정하고, 측정값을 활용하여 Bellhop 모델링을 거쳐 음파 전달 특성을 확인하는 절차가 일반적이나, 실제 해상에서는 제한된 시험 시간, 해상 환경 등 현실적인 여건으로 거리별 음속 구조에 대한 수시 측정에 제한이 있다. 이러한 이유로 일반적으로는 분석 구역이 일정한 음속 구조를 가진다고 가정하고 모델링 하는 경우가 많은데, 이는 거리에 따라 음속 구조가 변화하는 실제 해양 환경 특성^[19]을 반영하지 못하는 한계점이 있다. 본 논문에서 제안한 물리정보신경망이 적용된 학습 모델을 통해 해상 시운전 구역 내의 위도와 경도, 특정 시점에 대한 음속 구조를 예측할 수 있으므로 거리에 관계 없이 일정한 음속 구조를 가정하는 탐지 성능 분석 방법의 한계를 해소할 수 있다.

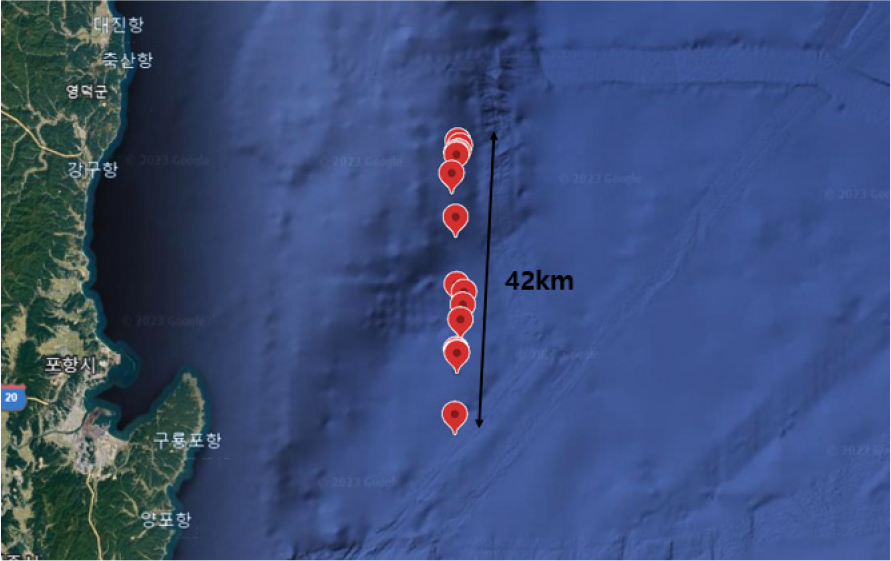
학습 모델의 효용성 검증을 위해 실제 해상 실험을 통해 거리별로 확보된 음속 구조를 이용하여 Bellhop 모델링을 수행한 결과와 학습 모델 기반의 예측 음속 구조를 이용한 Bellhop 모델링 결과를 비교 분석하였다. Fig. 10은 2022년 5월에 실시한 해상 실험 수행 구역을 나타내며, 위도 36.3721°N, 경도 130.0105°E에서 시작하여 위도 35.9993°N, 경도 130.0072°E까지 총 15개 지점에서 XBT를 이용하여 음속 구조를 측정하였다. 측정 시작 지점과 종료 지점 사이의 거리는 약 42 km이며, 개별 측정 지점 간의 거리는 약 0.31 km에서 9.32 km까지이다.

Fig. 10.

(Color available online) Sea experimental area.

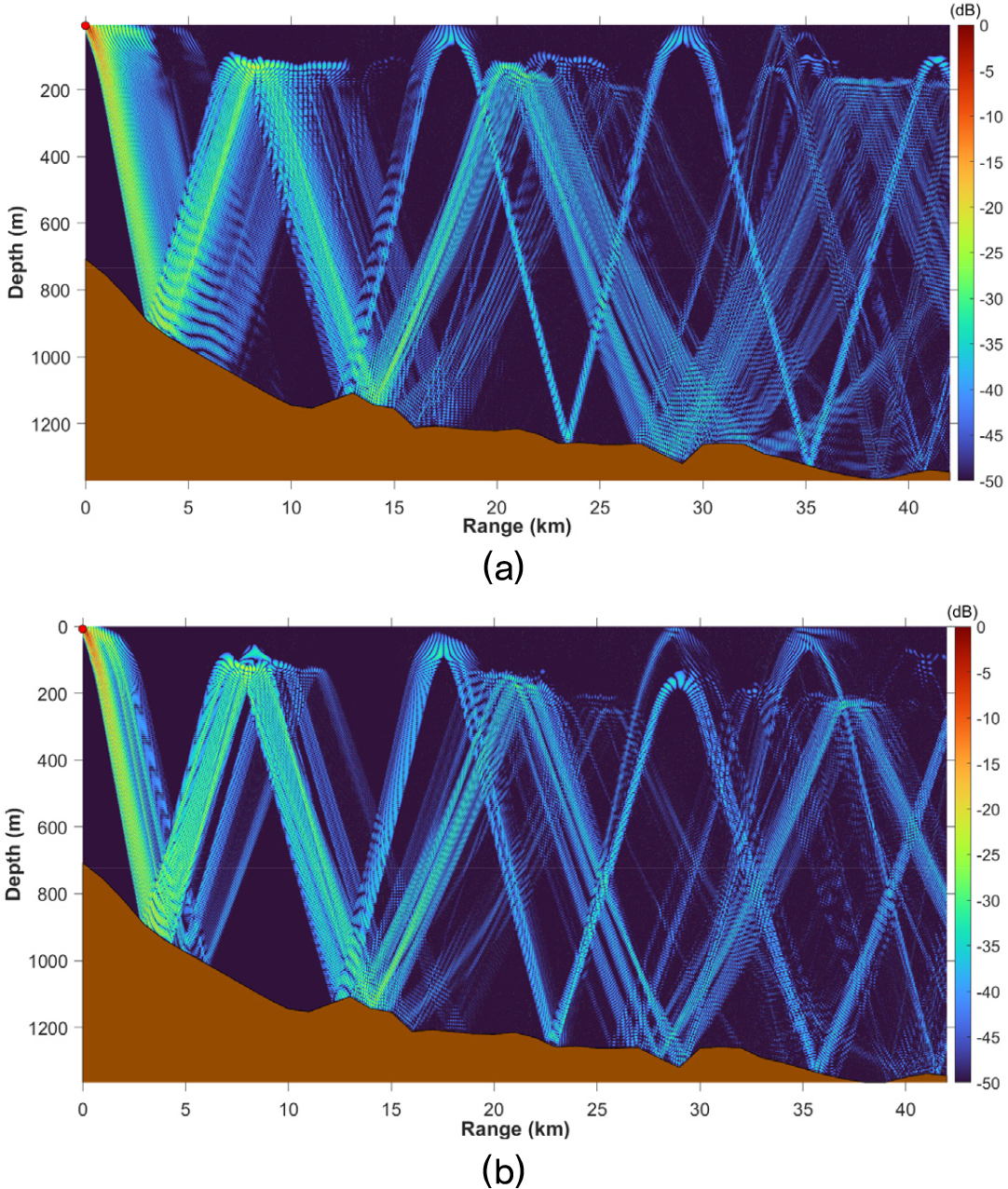
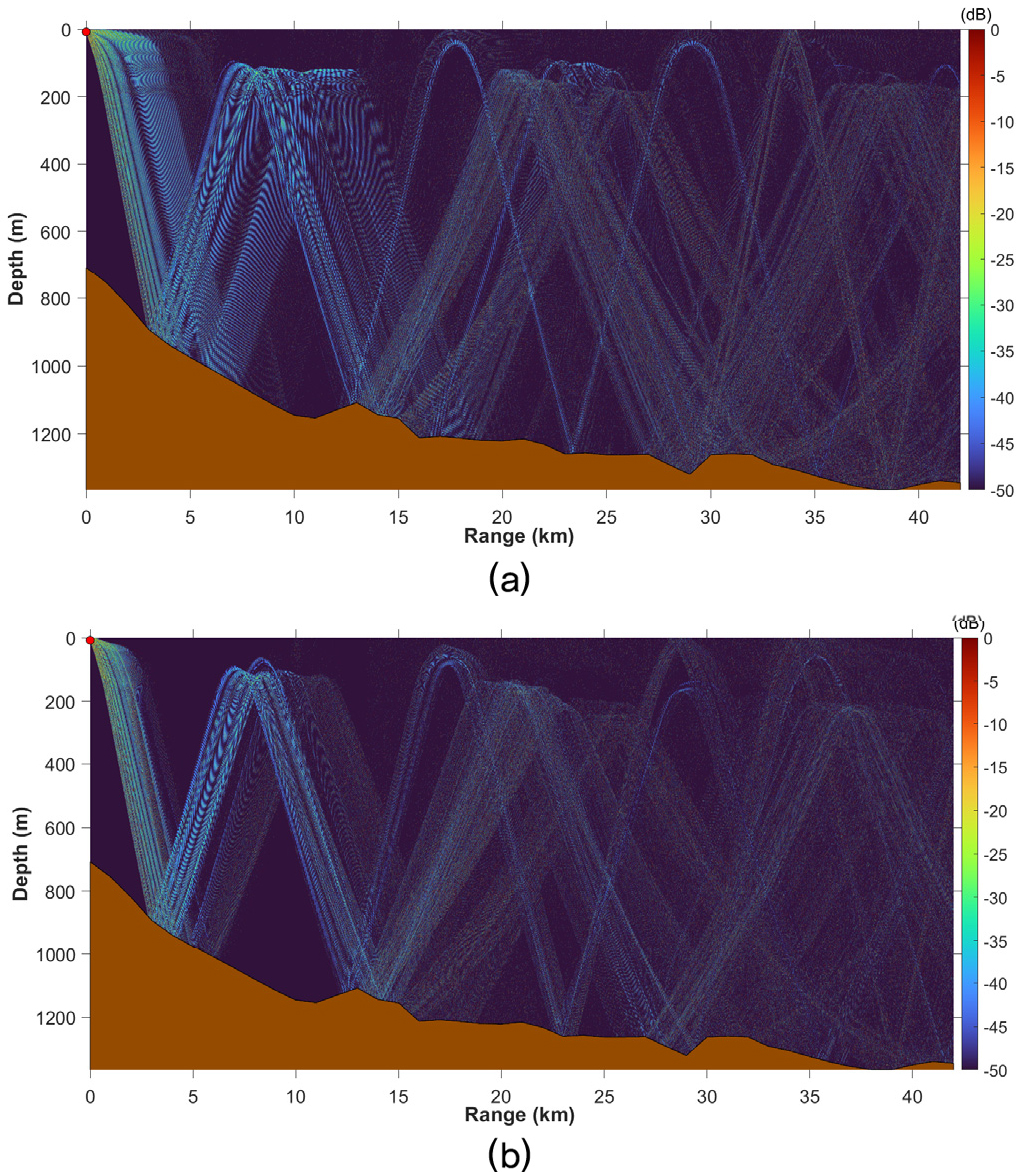
Bellhop 모델링 주파수는 500 Hz, 3.5 kHz, 7 kHz로 설정하였고, 음원 준위, 음원 수심, 주변 잡음 등의 변수는 앞서 언급한 선체고정형소나 수치 실험과 동일한 조건으로 적용하고, 모델링을 수행하였다. Fig. 11(a) 및 Fig. 12(a)는 실제 해상 실험을 통해 거리별로 확보된 음속 구조를 이용하여 계산된 전달 손실 결과를 나타내며, Fig. 11(b) 및 Fig. 12(b)는 기계학습 모델을 통한 예측 음속 구조를 이용하여 계산된 전달 손실을 나타낸다. 해저면/해수면 반사가 발생하는 지점과 수렴 영역 생성 지점을 비교했을 때, 두 경우가 서로 유사하게 나타나는 것을 확인할 수 있다. 음영구역은 총 격자에서 계산된 전달 손실 중 하위 10 %에 해당하는 영역으로 정의하고 정규화 후 비교하였으며, 계산된 음영구역 발생 비율은 Table 3과 같다. 해상 실험 음속 구조를 이용한 계산 결과를 참값이라고 할 때, 주파수를 고려하지 않은 경우 수심이 깊어질수록 오차 발생 비율이 증가하는 경향이 있다. 이는 기계학습에 사용된 데이터인 ARGO 플로트 및 정선 해양관측 정점 데이터가 주로 수심이 얕은 지점과 수심 500 m 이하에서 산포가 집중되어 있기 때문으로 판단된다. 또한 같은 수심에서 주파수가 높아질수록 오차 발생 비율이 증가하는 경향이 있지만, 수심과 비교하면 그 영향은 상대적으로 크지 않다. 월별 평균 음속 구조를 이용한 음영구역 계산 결과는 해상 실험 음속 구조를 이용한 결과와 큰 차이를 보인다. 이는 월별 평균 음속 구조가 특정 년도나 월의 특징을 반영하지 못하고, 측정되지 않은 수심에 대한 값들은 보간을 통해 산출되어 누적된 오차를 발생시킨 것으로 보인다. 이는 기계학습을 이용한 전달 손실 계산이 월별 평균 음속 구조를 이용한 계산보다 신뢰성이 더 높다는 것을 나타낸다.

Fig. 11.

(Color available online) Transmission loss for 500 Hz source. (a) sea experimental SSP, (b) predicted (machine learning) SSP.

Fig. 12.

(Color available online) Transmission loss for 7 kHz source. (a) sea experimental SSP, (b) predicted (machine learning) SSP.

선체고정형소나 해상 시운전 표적의 운용 수심이 300 m 이하인 점을 고려할 때, 해당 수심 범위에서는 오차가 크지 않으므로 기계학습 모델을 이용한 탐지 성능 예측 결과는 타당하며, 해상 시운전 수행 방법으로 활용 가능하다. 앞서 분석한 결과를 통해 제안하는 최종적인 선체고정형소나 해상 시운전 세부 수행 방안은 Table 4와 같다. 또한 누적탐지거리(Cumulative Detection Range, CDR)를 최대탐지거리(Max Detection Range, MDR)로 나눈 값으로 나타낼 수 있는 탐지 성능 예측을 위한 지표인 탐지 가능성(Detection Probability, DP)을 계산할 수 있는데 이러한 탐지 가능성을 통해 수중 표적에 대한 탐지 성능 정도를 예측하는데 활용할 수 있다.^[14,15]

결과적으로 제안하는 선체고정형소나 시운전 절차는 다음과 같이 요약할 수 있다. Table 4에서 제시한 조건에 부합하는 해상 시운전 구역을 선정하고, 위도, 경도 및 해상 시운전 수행 시점 정보를 기계학습 산출 모델에 입력한다. 다음으로 학습 모델을 통해 예측된 거리별 음속 구조를 사용하여 신호 초과량, 누적탐지거리 및 탐지 가능성을 모델링을 통해 계산하고, 상기 계산값을 활용하여 해상 시운전 거리 설정에 참고값으로 활용한다.

V. 결 론

건조 중인 선박의 선체고정형소나의 탐지 거리, 방위 정확도, 경보 기능과 같은 주요 성능 확인 과정을 포함한 해상 시운전 절차는 수중 환경 정보가 고려된 세부 수행 방안이 제시되지 않은 실정이다. 본 논문은 효율적이고 신뢰할 수 있는 선체고정형소나 해상 시운전 수행을 위한 방법으로 해상 시운전 구역 내의 해저 지형 선택, 선체고정형소나와 표적함의 배치, 음파 전송 방향 설정, 빔 조향각 설정 조건을 제시하였다.

더불어, 계절적 요인이 반영된 탐지 성능 변동성을 고려한 해상 시운전 세부 수행 방안을 제시하였다. 이 절차에는 ARGO 플로트 및 정선 해양관측 정점 데이터를 통한 기계학습 기반의 예측 음속 구조를 도출하고, Bellhop 모델링을 통해 신호 초과량, 누적탐지거리, 탐지 가능성을 계산하여 해상 시운전 시 탐지거리 설정에 활용 가능한 방안을 제시하였다.

동해는 동한난류와 북한한류, 중규모 순환 등으로 인한 시공간 변동성이 매우 크므로^[20,21] 향후, 해상 시운전 구역에서의 수온, 염도에 대한 더 많은 데이터 확보를 통해 음속 구조의 시공간 통계적 변동성을 더욱 충실히 대변할 수 있도록 음속 구조 예측 모델의 신뢰성 향상이 필요하다. 또한 선체고정형소나 성능에 영향을 미칠 수 있는 경계면에서의 반사 및 산란과 잔향 모델링 결과를 포함하고, 염도 예측을 위한 지배 방정식을 물리정보신경망에 반영하여 기계학습 모델을 개선함으로써 보다 현실적이고 신뢰할 수 있는 선체고정형소나의 해상 시운전 활용 방안을 제시할 수 있을 것으로 기대된다.