A study on inversion method of rotating monopole source for estimating the location of propeller singing noise source

Minseuk Park; Keunhwa Lee; Youngmin Choo; Myungsung Koo; Jungmo Jung

doi:10.7776/ASK.2024.43.6.644

Preview

Research Article

The Journal of the Acoustical Society of Korea. 30 November 2024. 644-655
https://doi.org/10.7776/ASK.2024.43.6.644

A study on inversion method of rotating monopole source for estimating the location of propeller singing noise source

프로펠러 명음소음원의 위치 추정을 위한 단극자 회전소음원의 역산 기법

Minseuk Park¹

Keunhwa Lee²^*

Youngmin Choo²

Myungsung Koo¹

Jungmo Jung¹

박 민석¹

이 근화²^*

추 영민²

구 명성¹

정 정모¹

¹국립수산과학원 수산공학과

²세종대학교 국방시스템공학과

^{*Corresponding Author}

License (open-access, http://creativecommons.org/licenses/by-nc/4.0/):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

Singing noise refers to the strong noise phenomenon that occurs when vortices separated from the propeller blades resonate with structures. This noise hinders the comfort of the crew and negatively impacts the marine ecosystem, necessitating effective mitigation measures. However, effective analysis of this noise source is challenging due to the frequency modulation phenomenon of the received signal. In this study, we propose an acoustic signal model for analyzing the singing noise and suggest an inversion technique to estimate the location of noise source, assuming it is of a monopole type. This technique provides a method for analyzing singing noise using only a single hydrophone, making it possible to establish the noise reduction measures during the design and operation stages. The proposed inversion technique using the signal model has been validated through experiments and numerical analysis.

Keywords

Singing noise

Doppler effect

Rotating source

Source localization

명음소음은 프로펠러 날개에서 박리되는 와류가 구조물과 공진하여 발생하는 강한 소음현상이다. 명음소음은 발생 시 선원의 안락성을 저해하고 해양생태계에 악영향을 미치기 때문에 효과적인 저감대책이 필요하나, 수신되는 신호의 주파수 변조현상으로 인해 해당 소음원에 대한 효과적인 분석이 어렵다. 본 연구에서는 명음소음의 위치추정을 위한 음향 신호모델을 제안하였고, 명음소음원을 단극자 소음원으로 가정하고 발생위치를 추정할 수 있는 역산기법을 제안하였다. 해당 기법은 단일 청음기만을 이용한 명음소음 분석 방법을 제공하여 설계 및 운용 단계에서 명음소음 방지대책 수립을 가능하게 한다. 제안된 신호모델을 이용한 역산기법은 실험과 수치해석 분석을 통해 성능의 유효성을 검증하였다.

키워드

명음소음

도플러효과

회전 소음원

위치추정

MAIN

I. 서 론
II. 명음소음의 탐지 및 위치추정
2.1 명음소음원의 기전
2.2 명음소음의 소음원 신호모델
2.3 전달거리 및 지연시간
2.4 명음소음의 수신음장 신호모델
2.5 소음원과 수신신호의 관계
III. 명음소음의 탐지 및 위치추정
3.1 명음소음원의 음향 신호모델
3.2 수신신호를 이용한 명음소음원의 역산
3.3 명음소음원의 위치 추정 기법
IV. 결 과
4.1 수치해석 실험
4.2 소음원 실험
V. 고 찰
5.1 명음소음의 단극자 소음원 가정
5.2 역산기법: 소음원의 단일 위치 추정
5.3 음파모델: 이상적인 유체환경 가정
VI. 결 론

I. 서 론

선박의 프로펠러에서 발생하는 명음소음현상은 일반적으로 프로펠러 끝단의 와류박리(vortex shedding)에 의한 가진 주파수 성분과 프로펠러 구조물의 고유주파수가 일치할 경우 발생하는 공진현상에 의한 것으로 알려져 있다.^[1,2,3] 이러한 명음소음은 프로펠러 운용 중 발생하는 조건이 명확하게 알려져 있지 않기 때문에 선박 설계 및 운용 단계에서 구체적인 사전예방 대책의 수립이 어렵고, 명음소음이 발생하여도 이를 명확히 판단하기 어렵다. 이러한 이유로 명음소음으로 추정되는 소음이 발생할 시 프로펠러 날개 전체를 연삭 가공하는 것이 소음저감을 위한 유일한 해결책으로 알려져 있다.^[4,5,6]

선박의 프로펠러에서 발생하는 소음은 선원의 거주 안락성 저해,^[7] 해양포유류의 생태계 교란,^[8] 어업피해^[9] 등의 문제점을 유발하기 때문에 해당 소음의 저감대책에 대한 연구가 지속적으로 수행되어지고 있다. 다만 명음소음의 경우, 프로펠러에서 발생하는 일반적인 소음(공동소음, 날개두께소음 및 날개하중소음 등)과는 달리 회전하는 프로펠러 날개 자체의 자려진동(self-sustained oscillation)에 의해 발생하는 소음으로, 수신되는 신호는 도플러 효과에 의한 주파수 변조 현상을 포함하게 된다. 주파수 변조현상으로 인해 수신되는 신호는 소음원의 신호와 상이한 특성을 가지게 되어, 수신신호의 분석을 통한 명음소음 발생여부 및 발생위치의 명확한 추정을 어렵게 만든다. 최근 빔형성기법을 이용하여 모형 프로펠러에서 발생하는 명음소음원의 위치를 추정한 연구 결과가 있었으나, 주파수 변조현상에 대한 고려가 없어 낮은 해상도의 위치추정 결과를 보여주었다.^[10]

해외 연구에서는 회전하는 소음원의 위치 추정을 위해, 주파수 변조현상을 고려한 빔형성 기반의 위치추정 기법들이 연구되었다.^[11,12,13] 해당 기법들은 다수의 청음기배열을 이용해 신호를 수집하여, 신호 변조에 강인하고 고해상도의 위치 추정 결과를 보여주었다. 다만, 해당기법들은 청음기배열이 회전체 정면에 배치되어 매질의 유동에 의한 잡음에 취약하고 수중에서 운용이 어려운 물리적 크기를 가지고 있어, 선박 프로펠러의 명음소음 위치추정 문제에 적용하기에는 어려움이 있다.

본 연구에서는 명음소음의 발생위치를 추정하기 위한 음향 신호모델과 소음원의 역산기법을 제안하였다. 제안된 기법은 단극자 소음원으로 단순화된 명음소음원이 회전 시 발생하는 수신신호의 왜곡을 정량화 하였고, 역산(inversion)을 통한 주파수 역변조를 수행하여 명음소음원의 발생위치를 추정할 수 있게 고안되었다. 역산기법은 역산된 소음원의 정현파와의 유사도에 대한 모호평면을 제공하고, 이 중 가장 유사도가 높은 하나의 지점을 명음소음원의 초기 위치로 추정할 수 있다. 제안된 기법은 하나의 수중청음기로부터 수신된 음향신호를 이용하여 역산을 수행할 수 있으며, 모의 데이터와 회전소음원 실험데이터를 이용하여 추정성능의 유효성을 검증하였다.

II. 명음소음의 탐지 및 위치추정

2.1 명음소음원의 기전

일반적으로 명음소음은 유동박리에 의해 발생하는 소음으로, Eq. (1)의 무차원수인 Strouhal Number (St)의 영향을 받는 것으로 알려져 있다.^[1]

(1)

St = \frac{f_{s} \times d}{ν},

여기서 $f_{s}$ 는 와류박리 주파수, $d$ 는 프로펠러trailing edge의 유효직경, 그리고 𝜈는 유체의 유속을 의미한다.

일반적으로 프로펠러 반류의 세기는 불균일한 분포를 가지기 때문에, 유속 𝜈는 프로펠러 회전반경 내 위치에 따라 변동성을 가진다. 따라서 구조물의 공진은 날개가 특정 반류장을 통과할 때만 발생하게 되나,^[1] 본 연구에서는 음향 신호모델의 단순화를 위해 균일한 유속 𝜈를 가정하였다. 또한, 소음원의 모델링에 와류박리 주파수성분 $f_{s}$ 를 가지는 단극자를 이용하였고, 매질의 유동에 의한 음장(wave)의 왜곡은 발생하지 않는다고 가정하였다.

2.2 명음소음의 소음원 신호모델

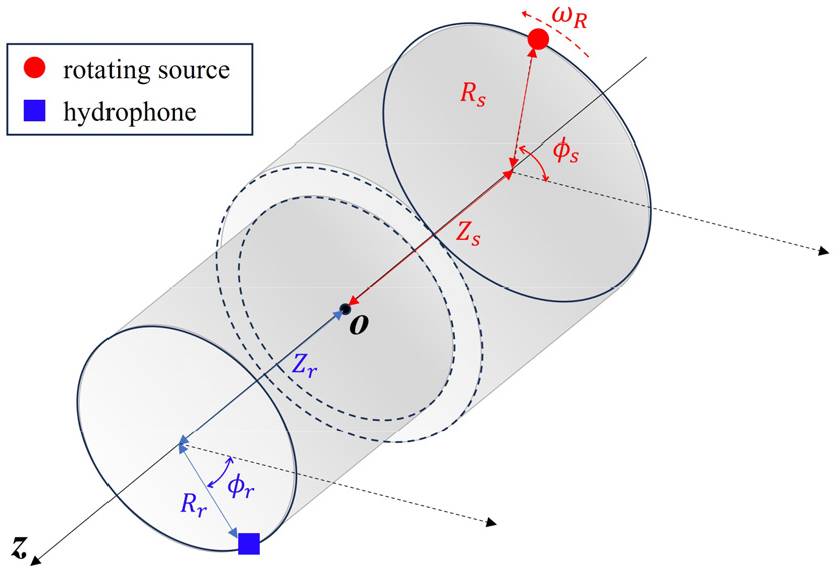
회전하는 단극자 소음원과 수중청음기의 상대적인 거리를 계산하기 위해 Fig. 1의 원통형 좌표계를 사용하였다. 원통형 좌표계에서 z-축과 프로펠러의 회전축은 서로 일치하게 설정하였으며, 단극자 소음원이 z-축을 중심으로 일정한 반경 $R$ 과 각속도 $ω_{R}$ 로 회전하는 상황을 가정하였다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430607/images/ASK_43_06_07_F1.jpg

Fig. 1.

(Color available online) Cylindrical coordinates for the rotating system, showing the rotating source (red circular dot) and a hydrophone (blue square dot).

해당 좌표계에서 단극자 소음원의 초기 위치는 $(Z_{s}, R_{s}, ϕ_{s})$ , 수중청음기의 위치는 $(Z_{r}, R_{r}, ϕ_{r})$ 로 각각 정의하였다. 또한 단극자 소음원의 회전에 따른 전달거리 변화를 계산하기 위해 단극자 소음원과 수중청음기에서의 시간 매개변수를 $t_{q}$ 와 $t_{r}$ 로 각각 다르게 정의하였다. 와류박리 주파수를 $f_{s}$ 라고 하면, 소음원 영역의 시간 $t_{q}$ 에 따른 단극자 소음원의 신호 $s (t_{q})$ 는 Eq. (2)의 정현파 함수로 정의된다.

(2)

s (t_{q}) = A \cdot c o s (2 π f_{s} t_{q} + θ_{s}),

여기서 $A, f_{s}, θ_{s}$ 는 각각 소음원의 진폭, 주파수, 그리고 초기위상을 의미한다(이때, $ϕ_{s}$ 는 소음원의 공간적 초기 위치, $θ_{s}$ 는 정현파 신호의 초기 위상을 의미).

2.3 전달거리 및 지연시간

소음원에서 수중청음기까지 음장의 전달거리를 나타내는 $r$ 은 소음원의 회전으로 인해 시간 $t_{q}$ 에 따라 Eq. (3)의 수식으로 표현된다.^[14]

(3)

r (t_{q}) = [(- Z_{r})^{2} + (R_{s})^{2} + (R_{r})^{2} - 2 R_{s} R_{r} \cos (ω_{R} t_{q} + ϕ_{s} - ϕ_{r})]^{1 / 2} .

$c$ 를 매질의 음속이라고 하면, 전달거리 $r (t_{q})$ 를 음파가 이동하는데 걸리는 시간 $τ (t_{q})$ 는 Eq. (4)와 같다.

(4)

τ (t_{q}) = r (t_{q}) / c .

전달거리에 따른 음장의 전달시간 $τ (t_{q})$ 를 본 논문에서는 지연시간(retarded time)으로 표기하였다. 지연시간은 소음원의 회전주파수인 $f_{R}$ 에 따라 주기적으로 변화하게 되고, 이에 따라 소음원의 신호 $s (t_{q})$ 는 도플러 효과에 의해 시간영역 및 주파수영역에서 변조된 신호가 수중청음기로 전달되게 된다.

2.4 명음소음의 수신음장 신호모델

소음원의 시계열 신호를 $s (t_{q})$ , 해당 소음원 신호가 수중청음기에서 수신되는 시계열 신호를 $p (t_{r})$ 라고 하자. 여기서 소음원 신호의 시간 $t_{q}$ 는 균일간격 $d t$ 를 가지는 $L$ 개의 요소로 구성된 이산시간 샘플(discrete time sample)로 가정하며, 각 요소들에 대응되는 지연시간들을 $τ (t_{q})$ 로 정의한다. 지연시간의 정의 Eq. (4)에 의해 $t_{q}$ 와 $t_{r}$ 은 Eq. (5) 로 표현할 수 있으며,

(5)

t_{q} = [0, d t, \dots, (L - 1) d t], t_{r} = t_{q} + [τ (t_{q, 1}), \dots, τ (t_{q, L})],

이때 수중청음기 신호의 시간 $t_{r}$ 은 불균일한 간격을 가지게 되며, $t_{q, l}$ 은 시간 $t_{q}$ 의 $l$ 번째 요소를 의미한다.

근거리음장영역에서 소음원이 구면파를 발산하는 상황을 가정한다면, 명음소음원에 의한 수신신호 $p (t_{r})$ 는 Eq. (6)과 같다.

(6)

p (t_{r}) = p (t_{q} + τ (t_{q})) = s (t_{q}) / 4 π r (t_{q}) .

Polett와 Teal^[14]에 의하면 회전하는 단극자 소음원의 수신신호는 Eq. (7)의 변조함수의 형태로 표현할 수 있으며,

(7)

p (t_{r}) = \cos (2 π f_{s} t_{r} + θ_{s}) \cdot \sum_{k = - \infty}^{\infty} A_{k} \cos (2 π f_{R} k t_{r} + θ_{R}^{(k)}),

Eq. (7) 우변 좌측의 carrier function과 우측의 modulation function의 조합으로 표현되어진다. 여기서 $f_{R}$ 은 프로펠러 회전주파수, $A_{k}$ 와 $θ_{R}^{(k)}$ 는 각 modulation function의 진폭과 초기위상을 의미한다. 따라서, 수신신호는 진폭 $A_{k}$ 와 주파수 $f_{s} + f_{R} k$ 를 가지는 여러 개의 정현파 성분들로 표현되어진다.

2.5 소음원과 수신신호의 관계

회전하는 소음원의 신호와 수신되는 신호의 특성을 분석하기 위해, Table 1의 음향인자들을 이용한 시뮬레이션 분석을 수행하였다.

Table 1.

Acoustic parameters for the singing noise model.

Parameters	Value
Central frequency ( $f_{s}$ )	1.8 kHz
Source No. ( $N$ )	1
Source amplitude ( $A$ )	1
Source initial phase ( $θ_{s}$ )	0°
Rotating speed ( $f_{R}$ )	500 RPS
Initial phase ( $θ_{s}^{(i)}$ )	0𝜋
Initial source location ( $Z_{s}, R_{s}, ϕ_{s}$ )	$(0.0 m, 0.2 m, \frac{1}{2} π)$
Hydrophone location ( $Z_{r}, R_{r}, ϕ_{r}$ )	$(0.2 m, 0.3 m, \frac{1}{2} π)$

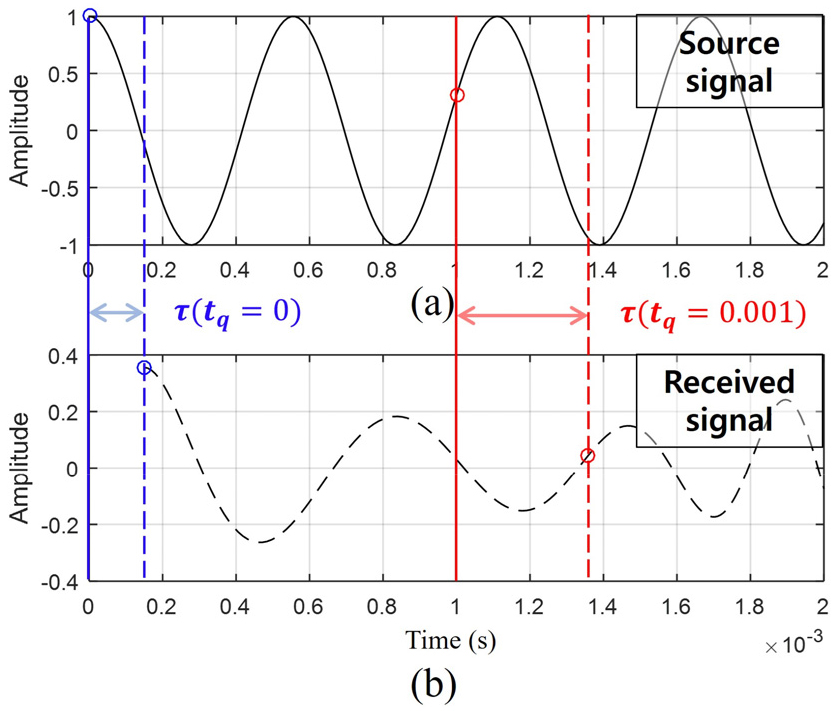
Fig. 2는 시계열 영역에서 모의된 소음원의 신호 $s (t_{q})$ 와 수신신호 $p (t_{r})$ 를 나타낸다. 신호 모의에는 진폭 A = 1의 값을 가지는 단극자 소음원 N = 1개를 사용하였고, 도플러 효과에 의한 명확한 변조현상을 관측하기 위해 일반적인 선박 운용상황에서의 프로펠러보다 훨씬 빠른 500 RPS로 회전하는 상황을 가정하였으며, 청음기를 프로펠러 끝단과 인접한 $(Z_{s}, R_{s}, ϕ_{s}) = (0.45 m, 0.40 m, 0.5 π)$ 위치에 설치하여 시간에 따른 전달거리의 변화가 크게 발생하게 하였다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430607/images/ASK_43_06_07_F2.jpg

Fig. 2.

(Color available online) Synthetic time signal: (a) source signal ( $t_{q}$ =[0 ms, 1 ms] are marked with 2 lines), (b) received signal from the rotating source (retarded times for $t_{q}$ =[0 ms, 1 ms] are marked as $τ (t_{q} = 0 m s)$ and $τ (t_{q} = 1 m s)$ with dashed lines.

Fig. 2(a)의 소음원 신호 $s (t_{q})$ 는 일정한 지연시간 $τ (t_{q})$ 이 지난 후 Fig. 2(b)의 $p (t_{r})$ 로 수신되게 되며, 이산시간 $t_{r}$ 과 신호의 진폭은 도플러 효과에 의해 주기적으로 변화하게 된다. 지연시간 $τ (t_{q})$ 를 예로 들면, $t_{q} = 0 m s$ 에서 소음원은 $ϕ_{s} = ϕ_{r}$ 에 위치하여 거리에 따른 지연시간 $r (t_{q}) / c = \sqrt{(0.2)^{2} + (0.3 - 0.2)^{2}} / c \approx 0.15 m s$ 가 발생하는데 반해, $t_{q} = 1 m s$ 에서 소음원은 $ϕ_{s} = - ϕ_{r}$ 에 위치하여 거리에 따른 지연시간이 $r (t_{q}) / c = \sqrt{(0.2)^{2} + (0.3 + 0.2)^{2}} / c \approx 0.54 m s$ 가 발생하게 된다.

Fig. 3은 모의된 주파수영역의 신호를 나타낸다. Fig. 3(a)는 소음원의 스펙트럼 $S (f)$ 를 나타내며, 중심주파수( $f_{s}$ =1.8 kHz)에서 하나의 peak 성분을 확인할 수 있다. 반면, Fig. 3(b)의 수신신호 스펙트럼 $P (f)$ 는 도플러 효과에 의해 변조되어 중심주파수( $f_{s}$ =1.8 kHz)성분과 주변으로 500 Hz의 일정한 간격으로 side peak 성분들이 동시에 발생함을 알 수 있다. Side peaks의 간격은 회전속도 $f_{R}$ =500 RPS에 대응되는 값이며, Eq. (7) 변조함수를 따르는 형태임을 확인할 수 있다.^[14]

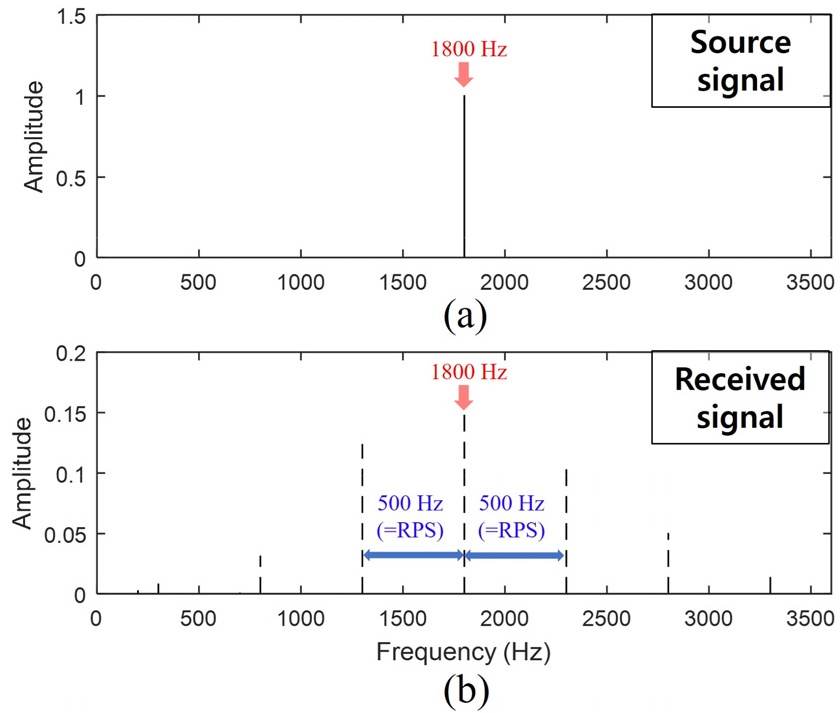
https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430607/images/ASK_43_06_07_F3.jpg

Fig. 3.

(Color available online) Spectrums for the synthetic signal: (a) Spectral signal $S (f)$ for monopole noise source involving 1-peak component ( $f_{s}$ =1.8 kHz), (b) received spectral signal $P (f)$ from the rotating source involving 1 central component ( $f_{s}$ =1.8 kHz) and several side peaks with the interval of 500 Hz. The spectrum was acquired through non-uniform fast Fourier transform.

III. 명음소음의 탐지 및 위치추정

일반적으로 수중청음기에 수신된 샘플들은 균일한 시간간격을 가지기 때문에, 본 장에서는 $t_{r}$ 이 균일간격을 가지는 경우 명음소음원을 역산할 수 있는 기법을 기술하였고, 가상소음원을 이용한 역산 결과를 이용하여 명음소음원의 발생위치를 추정할 수 있는 방법에 대해 기술하였다.

3.1 명음소음원의 음향 신호모델

수중청음기의 수신신호가 $p (t_{r})$ 라고 할 때, 명음소음원의 신호 $s (t_{q})$ 는 Eqs. (3), (4), (5)를 이용해 아래의 Eq. (8)로 유도될 수 있다.

(8)

s (t_{q}) = \frac{4 π \cdot τ (t_{q})}{c} \cdot p (t_{q} + τ (t_{q})),

여기서 Eq. (8)의 우변항의 미지수는 $τ (t_{q})$ 이고, Eqs. (3)과 (4)에 의해 초기 소음원의 위치인 $(Z_{s}, R_{s}, ϕ_{s})$ 를 매개변수로 가진다. 프로펠러 회전 중심축을 $Z$ =0에 놓는다면 지연시간 $τ (t_{q})$ 는 소음원의 초기위치 중 $R_{s}$ 와 $ϕ_{s}$ 에 의해 결정되므로, 지연시간은 $τ (t_{q}, R_{s}, ϕ_{s})$ 로 표현할 수 있다. 따라서, 프로펠러 회전반경 내 가상 소음원이 $(0, R_{s}, ϕ_{s})$ 위치에 존재한다고 가정하면, Eq. (8)을 이용해 수신신호로부터 소음원신호 $s (t_{q})$ 를 역산해낼 수 있다.

3.2 수신신호를 이용한 명음소음원의 역산

2.2 ~ 2.4장에서는 불균일 시간 $t_{r}$ 에 샘플링 되는 수신신호 $p (t_{r})$ 에 관한 음향 신호모델을 기술하였다. 하지만 일반적으로 우리가 얻게 되는 수신신호는 균일한 샘플링 지점에서 획득하기 때문에, 균일간격으로 샘플링 된 수신신호 $p (t_{r})$ 를 이용한 소음원의 시계열 신호 $s (t_{q})$ 를 역산하는 방법이 필요하다.

소음원으로부터 수신되는 신호가 $p (t_{r}^{'})$ 이고, $(t_{r}^{'})$ 은 $t_{r}^{'} = [0, d t, \dots, (L - 1) d t]$ 를 만족하는 균일한 샘플 지점이라고 가정하자. Eq. (6)에 의해 $t_{r}^{'} = t_{q}^{'} + τ (t_{q}^{'})$ 를 만족하여야 하며, 여기서 $(t_{q}^{'})$ 는 소음원의 불균일한 간격을 가지는 시간이 된다. $(t_{r}^{'})$ 에 대응되는 시간 $(t_{q}^{'})$ 는 Eq. (9)의 이차방정식 풀이를 통해 값을 계산할 수 있다.^[14]

(9)

c^{2} (t_{r}^{'} - t_{q}^{'})^{2} - (- Z_{r})^{2} + (R_{s})^{2} + (R_{r})^{2} - 2 R_{s}^{(i)} R_{r} \cos (ω_{R} t_{q}^{'} + ϕ_{s} - ϕ_{r}) = 0 .

하지만 샘플의 개수가 많을 경우, Eq. (9)의 풀이에 지나친 시간이 소요되고 소음원 신호 역산에 추가적인 신호처리 과정이 필요하기 때문에, 본 연구에서는 시계열 신호의 리샘플링^[15]을 통해 직접적으로 $t_{q} = [0, d t, \dots, (L - 1) d t]$ 에 대응되는 소음원의 신호 $s (t_{q})$ 를 역산하고자 한다.

우선, 임의의 가상 소음원의 위치 $(0, R_{s}, ϕ_{s})$ 를 정하여 Eqs. (3)과 (4)에 의해 $τ (t_{q})$ 를 계산한 뒤, 수신된 균일 이산신호로부터 다음의 값을 구한다.

(10)

p (t_{q} + τ (t_{q})) \approx L_{n} (p (t_{r}^{'})),

여기서 $L_{n}$ 은 리샘플링 연산자로 사용되었으며, Eq. (10)은 $(t_{r}^{'})$ 에서 샘플링된 수신신호를 $t_{q} + τ (t_{q})$ 의 시간으로 리샘플링함을 의미한다. 지연시간 $τ (t_{q})$ 는 3.1장에 언급한 것과 같이 초기 소음원의 위치 $R_{s}$ 와 $ϕ_{s}$ 에 관한 함수 $τ (t_{q}) = τ (t_{q}, R_{s}, ϕ_{s})$ 이므로, Eq. (6)은 Eq. (11)로 표현할 수 있다.

(11)

s (t_{q}, R_{s}, ϕ_{s}) = \frac{4 π \cdot τ (t_{q}, R_{s}, ϕ_{s})}{c} \cdot p (t_{q} + τ (t_{q}, R_{s}, ϕ_{s})) .

Eq. (11) 우변의 좌측항은 Eqs. (3)과 (4)에 의해, 우측항은 Eq. (10)에 의해 얻을 수 있으며, 균일하게 샘플링된 수신신호에서 임의로 정한 초기소음원의 위치 $R_{s}$ 와 $ϕ_{s}$ 에 의해 명음소음의 소음신호를 역산함을 의미한다.

정리하면, 수신신호로부터 명음소음원 신호 $s (t_{q})$ 의 역산은 다음의 순서로 이루어진다.

1) 균등 이산시간 $(t_{r}^{'})$ 에서 수신신호 $p (t_{r}^{'})$ 를 계측[Fig. 4(a)]

2) 초기 소음원의 위치 $(0, R_{s}, ϕ_{s})$ 에 대한 지연시간 $τ (t_{q}, R_{s}, ϕ_{s})$ 를 계산

3) 수신신호 $p (t_{r}^{'})$ 를 $t_{q} + τ (t_{q}, R_{s}, ϕ_{s})$ 에서 리샘플링 한 $p (t_{q} + τ (t_{q}))$ 신호를 생성[Fig. 4(b)]

4) $τ (t_{q}, R_{s}, ϕ_{s})$ 및 $p (t_{q} + τ (t_{q}))$ 를 Eq. (11)에 대입하여 소음원의 신호 $s (t_{q}, R_{s}, ϕ_{s})$ 를 역산[Fig. 4(c)]

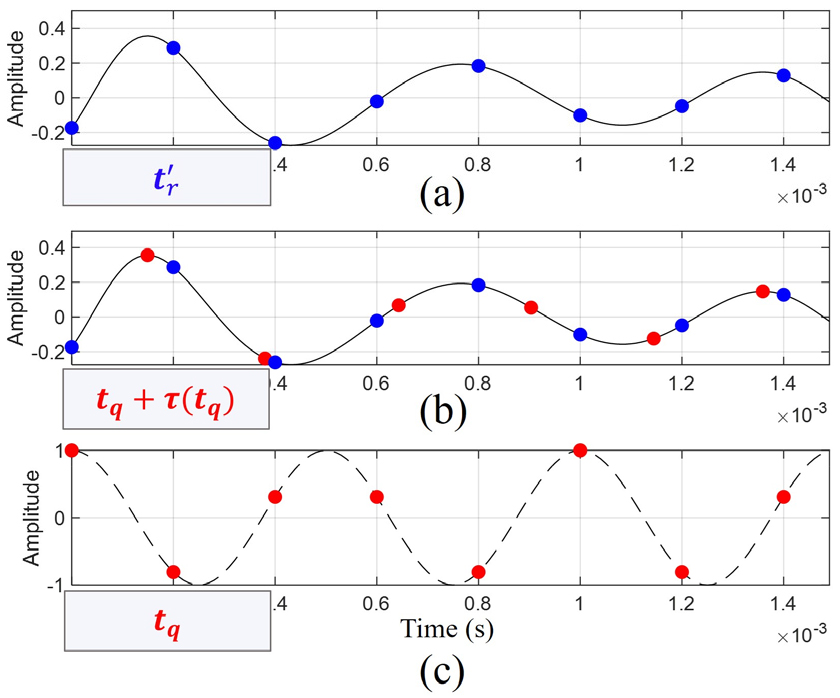
https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430607/images/ASK_43_06_07_F4.jpg

Fig. 4.

(Color available online) Resampling method for obtaining the inversely calculated source signal: (a) Measuring the uniform samples using the hydrophone (marked with blue dots), (b) calculating the $τ (t_{q})$ with initial source position { $R_{s}, ϕ_{s}$ } and resampling the signal at $t_{q} + τ (t_{q}, R_{s}, ϕ_{s})$ to obtain $p (t_{q} + τ (t_{q}))$ (marked with red dots), (c) calculating the $s (t_{q}, R_{s}, ϕ_{s})$ (marked with red dots).

3.3 명음소음원의 위치 추정 기법

회전하는 단극자 소음원은 도플러 효과에 의해 Fig. 3(b)와 같은 주파수신호의 변조가 발생한다. 수신신호에서 Eq. (11)과 실제 초기 소음원의 위치 매개변수 $R_{s}$ 와 $ϕ_{s}$ 를 이용해 소음원신호 $s (t_{q}, R_{s}, ϕ_{s})$ 를 역산한 경우, 역산된 소음원의 신호는 단극자 소음원과 유사한 정현파 스펙트럼을 가지게 된다. 따라서, 탐색공간 내에 다수의 가상소음원을 골고루 분포시킨 뒤 각 가상소음원에 대해 역산을 수행하면, 정현파의 형태와 가장 유사한 $s (t_{q}, R_{s}, ϕ_{s})$ 신호를 찾을 수 있다. 이 신호의 소음원을 판단할 수 있다면 실제 소음원의 발생위치를 추정할 수 있다. 즉, 소음원의 신호모델 Eq. (2)와 유사한 역산신호가 존재한다면, 명음소음이 발생하였고 해당 역산 위치를 소음원의 위치로 추정할 수 있다.

본 연구에서는 역산된 소음원의 주파수 스펙트럼이 정현파에 가까울 수록 소음원 모델과 유사한 것으로 가정하였다. 분석을 위해 역산된 소음원의 신호 $s (t_{q}, R_{s}, ϕ_{s})$ 는 푸리에 변환을 통해 Eq. (12)의 주파수 신호로 정의하였고,

(12)

S (f, R_{s}, ϕ_{s}) = F {s (t_{q}, R_{s}, ϕ_{s})},

$f$ 는 주파수 요소를 의미한다. 중심주파수에 신호의 에너지가 집중되어 있고, side peaks의 에너지가 작을수록 소음원 신호인 정현파에 가깝다고 판단할 수 있다. 따라서, 정현파 특성을 정량화 하기 위해 Eq. (13)의 목적함수를 정의하였다.

(13)

E (R_{s}, ϕ_{s}) = [S (f^{(l_{\max})}, R_{s}, ϕ_{s})]^{2} - \sum_{l = 1, l \neq l_{\max}}^{L} [S (f^{(l)}, R_{s}, ϕ_{s})]^{2},

여기서 $f^{(l)}$ 은 주파수 요소 $f$ 의 $l$ 번째 성분을, $f^{(l_{\max})}$ 는 가장 큰 주파수 성분을 의미한다. Eq. (13)의 목적함수는 중심주파수 대역에 에너지가 집중되어 있을수록 더욱 큰 값을 가지게 되며, 자체적으로 $(R_{s}, ϕ_{s})$ 에 대한 모호평면이 된다. 마지막으로, 각 가상소음원들의 $E (R_{s}, ϕ_{s})$ 값을 Eq. (14)에 대입하여 명음소음원의 초기위치인 ${{\bar{R}}_{s}, {\bar{ϕ}}_{s}}$ 를 판단할 수 있다.

(14)

{{\bar{R}}_{s}, {\bar{ϕ}}_{s}} = \underset{R_{s}, ϕ_{s}}{argmax} E (R_{s}, ϕ_{s}) .

${{\bar{R}}_{s}, {\bar{ϕ}}_{s}}$ 는 초기위치 $(R_{s}, ϕ_{s})$ 로 설정한 가상소음원들의 집합 중 가장 강한 정현파 특성을 가진 소음원으로 역산되는 위치를 의미하며, 여기서 초기위치는 $t_{r}^{'} = t_{q} + τ (t_{q}) = 0$ 을 만족하는 시간 $t_{q}$ 에서의 소음원의 위치를 의미한다. 가상소음원들은 이산 탐색공간에 균등하게 배치하여 초기위치 $(R_{s}, ϕ_{s})$ 를 설정한 뒤 역산을 수행한다.

정리하면, 명음소음원의 위치추정은 다음의 순서로 이루어진다.

1) 프로펠러 회전 단면에 균일한 간격으로 가상소음원을 생성하고 각 위치의 $(R_{s}, ϕ_{s})$ 를 통해 $s (t_{q}, R_{s}, ϕ_{s})$ 를 계산

2) Eqs. (12)와 (13)을 통해 각 가상소음원의 $S (f, R_{s}, ϕ_{s})$ 와 $E (R_{s}, ϕ_{s})$ 를 계산

3) Eq. (14)를 통해 $E (R_{s}, ϕ_{s})$ 가 최대가 되는 ${{\bar{R}}_{s}, {\bar{ϕ}}_{s}}$ 의 위치를 추정

IV. 결 과

본 장에서는 수치해석 및 소음원 실험결과 분석을 통해 제안된 기법의 성능을 검증하였다. 수치해석 및 실험에는 Table 2의 음향인자 값들이 활용되었다.

Table 2.

Acoustic parameters for the synthetic and experimental tests.

Parameters	Value
Central frequency	2982 Hz
Source No. ( $N$ )	1
Source amplitude ( $A$ )	1
Source initial phase ( $θ_{s}$ )	0°
Rotating speed	11.13 RPS
Sampling rate	48 kHz
Initial source location $(Z_{s}, R_{s}, ϕ_{s})$	$(0.0 m, 0.13 m, 0.0 π)$
Hydrophone location $(Z_{r}, R_{r}, ϕ_{r})$	$(0.45 m, 0.40 m, 0.5 π)$

여기서 역산을 수행할 탐색 공간은 프로펠러 회전단면에 해당하는 $R_{s} = [0 : 0.01 : 0.2] m$ , $ϕ_{s} = [0 : 10 : 360] °$ 로 설정하였고, 청음기는 유동소음의 영향이 적으면서 소음원으로부터 근거리에 위치한 지점을 선정하였다.

4.1 수치해석 실험

실험에 앞서 제안된 기법의 추정 성능을 검증하기 위해, 회전하는 단극자 소음원에 대한 모의실험 결과를 분석하였다. Table 2에 주어진 음향인자에 대한 모의신호를 생성한 뒤, 백색 가우시안 잡음(white Gaussian noise)을 중첩시켜 청음기에 신호 대 잡음비(Signal-to-Noise Ratio, SNR) 10 dB의 신호를 수신되게 생성하였다. 이후 실험 환경과 유사한 impulse 신호를 모의하여 시계열 신호에 중첩하였다.

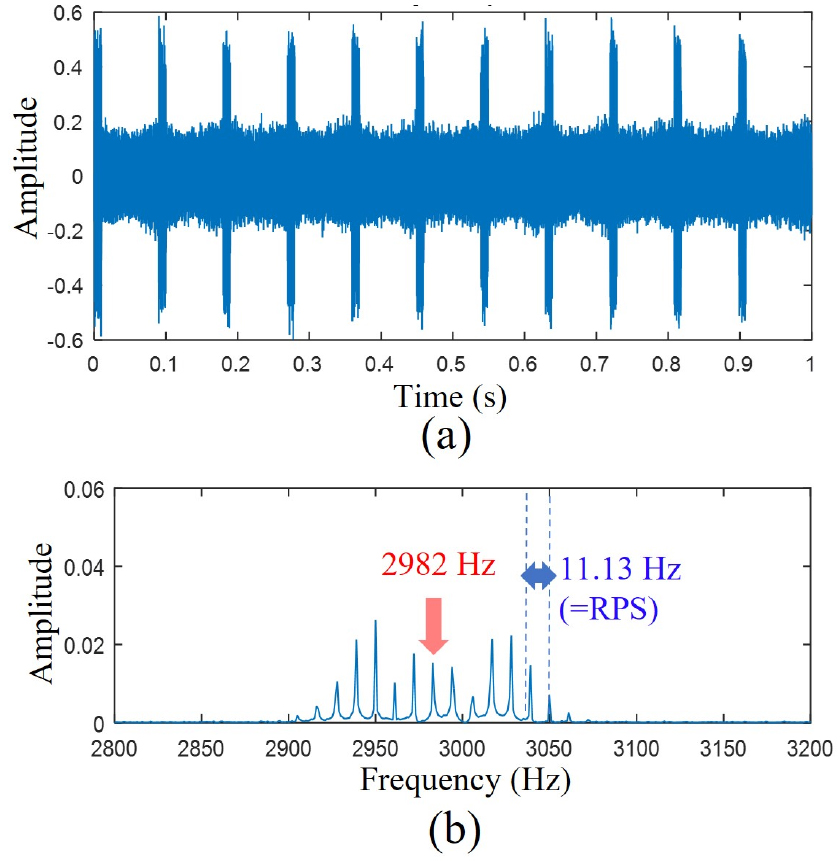
Fig. 5는 수신된 시계열 신호 $p (t_{r}^{'})$ 과 해당신호의 주파수 스펙트럼을 나타낸다. 시간영역에서는 회전에 따라 진폭이 주기적으로 변화하는 특성이 관찰되며[Fig. 5(a)], 스펙트럼상에서 중심주파수 신호인 2,982 Hz 대역의 peak값은 side peaks들에 비해 낮은 값을 가지는 것으로 확인되었다[Fig. 5(b)].

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430607/images/ASK_43_06_07_F5.jpg

Fig. 5.

(Color available online) Simulated signals: (a) time signal, (b) spectrum.

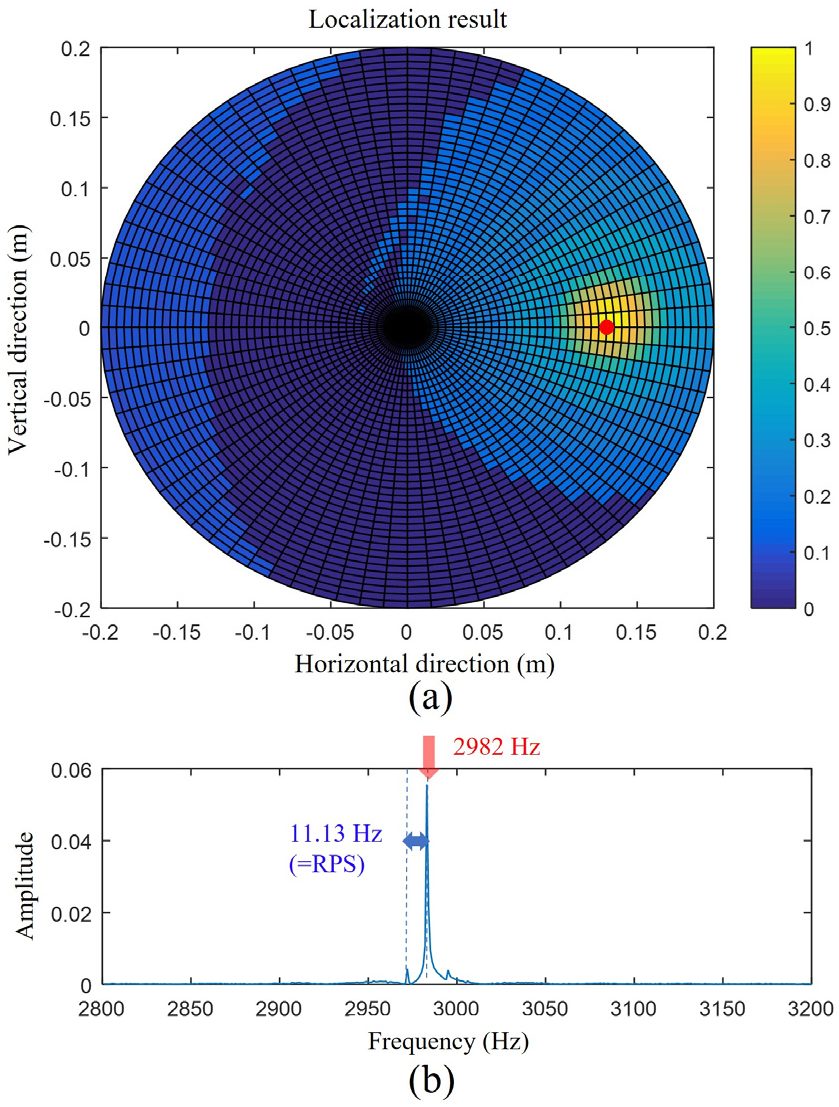
해당 신호를 탐색공간 $R_{s} = [0 : 0.01 : 0.2] m$ , $ϕ_{s}$ =[0:10:360]°에 분포하는 777개의 가상소음원에 대하여 역산을 수행하여 각각의 소음원의 신호를 생성하였으며, Fig. 6은 Eq. (13) 목적함수의 모호평면과 Eq. (14)를 통해 추정한 ${{\bar{R}}_{s}, {\bar{ϕ}}_{s}}$ 위치에서의 스펙트럼 $S (f, {\bar{R}}_{s}, {\bar{ϕ}}_{s})$ 를 나타낸다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430607/images/ASK_43_06_07_F6.jpg

Fig. 6.

(Color available online) Inversion result: (a) Ambiguity surface for $E (R_{s}, ϕ_{s})$ , (b) demodulated spectrum.

Fig. 6(a)는 각 가상소음원들에 대한 목적함수값 $E (R_{s}, ϕ_{s})$ 의 모호평면이다. 여기서 목적함수값이 최대가 되는 가상소음원의 위치는 ${{\bar{R}}_{s}, {\bar{ϕ}}_{s}} = {0.13 m, 0.0 π}$ 였으며, 이는 모의신호에 사용된 실제 소음원의 위치 ${0.13 m, 0.0 π}$ 와 동일하다. Fig. 6(b)는 해당위치에 대한 소음원 역산신호의 스펙트럼이다. 역변조를 통해 생성된 주파수 스펙트럼은 2,982 Hz에 주된 peak 성분이 존재하였으며, 단일 주파수 성분을 가지는 정현파와 유사한 소음원신호가 역산되었다.

따라서, 역산결과를 통해 2,982 Hz 주파수 성분을 가진 회전하는 단극자 소음원이 존재하고 있으며, 소음원의 초기위치는 ${0.13 m, 0.0 π}$ 임을 추정할 수 있다. 또한, 해당 수치해석 실험에서 impulse 신호의 유무는 역산 결과의 품질에 영향을 미치지 않았다.

4.2 소음원 실험

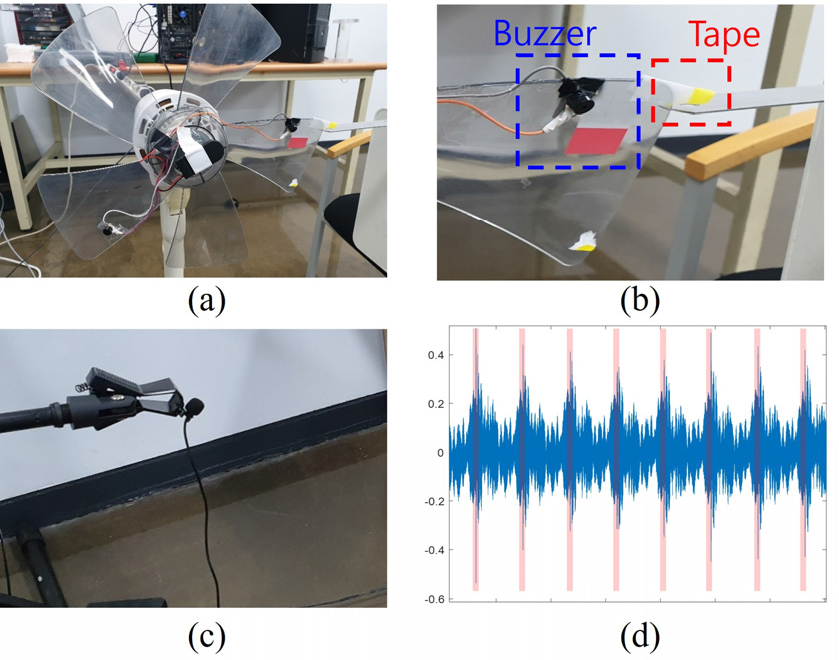
5개의 프로펠러 날개 중 1개의 날개에 소음원(buzzer)을 부착하여 명음소음원을 모의하였고, 1개의 청음기를 $(Z_{s}, R_{s}, ϕ_{s}) = (0.45 m, 0.40 m, 0.5 π)$ 위치에 설치하여 소음원의 신호를 수신하였다. Buzzer가 붙어있는 날개 끝에는 테이프를 부착하였으며, 회전 시 테이프의 충격에 의해 발생하는 impulse 신호를 이용해 수신되는 시계열 신호에서 소음원인 buzzer의 위치를 파악하였다[Fig. 7(d)]. 이때, 테이프에 의해 발생하는 impulse 신호는 소음원의 초기 위치인 $(Z_{s}, R_{s}, ϕ_{s}) = (0.0 m, 0.13 m, 0.0 π)$ 를 지나는 시점을 시계열 신호 상에서 파악할 수 있게 하는 역할을 한다. 실험환경 및 계측된 신호의 개형은 Fig. 7과 같다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430607/images/ASK_43_06_07_F7.jpg

Fig. 7.

(Color available online) Experimental setup for rotating noise source: (a) propeller with 1 attached buzzer, (b) tape attached to the end of the propeller, (c) microphone with sampling rate of 48 kHz, (d) measured time signal with impulsive signal (red bar).

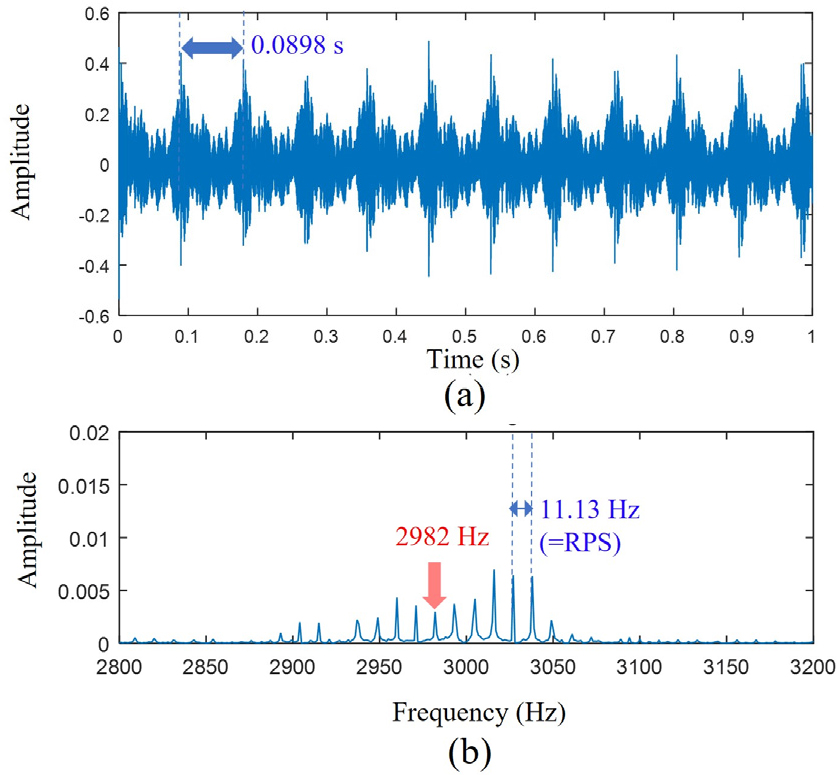
Fig. 8은 실험에서 계측된 시계열 신호와 주파수영역 스펙트럼을 보여준다. 시계열 신호인 Fig. 8(a)는 회전에 의한 주기적인 진폭의 변화가 관측되었으며, 해당 스펙트럼인 Fig. 8(b)에서 중심주파수 대역인 2,982 Hz 신호가 변조현상으로 인해 side peaks에 비해 약한 신호로 관측됨을 확인하였다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430607/images/ASK_43_06_07_F8.jpg

Fig. 8.

(Color available online) Measured signals: (a) time signal, (b) spectrum.

수치해석과 동일한 방법으로, 탐색공간 내의 가상소음원에 대해 수신신호의 역산을 수행하였다. Impulse 신호가 첫번째 샘플에 위치하게 1초의 계측 데이터를 잘라내어 역산에 사용하였다.

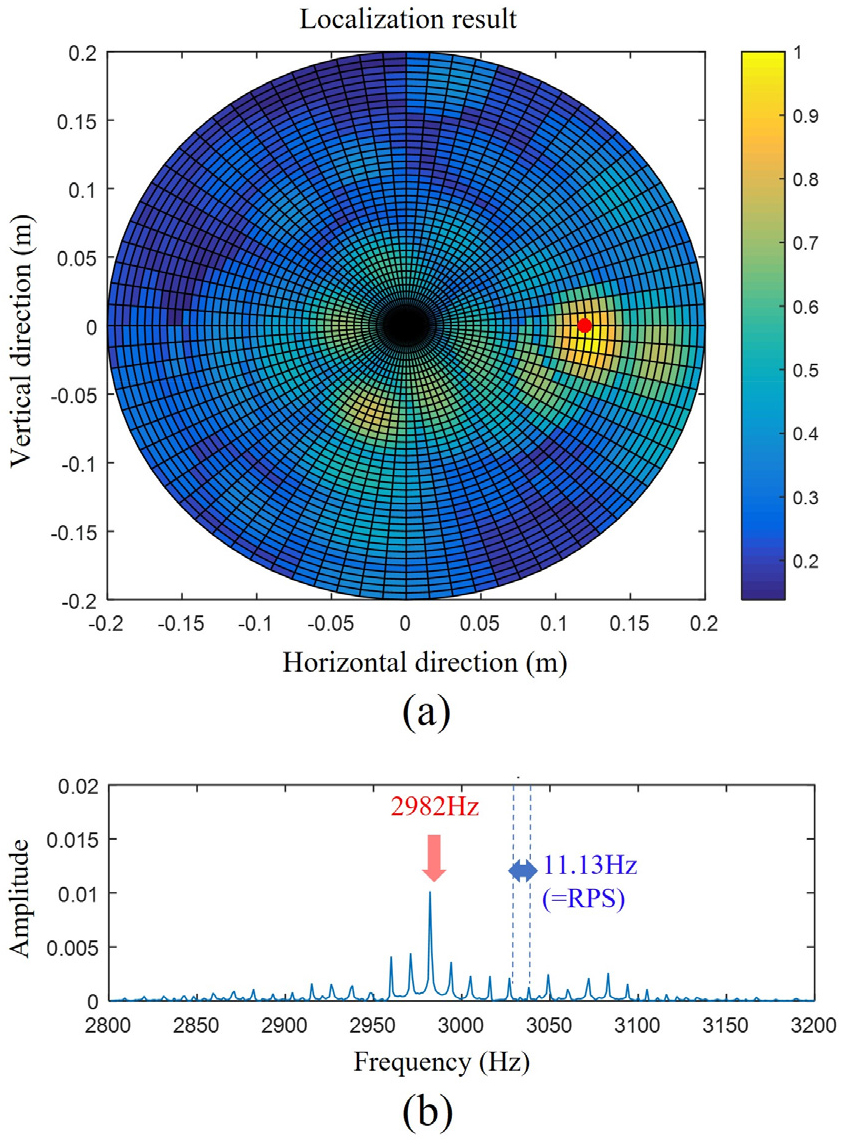
Fig. 9(a)는 역산에 의해 생성된 $E (R_{s}, ϕ_{s})$ 의 모호평면이며, Fig. 9(b)는 ${{\bar{R}}_{s}, {\bar{ϕ}}_{s}}$ 위치에서의 역산신호에 대한 주파수 스펙트럼이다. 추정된 소음원의 초기위치는 ${{\bar{R}}_{s}, {\bar{ϕ}}_{s}} = {0.12 m, 0.0 π}$ 였으며, 이는 실제 소음원의 위치인 ${0.13 m, 0.0 π}$ 와 거의 일치함을 알 수 있다. 하나의 main lobe가 생성되던 모의신호의 모호평면[Fig. 6(a)]과는 달리, 실제신호의 모호평면은 main lobe와 여러 개의 side lobe가 동시에 발생하였다. 이는 실험에 사용된 음향인자들의 미세한 실험적 오차값과 buzzer 소음원의 음전달 특성에 기인하는 것으로 판단되어진다. 역산된 신호의 스펙트럼에서 side peaks들이 존재하나, 모의신호의 결과와 마찬가지로 중심주파수 대역인 2,982 Hz에 명확한 신호성분이 존재함을 확인할 수 있었다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430607/images/ASK_43_06_07_F9.jpg

Fig. 9.

(Color available online) Inversion results: (a) Ambiguity surface for $E (R_{s}, ϕ_{s})$ and the location of virtual source corresponding to the maximum value, (b) demodulated spectrum.

따라서, 역산 결과를 통해 2,982 Hz 성분의 단극자 소음원이 회전하고 있고, 해당 소음원의 초기위치를 ${0.12 m, 0.0 π}$ 로 추정할 수 있다.

V. 고 찰

본 장에서는 제안된 음향신호모델과 분석결과들의 유효성을 검토하였고, 추후 보완되어야 할 연구의 한계점들에 대해 기술하였다.

5.1 명음소음의 단극자 소음원 가정

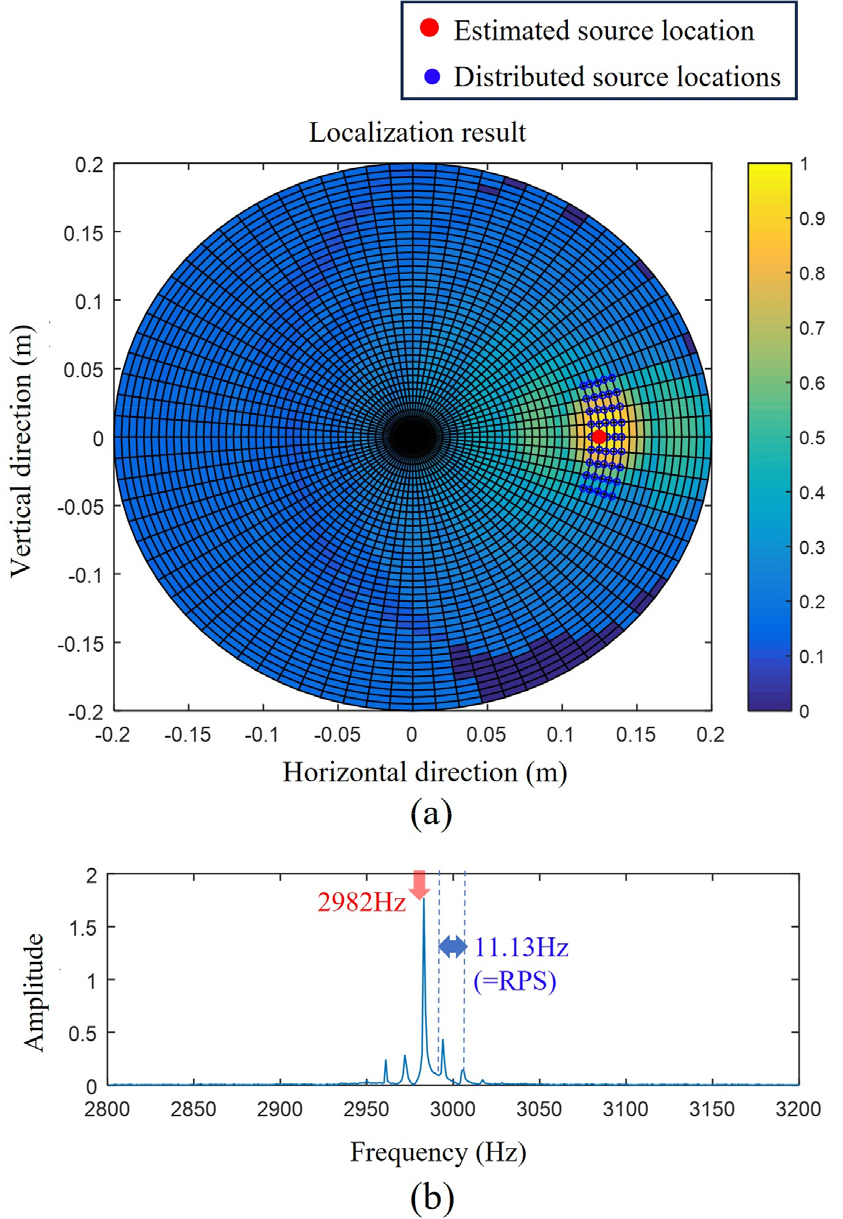
실질적인 프로펠러에서 발생하는 명음소음은 구조물의 공진에 기인한 구조방사소음에 가까운 형태를 가지게 된다. 본 연구에서 제안된 단극자 소음원 모델로는 이러한 복잡한 구조방사소음의 모의가 어렵다는 점이 연구의 한계점이다. 다만, 구조방사소음이 단순한 1차모드 진동에 기인한 면소음일 경우 하나의 단극자 소음원의 가정은 여전히 유효하게 활용될 수 있으며, 이러한 유효성을 검증하기 위해 여러 개의 단극자 소음원들을 분포시켜 구조물에서 방사되는 소음신호를 모의하였고, 역산기법을 통해 위치 추정을 수행하였다.

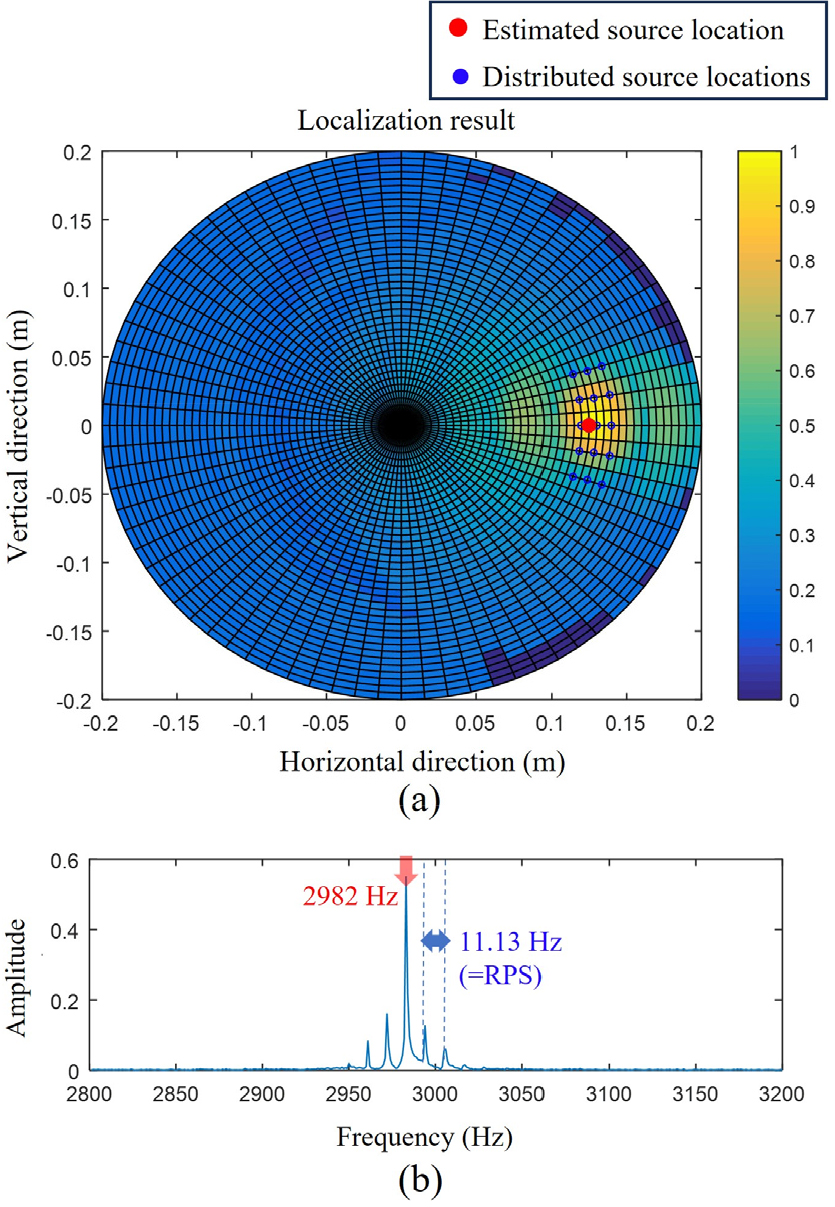
Fig. 10은 Table 2의 acoustic parameters $R_{s} = [0.12 : 0.01 : 0.14] m$ , $ϕ_{s}$ =[-18:9:18]°의 범위에 해당하는 15개의 단극자 분포 소음원을, Fig. 11은 $[0.12 : 0.005 : 0.14] m$ , $ϕ_{s}$ =[-18:4.5:18]°의 범위에 해당하는 45개의 단극자 분포 소음원을 모의한 후 역산한 결과이다. 모의에 사용된 단극자 소음원들은 동일한 진폭( $A$ =1)과 초기위상값( $θ_{s} = 0 °$ =0°)을 가지고 있고, 각 케이스는 동일한 면적 내에 다른 분포밀도 신호에 대한 역산결과이다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430607/images/ASK_43_06_07_F10.jpg

Fig. 10.

(Color available online) Inversion results for 15 distributed sources: (a) Ambiguity surface for $E (R_{s}, ϕ_{s})$ and the location of virtual source corresponding to the maximum value, (b) demodulated spectrum.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430607/images/ASK_43_06_07_F11.jpg

Fig. 11.

(Color available online) Inversion results for 45 distributed sources: (a) Ambiguity surface for $E (R_{s}, ϕ_{s})$ and the location of virtual source corresponding to the maximum value, (b) demodulated spectrum.

Fig. 10(a)와 Fig. 11(a)는 각 가상소음원들의 목적함수값 $E (R_{s}, ϕ_{s})$ 의 모호평면이다. 모의된 단극자가 공간적으로 분포된 상황이지만, 초기위치 ${{\bar{R}}_{s}, {\bar{ϕ}}_{s}}$ 를 역산하여 분포소음의 acoustic center point를 추정하였으며, Fig. 10(b)와 Fig. 11(b)의 스펙트럼과 같이 정현파에 가까운 역산된 소음원을 생성하였음을 확인할 수 있다. 이는 구조방사소음이 발생하는 경우에도 동일위상의 분포소음들로 모의될 수 있는 경우, 해당 기법의 성능이 유효함을 보여준다.

본 연구에서 제안된 단극자 음향신호모델은 명음소음의 물리 특성을 현실적으로 반영할 수 없다는 한계점을 가지고 있다. 다만, 본 연구에서 정립한 기초적인 음향신호모델을 기초로 하여 여러 개의 단극자 소음원으로 명음소음을 모의하는 연구를 수행하고 있으며, 해당 기법의 개발을 통해 향후 보다 실질적이고 효과적인 명음소음원 역산을 수행할 예정이다.

5.2 역산기법: 소음원의 단일 위치 추정

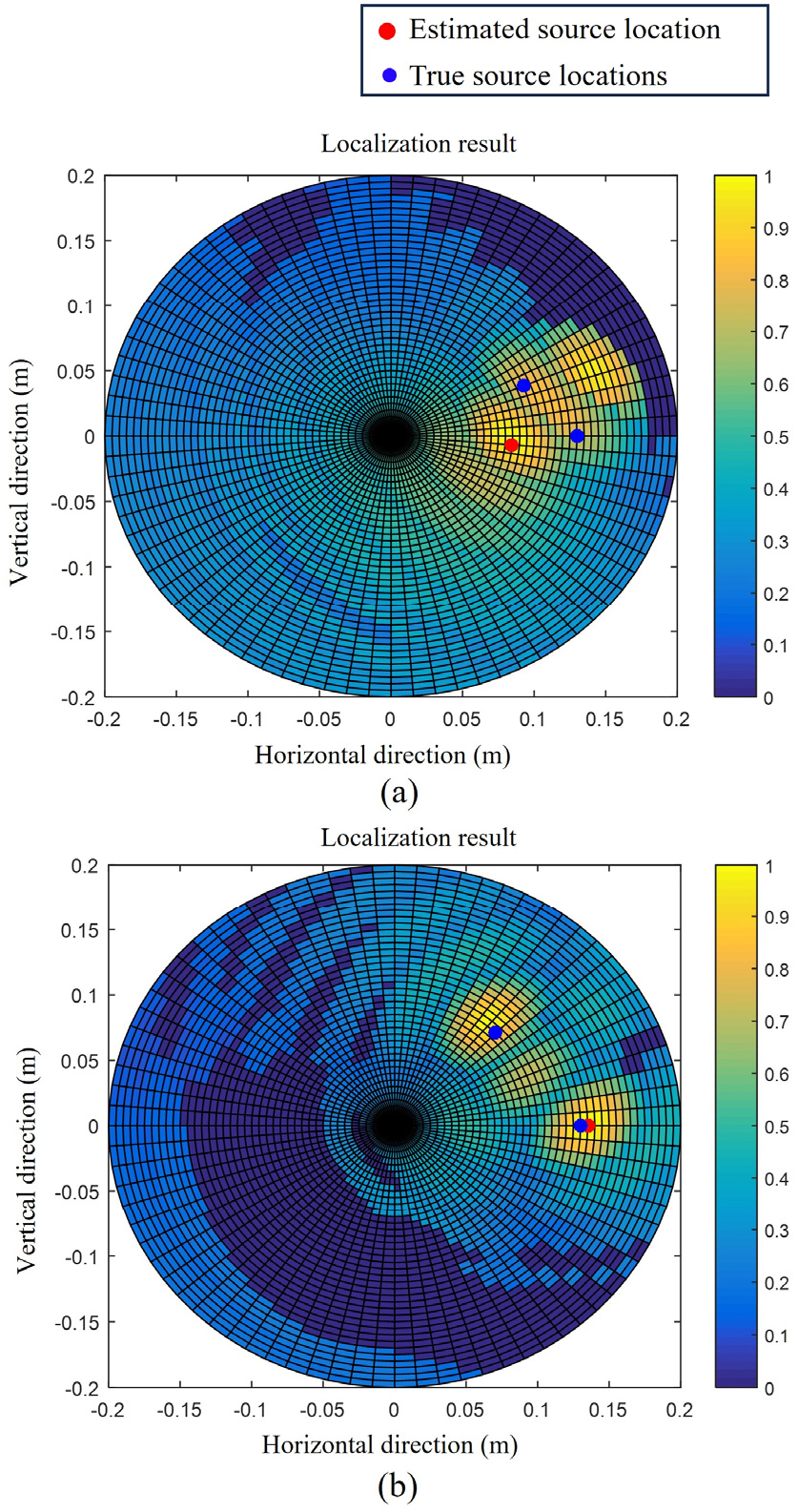
본 연구에서 제안된 역산기법은 Eq. (14)에 의한 초기위치 ${{\bar{R}}_{s}, {\bar{ϕ}}_{s}}$ 를 추정하므로, 해당 기법은 하나의 명음소음원의 위치에 대해서만 추정할 수 있다는 한계점을 가진다.

다만, 두개 이상의 소음원이 프로펠러에 존재할 경우에도, 모호평면을 이용해 해당 소음원들의 개략적인 위치 추정을 수행할 수 있다.

Fig. 12(a)는 ${R_{s}, ϕ_{s}} = {0.13 m, 0 °}$ , ${0.10 m, 22.5 °}$ 의 초기위치에 있는 두개의 단극자 소음원에 대한 모호평면 역산 결과이다. 두 소음원은 진폭( $A$ =1)과 초기위상값( $θ_{s}$ =0°)을 가진 동일한 단극자 소음원이며, 가까운 거리로 인해 두 소음원과 상관없는 위치에 main lobe가 발생하게 되고, 해당 케이스는 모호평면을 통한 소음원의 위치추정이 어렵다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430607/images/ASK_43_06_07_F12.jpg

Fig. 12.

(Color available online) Inversion results: (a) Ambiguity surface for $E (R_{s}, ϕ_{s})$ and the location of virtual source corresponding to the maximum value, (b) demodulated spectrum.

Fig. 12(b)는 ${R_{s}, ϕ_{s}} = {0.13 m, 0 °}$ , ${0.10 m, 45 °}$ 의 초기위치에 두개의 단극자 소음원이 위치한 경우의 모호평면 역산 결과이다. 물리적 거리가 충분히 확보될 경우, 모호평면 상에서 실제 소음원이 존재하는 두 위치에 명확한 main lobe가 발생하는 것을 확인할 수 있다.

정합장(Matched Field Processing, MFP)기법을 통한 소음원 위치추정 문제^[16]와 같이, 명음소음 역산기법은 모호평면을 결과값으로 제공하며 분해능이 확보될 경우 다수의 소음원에 대한 개략적인 위치 정보를 추정할 수 있다. 수학적 해석을 통해 다수의 소음원을 분리하는 연구를 진행중에 있으며, 이를 통해 제안된 역산기법이 가지고 있는 한계점을 극복하고자 한다.

5.3 음파모델: 이상적인 유체환경 가정

본 연구에서 제안한 음향신호모델은 근거리음장 영역에서 프로펠러 주위의 반류장이 균일하게 분포하며 유동에 의한 음장 왜곡이 없는 이상적인 유체 환경을 가정하였다. 하지만 실제 환경에서는 근거리 음장의 형태로 전달되지 않을 수 있고, 반류장은 불균일하며, 프로펠러 후류에 의한 음장의 왜곡이 발생할 수 있다. 모델의 단순화를 위해 가정한 이상적 음향신호모델과 실제 유체환경의 환경적 불일치(environmental mismatch)가 제안된 기법의 한계점이며, 이는 추후 실제환경에서의 실험을 통해 환경변수들에 대한 분석을 수행하여 보완되어야 할 것이다.

VI. 결 론

본 연구에서는 명음소음원의 발생위치를 추정하는 기법을 연구하였으며, 이를 위해 하나의 단극자 소음원을 이용한 기초적인 음향신호모델과 해당 소음원신호의 역산 알고리즘을 제안하였다.

제안된 기법은 모의데이터와 실제 실험 데이터를 이용해 성능의 유효성을 검증하였고, 회전하는 단극자 소음원의 위치를 1 mm 내외의 오차범위로 추정하는 성능을 가지고 있음을 검증하였다. 해당 역산기법은 단일 청음기의 수신신호를 활용하기 때문에, 향후 모형실험 및 실선 운용과정에서 발생하는 명음소음 분석에서 유용하게 활용할 수 있을 것으로 기대한다.

다만, 제안된 음향 신호모델은 명음소음원을 단극자 소음원으로 단순 모델링하였고, 균일한 반류장 내에 수신되는 신호가 매질의 유동에 의한 왜곡이 없는 이상적인 환경을 가정하였다는 한계점을 가진다.

향후 연구에서는 실질적인 명음소음원을 모의할 수 있는 음향신호모델과 다수의 단극자 소음원의 위치를 추정할 수 있는 역산 기법을 개발하여 본 연구의 한계점을 보완할 예정이다. 또한, 실제 프로펠러 운용환경에서의 음파전달특성에 대한 연구를 수행하여 명음소음원의 위치 추정 성능을 개선하고자 한다.

Acknowledgements

이 논문은 국립수산과학원 수산과학연구 사업인 자원관리형 어구어법 연구(R2024007)(0.5)와 2023년도 정부(방위사업청)의 재원으로 국방기술진흥연구소(No. 21-107-B00-008(KRIT-CT-23-009), 광해역 수중감시 및 심해 음향환경 분석 기술)(0.5)의 지원으로 수행된 연구입니다.

References

W. Kerr, J. F. Shannon, and R. N. Arnold, "The problems of the singing propeller," IMechE, 144, 54-90 (1940).

10.1243/PIME_PROC_1940_144_015_02

S. Makiya, A. Inasawa, and M. Asai, "Vortex shedding and noise radiation from a slat trailing edge," AIAA J. 48, 502-509 (2010).

10.2514/1.45777

D. Kim and K. Chung, "A study on the propeller blade singing place of an 86,000 ton deadweight crude oil tanker," SNAK, 31, 59-64 (1994).

T. Kim and H. Lee, "A study on the identification of underwater propeller singing phenomenon" (in Korean), J. Acoust. Soc. Kr. 37, 92-98 (2018).

B. Ahn, J. Lee, W. Rhee, and J. Choi, "Theoretical and experimental study on airfoil singing," Trans. Korean Soc. Noise Vib. Eng. 20, 115-121 (2010).

10.5050/KSNVE.2010.20.2.115

R. Fischer, "Singing propellers-solutions and case histories," Mar. Technol. SNAME News, 45, 221-227 (2008).

10.5957/mt1.2008.45.4.221

M. Park, Y. Park, K. Lee, and W. Seong, "Incipient tip vortex cavitation localization using block-sparse compressive sensing," J. Acoust. Soc. Am. 147, 3454-3464 (2020).

10.1121/10.000126532486828

C. Erbe, S. A. Marley, R. P. Schoeman, J. N. Smith, L. E. Trigg, and C. B. Embling, "The effects of ship noise on marine mammals-A review," Front. Mar. Sci. 6, article 606 (2019).

10.3389/fmars.2019.00606

I. Han, E. Yoon, W. Oh, and K. Lee, "The influences of encircling gill net fishery on fish organisms" (in Korean), J. Korean Soc. Fish Technol. 53, 41-48 (2017).

10.3796/KSFT.2017.53.1.041

C. Park, G. Kim, Y. Park, K. Lee, and W. Seong, "Noise localization method for model tests in a large cavitation tunnel using a hydrophone array," Remote Sens. 8, 195 (2016).

10.3390/rs8030195

W. Pannert and C. Maier, "Rotating beamforming - motion-compensation in the frequency domain and application of high-resolution beamforming algorithms," J. Sound and Vib. 333, 1899-1912 (2014).

10.1016/j.jsv.2013.11.031

G. Herold and E. Sarradj, "Microphone array method for the characterization of rotating sound sources in axial fans," NCEJ, 63, 546-551 (2015).

10.3397/1/376348

N. Chu, Q. Huang, L. Yu, Y. Ning, and D. Wu, "Rotating acoustic source localization: A power propagation forward model and its high-resolution inverse methods," Measurement, 174, 109006 (2021).

10.1016/j.measurement.2021.109006

M. A. Poletti and P. D. Teal, "Comparison of methods for calculating the sound field due to a rotating monopole," J. Acoust. Soc. Am. 129, 3513-3520 (2011).

10.1121/1.358948121682378

F. J. Harris, Multirate Signal Processing for Communication Systems (Prentice Hall PTR, New York, 2004), pp. 28-45.

K. Lee, J. Lee, D. Kim, K. Kim, and W. Seong, "Propeller sheet cavitation noise source modeling and inversion," J. Sound and Vib. 333, 1356-1368 (2014).

10.1016/j.jsv.2013.11.002

The Journal of the Acoustical Society of KoreaISSN:1225-4428(Print) 2287-3775(Online)한국음향학회

Preview

A study on inversion method of rotating monopole source for estimating the location of propeller singing noise source

ABSTRACT

MAIN

(1)

Fig. 1.

(Color available online) Cylindrical coordinates for the rotating system, showing the rotating source (red circular dot) and a hydrophone (blue square dot).

(2)

(3)

(4)

(5)

(6)

(7)

Table 1.

Acoustic parameters for the singing noise model.

Fig. 2.

(Color available online) Synthetic time signal: (a) source signal (tq=[0 ms, 1 ms] are marked with 2 lines), (b) received signal from the rotating source (retarded times for tq=[0 ms, 1 ms] are marked as τ(tq=0ms) and τ(tq=1ms) with dashed lines.

Fig. 3.

(8)

(9)

(10)

(11)

Fig. 4.

(12)

(13)

(14)

Table 2.

Acoustic parameters for the synthetic and experimental tests.

Fig. 5.

(Color available online) Simulated signals: (a) time signal, (b) spectrum.

Fig. 6.

(Color available online) Inversion result: (a) Ambiguity surface for E(Rs,ϕs), (b) demodulated spectrum.

Fig. 7.

(Color available online) Experimental setup for rotating noise source: (a) propeller with 1 attached buzzer, (b) tape attached to the end of the propeller, (c) microphone with sampling rate of 48 kHz, (d) measured time signal with impulsive signal (red bar).

Fig. 8.

(Color available online) Measured signals: (a) time signal, (b) spectrum.

Fig. 9.

(Color available online) Inversion results: (a) Ambiguity surface for E(Rs,ϕs) and the location of virtual source corresponding to the maximum value, (b) demodulated spectrum.

Fig. 10.

(Color available online) Inversion results for 15 distributed sources: (a) Ambiguity surface for E(Rs,ϕs) and the location of virtual source corresponding to the maximum value, (b) demodulated spectrum.

Fig. 11.

(Color available online) Inversion results for 45 distributed sources: (a) Ambiguity surface for E(Rs,ϕs) and the location of virtual source corresponding to the maximum value, (b) demodulated spectrum.

Fig. 12.

(Color available online) Inversion results: (a) Ambiguity surface for E(Rs,ϕs) and the location of virtual source corresponding to the maximum value, (b) demodulated spectrum.

Acknowledgements

References

(Color available online) Synthetic time signal: (a) source signal ( $t_{q}$ =[0 ms, 1 ms] are marked with 2 lines), (b) received signal from the rotating source (retarded times for $t_{q}$ =[0 ms, 1 ms] are marked as $τ (t_{q} = 0 m s)$ and $τ (t_{q} = 1 m s)$ with dashed lines.

(Color available online) Inversion result: (a) Ambiguity surface for $E (R_{s}, ϕ_{s})$ , (b) demodulated spectrum.

(Color available online) Inversion results: (a) Ambiguity surface for $E (R_{s}, ϕ_{s})$ and the location of virtual source corresponding to the maximum value, (b) demodulated spectrum.

(Color available online) Inversion results for 15 distributed sources: (a) Ambiguity surface for $E (R_{s}, ϕ_{s})$ and the location of virtual source corresponding to the maximum value, (b) demodulated spectrum.

(Color available online) Inversion results for 45 distributed sources: (a) Ambiguity surface for $E (R_{s}, ϕ_{s})$ and the location of virtual source corresponding to the maximum value, (b) demodulated spectrum.

(Color available online) Inversion results: (a) Ambiguity surface for $E (R_{s}, ϕ_{s})$ and the location of virtual source corresponding to the maximum value, (b) demodulated spectrum.