I. 서 론
II. 수치해석
2.1 대상 원심팬 시스템
2.2 3차원 수치해석 기법
2.3 2차원 수치해석 기법
2.4 수치해석 기법 유효성 검증
III. 다중 충실도 모델 기반 가상제품개발
3.1 설계 변수 선정 및 데이터 구축
3.2 다중 충실도 모델 개발
3.3 스크롤 컷오프 각도 영향도 분석
3.4 임펠러 유량 성능 최적화
3.5 최적 모델 수치적 분석
IV. 결 론
I. 서 론
최근 제조업에서는 제품의 다양성 증가와 시장의 세분화에 따라 제품 개발 과정에서 제품 시험 횟수가 기하급수적으로 증가하여 제품 개발 비용 절감에 대한 중요성이 강조되고 있다. 이로 인해 제품 개발 과정에서 발생하는 비용을 절감하기 위해 가상제품개발 기술이 적용되고 있는 추세이다. 가상제품개발은 제품 개발 과정에서의 물리적 현상이 반영된 가상 프로토 타입 제품을 구현함으로써 제품의 개발 및 시험을 가상 시뮬레이션 상에서 구축하는 것을 의미한다. 최근 가전제품 시장에서 꾸준히 수요가 증가하고 있는 의류 건조기를 대상으로도 3차원 수치해석 기반의 가상제품개발 기술이 활발히 적용되고 있다. 의류 건조기는 소비자가 가정에서 직접 실시간으로 성능을 체감할 수 있다는 특징 때문에 특히 건조 성능과 소음 성능이 주요 성능지표로 인식되고 있다. 이러한 건조기의 건조 성능은 건조기의 순환 팬의 유량 성능과 직결되며, 의류 건조기 소음 성능은 내부 팬 시스템이 지배적인 소음원으로 작용한다. 의류 건조기의 내부 유로 순환을 담당하는 팬 시스템에는 주로 원심팬이 사용되며, 원심팬의 유량 성능 개선 및 소음 저감을 위한 가상제품개발을 목표로 3차원 수치해석을 통한 팬 성능 개선 연구가 다양하게 진행되고 있다.
이와 관련된 연구로 Heo et al.[1]은 전산유체역학(Computational Fluid Dynamics, CFD)과 복합전산음향학(Hybrid Computational Aeroacoustics, Hybrid-CAA)을 기반으로 냉장고용 원심팬의 날개 뒷전 형상에 S자 형상을 적용하여 소음 저감을 시킨 바가 있으며, Shin et al.[2]은 냉장고의 냉동실 냉기 순환용 원심팬을 대상으로 전산유체역학을 이용하여 원심팬의 유동 특성을 분석하고 날개 형상을 변경하여 원심팬의 허브 밑단에서 발생하는 와류를 저감해 유동 성능을 향상시켰다. Shin et al.[3]은 팬 설계 인자 중 날개 입구각, 출구각, 내경을 대상으로 반응표면법을 적용하여 원심팬의 성능을 최적화하였다. Kim et al.[4]은 자동차 시트 쿨링용 원심팬에서 발생하는 와류 및 정체 유동을 줄이기 위해 팬 날개와 팬 하우징 최소 간극(cut-off)과 허브 형상을 변경하여 유동과 소음 성능을 향상시켰다. Choi et al.[5]은 의류 건조기용 원심팬과 덕트 및 하우징 등을 포함한 공기배출 시스템에 대하여 전산유체역학과 Ffowcs-Williams and Hawkings(FW-H) 방정식에 기초한 복합방법을 이용하여 유동 및 소음 특성을 분석하였으며 원심팬의 날개 형상 최적화를 통해 유량 성능 향상과 공력 소음 저감에 관한 연구를 수행하였다. Jung et al.[6]은 냉장고 냉동실 냉기순환용 후향익 원심팬 시스템을 대상으로 익형을 최적 설계하여 유동 성능 및 소음 성능을 향상시킨 바 있다. Song et al.[7]은 식기세척기 내 원심펌프의 유량 성능 및 소음 성능을 개선하기 위해 원심펌프 내 임펠러 형상에 대한 최적 설계 연구를 진행한 바 있다. 이러한 선행연구들과 같이 3차원 수치해석을 활용한 원심팬의 가상제품개발이 활발히 이루어지고 있지만 다양한 운전 조건과 많은 설계 변수를 고려한 3차원 수치해석에는 상당한 개발 비용이 소요된다는 한계점이 아직 존재하는 실정이다.
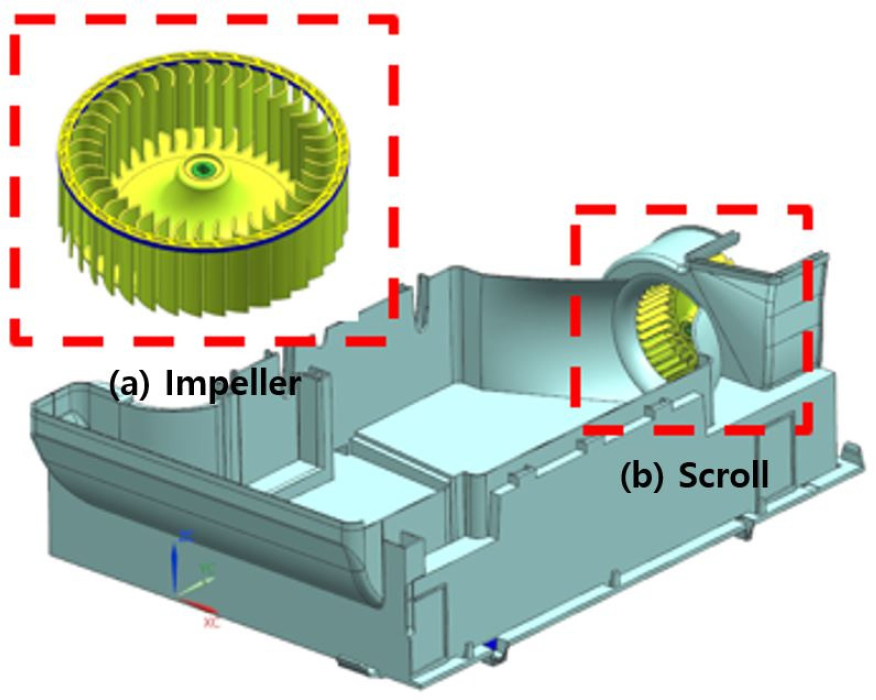
본 연구에서는 수치해석 비용을 저감한 효율적인 가상제품개발을 목표로, 3차원 수치해석에 비해 상대적으로 성능 예측 정확도는 떨어지지만 계산 비용이 적은 2차원 수치해석의 특징을 활용하고자 하였다. 이를 위해 계산 비용이 비싸고 정확한 고충실도 데이터와 계산 비용이 싸지만 정확도가 떨어지는 저충실도 데이터를 융합하여 최소의 비용으로 고충실도 모델을 유사한 정확도로 예측할 수 있는 대체 모델을 생성하는 기법인 다중 충실도 모델링 기법을 적용하였다. 이와 관련된 최근 선행 연구로 Guo et al.[8]은 매개 변수화된 형태와 주파수를 가진 음향 혼에 압력파가 전파되는 문제를 다루어 반사 강도 지수를 인공신경망을 이용한 다중 충실도 모델을 통해 근사한 바 있으며, 고충실도 모델로는 유한 요소 기반의 완전 차수 모델을, 저충실도 모델로는 차수 축소 모델을 사용하였다. 본 연구에서는 3차원 수치해석 데이터를 고충실도 데이터로 선정하고 2차원 수치해석 데이터를 저충실도 데이터로 선정하여 인공신경망을 이용한 다중 충실도 모델을 개발하여 목표 작동 영역에 대한 원심팬의 성능을 예측하였다. 개발한 다중 충실도 모델의 성능 예측 데이터를 기반으로 대상 원심팬 시스템에 대해 가상제품개발을 수행하여 유량 및 소음 성능을 향상시키고자 한다. 원심팬 시스템은 Fig. 1과 같이 스크롤과 임펠러로 구성되며 본 연구에서는 Fig. 2의 스크롤의 컷오프 각도, 원심팬의 날개 입구각, 출구각을 주요 설계 변수로 선정하였다. 스크롤 컷오프 각도를 고려한 스크롤 설계와 임펠러의 날개 입구각, 출구각을 고려한 임펠러 최적 설계를 수행하였으며 최적 설계 기법으로 반응표면법을 사용하였다. 이를 통해 도출한 최적 형상을 적용한 원심팬 시스템의 유동 성능 향상과 공력 소음 저감 결과를 제시하였다.
II. 수치해석
2.1 대상 원심팬 시스템
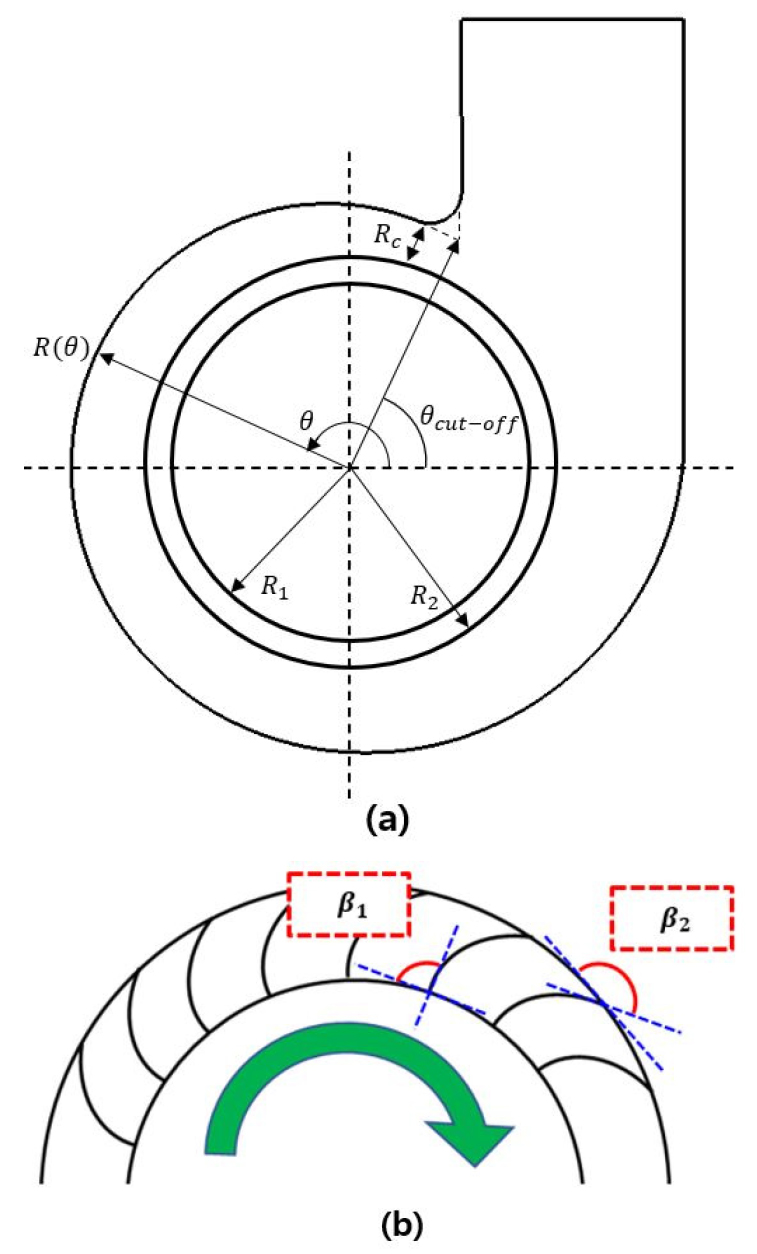
본 연구에서는 수치해석 기법 검증을 위해 지름이 149 mm, 날개 수가 38개로 구성된 임펠러에 대하여 스크롤 설계를 수행하여 수치해석과 실험을 진행하였다. Fig. 2와 Table 1에서 볼 수 있듯이 임펠러 설계 변수는 대표적으로 임펠러 내경, 외경, 날개 입구각, 출구각 등을 들 수 있고, 스크롤에 대해서는 컷오프 각도, 컷오프 간극, 나선의 반경, 스크롤 확장 각도 등을 고려할 수 있다. 스크롤 나선 설계를 위해서 대수나선형 식을 채택하였으며 나선의 반경 은 다음 식과 같다.[9]
Table 1.
Definition of design parameters.
| Symbol | Term | Symbol | Term |
| Inner radius | Cut-off angle | ||
| Outer radius | Cut-off gap | ||
| Blade inlet angle | Scroll spiral radius | ||
| Blade outlet angle | Scroll expansion angle |
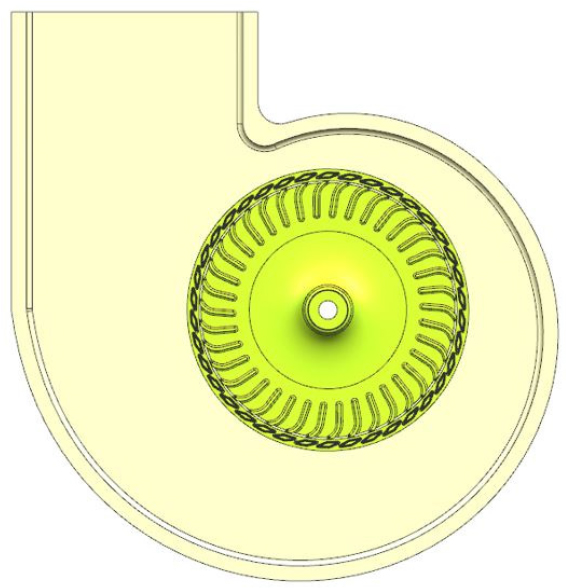
여기서 는 임펠러 내경 반지름과 컷오프 간극의 합으로 정의된다. Eq. (1)의 스크롤 확장 각도 는 스크롤의 출구 면적과 전체적인 크기를 결정하는 중요한 설계 인자이며, 임펠러 출구의 절대 유동각과 같은 값을 가지도록 설계하는 것이 가장 효율적이라고 연구한 바가 있는 Yamazaki의 선행연구를 참고하여 6.225°로 적용하였다.[10,11,12] 다음으로 스크롤 컷오프 각도 는 임펠러가 스크롤 출구를 기준으로 노출되는 정도를 결정하는 설계 변수로, 임펠러를 통과하여 스크롤 내부에서 혼합되면서 나선을 따라 모아진 유동을 토출구로 유인하는 중요한 역할을 한다. Kang et al.[9]은 컷오프 각도가 약 60°일 때 출구에서의 속도분포가 가장 균일하여 소음이 적다는 결론을 얻었으며, 본 연구에서는 이를 참고하여 스크롤 컷오프 각도를 60°로 적용하였다. 설계한 스크롤 형상과 대상 임펠러 형상은 Fig. 3에서 제시하였다.
2.2 3차원 수치해석 기법
본 연구에서는 대상 원심팬 시스템의 유동 성능을 수치적으로 분석하기 위하여 상용 프로그램인 ANSYS Fluent v23.2을 사용하여 수치해석을 수행하였다. 또한, 본 연구에서 개발할 다중 충실도 모델에 필요한 데이터를 구축하기 위해 3차원 수치해석과 2차원 수치해석을 모두 진행하였다. 먼저 본 절에서 3차원 수치해석 기법에 대해 다루고, 다음 절에서 2차원 수치해석 기법에 대해 다룰 예정이다. 지배방정식은 비정상 비압축성 레이놀즈 평균 나비에 스토크스(Reynolds-Averaged Navier-Stokes, RANS) 방정식을 사용하였으며 아래의 연속방정식과 운동량 방정식으로 나타낼 수 있다.
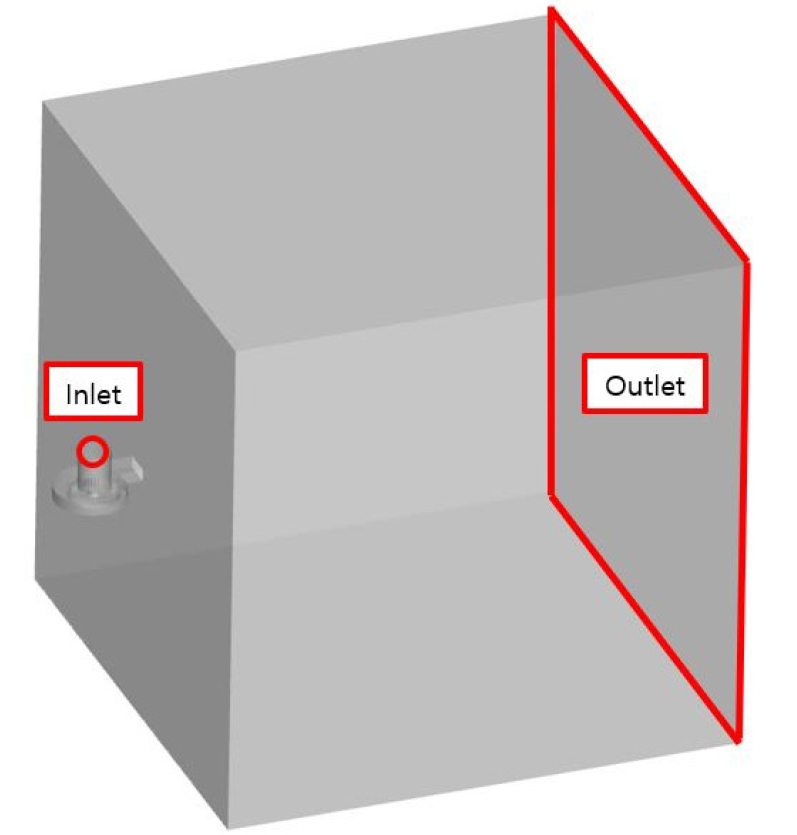
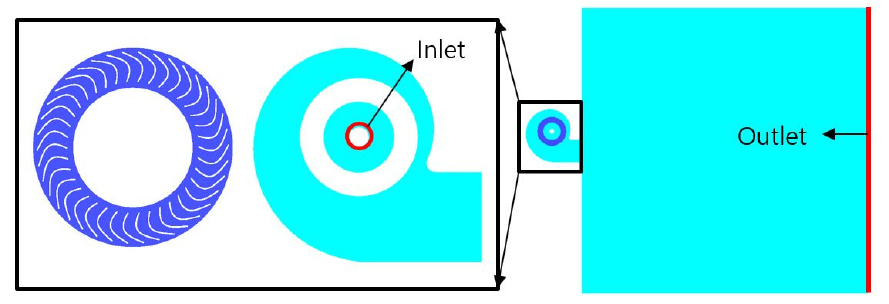
여기서 항은 난류에 의한 영향을 모사하기 위한 Reynolds stress tensor 항이며 난류 모델에 의해 정의된다. 임펠러 날개 벽면 근처의 난류의 거동을 해석하기 위한 난류 모델로는 경계층 내부는 난류 모델을 사용하여 벽면 함수를 사용하지 않고 벽면 난류 경계층에 대한 모사를 가능하게 하며, 경계층 외부 영역에 대해 난류 모델을 통해 계산하여 벽면 근처 흐름 예측에 이점을 가진 Menter의 Shear Stress Transport(SST) 난류 모델[13]을 적용하였다. 수치해석 계산 영역은 정확한 유동 특성 분석을 위해 실제 유동 실험에 사용하는 팬 성능 시험기을 모사한 3차원 가상 팬 성능 시험기를 구축하였으며, 구체적인 구성은 Fig. 4와 같다. 격자 구성은 벽면 근처 흐름 예측에 신뢰성을 더하기 위해 Fig. 5와 같이 분포가 5 이하를 만족하도록 표면 격자 크기를 조정하였으며 체적 격자는 약 2,600만 개의 사면체 격자들로 구성하였다. 임펠러 회전 영역의 경우, 운전 속도 2,500 r/min을 부여하고 Sliding Mesh 기법을 적용하였으며 경계조건으로는 pressure inlet & pressure outlet 조건을 적용하였다.
2.3 2차원 수치해석 기법
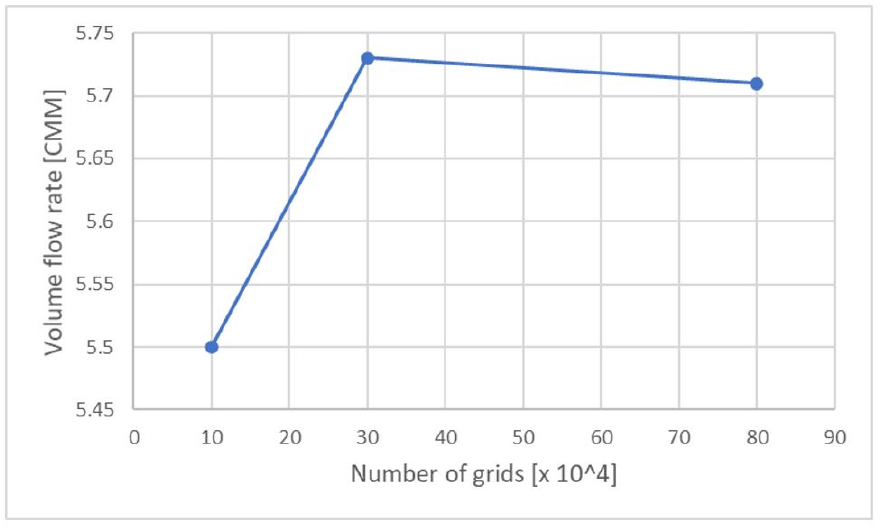
2차원 수치해석의 경우, 동일한 상용프로그램인 ANSYS Fluent v23.2를 사용하였으며 Eqs. (3)과 (4)의 비정상 비압축성 RANS 방정식을 지배방정식으로 수치해석을 수행하였다. 난류 모델은 동일하게 SST 모델을 사용하였으며 계산 영역은 Fig. 6과 같이 2차원 가상 팬 성능 시험기를 구축하였다. 격자 구성은 3차원 수치해석의 표면 격자 크기와 동일하게 적용하여 약 30 만 개 수준의 삼각형 표면 격자를 구성하였다. 또한 Fig. 7의 grid refinement study를 통해 격자 수준을 평가하였을 때, 격자 80만 개 수준에서 유량 성능과의 차이가 약 0.3 % 정도로 30만 개 격자 수준의 신뢰도를 확인하였다. 회전 영역의 경우, 3차원 수치해석과 동일하게 회전속도 2,500 r/min을 부여하고 Sliding Mesh 기법을 적용하였으며, 경계 조건으로 pressure inlet & pressure outlet 조건을 적용하였다.
2.4 수치해석 기법 유효성 검증
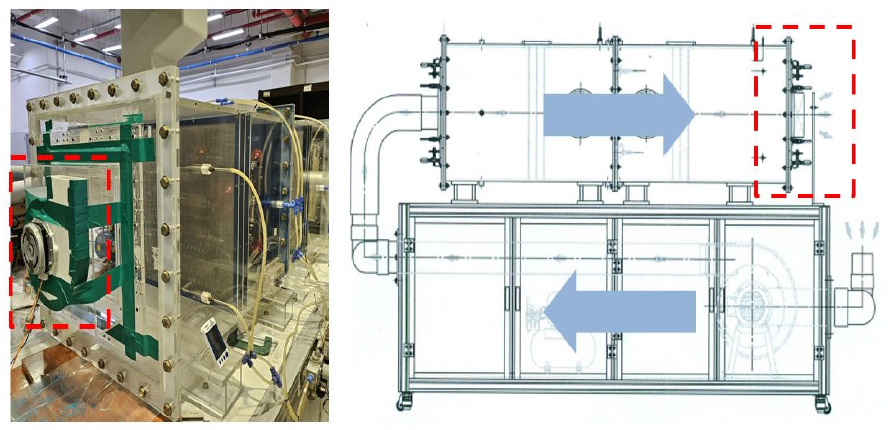
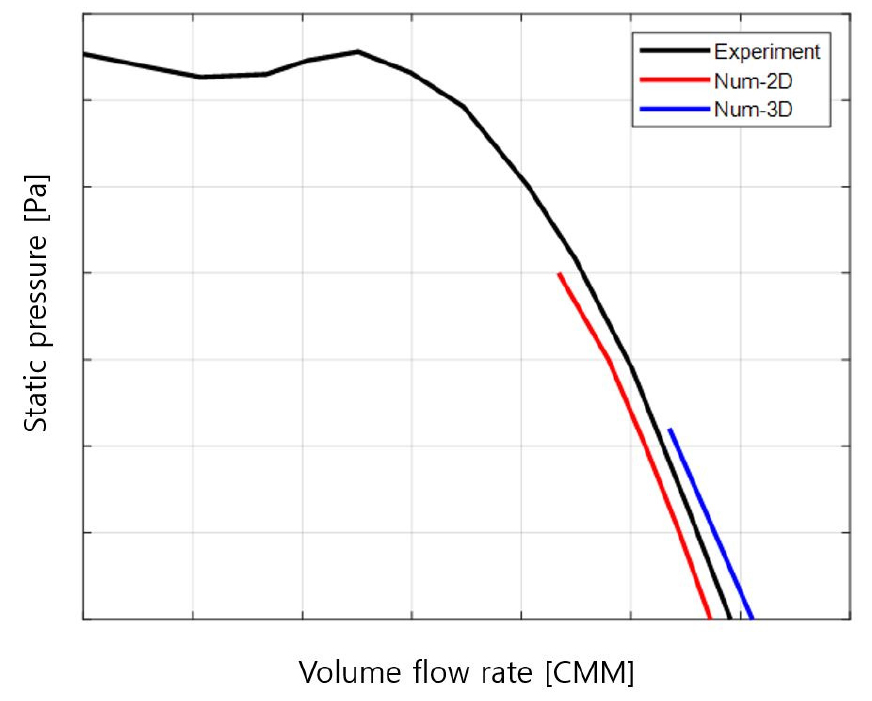
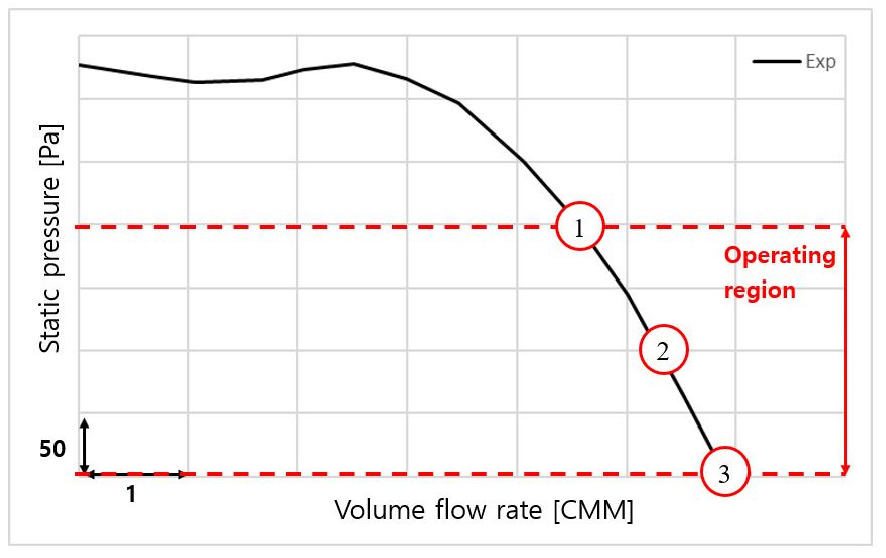
본 연구에서 사용된 3차원 & 2차원 수치해석 기법의 유효성을 검증하기 위하여 수치해석 결과와 유동 실험 결과를 함께 비교하였다. 유동 실험의 경우, 대상 원심팬 시스템의 유량 성능을 도출하기 위해 Fig. 8의 팬 성능 시험기를 사용하였다. 실험에 사용한 팬 성능 시험기는 AMCA 210-07[14] 규정을 충족시키며, 0.6 m(W) × 0.6 m(H) × 1.5 m(L)의 크기를 가진다. 실험 방식은 흡입모드와 배출모드가 있으며 본 실험에서는 흡입모드를 사용하였다. 대상 원심팬을 2,500 r/min으로 작동시켜 P-Q 선도를 도출하였으며 수치해석 결과와 함께 비교한 P-Q 선도를 Fig. 9에 나타내었다. 무부하 지점을 기준으로 실험과 수치해석 결과값을 비교했을 때, 2차원 수치해석과 3차원 수치해석 모두 실험과 약 3 %의 오차를 가지는 것을 확인하였다.
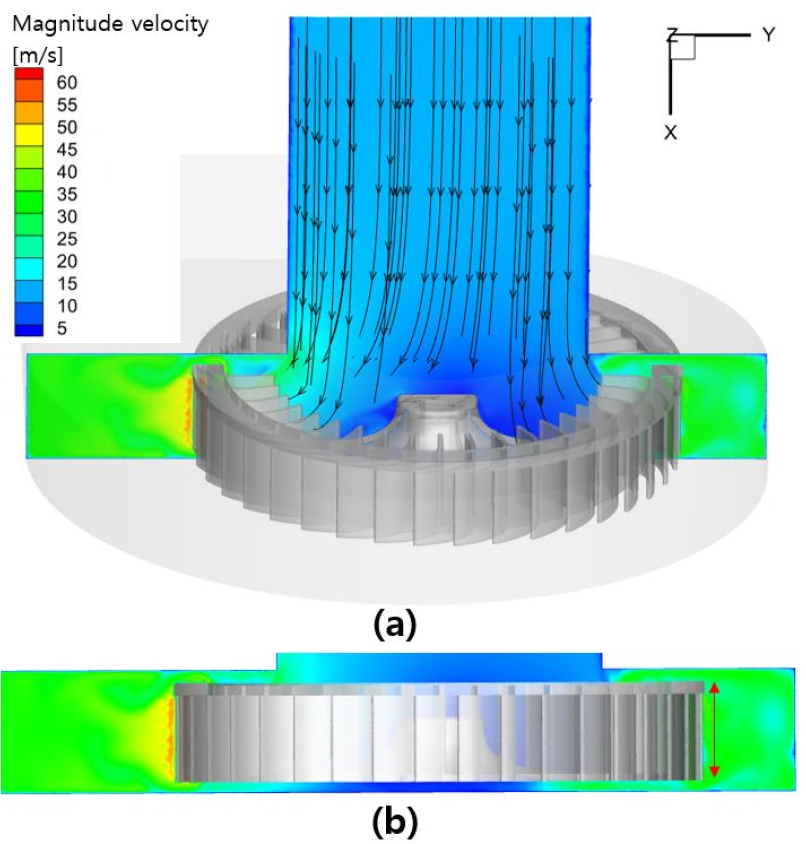
3차원 수치해석의 경우, 실험 결과에 비해 유량 성능을 과도 예측하는 경향을 나타내는 것을 알 수 있다. 이는 원심팬의 특성 상 스크롤 입구와 출구의 방향이 수직으로 꺾여 있어 실제 실험처럼 스크롤 입구단이 팬 성능 시험기의 대형 챔버와 연결되어 있는 형상을 계산 영역 상에서 구현하기 힘든 이유로 입구단과 연결된 대형 챔버 형상을 덕트 형상으로 변경한 영향으로 판단된다. Fig. 10의 속도장 (a)의 streamline에서 볼 수 있듯이 계산 영역에서 inlet 영역인 덕트 형상에서 스크롤 입구단으로 들어가는 유동의 손실이 없어 실험보다 유량 성능이 높게 예측됨을 알 수 있다. 하지만 압력이 높아질수록 유량 성능이 낮아지는 전반적인 실험 결과의 경향성은 3차원 수치해석 모델이 잘 따라감을 확인할 수 있다.
2차원 수치해석의 경우, 전반적인 경향성은 일치하나 실험 결과에 비해 유량 성능을 과소 예측하는 경향을 나타낸다. 이는 2차원 수치해석의 특성 상 계산 영역을 Fig. 10(b)에서 붉은 화살표로 표시한 임펠러의 날개 폭 영역까지만 고려할 수 있기 때문에 실제로 임펠러를 통과해 스크롤의 전체 영역에 모이는 유동을 계산하지 못한 영향으로 판단된다. 이와 같이 2차원 수치해석 상에서 고려하지 못하는 물리적 차이로 인한 유량 성능 예측 오차를 극복하기 위해 다음 절에서는 다중 충실도 모델 개발을 통해 2차원 수치해석 모델의 정확도를 높이고자 한다.
추가로 수치해석 기법의 계산 효율성을 평가하기 위해 2차원과 3차원 수치해석의 동일 CPU core 수 대비 수치해석 소요 시간을 비교하였다. 수치해석에 사용한 CPU 제원은 Intel-Xeon Silver 4210R이며 비교 결과는 Table 2에 제시하였다. 수치해석의 시간 간격 는 임펠러 1° 회전과 동일하도록 설정하였고 계산식은 다음과 같다.
Table 2.
Comparison result of time required for 2D/3D numerical analyses.
| Num.method | CPU core | CPU hours |
| 2D RANS | 14 cores | 6 h |
| 3D RANS | 14 cores | 360 h |
임펠러가 1바퀴 회전할 때 평균 유량을 계산하여 다음 바퀴의 평균 유량과의 오차가 1 % 이하일 때를 수렴 기준으로 정했을 때, 10바퀴 회전했을 때 수렴함을 알 수 있었다. 따라서 10바퀴 회전할 때를 기준으로 소요시간을 비교하였으며, 14개의 CPU core 수를 사용하였을 때, 2차원 수치해석의 소요 시간이 3차원 수치해석의 소요 시간의 1/60 수준임을 확인할 수 있다. 따라서 본 연구에서는 3차원 수치해석에 비해 상대적으로 계산 비용이 적고 성능 예측 정확도가 낮은 2차원 수치해석 기법을 활용할 수 있는 방법으로 다중 충실도 모델을 선정하였으며, 다중 충실도 모델 개발을 통해 고효율 고적확 가상제품개발을 수행하고자 한다.
III. 다중 충실도 모델 기반 가상제품개발
3.1 설계 변수 선정 및 데이터 구축
본 연구에서는 목표 작동 영역에서 설계 변수를 기반으로 원심팬의 성능 예측을 할 수 있는 다중 충실도 모델을 개발하고자 하였다. 서론에서 소개한 인공신경망을 이용한 다중 충실도 모델[8]을 개발하기 위해 3차원 수치해석 데이터를 고충실도 데이터로 사용하고 2차원 수치해석 데이터를 저충실도 데이터로 사용하여 2차원 수치해석의 계산 비용으로 3차원 수치해석과 유사한 정확도로 원심팬의 성능을 예측하는 모델을 개발하고자 하였다.
다중 충실도 모델을 개발하기 위한 데이터를 구축하기에 앞서 2.1절에서 소개한 원심팬 시스템의 유동 성능 및 소음 성능에 영향을 미치는 주요 변수인 스크롤의 컷오프 각도와 임펠러의 유동 성능 및 소음 성능에 영향을 미치는 주요 변수인 임펠러 날개 입구각, 출구각을 본 연구의 설계 변수로 선정하였다. 먼저 스크롤 컷오프 각도의 경우, Fig. 1에서 볼 수 있듯이 스크롤이 설치되는 실제 건조기 기계실 내부의 협소한 공간을 고려하여 최소 20°에서 최대 80° 범위에서 4수준으로 선정하였고, 스크롤의 전체적인 크기를 결정하는 스크롤 확장 각도 는 4°로 고정하였다. 임펠러 형상의 경우, 2.1절에서 제시한 임펠러 날개 형상을 기준으로 Fig. 2(b)에서 정의한 날개 입구각과 출구각의 각도 변경을 고려하였다. 전향익 원심팬은 일반적으로 입구각의 경우 80°에서 120° 사이의 범위를 가지며, 출구각의 경우 120°에서 160° 사이의 범위를 가지는 것으로 알려져 있다.[15] 본 연구에서는 임펠러의 구조 상 설계 가능한 범위를 고려하여 Table 3과 같이 범위를 선정하였으며, 반응표면기법 중 하나인 중심합성계획법[6]을 사용하여 9개의 임펠러 실험 모델을 Table 4와 같이 정의하였다. 그리고 목표 작동 영역과 작동 영역 내 대표 작동점 3개를 Fig. 11와 같이 도시하였다.
Table 3.
Range of inlet angle and outlet angle for optimization.
| Level | -1.414 | -1 | 0 | 1 | 1.414 |
| [°] | -22 | -15 | +15 | +22 | |
| [°] | -12 | -8 | +8 | +12 |
Table 4.
Definition of 9 models for Response Surface Method (RSM) about inlet angle and outlet angle.
| Model | Level | [°] | [°] | |
| 1 | 0 | 0 | ||
| 2 | 1.414 | 0 | +22 | |
| 3 | -1.414 | 0 | -22 | |
| 4 | 0 | -1.414 | -12 | |
| 5 | -1 | 1 | -15 | +8 |
| 6 | 1 | 1 | +15 | +8 |
| 7 | -1 | -1 | -15 | -8 |
| 8 | 0 | 1.414 | +12 | |
| 9 | 1 | -1 | +15 | -8 |
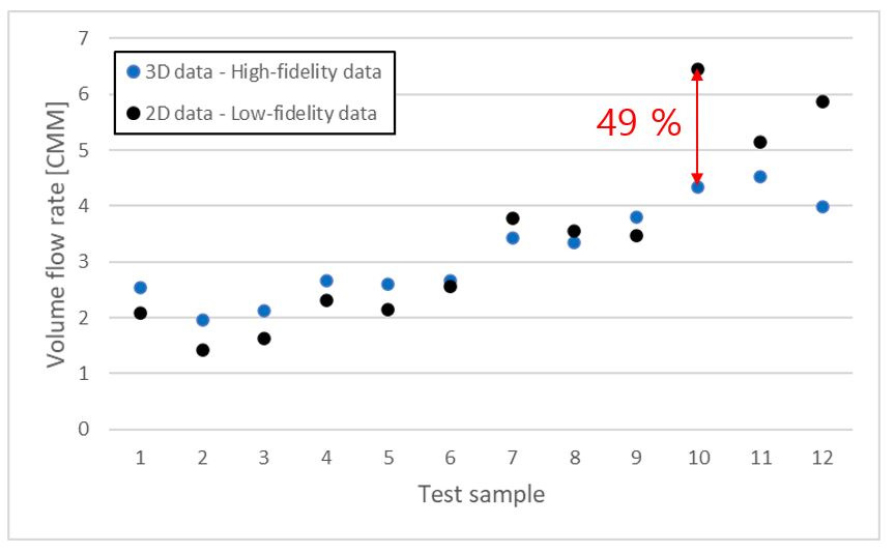
저충실도 데이터를 구축하기 위해 스크롤 컷오프 각도에 따른 4개의 스크롤 형상과 임펠러의 날개 입구각, 출구각을 고려한 9개의 임펠러 실험 모델에 대하여 3개의 대표 작동점에서 2차원 수치해석을 수행하였으며, 컷오프 각도, 입구각, 출구각, 작동점 압력은 입력 데이터로, 유량은 출력 데이터로 구성된 총 108개의 저충실도 데이터를 구축하였다. 고충실도 데이터의 경우, 4개의 스크롤 형상 각각에 대하여 9개 중 3개의 임펠러 실험 모델을 임의로 선정하여 총 12번의 3차원 수치해석을 수행하였다. 9개의 임펠러 모델이 모두 고려되도록 선정하였으며, 작동점의 경우는 동일 작동점에서 저충실도 데이터와의 과적합을 방지하기 위해 2차원 수치해석에서 적용한 작동점을 제외하고 목표 작동 영역 내에서 임의로 선정하였다. 저충실도 데이터와 동일하게 컷오프 각도, 입구각, 출구각, 작동점 압력은 입력 데이터로, 유량은 출력 데이터로 구성된 총 12개의 고충실도 데이터를 구축하였다.
3.2 다중 충실도 모델 개발
본 절에서는 3.1절에서 구축한 저충실도 데이터와 고충실도 데이터를 기반으로 인공신경망을 이용한 다중 충실도 모델을 개발하였다. 인공신경망 학습 모델은 순전파, 역전파, 경사하강법 순으로 반복 학습 과정을 거쳐 생성되며 학습 과정은 다음 식과 같이 나타낼 수 있다.[8]
이때, 이고 이다. 여기서 은 hidden layer의 개수이며, 을 입력 데이터로 정의하고, 을 출력 데이터로 정의한다. 𝜙는 비선형 활성화 함수이며, 는 가중치, 는 편향 값을 의미한다.
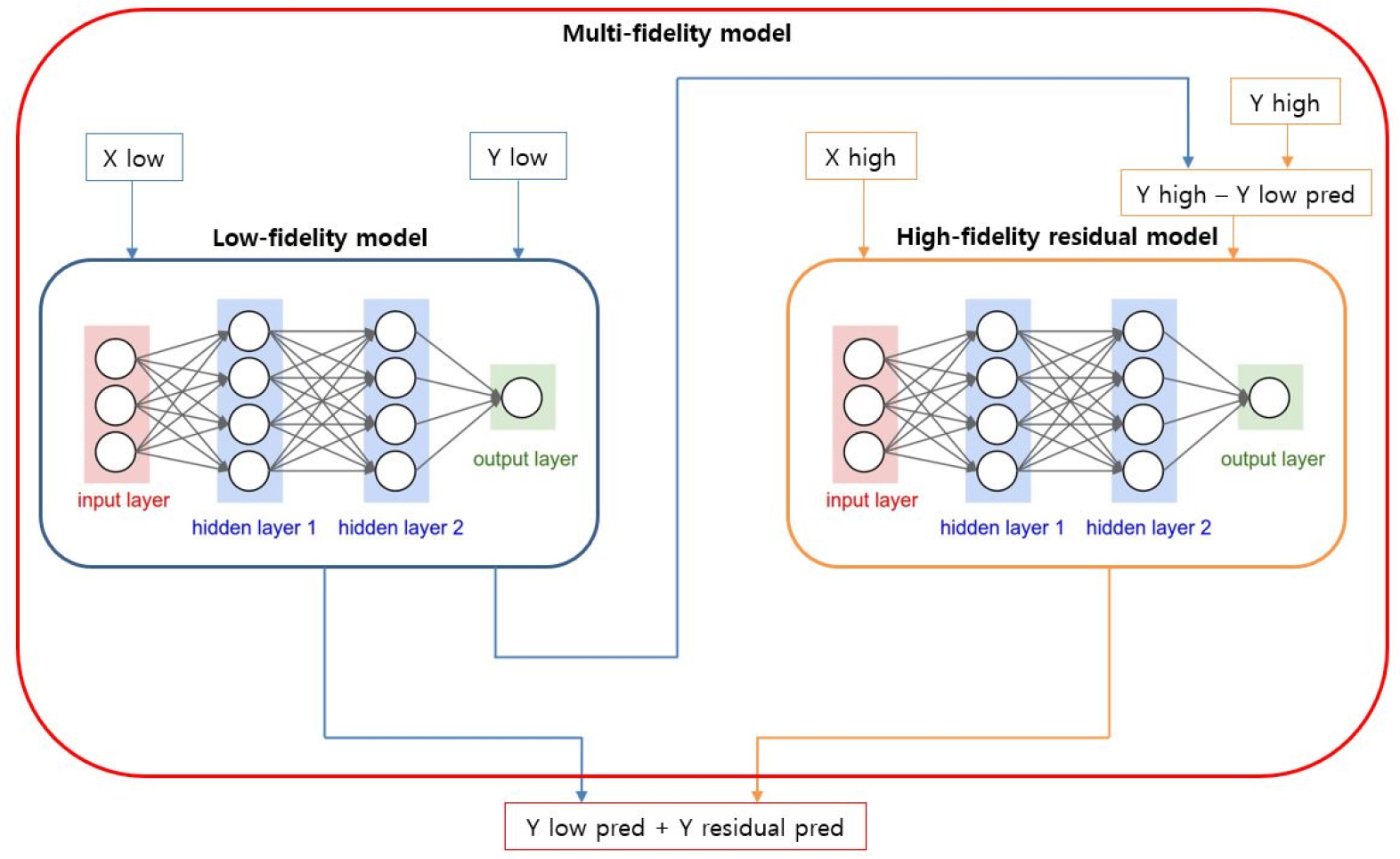
위와 같은 인공신경망 학습 알고리즘을 통해 먼저 저충실도 데이터를 학습하는 저충실도 인공신경망 모델을 생성하고 학습을 진행하였다. 저충실도 데이터에서 80 %는 학습 데이터로, 10 %는 검증 데이터, 그리고 나머지 10 %는 테스트 데이터로 활용하였다. 다음으로 고충실도 데이터의 입력값을 저충실도 인공신경망 모델을 통해 예측한 값과 실제 고충실도 데이터의 출력값의 차이인 잔차를 계산하였으며, 계산된 고충실도 잔차를 학습하는 고충실도 잔차 인공신경망 학습 모델을 생성하였다. 최종적으로 입력 데이터에 대해 저충실도 인공신경망 모델로 예측한 값과 고충실도 잔차 인공신경망 모델로 예측한 잔차를 더해 최종 예측값을 계산하는 다중 충실도 모델을 개발하였다. 다중 충실도 모델의 알고리즘은 다음 식과 같다.
여기서 는 저충실도 인공신경망 모델이며 는 고충실도 잔차 인공신경망 모델이다. 개발한 다중 충실도 모델의 알고리즘 개략도는 Fig. 12에 도시하였으며, 인공신경망 모델은 64개, 36개의 뉴런으로 구성된 2개의 은닉층이 포함되고 Batch size는 64, Epoch는 300으로 설정하였다.
개발한 다중 충실도 모델의 예측 성능을 평가하기 위해 먼저 2차원 수치해석 데이터를 학습한 저충실도 모델의 성능 예측 정확도를 고충실도 데이터와 비교하여 Fig. 13에 나타냈다. 예측 정확도를 평가하기 위해 평균제곱오차(Mean Squared Error, MSE) 지표를 적용하였으며 아래와 같은 식을 통해 계산하였다.
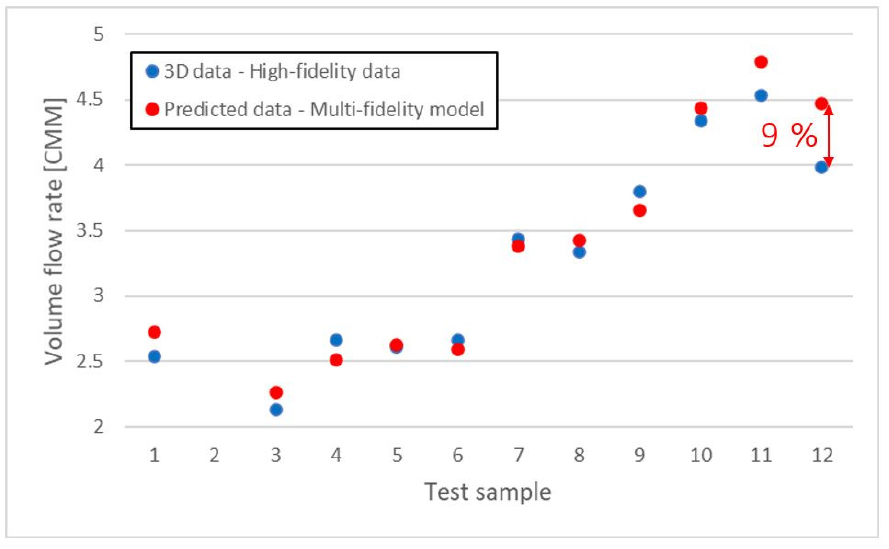
계산한 결과, MSE = 0.812로 1에 가까운 높은 값으로 예측 정확도가 좋지 않음을 확인하였다. 다음으로 다중 충실도 모델의 예측 정확도를 평가하기 위해 예측값과 고충실도 데이터를 Fig. 14에서 비교하였으며 MSE 지표로 계산하였을 때, MSE = 0.022로 0에 가까운 낮은 값으로 예측 정확도가 높은 것을 확인할 수 있었다.
3.3 스크롤 컷오프 각도 영향도 분석
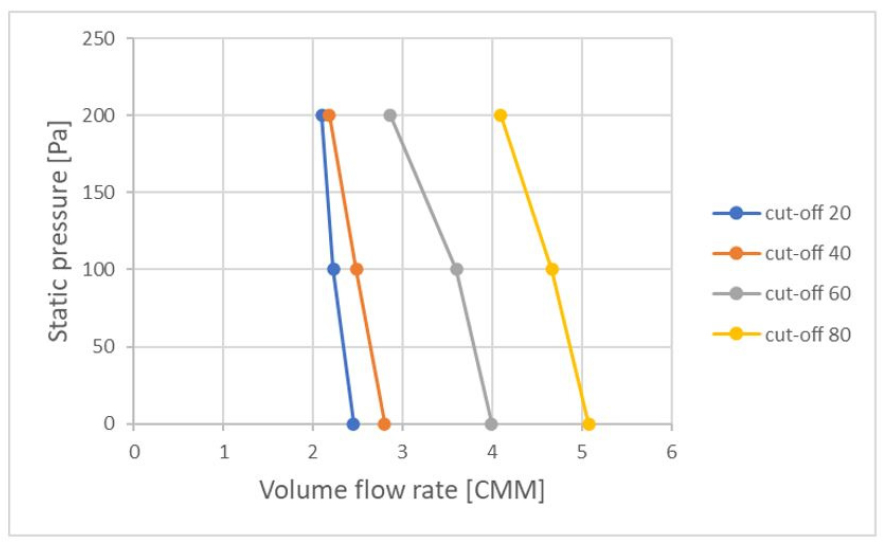
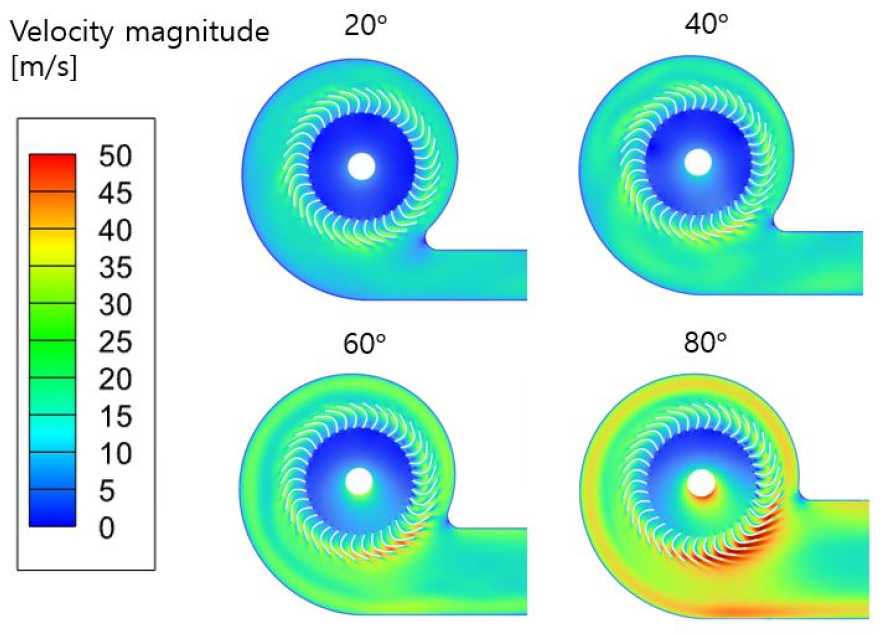
앞 절에서 개발한 다중 충실도 모델을 이용하여 108개의 저충실도 입력 데이터에 대한 고충실도 데이터와 유사한 정확도를 가지는 유량 성능 데이터를 확보하였다. 이를 활용하여 스크롤 컷오프 각도에 따른 유량 성능의 변화를 분석하고자 하였다. Fig. 15에 컷오프 각도 20°, 40°, 60°, 80°의 스크롤 형상에 대해 3개의 대표 작동점에서 유량 성능을 비교하여 나타내었다. 이를 통해 컷오프 각도가 증가함에 따라 유량도 함께 증가함을 확인하였으며 무부하 지점에서의 Fig. 16의 2차원 수치해석 속도 유동장을 확인해 보았을 때, 스크롤 내부 유동의 속도 성분이 컷오프 각도가 증가할수록 커지는 것을 알 수 있었다. 따라서 유량 성능이 최대가 되는 컷오프 각도 80°의 스크롤을 선정하여 다음 절에서 임펠러의 날개 입구각 출구각에 따른 유량 성능을 최적화할 예정이다.
3.4 임펠러 유량 성능 최적화
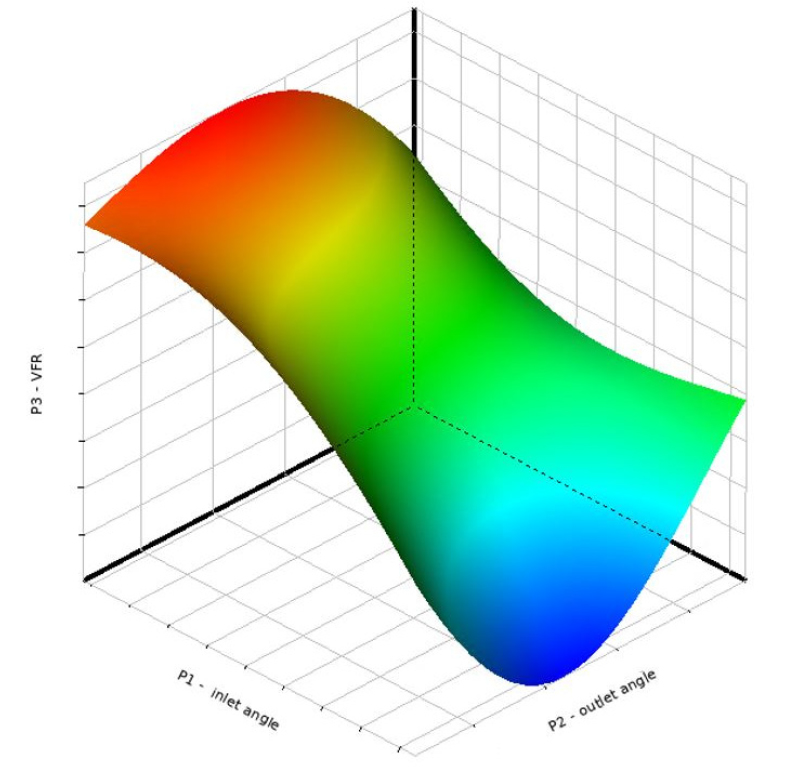
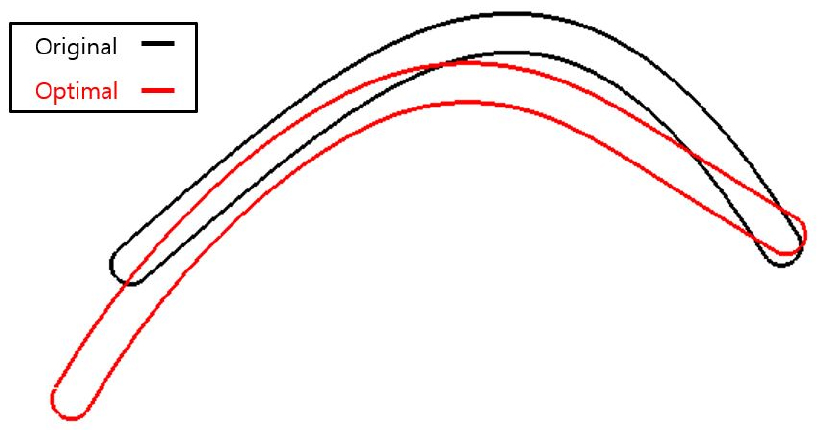
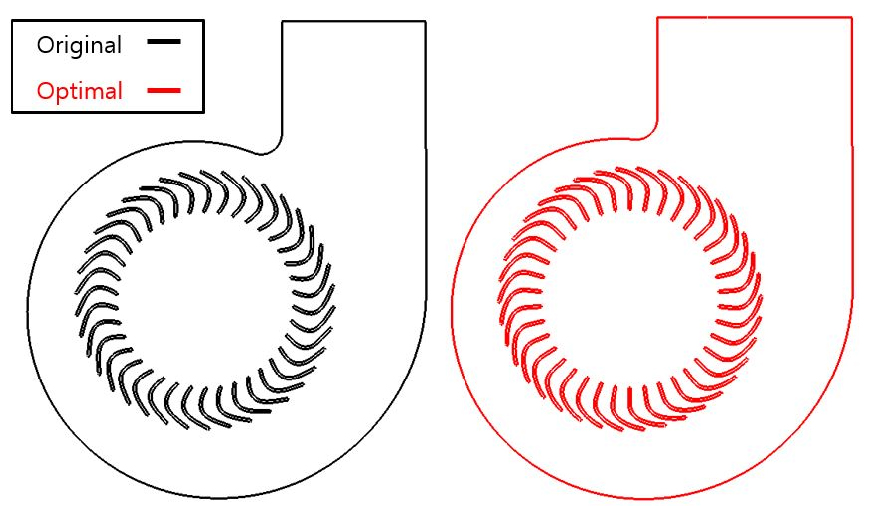
본 절에서는 컷오프 각도 80°의 스크롤에 대하여 유량 성능을 목적함수로 임펠러의 날개 입구각, 출구각에 대한 최적 설계를 수행하였다. 3개의 작동점 중 대표로 2번 작동점에 대하여 최적 설계를 수행하였으며 3.3절에서 확보한 다중 충실도 모델의 예측 데이터 중에서 3.1절에서 중심합성법을 적용하여 정의한 9개의 실험 모델의 유량 성능 데이터를 도출하였다. 중심합성법 기반의 도출한 데이터를 바탕으로 유량 성능을 목적함수로 입구각과 출구각의 변화에 따라 달라지는 반응 표면을 Fig. 17에 도시하였다. 도출된 반응 표면을 통해 유량 성능이 최대가 되는 최적의 입구각과 출구각을 도출하여 기존 날개 형상과 Fig. 18과 Table 5에서 비교하였다. 최종적으로 최적의 입구각과 출구각을 적용한 최적 모델을 설계하여 3.1절의 기존 모델과 함께 Fig. 19에 나타내었다.
Table 5.
Range of inlet angle and outlet angle for optimization.
| Model | [°] | [°] |
| Original | ||
| Optimal | -22 | +1 |
3.5 최적 모델 수치적 분석
다중 충실도 모델의 유량 성능 예측 데이터 기반으로 예측한 유량 최적 성능과 최적 모델에 대하여 3차원 수치해석을 통해 얻은 수치해석 결과를 비교하여 약 6 %의 차이로 비교적 정확한 예측성을 가지는 것을 확인하였다. 다음으로 3.3절에서 고려한 컷오프 각도 기존 60° 모델과 80° 모델의 3차원 수치해석 결과를 통해 유량 성능이 약 19 % 증가하는 것을 알 수 있었다. 그리고 컷오프 각도 80° 스크롤 형상에 대해 임펠러 기존 모델과 최적 모델의 유량 성능을 비교 분석하기 위해 3차원 수치해석을 수행하였으며 3차원 수치해석 결과, 최적 모델의 유량 성능이 기존 모델 대비 약 5 % 증가하였다. 스크롤 형상 변경에서의 유량 성능 개선량과 임펠러 최적 설계를 통한 유량 성능 개선량을 합하면 최종적으로 약 24 % 유량 성능이 개선됨을 확인하였다. 또한 스크롤 컷오프 각도 변경이 유량 성능 변화에 미치는 영향이 임펠러의 날개 입, 출구각 변화가 미치는 영향보다 상대적으로 큰 것을 알 수 있었다.
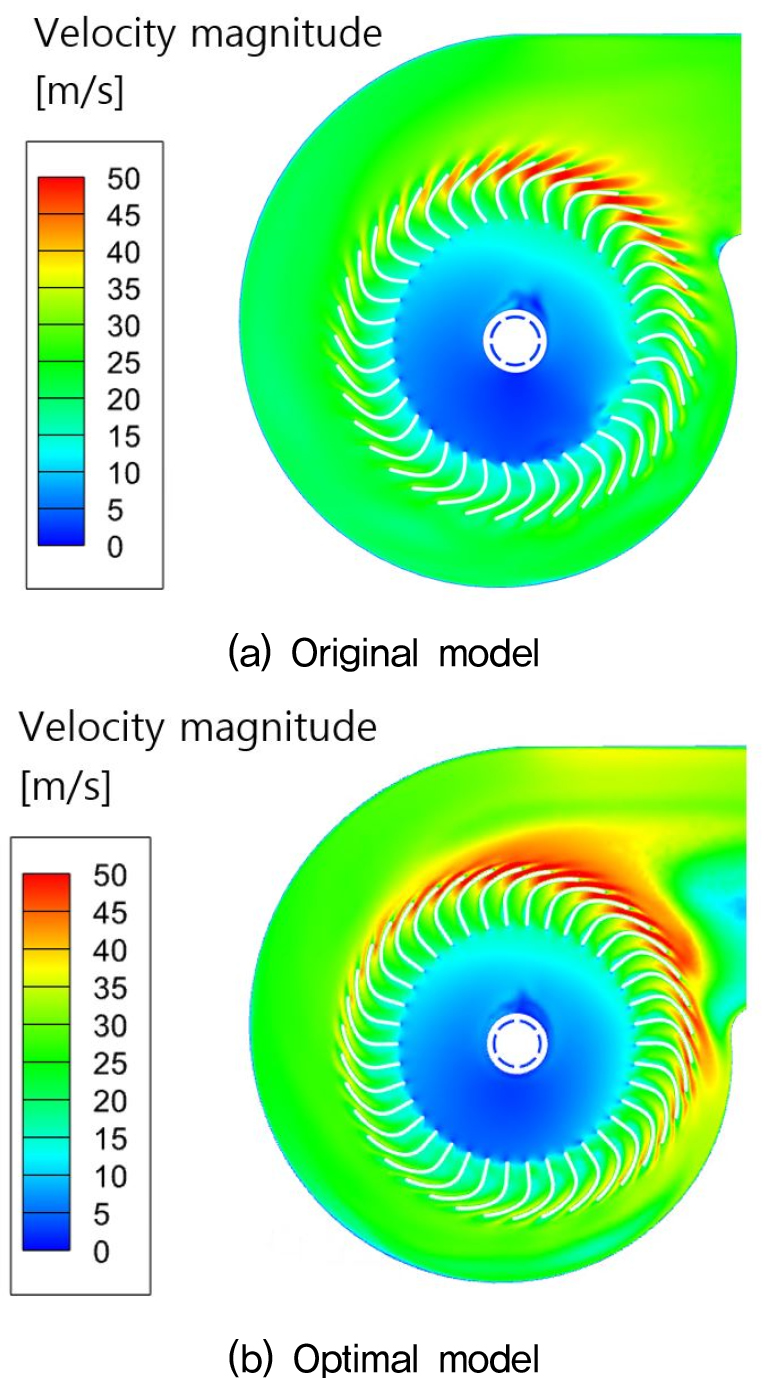
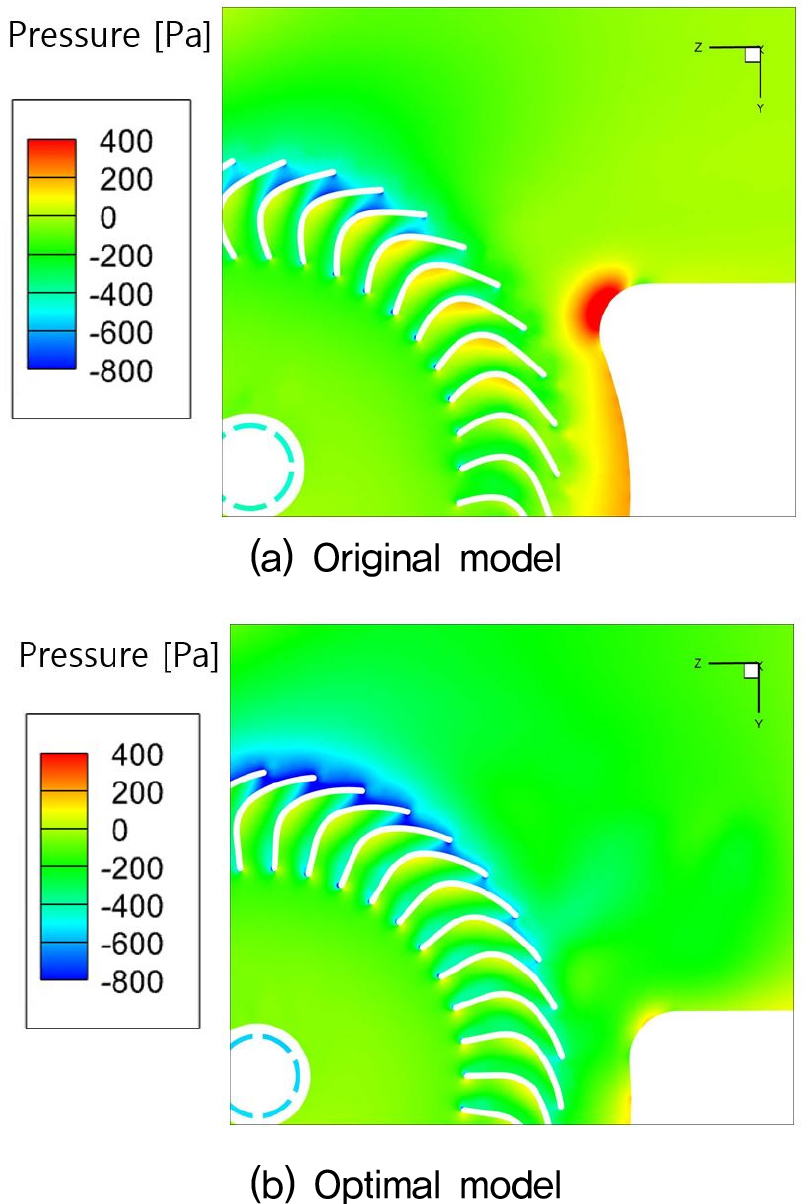
다음으로 유동장 분석을 통해 기존 모델과 최적 모델의 유동 특성을 분석하였다. 먼저 Fig. 20의 속도장을 통해 임펠러를 통과해 나가는 유동의 속도가 전체적으로 증가하는 것을 볼 수 있으며, 특히 스크롤 출구 근처에서 임펠러를 통과해 나오는 유동의 유속이 기존 모델에 대비해 크게 증가한 것을 확인할 수 있다. 또한, Fig. 21을 통해 스크롤 컷오프 영역 근처의 압력장을 분석하였다. 기존 모델의 컷오프 영역에서 볼 수 있는 높은 압력 성분이 최적 모델의 컷오프 영역에서는 크게 감소한 것을 확인할 수 있다. 이를 통해 컷오프 영역 근처 유로에서 발생하는 저항이 감소하여 최적 모델의 유량 성능 증가에 영향을 미친 것으로 판단된다.
마지막으로 팬 법칙을 적용하여 기존 모델과 최적 모델의 동일 유량 기준 소음 차이를 예측하였다.[15] 팬 법칙의 식은 다음과 같다.
Eq. (6)을 통해 약 24 % 개선된 유량을 기존 모델의 유량과 동일하게 환산하면 최적 모델은 작동 r/min이 2,500 r/min에서 약 2,016 r/min으로 감소하며, 감소한 r/min을 Eq. (7)에 대입하면 동일 유량에서 최적 모델의 소음이 약 4.7 dB 감소함을 예측할 수 있다.
IV. 결 론
본 논문에서는 3차원 수치해석을 이용한 가상제품개발 과정에서 발생하는 수치 비용을 대폭 줄이는 효율적인 가상제품개발 모델을 만들어 보고자 2차원 수치해석 기법의 특징을 다중 충실도 모델을 통해 활용한 가상제품개발을 수행하였다. 상대적으로 계산 비용이 싸고 예측 정확도가 낮은 2차원 수치해석의 특징을 활용하기 위해 인공신경망을 이용한 다중 충실도 모델링 기법을 적용하였다. 3차원 수치해석 기법과 2차원 수치해석 기법을 정립하고 실험과의 비교를 통해 유효성을 검증하였으며 동일 CPU core를 사용하였을 때, 해석 소요 시간을 3차원 수치해석과 비교하여 2차원 수치해석 기법의 효율성을 평가하여 2차원 수치해석의 소요 시간이 1/60 수준인 것을 확인하였다. 스크롤 컷오프 각도 날개 입구각, 출구각을 설계 변수로 선정하고 목표 작동 영역 내의 작동점에 대하여 2차원 수치해석 데이터 총 108개를 저충실도 데이터로 선정하고 3차원 수치해석 데이터 총 12개를 고충실도 데이터로 선정하였다. 저충실도 데이터와 고충실도 데이터를 융합하여 계산 비용이 싸고 예측 정확도가 높은 다중 충실도 인공신경망 모델을 개발하였으며 유량 성능이 최대인 스크롤에 대해 임펠러의 날개 입구각과 출구각 최적 설계를 통해 최적 원심팬 시스템 모델을 도출하였다. 3차원 수치해석을 통해 기존 모델과 최적 모델의 유량 성능을 비교하였을 때, 유량 성능이 약 24 % 증가함을 확인하였다. 그리고 팬 법칙을 적용하여 기존 모델 대비 동일 유량에서 최적 모델의 소음이 약 4.7 dB 감소함을 예측하였다.