The relationship between the array invariant-based ranging and the effective range in a weakly range-dependent environment

Donghyeon Kim; Gihoon Byun; Daehwan Kim; Jeasoo Kim

doi:10.7776/ASK.2024.43.4.455

Preview

Research Article

The Journal of the Acoustical Society of Korea. 31 July 2024. 455-465
https://doi.org/10.7776/ASK.2024.43.4.455

The relationship between the array invariant-based ranging and the effective range in a weakly range-dependent environment

거리 종속 환경에서의 배열 불변성 기반 거리추정과 상응 거리와의 관계

Donghyeon Kim¹

Gihoon Byun²^*

Daehwan Kim³

Jeasoo Kim³

김 동현¹

변 기훈²^*

김 대환³

김 재수³

¹한국해양대학교 수중운동체특화연구센터

²한국해양대학교 해양과학기술융합학과

³한국해양대학교 해양공학과

^{*Corresponding Author}

License (open-access, http://creativecommons.org/licenses/by-nc/4.0/):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

In shallow water, the array invariant, known as the effective range estimation method, is developed based on the broadband dispersion characteristics in an ideal waveguide, which can be summarized by the waveguide invariant. It is robust enough to estimate both the array tilt and range simultaneously, even in situations where array tilt exists. Recently, it has been extended to fully consider the angle dependence of the waveguide invariant. However, applying the array invariant in range-dependent environments instead of range-independent environments can lead to range estimation errors due to bathymetry mismatch. In this paper, we interpret such range estimation errors by introducing the concept of effective range. Through numerical simulations and experimental data in a weakly range-dependent environment, we demonstrate the relationship between range estimation errors and effective range.

Keywords

Shallow water

Waveguide invariant

Array invariant

Array tilt

Range estimation

Range-dependent environment

Effective range

천해역에서 효과적인 거리추정 방법으로 알려진 배열 불변성은 도파관 불변성으로 요약될 수 있는 이상적인 도파관 내에서의 광대역 확산 특징을 기반으로 개발되었으며, 배열 기울기가 존재하는 상황에서도 배열 기울기와 거리를 동시에 추정할 정도로 강인하다. 최근에는 도파관 불변성의 각도 종속성을 완전히 고려할 수 있도록 확장되었다. 하지만, 거리-종속 환경에 대해 거리-독립 환경의 배열 불변성 기법을 적용한다면, 해저 지형 오정합에 의해 거리추정오차가 발생하게 된다. 본 논문에서는 이러한 거리추정 오차를 상응 거리 개념을 도입하여 해석하고자 한다. 거리-종속 환경에서의 수치 시뮬레이션 수행과 해상 실험 데이터를 통해 거리추정의 오차와 상응 거리 사이의 관계를 입증하였다.

키워드

천해역

도파관 불변성

배열 불변성

배열 기울기

거리추정

거리 종속 환경

상응 거리

MAIN

I. 서 론
II. 배열 불변성 기반 거리추정
2.1 RADAR07 실험
2.2 배열 불변성
III. 상응 거리
IV. 시뮬레이션
V. 해상실험 데이터
VI. 결 론

I. 서 론

배열 불변성은 천해역에서 강인한 거리추정을 위해 개발되었으며, 2000년대 후반 Søstrand와 Lee에 의해 처음 제안된 이후 2010년대 후반부터 다양한 환경에 대해서 개발되면서 발전하였다.^[1,2,3,4]

𝜒라는 파라미터로 정의할 수 있는 배열 불변성은 도파관 불변성(i.e., $β = \cos^{2} θ$ )으로 요약할 수 있는 이상적인 도파관에서의 분산 특징들을 기반으로 거리를 추정한다.^[3] 많은 경우에 대해 천해역에서는 이상적인 도파관과 마찬가지로 해수면/해저면 반사파에 의해 지배되며, 임계각에 의해 낮은 각도(e.g., $| θ | < 20$ °)로 수신되므로 𝛽를 1로 가정할 수 있다.^[5]

초기의 배열 불변성은 임펄스성 송신 신호에 대해서만 시간 영역 빔형성 기법을 적용한 후 빔-시간 그래프를 통해 거리를 추정할 수 있는 제약이 존재했다. 이후 Song과 Cho^[6]는 알고 있는 송신 신호에 대해 정합 필터 또는 블라인드 디컨볼루션^[7]을 적용함으로써 채널 임펄스 응답을 얻어 거리를 추정하도록 확장하였으며, Cho는 배열 기울기에 대한 거리추정 영향을 살펴봤다.^[8] 더 나아가 Byun은 임의의 신호라고 할 수 있는 선박 방사소음에 대해 어떠한 환경 정보 없이 거리를 추정하도록 확장하였으며,^[9,10,11,12] 그뿐만 아니라 목적 함수를 기반으로 배열의 기울기와 거리추정을 동시에 수행할 수 있는 알고리즘을 제안하였다.^[13]

하지만, 이마저도 𝜒와 𝛽가 분리되어있는 형태로 제안되고 있어 𝛽의 각도 종속성을 고려할 수 없는 즉, 상수로 표현할 수밖에 없는 구조이고, 이를 표준형 배열 불변성이라 정의하였다.^[14] 이러한 각도 종속성을 해결하기 위해 Byun은 𝜒와 𝛽를 하나의 파라미터로 정의하는 $χ_{β}$ 를 제안하였고, 이를 적응형 배열 불변성이라 정의하였다.^[14] 이로부터 각도 편차가 커 거리추정 오차가 커질 수 있는 환경에서도 2 % 이내의 거리추정 오차율이라는 매우 강인한 연구 결과를 보였다.

대부분의 천해역에서 형성되는 이상적인 도파관의 특징에서는 $β = \cos^{2} θ$ 이지만, 거리-종속 환경에서는 𝛽를 해저 지형에 대해서도 고려해야 한다. Cho와 Byun은 모두 해저 지형 변화가 고려된 𝛽를 반영한 거리추정 연구를 발표하였으며,^[15,16] Cho는 선형 기울기를 가진 해저 지형 환경에서^[15] 그리고 Byun et al.^[16]은 곡선 형태(e.g., 활과 같은 형상)를 갖는 해저 지형 환경에서의 거리추정 결과를 발표하였다. 특히, Byun의 연구에 따르면, 거리-종속 환경의 데이터에 대해 거리-종속 환경에서의 적응형 배열 불변성을 적용할 때 평균적으로 3 %의 오차율을 보였지만, 거리-독립 환경에서의 적응형 배열 불변성을 적용할 때, 평균적으로 53 %의 오차율이 나타남을 보였다.

위와 같은 큰 오차율은 결국 해저 지형에 의한 오정합에 기인한 결과라고 할 수 있으며, 이러한 오정합은 기존의 정합장 처리 연구에서 일부 설명된 바 있다. 정합장 처리는 배열 센서로 획득한 수신 신호와 파동방정식을 이론적/수치적으로 계산하여 얻은 음장 사이의 상관성을 통해 음원의 위치를 찾는 기법으로, 많은 관련 연구가 수행되었다.^{[17,18,19,20,21,22]} 음장을 계산하기 위해서는 해양 환경 정보를 정확하게 알아야 하는데, 계산에 적용된 해저 지형과 실제 해저 지형이 다를 경우 음원이 실제가 아닌 다른 위치에 있는 것과 같은 결과를 도출하게 된다. 이를 신기루(mirage) 현상이라고도 한다.^[23] 따라서, 정합장 처리 관점에서의 신기루 현상을 정리하면, 다음과 같다:

1) 음장 계산 시 실제 수심보다 낮은 수심을 반영한다면, 음원이 더 가까이 있는 것과 같은 결과 도출

2) 음장 계산 시 실제 수심보다 깊은 수심을 반영한다면, 음원이 더 멀리 있는 것과 같은 결과 도출

즉, 이는 해저 지형 차이로 인해 실제 음장과 동일한 위상을 갖는 위치가 실제 음원 위치와 달라지는 것을 의미한다. Harrison은 거리-종속 환경에서 상응 파라미터(effective parameters) 개념을 도입하여, 서로 다른 두 해저 지형에 대해 한 위치에서의 음장의 위상과 동일한 위상을 갖는 위치를 수치적으로 계산하였다.^[24] Harrison은 이러한 등가 위치들을 상응 파라미터로 정의하고 있으며, 정합장 처리에서의 신기루 현상과 관련이 있을 수 있다고 언급하고 있다. 상응 파라미터에 대한 수식은 단열 근사(adiabatic approximation)를 가정할 수 있는 약한(weakly) 거리-종속 환경에서 전개하고 있다. 약한 거리-종속 환경을 거리-독립으로 변환했을 때의 등가가 되는 네 개의 파라미터[i.e., 수심( $H$ ), 음원( $z_{s}$ )과 수신기( $z_{r}$ )의 깊이, 거리( $r$ )]에 대한 수식을 정의하였다.

정합장 처리와 배열 불변성 모두 수동 신호 처리 기법일 뿐만 아니라, 해저 지형 오정합에 의한 오차가 발생할 수 있다는 공통점이 있다. 따라서, 본 논문에서는 앞서 언급한 거리-종속 환경의 데이터에 대해 거리-독립 환경에서의 적응형 배열 불변성 기법을 적용함으로써 나타나는 오차율(53 %)에 대한 원인을 상응 파라미터 중 상응 거리(effective range) 관점에서 해석하고자 한다. 즉, 배열 불변성과 상응 거리와의 관계를 확인하고자 한다. 본 논문 내에서의 모든 거리추정 결과는 각도 종속성을 고려함으로써 매우 효과적으로 거리를 추정하는 적응형 배열 불변성을 통해 도출한다. 따라서, 표현의 단순화를 위해, 이 부분 이후부터는 편의상 ‘적응형 배열 불변성’을 ‘배열 불변성’으로 표현한다.

이후의 본 논문의 구성은 다음과 같다. II장에서는 거리-종속 환경의 해상 실험에 대한 소개와 함께, 거리-독립 환경 기반의 배열 불변성 거리추정 결과를 보여줌으로써 문제점을 제시한다. III장에서는 Harrison에 의해 제안된 상응 거리 개념에 대해 리뷰한다. IV장에서는 시뮬레이션을 기반으로 배열 불변성과 상응 거리 사이의 관계를 검증하고, 이를 해상 실험 데이터와 비교한 결과를 V장에 나타낸다. 마지막으로 VI 장에서는 본 논문의 결론을 맺는다.

II. 배열 불변성 기반 거리추정

2.1 RADAR07 실험

2007년 7월, 포르투갈 서쪽 연안의 낮은 기울기를 가진 대륙붕에서 Random Array of Drifting Acoustic Receivers(RADAR) 07 해상 실험이 수행되었다. 이 지역은 낮은 대륙붕과 협곡, 해산으로 이루어진 복잡한 해저 지형적인 특징으로 인해 중요한 내부 조석 활동이 이루어진 해역이다.^[3,15,16] Fig. 1은 RADAR07 해상 실험이 수행된 해역 및 모식도로, 본 논문의 저자가 발표한 기존 논문의 그림을 재사용하였다.^[16] Fig. 1(a)는 해상 실험이 수행된 지역에 대한 해저 지형 지도를 보여주는 그림으로, 노란색 선과 화살표는 본 논문에서 활용된 음원의 경로 및 방향을 의미한다. 이 경로는 JD 194(7월 13일)의 17시 37분부터 18시 18분까지 총 42분 동안의 경로이며, 이 기간에 획득한 데이터를 분석한다. 또한, 본 논문에서는 수직 배열 센서 데이터를 분석하였으며, 해당 위치는 Fig. 1(a)에서 “VA”로 표기하였다.

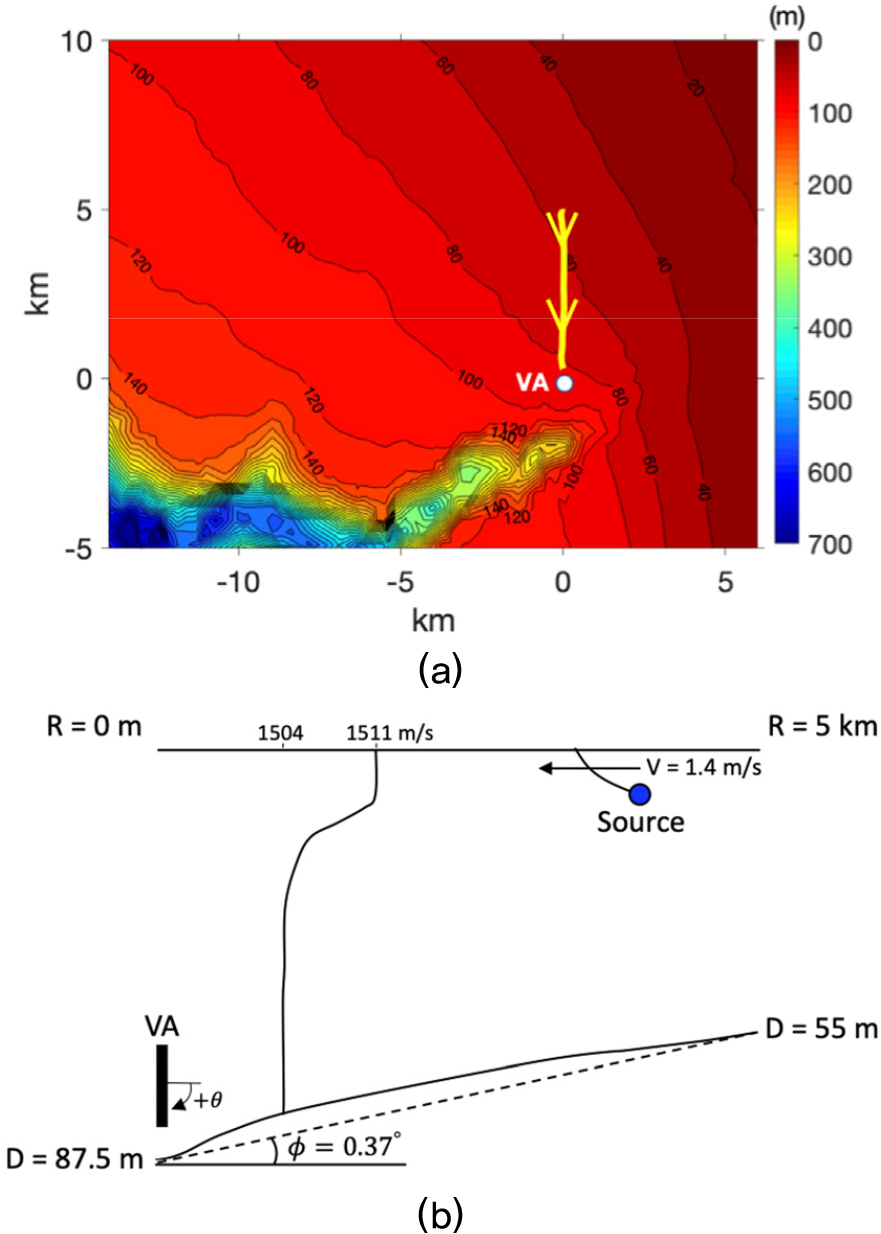
https://cdn.apub.kr/journalsite/sites/ask/2024-043-04/N0660430410/images/ASK_43_04_10_F1.jpg

Fig. 1.

(Color available online) (a) Bathymetry map around the experimental site. This map feature contours at 20 m intervals. The white color denotes the location of the vertical array, while the yellow arrow signifies the ship track descending towards the receiver over a duration of about 42 min (17:37-18:18 UTC) during a source-tow run. (b) Schematic of a source-tow run on JD 194 (July 13) using the R/V NRP D. Carlos 1 during RADAR07. The actual bathymetry exhibit a bow-shaped curve (solid line), ranging from 87.5 m at the receiver to 55 m over a range of 5 km. The slope between the 5 km range measures about 0.37°.

Fig. 1(b)는 본 논문에서 분석하고자 하는 해양 환경 모식도를 보여주는 그림으로, 음원은 R/V NRP D. Carlos 1이라는 실험선에 의해 약 3 노트(1.4 m/s)의 속도로 6 m의 깊이에서 예인되었다. 실제 해상 실험 당시 수직 배열 센서는 세 개의 설계 주파수로 구성된 네스티드 배열이 사용되었으나, 본 논문에서는 중앙이 70 m에 위치하면서 32개의 센서가 등간격으로 구성된 2.8 m 길이의 수직 배열 센서를 분석한다. 해상 실험 동안, 음원에서는 3 kHz의 대역폭(0.5 kHz ~ 3.5 kHz)을 갖는 광대역 신호를 송신하였다. Fig. 1(a)에서 보여진 음원의 이동 경로에서 수신기 위치의 수심은 87.5 m이며, 초기 음원 위치인 5 km 거리에서의 수심은 55 m이다. 5 km 거리 구간의 해저 지형은 Fig. 1(b)에서 실선으로 나타낸 것과 같이 활 모양으로 변하는 형태이며, 양 끝 지점의 수심을 직선으로 이었을 때[Fig. 1(b)에서의 파선(dashed line)] 기울기는 약 0.37°로 이루어져 있다.

Fig. 1(b)에 나타낸 음속 구조는 Conductivity, Temperater, and Depth(CTD)에 의해 측정되었으며, 10 m까지는 혼합층 그리고 급격한 수온약층으로 구성되어 하향 굴절 환경의 특징을 지니는 환경이다. 하지만, 음원이 해수면 근처에 위치함에 따라, 해수면 및 해저면 반사에 의해 전파되는 고차 모드들이 우세한 환경이다. 따라서, 모드 분산 관점에서 이상적인 도파관과 같은 환경임을 예상할 수 있다.^[16]

2.2 배열 불변성

배열 불변성은 도파관 불변성( $β = \cos^{2} θ$ )과 배열 불변성(𝜒)이라는 두 개의 파라미터가 분리된 형태의 기존의 표준형 배열 불변성을 하나의 배열 불변성 파라미터( $χ_{β}$ )으로 나타냄으로써, 모든 파면의 각도들에 대한 정보를 활용하여 거리를 추정하는 기법이다.^[15,16]

Eq. (1)은 배열 불변성 기반 거리추정 식을 의미하며, 여기서 $r$ 은 추정된 거리, 그리고 $c$ 는 음속 값을 나타내며 음속은 1500 m/s으로 설정해도 무방하다.

(1)

r = - \frac{c}{χ_{β}} .

배열 불변성 파라미터( $χ_{β}$ )는 Eq. (2)와 같이 정의된다. 여기서 𝜃는 접지각(grazing angle)에 대한 정보를 나타낸다.

(2)

χ_{β} \equiv χ / β = \frac{d (\cos θ)}{d t} \frac{1}{\cos^{2} θ} = - [\frac{\sin θ}{\cos^{2} θ}] \frac{d θ}{d t},

여기서 𝜒는 배열 불변성이라는 파라미터로써 $\frac{d (\cos θ)}{d t}$ 로 표현될 수 있고, 도파관 불변성 𝛽는 $\cos^{2} θ$ 로 표현된다.^[3]

Eq. (2)의 양변을 적분하면 Eq. (3)과 같이 나타낼 수 있으며, 여기서 $d_{β}$ 는 적분 상수이다.

(3)

χ_{β} t + d_{β} = - \frac{1}{\cos θ} = - \frac{1}{\sqrt{1 - \sin^{2} θ}} .

수직 배열 센서를 통해 수신 신호에 시간 영역 빔 형성을 적용하면 여러 파면들에 대한 상대적 도달 시간과 접지각을 얻을 수 있다. 이러한 상대적 도달 시간과 접지각 정보들은 $χ_{β}$ 를 추정하기 위해 활용되며, 최소자승법 기법을 통해 최적의 $χ_{β}$ 를 추정할 수 있다.

Eq. (3)에서 수직 배열 센서 환경에서의 $χ_{β}$ 추정을 위한 최소자승법 식은 Eq. (4)와 같이 정의할 수 있다. Eq. (4) 내부의 $S$ 와 $T$ 는 Eq. (5)와 같다.

(4)

[\hat{χ_{β}} \hat{d_{β}}] = (T^{T} T)^{- 1} T^{T} S,

(5)

S = - [\begin{matrix} (1 - \sin^{2} θ_{1})^{- 1 / 2} \\ (1 - \sin^{2} θ_{2})^{- 1 / 2} \\ \dots \\ (1 - \sin^{2} θ_{K})^{- 1 / 2} \end{matrix}], T = [(t_{1}, t_{2}, \dots, t_{K})^{T} 1^{T}],

여기서 $T$ 는 전치 행렬을 의미하며, $1$ 은 $K$ 개 성분을 가진 행벡터이다. 또한, $K$ 는 파면의 개수를 나타낸다.

또한, Eq. (3)의 양변에 제곱하여 정리하면 Eq. (6)과 같은 형태의 빔-시간 그래프가 얻어지게 된다.

(6)

{(\frac{t - t_{c}}{1 / χ_{β}})}^{2} - \frac{1}{1 - \sin^{2} θ} = 0 .

Eqs. (1), (2), (3), (4), (5), (6)은 거리-독립 환경에서의 배열 불변성에 대한 수식들이며, 이를 거리-종속 환경의 데이터에 적용하고자 한다.

Fig. 2는 앞서 언급한 RADAR07 데이터 중 약 2,485 m 거리에서의 데이터에 대한 분석 결과이다. Fig. 2(a)는 수신 신호와 알고 있는 송신 신호와의 정합 필터를 통해 얻은 채널 임펄스 응답을 의미한다. 채널 임펄스 응답에는 크고 작은 파면들이 보이며, 가로축과 세로축은 각각 상대적인 시간과 깊이를 의미한다.

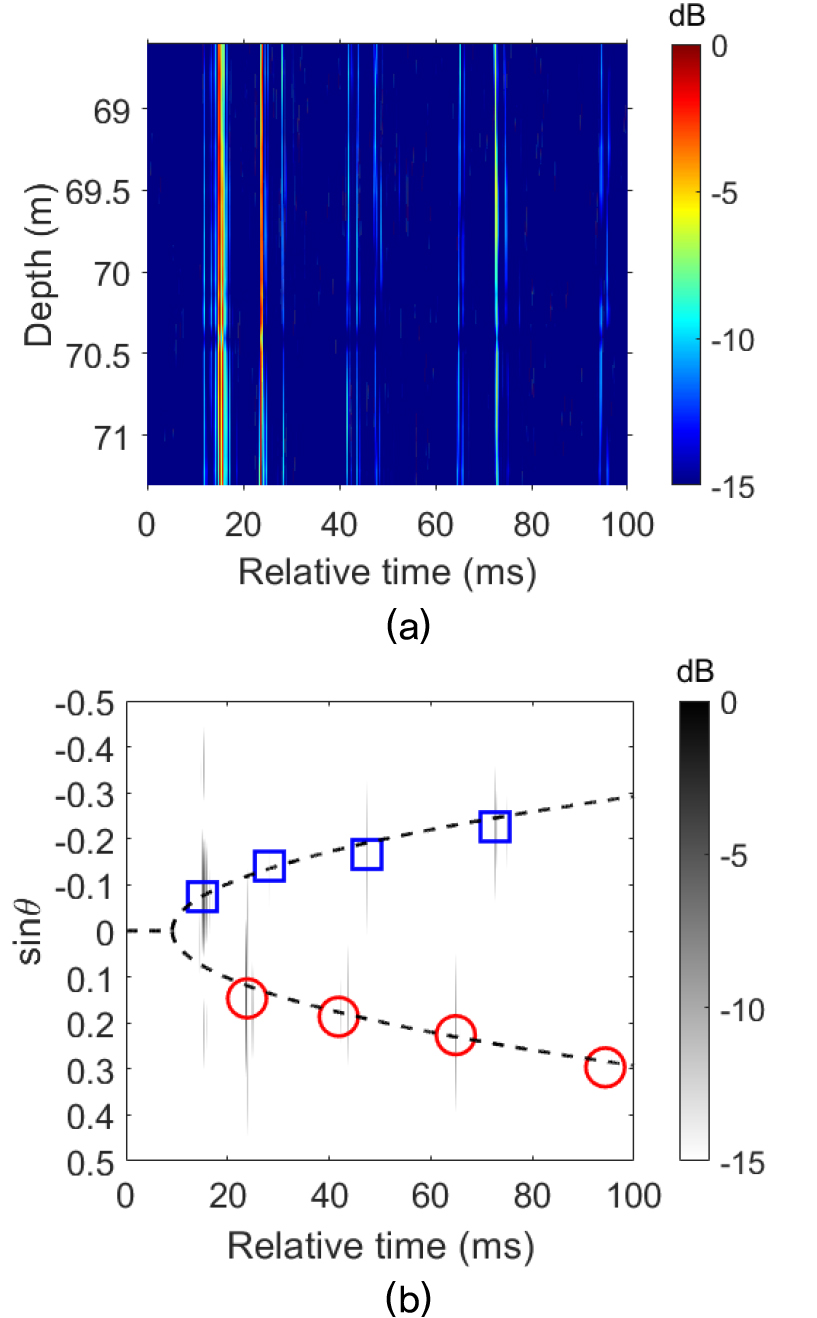
https://cdn.apub.kr/journalsite/sites/ask/2024-043-04/N0660430410/images/ASK_43_04_10_F2.jpg

Fig. 2.

(Color available online) (a) Channel impulse response (CIR) measured after matched filtering at 2,485 m. (b) Beam-time migration (dashed line) of the CIR in ( $t$ , $\sin θ$ ) coordinate, corresponding to (a). The eight reflected arrivals with four up-going (blue circles) and four down-going (red squares) paths are selected, and the corresponding least-square estimate of $χ_{β}$ is calculated for source-range estimation.

파면의 개수와 각 파면들의 정보를 알기 위해서 채널 임펄스 응답에 대해 시간 영역 빔형성 기법을 적용하면, Fig. 2(b)와 같은 결과가 도출된다. 이로부터 8개의 파면들의 상대적인 도달 시간 및 접지각을 얻을 수 있다. 여기서, 빨간색 원과 파란색 사각형들은 각각 양과 음의 각도로 수신되는 파면들의 상대적인 도달 시간 및 접지각이다. 이 파면 정보들(i.e., 상대적인 도달 시간 및 접지각)은 특정 문턱치를 기준으로, 기준보다 높은(즉, 지배적인) 파면만을 추출한 것이다.

상대적인 도달 시간과 접지각을 Eqs. (4)에서 (6)에 적용하면 $\hat{χ_{β}}$ 와 함께, Fig. 2(b)의 검은색 파선과 같은 빔-시간 그래프를 얻게 된다. Fig. 2(b)에서도 알 수 있듯이 모든 파면의 정보들이 빔-시간 그래프 위에 위치하고 있으며, 이는 $\hat{χ_{β}}$ 가 성공적으로 추정됨을 의미한다. 모든 접지각들은 부호 상관없이 크기만을 표현할 때 4°에서 19° 사이에 분포하였고, 이는 작은 각도를 가정할 수 할 수 있는 범위( $| θ | < 20 °$ ) 안에 포함된다.^[16] 상대적인 도달 시간과 접지각을 통해 추정한 거리는 3,531 m이며, Global Positioning System (GPS) 수치와의 오차는 약 42 %로 매우 크다.

이러한 과정을 모든 데이터에 적용함으로써, 추정된 $\hat{χ_{β}}$ 과 Eq. (1)를 활용하여 거리를 추정한다면 Fig. 3과 같은 결과를 얻게 된다. 여기서 검은색 실선은 GPS로 측정한 거리이며, 빨간색 원은 배열 불변성으로 추정한 거리이다. 검은색 화살표는 Fig. 2에서 분석한 데이터에 대응하는 시간대를 의미한다.

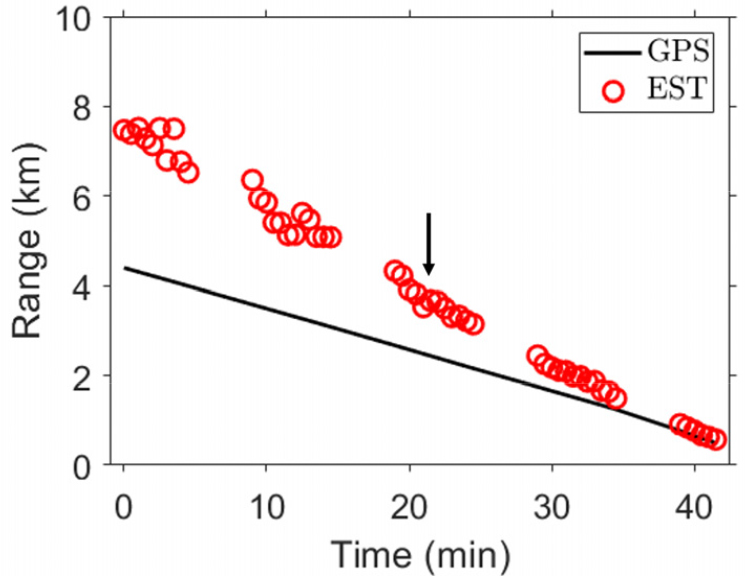
https://cdn.apub.kr/journalsite/sites/ask/2024-043-04/N0660430410/images/ASK_43_04_10_F3.jpg

Fig. 3.

(Color available online) The array invariant (AI)-based ranging in a range-independent environment (red circles) during the source-tow run for about 42 min (17:37-18:18 UTC). The solid line is based on the ship’s GPS, and the black arrow indicates the time corresponding to Fig. 2.

Fig. 3으로부터 거리-독립 환경 기반의 배열 불변성 결과와 GPS 수치를 비교했을 때, 오차가 확연하게 드러나고 있으며 이는 거리가 멀수록 두드러지고 있다. 거리가 멀어질수록 오차가 증가하는 이 현상은 해저 지형의 차이로 인한 것으로 예상할 수 있다.

본 절에서는 거리-종속 환경의 데이터에 거리-독립 환경의 배열 불변성을 적용했을 때의 문제점(거리추정 오차 발생)을 제시하였으며, 다음 장부터는 원인에 대해 해석하고자 한다.

III. 상응 거리

본 장에서는 거리-종속 환경에서의 음장 계산 식으로부터 유도되는 상응 거리에 대한 개념에 대해서 리뷰한다. Harrison은 2003년 상응 거리에 대한 개념을 등음속 환경 기준 모드 이론을 바탕으로 발표하였으며, 이를 정리하고자 한다.^[24]

Fig. 1(b)와 같이 공간적인 변화가 크지 않은 해저 지형은 단열 근사가 사용될 수 있으며, 모드 사이의 에너지 결합(coupling)을 무시할 수 있다.^[23,25] 즉, 이러한 약한 거리-종속 환경에서의 음장은 아래의 Eq. (7)과 같이 단열 모드 이론을 활용하여 표현할 수 있다.^[24]

(7)

p (r, z) = (2 π)^{1 / 2} e^{- i π / 4} \times \sum_{m} \{ϕ_{m} (0, z_{s}) ϕ_{m} (r, z_{s}) \times \frac{\exp (i \int_{0}^{r} K_{m} (r') d r')}{{[\int_{0}^{r} K_{m} (r') d r']}^{1 / 2}}\} .

$m$ 번째 모드에 대한 지수항(또는 분모)은 $\int K_{m} (r) d r$ 의 형태를 가지며, 등음속 환경에서 파수 $k$ 를 가질 때의 모드는 Eq. (8)과 같다.

(8)

ϕ_{m} (r, z) = {(\frac{2}{H (r)})}^{1 / 2} \sin (\frac{m π z}{H (r)}) .

따라서, 파수의 수평방향 성분은 Eq. (9)와 같이 나타낼 수 있다.

(9)

K_{m}^{2} = k^{2} - {(\frac{m π}{H (r)})}^{2} .

Eq. (7)의 우변에 있는 $m$ 번째 모드에 대한 지수항(또는 분모)에 있는 $\int K_{m} (r) d r$ 에 Eq. (9)를 대입한 후 테일러 급수를 활용하면 Eq. (10)과 같이 전개할 수 있다. 이때, 작은 접지각 즉, 저차 모드만을 고려함으로써, 테일러 급수의 이차항부터는 무시한다.^[24]

(10)

\int_{0}^{r} K_{m} (r) d r = \int_{0}^{r} k \sqrt{1 - {(\frac{m π}{k H (r)})}^{2}} d r = \int_{0}^{r} k (1 - \frac{1}{2} \frac{m^{2} π^{2}}{k^{2} H (r)^{2}} + \dots) d r \approx \int_{0}^{r} k (1 - \frac{1}{2} \frac{m^{2} π^{2}}{k^{2} H (r)^{2}}) d r = \int_{0}^{r} k d r - \frac{m^{2} π^{2}}{2 k^{2}} \int_{0}^{r} \frac{1}{H (r)^{2}} d r .

(11)

\int_{0}^{r} K_{m} (r) d r \approx k r - \frac{m^{2} π^{2}}{2 k^{2}} \int_{0}^{r} \frac{1}{H (r)^{2}} d r .

Eq. (10)을 최종적으로 정리한 Eq. (11)을 통해, 같은 위상을 얻는 데 있어 $\int_{0}^{r} \frac{1}{H (r)^{2}} d r$ 은 모드 번호에 독립임을 알 수 있으며 이를 기반으로 동일 수신기 환경에서의 상응 거리를 정의할 수 있다.

Fig. 4는 상응 거리( $r_{e}$ ) 정의에 관한 이해를 돕기 위해 표현한 개념도이다. 수신기 깊이 및 수신기 위치의 수심이 고정된 환경에 대하여, 거리-종속 환경에서의 위상과 동일한 위상을 갖는 거리-독립 환경을 나타내기로 한다. 이를 위해서는 결국 우변 중 적분항만 같아지면 된다. 거리-독립 환경은 수심이 유지되는 환경이므로, Eq. (11)에서 우변 중 적분항을 거리-종속과 거리-독립 환경에 대한 비교로 다시 표현한다.

(12)

\int_{0}^{r} \frac{1}{H (r)^{2}} d r = \frac{r_{e}}{H_{r}^{2}},

(13)

r_{e} = H_{r}^{2} \int_{0}^{r} \frac{1}{H (r)^{2}} d r,

여기서 $H_{r}$ 은 수신기 위치의 수심을 의미한다.

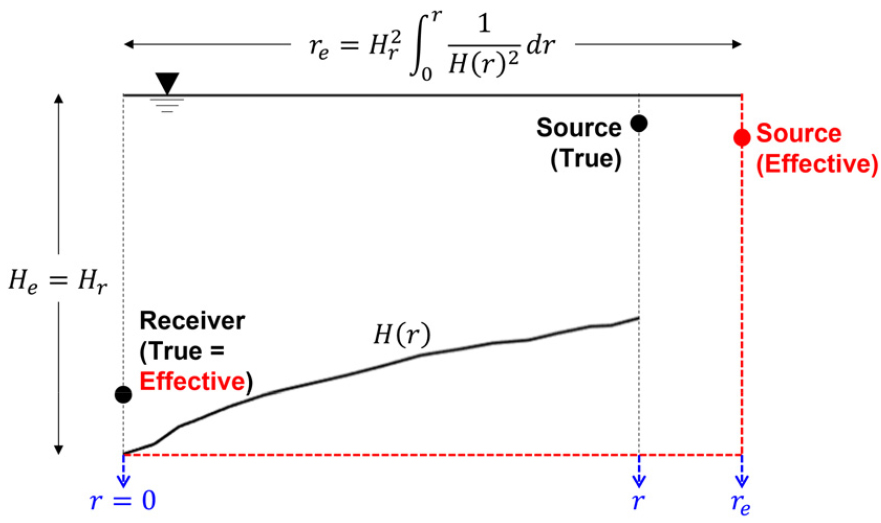
https://cdn.apub.kr/journalsite/sites/ask/2024-043-04/N0660430410/images/ASK_43_04_10_F4.jpg

Fig. 4.

(Color available online) True and effective geometries. Effective depth equals depth at receiver and effective range is determined by the receiver depth and the actual bathymetry as a function of range. The black and red circles represent the true and effective parameters (e.g., depth or/and range), respectively.

Eq. (12)에서 좌변과 우변은 각각 거리-종속과 거리-독립 환경에서의 표현이다. 그리고 정합장 처리를 포함한 모든 수동 신호 처리 시스템은 수신기 위치의 수심을 기반으로 수행되므로, 우변에서 수심은 수신기의 수심으로 표현된다. 따라서, 우변의 분자인 $r_{e}$ 은 결국, 거리-종속 환경과 수신기 수심으로 구성된 거리-독립 환경의 위상이 등가가 되는 거리를 의미한다. 이를, 상응 거리라고 정의하며, 상응 거리를 기준으로 Eq. (12)를 다시 표현하면 Eq. (13)과 같다.

즉, 신호 처리 관점에서 상응 거리를 설명한다면, 거리-종속 환경을 통해 수신된 신호를 거리-독립 환경으로 처리했을 경우, 나타나게 되는 음원의 거리를 의미한다고 할 수 있다.

다음 장에서는 시뮬레이션을 기반으로 거리-종속 환경의 데이터에 대한 거리-독립 환경 기반의 배열 불변성 거리추정 결과와 상응 거리 개념과의 관계를 살펴보고자 한다.

IV. 시뮬레이션

Fig. 1(b)와 같은 해저 지형은 단열 근사 가정을 적용할 수 있을 정도로 약한 거리-종속 환경이라 할 수 있으므로, 단열 모드 이론을 기반으로 채널 임펄스 응답을 모의한다.^[23,25] 모의를 위한 해양 환경 정보로는 Fig. 1(b)에 나타낸 음속 구조와 해저 지형을 활용하였으며, 음원의 거리는 2.2절과 같이 2,485 m로 설정하였다.

Fig. 5(a)는 시뮬레이션을 통해 계산한 채널 임펄스 응답을 나타내며, 8개의 파면 그룹이 도달하고 있음이 확인된다. 모의한 채널 임펄스 응답에 시간 영역 빔형성 기법을 적용하면 Fig. 5(b)와 같은 결과를 얻을 수 있으며, 데이터와 마찬가지로 빨간색 원과 파란색 사각형들은 각각 양과 음의 각도로 수신되는 파면들의 상대적인 도달 시간 및 접지각을 의미한다. 8개의 파면 그룹 중 두 개씩 겹쳐진 파면들도 보이는데, 이는 얕은 깊이에 위치한 음원으로 인한 로이드 미러 효과이다.^[5]

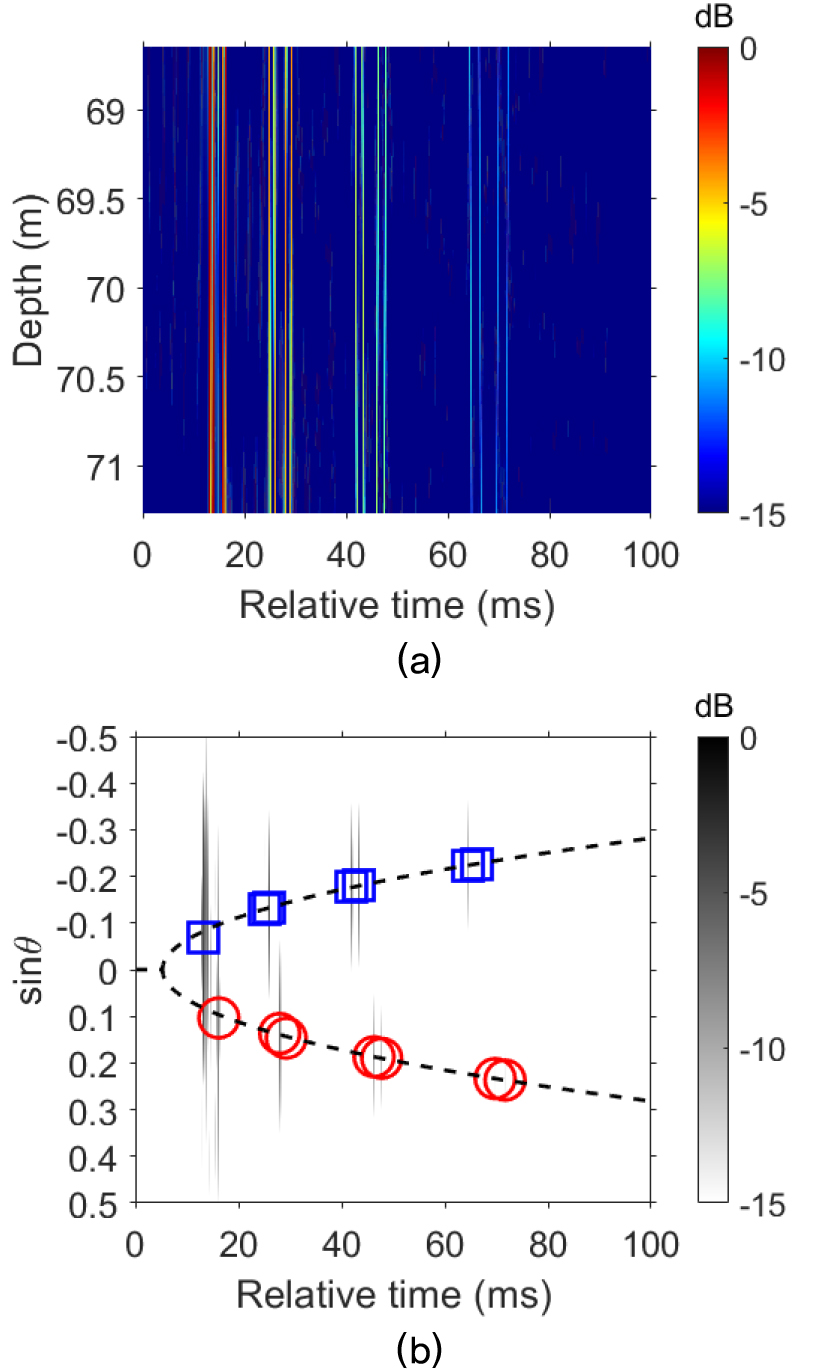
https://cdn.apub.kr/journalsite/sites/ask/2024-043-04/N0660430410/images/ASK_43_04_10_F5.jpg

Fig. 5.

(Color available online) (a) CIR at 2,485 m simulated in a range-dependent environment. (b) Beam-time migration (dashed line) of the CIR, corresponding to (a). The eight reflected arrival groups with four up-going (blue circles) and four down-going (red squares) paths are selected. Some of the eight groups exhibit the effect of Lloyd’s mirror, revealing two arrivals. The corresponding least-square estimate of $χ_{β}$ is calculated for source-range estimation.

8개의 파면 그룹의 각도는 크기 기준으로 4°에서 13° 사이에 분포하였고, 이 역시 작은 각도를 가정할 수 있는 범위( $| θ | < 20$ °) 안에 포함된다.^[5] 이러한 파면 정보들을 통해 $\hat{χ_{β}}$ 를 추출하면, Fig. 5(b)에서의 파선과 같이 빔-시간 그래프를 그릴 수 있을 뿐만 아니라 거리를 추정할 수 있다. 상대적인 도달 시간과 접지각을 통해 추정한 거리는 3,393 m이며, GPS 수치와의 오차는 약 37 %로 데이터와 마찬가지로 매우 크다.

이를 바탕으로 2,485 m 뿐만 아니라 실제 데이터에 대응하는 모든 경로에 대해 신호를 모의하였으며, 모든 경로에 대한 거리-독립 환경에서 정의된 배열 불변성 기반 거리추정 결과를 Fig. 6(a)에 파란색 원으로 나타냈다. Fig. 6(a)에서 검은색 실선은 모든 경로에 대한 GPS를 의미한다. 또한, 배열 불변성 거리추정 결과와 상응 거리와의 관계를 확인하기 위해 Eq. (13)으로 모든 경로에 대한 상응 거리를 계산하고, 이 역시도 Fig. 6(a)에 녹색 사각형으로 표현한다. Fig. 6(a)에서 화살표는 Fig. 5를 모의한 위치에 해당하는 시간대를 나타낸다.

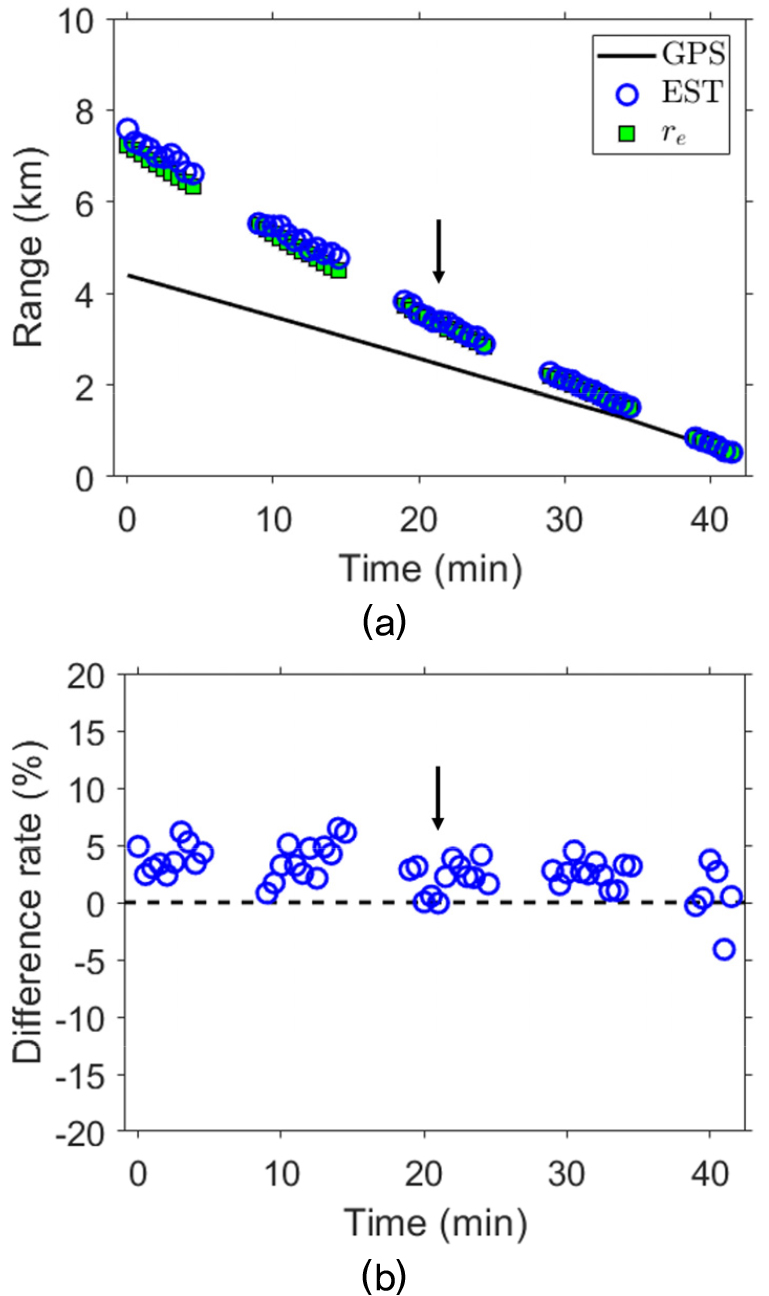
https://cdn.apub.kr/journalsite/sites/ask/2024-043-04/N0660430410/images/ASK_43_04_10_F6.jpg

Fig. 6.

(Color available online) (a) Comparison between the AI-based ranging in a range-independent environment (blue circles) and the effective range (green squares). AI-based ranging is calculated from the data that simulate the source-tow run for about 42 min. The solid line is based on the ship’s GPS. (b) Difference rate between the two results in (a) with respect to the effective range. The black arrows in (a) and (b) indicate the time corresponding to Fig. 5.

Fig. 3에 보여진 실제 데이터와 마찬가지로, 시뮬레이션에서도 배열 불변성 기반 거리추정 오차가 거리가 멀어질수록 증가함을 확인할 수 있다. 하지만, 이러한 오차가 포함된 거리추정 결과는 상응 거리와 일치하고 있음을 알 수 있다. 2,485 m 환경의 경우 계산된 상응 거리 3,391 m이며, 배열 불변성 거리 추정 결과(3,393 m)와의 오차는 ‑0.05 %로 두 결과는 일치한다고 할 수 있다.

따라서, 이러한 GPS와 배열 불변성 거리 추정 결과 사이의 오차는 Eq. (13)을 이용하면 설명할 수 있다. 상응 거리 개념을 다시 표현하면 거리-종속 환경의 음장과 등가가 되는 거리-독립 환경의 위치를 나타내는 것이다. 즉, 데이터가 거리-종속 환경을 통해 수신되었더라도, 거리-독립 환경의 신호 처리를 수행한다면 음원과 수직 배열 센서 사이의 음장이 실제 위치가 아닌 상응 거리가 위치하는 곳으로부터 계산된 것과 같은 모호성이 드러나는 것이라고 할 수 있다. 이로부터 거리-독립 배열 불변성과 상응 거리 사이의 관계가 정의된다고 할 수 있다.

또한, 거리-독립 환경의 배열 불변성은 수심에 대한 항이 포함되지 않는데 거리추정 결과가 수신기 위치의 수심이 고려된 상응 거리와 일치하는 것으로 보아, 거리-독립 환경의 배열 불변성은 해저 지형을 수신기 위치의 수심으로 이루어진 평탄한 환경으로 간주하고 있음을 유추할 수 있다.

추가로 GPS 대비 거리추정 오차에 대해 해저 지형 관점에서 자세하게 분석하면, 다음과 같다. Fig. 1(b)와 같은 해저 지형에서 음원과 수신기가 가까울수록 음원과 수신기 사이의 해저 지형이 평탄하다고 가정할 수 있으므로, 오차가 크지 않다. 하지만, 거리가 멀어질수록 수신기 위치의 수심과 송신기 위치의 수심의 차이가 증가한다. 이때, Eq. (13)과 같이 거리-종속 환경과 거리-독립 환경이 등가를 이루는 상응 거리를 고려한다면, 해저 지형의 제곱의 적분항과 관계가 있으므로 거리 증가에 따라 거리추정 오차는 점차 증가하게 된다. 따라서, 위와 같이 GPS 대비 거리추정 오차는 해저 지형 오차로 해석할 수 있다.

배열 불변성과 상응 거리 사이의 관계는 Fig. 6(a)에서 상응 거리(녹색 사각형)와 배열 불변성 거리추정 결과(파란색 원)의 결과의 수치적인 비교를 통해서도 검증된다. 두 결과의 차이를 비교하기 위해, 상응 거리 대비 배열 불변성 거리추정 결과의 오차율을 Fig. 6(b)에 나타냈다. 두 결과의 차이는 평균적으로 2.9 %(최대 약 5.0 % 이내)를 보이고 있으므로, 상응 거리 기반의 해석은 합리적인 해석이라 할 수 있다.

위 오차를 다시 표현하면, ‘거리-종속 환경에서의 압력과 등가의 압력을 갖는 거리-독립 환경에서의 거리를 의미하는 상응 거리’와 ‘배열 불변성 기반 거리 추정 결과’의 차이이다. 하지만, References [14]와 [16]에 따르면 배열 불변성 기반 거리 추정 결과 자체에 약 3 %의 오차가 나타나고 있으며,^[14,16] 이는 위에서의 2.9 %의 평균적인 오차가 배열 불변성 기법 자체에 의한 오차일 수 있음을 알려준다. 거리-독립 환경에서의 배열 불변성은 $β = \cos^{2} θ$ 라는 가정을 활용하고 있으며, Eq. (1)과 같은 거리 추정 시 1500 m/s를 활용한다. 따라서, 이러한 배열 불변성 기법이 갖는 구조적인 오차를 감안할 때, 상응 거리와 배열 불변성 거리추정 결과가 매우 유사하다고 할 수 있다.

V. 해상실험 데이터

시뮬레이션 결과 및 해석을 바탕으로, 본 장에서는 상응 거리 개념을 해상 실험 데이터에 적용함으로써 간단하게 살펴본다.

Fig. 7은 Fig. 3을 다시 그리고, 그 위에 Fig. 6(a)에 있는 상응 거리를 같이 그린 그림이다. 시뮬레이션과 비교했을 때, 실제 데이터의 거리추정 결과가 시뮬레이션으로부터 예측한 상응 거리보다 조금 더 차이가 나고 있다. 이러한 차이는 실제 해상 실험 데이터에 포함된 환경적 불확실성에 의한 것으로 추정된다. 동일한 거리에 대한 시뮬레이션[Fig. 2(a)] 및 해상 실험 데이터[Fig. 5(a)]의 채널 임펄스 응답을 비교했을 때, 두 채널 임펄스 응답 간의 차이는 매우 유사해 보이지만 두 빔-시간 그래프[Figs. 2(a)와 5(a)]를 비교해보면 파면의 정보에서 조금의 차이가 보인다. 이는 곧 실제 해저 지형의 거칠기 또는 시뮬레이션 시 활용된 샘플링된 해저 지형 격자 사이의 지형 정보 공백 등과 같은 해양 환경에 의한 차이라고 예상할 수 있다. 하지만, 그럼에도 불구하고 해상 실험 데이터로부터 거리-독립의 배열 불변성을 통해 얻은 거리추정 결과의 경향과 시뮬레이션 기반 상응 거리의 경향이 매우 유사함을 알 수 있으며, 이는 이미 시뮬레이션 결과 및 해석을 통해서 입증된 결과와 일치한다.

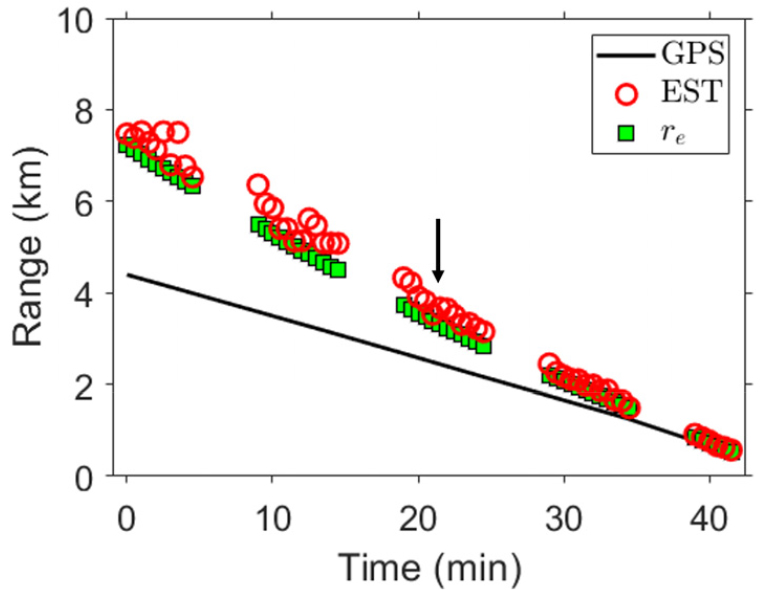
https://cdn.apub.kr/journalsite/sites/ask/2024-043-04/N0660430410/images/ASK_43_04_10_F7.jpg

Fig. 7.

(Color available online) Comparison between the AI-based ranging in a range-independent environment during the entire source-tow run for about 42 min (red circles) and the effective range (green squares). AI-based ranging is calculated from the data that simulate the source-tow run for about 42 min. The solid line is based on the ship’s GPS.

VI. 결 론

배열 불변성은 파면의 도달 각도를 모두 고려할 때, 음원의 거리를 추정하는 데 있어 강인하다고 알려져있다. 하지만, 거리-종속 환경 데이터에 대해 거리-독립 환경으로 정의된 배열 불변성을 적용한다면, 해저 지형 오정합으로 인해 오차가 발생한다.

이러한 오차를 해석하기 위해 본 논문에서는 상응 거리 개념을 도입하고, 수치 시뮬레이션을 통해 해저 지형 오정합 요소가 포함된 거리추정 결과와 상응 거리 사이의 밀접한 관계를 갖는다는 것을 입증하였다. 이를 바탕으로, 해상 실험 데이터와의 비교를 통해 해양 환경의 불확실성으로 인해 얻은 결과라 할지라도, 거리추정 결과의 경향이 상응 거리의 경향과 매우 유사함을 확인하였다.

또한, 거리-독립 환경의 배열 불변성은 해저 지형을 수신기 위치의 수심으로 평탄한 환경으로 간주하고 있다는 사실을 유추할 수 있다. 이러한 결과를 통해, 거리-종속 데이터에 대한 거리-독립 환경의 배열 불변성을 통한 거리추정 오차의 원인을 보다 정확하게 이해할 수 있다는 점이 이 논문의 주요 의의이다.

Acknowledgements

이 논문은 2022학년도 한국해양대학교 신진교수 정착연구지원사업 연구비의 지원을 받아 수행된 연구임.

References

K. A. Søstrand, "Range localization of 10-100 km explosions by means of an endfire array and a waveguide invariant," IEEE J. Ocean. Eng. 30, 207-212 (2005).

10.1109/JOE.2004.834598

S. Lee and N. C. Makris, "The array invariant," J. Acoust. Soc. Am. 119, 336-351 (2006).

10.1121/1.213907416454289

H. C. Song and G. Byun, "An overview of array invariant for source-range estimation in shallow water," J. Acoust. Soc. Am. 151, 2336-2352 (2022).

10.1121/10.000982835461510

H. C. Song and C. Cho, "The relation between the waveguide invariant and array invariant," J. Acoust. Soc. Am. 139, 899-903 (2015).

10.1121/1.492709026328705

F. B. Jensen, W. A. Kuperman, M. B. Porter, and H. Schmidt, Computational Ocean Acoustics (Springer, New York, 2011), pp. 136.

10.1007/978-1-4419-8678-8

H. C. Song and C. Cho, "Array invariant-based source localization in shallow water using a sparse vertical array," J. Acoust. Soc. Am. 141, 183-188 (2017).

10.1121/1.497381228147576

H. C. Song, C. Cho, G. Byun, and J. S. Kim, "Cascade of blind deconvolution and array invariant for robust source-range estimation," J. Acoust. Soc. Am. 141, 3270-3273 (2017).

10.1121/1.498330328599546PMC5433883

C. Cho and H. C. Song, "Impact of array tilt on source-range estimation in shallow water using the array invariant," J. Acoust. Soc. Am. 141, 2849-2856 (2017).

10.1121/1.498177628464645

G. Byun, J. S. Kim, C. Cho, H. C. Song, and S. Byun, "Array invariant-based ranging of a source of opportunity," J. Acoust. Soc. Am. 142, EL286-EL291 (2017).

10.1121/1.500332728964101

H. C. Song and G. Byun, "Simultaneous localization of a surface ship and a submerged towed source," J. Acoust. Soc. Am. 144, 2238-2241 (2018).

10.1121/1.506335230404518

G. Byun, H. C. Song, J. S. Kim, and J. S. Park, "Real-time tracking of a surface ship using a bottom-mounted horizontal array," J. Acoust. Soc. Am. 144, 2375-2382 (2018).

10.1121/1.506479130404486

G. Byun, H. C. Song, and S. Byun, "Localization of multiple ships using a vertical array in shallow water," J. Acoust. Soc. Am. 145, EL528-EL533 (2019).

10.1121/1.511177331255094

G. Byun, C. Cho, H. C. Song, J. S. Kim, and S. Byun, "Array invariant-based calibration of array tilt using a source of opportunity," J. Acoust. Soc. Am. 143, 1318-1325 (2018).

10.1121/1.502584429604662

G. Byun and H. C. Song, "Adaptive array invariant," J. Acoust. Soc. Am. 148, 925-933 (2020).

10.1121/10.000176832873004

C. Cho, H. C. Song, P. Hursky, and S. M. Jesus, "Iterative range estimation in a sloping-bottom shallow- water waveguide using the generalized array invariant," J. Acoust. Soc. Am. 142, 55-60 (2017).

10.1121/1.499067028764451

G. Byun, H. C. Song, and C. Cho, "Adaptive array invariant in range-dependent environments with variable bathymetry," J. Acoust. Soc. Am. 149, 1363-1370 (2021).

10.1121/10.000356233639832

A. B. Baggeroer, W. A. Kuperman, and P. N. Mikhalevsky, "An overview of matched field methods in ocean acoustics," IEEE J. Ocean. Eng. 18, 401-424 (1993).

10.1109/48.262292

A. Tolstoy, Matched Field Processing for Underwater Acoustics (World Scientific, Singapore, 1993), pp. 1-228.

Z. H. Michalopoulou and M. B. Porter, "Matched-field processing for broadband source localization," IEEE J. Ocean. Eng. 21, 384-392 (1996).

10.1109/48.544049

G. J. Orris, M. Nicholas, and J. S. Perkins, "The matched-phase coherent multi-frequency matched field processor," J. Acoust. Soc. Am. 107, 2563-2575 (2000).

10.1121/1.42864410830380

C. Soares and S. M. Jejus, "Broadband matched-field processing: Coherent and incoherent approaches," J. Acoust. Soc. Am. 113, 2587-2598 (2003).

10.1121/1.156401612765377

C. Debever and W. A. Kuperman, "Robust matched-field processing using a coherent broadband white noise constraint processor," J. Acoust. Soc. Am. 122, 1979-1986 (2007).

10.1121/1.276983017902834

G. L. D'Spain, J. J. Murray, W. S. Hodgkiss, N. O. Booth, and P. W. Schey, "Mirages in shallow water matched field processing," J. Acoust. Soc. Am. 105, 3245-3265 (1999).

10.1121/1.424653

C. H. Harrison and M. Siderius, "Effective parameters for matched field geoacoustic inversion in range-dependent environments," IEEE J. Ocean. Eng. 28, 432-445 (2003).

10.1109/JOE.2003.816693

G. L. D'Spain and W. A. Kuperman, "Application of waveguide invariants to analysis of spectrograms from shallow water environments that vary in range and azimuth," J. Acoust. Soc. Am. 106, 2454-2468 (1999).

10.1121/1.428124

The Journal of the Acoustical Society of KoreaISSN:1225-4428(Print) 2287-3775(Online)한국음향학회

Preview

The relationship between the array invariant-based ranging and the effective range in a weakly range-dependent environment

ABSTRACT

MAIN

Fig. 1.

(1)

(2)

(3)

(4)

(5)

(6)

Fig. 2.

Fig. 3.

(Color available online) The array invariant (AI)-based ranging in a range-independent environment (red circles) during the source-tow run for about 42 min (17:37-18:18 UTC). The solid line is based on the ship’s GPS, and the black arrow indicates the time corresponding to Fig. 2.

(7)

(8)

(9)

(10)

(11)

(12)

(13)

Fig. 4.

Fig. 5.

Fig. 6.

Fig. 7.

Acknowledgements

References