I. 서 론
II. 음향메타물질 FEM 해석
2.1 Thermo-viscous acoustic mesh
2.2 4-Microphone method를 이용한 메타물질 소음기 해석
2.3 원형 덕트 내 지그재그 메타물질 소음기 해석
2.4 직렬(Series) 메타물질 소음기 해석
2.5 병렬(Parallel) 메타물질 소음기 해석
III. 결 론
I. 서 론
메타물질은 화학적 성질로 이루어지는 물질이 아니라 주기적인 인공구조물을 이용하여, 음의 굴절률[1] · 음의 탄성률[2] · 음의 밀도[3] 같이 자연계에서 존재하지 않는 파동 현상을 구현할 수 있는 주기적인 구조체이다. 과거에는 물리학 및 전자기학 분야에서 연구되었지만, 현재는 음향학 및 탄성학 분야에서 자연에서 발견할 수 없는 파동 현상을 구현하기 위해 활발하게 연구되고 있다. 예를 들어, 파장보다 매우 작은 구조체의 주기적 배열을 통해 역학적인 탄성률[2]과 밀도[3]를 자유자재로 조절할 수 있다. 이러한 현상을 이용하여, 음향 에너지를 파장보다 매우 작은 영역에 국소적으로 집중시키거나,[4] 기존 방식으로 불가능한 음향 진행경로를 구현하거나,[5] 파장보다 매우 작은 초음파 이미징을[6] 구현하기 위해 메타물질을 이용할 수 있다.
메타물질을 이용하여 음향에너지를 효과적으로 제어하는 것은 과학 및 공학 분야에서 매우 중요한 분야이고, 특히 저주파 대역에서 음향에너지를 효과적으로 흡수 및 차단하는 구조체 설계 및 제작에 많은 관심이 쏠리고 있다. 전통적인 질량 법칙으로 인해, 저주파 에너지를 효과적으로 흡수 및 차단하기 위해 다공성 및 섬유질 재료를 사용할 경우 부피가 크고 무거운 재료를 사용해야 한다. 그러나 음향 메타물질을 활용하면 파장보다 매우 작은 두께의 박막 구조로도 저주파 에너지를 차단 및 흡수할 수 있다. 이를 통해 다양한 경량 음향 차단제 및 흡수제가 최근 들어 개발되고 있다. 예를 들어, 저주파 대역의 음향 에너지를 제어하기 위해 헬름홀츠 형상의 공진 구조 어레이를 이용하여 음의 탄성률을 구현하거나,[2] 멤브레인 타입 메타물질을 이용하여 음의 밀도[7] 및 제로 밀도[8]를 구현하여 음향 에너지를 효과적으로 차단 및 흡수가 가능하다. 또한 지그재그 구조를 이용하여,[4,9] 소리의 공간상의 진행 속도를 감소시켜 파장보다 매우 작은 구조물로 저주파 대역에서 효과적으로 작동하는 소음 저감 구조를 구현할 수 있다.
최근 들어 덕트 내의 소음을 저감하는 분야에서 음향 메타물질을 접목하려는 연구가 활발히 수행되고 있다.[10,11] 덕트 내의 소음 저감은 기계 산업 전반에 사용되고 있는 핵심 분야이다. 특히, 전자기기가 소형화 될수록 유동 및 소음문제가 발생하는데, 이러한 문제점을 해결하기 위해 소음을 저감하는 얇은 두께의 음향 소음기가 필요하다.
본 연구에서는 지그재그 형상 구조를 이용하여, 고 굴절 메타물질과 헬름홀츠 형상을 기본으로 저주파에서 작동하는 초소형 소음기를 개발하는데 목적이 있다. 구체적으로, 10 cm 지름을 갖는 덕트 내의 소음을 저감하기 위해 2 cm의 반경 방향 두께를 갖는 고 굴절 메타물질 음향 소음기를 설계하였다. 또한, 지그재그 구조 내 점성 및 열의 기여를 예측하기 위해서 Thermo-viscous acoustic mesh를 사용해 Finite Element Method(FEM) 해석을 수행하고, 이로부터 음파분리법을 이용하여 메타물질 소음기의 투과율, 반사율, 흡음률과 투과손실을 구하였다. 지그재그 내부 구조물의 간격을 조절하며 위의 과정을 반복하여 차단 주파수 및 투과손실의 변화를 관찰하였고, 3가지 형상의 메타물질들을 직렬 및 병렬 배치하여 음향 에너지 차단 효과를 비교하였다.
II. 음향메타물질 FEM 해석
2.1 Thermo-viscous acoustic mesh
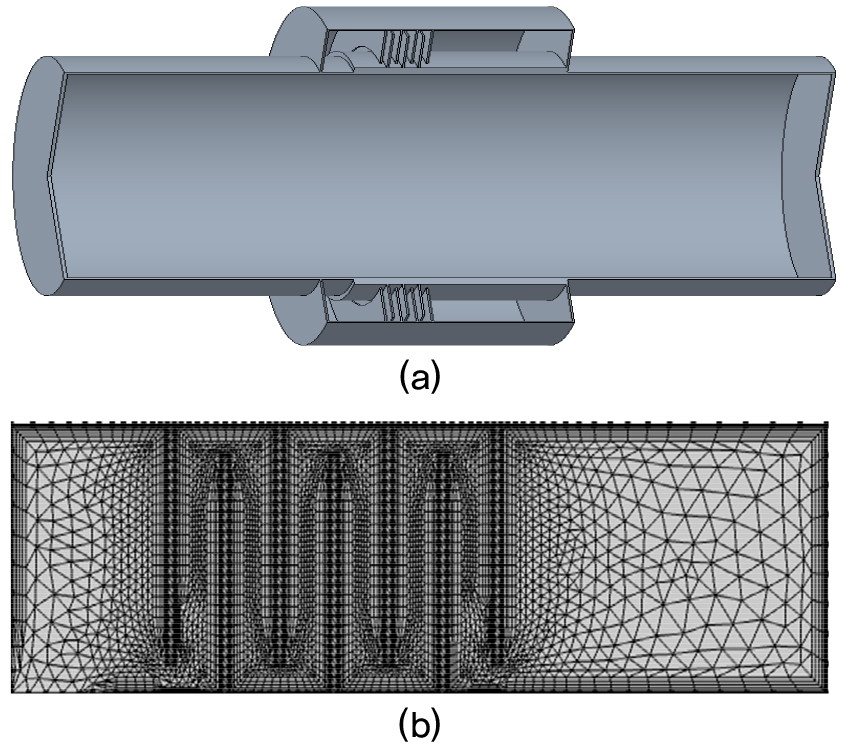
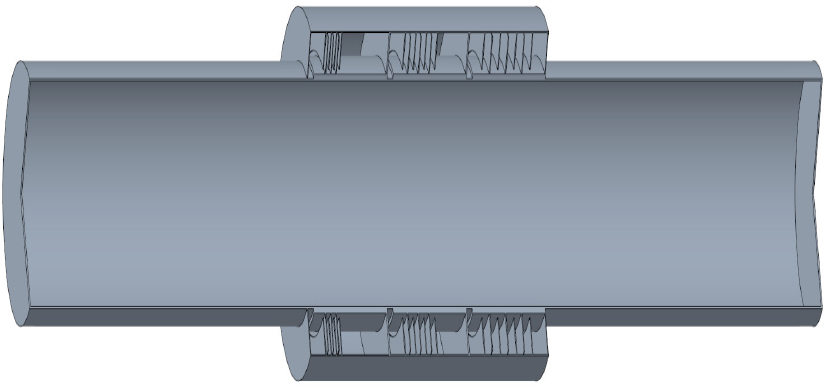
본 연구에서는 지그재그 구조를 이용하여 저주파에서 작동하는 소음기를 개발한다. 소음기의 내부 구조는 Fig. 1(a)에 나타나 있다. 파장보다 매우 작은 도파관으로 이루어진 지그재그 구조를 이용하기 때문에 도파관 내에서 발생하는 점성 및 열 감쇠 항에 대한 정확한 해석이 필요하다. 이를 이론적으로 해석하기 위해, 경계층 근처의 입자 속도 구배를 COMSOL Multiphysics에서 경계층 매쉬를 이용해 계산하였다. 점성 및 열 경계층 두께는 주파수 에 따른 값 과 지그재그 구조물 간격의 1/3 중 큰 값으로 설정하고, 6개의 층으로 매쉬를 구성하여 점성 및 열 경계층을 나타내었다. Fig. 1(b)에 이러한 매쉬 구성이 나타나 있다. 경계층에 대한 점성 및 열에너지 감쇠 항을 계산하기 위해서 공기의 질량 밀도 = 1.2043 kg/m3, 비열 비 = 1.4, 역학 점도 = 1.814 × 10−5 kg/m·s, 프란틀 수 = 0.707과 같은 공기 물성을 사용하였다.
2.2 4-Microphone method를 이용한 메타물질 소음기 해석
본 연구는 음향 메타물질로 구성된 소음기의 성능을 평가하기 위해, 소음기의 음향 에너지 투과율, 반사율, 흡음률 그리고 투과손실을 계산하였다. 이를 위해 두 개의 도파관에 각각 음파분리법을 적용하는 4-Microphone method를 이용하였다.
음파분리법은 도파관 내부의 음압분포를 이용해 진행파와 반사파를 역으로 추정하는 이론이다. 동일한 매질과 일정한 단면적을 갖는 도파관의 내부에 평면파 가정이 성립할 때, 한 지점의 음압은 음원에서 발생한 진행파와 도파관의 끝에서 발생한 반사파가 중첩되어 Eq. (1)와 같이 표현된다. 이는 여러 지점에 대한 음압을 측정할 수 있다면, 역으로 도파관 내부의 진행파와 반사파를 분리할 수 있다는 것을 의미한다.
: Pressure at a point [Pa]
: Angular frequency [rad/s]
: Wavenumber [rad/m]
: Amplitude of Incident wave [Pa]
: Amplitude of Reflected wave [Pa]
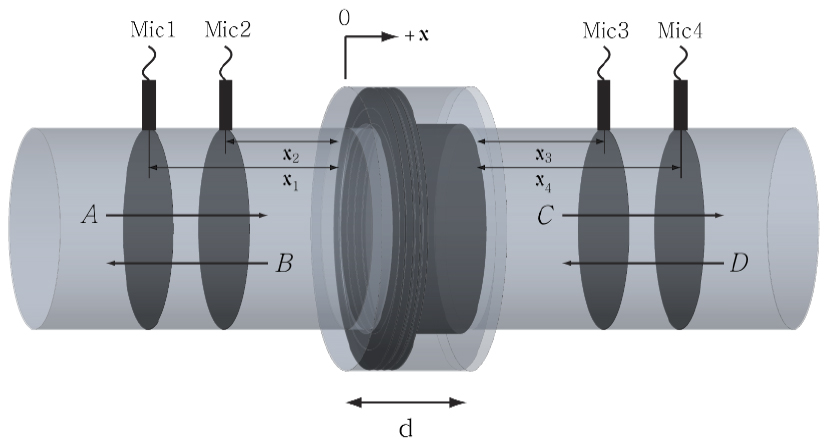
Fig. 2는 두 개의 도파관이 소음기의 양 끝에 연결된 형태의 음파분리법 모델이다. 소음기의 투과율, 반사율 및 흡음률을 측정하기 위해서는 두 도파관의 진행파와 반사파를 모두 분리해야 하며 각 도파관 당 두 지점의 음압 정보가 필요하다. 이를 측정하기 위해 총 4개의 마이크가 사용되어 이러한 방식을 4-Microphone method라고 부른다.
4-Microphone method에서 각 도파관 내부의 임의의 위치에서 측정한 음압은 Eq. (2)로 표현된다.
: Amplitude of Incident wave in waveguide 1 [Pa]
: Amplitude of Reflected wave in waveguide 1 [Pa]
: Amplitude of Incident wave in waveguide 2 [Pa]
: Amplitude of Reflected wave in waveguide 2 [Pa]
각 도파관 내부의 진행파 및 반사파의 진폭은 임의의 네 위치에서 측정한 음압()과 기준면()에서 측정지점까지의 거리()를 이용해 계산할 수 있으며, 이는 Eqs. (3), (4), (5), (6)과 같이 표현된다.
소음기의 투과계수 및 반사계수는 각각 소음기에 입사된 음파에 대한 투과된 음파 그리고 반사된 음파의 진폭비로 정의된다. 두 도파관에서 분리된 음파로부터 소음기의 투과계수 및 반사계수 을 계산할 수 있으며, 이는 Eqs. (7), (8)과 같다.
메타물질 소음기의 음향 에너지 반사율 , 투과율 및 흡음률 는 투과계수 및 반사계수로부터 Eqs. (9), (10), (11)과 같이 계산할 수 있다.
최종적으로, 음향에너지 투과율을 이용해 투과손실 을 Eq. (12)와 같이 계산할 수 있다.
2.3 원형 덕트 내 지그재그 메타물질 소음기 해석
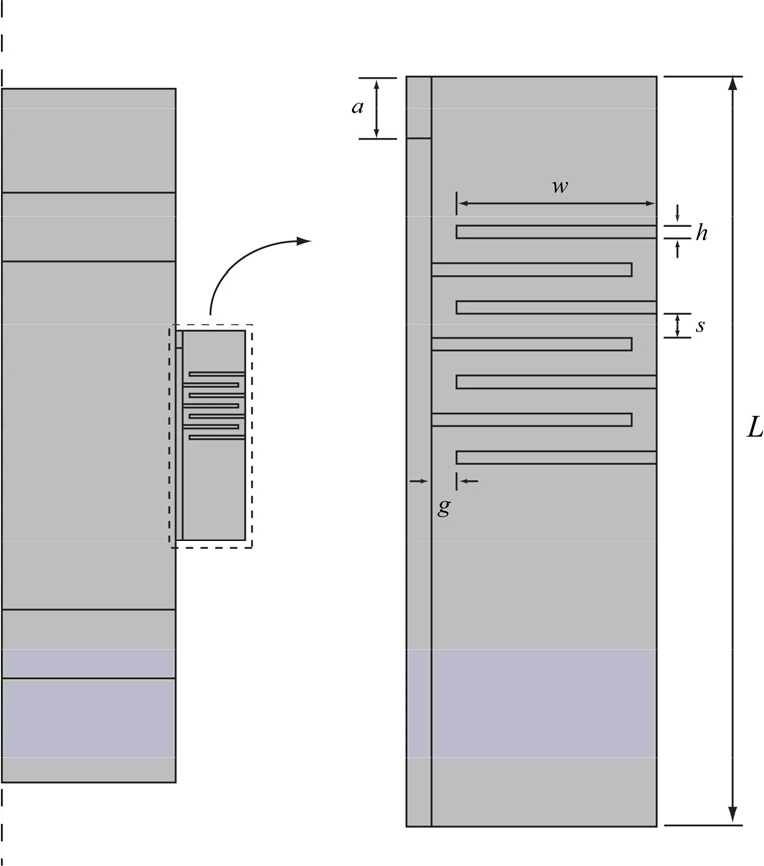
Fig. 3에 지그재그 구조물 기반 메타물질의 단면이 나타나 있다. 좌측 그림은 원형 덕트와 그에 부착된 소음기를 나타내며, 소음기를 확대하여 우측 그림에 나타내었다. 소음기의 길이는 = 6 cm, 음파가 들어오는 입구는 = 0.5 cm이고 지그재그 구조물의 크기는 = 1.6 cm, = 0.05 cm, 간격은 s이다. 지그재그 구조물과 소음기 벽과의 간격은 = 0.2 cm이다. 지그재그 구조물의 간격 를 0.15 cm, 0.35 cm, 0.55 cm로 변경해가며 3가지 형상의 메타물질 소음기들을 설계하고, 투과율, 흡음률, 반사율과 투과손실에 대한 FEM 해석을 수행하였다. 그 중 반사율, 흡음률과 투과율이 Fig. 4(a) ~ (c)에 나타나 있다. Fig. 4(a) ~ (c)와 같이, 지그재그 구조물의 간격이 작아질수록( = 0.15 cm) 반사율은 작아지고, 투과율과 흡음률은 커짐을 알 수 있다. 흡음률은 구조물의 간격이 작을수록 도파관 내에서 점성 및 열 경계층이 차지하는 두께가 상대적으로 커지므로 점성 및 열에 의한 에너지 손실이 지배적으로 나타나 증가한다. 또한, 구조물의 간격이 작을수록 유효질량이 증가하여, 헬름홀츠 형상에서 공진주파수(230 Hz)가 낮아짐을 확인할 수 있다. 그러나 지그재그 구조물의 간격이 커질수록( = 0.55 cm), 지그재그 도파관 내의 음파에 작용하는 점성과 열의 영향은 작아져, 흡음계수는 공진주파수(450 Hz)에서 대략 0.34, 반사계수는 대략 0.61로 측정된다.
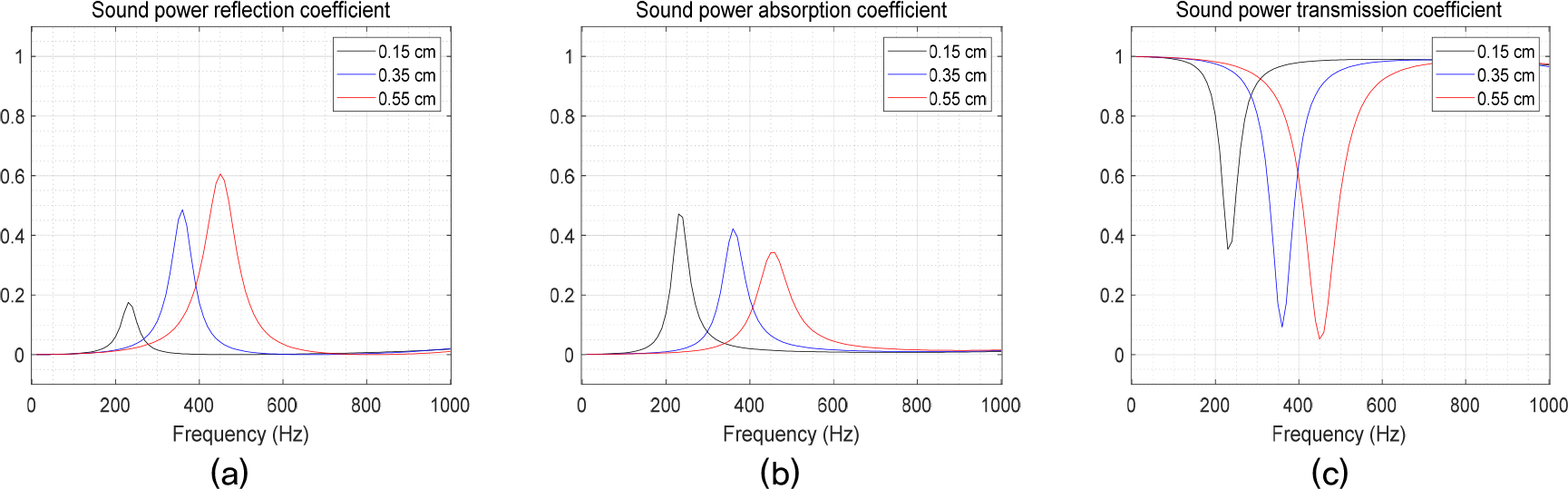
Fig. 4
(Color available online) Variation of (a) simulated sound power reflection coefficients; (b) simulated sound power absorption coefficients; (c) simulated sound power transmission coefficients with the intervals = 0.15 cm, 0.35 cm and 0.55 cm. The peak frequencies are identically at = 230 Hz, 360 Hz, 450 Hz.
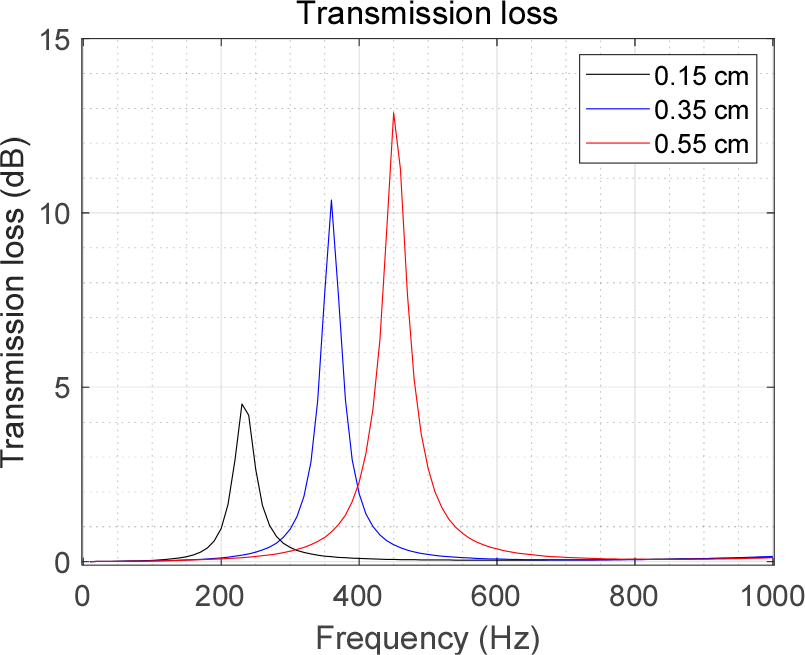
Fig. 5는 3가지 형상의 메타물질 소음기들에 대한 투과손실 그래프이다. 투과손실은 소음기의 반사율 및 흡음률에 영향을 받는다. 지그재그 구조물의 간격이 작을수록 흡음률은 커지지만 반사율은 작아져 공진주파수 근처(230 Hz)에서 투과손실은 대략 4.5 dB으로 측정되었다. 그러나 지그재그 구조물의 간격이 커질수록 흡음률은 작아지지만, 반사율이 커지기 때문에 공진주파수 근처에서(450 Hz)에서 투과손실은 대략 12.9 dB으로 측정되었다. 이로부터, 3가지 형상의 메타물질 소음기들이 각기 다른 공진주파수에서 음향 에너지를 차단함을 확인하였다.
2.4 직렬(Series) 메타물질 소음기 해석
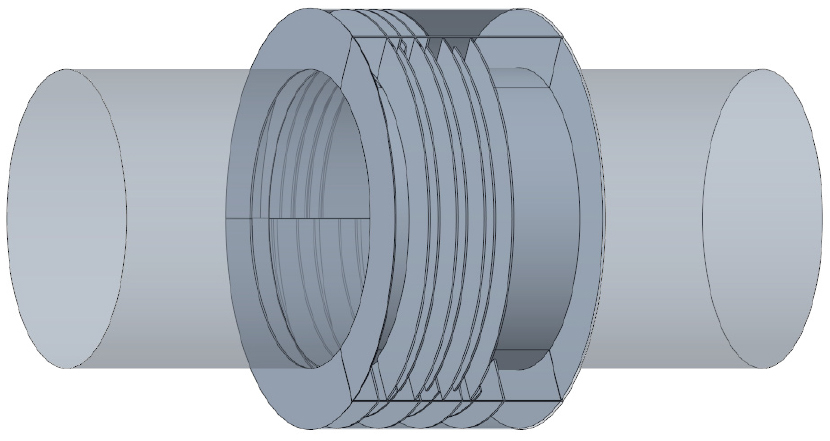
광대역으로 음향 에너지를 차단하기 위해서 3가지 형상을 갖는 메타물질을 Fig. 6과 같이 직렬로 배열하고, 음파분리법으로 직렬배열 메타물질 소음기의 투과율, 흡음률, 반사율과 투과손실에 대한 FEM 해석을 수행하였다. Fig. 7(a)와 같이, 직렬 메타물질 소음기에서 기존 3가지 형상의 메타물질에서 나타나는 공진 주파수(230 Hz, 360 Hz, 450 Hz)와 동일한 공진 주파수가 나타나는 것을 확인할 수 있다. 또한, 각 공진 주파수에서 지그재그 구조물의 간격이 작을수록 흡음률이 크고(0.35, 0.33, 0.32) 반사율이 작은(0.27, 0.55, 0.64) 경향이 동일하게 나타났다. 그러나 각각의 메타물질에서 측정했을 때보다 흡음률은 전반적으로 감소하고, 반사율은 증가했다.
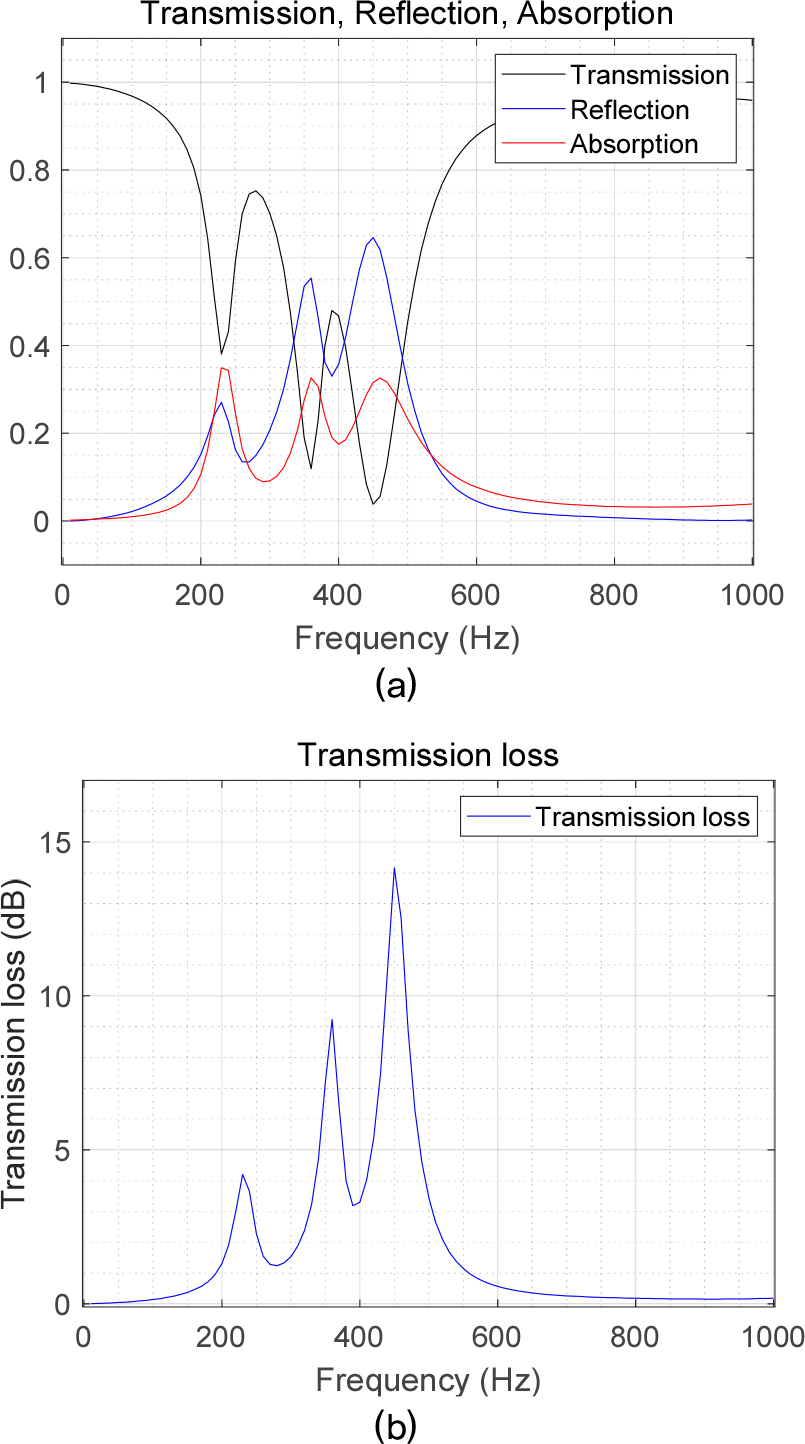
Fig. 7
(Color available online) (a) Simulated sound power transmission, reflection, and absorption coefficient of serially connected silencer; peak frequencies are identically at = 230 Hz, 360 Hz, 450 Hz. (b) simulated transmission loss of serially connected silencer; peak frequencies are identically at = 230 Hz, 360 Hz, 450 Hz.
Fig. 7(b)는 직렬 메타물질에 대한 투과손실을 나타내는 그래프이다. 기존 3가지 형상의 메타물질 소음기들에서 나타나는 투과손실(4.5 dB, 10.4 dB, 12.9 dB)과 비교했을 때, 직렬 메타물질 소음기에서 각 공진주파수의 투과손실(4.2 dB, 9.2 dB, 14.2 dB)은 큰 차이가 없다. 이로부터, 직렬로 메타물질을 배열함으로써 큰 성능 차이 없이 광대역으로 음향 에너지를 차단하는 소음기를 구현할 수 있음을 확인하였다.
2.5 병렬(Parallel) 메타물질 소음기 해석
광대역으로 음향 에너지를 차단하기 위해서 3가지 형상을 갖는 메타물질을 Fig. 8과 같이 병렬로 배열하고, 음파분리법으로 병렬 메타물질 소음기의 투과율, 흡음률, 반사율과 투과손실에 대한 FEM 해석을 수행하였다. Fig. 9(a)와 같이, 기존 3가지 형상의 메타물질에서 나타나는 공진 주파수(230 Hz, 360 Hz, 450 Hz)와 동일한 공진 주파수가 나타나는 것을 확인할 수 있다. 그러나 지그재그 구조물의 간격이 작을수록 흡음률과 반사율이 모두 작게 나타나 앞선 경우들과 다른 경향성을 나타냈다. 또한, 앞선 경우들과 비교하여 반사율(0.04, 0.21, 0.32)이 매우 작게 측정되었다.
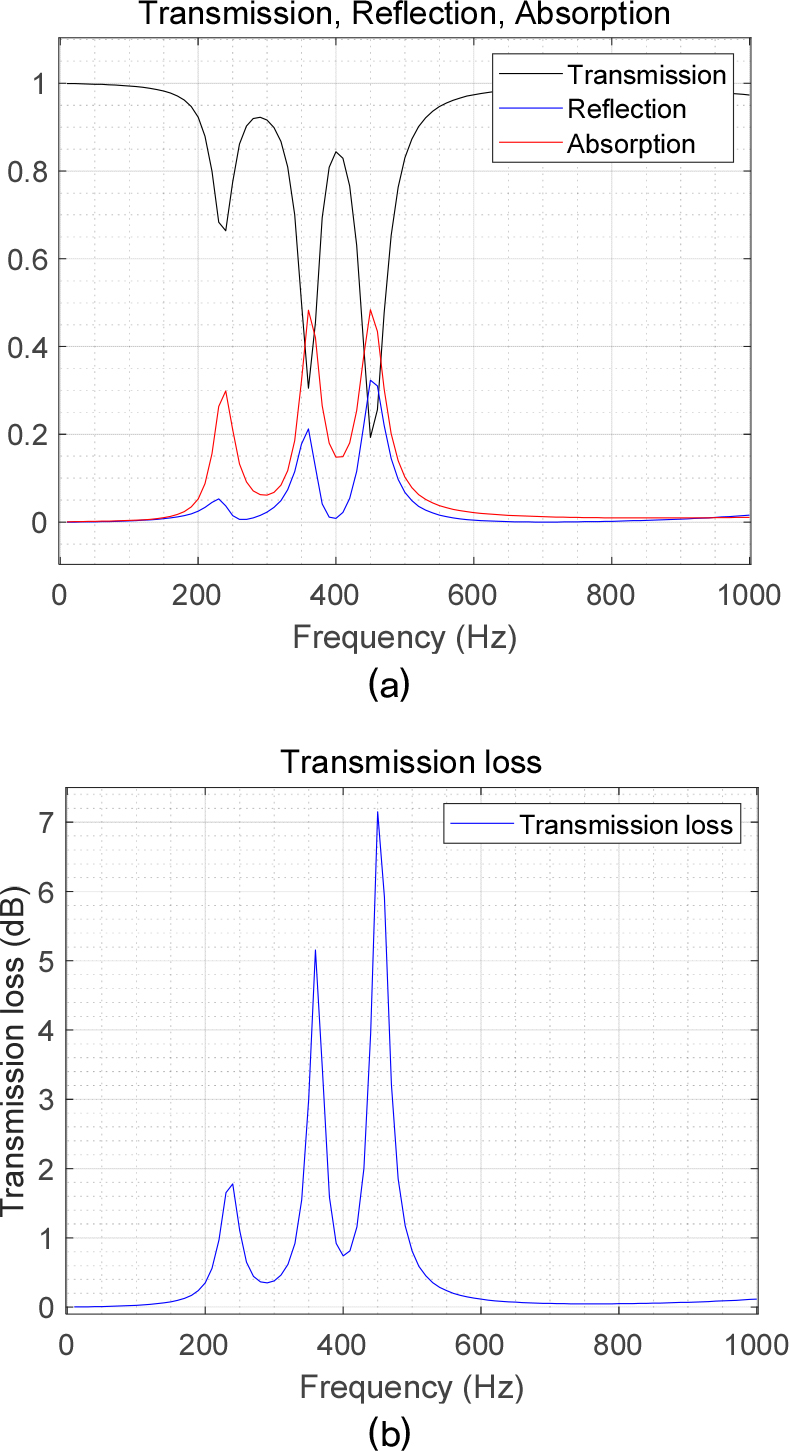
Fig. 9
(Color available online) (a) Simulated sound power transmission, reflection, and absorption coefficient of parallel connected silencer; peak frequencies are identically at = 230 Hz, 360 Hz, 450 Hz. (b) Simulated transmission loss of parallel connected silencer; peak frequencies are identically at = 230 Hz, 360 Hz, 450 Hz.
Fig. 9(b)는 병렬 메타물질에 대한 투과손실을 나타내는 그래프이다. 흡음률에서 큰 차이가 나지 않는데 비해, 반사율이 크게 감소하여 기존 3가지 형상의 메타물질 소음기들에서 나타나는 투과손실(4.5 dB, 10.4 dB, 12.9 dB)과 비교했을 때 매우 작은 투과손실(1.8 dB, 5.2 dB, 7.15 dB)이 측정되었다. 즉, 병렬 메타물질 소음기는 광대역으로 음향 에너지를 차단할 수 있고 직렬 메타물질 소음기에 비해 적은 공간을 차지하지만, 투과 손실에 있어 약 50%의 성능 저하가 있음을 확인하였다.