I. 서 론
II. RLS(Recursive Least Squares) and RTLS(Recursive Total Least Squares)
III. IWF 기반 RTLS(Recursive Total Least Squares)
IV. 시뮬레이션을 통한 성능 검증
4.1 채널 추정을 통한 기존 RTLS의 성능 비교
4.2 알고리즘의 견실성 실험
V. 결 론
I. 서 론
잡음 섞인 데이터를 사용하는 시스템 인식 문제는 출력에 잡음이 부가된 경우뿐 아니라, 때에 따라 입력에도 잡음이 부가되는 경우도 포함한다. 전형적인 최소 자승 알고리즘(Least Squares, LS)은 출력에만 잡음이 부가된 경우에 최적의 시스템 인식을 해내는 것으로 알려져 있다. 입력과 출력이 동시에 잡음에 오염된 경우에 시스템인식은 완전 최소 자승법(Total Least Squares, TLS)이 최소 자승법보다 좋은 결과를 낸다고 알려져 있다.[1,2] Choi et al.[3]에 의해서 Recursive Least Squares(RLS)와 유사한 방법으로 계산하는 Recursive Total Least Squares(RTLS)를 제안하였다. 이 알고리즘은 다른 연구자들에 의해서 인용 발전되었다.[4,5,6,7,8]
Reference [3]에서 제안된 알고리즘은 RLS의 재귀적 갱신법을 충분히 이용하고 있어서 실시간으로 관측되는 데이터를 사용할 경우에 잘 맞는 방법이지만 RLS가 지닌 단점 또한 함께 가지고 있다. 즉 알고리즘 상에 자기 상관 행렬의 역행렬을 계산하는 과정에 수치적 불안정성이 내재되어 있다. 이런 수치상 불안정 상태의 주된 원인중 하나가 자기상관 행렬의 역행렬에 대칭성이 유지되지 못할 때라는 것이 알려져 있다.[9]
본 논문은 RTLS와 유사한 성능을 내면서도 역행렬이 내재되어 있지 않은 RTLS 알고리즘을 제안한다. 이를 위해서 Iterative Wiener Filter(IWF)[10] 방법을 응용한 새로운 RTLS 알고리즘을 제안한다. IWF[10]는 Xi 등이 제안한 역행렬이 내재되어 있지 않은 RLS 대체 알고리즘이다. 이 알고리즘의 수렴 성능은 전통적인 RLS와 유사한 것이 알려져 있다. 그리고 후속 연구에서 IWF기반 알고리즘이 수치적 불안정성도 매우 개선됨도 보였다.[11] 따라서 제안된 RTLS 알고리즘은 전통적인 RTLS와 유사한 수렴 특성을 지니면서 수치적 안정성이 개선된 특성을 지닌다.
본 논문은 2장에 기존의 RTLS를 정리하고, 3장에 새로운 알고리즘을 제안한다. 4장에는 시뮬레이션을 통해서 새 알고리즘의 성능이 기존의 RTLS와 유사함을 보이고, 또 양자화 오차에 대한 견실성도 있음을 보인다.
II. RLS(Recursive Least Squares) and RTLS(Recursive Total Least Squares)
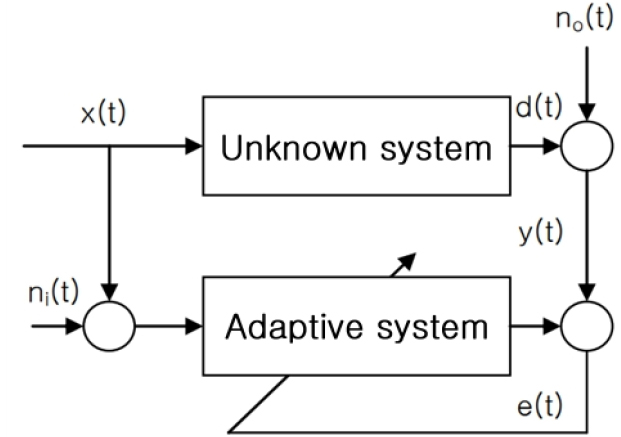
미지의 시스템이 주어지고, 입력과 출력 양쪽에 잡음이 부가된 경우를 가정할 때, Fig. 1과 같이 모델링 할 수 있다. 그리고 그 미지의 시스템은 다음과 같이 기술 된다.
여기서 w는 시변 또는 시불변 이다. 출력은 다음과 같다.
여기서 no(k)는 출력 잡음이고 의 분산을 갖는 정규분포를 따른다. 잡음이 없는 입력신호 벡터는 다음과 같다.
그리고 앞서와 같은 환경에서 최소자승법을 사용하여 시스템 파라미터를 인식하기 위해서 다음과 같은 최적화용 비용 함수를 사용한다.
여기서 k번째 표본에 대한 추정 오차 eLS(k)는 다음과 같다.
RLS 알고리즘은 위 최소 자승 풀이를 위한 재귀 형식 알고리즘이다.[3] 이 알고리즘의 매 단계 과정은 다음 Table 1과 같다.
Eq. (2)와 같이 출력에 잡음이 낀 경우와 함께, 다음과 같이 입력에도 의 분산을 갖는 백색 정규 분포를 따르는 잡음이 낀 경우
완전 최소 자승법이 최적의 해를 제공 한다.[1,2] Reference [3]의 저자들에 의해서 완전 최소 자승법을 재귀형으로 만든 Recursive Total Least Squares(RTLS) 알고리즘이 제안되었다. RTLS알고리즘은 다음과 같은 비용함수의 최소화로부터 유도할 수 있다.
여기서 이고 이다. 이 알고리즘은 형식이 위의 Table 1과 유사한 재귀 형식이고 전체 알고리즘은 Table 2와 같다.
III. IWF 기반 RTLS(Recursive Total Least Squares)
IWF[10]방법을 기반으로 하여 역행렬 연산이 없는 RTLS를 구현하기 위해서 Eq. (7)의 목적함수를 다음과 같이 변형하였다.
위 목적함수에 대해서 Reference [10]에 IWF 알고리즘 개발 방법을 적용하면 다음과 같은 갱신식을 얻는다.
여기서 이고 그 자세한 식은 다음과 같다.
그리고 갱신식의 갱신 스텝 사이즈는 다음과 같이 목적함수를 스텝 사이즈로 미분한 것으로부터 얻을 수 있다.
이고, Eq. (12)와 같이 Eq. (11)이 ‘0’이 되는 스텝 사이즈를 구하면 Eq. (13)과 같은 스텝 사이즈를 구할 수 있다.
이와 같이 IWF를 적용한 새로운 RTLS 알고리즘을 정리하면 다음 Table 3과 같다.
IV. 시뮬레이션을 통한 성능 검증
4.1 채널 추정을 통한 기존 RTLS의 성능 비교
본 실험에서는 총 64차의 가상의 유한 임펄스 응답을 갖는 채널을 사용하였다. 채널의 다양성을 위해서 64개의 임펄스 응답 계수 중 임의로 각각 32개, 16개, 8개의 영이 아닌 계수를 갖는 3종류의 가상 채널을 발생 시켜서 각각 100 회씩 반복 실험을 하였다. 반복 실험 시에 영이 아닌 계수의 위치와 크기를 각각 N(0, 1/(영이 아닌 계수의 갯수))인 정규 분포를 갖도록 발생시켰다.
실험에서 본 논문에서 제안한 RTLS와 Reference [3]에서 제안한 기존 RTLS 및 제안한 알고리즘의 모태인 Reference [10]의 IWF 알고리즘의 추정 성능을 서로 비교하여 Fig. 2에 나타내었다. Fig. 2는 다음 식으로 정의된 평균 표준 편차(Mean Standard Deviation, MSD) 곡선을 보여준다.
Fig. 2의 결과는 제안된 알고리즘의 추정 성능이 기존RTLS와 유사함을 보이고 있다.
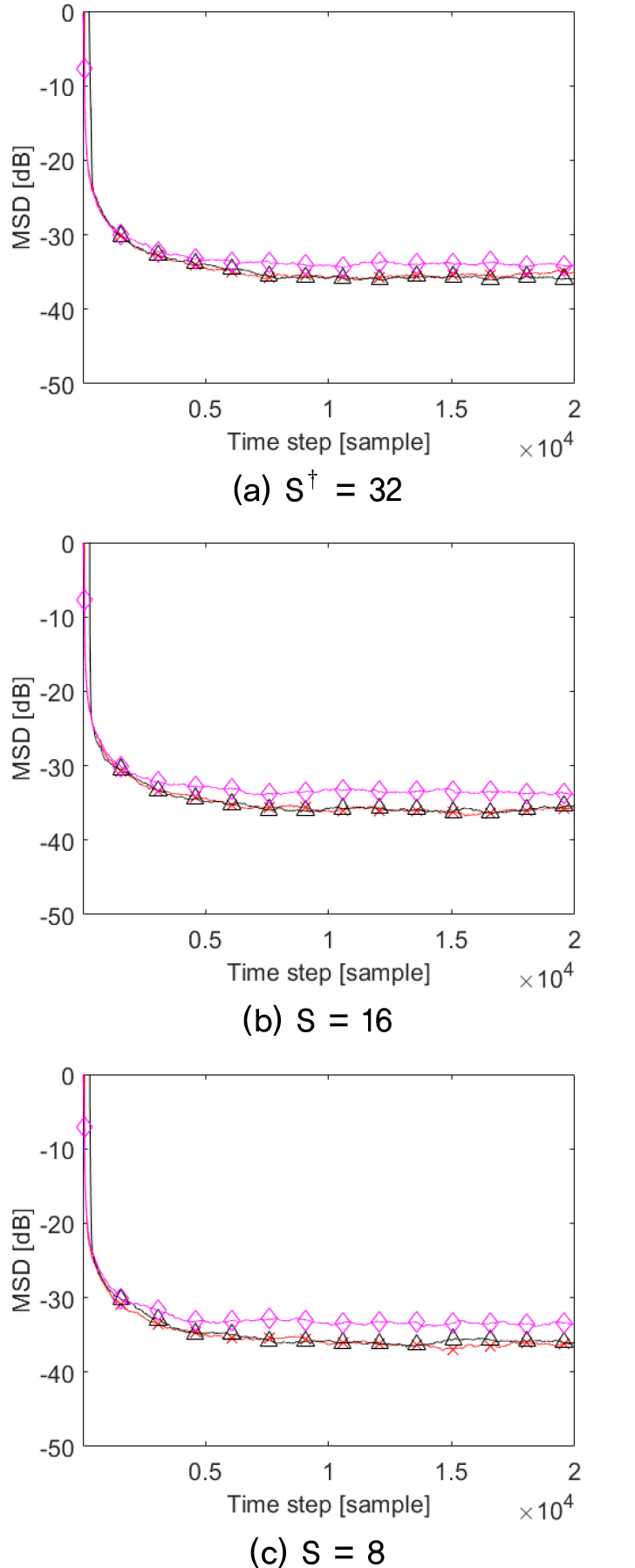
Fig. 2.
(Color available online) Convergence comparison between conventional RTLS and the proposed algorithm (-x-: the conventional RTLS , -△-: the proposed algorithm, -◇-: the algorithm in Reference [10]) †(S is the number of non-zero coefficients).
4.2 알고리즘의 견실성 실험
본 실험은 제안된 알고리즘이 자기 상관의 역행렬을 사용하는 기존 RTLS에 대해 수치적으로 더 견실하다는 것을 보여준다. 수치적 견실성을 보여주기 위해 양자화를 사용하여 유한 정밀도 환경 하에서 채널 추정을 수행한다. 유한한 비트를 사용하는 양자화 실험의 이유는 알고리즘 연산중에 수치 오류를 유도하기 위해 양자화 노이즈 상황을 도출하고 자기 상관 행렬의 역행렬 연산에 오류를 포함하기 위함이다.
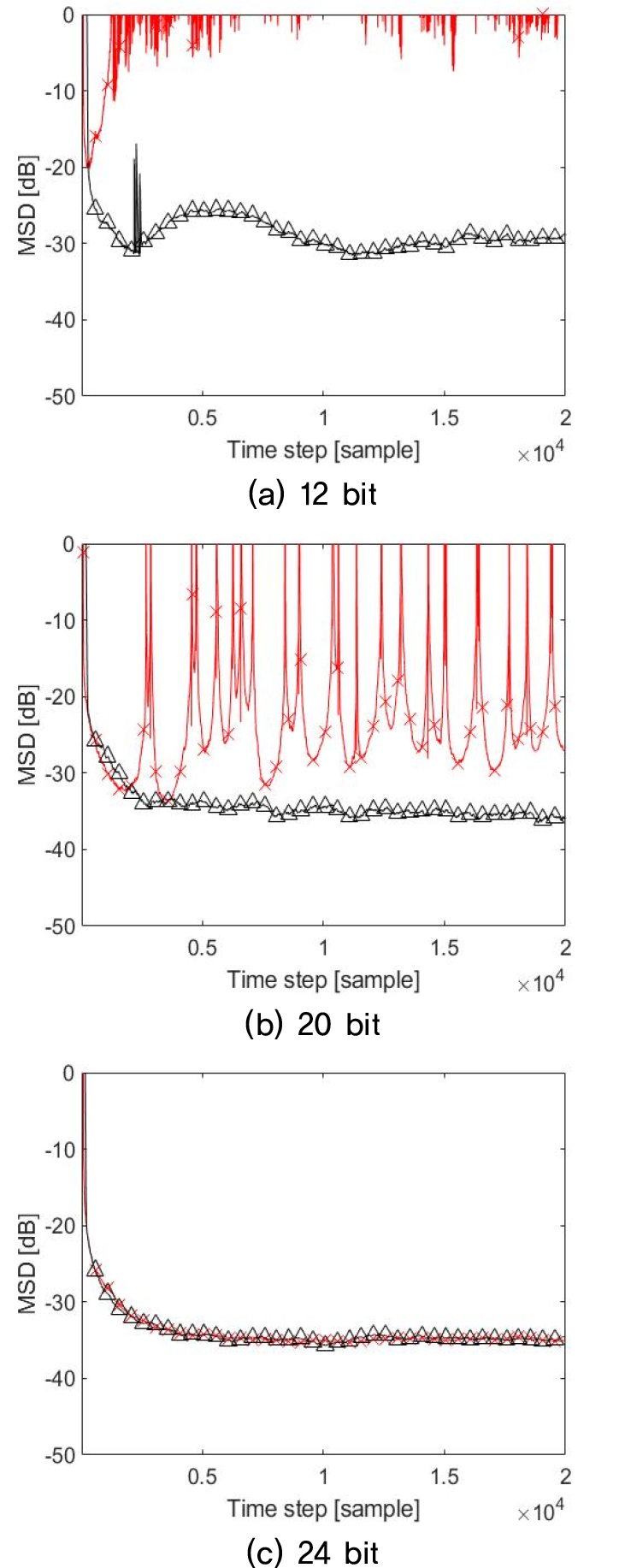
이러한 상황을 보이기 위해 양자화 비트 수를 24 비트, 20 비트와 12 비트로 변경하여 채널 추정 성능을 비교 했다. 이 때 채널 중 영이 아닌 계수의 숫자는 32개로 하였다.
Fig. 3은 제안 된 알고리즘과 기존 RTLS의 성능을 서로 다른 양자화 비트 수를 갖는 MSD 측면에서 비교 한 결과를 보여준다. Fig. 3의 결과를 통해 보면, 유한 비트를 사용하여 양자화 된 환경에서 사용할 경우 Reference [3]의 RTLS는 20 비트 상황부터 양자화 잡음의 오류 누적 효과로 인해 발산되는 것을 볼 수 있다. 이에 반하여 제안된 알고리즘은 16 비트까지는 정상적으로 수렴하는 것도 관찰 할 수 있고, 12 비트부터 발산하기 시작함을 관찰 할 수 있다. 본 실험을 통하여 제안 된 알고리즘이 기존 RTLS보다 수치적으로 더 견실함을 보여준다.