Design of the broadband pattern of a cymbal transducer array

Donghyun Kim; Changmin Oh; Hayeong Shim; Soonkwan Kang; Yongrae Roh

doi:10.7776/ASK.2021.40.1.010

Preview

Research Article

The Journal of the Acoustical Society of Korea. 31 January 2021. 10-17
https://doi.org/10.7776/ASK.2021.40.1.010

Design of the broadband pattern of a cymbal transducer array

심벌 트랜스듀서 배열의 광대역 패턴 설계

Donghyun Kim¹

Changmin Oh¹

Hayeong Shim¹

Soonkwan Kang¹

Yongrae Roh¹^*

김 동현¹

오 창민¹

심 하영¹

강 순관¹

노 용래¹^*

¹경북대학교 기계공학부

^{*Corresponding Author}

ABSTRACT

The cymbal transducer is a miniaturized version of the Class V flextensional transducer. It has low resonant frequency and high output pressure characteristics compared with its size. However, since it has high quality factor and low energy conversion efficiency as well, it is often used as an array rather than single. When used as an array, a big change in the frequency characteristics occurs in comparison with that of the single transducer due to the interaction between constituent transducers. In this study, we designed a pattern of cymbal array with a view to having broadband characteristics. Three transducers having different center frequencies were designed first. The designed cymbal transducers were used to construct all possible patterns of a 3 × 3 planar array. After analyzing frequency characteristics of these patterns, based on the results, we derived the most effective pattern to achieve a higher fractional bandwidth. The derived array pattern showed an improvement of the fractional bandwidth by 24.9 % in comparison with the reference model.

Keywords

Cymbal transducer

Array pattern

Fractional bandwidth

Broadband

심벌 트랜스듀서는 Class V flextensional 트랜스듀서의 소형화된 버전으로서 크기에 비해 낮은 공진 주파수와 고출력 특성을 가진다. 하지만, 높은 품질계수와 낮은 에너지 변환 효율성 때문에 단일보다는 배열형으로 많이 사용된다. 배열형으로 사용하면 구성 트랜스듀서들 간의 상호작용으로 인해 단일 트랜스듀서에 비해 주파수 특성에 많은 변화가 나타난다. 본 연구에서는 이러한 성질을 이용하여 심벌 어레이가 광대역 특성을 가지게 하는 패턴을 설계하였다. 특정 중심 주파수를 가지는 세 개의 심벌 트랜스듀서를 먼저 설계하였고, 설계된 심벌 트랜스듀서들로 3 × 3 평면 배열을 구성할 수 있는 모든 패턴을 찾았다. 그 후, 이들 패턴들의 주파수 특성을 분석하고, 그 결과를 바탕으로 높은 비대역폭을 구현하기 위해 가장 효과적인 배열 패턴을 도출하였다. 도출된 배열 패턴은 기준 모델에 비해 비대역폭이 최대 24.9 % 개선되었다.

키워드

심벌 트랜스듀서

배열 패턴

비대역폭

광대역

MAIN

I. 서 론
II. 심벌 어레이 구성
III. 배열 패턴에 따른 3×3 심벌 어레이 성능 분석
IV. 결 론

I. 서 론

수중에서의 효과적인 통신 및 탐지를 위한 수중 센서 네트워크(Underwater Sensor Networks, UWSN)에서 센서 노드로 사용되는 각종 음향 센서는 UWSN의 성능을 좌우하는 핵심요소이다. 따라서, UWSN의 효과적인 작동을 위해서 고성능 센서 관련 기술 확보는 필수적이다. 특히, 대용량의 고속 통신과 데이터 전송을 위해서는 광대역 주파수 특성을 가지는 음향 센서가 요구된다.^[1] 본 연구에서는 위와 같은 조건을 만족하는 수중 음향 센서로 심벌 트랜스듀서를 연구하였다. Newnham et al.^[2]에 의해 개발된 이 트랜스듀서는 Class V flextensional 트랜스듀서의 소형화된 버전이다. 이는 심벌즈 모양의 금속 캡들 사이에 압전 세라믹 디스크가 끼워져 있는 구조이며, 접착제를 사용하여 서로 접착된다.^[3] 심벌 트랜스듀서는 크기가 작은 데에 비해 공진주파수가 낮고 고출력으로 작동된다.^[4] 또한, 기계적 변압기 역할을 하는 금속 캡은 통상 펀칭 공정을 이용하여 제작하기 때문에 다른 트랜스듀서에 비해 제작비용이 저렴하다.^[5,6]따라서, UWSN 특징인 대규모 노드 망을 구성하기에 적합하다. 하지만 심벌 트랜스듀서는 높은 품질계수와 낮은 에너지 변환 효율을 가지기 때문에 원하는 소스 레벨과 주파수 대역폭을 달성하기 위해서 단일보다는 배열형으로 많이 사용된다. 이렇게 배열형으로 사용하게 되면 고출력을 구현할 수 있을 뿐만 아니라 소자들 간의 상호방사작용으로 인해 광대역의 고효율 트랜스듀서를 만들 수 있다.^[7,8]

심벌 어레이에 관해서는 많은 연구들이 수행된 바 있다. Tressler et al.^[9]은 심벌 어레이의 금속 캡 재료와 포팅의 유무에 따른 성능을 비교하였다. Zhang et al.^[10]은 장착 방식에 따른 배열 구조의 성능 차이를 비교하며 요소 간 간격에 따른 상호 작용을 분석하는 연구도 수행하였고, Newnham et al.^[11]은 3 × 3과 5 × 20의 두 종류 어레이들을 제작하여 Transmitting Voltage Response(TVR)을 비교하였다. Zhang et al.^[12]은 유한 요소 해석과 적분 방정식을 결합하여 심벌 어레이의 특성을 해석하고, 그 결과를 제작된 시편의 특성과 비교하였다. 이 외에도, 심벌 어레이 모듈을 직렬, 병렬 또는 두 가지의 조합으로 배열한 프로젝터 설계,^[13] 3 × 3 원형 심벌 어레이와 3 × 1 직사각형 심벌 어레이의 TVR 비교,^[14] 직렬 또는 병렬 회로로 연결된 수중 청음기용 평면 배열형 심벌 어레이의 수신감도 및 지향성 특성 비교 평가,^[15] 하이드로폰용 1 × 3 심벌 어레이의 성능 평가^[16] 등과 같은 연구들이 이루어진 바 있다. 그러나 이들 연구는 대부분 동일한 중심 주파수를 가지는 심벌 트랜스듀서들로만 이루어진 어레이의 성능 평가와 활용에 중점을 둔 것으로서, UWSN 체계에 필요한 트랜스듀서의 대역폭 개선과 직접 관련된 사례는 없다.

따라서 본 연구에서는 UWSN에 적용할 수 있도록 광대역 주파수 특성을 가질 수 있는 심벌 어레이의 효과적인 배열 패턴에 관해 연구하였다. 본 저자들은 구성 트랜스듀서들의 주파수 차이와 소자들 중심 간의 간격이 2 × 2 심벌 어레이의 주파수 대역폭에 미치는 영향을 분석한 바 있다.^[17] 본 연구에서는 이를 더 발전시켜 세 개의 서로 다른 중심 주파수를 가지는 심벌 트랜스듀서들을 배열한 3 × 3 어레이에서 주파수 대역폭을 최대화할 수 있는 배열 패턴을 도출하고자 하였다. 이를 위해 먼저 특정 주파수에서 작동하는 개별 심벌 트랜스듀서들을 설계한 다음, 이들을 배열해서 구현할 수 있는 모든 경우의 패턴들을 선정하였다. 그 후, 패턴들이 심벌 어레이의 대역폭에 미치는 영향을 분석하고 그 결과를 바탕으로 비대역폭을 효과적으로 넓힐 수 있는 패턴들을 선정하였다. 선정된 패턴들에 대해 비대역폭이 확장되는 원리를 논하고, 기준 모델과 TVR 스펙트럼을 비교함으로써 패턴 선정 기준의 타당성을 입증하였다.

II. 심벌 어레이 구성

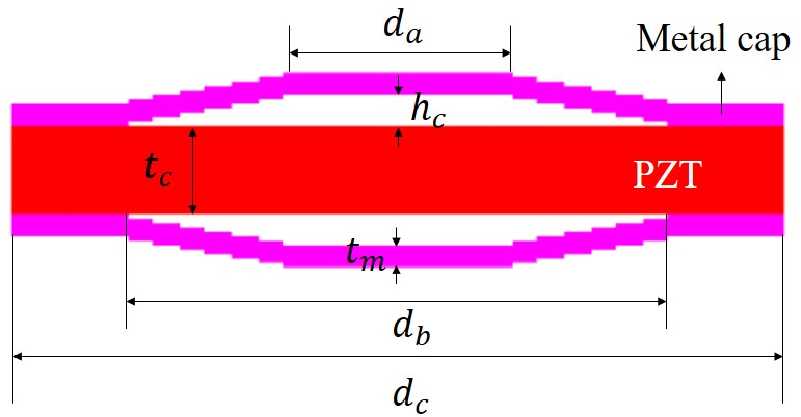
이 연구의 목적은 서로 다른 중심 주파수를 가지는 세 가지의 트랜스듀서를 세 개씩 사용하여 넓은 대역폭을 가질 수 있는 배열 패턴을 찾는 것이다. 이를 달성하기 위해서 3 × 3 심벌 어레이에서 나올 수 있는 경우의 수들을 모두 찾고, 패턴에 따른 심벌 어레이의 성능을 유한요소해석을 통해 분석하였다. 본 연구에서는 상용 프로그램인 PZFlex^®를 이용하여 심벌 트랜스듀서의 유한요소해석 모델을 구축하고 음향특성을 분석하였다. 단일 심벌 트랜스듀서의 2D 모델과 구조를 Fig. 1에 나타내었다. Fig. 1에서 d_a는 공동 위 직경, d_b는 공동 아래 직경, d_c는 압전 세라믹 직경, h_c는 공동 높이, t_c는 압전 세라믹 두께, t_m은 금속 캡 두께를 가리킨다. 압전 세라믹으로는 PZT-5A, 금속 캡으로는 황동을 사용하였다. 각 재료의 물성은 Reference [18]의 값을 인용하였다.

https://static.apub.kr/journalsite/sites/ask/2021-040-01/N0660400102/images/ASK_40_01_02_F1.jpg

Fig. 1

(Color available online) Schematic structure of the individual cymbal transducer.

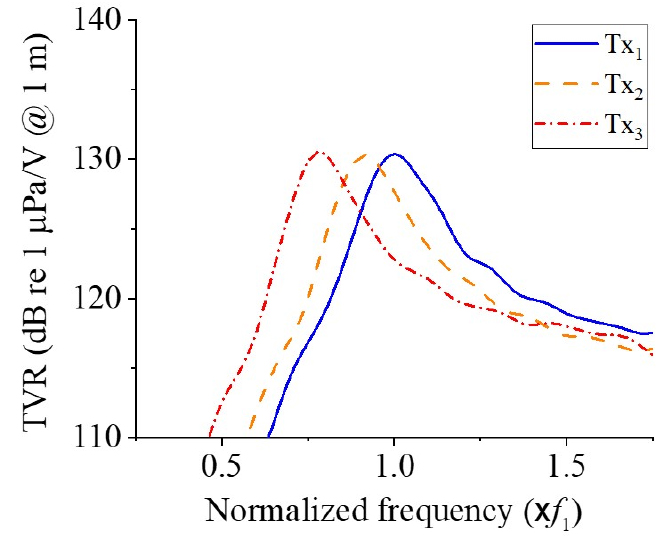
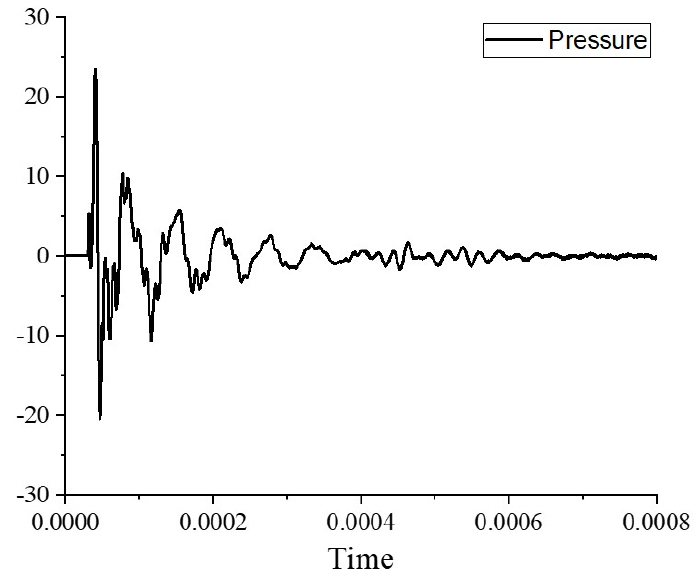
우선 3 × 3 심벌 어레이를 구성하기 위한 특정 중심 주파수와 TVR 값을 가지는 단일 심벌 트랜스듀서들을 설계하였다. 이는 Reference [17]에서와 같이 특정 구조 변수의 치수를 조정함으로써 원하는 특성 값을 가지는 심벌 트랜스듀서들의 최적 구조 변수 값들을 도출하는 과정을 거친 것이다. 목적함수로는 대역폭을 최대화하는 것으로 설정하였고, 제한조건으로 제작상의 오차 범위를 감안해 0.3 kHz 편차 내에서 중심 주파수가 원하는 값을 가지도록 했으며, TVR 레벨은 또한 0.3 dB 편차 내에서 특정 크기를 가지도록 하였다. 첫 번째로, 중심 주파수가 f₁인 심벌 트랜스듀서(Tx₁)의 구조를 설계하였으며, 설계된 Tx₁의 치수를 Table 1에 나타내었다. 다음으로, f₂, f₃을 각각 중심 주파수로 가지는 심벌 트랜스듀서 Tx₂와 Tx₃을 마찬가지 방법으로 설계하였다. 심벌 어레이가 광대역 특성을 가지기 위해 Reference [17]에서의 최적 설계 결과를 바탕으로 Tx₂의 중심 주파수 f₂는 0.92f₁, Tx₃의 중심 주파수 f₃은 0.79f₁로 설정하였다. 설계된 Tx₁, Tx₂와 Tx₃의 TVR 스펙트럼을 Fig. 2에 나타내었으며, 각각의 정량적인 음향특성 값들을 Table 2에 나타내었다. 또한, 대표적으로 Tx₁의 펄스 형태를 Fig. 3에 나타내었으며, 이것으로부터 고속 Fourier 변환하여 Fig. 2와 같은 스펙트럼들을 얻었다. Fig. 3에서 펄스폭이 좁아지면 대역폭이 넓어지며, 펄스폭과 대역폭은 반비례 관계를 가진다.

Table 1.

Structural parameters and dimensions of the cymbal transducer Tx₁.

Structural Parameter	Symbol	Dimension (mm)
Diameter of the cavity apex	d_a	5.7
Diameter of the cavity base	d_b	15.0
Diameter of the piezoceramic	d_c	20.0
Thickness of the metal cap	t_m	0.5
Thickness of the piezoceramic	t_c	1.0
Height of the cavity	h_c	0.8

https://static.apub.kr/journalsite/sites/ask/2021-040-01/N0660400102/images/ASK_40_01_02_F2.jpg

Fig. 2

(Color available online) Underwater TVR spectra of the three cymbal transducers Tx₁, Tx₂ and Tx₃.

https://static.apub.kr/journalsite/sites/ask/2021-040-01/N0660400102/images/ASK_40_01_02_F3.jpg

Fig. 3

Pulse form of Tx₁.

Table 2.

Acoustic characteristics of the three cymbal transducers Tx₁, Tx₂ and Tx₃.

Cymbal transducer	Center frequency	Maximum TVR	Fractional bandwidth
Tx₁	f₁	130.4 dB	18.6 %
Tx₂	f₂ = 0.92f₁	130.3 dB	18.5 %
Tx₃	f₃ = 0.79f₁	130.5 dB	20.1 %

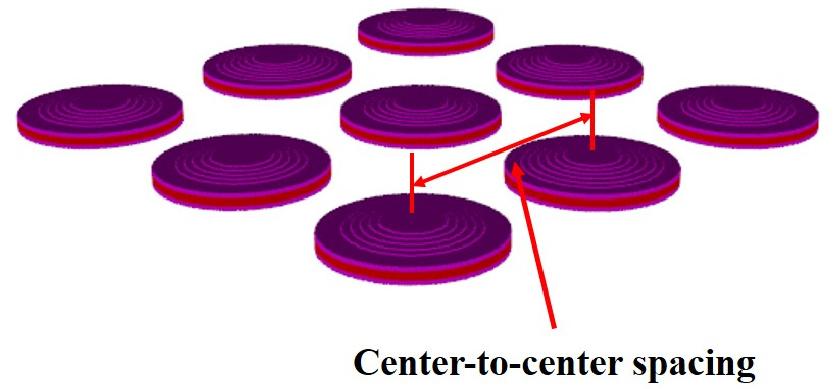
다음으로, 설계된 심벌 트랜스듀서 Tx₁, Tx₂와 Tx₃을 사용하여 Fig. 4와 같은 평면 배열을 구성하였다. 여기서 각 트랜스듀서들의 중심 간 간격은 Reference [17]의 최적 설계 결과를 따라 0.3λ로 설정하였다. λ는 f₁ 주파수에서의 수중 음파 파장이다. 수중에서 이 평면 배열의 송신특성을 확인하기 위해 어레이 외곽에 원거리 음장보다 충분히 큰 크기의 물을 설정하였고, 상부 캡의 수직방향 원거리 음장 지점에서 트랜스듀서로부터 방출된 음압을 계산하였다. 또한, 유한요소해석 모델의 물 경계부분에서는 반사가 일어나지 않도록 흡수 경계조건을 설정하였다.

https://static.apub.kr/journalsite/sites/ask/2021-040-01/N0660400102/images/ASK_40_01_02_F4.jpg

Fig. 4

(Color available online) 3D finite element analysis model of the 3×3 cymbal array.

III. 배열 패턴에 따른 3×3 심벌 어레이 성능 분석

패턴에 따른 심벌 어레이의 성능을 파악하기 위해서 우선 서로 다른 중심 주파수를 가지는 세 가지의 심벌 트랜스듀서를 각각 세 개씩 사용하였을 때 나올 수 있는 모든 경우의 수를 찾았다. 여기서 각 주파수별 소자를 세 개씩 사용한 이유는 TVR 레벨을 동일하게 하기 위해서이다. 또한, Reference [17]에서의 결과를 보면 어레이에서 구성 트랜스듀서들의 중심 주파수 차이가 배열의 음향특성에 영향을 미치는 것을 확인할 수 있다. 이 결과를 바탕으로 대역폭을 극대화하기 위해서 서로 다른 중심 주파수를 가지는 심벌 트랜스듀서들이 각기 다른 위치에 배열되어있는 모든 패턴들을 구성하였다. 심벌 트랜스듀서의 전체 개수가 아홉 개, 같은 것이 세 개씩 있으며 횡축, 종축, 대각선 대칭을 고려하여 계산한 결과 Eq. (1)과 같이 총 210가지의 경우의 수가 나왔다.

(1)

\frac{9!}{3! \times 3! \times 3!} \times \frac{1}{2^{3}} = 210 .

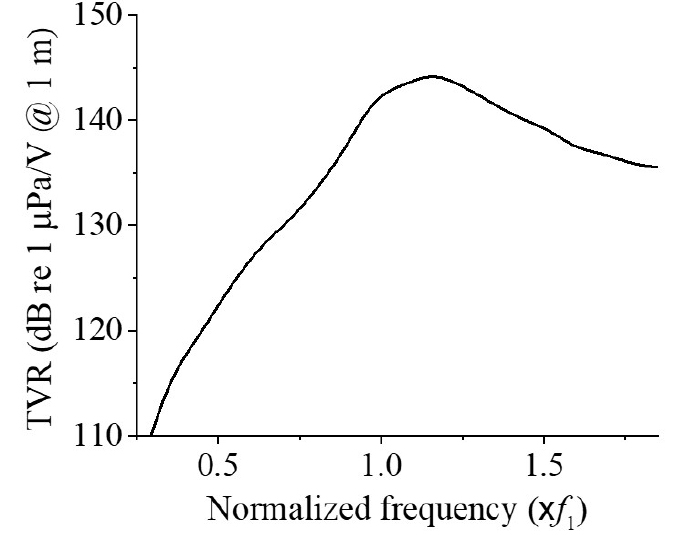
배열 형태가 비대칭인 패턴은 요소들의 개수가 많아서 해석 시간이 지나치게 오래 걸리기 때문에, 이들 210가지 경우들 중 면대칭인 33가지 패턴을 해석대상으로 선정하였다. 선정된 패턴들은 Fig. 5에 나타내었다. 이를 해석하기에 앞서, 선정된 패턴들과 비교할 기준 모델의 특성을 유한요소해석을 통해 분석하였다. 여기서, 기준 모델은 중심 주파수가 f₁인 심벌 트랜스듀서들로만 구성되어있는 3 × 3 배열 구조이다. Fig. 6는 기준 모델의 수중 TVR 스펙트럼으로 중심 주파수는 1.15f₁, 최대 TVR값은 144.1 dB, 대역폭은 6.5 kHz, 비대역폭은 34.6 %로 나타났다.

https://static.apub.kr/journalsite/sites/ask/2021-040-01/N0660400102/images/ASK_40_01_02_F5.jpg

Fig. 5

(Color available online) Patterns of the thirty three 3×3 cymbal array.

https://static.apub.kr/journalsite/sites/ask/2021-040-01/N0660400102/images/ASK_40_01_02_F6.jpg

Fig. 6

Underwater TVR spectrum of the reference model.

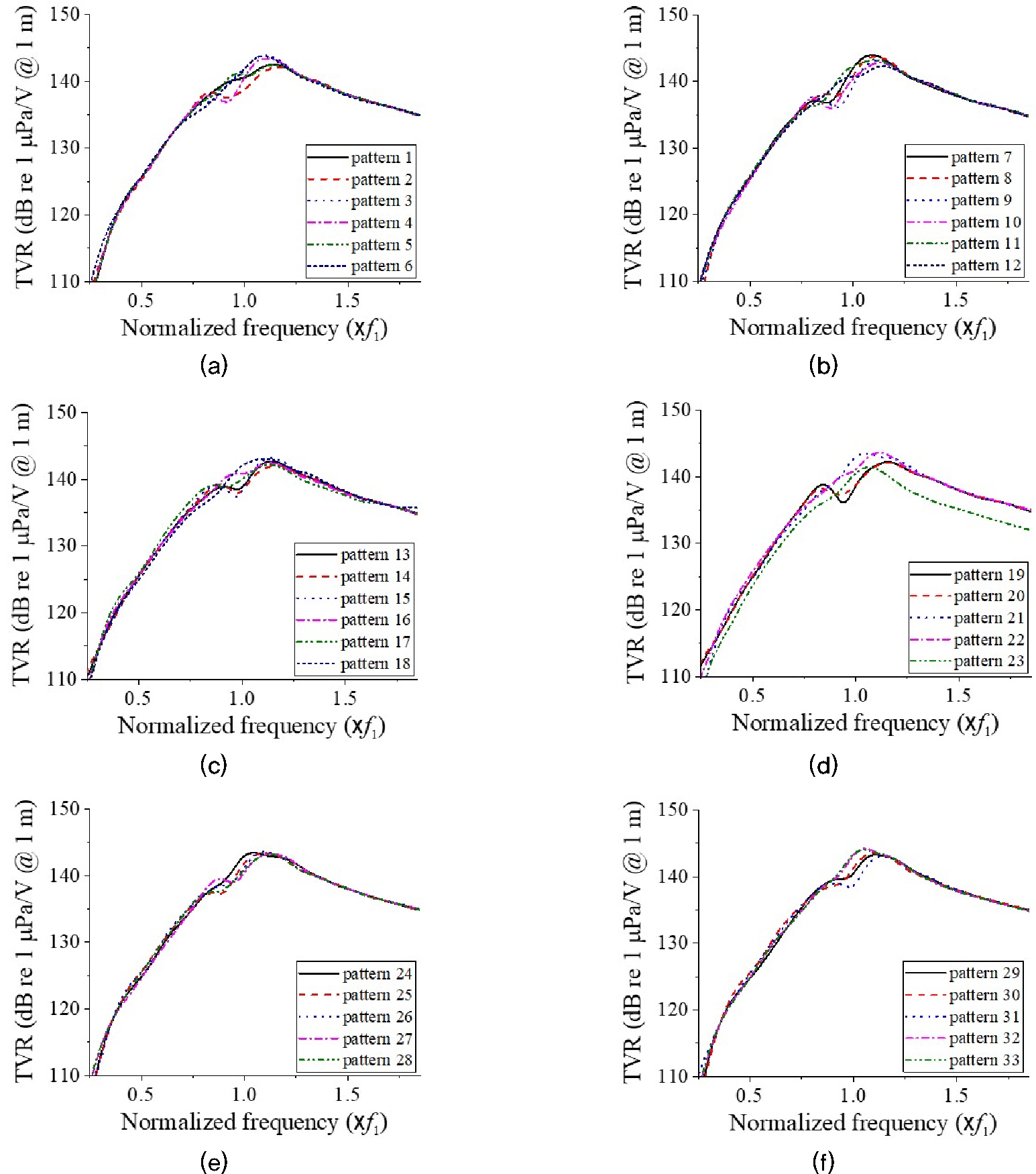
다음으로, 선정된 33가지 3 × 3 심벌 어레이 패턴의 주파수 특성을 유한요소해석을 통해 분석하여 Fig. 7에 나타내었다. 이 가운데 기준 모델에 비해 비대역폭이 넓은 패턴들은 6가지가 있었으며, 비대역폭이 40 %가 넘는 패턴들은 총 4가지가 있었다. 이 4가지 패턴들의 번호는 1, 5, 12, 16번이며, Table 3에 이들의 음향특성 값을 나타내었다. 이들의 공통점을 보면 사용한 세 개의 중심 주파수 가운데가 가장 높은 주파수인 f₁을 가지는 심벌 트랜스듀서가 중앙과 대각선에 있으며, 가장 낮은 주파수인 f₃을 가지는 심벌 트랜스듀서가 인접해있거나 뭉쳐져 있으면 높은 대역폭을 가지는 것을 확인할 수 있었다. 따라서 이와 같은 배열 구조를 가지면 비대역폭이 넓어질 것이라는 가설을 세울 수 있다.

https://static.apub.kr/journalsite/sites/ask/2021-040-01/N0660400102/images/ASK_40_01_02_F7.jpg

Fig. 7

(Color available online) Comparison of TVR spectra of the thirty three selected patterns : (a) pattern 1~6, (b) pattern 7~12, (c) pattern 13~18, (d) pattern 19~21, (e) pattern 22~28. (f) pattern 29~33.

Table 3.

Acoustic characteristics of the four patterns showing more than 40 % fractional-bandwidth.

Pattern	Center frequency	Maximum TVR	Bandwidth	Fractional bandwidth
1	1.14f₁	142.5 dB	7.7 kHz	42.3 %
5	1.14f₁	142.4 dB	7.9 kHz	43.2 %
12	1.16f₁	142.3 dB	7.9 kHz	42.5 %
16	1.13f₁	142.5 dB	7.7 kHz	42.4 %

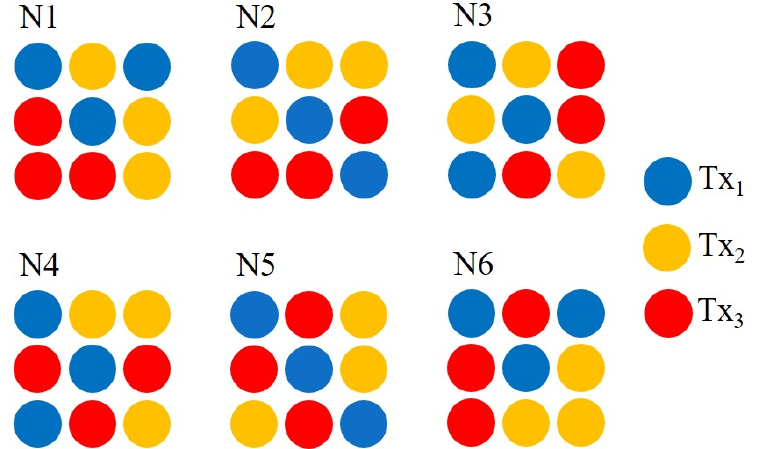
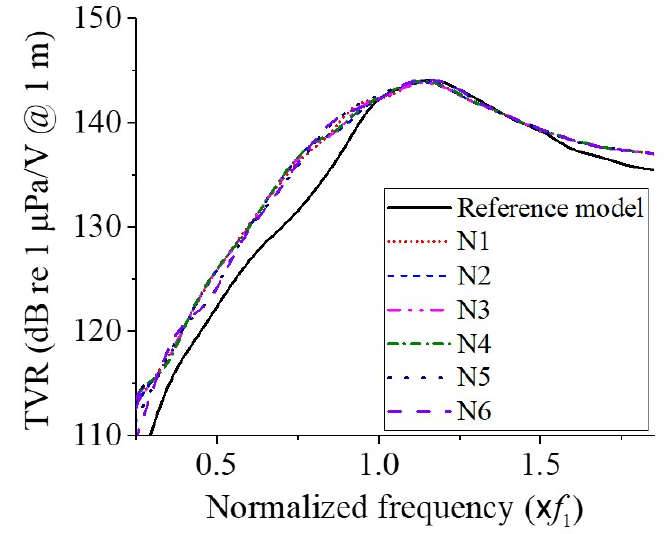
이 가설을 입증하기 위해, 전체 210가지의 패턴들 중에서 대칭 구조인 33가지 패턴을 제외한 나머지 경우들에서도 이 가설에 해당되는 것들을 찾아 추가적인 해석을 하였다. 추가적으로 해석된 N1 ~ N6 패턴들을 Fig. 8에 나타내었고, 이들의 TVR 스펙트럼을 Fig. 9에 보였다. Fig. 9는 기준 모델의 TVR 스펙트럼과 비교하여 N1 ~ N6 패턴들의 TVR 스펙트럼을 나타낸 것이며, 정량적인 음향특성 값들을 Table 4에 비교하였다.

https://static.apub.kr/journalsite/sites/ask/2021-040-01/N0660400102/images/ASK_40_01_02_F8.jpg

Fig. 8

(Color available online) Six additional patterns of the cymbal array.

https://static.apub.kr/journalsite/sites/ask/2021-040-01/N0660400102/images/ASK_40_01_02_F9.jpg

Fig. 9

(Color available online) TVR spectra of the N1~N6 patterns compared with that of the reference model.

Table 4.

Acoustic characteristics of the N1~N6 patterns compared with that of the reference model.

	Center frequency	Maximum TVR	Bandwidth	Fractional bandwidth
Reference model	1.15f₁	144.1 dB	6.5 kHz	34.6 %
N1	1.14f₁	143.9 dB	7.8 kHz	42.4 %
N2	1.16f₁	143.9 dB	7.1 kHz	38.5 %
N3	1.15f₁	143.9 dB	7.5 kHz	40.4 %
N4	1.15f₁	144.0 dB	7.1 kHz	38.4 %
N5	1.13f₁	144.0 dB	7.5 kHz	41.4 %
N6	1.14f₁	144.2 dB	7.0 kHz	38.7 %

Table 4의 결과를 통해, 가설로 세워진 배열 패턴을 가지는 N1 ~ N6 패턴들이 기준 모델보다 비대역폭이 더 넓은 것을 확인하였다. 도출된 배열 패턴들 중 비대역폭이 가장 넓었던 pattern 5는 기준 모델에 비해 비대역폭이 24.9 % 개선되었다. 이러한 광대역 배열 패턴이 성립되는 이유를 알고자 각 심벌 트랜스듀서의 어레이 내 위치에 따른 방사 저항을 계산하였다. 먼저, 심벌 트랜스듀서를 피스톤 음원으로 가정하여 Eq. (2)를 통해 자기방사 임피던스를 구하고, Eq. (3)을 사용하여 상호방사 임피던스를 구하였다. Eq. (2)에서 $ρ$ 는 밀도, $c$ 는 음속, $a$ 는 트랜스듀서 반지름이며, Eq. (3)에서 $Γ$ 는 감마 함수, $h_{p}^{(2)}$ 는 2종 구형 Hankel 함수, $d_{i j}$ 는 피스톤의 중심간 거리, $J$ 는 Bessel 함수이다.

(2)

Z_{i i} = ρ c π a^{2} .

(3)

Z_{i j} = 2 ρ c π a^{2} \sum_{p = 0}^{\infty} \frac{1}{π^{1 / 2}} Γ (p + 1 / 2) (\frac{a}{d_{i j}})^{p} h_{p}^{(2)} (k d_{i j}) \times \sum_{n = 0}^{p} (\frac{J_{p - n + 1} (k a) J_{n + 1} (k a)}{n! (p - n)!}) (i \neq j) .

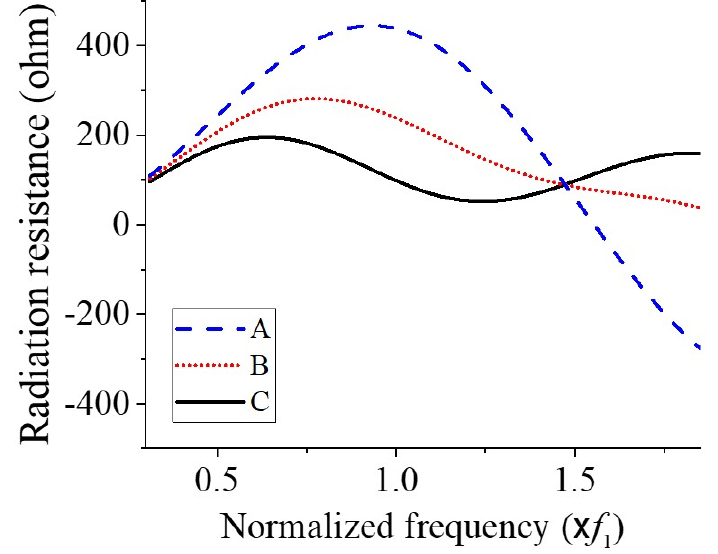
이 두 개의 임피던스를 더하여 전체 방사 임피던스를 구하였으며, 여기서 실수부인 방사 저항의 결과 값을 추출하여 Fig. 10에 나타내었다. Fig. 10은 동일한 중심 주파수의 트랜스듀서로 이루어진 3 × 3 어레이에서 서로 다른 위치에 있는 트랜스듀서들의 방사 저항 스펙트럼을 나타낸 것이다. Fig. 10에 보인 트랜스듀서들의 3 × 3 배열 내 위치는 Fig. 11에 나타내었다. Fig. 11에서 배열 내 소자마다 알파벳으로 기재된 것을 볼 수 있는데, 이것은 동일한 방사 저항을 가지는 소자들을 같은 알파벳으로 나타낸 것이다. Fig. 10의 결과를 보면 Fig. 11에서 A에 위치한 소자의 방사 저항이 가장 높은 것으로 보아 어레이에서 중심에 위치할수록 주변 소자들과 강한 상호작용이 일어나는 것을 알 수 있다. 여기서 상호작용이란 소자들 간의 음향 간섭작용에 의해 각 소자에 의해 발생되는 음파의 주파수 특성과 방사 특성이 변경되는 crosstalk 현상을 지칭한다.^[18,19] 그리고 C에 위치한 소자의 방사 저항이 가장 낮은데, 이로써 어레이의 모서리에 위치할수록 방사 응답이 낮다는 것을 알 수 있다. 위의 결과를 통해 서로 다른 세 개의 중심 주파수를 가지는 트랜스듀서들의 개수를 동일하게 사용했음에도 불구하고 소자들을 어떻게 배열하는가에 따라 음향특성이 바뀌는 것을 확인하였다. 이상의 현상을 반영해서 광대역 심벌 어레이를 구현하기 위한 방안을 다음과 같이 제시한다. 우선, 통과대역 우측단에 먼저 가장 높은 중심 주파수 f₁을 가지는 Tx₁을 발생 음압이 가장 강한 중앙과 가장 약한 모서리에 두어 레벨의 균형을 이루도록 한다. 다음으로 가장 낮은 중심 주파수 f₃을 가지는 Tx₃을 두 번째로 방사 음압이 높은 B에 위치시켜 통과대역 하단의 레벨을 앞서 설치한 고주파 대역에서의 레벨과 근사하도록 한다. 마지막으로, 중심 주파수가 f₂인 Tx₂를 앞서 설치한 어레이의 나머지 위치에 설치해서 대역폭 내 고주파와 저주파 성분 사이에 해당하는 골을 채우도록 한다. Figs. 7과 9에서 이상과 같은 방법으로 배열된 패턴들은 기준 모델에 비해 비대역폭이 최대 24.9 % 개선되었다. 결론적으로, 본 연구에서 의도했던 UWSN용 광대역 배열형 센서를 위한 패턴의 설계 방안을 도출했다고 할 수 있다.

https://static.apub.kr/journalsite/sites/ask/2021-040-01/N0660400102/images/ASK_40_01_02_F10.jpg

Fig. 10

(Color available online) Radiation resistance of the elements of different positions inside the 3×3 cymbal array.

https://static.apub.kr/journalsite/sites/ask/2021-040-01/N0660400102/images/ASK_40_01_02_F11.jpg

Fig. 11

Configuration of the 3×3 cymbal array.

IV. 결 론

본 연구에서는 수중 센서 노드용 광대역 음향 센서를 만들기 위한 심벌 트랜스듀서의 배열 패턴에 관한 연구를 수행하였다. 여러 패턴이 심벌 어레이의 음향특성에 미치는 영향을 분석하였고, 분석된 결과를 바탕으로 심벌 어레이의 비대역폭을 최대화시킬 수 있는 패턴을 도출하였다. 도출된 배열 패턴은 배열에 사용되는 트랜스듀서들 가운데 고주파인 심벌 트랜스듀서를 중앙인 A 위치에 1개, 모서리인 C 위치에 2개, 저주파인 심벌 트랜스듀서를 B 위치에 각각 3개 위치시키고, 중주파 트랜스듀서 3개를 남은 자리에 위치시킴으로써 비대역폭을 증대시킬 수 있었다. 이러한 구조를 가지는 패턴들은 동일한 주파수의 트랜스듀서들로만 구성된 기준 모델에 비해 비대역폭이 최대 24.9 % 개선되었다. 이 연구결과는 UWSN용 다양한 광대역 음향센서 기술 개발에 활용될 수 있다.

Acknowledgements

이 논문은 2020학년도 경북대학교 연구년 교수 연구비에 의하여 연구되었음.

References

J. H. Cui, J. Kong, M. Gerla, and S. Zhou, "The challenges of building scalable mobile underwater wireless sensor networks for aquatic applications," IEEE Netw. 20, 12-18 (2006). 10.1109/MNET.2006.1637927

Q. C. Xu, S. Yoshikawa, J. R. Belsick, and R. E. Newnham, "Piezoelectric composites with high sensitivity and high capacitance for use at high pressures," IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 38, 634-639 (1991). 10.1109/58.10886218267628

F. Bejarano, A. Feeney, and M. Lucas, "A cymbal transducer for power ultrasonics applications," Sens. Actuators, A: Phys. 210, 182-189 (2014). 10.1016/j.sna.2014.02.024

J. Zhang, W. J. Hughes, P. Bouchilloux, R. J. Meyer Jr., K. Uchino, and R. E. Newnham, "A class V flextensional transducer: The cymbal," Ultrasonics, 37, 387-393 (1999). 10.1016/S0041-624X(99)00021-9

A. Dogan, J. F. Fernandez, K. Uchino, and R. E. Newnham, "The 'cymbal' electromechanical actuator," Proc. 10th IEEE Int. Symp. Appl. Ferroelectr. 213-216 (1996).

A. Dogan, K. Uchino, and R. E. Newnham, "Composite piezoelectric transducer with truncated conical endcaps 'cymbal'," IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 44, 597-605 (1997). 10.1109/58.658312

R. E. Newnham, A. Dogan, D. C. Markley, J. F. Tressler, J. Zhang, E. Uzgur, R. J. Meyer Jr., A. C. Hladky-Hennion, and W. J. Hughes, "Size effects in capped ceramic underwater sound projectors," Ocean. Conf. Rec. 4, 2315-2321 (2002).

A. Dogan, Z. O. Yazici, and E. Uzgur, "Tailoring the Q of cymbal transducer," Key Eng. Mater. 264-268, 1305-1308 (2004). 10.4028/www.scientific.net/KEM.264-268.1305

J. F. Tressler, R. E. Newnham, and W. J. Hughes, "Capped ceramic underwater sound projector: The 'cymbal' transducer," J. Acoust. Soc. Am. 105, 591-600 (1999). 10.1121/1.426249

J. Zhang, W. J. Hughes, R. J. Meyer Jr., K. Uchino, and R. E. Newnham, "Cymbal array: A broad band sound projector," Ultrasonics, 37, 523-529 (2000). 10.1016/S0041-624X(99)00111-0

R. E. Newnham, J. Zhang, and R. J. Meyer Jr., "Cymbal transducers: A review," IEEE Int. Symp. Appl. Ferroelectr. 1, 29-32 (2000).

J. Zhang, A. C. Hladky-Hennion, W. J. Hughes, and R. E. Newnham, "Modeling and underwater characterization of cymbal transducers and arrays," IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 48, 560-568 (2001). 10.1109/58.91173911370370

J. F. Tressler, T. R. Howarth, and W. L. Carney, "Thin, lightweight electroacoustic projector for low frequency underwater applications," J. Acoust. Soc. Am. 116, 1536-1543 (2004). 10.1121/1.1778742

J. Luis, E. J. Park, R. J. Meyer Jr., and N. B. Smith, "Rectangular cymbal arrays for improved ultrasonic transdermal insulin delivery," J. Acoust. Soc. Am. 122, 2022-2030 (2007). 10.1121/1.276998017902839

L. Denghua and Y. Xi, "Cymbal transducer array for hydrophone applications," Ferroelectrics, 263, 131-136 (2001). 10.1080/00150190108225188

C. Kannan, R. Dhilsha, and P. M. Rajeshwari, Shibu Jacob, and M. A. Atmanand, "Performance evaluation of cymbal hydrophones for underwater applications," Int. J. Mech. Eng. Appl. 1, 43-48 (2013). 10.11648/j.ijmea.20130102.13

D. H. Kim and Y. Roh, "Design of a wideband cymbal transducer array" (in Korean), J. Acoust. Soc. Kor. 39, 170-178 (2020).

J. L. Butler and C. H. Sherman, Transducers and Arrays for Underwater Sound (Springer, Switzerland, 2016), pp. 547-552.

Y. Roh and M. S. Afzal, "Optimum design of a sparse planar array transducer for underwater vehicles by inclusion of crosstalk effect," Jpn. J. Appl. Phys. 57, 07LG02-1-7 (2018). 10.7567/JJAP.57.07LG02

The Journal of the Acoustical Society of Korea ISSN:1225-4428(Print) 2287-3775(Online) 한국음향학회지

Preview

Design of the broadband pattern of a cymbal transducer array

ABSTRACT

MAIN

Fig. 1

(Color available online) Schematic structure of the individual cymbal transducer.

Table 1.

Structural parameters and dimensions of the cymbal transducer Tx1.

Fig. 2

(Color available online) Underwater TVR spectra of the three cymbal transducers Tx1, Tx2 and Tx3.

Fig. 3

Pulse form of Tx1.

Table 2.

Acoustic characteristics of the three cymbal transducers Tx1, Tx2 and Tx3.

Fig. 4

(Color available online) 3D finite element analysis model of the 3×3 cymbal array.

(1)

Fig. 5

(Color available online) Patterns of the thirty three 3×3 cymbal array.

Fig. 6

Underwater TVR spectrum of the reference model.

Fig. 7

(Color available online) Comparison of TVR spectra of the thirty three selected patterns : (a) pattern 1~6, (b) pattern 7~12, (c) pattern 13~18, (d) pattern 19~21, (e) pattern 22~28. (f) pattern 29~33.

Table 3.

Acoustic characteristics of the four patterns showing more than 40 % fractional-bandwidth.

Fig. 8

(Color available online) Six additional patterns of the cymbal array.

Fig. 9

(Color available online) TVR spectra of the N1~N6 patterns compared with that of the reference model.

Table 4.

Acoustic characteristics of the N1~N6 patterns compared with that of the reference model.

(2)

(3)

Fig. 10

(Color available online) Radiation resistance of the elements of different positions inside the 3×3 cymbal array.

Fig. 11

Configuration of the 3×3 cymbal array.

Acknowledgements

References

Structural parameters and dimensions of the cymbal transducer Tx₁.

(Color available online) Underwater TVR spectra of the three cymbal transducers Tx₁, Tx₂ and Tx₃.

Pulse form of Tx₁.

Acoustic characteristics of the three cymbal transducers Tx₁, Tx₂ and Tx₃.