I. 서 론
잠수함의 외부 유동에 의해 발생하는 소음을 수치적으로 예측하기 위한 방법으로는 크게 직접법과 하이브리드법이 있다. 하이브리드법은 유동장과 음향장을 구분하여 유동소음을 예측하는 방법으로, Ffowcs Williams-Hawkings(FW-H) 음향상사법이 보편적으로 사용된다. FW-H를 활용한 유동소음 예측은 Computational Fluid Dynamics(CFD)를 수행한 후, 적분면에서의 데이터로 수음점에서 발생하는 소음을 예측하는 방법이다. 특히 합리적인 계산 비용으로 수중에 방사되는 소음을 효과적으로 예측할 수 있어 해석에 많은 시간이 소요되는 잠수함 추진기에 의해 발생하는 소음 예측에 활용된다.[1,2] 잠수함 수중익형과 소나돔의 난류 경계층에서 발생하는 근거리장 소음은 잠수함 자체소음에 기여하며, 이 소음 성분을 입사 음향 신호와 구분하지 못할 경우 소나성능 저하로 이어지므로 정확한 분석이 필요하다.[3] 하이브리드법은 소음이 선형적으로 전파되는 원거리장을 가정하여 계산을 수행하며, 관측점에서의 에너지가 거리에 반비례하여 감소한다. 유동과 구조물의 상호작용에 의해 반사, 산란되는 성분을 고려해야 하는 근거리장에서 발생하는 소음을 예측하기 위해서는 직접법을 활용해야 한다. 직접법은 유동장 내부의 수음점에서 압력값을 직접 활용하기 때문에 위치에 따라 급변하며 선형적인 관계를 띄지 않는 근거리장에서의 유동소음을 예측할 수 있다.[4]
최근 컴퓨팅 자원을 많이 소모하는 CFD 해석에 소요되는 시간을 단축하고자 딥러닝을 활용하여 결과를 예측하는 연구가 수행되었다. Lee et al.[5]는 비정상 와류 흐름장을 예측하기 위해 합성곱 신경망(Convolutional Neural Network, CNN)을 활용한 모델을 제안하고 분석하였다. 다중 해상도 CNN을 설계하여, 다양한 시간 및 공간 규모에서 발생하는 와류 구조를 학습하고 예측하도록 하였다. 학습 데이터는 Large Eddy Simulation(LES) 난류 모델을 통해 생성된 원형 실린더 주위의 유동장 데이터로 구성되었으며, CNN은 압력 및 속도 필드로부터 유동장 전체의 변화를 예측하도록 학습되었다. 검증 결과, 기존 CFD 대비 3배 이상 단축된 계산시간으로 비정상 유동장을 예측하였다. Meng et al.[6]은 원형 실린더 주위 유동으로 인해 발생하는 유동소음을 심층 신경망(Deep Neural Network, DNN)을 활용하여 빠르고 정확하게 예측하는 방법을 제안하였다. 유동소음 데이터는 FW-H 음향 상사식으로 유속에 따른 수음점에서의 Overall Sound Pressure Level(OASPL)을 계산하였다. DNN 모델의 입력 변수는 수음점 좌표와 유속을 선정하였고, 출력층에서 OASPL을 예측하도록 모델을 구성하였다. 이를 통해 제안된 DNN 모델 프레임워크는 실린더 주위 유동으로 발생하는 공력 소음을 빠르고 정확하게 예측할 수 있음을 확인하였다.
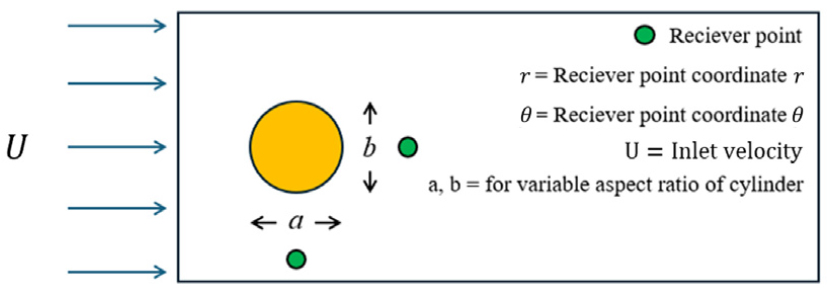
본 연구에서는 잠수함 부가물의 형상과 운항 환경에 따른 유동소음 예측에 앞서, 비교적 단순한 형상인 실린더 모델을 대상으로 연구를 진행하였다. 이를 위해 상용 소프트웨어인 Star-CCM+를 활용하여 실린더의 형상과 유속을 설계 변수로 하는 CFD 해석 케이스를 생성하고 Detached Eddy Simulation(DES) 난류 모델[7]로 해석을 수행하였다. 또한 각 케이스에 극좌표계 기준으로 등간격의 수음점을 생성하였고, 직접법을 활용하여 근거리장에서의 유동소음 데이터를 생성하였다. 각 수음점에서의 데이터는 후처리를 통해 옥타브 밴드로 정형화하였고, Fig. 1의 설계 변수와 옥타브 밴드의 중심 주파수에 따른 음압레벨(Sound Pressure Level, SPL)을 데이터베이스로 구성하였다. 생성된 데이터베이스를 활용하여 복수의 입력값에 따른 SPL 값을 예측할 수 있도록 DNN 모델을 구성하였고, 학습 과정에서 모델의 수렴 여부를 학습곡선(learning curve)으로 분석하였다. 마지막으로 학습에 사용되지 않은 데이터를 통해 모델의 정확도와 적합성을 측정하였고, DNN 모델을 활용한 유동소음 예측 기법의 유효성을 평가하였다.
II. 실린더의 유동소음 해석
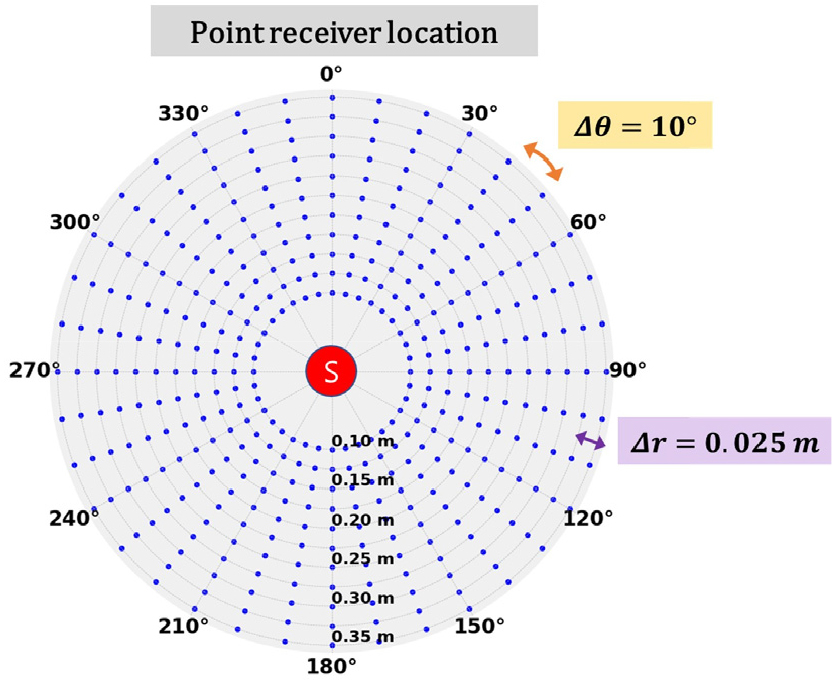
유동소음 예측 모델의 학습 데이터를 생성하기 위해 해석 케이스를 선정하였다. 초기 형상은 CFD 해석에서 표준으로 사용하는 원형 실린더 모델로 선정하였고, 잠수함 세일의 형상을 모사하기 위해 원형 실린더의 직경에 따른 종횡비를 조정하여 타원형 실린더 형상으로 구현하였다. 또한 각 실린더 형상에 대해 유속을 변경하여 유동소음 해석 케이스로 선정하였다. 실린더 직경은 0.02 m, 0.03 m로 설정하였으며, 각 직경에 대한 종횡비는 각 직경에 대해 1부터 3까지 0.5 간격으로 증가시켰다. 유속은 5 m/s, 7.5 m/s, 10 m/s로 설정하여 해석을 수행하였으며, 전체 해석 케이스 목록은 Table 1에 명시하였다. 실린더 형상과 유속 외에 직교 좌표계의 기준으로 0.25 m, 10° 간격의 수음점을 Fig. 2와 같이 생성하였다. 각 수음점의 압력 데이터를 활용하여 직접적으로 유동소음을 예측하는 직접법 기반의 해석을 수행하였고, 신호처리 결과는 각 주파수별 SPL 형태로 출력된다. 주파수 해상도에 따라 SPL 데이터의 분포와 개수가 상이하므로, 데이터 개수가 정형화된 옥타브 밴드 데이터를 학습 데이터로 선정하였다.
Table 1.
Variables in CFD simulations.
| Design variables | Value |
| Inlet velocity (m/s) | 5, 7.5, 10 |
| Cylinder aspect ratio | 1, 1.5, 2, 2.5, 3 |
| Cylinder diamater (m) | 0.02, 0.03 |
정확한 유동소음 데이터를 얻기 위해 공간 필터링 난류 모델인 DES 모델을 활용하여 비정상 상태의 해석을 수행하였다. 유동소음을 정확하게 계산하기 위해서는 복잡한 난류 형상을 모사할 수 있는 LES 모델을 사용해야 하지만, 벽면 근처에서 과도한 격자가 생성되어 계산량이 크게 증가한다. DES 모델은 벽면 근처 경계층에서 Reynolds Averaged Navier Stokes(RANS) 모델을 적용하는 방법을 통해 LES 모델 수준의 난류 정확도를 유지하면서도 합리적인 계산이 가능하다. 실린더 주위에 난류가 발생할 수 있는 영역은 Fig. 3과 같이 격자를 조밀하게 생성하였고, 실린더 경계층에서 벽면 근처의 유동 박리점을 정확하게 계산하기 위해 Y+는 1 이하가 되도록 격자를 생성하였다. 시간 간격은 2.5E-5로 설정하였고, Courant Friedrichs Lewy number(CFL 수)의 값이 0.7인 것을 통해 격자 크기와 시간 간격이 비정상 해석을 수행하는 데 적합함을 확인하였다. 격자와 해석 조건에 대한 상세한 내용은 Tables 2와 3에 명시하였다.
Table 2.
Mesh specifications in the CFD grids.
| Design variables | Value |
| Y+ | 1 |
| CFL | 0.7 |
| # of nodes (M) | 2.8 ~ 3.7 |
| # of prism layers | 40 |
Table 3.
Star-CCM+ simulation condition.
딥러닝 모델은 일반적으로 데이터의 개수가 많을수록 예측 정확도가 증가하지만, 데이터를 생성하는 수음점의 수가 증가하게 되면 전처리와 후처리에 소요되는 시간 또한 증가하게 된다. 이를 보완하고자 프로그래밍 언어인 Python과 Java를 활용하여 자동화를 수행하였고, 해석 케이스 생성 및 데이터 처리 시간을 단축하였다. 또한 자동화 코드를 활용하여 Fig. 2와 같은 간격으로 수음점을 생성하였고, 부가물의 설계 변수, 수음점 좌표에 따른 SPL 값을 데이터베이스로 구성하였다.
III. 심층 신경망 모델 개발
DNN은 딥러닝 알고리즘의 한 종류로, 입력층(input layer)과 출력층(output layer) 사이에 다중의 은닉층(hidden layers)이 구성된 인공 신경망(Artificial Neural Network, ANN) 모델을 지칭한다. 각 은닉층에는 다수의 노드가 각각의 가중치를 가지며, 순전파와 역전파를 반복하여 가중치를 수정하는 과정을 반복하여 스스로 학습을 수행한다. 순전파 과정에서는 우선 아래 식의 가중치 행렬 W(l)과 이전 층의 출력값 h(l-1)의 곱에 편향 b(l)를 더한다. 이어서 연산값에 활성화함수(activation function) g를 적용하여 현재 층의 출력값 h(l)를 계산한다. 각 은닉층은 위 과정을 반복하여 마지막 층에서 출력값을 산출한다.
일차적으로 연산을 수행한 출력층에서의 값과 실제 값의 차이를 손실함수(loss function) L로 정의하고, 이를 최소화하는 방향으로 업데이트를 수행한다. 손실함수를 최소화하기 위해 사용하는 알고리즘인 최적화 알고리즘(optimizer)을 활용하여 각 층의 가중치와 편향은 업데이트를 수행하며, 이 과정을 반복하여 학습된 DNN 모델은 복잡한 데이터를 예측할 수 있게 된다.
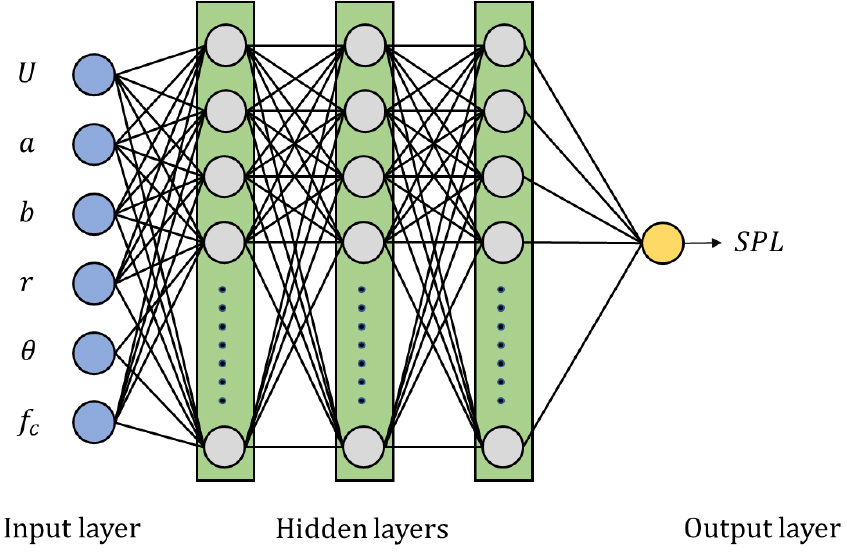
본 연구에서는 실린더 주위 유동소음 예측 모델 개발을 위해 설계 변수, 수음점 위치, 중심 주파수를 DNN 모델의 입력 변수로 선정하였고, 출력층에서 SPL 값을 출력하도록 Fig. 4와 같이 초기 모델을 구성하였다. 수음점에서의 유동소음 결과를 빠르고 정확하게 예측하기 위해 DNN 모델을 다층 퍼셉트론(Multilayer Perceptron, MLP) 아키텍처로 구성하였다. 모델의 하이퍼파라미터는 MLP 아키텍처에서 보편적으로 사용하는 값들로 설정하였다. 활성화 함수는 Rectified Linear Unit(ReLU), 손실함수는 Mean Squared Error(MSE), 최적화 알고리즘은 Adaptive Moment Estimation(Adam)으로 Table 4에 명시하였다. 전체 데이터셋을 학습, 검증, 테스트셋으로 각각 0.7:0.15:0.15 비율로 분할하여 DNN 모델 학습을 진행하였다.
IV. 유동소음 예측 결과
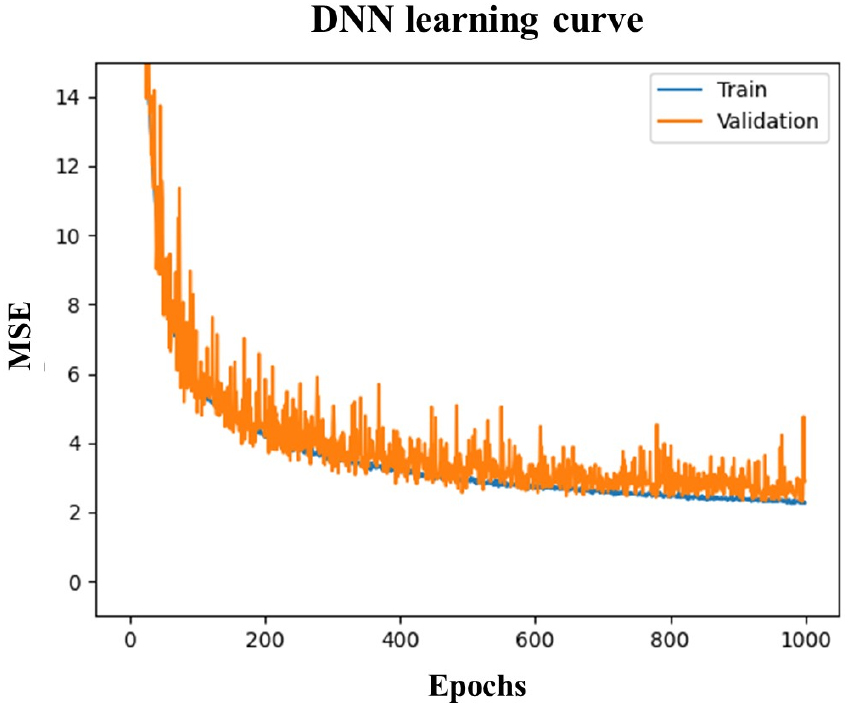
DNN 모델의 예측 성능을 평가하기 위해 하이퍼파라미터를 Table 4의 값으로 설정한 뒤 학습을 수행하였다. 또한 학습 과정과 개선 방향성을 확인하기 위해 학습곡선으로 모니터링하였다. 학습의 진행도는 Fig. 5의 학습곡선에서 학습 데이터의 손실값인 MSE가 점차 감소하는 것을 통해 확인하였다. 또한 학습 데이터가 제한적일 경우 모델이 학습 데이터에만 과도하게 최적화되어 새로운 데이터에 대한 예측 성능이 떨어지게 되는 과적합이 발생할 수 있다. 과적합이 발생할 경우 학습 데이터의 손실은 감소하는 반면 검증 데이터의 손실은 증가하는 경향을 보인다. 따라서 모델 학습 과정에는 과적합을 방지하기 위해 주기적으로 확인하고 필요하다면 학습 조기 종료와 같은 대응이 필요하다. 본 연구의 DNN 모델의 경우 Fig. 5를 통해 학습이 안정적으로 진행되었음을 확인할 수 있다. 전체 학습 과정에서 학습 데이터와 검증 데이터의 손실 값이 함께 감소하는 경향을 보였으며, 손실 값이 더 이상 감소하지 않는 1,000 epochs에서 학습을 종료하였다.
Table 4.
Hyperparameters of DNN model.
학습이 완료된 DNN 모델의 성능을 테스트 데이터로 평가하였다. DNN 모델로 회귀분석을 수행한다면, 모델의 성능은 오차와 결정계수를 고려하여 평가한다. 오차는 DNN 모델의 예측값과 CFD 결괏값의 차이를 기반으로 평가하며, 일관성을 유지하기 위해 손실과 동일하게 MSE로 평가하였다.
결정계수( score)는 회귀모델에서 독립변수가 종속변수의 변동에 기여하는 수치를 나타내는 척도이다. 결정계수가 높을수록 모델이 관측된 데이터의 변동성을 효과적으로 설명함을 의미하며, 그 식은 다음과 같다.
위 식에서 총제곱합(Total Sum of Squares, SST)은 실제값()과 평균값()의 차이를 제곱한 값들을 합한 것으로, 데이터 전체 변동성을 나타낸다. 잔차제곱합(Regression Sum of Squares, SSR)은 모델 예측값()과 평균값의 차이의 제곱합이며, 데이터와 모델의 적합도를 설명한다. 회귀제곱합(Error Sum of Squres, SSE)은 모델의 예측값과 실제값의 차이의 제곱합으로, SST와 SSR의 차이로도 계산이 가능하다.
하지만 결정계수는 변수가 증가할수록 값이 증가하는 경향이 있으며 모델의 성능평가에 이를 반영해야 한다. 수정된 결정계수(adjusted , )는 표본 크기(n)와 독립변수의 수(k)를 고려하여 결정계수를 조정하며 아래와 같이 계산한다.
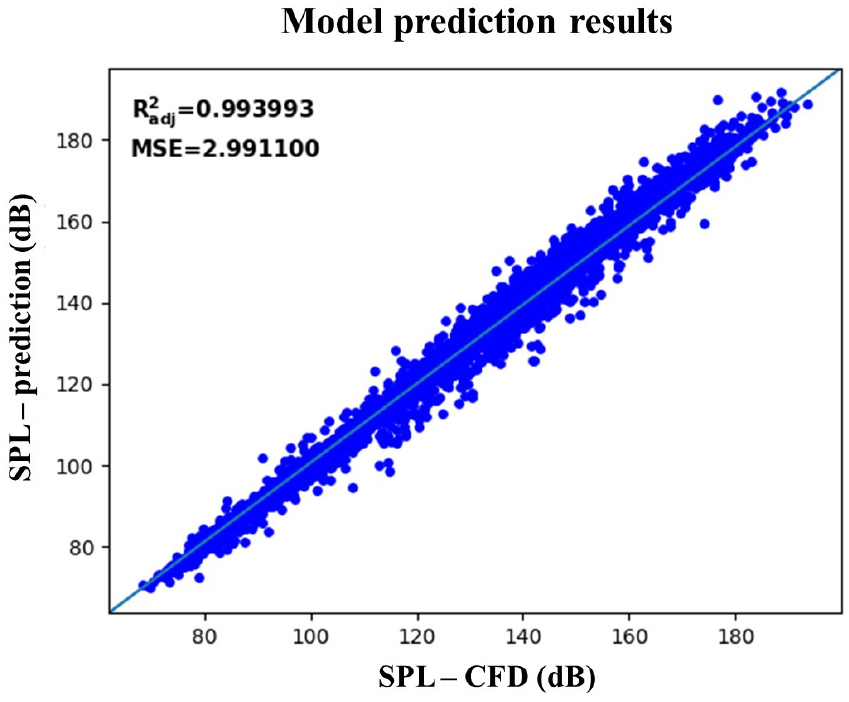
앞서 정의한 평가지표로 DNN 모델의 성능을 테스트 데이터를 통해 평가하였으며, 예측 결과를 Fig. 6의 산점도로 표기하였다. 모델의 평가지표는 Table 5의 수정된 결정계수가 0.994로 충분한 설명력을 가짐을 확인할 수 있다. 또한 테스트 데이터에 대한 MSE 값인 2.99를 통해 학습된 유동소음 예측 DNN 모델의 정확도를 검증하였다.
V. 결 론
본 연구에서는 잠수함 부가물 주위의 유동소음을 딥러닝 알고리즘인 DNN 모델로 예측하고자 하였다. 학습 데이터 생성을 위해 실린더 형상과 유속을 설계 변수로 하여 CFD 해석 케이스를 선정하고, 난류를 정확하게 모사하기 위해 DES 난류 모델을 활용하여 해석을 수행하였다. 각 케이스에는 극좌표계를 기준으로 동간격의 수음점을 생성하였고, 직접법으로 근거리장의 유동소음 데이터를 생성하였다. 생성된 데이터를 활용하여 설계 변수, 수음점 좌표, 옥타브 밴드 중심 주파수에 따른 SPL을 예측하는 DNN 모델을 학습하였다. 마지막으로 학습이 완료된 DNN 모델의 성능을 테스트 데이터로 평가하였고, 개발한 모델이 실린더 주위의 유동소음을 정확하게 예측하고 충분한 적합도를 가짐을 확인하였다.
현재 본 연구에서는 잠수함 부가물을 실린더 형상으로 단순화하여 유동소음 예측 연구를 수행하였으나, 추후 실 형상에 유사한 수중익형과 복잡한 구조를 적용하여 예측 성능을 추가적으로 검증할 필요가 있다. 또한 수중으로 전파되는 소음의 공간적 특성을 보다 정확히 고려하기 위해 3차원 구면좌표계 기반 예측으로 확장하고자 한다. 이러한 추가 연구를 통해 잠수함 운용 환경에서의 실제 소음 특성을 보다 현실적으로 반영할 수 있으며, 향후 잠수함 설계 단계에서 소음 저감 방안을 도출하는 데 기여할 것으로 사료된다.