I. 서 론
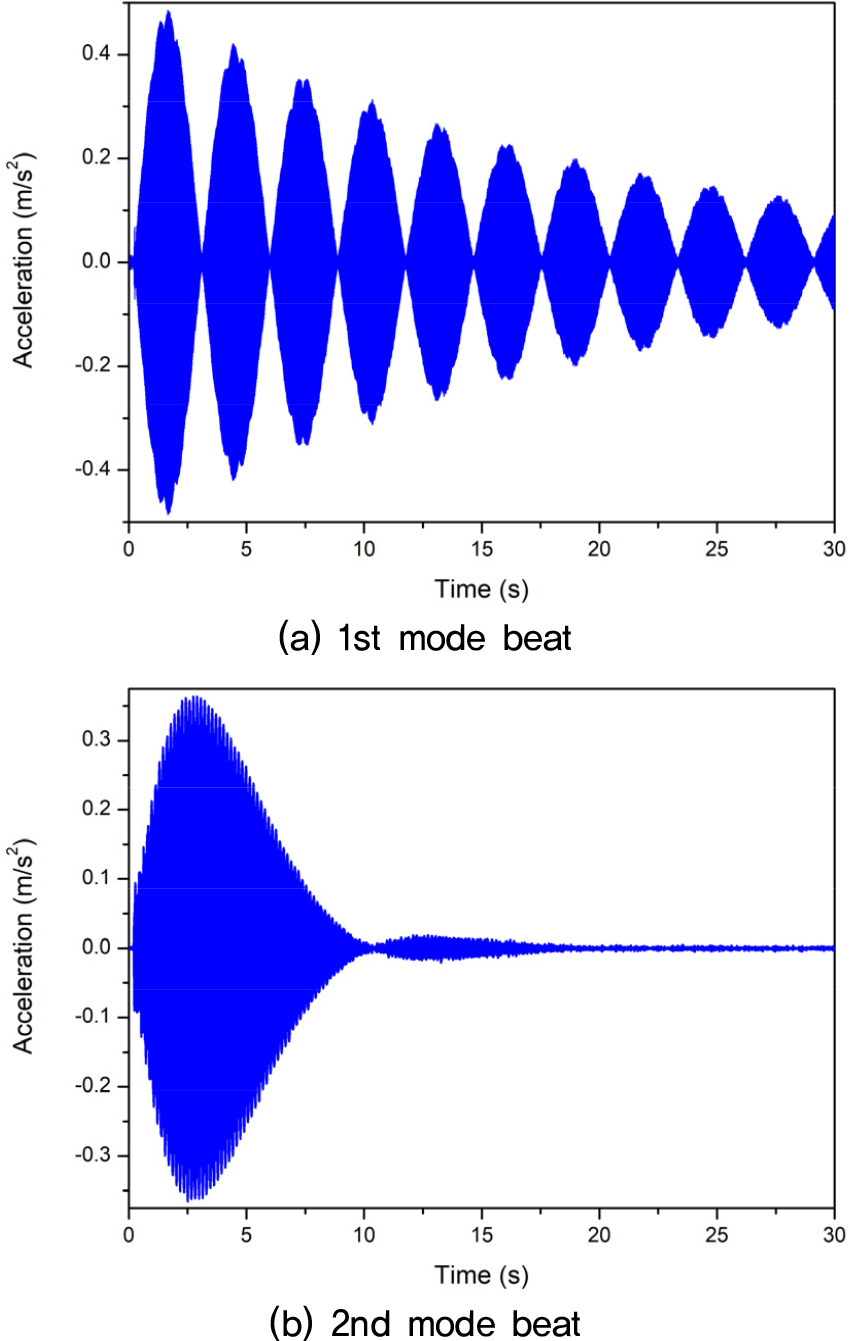
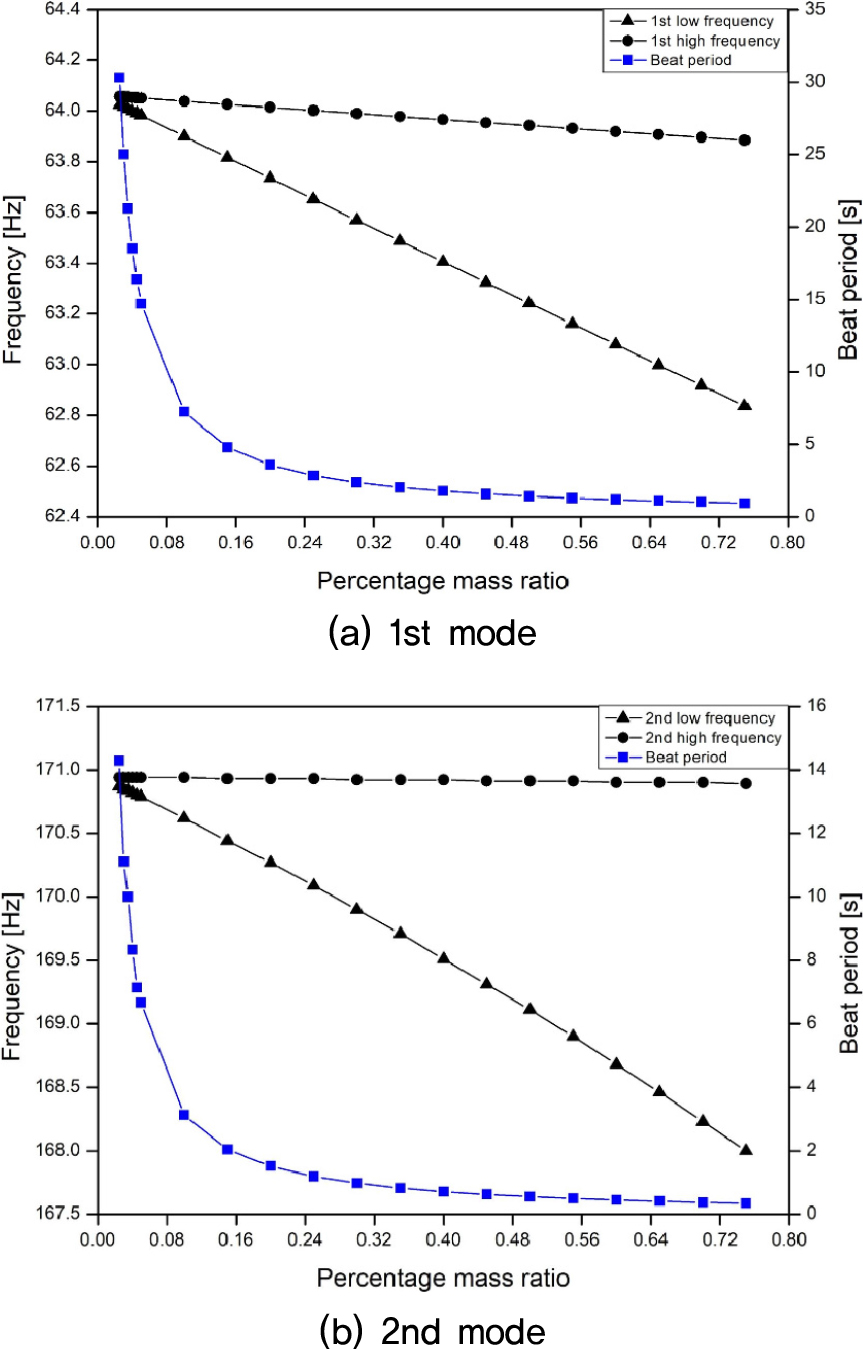
성덕대왕신종으로 대표되는 한국종에서 타격음의 웅장함과 여음의 생동감은 맥놀이라는 물리 현상이 만들어 낸다.[1] Fig. 1(a)는 성덕대왕신종의 1차 진동모드가 만드는 여음의 맥놀이다.[2] 이 맥놀이는 저주파수 여음의 크기에 변화를 주어 오래 들리도록 한다. Fig. 1(b)는 2차 진동모드가 만드는 기본음의 맥놀이로, 강하게 뿜어 나오는 타격음이 사라지는 듯하다가 다시 살아나면서 소리에 역동감을 준다. 이처럼 각각의 진동모드에서 발생하는 맥놀이는 종 표면의 복잡한 문양과 주조 오차에 의한 비대칭성에 기인한다. 비대칭성은 하나의 진동모드를 미세한 주파수 차이를 갖는 모드 쌍으로 분리시킨다.[3] 이하 미세하게 낮은 고유주파수의 모드를 L 모드로, 이보다 약간 높은 주파수의 모드를 H 모드로 표기한다. 미세한 주파수 차이를 갖는 모드 쌍이 상호 간섭하여 맥놀이를 만든다. 한국종에서 맥놀이는 선명하면서도 적절한 주기를 가져야 소리의 우수성을 극대화시킬 수 있다.
맥놀이가 얼마나 선명한가는 타격점인 당좌와 L, H 모드 쌍의 상대적 위치 관계로 결정된다. 타격점인 당좌가 L, H 모드 쌍의 배의 정중앙에 위치하면 두 모드는 같은 크기로 가진된다. 따라서 모드 쌍이 대등하게 응답하는 지점에서 완벽한 보강과 상쇄가 이루어져 매우 선명한 맥놀이가 발생한다. 반대로 당좌가 L, H 모드 쌍 중 어느 하나만 가진하는 위치에 있으면 맥놀이는 모든 위치에서 발생하지 않는다.
맥놀이의 주기는 비대칭성의 크기에 따라 결정되는데, 주조 후에 적절한 주기를 갖도록 교정이 가능하다.[4,5]
문제는 타격점인 당좌가 맥놀이를 만들지 못하는 위치에 오는 경우, 맥놀이 주기가 적절하더라도 선명하게 들리지 않는다는 것이다.
이를 위해 본 연구에서는 인공 덤쇠를 사용하여 선명한 맥놀이를 만드는 방법을 제시한다. 덤쇠란 성덕대왕신종의 종합학술조사에서 처음 관찰되었는데, 종 내부에 떡처럼 돌출된 작은 부분을 의미한다.[6,7] 뜨거운 쇳물의 주입과정에서 주물사의 일부가 훼손되어 종 내면의 일부가 돌출된 것으로 추정된다.
덤쇠는 종 구조의 비대칭성에 영향을 준다. 인공적으로 덤쇠를 만들어 문양이나 주조 오차로 인한 작은 비대칭성을 압도할 수 있다면, 당좌가 선명한 맥놀이를 만드는 위치가 되도록 L, H 모드쌍의 배를 이동시킬 수 있을 것이다.
선행연구에서는 링을 대상으로 인공 덤쇠를 적용하여 선명한 맥놀이를 만드는 방법을 검토하였다.[6] 또 소형 모형종의 비대칭성을 집중질량으로 모델링하고 덤쇠가 맥놀이 특성에 미치는 영향을 검토하였다.[7] 그러나 한국종의 비대칭성이 어느 정도인지를 가늠하기 어려워 실제 적용 가능한 인공 덤쇠의 제원을 제시하지 못했다. 이 방법을 주조 현장에 적용하기 위해서는 종의 문양이나 주조 오차에 의한 비대칭성이 어느 정도 발생하는가를 먼저 파악하고 이를 정량화해야 한다. 이를 위해 선행연구에서 현대에 제작된 여러 대형 한국종을 대상으로 비대칭성의 크기를 반영하는 맥놀이 주기 데이터를 취득하였다.[8]
본 연구에서는 성덕대왕신종과 현대에 제작된 대형 한국종의 맥놀이 주기 데이터로부터 복잡한 문양과 주조 오차로 인한 비대칭성의 크기를 정량화시켰다. 비대칭성의 정량화를 위해 선행연구에서 제시한 등가종 모델[9]을 이용하였다. 등가종은 실제 종과 동일한 맥놀이 주기를 갖는 유한요소 해석 모델로, 종의 축 대칭 유한요소해석 모델에 한 개의 등가 집중질량을 부착해서 만들었다. 20 t 규모의 한국종의 등가종 모델을 대상으로 당좌가 선명한 맥놀이를 내는 위치에 오도록 만드는 덤쇠의 위치와 크기를 제시하고자 한다.
II. 한국종의 비대칭성
Table 1은 성덕대왕신종을 포함하는 12개의 대표적인 대형 한국종에서 맥놀이를 만드는 1, 2차 고유주파수 쌍의 측정 결과다. 가장 오래 지속되는 여음을 만드는 1차 고유주파수 쌍과 타격음의 음높이를 지배하는 2차 고유주파수 쌍을 보인다.
맥놀이 이론에 따라 각각의 모드에서 고유주파수 쌍의 차이의 역수가 맥놀이 주기다. ①King Sungdeok 종의 1차 음의 맥놀이 주기는 주파수 쌍의 차이 0.35 Hz의 역수인 2.9 s이고, 2차 음의 맥놀이 주기는 주파수 차이 0.11 Hz의 역수인 9.1 s다. 맥놀이 주기는 모드별 비대칭성을 반영하면서, Fig. 1의 모드별 맥놀이를 발생시킨다.
Table 1.
Frequency pairs of Korean bells.[8]
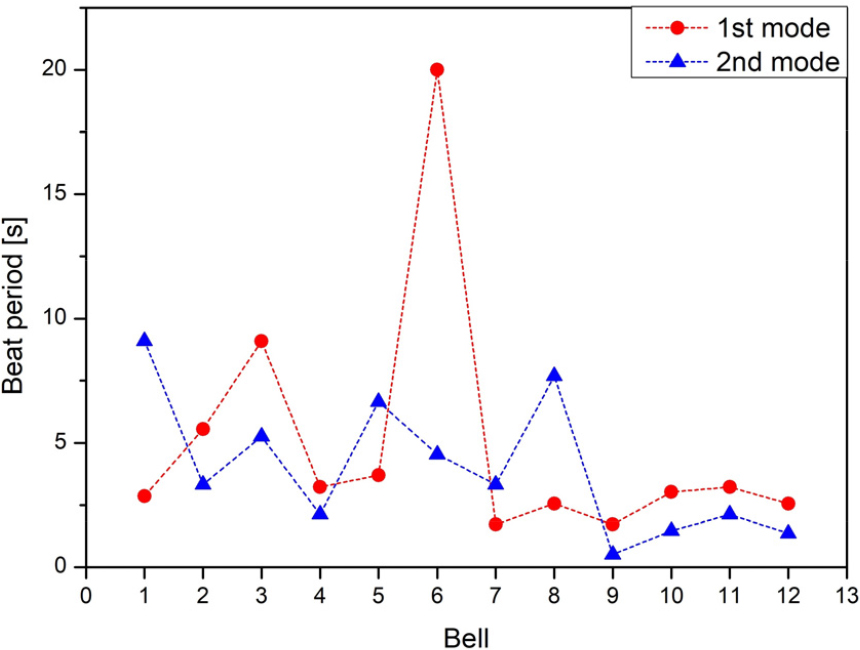
Fig. 2는 Table 1의 값으로부터 구한 1차 및 2차 음의 맥놀이 주기를 비교한다. 맥놀이 주기가 길수록 비대칭성이 작고, 주기가 짧을수록 비대칭성이 크다. 1차 모드에서 ⑥Hwasung 종은 맥놀이 주기가 20 s로 가장 길다. 반대로 ⑦Yangsan 종과 ⑨Baekje 종의 맥놀이 주기는 1.7 s로 가장 짧으므로 비대칭성이 가장 크다. 2차 모드에서 가장 짧은 맥놀이 주기는 ⑨Baekje 종의 0.5 s이고, 따라서 이 종은 2차 모드의 비대칭성이 가장 크다. 반대로 ①King Sungdeok 종의 2차 맥놀이 주기는 9.1 s로 가장 길고 따라서 비대칭성은 가장 작다.
Fig. 2에서 맥놀이 주기는 종의 크기가 작아지면서 짧아지는 경향이 있다. 종이 작아지면 중량대비 주조 오차로 인한 비대칭성이 커지기 때문이다. Table 1과 Fig. 2의 결과는 현대 한국종의 주조 기술이 어느 정도의 비대칭성을 만드는가를 반영한다.
본 연구에서는 20 t 이상의 대형 종에 인공 덤쇠를 적용하기 위해 성덕대왕신종을 포함 ① ~ ⑥의 6개 종의 비대칭성을 고려하였다. Fig. 2에서 ① ~ ⑥번 종의 1차 모드의 맥놀이 주기는 2.9 s ~ 20 s이고, 2차 모드의 맥놀이 주기는 2.1 s ~ 9.1 s 범위다.
이 범위의 맥놀이 주기를 고려하여 비대칭성을 등가종으로 모델링 한 후, 인공 덤쇠를 적용하고자 한다.
III. 등가종
등가종은 실제와 동일한 맥놀이 주기, 즉 비대칭성을 갖는 유한요소해석 모델이다. 이에 관해 컷이나 집중 질량을 갖는 등가링의 고유주파수 쌍과 맥놀이 주기 해석방법이 제시되었고,[10,11] 최근에는 평창 동계올림픽대종에서 등가종을 이용하여 맥놀이 주기를 조절한 연구가 있었다.[12]
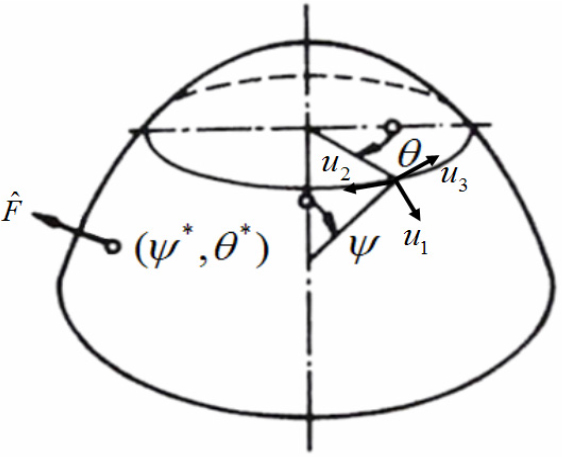
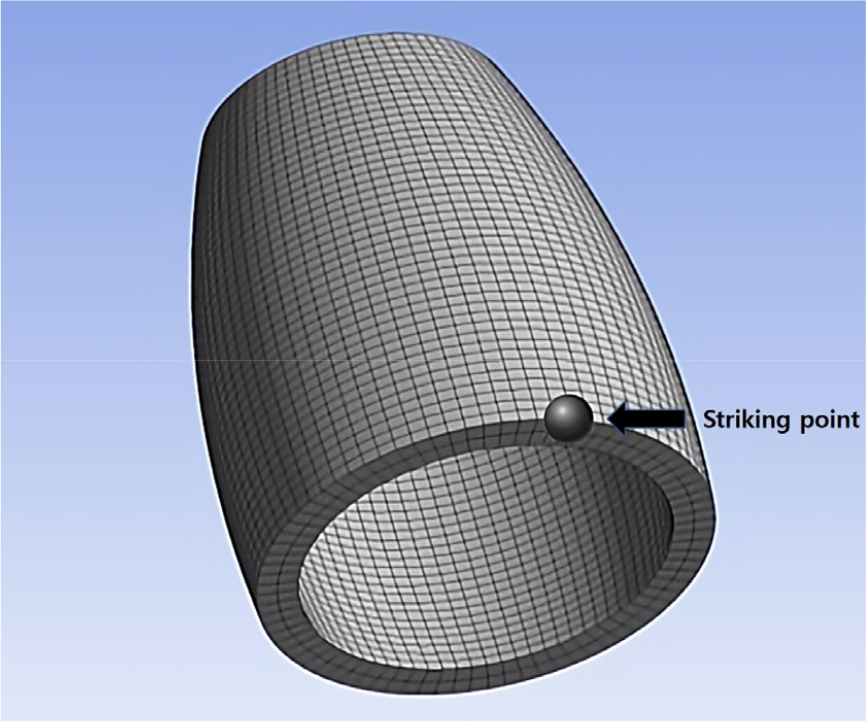
등가종의 맥놀이 특성을 이론적으로 파악하기 위해 종을 단순화시킨 비대칭 회전쉘의 모드 응답을 검토한다. Fig. 3에서 쉘 표면의 임의의 위치 에 충격량 이 가해질 때, 위치 에서의 변위 응답은 표면에 접하는 성분 와 표면에 수직인 성분 로 표시된다. 접선 성분은 소리를 내지 못하고 수직 성분 만이 소리를 방사한다.
Donnell-Mushtari-Vlasov의 쉘 운동방정식[13]에 모드 중첩법을 적용하면, 쉘 원주상에서 의 모드 응답을 Eq. (1)로 구할 수 있다.[14]
은 수직 축 상에서 충격량 의 위치와 크기로 결정되는 상수이고, 는 원주 상에서의 타격 지점이다. 미소 비대칭성 때문에 차 모드는 원주 상에서 위상차를 갖는 L, H 모드 쌍으로 분리된다. 이 모드 쌍은 미세하게 낮은 주파수 과 이보다 높은 의 주파수 쌍을 갖는다.
는 각각 L, H 모드 쌍의 배의 위상각으로 Eq. (2)의 관계를 갖는다.
과 은 고유주파수 쌍의 평균치와 평균 감쇠비로 L, H 모드 쌍은 같은 감쇠비를 갖는다고 가정한다.
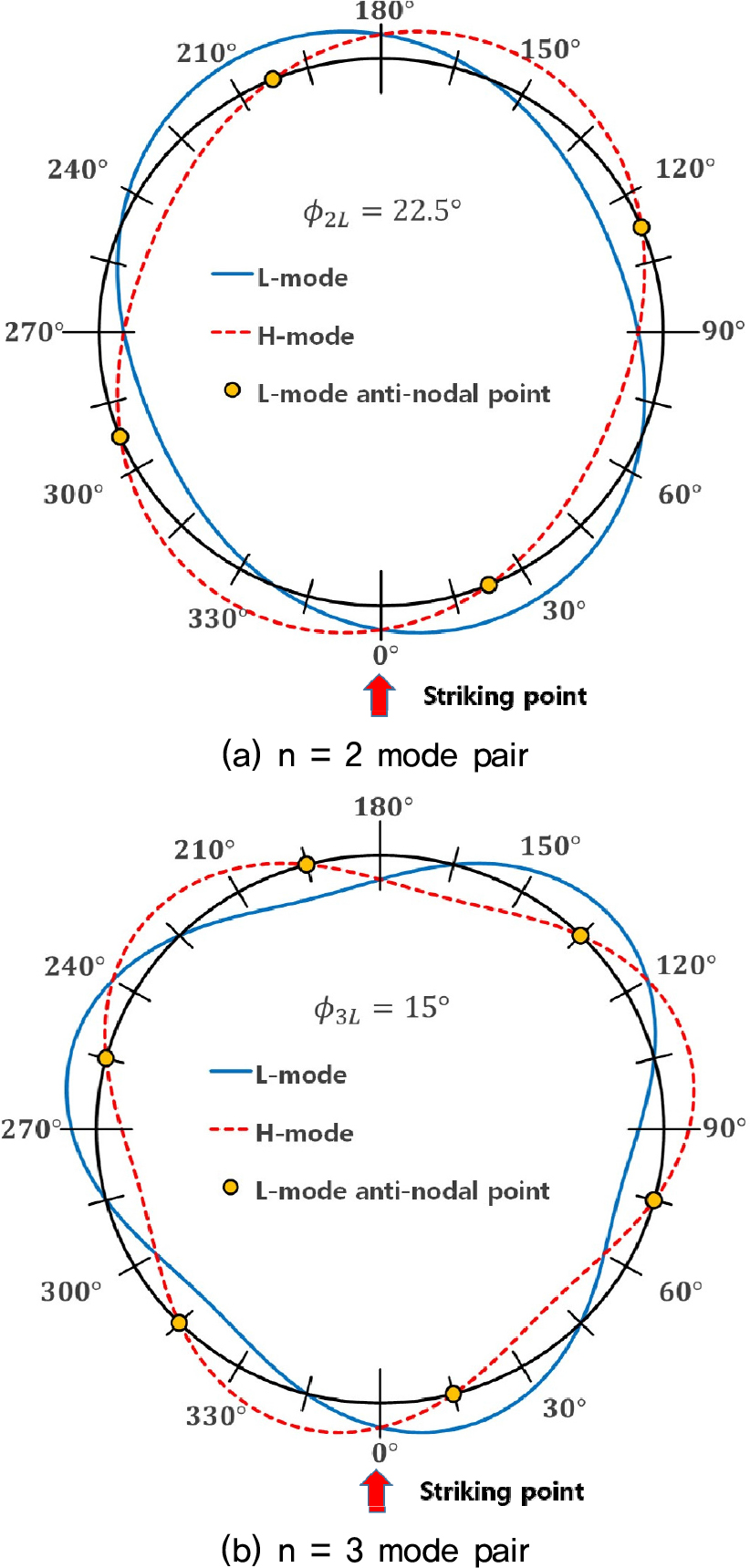
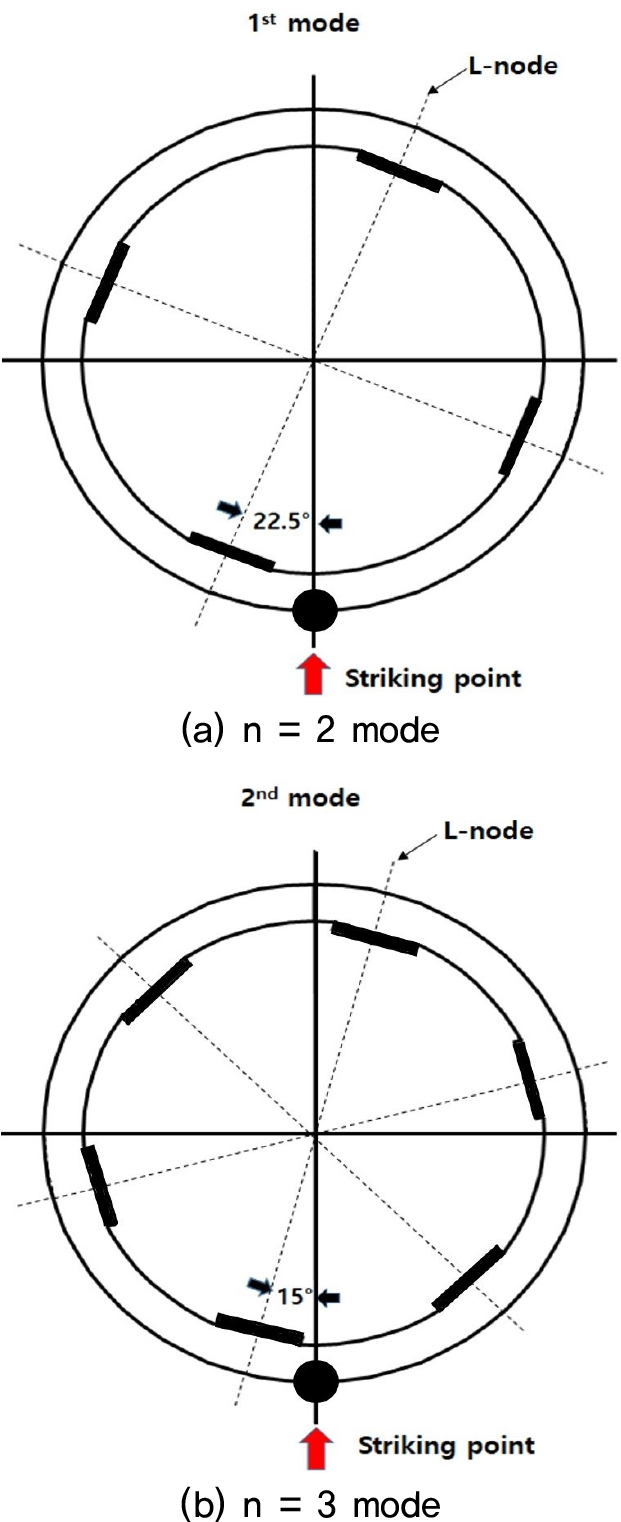
Fig. 4(a)는 1차(n = 2) 모드 쌍의 원주 상 분포도다. L, H 모드 쌍은 각각 원주 상에서 4개의 절점을 가지며 서로 45°의 위상차를 보인다. Fig. 4(b)는 2차(n = 3) 모드 쌍의 분포도다. 원주상에서 6개의 절점을 가지며 L, H 모드 쌍의 절점은 서로 30°의 위상 차이를 보인다.
Fig. 4(a), (b)처럼 타격점이 모드 쌍을 대등하게 가진하는 위치에 있으면, 모드 쌍이 대등하게 응답하는 위치에서 Fig. 1(a), (b)의 선명한 맥놀이가 발생한다. 타격점이 L 또는 H 모드의 절점에 오면 하나의 모드만 가진하므로 모든 위치에서 맥놀이가 생기지 않는 최악의 상황이 되고 맥놀이 교정이 가장 어려워진다.
1단계로 Table 2의 치수를 갖는 20 t 규모의 축대칭 유한요소해석 모델을 만들었다. 이 치수는 성덕대왕신종을 복원한 신라대종의 제원을 따랐다.[5] 원주를 80 등분하고, 높이를 45 등분하여, 총 6,989개의 HEX20 요소로 축 대칭 모델을 만들었다. 고유주파수 해석에는 ANSYS 2019 R2를 사용하였다.[15]
Table 2.
Specification of Korean bell.
| Mass | 20,560 kg |
| Density | 8,700 kg/m3 |
| Young's modulus | 127.5 GPa |
| Poisson's ratio | 0.35 |
| Height (h) | 2,978 mm |
| Bottom thickness (t) | 203 mm |
| Bottom diameter (D) | 2,233 mm |
등가종 모델로 Fig. 5와 같이 타격점인 0° 위치에 하나의 집중 질량을 부착하였다. 이 경우 타격점은 L 모드의 배(H 모드의 절점)가 되어 맥놀이를 전혀 만들지 못하는 최악의 상황이 된다.
2단계에서는 등가종의 집중 질량을 구하였다. Fig. 6은 총중량대비 집중질량의 비에 따른 고유주파수 쌍의 변화와 맥놀이 주기의 해석 결과다. 앞에서 20 t급 한국종의 1차 맥놀이 주기는 2.9 s ~ 20 s 범위였다. Fig. 6(a)에서 이 주기를 만드는 등가종의 집중 질량은 7 kg ~ 50 kg(질량비 0.035 % ~ 0.25 %)로 나온다. 또 2차 맥놀이 주기는 2.1 s ~ 9.1 s 범위였다. 이 범위의 맥놀이 주기를 내는 집중 질량은 7 kg ~ 30 kg(질량비 0.035 % ~ 0.15 %)로 나온다.
이와 같이 20 t급 한국종에서 맥놀이 주기 범위를 고려한 등가종 모델을 만들 수 있다.
IV. 인공 덤쇠의 설계
4.1 인공 덤쇠의 위치
1차 모드의 선명한 맥놀이가 나오려면, Fig. 4(a)처럼 타격점인 당좌 좌우 22.5° 지점에 L 또는 H 모드 절점이 와야 한다. 이 경우 당좌가 L, H 모드 쌍을 대등하게 가진하는 위치가 되기 때문이다. 이때 L, H 모드 쌍이 대등하게 응답하는 위치(45°, 90°, 135° 등 45° 간격 위치)에서는 완전 상쇄와 완전 보강이 이루어지고 Fig. 1(a)처럼 선명한 맥놀이가 발생한다. 같은 이유로 2차 모드에서는 당좌 좌우 15° 위치에 L 또는 H 모드 절점이 와야 선명한 맥놀이가 발생한다. 이러한 조건을 만드는 덤쇠를 검토한다. 덤쇠는 주형의 내형 표면을 부분적으로 파내고 용탕을 주입해 Fig. 7처럼 종의 내면이 돌출되도록 만들어 준다.
덤쇠 위치에서는 두께에 비례하는 질량 증가보다는 두께의 세제곱에 비례하는 굽힘 강성의 증가가 더 크다. 그 결과 덤쇠는 부착 지점을 H 모드의 배(L 모드의 절점)으로 만드는 효과를 낸다. 따라서 Fig. 7(a)의 돌출된 4개 위치에 인공 덤쇠를 부착하면, 1차 L, H 모드 쌍의 절점이 당좌를 중앙으로 좌우 22.5° 위치로 이동하게 된다. 그 결과 선명한 맥놀이를 내는 가진 조건을 구현할 수 있다.
같은 이유로 n = 3 모드에서는 Fig. 7(b)처럼 당좌 좌측 15° 지점, 또는 같은 효과를 내는 6개 지점에 덤쇠를 부착하면 당좌가 선명한 맥놀이를 만드는 위치에 온다.
종 높이 상에서는 종의 하대(하단 두꺼운 부분)에 덤쇠를 만드는 것이 유리하다. 하대의 자유단에서 1, 2차 모드의 굽힘 변형이 최대이므로 강성증가 효과가 극대화되기 때문이다.
이와같이 1차와 2차 모드중 어느 모드의 맥놀이를 선명하게 만들려 하는가를 고려하여 덤쇠의 부착 위치를 정할 수 있다.
4.2 인공 덤쇠의 크기
종의 비대칭성을 이겨내고 Fig. 4와 같은 모드 쌍의 배치를 이루기 위한 덤쇠의 크기를 검토하였다.
본 연구사례에서는 20 t 종의 크기와 하대의 평균 높이 20 cm를 감안하여, 덤쇠 크기를 높이 20 cm, 원주상의 폭 30 cm로 하였다. 1차 모드 맥놀이를 위해서는 Fig. 7(a)와 같이 분산해서 4개의 동일한 덤쇠를 만들었다. 비대칭성이 가장 작은 경우(집중질량 7 kg)과 가장 큰 경우(집중질량 50 kg)의 두 개 등가종에 덤쇠를 만들고 두께 변화에 따른 효과를 검토했다. 덤쇠 두께는 5 mm ~ 50 mm 범위에서 변화시켰는데, 이는 20 t 종의 질량을 10.4 kg ~ 104 kg(질량비 0.052 % ~ 0.52 %) 증가시킨다.
2차 모드의 선명한 맥놀이를 위해서는 비대칭성이 가장 작은 경우(집중질량 7 kg)과 가장 큰 경우(집중질량 30 kg)을 대상으로, Fig. 7(b)의 6개 위치에 분산해서 덤쇠를 만들었다. 이때 덤쇠는 종의 질량을 15.6 kg ~ 156.8 kg(질량비 0.078 % ~ 0.78 %) 증가시킨다.
4.3 인공 덤쇠의 효과
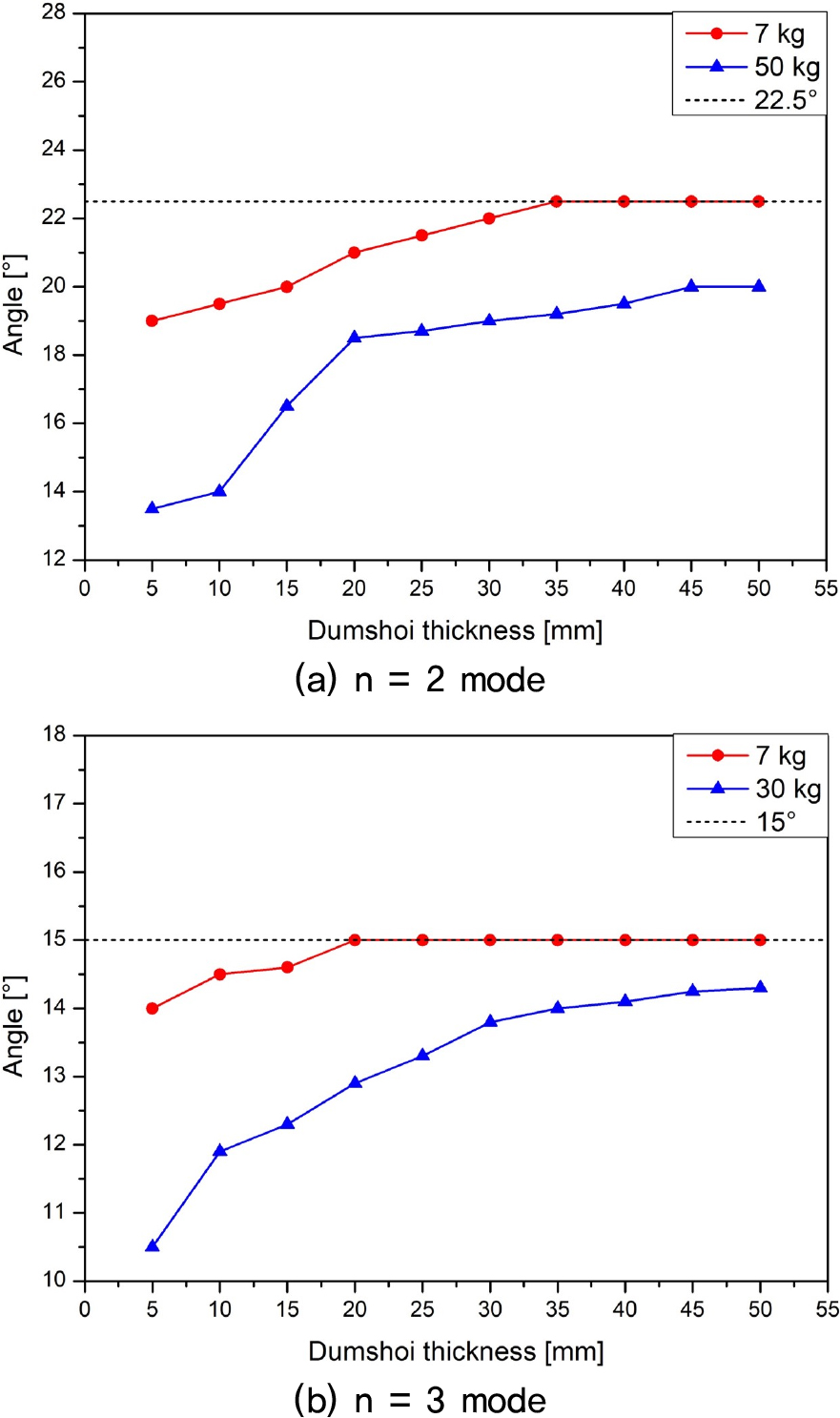
덤쇠를 부착할 때 모드 쌍의 이동 효과가 어느 정도 발생하는가를 검토하였다. Fig. 8은 덤쇠 두께 증가에 따른 L 모드 배의 위상각 변화를 보인다. Fig. 8(a)의 1차 모드에서 집중 질량 때문에 덤쇠 설치 전에 0° 위치에 있던 L 모드 배는 두께 증가에 따라 목표치인 당좌 우측 22.5° 위치로 이동한다. 비대칭성이 작은 경우(집중질량 7 kg) 두께 35 mm 정도(종 질량의 0.18 %)면 목표치인 22.5°로 이동하여 Fig. 4(a)처럼 L, H 모드 쌍이 배치된다. 그러나 비대칭성이 큰 경우(집중질량 50 kg), 50 mm의 두께에서도 목표치에 조금 못 미치는 20°에 접근한다.
Fig. 8(b)는 2차 모드에서의 덤쇠 효과로, 당좌 좌측 15° 위치와 등가적인 6개 지점에 덤쇠를 분산 배치할 때의 두께 증가비에 따른 L 모드 배의 위상을 보인다. 비대칭성이 가장 작은 경우 L 모드 배는 20 mm 두께의 덤쇠로 목표치인 15°로 이동한다. 비대칭성이 큰 경우 50 mm 두께에서 목표치 부근 14°에 온다. 집중 질량이 큰 경우, 50 mm 두께의 덤쇠로 목표치에 완전히 도달하지 못하는 원인은 등가종에서 집중 질량을 0°의 한 지점에 위치시킨 최악의 비대칭 조건을 적용한 반면, 덤쇠는 면적을 갖고 분포하는 데에 기인한다. 이러한 인공 덤쇠가 얼마나 선명한 맥놀이를 발생시키는가를 맥놀이지도를 통해 예측해보았다. 맥놀이지도는 Eq. (1)에 L, H 모드쌍의 배의 위상각 를 적용하여 그릴 수 있다. 그 결과는 선행연구에서 측정 결과와 일치함을 검증한 바 있다.[14]
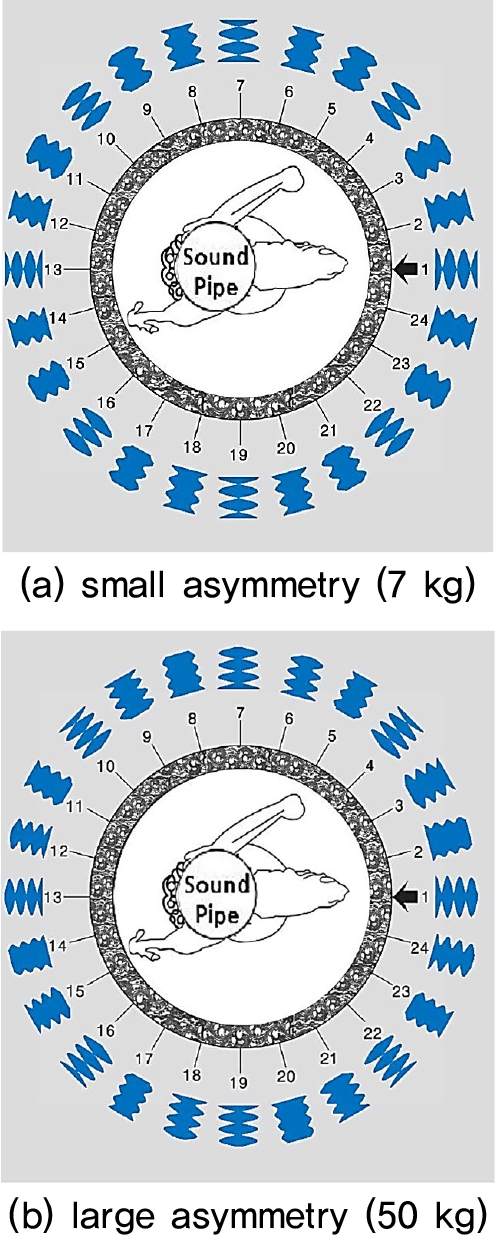
Fig. 9는 1차(n = 2) 모드의 맥놀이지도다. (a)의 작은 비대칭의 경우, 타격점으로부터 45° 간격으로 완벽하게 선명한 맥놀이가 발생한다. (b)의 큰 비대칭의 경우에도 유사한 지점에서 상당히 선명한 맥놀이를 만들고 있다.
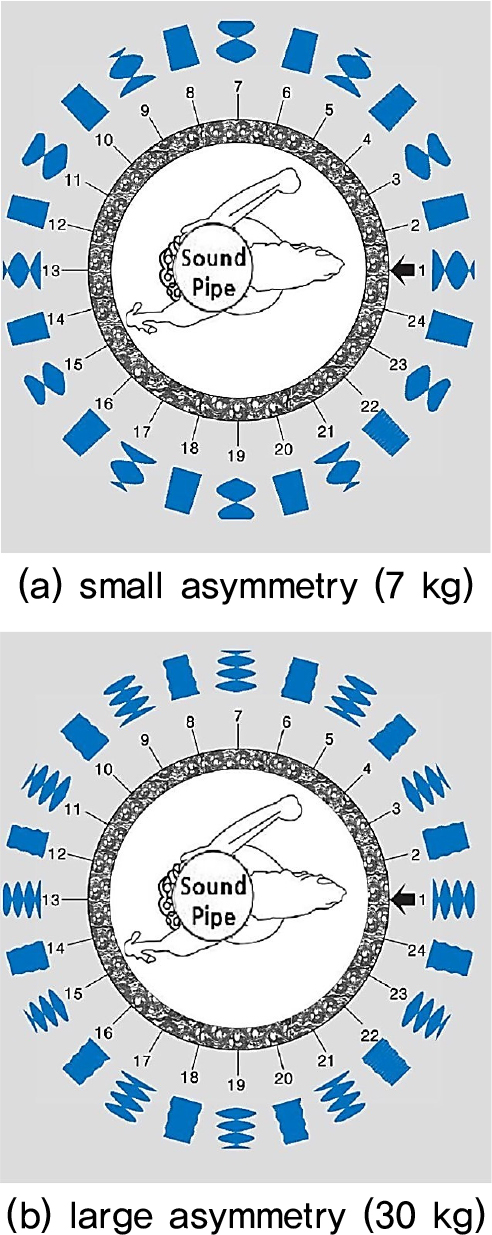
Fig. 10은 2차(n = 3) 모드의 맥놀이지도다. 작은 비대칭성의 경우, 타격점으로부터 30° 간격으로 완벽한 맥놀이가 발생하며, 큰 비대칭성의 경우에도 상당히 선명한 맥놀이가 발생하고 있다. 일단 선명한 맥놀이를 만들면, 주기는 주조 후에 교정법을 적용해 조절이 가능하다.[5,12]
V. 결 론
성덕대왕신종과 현대에 제작된 12개 종을 대상으로 1, 2차 모드의 고유주파수 쌍 데이터로부터 맥놀이 주기를 구하였다. 이에 근거하여 6개의 20 t급 한국종이 갖는 1, 2차 모드의 비대칭성을 등가종 모델을 사용하여 정량적으로 표시하였다.
20 t 규모의 등가종 모델에서 1차 모드의 비대칭성은 7 kg ~ 50 kg의 집중 질량으로 등가화시킬 수 있었으며, 2차 모드의 비대칭성은 7 kg ~ 30 kg의 집중 질량으로 등가화시킬 수 있었다.
20 t 규모의 한국종에서 1차 모드의 선명한 맥놀이를 만들기 위해 당좌 좌측 22.5° 위치를 포함하는 총 4개 위치에 덤쇠를 분산 배치하고, 덤쇠 두께의 증가에 따른 1차 모드 쌍의 배의 이동을 구하였다.
비대칭성이 가장 작은 경우, 종 중량 대비 0.052 %의 덤쇠로 가장 선명한 1차 맥놀이 조건이 달성되었다. 비대칭성이 가장 큰 경우에는 종 중량 대비 0.52 %의 덤쇠로 선명한 1차 맥놀이를 만들 수 있었다.
2차 모드의 선명한 맥놀이를 위해 당좌 좌측 15° 및 그 등가적인 6개 위치에 덤쇠를 적용하였다. 비대칭성이 가장 작은 경우 종 중량 대비 0.078 %의 덤쇠로 가장 선명한 2차 맥놀이 조건이 달성되었다. 비대칭성이 가장 큰 경우에도 종 중량 대비 0.78 %의 덤쇠로 선명한 2차 맥놀이를 만들 수 있었다.
덤쇠 효과를 보기 위해 맥놀이지도를 그린 결과, 1, 2차 모드에서 매우 선명한 맥놀이를 얻을 수 있었다.
본 연구에서 제시한 인공 덤쇠법은 종 설계 단계에서 선명한 맥놀이를 만들고 주조 후에 맥놀이 주기를 조절함으로써, 선명하고 적절한 주기의 맥놀이를 만드는 데에 효과적으로 적용할 수 있다.