Development of numerical method to predict broadband radiation noise resulting in fluid-induced vibration and acoustic-induced vibration of pipe

Sangheon Lee; Cheolung Cheong; Songjune Lee

doi:10.7776/ASK.2024.43.1.112

Preview

Research Article

The Journal of the Acoustical Society of Korea. 31 January 2024. 112-121
https://doi.org/10.7776/ASK.2024.43.1.112

Development of numerical method to predict broadband radiation noise resulting in fluid-induced vibration and acoustic-induced vibration of pipe

배관의 유동 유발 진동 및 음향 유발 진동 기인 광대역 방사 소음 예측을 위한 수치 해석 기법 개발

Sangheon Lee¹

Cheolung Cheong¹²^*

Songjune Lee³

이 상헌¹

정 철웅¹²^*

이 송준³

¹부산대학교 기계공학부

²부산대학교 첨단냉동공조에너지센터

³한국에너지기술연구원

^{*Corresponding Author}

ABSTRACT

The pipping system is widely used in many industries as equipment for transporting fluids over long distances. In high-pressure pipe, as the speed of the fluid increases, a loud noise is generated. Therefore, various studies have been conducted to reduce pipe noise. In this paper, a pipe noise analysis was developed to predict and quantitatively assess the flow-induced vibration and acoustic-induced vibration due to valve flow in high-temperature and high-pressure. To do this, a high-fidelity fluid analysis technique was developed for predicting internal flow in the pipe with valve. In additional, the contribution of compressible/incompressible pressure by frequency band was evaluated using the wavenumber-frequency analysis. To predict a low/middle frequency pipe noise, the vibroacoustic analysis method was developed based on Finite Element Method (FEM). And the pipe noise prediction method for the middle/high frequency was developed based on Statistical Energy Analysis (SEA).

Keywords

Pipe flow

Fluid-induced vibration

Acoustic-induced vibration

Finite Element Method (FEM)

Statistical Energy Analysis (SEA)

배관시스템은 유체를 장거리로 이송시키는 장비로서 많은 산업군에서 사용되고 있다. 고압의 배관에서는 빠른 유속으로 인하여 소음이 크게 발생하고 있으며, 이러한 소음을 저감 시키기 위한 많은 연구가 수행되고 있다. 이 논문에서는 고온․고압의 배관내 밸브 유동을 원인으로 발생하는 유동유발진동과 음향유발진동을 설계단계에서 예측하고 정량적으로 분석을 위한 배관 소음 해석 기법을 개발하였다. 이를 위하여 배관의 내부 유동 예측을 위한 고정밀 유동 해석기법을 개발하였으며, 파수-주파수 분석법을 이용하여 주파수 대역별 압축성/비압축성 압력의 기여도를 평가하였다. 그리고 유한요소 해석법(Finite Element Method, FEM)을 기반으로 한 저․중 주파수 대역의 진동소음 해석기법을 개발하였으며, 통계적 에너지 분석법(Statistical Energy Analysis, SEA)을 기반으로 한 중․고 주파수 대역에서의 방사소음해석 기법을 개발하였다.

키워드

배관 유동

유동유발진동

음향유발진동

유한요소법(Finite Element Method, FEM)

통계적에너지분석법(Statistical Energy Analysis, SEA)

MAIN

I. 서 론
II. 수치해석 기법 정립
2.1 고정밀 유동 해석 기법
2.2 FEM 기반 저․중 주파수 대역 유동유발진동(FIV) 해석 모델 개발
2.3 SEA 기반 중․고 주파수 대역 유동유발진동(FIV) 해석 모델 개발
III. 결 론

I. 서 론

배관 시스템은 단거리에서부터 장거리까지 유체를 전달하는 역할을 수행하며, 가전, 자동차에서부터 선박, 플랜트와 같이 다양한 산업군에서 사용된다. 일반적으로 배관시스템은 고압의 상태로 작동하며, 이는 배관에 큰 유동 소음을 유발하게 된다.

배관 내부 유동에 의한 소음은 저/중 주파수 대역의 유동 유발 진동(Fluid Induced Vibration, FIV)에 의한 소음과 중/고 주파수 대역의 음향 유발 진동(Acoustic Induced Vibration, AIV)에 의한 소음으로 나눌 수 있다. 유동유발진동과 음향유발진동에 의한 소음의 주파수 대역은 그 가진원의 주파수 대역의 영향을 받게 되며, 유동유발진동을 유발하는 가진원을 비압축성 압력이 기여도가 크며, 음향유발진동을 유발하는 가진원을 압축성 압력이 기여도가 크다고 알려져 있다.

일반적으로, 비압축성 압력은 배관의 요소에서 발생한 와류의 압력 섭동이 벽면에 닿으면서 형성되는 압력이며, 주로 밸브, 오리 피스 및 고관과 같은 배관의 요소 주변에서 크게 발생하게 되며, 난류가 소산하면서 가진력의 크기가 작아진다. 반면에 압축성 압력은 와류의 압력 섭동이 음향파를 발생시키고, 이러한 음향파가 배관의 길이방향을 따라 전파하면서 배관에 형성된 압력이다. 이러한, 두 성분을 설계 단계에서 평가하기 위해선, 배관 내의 난류 유동뿐만 아니라, 압력의 크기가 작은 음향파까지 정확하게 예측되야 하며, 고정밀한 해석 방법을 필요로 하게 된다.

유체의 이동에 의한 압축성 압력과 비압축성 압력에 대한 연구는 다양한 분야에서 많은 연구가 진행되어 왔다. Kim et al.^[1]은 수축․팽창 밸브가 포함된 배관에 대하여 고정밀 유동해석을 진행하였으며, 파수-주파수 분석법(Wave-number Frequency Analysis, WFA)기법을 이용하여 배관 표면의 압력으로부터 압축성 압력과 비압축성 압력을 분리하였다. 그는 파수 주파수 분석법을 이용하여 음향유발진동의 가진원이 되는 압축성 압력이 중․고 주파수 대역에서의 기여도가 큼을 확인하였다. 또한, Ku et al.^[2]은 임계 밸브가 포함된 배관에 대하여 유동해석을 진행하였으며, WFA를 이용하여 압축성 압력과 비압축성 압력의 주파수별 기여도를 비교하였다. 그는 압축성 압력이 고주파에서의 기여도가 큼을 확인하였다. 추가적으로, 비압축성 압력이 배관 요소인 밸브에서 멀어질수록 가진력이 크게 감소하는 것을 확인하였으며, 이에 따라, 압축성 압력의 기여도가 커짐을 확인하였다. 하지만, 많은 배관 산업계에서 유발유동진동과 음향유발진동에 의한 소음을 저감하기 위하여 실험적인 방법을 통하여 접근하고 있는 실정이다.

따라서, 본 논문에서는 배관의 설계 단계에서 유발유동진동 그리고 음향유발진동에 의한 소음을 예측할 수 있는 기법을 정립하였다. 이를 위하여, 먼저 밸브가 포함된 배관에 대하여 난류뿐만 아니라 소음원을 예측하기 위하여 고정밀 유동 해석 기법을 정립하였으며, 그 유효성을 실험과 비교하였다. 이후, 유한요소법(Finite Element Method, FEM)을 이용하여 밸브 유동에 의한 배관 진동과 방사소음을 예측하였다. 유한요소기법은 구조물의 모드가 많아지는 고주파에서는 잘 맞지 않다고 알려져 있으며, 저․중 주파수 대역에서만 해석을 진행하였다. 중․고 주파수 대역에서는 통계적 에너지 분석(Statistical Energy Analysis, SEA)법을 적용하였으며, 통계적 에너지 분석법을 위한 변수를 수치적으로 계산하였다. 최종적으로 정립된 해석기법을 이용하여 저주파수 대역부터 고주파수 대역까지 유동에 의한 배관 소음을 효율적으로 예측할 수 있는 해석 기법을 정립하였다.

II. 수치해석 기법 정립

2.1 고정밀 유동 해석 기법

먼저, 배관의 내부 유동을 예측하기 위하여 고정밀 유동해석 기법을 정립하였으며, 실험과의 비교를 통하여 유효성을 검증하였다. Fig. 1은 해석 기법의 검증을 위한 유동 해석 대상 형상을 나타내었다. Fig. 1의 임계 노즐은 ISO 규정에 따라 설정하였다.^[3]

https://static.apub.kr/journalsite/sites/ask/2024-043-01/N0660430113/images/ASK_43_01_13_F1.jpg

Fig. 1.

Geometry of pipe with critical nozzle.

유동 해석의 지배방정식으로 대와류모사기법(Large Eddy Simulation, LES)를 적용하였으며, 아래와 같이 정의된다.

(1)

\frac{\partial ρ}{\partial t} + \frac{\partial}{\partial x_{i}} (ρ {\bar{u}}_{i}) = 0 .

(2)

\frac{\partial}{\partial t} (ρ {\bar{u}}_{i}) + \frac{\partial}{\partial x_{j}} (ρ {\bar{u}}_{i} {\bar{u}}_{j}) = \frac{\partial}{\partial x_{i}} (σ_{i j}) - \frac{\partial \bar{p}}{\partial x_{i}} - \frac{\partial τ_{i j}}{\partial x_{j}} .

(3)

\frac{\partial}{\partial t} (ρ {\bar{h}}_{s}) + \frac{\partial}{\partial x_{i}} (ρ {\bar{u}}_{i} h_{s}) - \frac{\partial \bar{p}}{\partial t} - {\bar{u}}_{j} \frac{\partial \bar{p}}{\partial x_{j}} - \frac{\partial}{\partial x_{i}} (λ \frac{\partial \bar{T}}{\partial x_{i}}) = - \frac{\partial}{\partial x_{j}} [ρ (\bar{u_{i} h_{s}} - \bar{u_{i} h_{s}})] .

Eqs. (1), (2), (3)은 각각 연속방정식, momentum 방정식 그리고 energy 방정식이다. 여기서, Eq. (2)의 $σ_{i j}$ 와 $τ_{i j}$ 는 전단 변형 텐서와 아격자에서의 전단 텐서이며 다음과 같다.

(4)

σ_{i j} = 2 μ S_{i j} - \frac{2}{3} μ δ_{i j} {\bar{S}}_{k k} .

(5)

τ_{i j} = - 2 μ_{t} {\bar{S}}_{k k} .

Eq. (5)의 ${\bar{S}}_{k k}$ 는 변형률 텐서이며, 다음과 같이 정의된다.

(6)

{\bar{S}}_{k k} = \frac{1}{2} (\frac{\partial {\bar{u}}_{i}}{\partial {\bar{x}}_{j}} + \frac{\partial {\bar{u}}_{j}}{\partial {\bar{x}}_{i}}) .

Eq. (5)의 난류 점성항을 계산하기 위한 아격자 모델로는 Smagorinsky-Lilly 모델을 적용하였으며, 식은 다음과 같이 정의된다.

(7)

μ_{t} = ρ (C_{s} ∆) | \bar{S} |,

여기서

(8)

| \bar{S} | = \sqrt{2 {\bar{S}}_{i j} {\bar{S}}_{i j}} .

(9)

∆ = V^{1 / 3} .

Eq. (7)의 $C_{s}$ 는 Smagorinsky상수이며, Eq. (9)의 V는 격자의 부피이다. 시간 및 공간 차분법으로서 Bounded 2^nd order implicit와 2^nd order upwind 기법을 적용하였다. 해석을 위한 시간 간격은 5e-4 s로 적용하였다. 경계조건은 입구단과 출구단에 각각 10 bar와 5 bar를 적용하였다.

유동 해석기법의 검증을 위한 실험은 한국 표준과학연구원(Korea Research Institute of Standards and Science, KRISS)의 High-pressure flow standard system을 이용하였으며, Fig. 2에 나타낸 바와 같이 배관 내부 벽면의 표면 압력을 측정하였다.

https://static.apub.kr/journalsite/sites/ask/2024-043-01/N0660430113/images/ASK_43_01_13_F2.jpg

Fig. 2.

(Color available online) Measurement setup of high-pressure gas flow system.

Fig. 3은 센서1과 센서2의 위치에서의 측정값과 예측 값을 비교한 결과이다. 센서 1의 저주파에서 다소 차이가 보이는데 이는, 센서가 위치한 지점이 교란이 크게 발생한 영역에 근접했기 때문으로 판단된다. 이러한 교란은 후향 단차(Backward-Facing Step, BFS) 유동의 문제에서 발생하는 유동 특성과 유사하다고 판단된다. 후향 단차 문제에서 고속으로 빠져나가는 유동장 아래에는 전단응력에 의해 회전하는 유동이 발생하게 되며, 이러한 유동특성은 압력섭동을 유발한다고 알려져 있다.^[4] 후향 단차 문제에서 발생하는 압력섭동의 편차는 경계층영역에 조밀한 격자를 구성하여 해석할 수 있다.^[5] 센서 2에서는 실험결과와 해석 결과가 잘 일치하는 것을 확인할 수 있다. 하지만, 센서1 과 센서2의 고주파수 대역에서의 편차가 발생하고 있다. 고주파수 대역은 해석의 압축성 압력이 지배적인 영역으로 음압을 유발하는 작은 크기의 와류를 예측하기 위해 조밀한 격자와 해석에 사용된 시간간격을 줄임으로서 완화할 수 있을 것으로 판단된다.^[6]

https://static.apub.kr/journalsite/sites/ask/2024-043-01/N0660430113/images/ASK_43_01_13_F3.jpg

Fig. 3.

(Color available online) Comparison results of pressure at (a) sensor 1 and (b) sensor 2.

검증된 유동 해석 기법을 이용하여, 실제 밸브와 포함된 배관에 대하여 유동해석을 진행하였다. Fig. 4는 해석 대상 및 해석 영역을 나타내었다. 유동해석 시 곡관을 중심으로 상류(Region 1)과 하류(Region 2)로 구분하여 유동의 영향을 분석하였다. 분석을 하고자 하는 목표 주파수 대역을 10,000 Hz로 선정하였으며, 시간 간격은 목표 주파수의 10배인 1/100,000 s로 선정하였으며, 목표 주파수의 파장을 고려하여 격자 크기가 4.62 mm를 넘지 않도록 구성하였다. 또한, 경계층에서의 유동을 예측하기 위하여 30장의 프리즘격자를 구성하였다. 총 해석에 사용된 격자수는 약 2천만개를 사용하였다. 작동 유체는 천연가스의 주 성분인 메탄을 적용하였으며, 이상기체로 모델링 하였다.

https://static.apub.kr/journalsite/sites/ask/2024-043-01/N0660430113/images/ASK_43_01_13_F4.jpg

Fig. 4.

(Color available online) Target geometry and computational domain.

Fig. 5에는 해석 결과로서 압력장과 유동장을 나타내었다.

https://static.apub.kr/journalsite/sites/ask/2024-043-01/N0660430113/images/ASK_43_01_13_F5.jpg

Fig. 5.

(Color available online) Snapshot results of (a)Static pressure and (b) velocity contour.

Fig. 5에서 밸브 부근에서 속도장이 매우 복잡하 나오는 것을 확인할 수 있으며, 압력 섭동이 나타나는 것을 볼 수 있다. 이는 밸브를 만나 발생한 와류의 영향으로 판단되며, 유동이 길이방향으로 흐름에 따라 소산되는 것을 확인할 수 있다.

벽면에 형성되는 압력성분을 분석하기 위하여 파수 주파수 분석 기법을 적용하였다. 일반적으로 유발유동진동의 가진원이 되는 비압축성 압력은 와류와 벽면의 직접적인 상호작용으로 인하여 발생하며, 유동의 평균 유속의 전파속도를 가지고 있다고 알려져 있으며, 압축성 압력 섭동은 와류에 의해 발생한 음향파로 인하여 발생하며, 매질의 전파속도로 전파한다고 알려져 있다. 이러한 전파속도 차이를 이용하여 압축성 압력과 비압축성 압력을 분리할 수 있으며, 이를 위한 WFA는 아래와 같이 공간 및 시간 영역에서의 푸리에 변환을 이용하여 계산할 수 있다.

(10)

F \{f (r, θ, z, t)\} = \int_{t = - \infty}^{\infty} \int_{z = - \infty}^{\infty} 2 π \sum_{n = - \infty}^{\infty} (- i)^{n} e^{i π ϕ} \times \int_{r = 0}^{\infty} a_{n} (r, z, t) J_{n} (r ρ) e^{2 π i (f t - k_{z} z)} r d r d z d t .

(11)

a_{n} (r, z, t) = \frac{1}{2 π} \int_{θ = - π}^{π} f (r, θ, z, t) e^{- i n θ} d θ .

(12)

S (m, p ∆ k_{z} z, o ∆ f) = \frac{1}{N_{t} N_{z} N_{θ}} \sum_{J_{m} (k_{r_{0, m, n}} r_{0})}^{\infty} \sum_{k = 1}^{N_{t - 1}} \sum_{l = 1}^{N_{z - 1}} \sum_{j = 1}^{N_{θ - 1}} ω_{k l j} P_{k j l} e^{- 2 π i (\frac{k_{0}}{N_{t}} + \frac{m θ}{N_{θ}} + \frac{l_{p}}{N_{z}})}

파수-주파수 분석을 위하여 총 0.4 s의 해석 데이터를 이용하였으며, 주파수 간격은 2.44 Hz이다. 또한, region 1의 길이는 유동 방향의 길이는 0.715 m이며, region 2의 길이는 유동 방향으로 0.529 m이다. 파수-주파수 분석을 통하여 변환된 압력을 Power Spectral Density(PSD)로 나타내었으며, 그 결과 Fig. 6에 나타내었다. 표시된 직선의 기울기는 압력 성분의 전파속도를 나타내며, 낮은 기울기의 성분은 비압축성 압력, 높은 기울기에서의 성분은 압축성 압력이다. region1에 비하여 region2의 비압축성 압력의 PSD값이 감소하는 것을 알 수 있으며, 이는 앞서 설명한 바와 같이 유동이 밸브에서 멀어짐에 따라 난류가 소산하여 난류의 강도가 약해진 것으로 판단된다. 또한, 압축성 압력 장의 PSD 값도 다소 감소하는 것을 확인할 수 있는데, 이는 곡관의 영향으로 인한 감쇠라고 판단된다. 압축성 압력장의 경우 1,000 Hz 이상에서부터 비압축성에 대한 상대적 기여도가 커지는 것을 확인할 수 있으며, 1,500 Hz 이상에선 압축성 압력만이 크게 기여하는 것을 확인할 수 있다.

https://static.apub.kr/journalsite/sites/ask/2024-043-01/N0660430113/images/ASK_43_01_13_F6.jpg

Fig. 6.

(Color available online) Power spectral density spectrum (a) at region1 and (b) region 2 [P_ref = 20 μPa].

2.2 FEM 기반 저․중 주파수 대역 유동유발진동(FIV) 해석 모델 개발

일반적으로 배관 소음은 구조물의 모드를 전달경로로 하여 전파된다. 따라서, 구조물의 모드와 방사소음을 예측하기위해 유한요소법(Finite Element Method, FEM)을 적용하였다. 진동 및 소음해석 기법으로 직접 계산법을 적용하였다.^[7]

(13)

[M] \{\ddot{X}\} + [B] \{\ddot{X}\} + [K] \{X\} = \{F\},

여기서

(14)

\dot{X} = i ω X .

(15)

\ddot{X} = - ω^{2} X .

이다. Eqs. (13), (14), (15)까지의 윗첨자의점은 시간 미분을 나타내며, ω는 각속도를 나타낸다. Eq. (13)의 [M], [B] 그리고 [K] 행렬은 각각 구조 격자와 음향격자가 결합된 질량, 감쇠 및 강성 행렬을 나타내며, 아래와 같이 정의된다.

(16)

[M] = [\begin{matrix} M_{s} & 0 \\ - A^{T} & M_{a} \end{matrix}] .

(17)

[B] = [\begin{matrix} B_{s} & 0 \\ 0 & B_{a} \end{matrix}] .

(18)

[K] = [\begin{matrix} K_{s} & 0 \\ C & K_{a} \end{matrix}] .

(19)

\{F\} = \{\begin{matrix} F_{s} \\ F_{a} \end{matrix}\} .

(20)

[A] = \int_{S} N_{s}^{T} N_{a} \{n_{s}\} d S .

Eqs. (16), (17), (18), (19), (20)까지의 식에서 아랫첨자 s는 구조물을 의미하며 a는 음향격자를 나타낸다. Eq. (20)은 연성 행렬이며, N은 형상 행렬이다. 구조 응답 정보와 소음 응답 정보 사이의 상호작용(Fluid Structure Interaction, FSI)은 단 방향 접근 법을 적용하였으며, Eq. (18)의 C의 값이 0이 된다.

직접 적분법은 Eqs. (14)과 (15)를 Eq. (13)에 대입 하여, 각 주파수 별로 아래의 식을 이용하여 계산하게 된다.

(21)

X = [- ω^{2} [M] + i ω [B] + [K]]^{- 1} \{F\} .

Fig. 7은 유한 요소 해석을 위한 구조 격자 및 음향 격자와 경계조건을 나타내었다. 구조 격자에 사용된 격자의 크기는 5 mm이며, 음향 격자에 사용된 격자의 크기는 20 mm이다.

https://static.apub.kr/journalsite/sites/ask/2024-043-01/N0660430113/images/ASK_43_01_13_F7.jpg

Fig. 7.

(Color available online) Snapshot results of (a)Static pressure and (b) velocity contour.

구조해석을 위한 경계조건으로 배관이 바닥에 고정된 상황을 모사하여, 6자유도 구속조건을 적용하였으며, 음향 해석을 위한 경계조건으로서 비 반사 경계조건을 모사하기 위하여 조머펠트(Sommerfeld) 경계조건을 적용하였으며, 아래와 같이 정의된다.

(22)

\lim_{r \to \infty} [r (\frac{\partial p}{\partial r} + \frac{1}{c} \frac{\partial p}{\partial t})] = 0 .

계산 주파수 대역 및 계산 비용을 고려하여 총 0.1초의 유동해석결과를 가진력으로 적용하였으며, 주파수 간격을 100 Hz로 적용하였다. 주파수의 간격이 100 Hz임에 따라 1/3 옥타브 밴드의 중심주파수가 500 Hz 이하의 영역에서는 밴드 폭 안에 1개 이하의 소음이 반영되게 된다. 따라서, 630 Hz 이상의 중심주파수에 대하여 분석을 진행하였다.

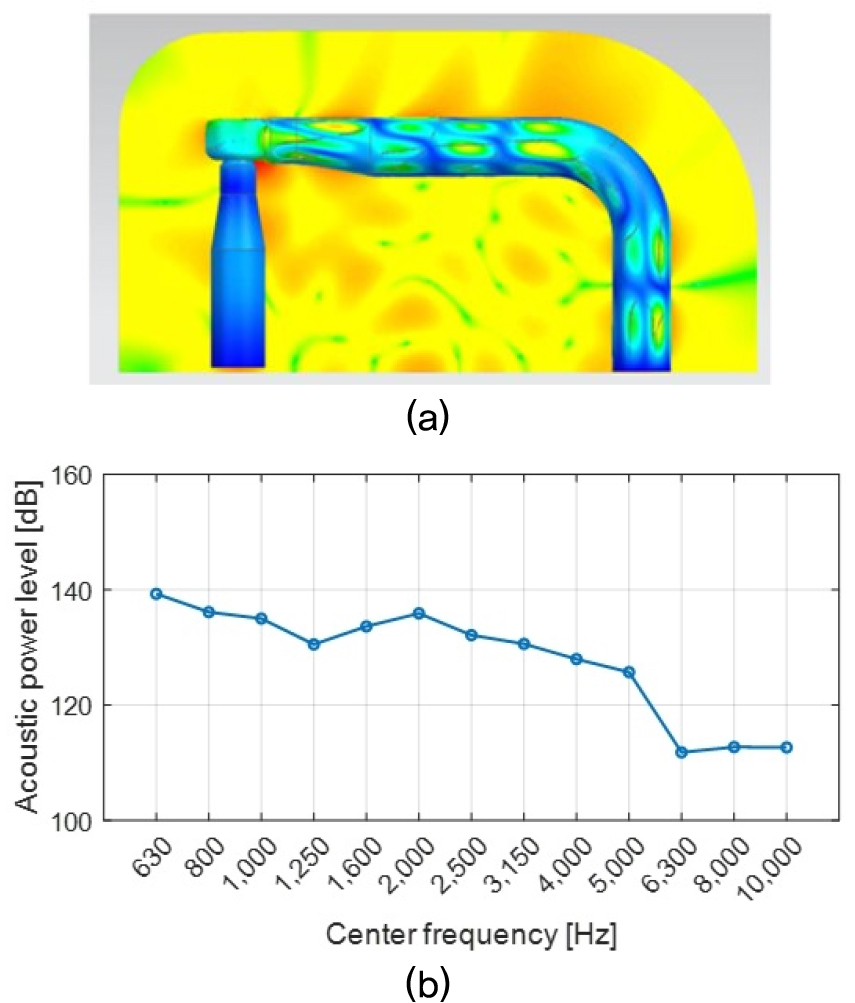
Fig. 8에서는 유동에 의한 배관의 진동 형상과 소음의 음향파워 레벨의 1/3 옥타브 밴드 결과 나타내었다.

저·중 주파수 대역에서는 특정 진동 모드를 통하여 소음이 발생하는 것을 확인할 수 있다. 또한, 해당 주파수 대역에서는 비압축성 압력의 기여도가 큼에 따라, 배관 요소 주변에서 진동과 소음이 크게 발생하는 것을 확인할 수 있다. Fig. 8(b)의 1/3 옥타브 밴드 결과에서 중심 주파수가 5,000 Hz 이상의 고주파영역에서의 소음이 크게 감소하는 것을 확인할 수 있다. 이는 유한요소법 기반의 해석이 고주파에서의 모드 간격이 짧아짐에 따라 모드를 정확하게 계산하지 내지 못함에 따라 발생하는 편차로 판단된다.

https://static.apub.kr/journalsite/sites/ask/2024-043-01/N0660430113/images/ASK_43_01_13_F8.jpg

Fig. 8.

(Color available online) Results of (a) pipe vibrational shape at 600 Hz and (b) 1/3 octave band of PWL.

2.3 SEA 기반 중․고 주파수 대역 유동유발진동(FIV) 해석 모델 개발

앞서 설명한바와 같이 FEM을 이용한 배관 진동 및 소음 해석이 고주파대역에서 적용이 힘듦을 확인하였으며, 따라서, SEA방법을 적용하여 중․고 주파수 대역에서의 소음을 예측하였다. Fig. 9는 SEA 해석을 위한 모델 구성을 나타내었다.

https://static.apub.kr/journalsite/sites/ask/2024-043-01/N0660430113/images/ASK_43_01_13_F9.jpg

Fig. 9.

(Color available online) SEA model configuration.

아래 첨자 1과 2는 각각 밸브 및 배관이 포함된 구조물과 음향공간의 sub-system을 의미한다. Fig. 9를 기반으로 통계적 에너지 분석법의 수식을 아래와 같이 나타내었다.^[8]

(23)

[\begin{matrix} π_{1, i n} \\ 0 \end{matrix}] = ω [\begin{matrix} η_{1, d i s s} + η_{12} & - η_{21} \\ η_{21} & η_{2, d i s s +} η_{21} \end{matrix}] [\begin{matrix} E_{1} \\ E_{2} \end{matrix}] .

𝛱_1,in는 유동에 의하여 배관에 전달된 전력(Power)이며, 음향 공간에서의 소음원이 없음으로 Eq. (23)의 좌변의 2번째 요소는 0이다. Eq. (23)의 우변행렬에서 E₁과 E₂ 각각 구조물과 음향공간이 가지고 있는 에너지이다. η₁₁과 η₂₂는 각각 구조물의 감쇠와 음향공간에서의 흡음을 나타내는 감쇠 손실 인자(Damping Loss Factor, DLF)이다. 또한, η₁₂와 η₂₁은 구조물에서 음향공간으로 전달되는 에너지와 음향공간에서 구조물로 전달되는 에너지인 연성 손실 인자(Coupling Loss Factor, CLF)를 의미한다.

입력 전력을 계산하기 위하여 구조물의 진동 모드와 벽면에 형성된 압력의 곱을 벽면 면적에 대하여 적분을 통하여 계산할 수 있으며, 다음과 같이 정의할 수 있다.^[9]

(24)

Π_{1, i n} (ω) = \int_{A} p (ω, x, y, z,) ϕ (ω, x, y, z) d A .

Eq. (24)의 p는 유동에 의해 벽면에 형성된 정압이며, 𝜙는 구조물의 속도 응답이다. 또한, 감쇠손실계수 및 연성손실계수를 다음의 식을 이용하여 계산하였다.^[8]

(25)

η_{11} = \frac{1}{Q} = 2 ξ = G .

(26)

η_{22} = \frac{C_{0} A}{4 π f V} \frac{\bar{α}}{2 - \bar{α}} .

(27)

η_{12} = \frac{η_{22} E_{2}}{(E_{1} - \frac{\bar{f_{2}}}{\bar{f_{1}}} E_{2})} .

(28)

n_{1} η_{12} = n_{2} η_{21} .

(29)

n_{i} = \frac{N_{i}}{∆ ω} .

Eq. (25)의 𝜁와 G는 각각 구조물의 점성 감쇠 계수와 이력 감쇠 계수이며, 본 해석에서는 G = 0.005로 적용하였다. Eq. (26)에서 $\bar{a}$ 는 흡음 계수이며, 음향공간에서는 반사파가 없는 공간임을 고려하여 흡음계수로서 1을 적용하여 비반사조건을 모델링 하였다. Eq. (27)의 E₁과 E₂는 다음의 식을 통하여 계산하였다.

(30)

E_{1} = M v^{2} .

(31)

E_{2} = \frac{P V}{c A} .

Eq. (30)의 m과 $v$ 는 각각 구조물의 질량과 속도이며, Eq. (31)의 P, V, c와 A는 각각 음향공간에서의 음향 파워, 부피, 공기에서의 음속과 음향 파워를 계산하는 면적이다. Fig. 10은 Eq. (25)에서부터 Eq. (29)까지의 식을 이용하여 계산한 손실 계수를 나타낸 결과이다.

https://static.apub.kr/journalsite/sites/ask/2024-043-01/N0660430113/images/ASK_43_01_13_F10.jpg

Fig. 10.

(Color available online) Damping and coupling loss factor of structure and acoustic domain.

음향 영역은 개방된 공간임으로 반사파가 없는 상태이며, 따라서 음향공간에서 구조물로의 에너지 이동에 영향을 주는 연성 손실 계수 값이 매우 작은 것을 확인할 수 있다. 또한, 음향공간의 감쇠 손실 계수 값이 가장 크게 계산되며, 이는 구조물에서 음향공간으로 전달된 에너지가 모두 소산된다는 것을 의미한다.

Fig. 11은 구조물의 전체에 1 Pa의 가진에 대한 유한요소법 및 통계적 에너지 분석법을 이용한 음향파워 레벨값을 1/3 옥타브 밴드로 비교한 결과이다. 이를 통하여 통계적 에너지 분석법의 유효성을 검증하였으며, 4,000 Hz이상의 결과에서의 편차는 유한요소법의 오차로 판단된다. 추가적으로 통계적 에너지 분석법의 유효 주파수를 판단하기 위하여 배관의 모달 중첩 인자(Modal Overlap Factor, MOF)를 Fig. 12에 나타내었다. 통계적 에너지 분석법의 유효 주파수를 모드 중첩 인자값이 1이상이 되는 주파수 대역으로 정의하였으며, 통계적 에너지 분석법의 유효 주파수 대역이 약 3,000 Hz 이상임을 알 수 있다.^[6]

https://static.apub.kr/journalsite/sites/ask/2024-043-01/N0660430113/images/ASK_43_01_13_F11.jpg

Fig. 11.

(Color available online) PWL comparison between FEM and SEA results for unit pressure input.

https://static.apub.kr/journalsite/sites/ask/2024-043-01/N0660430113/images/ASK_43_01_13_F12.jpg

Fig. 12.

(Color available online) MOF of structure mode including pipe and valve system.

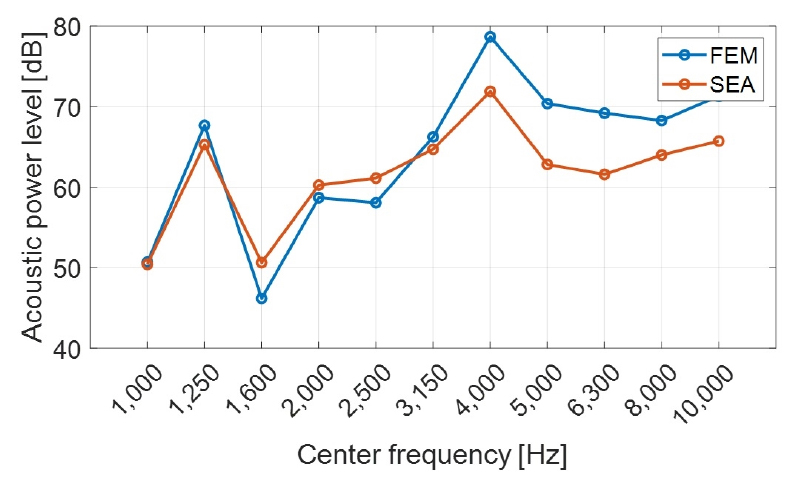
최종적으로, 유동 해석을 통하여 획득한 벽면 압력값을 입력으로 하여 통계적 에너지 분석법 계산을 진행하였으며, 주파수 대역별 유한요소법과 통계적 에너지 분석법를 통하여 계산한 음향 파워 레벨의 1/3 옥타브 밴드결과를 Fig. 13에 나타내었다.

https://static.apub.kr/journalsite/sites/ask/2024-043-01/N0660430113/images/ASK_43_01_13_F13.jpg

Fig. 13.

(Color available online) One-third octave band results of PWL computed by FEM and SEA.

이를 통하여 유한요소법 및 통계적 에너지 분석법을 이용하여 저주파수 대역에서부터 고주파수 대역까지의 소음을 잘 예측하는 것을 확인할 수 있다.

III. 결 론

본 연구에서는 배관의 설계단계에서 유동에 의한 소음을 평가할 수 있는 효율적인 소음해석 방법을 정립하였다. 먼저, 고정밀 유동 해석 기법을 이용하여, 고압의 배관 유동에 의한 벽면의 압력을 획득하였다. 유동 해석 기법은 실험과의 비교를 통하여 검증을 하였다. 또한, 파수-주파수 분석법을 적용하여 고압 배관에서의 유동에 의한 압축성․비압축성 압력의 주파수별 기여도를 분석하였다. 이를 통하여 배관의 밸브요소에서 비압축성 압력성분의 기여도가 큼을 확인하였으며, 곡관을 지나 하류로 갈수록 압축성 압력의 상대적 기여도가 커짐을 확인하였다. 이후, 유동해석을 통하여 획득한 압력을 가진력으로 하여 배관의 방사소음 해석을 진행하였다. 먼저, 저․중 주파수 대역에서의 방사소음해석을 위하여 유한요소법 기반의 해석 기법을 정립하였다. 유한요소법 해석 결과를 통하여 저․중 주파수 대역에서의 소음이 배관의 모드를 전달 경로로 하여 전파됨을 확인하였으며, 밸브 요소에서 소음이 크게 발생됨을 확인하였다. 또한, 모드의 수가 많아지는 중․고 주파수 대역에서는 통계적 에너지 분석법 기반의 해석 기법을 정립하였다. 통계적 에너지 분석법을 위한 감쇠 손실 계수 및 연성 손실 계수의 계산은 수치적 접근을 통하여 계산하였다. 모드 중첩 인자가 1이상이 되는 주파수 대역인 3,000 Hz 이상의 대역을 유효주파수로 선정하였다. 현재의 해석 방법에서는 연성 손실 계수 및 감쇠 손실 계수를 수치적 기법을 통하여 계산하였다. 이는 두개의 인자를 계산하는데 오차를 유발할 수 있다. 모달 시험 및 전달 경로 분석법과 같은 실험적 방법을 이용하여 연성 손실 계수 및 감쇠 손실 계수 인자를 선정하면 신뢰성 있는 소음을 예측할 수 있을 것 판단된다. 최종적으로 유한요소법 및 통계적 에너지 분석법을 기반으로 한 배관 방사소음 해석 기법이 배관의 설계단계에서 저주파수 대역에서 고주파수 대역까지 넓은 대역폭의 소음을 평가할 수 있을 것으로 기대된다.

Acknowledgements

본 과제(결과물)는 교육부와 한국연구재단의 재원으로 지원을 받아 수행된 3단계 산학연혁력 선도대학 육성사업(LINC 3.0)의 연구결과입니다.

References

K.-S. Kim, G. Ku, S.-J. Lee, S.-G. Park, and C. Cheong, "Wavenumber-frequency analysis of internal aerodynamic noise in constriction-expansion pipe," Appl. Sci. 7, 1137 (2017). 10.3390/app7111137

G. Ku, S. Lee, C. Cheong, W. Kang, and K. Kim, "Development of high-fidelity numerical methodology based on wavenumber-frequency transform for quantifying internal aerodynamic noise in critical nozzle," Appl. Sci. 9, 2885 (2019). 10.3390/app9142885

International Organization for Standardization, ISO 9300:2022 - Measurement of Gas Flow by Means of Critical Flow Nozzles (2022).

T. McQueen, D. Burton, J. Sheridan, and M. C. Thompson, "High-Reynolds number backward-facing step flow control," Proc. 22nd AFMC, 209-212 (2020). 10.14264/ac27693

F. Wang, S. Wu, and S. Zhu, "Numerical simulation of flow separation over a backward-facing step with high Reynolds number," Water Science and Engineering, 12, 145-154 (2019). 10.1016/j.wse.2019.05.003

S. Lee, S. Lee, and C. Cheong, "Development of high-fidelity numerical methodology for prediction of vehicle interior noise due to external flow disturbances using LES and vibroacoustic techniques," Appl. Sci. 12, 6345 (2022). 10.3390/app12136345

Siemens, Acoustics user's guide, PLM software Inc, (2019).

R. H. Lyon and R. G. Dejong, Theory and Application of Statistical Energy Analysis (Lyon Corp, Cambridge, 1998), pp. 3-19. 10.1016/B978-0-7506-9111-6.50005-17856448

W. K. Blake, Mechanics of Flow-Induced Sound and Vibration (Academic Press, New York, 1986), pp. 323-351.

The Journal of the Acoustical Society of Korea ISSN:1225-4428(Print) 2287-3775(Online) 한국음향학회지

Preview

Development of numerical method to predict broadband radiation noise resulting in fluid-induced vibration and acoustic-induced vibration of pipe

ABSTRACT

MAIN

Fig. 1.

Geometry of pipe with critical nozzle.

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

Fig. 2.

(Color available online) Measurement setup of high-pressure gas flow system.

Fig. 3.

(Color available online) Comparison results of pressure at (a) sensor 1 and (b) sensor 2.

Fig. 4.

(Color available online) Target geometry and computational domain.

Fig. 5.

(Color available online) Snapshot results of (a)Static pressure and (b) velocity contour.

(10)

(11)

(12)

Fig. 6.

(Color available online) Power spectral density spectrum (a) at region1 and (b) region 2 [Pref = 20 μPa].

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

Fig. 7.

(Color available online) Snapshot results of (a)Static pressure and (b) velocity contour.

(22)

Fig. 8.

(Color available online) Results of (a) pipe vibrational shape at 600 Hz and (b) 1/3 octave band of PWL.

Fig. 9.

(Color available online) SEA model configuration.

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

Fig. 10.

(Color available online) Damping and coupling loss factor of structure and acoustic domain.

Fig. 11.

(Color available online) PWL comparison between FEM and SEA results for unit pressure input.

Fig. 12.

(Color available online) MOF of structure mode including pipe and valve system.

Fig. 13.

(Color available online) One-third octave band results of PWL computed by FEM and SEA.

Acknowledgements

References

(Color available online) Power spectral density spectrum (a) at region1 and (b) region 2 [P_ref = 20 μPa].