I. 서 론
II. 마스크 기반 음성향상
2.1 복소값 스펙트럼을 이용한 음성향상
2.2 음성향상 모델
III. 이상치 강건 손실함수
3.1 선행 연구
3.2 Huber 손실함수
3.3 Berhu 손실함수
3.4 제안하는 손실함수 조합
IV. 실험 및 결과
4.1 데이터베이스
4.2 실험 설정
4.3 실험 결과
V. 결 론
I. 서 론
음성 인식 시스템은 실생활의 다양한 잡음 환경에서 그 성능이 저하되는 문제가 발생한다. 이러한 문제를 해결하기 위해 음성 향상 기술이 널리 연구되고 있으며, 음성 인식, 화자 인식, 음성 합성 등 다양한 음성 처리 분야에서 필수적인 기술로 활용되고 있다. 음성 향상 기술의 주요 목표는 잡음에 오염된 음성 신호에서 잡음을 억제하고, 원본 음성의 명료도를 회복하는 것이다.
마스크 기반 음성 향상 기법은 잡음 신호와 음성 신호를 분리하여 음성 품질을 향상시키는 데 효과적이다. 이러한 기법에서는 특히 심층 신경망(Deep Neural Network, DNN)을 활용하여 잡음 환경에서 음성 스펙트럼을 복원하는 방식이 주로 연구되고 있다.[1,2] DNN 기반의 음성 향상 모델은 다양한 잡음 조건에서도 우수한 성능을 보여주지만, 모델 학습에 사용되는 손실함수 선택에 따라 성능이 크게 좌우될 수 있다.[3,9]
기존 연구에서는 시간 영역의 Scale-Invariant Signal-to-Noise Ratio(SI-SNR) 손실함수와 주파수 영역의 Mean Squared Error(MSE) 손실함수를 조합하여 음성 향상 모델을 학습하는 방식을 제안하였다.[3] 이 조합은 음성의 명료도와 스펙트럼 재구성의 균형을 맞추는 데 효과적이지만, MSE 손실함수는 훈련 데이터에서 잡음의 불균일성이 이상치(outlier)로 작용할 경우 민감하게 반응하여 성능 저하를 초래할 수 있는 한계를 가진다.
본 연구에서는 이러한 문제를 해결하기 위해 이상치에 강건한(robust) Huber 손실함수(Huber Loss)[4]와 Berhu 손실함수(Berhu Loss)[5]를 SI-SNR 손실함수와 조합하여 음성 향상 성능을 개선하는 방법을 제안한다. Huber 손실함수는 고정된 임계값을 통해 이상치의 영향을 완화하며, Berhu 손실함수는 동적 임계값을 적용하여 잡음 환경에서도 적응적으로 작동한다. 이를 통해 기존 SI-SNR + MSE 조합의 한계를 극복하고 안정적인 학습과 더 나은 성능을 기대할 수 있다.
본 연구에서는 복소값 스펙트럼을 입력으로 활용하는 Deep Complex U-Net(DCUNET)에 Complex Attention(CA) 모듈을 적용한 모델[6,7]을 사용하여 제안한 방법의 효과를 검증하였다. 제안된 손실함수 조합이 다양한 잡음 환경에서도 안정적인 학습을 유도하며 SDR, PESQ, STOI 지표에서 기존 방식과 비교하여 성능이 향상됨을 확인하였다.
II. 마스크 기반 음성향상
2.1 복소값 스펙트럼을 이용한 음성향상
잡음에 오염된 음성 신호는 시간 영역에서 다음과 같은 수식으로 표현된다.
여기서 는 잡음이 섞인 음성 신호를, 는 깨끗한 음성을 은 잡음을 나타낸다. 이러한 신호는 단시간 푸리에 변환(STFT)을 사용하여 복소값 스펙트럼으로 변환되며, 변환된 복소값 스펙트럼은 다음과 같이 표현된다.
이때, Eq. (2)에서 는 잡음이 포함된 음성 신호의 복소값 스펙트럼으로, 실수부 와 허수부 로 구성된다. 본 연구에서는 복소값 스펙트럼 기반 음성향상 모델을 사용하여, STFT로 얻어진 복소 스펙트럼을 입력으로 받아 음성향상에 필요한 마스크를 추정한다. 추정된 마스크는 잡음이 포함된 입력 스펙트럼에 적용되고, 잡음이 제거된 향상된 음성 스펙트럼을 생성하여 이를 역 단시간 푸리에 변환 (ISTFT)를 통해 시간 영역의 신호로 복원한다.
복소값 스펙트럼을 이용한 음성향상은 다음과 같은 식을 따른다.
여기서 는 입력 음성 스펙트럼의 크기, 은 추정된 마스크의 크기를 나타내며, 와 은 각각 입력 스펙트럼과 마스크의 위상이다. 복소값 마스크를 추정하여 이를 스펙트럼과 곱함으로써 향상된 음성 스펙트럼 을 얻게 된다.
2.2 음성향상 모델
본 연구에서 사용한 음성향상 모델은 DCUNET 구조로, 이 모델은 복소값 스펙트럼에서 음성 신호를 복원하는 데 주로 사용된다. DCUNET은 Encoder와 Decoder로 구성되어 있으며, 각 계층은 CA 모듈을 통해 연결된다.[6,7] 모델에서 사용되는 복소 컨볼루션은 복소값 스펙트럼을 입력받아 실수부와 허수부를 독립적으로 처리하는 연산이다. 이를 위해 복소 컨볼루션 필터는 Eq. (4)와 같이 정의된다.
Eq. (4)에서 와 는 각각 실수부와 허수부의 컨볼루션 필터를 나타낸다. 중간 복소 스펙트럼 는 Eq. (5)와 같이 표현되며, 복소 컨볼루션 연산은 Eq. (6)와 같이 계산된다.[6,8]
본 연구에 사용된 모델의 구조는 Fig. 1과 같으며 8개의 Encoder(E0...E7)와 8개의 Decoder(D0...D7) 계층으로 구성된다, 각 Encoder 계층은 복소값 컨볼루션, 배치 정규화, 활성화 함수로 이루어져 있으며, E0부터 E7은 Eq. (6)의 복소 컨볼루션 연산을 통해 입력 특징을 추출하며, 배치 정규화와 활성화 함수가 순차적으로 적용된다. 추출된 특징은 Encoder와 Decoder 계층 간에서 전달되며 이때 모델의 처음 입력은 Eq. (2)의 복소 스펙트럼이 E0에 입력된다. Decoder는 Encoder와 유사한 구조이지만 D7부터 D0까지 복소 전치 컨볼루션을 수행하여 입력 신호를 복원한다. 배치 정규화와 활성화 함수는 복소 컨볼루션과 달리 Eq. (7)에 따라 실수부와 허수부를 각각 독립적으로 처리한다.
여기서 와 는 각각 실수부와 허수부에 적용되는 배치 정규화 연산 또는 활성화 함수이다.
모델에 적용된 CA 모듈은 Encoder와 Decoder의 출력을 결합하여 복원 과정을 더욱 효과적으로 진행한다. CA 모듈은 Global Average Pooling(GAP)과 Absolute (Abs) 연산을 포함하며 모두 Eq. (7)과 같은 방식으로 실수부와 허수부에 각각 별도로 적용된다.[6,7]
III. 이상치 강건 손실함수
3.1 선행 연구
음성향상 모델의 성능을 향상하기 위해, 선행 연구에서는 시간 영역과 주파수 영역에서 각각 다른 손실함수를 적용하는 방식을 제안하였다.[3] 시간 영역의 SI-SNR 손실함수는 음성 신호의 명료도를 향상시키는 데 효과적이며, MSE 손실함수는 마스크 기반 음성향상 기법에서 대중적으로 사용하는 손실함수로서,[9] 음성향상 처리 과정을 통해 얻은 향상된 음성 스펙트럼과 깨끗한 음성의 스펙트럼의 거리를 줄이도록 하는 손실함수로 정의된다.
SI-SNR 손실함수는 향상된 복소 스펙트럼을 ISTFT을 통해 시간 영역의 음성 파형으로 변환한 후, 향상된 음성 파형에서 깨끗한 음성 부분을 제거하여 얻은 잡음과 크기가 조정된 깨끗한 음성의 비율을 기반으로 손실 값을 계산한다. 수식적 정의는 아래와 같다.
Eqs. (8), (9), (10)에서 는 깨끗한 음성 파형, 는 향상된 음성 파형을 나타낸다. 는 두 벡터의 내적 연산이며, 는 L2 norm 연산이다.
주파수 영역에서 정의된 MSE 손실함수는 다음과 같이 계산된다.[3]
Eq. (11)에서 은 실제 정답 음성 스펙트럼을, 는 향상된 음성 스펙트럼을 나타내며, 와 는 각각 시간 축 프레임, 주파수 축 인덱스를 나타낸다. 와 각 시간축 프레임의 총 개수, 주파수 축 간격의 총 개수이다.
크기 스펙트럼에 대한 MSE 손실함수는 다음과 같다.
Eq. (12)에서 는 향상된 음성의 스펙트럼, 는 깨끗한 음성의 스펙트럼으로 는 크기 스펙트럼을 나타내며 는 크기 스펙트럼에 MSE를 적용한 손실함수이다.
MSE 손실함수는 모든 오차항에 대해 제곱 합을 계산함으로써 손실을 추정하며, 이는 매우 큰 오차, 또는 작은 오차값에 의해 손실 값이 기하급수적으로 커지거나 작아지게 되어, 이상치에 민감하게 반응하는 특성을 가진다. 이상치 민감성은 음성향상 모델의 학습 과정에서 다양한 크기의 잡음이 포함된 훈련 데이터의 잡음 불균일성이 MSE 손실함수에 이상치로 작용할 경우, 모델의 성능 저하를 유발할 수 있다. 이러한 이상치 민감성은 학습의 수렴 속도 저하와 모델의 안정성에 부정적인 영향을 미치며, 결과적으로 음성향상 성능 저하로 이어질 수 있다.
3.2 Huber 손실함수
Huber 손실함수는 회귀 문제에서 자주 사용되는 손실함수로, 평균 제곱 오차(MSE)와 평균 절대 오차(Mean Absolute Error, MAE) 의 장점을 결합한 형태이다.[4] Huber 손실함수는 작은 오차에 대해서는 MSE 손실함수처럼 동작하지만, 큰 오차에 대해서는 MAE 손실함수처럼 선형적으로 동작한다. 이는 이상치나 노이즈에 더 강인한 회귀 모델을 만들 수 있다.
Huber 손실함수의 수식적 정의는 다음과 같다.
여기서 는 예측값과 실제값 간의 차이를 의미하며 𝛿는 임계값(threshold) 이다. Huber 손실함수는 가 임계값 𝛿보다 작을 때 MSE 손실함수처럼 오차의 제곱을 Loss로 계산하고, 𝛿보다 크면 MAE 손실함수처럼 이상치에 덜 민감하게 선형적으로 Loss를 계산한다. 이러한 특성은 노이즈나 이상치가 많은 데이터에 유리하며 모델의 강건성을 향상시킨다. 임계값 𝛿는 사용자가 정의하며, 𝛿가 작을수록 Huber 손실함수는 MAE 손실함수처럼 동작하고, 𝛿가 클수록 MSE 손실함수처럼 동작한다. 따라서 𝛿의 값은 모델이 이상치에 대한 민감도를 조정하는 중요한 제어 변수이다. 본 실험에서는 𝛿의 범위를 [1, 5]으로 설정하여 1씩 증가시키며 실험을 진행하였고, 최종적으로 가장 높은 성능을 보인 𝛿 = 2를 선정하였다.
본 실험에서 선행 연구와 마찬가지로 Huber 손실함수를 크기 스펙트럼에 적용하였으며 수식적 정의는 아래와 같다.
위 식은 Eq. (12)의 설명과 동일하며 향상된 음성 스펙트럼과 깨끗한 음성 스펙트럼 간의 차이를 계산한다.
3.3 Berhu 손실함수
Berhu 손실함수(Reverse Huber)는 Huber 손실함수에서 변형한 형태로,[5] Huber 손실함수와 같이 두 구간으로 나누어 손실을 계산하지만 작은 오차에 대해 MAE를, 큰 오차에 대해서는 선형적으로 증가하는 손실함수로 Huber 손실함수와 반대로 동작하는 특성을 가진다.
Berhu 손실함수의 수식적 정의는 다음과 같다.
여기서 는 Eq. (13)과 동일하게 예측값과 실제값 간의 차이를 나타내며, 𝛿는 하이퍼파라미터, 는 임계값을 나타낸다.
Berhu 손실함수는 수식적 특성 중 하나인 이상치 강건성은 MSE 손실함수의 경우 이상치에 매우 민감하여 큰 오차가 발생하면 손실이 크게 증가하는 제곱 오차 형식을 가지지만, Berhu 손실함수는 큰 오차에 대해서도 선형적인 손실 계산을 통해 이상치에 강건한 특징을 가진다.
Huber 손실함수와 비교하여 Berhu 손실함수는 임계값을 설정하는데 있어 차이가 존재한다. Huber 손실함수는 고정된 임계값을 사용하지만 Berhu 손실함수는 데이터에 따라 동적으로 변하는 임계값을 사용한다. 일반적으로 최대 오차의 20 %(𝛿 = 0.2)로 설정된다. 데이터에 따라 동적으로 임계값이 변하는 동적 전환(Dynamic transition)으로 이상치나 데이터 규모가 다양할 때 데이터 크기 차이에 덜 민감하게 반응하며 학습 시 손실 분포가 다르더라도 자동으로 적응하여 효과적으로 손실 계산이 가능하다. 본 실험에서는 𝛿의 범위를 [0.1, 0.5]으로 설정하여 0.1씩 증가시키며 실험을 진행하였고, 최종적으로 가장 높은 성능을 보인 𝛿 = 0.4를 선정하였다.
본 실험에서 선행 연구와 마찬가지로 Berhu 손실함수를 크기 스펙트럼에 적용하였으며 수식적 정의는 아래와 같다.
Eq. (18)은 Eq. (12)에서 정의된 것처럼 향상된 음성 스펙트럼과 깨끗한 음성 스펙트럼 간의 차이를 계산한다.
3.4 제안하는 손실함수 조합
본 연구에서 시간 영역의 SI-SNR 손실함수와 주파수 영역의 Huber 손실함수 및 Berhu 손실함수를 조합한 두 가지 새로운 손실함수 조합을 제안한다. 이러한 조합은 각 손실함수의 장점을 활용하며 기존 SI-SNR + MSE 조합에서 MSE 손실함수의 잡음 데이터 불균일성으로 인한 이상치 민감성 문제를 개선하고 학습 수렴 속도와 성능을 높이고자 하는 시도이다.
SI-SNR과 Huber 손실함수 및 Berhu 손실함수 조합은 다음과 같이 정의된다.
이러한 손실함수 조합을 통해 SI-SNR 손실함수는 시간 영역에서 음성의 명료도를 향상시키며 Huber 손실함수 및 Berhu 손실함수는 주파수 영역에서 스펙트럼 차이를 효과적으로 줄인다. 또한, MSE 손실함수를 대체함으로써 훈련 데이터 잡음의 불균일성으로 인한 성능 저하를 방지할 수 있다. 특히 Berhu 손실함수는 동적 전환 특성으로 인해, 다양한 잡음 데이터 분포에 맞게 임계값이 자동으로 조정됨으로써 보다 효과적으로 음성향상 모델 학습이 가능할 것으로 기대된다.
IV. 실험 및 결과
4.1 데이터베이스
본 실험에서 사용한 깨끗한 음성은 CSTR VCTK Corpus를 사용하였다.[10] VCTK 데이터셋은 109명의 영어 화자가 약 400개의 문장을 낭독한 고품질 음성 데이터셋으로, 이 중 28명의 화자 데이터를 훈련에, 2명의 화자 데이터를 테스트에 사용하였다. 모든 음성은 48 kHz로 샘플링 되었으며, 실험에서는 16 kHz로 다운 샘플링하여 사용하였다.
훈련 데이터셋의 잡음 데이터는 DEMAND 데이터베이스[11]의 8가지 실제 환경 잡음과 2가지 인공 잡음(speech-shaped noise, babble noise)을 사용하였다. 각 깨끗한 음성에 대해 15 dB, 10 dB, 5 dB, 0 dB의 네 가지 신호 대 잡음 비(Signal-to-Noise Ratio, SNR)로 잡음을 합성하여, 음성 표본당 40가지의 서로 다른 잡음 조건을 생성하였다. 테스트 데이터셋은 훈련에 사용 되지 않은 DEMAND의 5가지 잡음을 17.5 dB, 12.5 dB, 7.5 dB, 2.5 dB의 SNR로 합성하여 구성하였다.[12]
스펙트럼 특징 추출을 위해 32 ms 크기의 Hamming 윈도우를 50 % 중첩으로 적용하였으며, 고속 푸리에 변환 개수는 512로 설정하여 총 257차원의 스펙트럼 특징을 얻었다.
4.2 실험 설정
훈련을 위한 Optimizer은 ‘Adam’을 사용하였으며 Learning rate는 0.001로 설정하였다. 활성화 함수는 디코더의 마지막 층을 제외하고 모두 Leaky_ReLU를 사용하였으며 디코더의 마지막 층에서 Tanh함수를 사용하였다. Huber손실함수와 Berhu손실함수의 임계값은 각각 초기 실험에서 다양한 𝛿 값으로 실험을 수행한 결과 가장 안정적이고 우수한 성능을 보인 2와 0.4로 설정하였다. 각각의 손실함수 조합 실험은 모두 동일한 실험환경에서 진행하였으며, 실험환경은 Ubuntu 22.04버전, pytorch 2.10버전, RTX4090 단일 GPU 환경에서 실험을 진행하였다.
4.3 실험 결과
모델에 대한 성능 평가는 총 3가지 지표를 이용하였다. 첫 번째는 깨끗한 음성과 원하지 않는 왜곡의 비율인 SDR로 dB단위로 표현하였다.[13] 두 번째는 PESQ로 음성의 지각적인 품질을 평가하는데 가장 많이 사용되며 ITU-T에서 표준화하였다.[14] PESQ 지표는 보통 1.0에서 4.5 사이의 값을 가진다. 세 번째는 음성의 명료도를 객관적으로 평가할 수 있는 STOI를 사용하였다.[15] STOI는 0에서 1사이의 값을 가지기 때문에 백분율(%)로 단위를 조정하여 비교를 진행하였다. 본 연구에서 성능 평가를 위해 각 손실함수 조합에 대해 모델별로 5회 학습을 진행하였으며, 각 학습은 모델이 충분히 학습 가능한 150,000 epoch로 진행되었다. 성능 평가의 일관성을 위해 모델이 과적합에 도달하기 이전에 성능이 충분히 수렴하는 지점인 100,000 epoch시점 모델을 저장하였으며, 손실함수 조합당 5개의 모델의 성능 평균을 최종 결과로 사용하였다.
실험 결과는 Table 1에 나타내었다. 표에서 No Processing은 음성향상을 수행하지 않은 잡음 오염 음성에 대한 평과 결과이다. 첫째, SI-SNR + MSE 손실 함수 조합에서 발생하는 문제점인 이상치에 민감하다는 단점을 고려할 때, Huber 손실함수와 Berhu 손실함수를 조합한 경우가 기존의 MSE 손실 함수 조합보다 SDR, PESQ, STOI성능 지표 모두에서 향상된 결과를 나타냈다. 특히, Huber 손실함수를 조합한 경우 평균 SDR 20.98 dB, PESQ 2.634, STOI 93.71 %로 개선되었으며, Berhu 손실함수 조합의 경우 평균 SDR 21.34 dB, PESQ 2.743, STOI 94.18 %로 가장 높은 향상을 보였다.
Table 1.
Results of speech enhancement trained with various loss function.
| DCUNET-CA | SDR [dB] | PESQ | STOI [%] |
| No processing | 8.53 | 1.970 | 92.13 |
| SI-SNR | 20.37 | 2.541 | 92.67 |
| SI-SNR + MSE | 20.59 | 2.604 | 93.44 |
| SI-SNR + huber_loss | 20.98 | 2.634 | 93.71 |
| SI-SNR + berhu_loss | 21.34 | 2.743 | 94.18 |
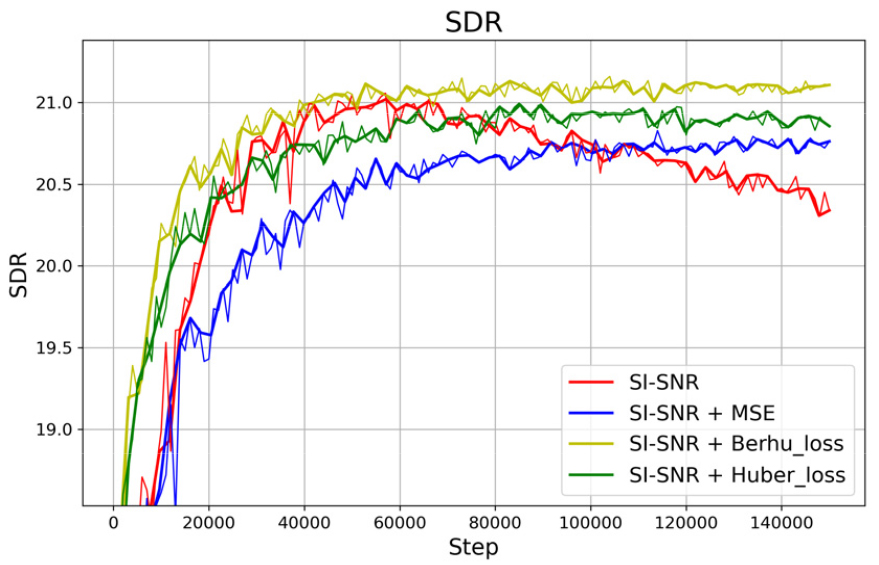
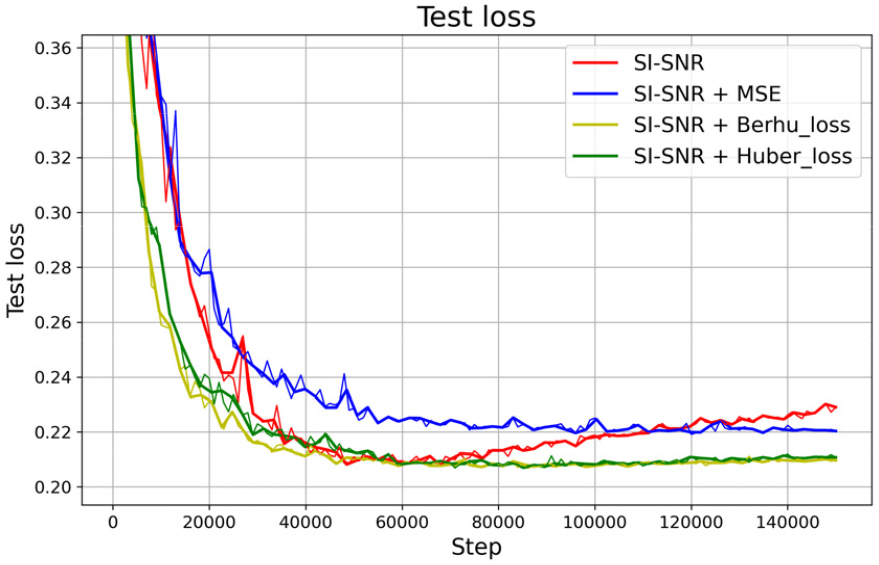
또한, 제안된 손실함수 조합(SI-SNR + Huber 및 SI-SNR + Berhu)은 Figs. 2와 3에서 확인할 수 있듯이 학습 초기 약 20,000 스텝 이내에 기존 SI-SNR + MSE 손실함수과 비교하여 빠르게 수렴하는 양상을 보였다. 이는 MSE 손실함수가 잡음 데이터의 불균일성으로 인해 이상치 데이터에 민감하게 반응하며, 손실 값의 변동성을 증가시키고, 결과적으로 수렴 속도를 저하시켰기 때문으로 해석할 수 있다. 반면, Huber 손실함수와 Berhu 손실함수는 이상치 데이터의 영향을 완화하여 손실 값의 변동을 억제하고, 안정적인 학습 과정을 가능하게 했다.
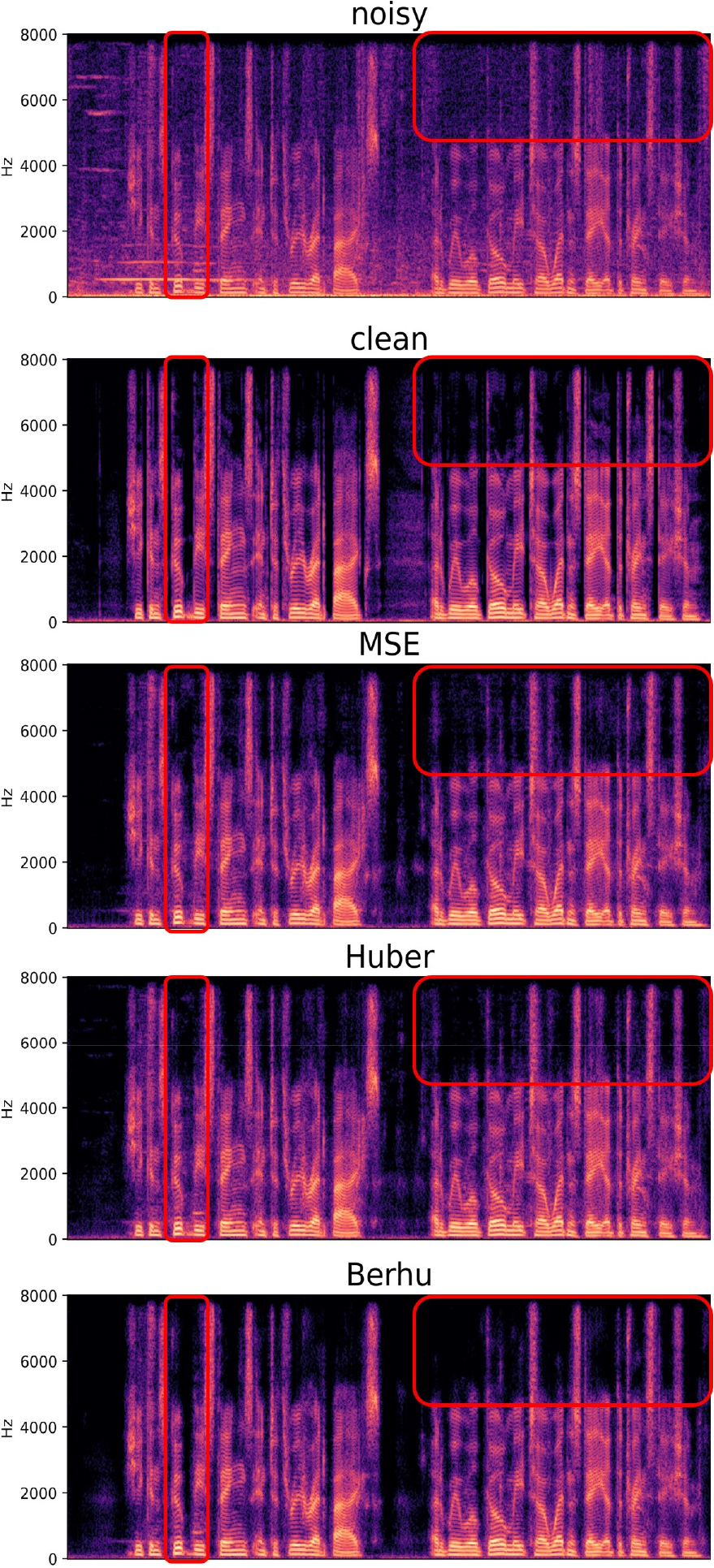
스펙트로그램 분석(Fig. 4)에서 빨간색 테두리로 강조된 영역을 비교한 결과, Berhu 손실함수를 적용한 모델이 잡음을 가장 효과적으로 억제하며 원본 음성을 선명하게 복원하는 성능을 보였다. 반면, MSE 손실함수는 잡음 억제 성능이 부족했으며, Huber 손실함수는 개선된 성능을 보였으나 Berhu 손실함수만큼 효과적이지 않았다. 이를 통해 제안하는 손실함수 조합이 학습 초기 안정성을 높이고, 잡음 데이터의 불균일성으로 인한 문제를 해결하여 음성향상 성능 개선에 기여했음을 보여준다.
V. 결 론
본 연구에서는 음성향상 모델의 성능을 높이기 위해 마스크 기반 음성향상 모델에서 MSE 손실함수 대신, 이상치에 강건한 Huber 손실함수와 Berhu 손실함수를 도입하는 방법을 제안하였다. 기존의 SI-SNR + MSE 조합에서 MSE 손실함수에서 발생하는 문제점인 훈련 데이터의 잡음 불균일성으로 인한 이상치에 대한 민감성을 해결하고자 하였다. 실험 결과, Huber 손실함수와 Berhu 손실함수를 SI-SNR과 결합한 모델이 기존 MSE 손실함수 조합보다 SDR, PESQ, STOI 성능 지표 모두 향상된 결과를 나타냈다. 특히 Berhu 손실함수를 조합하였을 때 평균 SDR은 0.76 dB, PESQ는 0.139, STOI는 0.74 % 개선된 성능을 보였다. 이를 통해, 이상치에 강건한 손실함수의 사용이 음성향상 모델 성능을 효과적으로 향상시킬 수 있음을 확인하였다.