I. 서 론

천해의 수중 음향 통신 채널은 경계면 시변동과 매질의 불균일성이 존재하는 시변 통신채널이다. 특히, 해면과 해저 면에 의해 형성된 다중경로는 시변적 환경 요인으로 통신성능을 시변적으로 변동시킨다. 다중경로 채널에서 송신 신호의 변동에 영향을 주는 해면 요인은 파고, 파주기, 입사각 등이 있으며, 해저 면은 해저 매질, 매질의 분포상태 등이 있다. 또한, 조수간만에 따른 수심의 변화, 해류에 따른 수온 층 변동, 송·수신기의 위치 변동, 부유물의 반사 경로변동 등이 다중경로 변동에 영향을 주는 요인이다.^[1,2,3]

수중 다중경로 채널로 송신된 신호는 각 경로의 경계면 특성에 따라 변동되어 반사되며, 경로의 길이에 따라 지연 확산되어 수신된다. 시변적 변동이 많은 해면 반사파는 입사각과 파고에 따라 도플러 천이 및 산란 특성을 가지며, 해저면 반사파는 매질의 특성에 따라 반사, 투과, 산란 등의 변동 영향을 받는다. 이로 인해 경계면 변동 영향을 받은 송신 신호는 각 경로를 통해 시간 지연되어 수신되고, 수신 신호는 지연 확산된다.^[4]

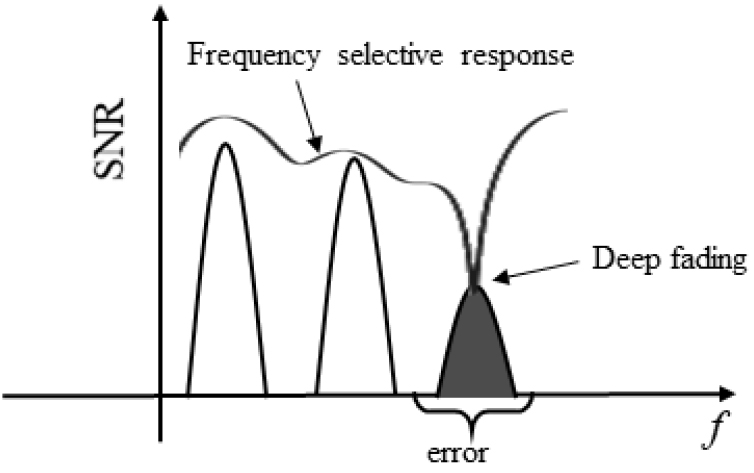
지연 확산된 신호는 경계면 변동 특성에 의해 각 경로 파는 다양한 형태의 상쇄 간섭과 보강 간섭 그리고 신호의 진폭, 주파수 그리고 위상 변동의 영향을 받는다. 이로 인해 채널의 대역폭 제한, 심벌 간 간섭(InterSymbol Interference, ISI)그리고 반송파의 주파수 선택적 페이딩(frequency selective fading)에 의한 상쇄 간섭 및 신호대잡음비(Signal to Noise Ratio, SNR)변동으로 수중 음향 통신 시스템의 전송성능을 감소시킨다.^[5,6]

수중 다중경로 주파수 선택성 채널에서 전파 경로 상의 매질 변동 등에 의해 수신 신호의 에너지가 불규칙하게 변동되는 현상을 해결하기 위한 기법으로 다이버시티 기법이 적용되고 있다. 수중 음향 통신에서는 공간 다이버시티와 주파수 다이버시티가 적용되고 있다.

이 중 단일 센서를 적용한 주파수 다이버시티는 동일한 전송정보를 다수의 주파수 채널로 전송하고 서로 다른 경로로 수신된 신호를 결합하거나 결정하는 기법이다.

주파수 다이버시티 기법에서 수신 신호 결합 및 결정하는 기법은 선택적 합성법(Selective Combining, SC), 동이득 합성법(Equal Gain Combining, EGC), 최대비 합성법(Maximum Ratio Combining, MRC)이 있다. SC는 다수의 채널 신호 중 높은 에너지의 신호를 선택하는 방법이며, EGC는 다수의 채널 신호를 정합 후 같은 이득으로 합성하는 방법이다. MRC는 정합 후 합성 전에 신호마다 신호대잡음비를 계산하여 그 크기에 따라 합성하는 방식으로, EGC와 MRC는 위상 정합(phase matched)과 처리 과정의 구현이 어렵다.^[7,8] 따라서 주파수 다이버시티의 합성법 중 적용이 용이한 SC 기법과 결정 값 오류를 해결하기 위한 최대우도추정(Maximum Likelihood Estimation, MLE)을 적용한 MLE-SC 기법을 제안한다.

본 논문에서는 수중 주파수 선택적 채널에서 MLE- SC 기법을 적용한 수중 주파수 다이버시티의 통신성능을 평가하였다. SC기법의 결정 값 추출은 송신 신호의 FFT(Fast Fourier Transform) 값을 바탕으로 MLE로 추출하였다. 실험 결과에서 MLE-SC 적용한 후 보호대역에 따라 약 3.6배와 약 2.8배의 성능 향상을 보였다.

II. 수중 다중경로 주파수 선택성과 주파수 다이버시티 MLE-SC기법

수중 다중경로 채널의 송신 신호는 경계면 변동성에 따라 반사파의 도플러 천이, 진폭변동, 위상천이 등의 변동성을 갖는다.

수중 다중경로 채널의 임펄스 응답은 Eq. (1)과 같다.^[3]

여기서 L은 다중경로 경로의 수이며, al(t)와 τl(t)는 l 번째 다중경로의 진폭과 지연시간이다.

해면 반사파에 영향을 주는 해면의 roughness Rrou 는 Eq. (2)와 같다.^[9,10]

여기서 Rrou=khssin(θ)이며, k는 파수, hs해면의 파고, θ는 해면 반사파의 입사각이다. 이런 해면의 roughness는 송신 신호의 파장과 관계되어 도플러 천이 및 산란특성에 영향을 준다.^[2,3]

수중 다중경로 채널의 주파수 선택성은 Fig. 1에서 보는 것과 같이 송신 신호의 시간지연과 주파수 간 상쇄 간섭으로 인해 발생되며, 신호의 신호대잡음비를 감소시킨다. 특히, 수중 다중경로 채널은 시변동성이 높은 빠른 페이딩 채널로 송신 신호의 세기와 위상이 시변적으로 변동되는 채널 환경이다.

Fig. 1.

Underwater acoustic multipath frequency selective channel.

이러한 채널의 주파수 선택성에 대한 통신성능 확보를 위해 다이버시티 기법이 적용되고 있다. 본 논문에서는 단일 센서 적용을 위해 다수의 주파수를 사용하는 주파수 다이버시티가 적용되었다. 동일한 정보 신호를 다수의 채널로 전송하기 위해 각 채널로 입력된 비트 또는 심벌에 대응되는 변조 방식과 반송파 주파수로 변조되어 송신된다.

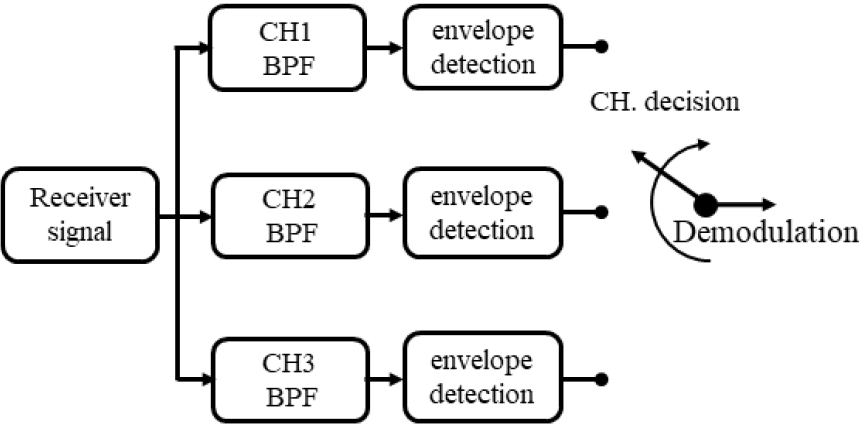
동일한 정보가 다수의 채널로 송신되는 주파수 다이버시티는 수신 신호의 합성법에 따라 복조 과정을 수행한다. 본 논문에서는 Fig. 2과 같이 SC기법을 적용한다.

Fig. 2.

Selective combining of block diagram.

SC는 신호가 L개의 독립적인 페이딩 채널에서 전송된다고 가정하면, k번째 채널에서 대한 equivalent low-pass 출력은 Eq. (3)과 같이 주어진다.^[8]

여기서 αk는 진폭 감쇠, ϕk는 위상 편이, zl(t)는 각각의 k번째 채널에서의 equivalent low-pass complex 가우시안 잡음이다. zl(t)의 실수부분과 허수부분 모두 동일한 전력 스펙트럼 Nb를 가진다고 가정하면, 수신기의 상관기 또는 정합 필터의 출력 SNR은 Eq. (4)와 같이 주어진다.^[8]

여기서 Es는 complex envelope signal sl(t)의 에너지이다. 선택적 합성법의 경우, 모든 페이딩 채널에서 신호대잡음비를 측정한 후, 해당 신호를 결정하기 위해 최댓값을 선택한다. 하지만 수중 다중경로 채널은 경계면 반사의 특성과 지연시간에 따라 직접파와 반사파 신호의 중첩으로 상쇄와 보강에 따른 판정오류 및 정보 복원 오류를 발생시킬 수 있다.

따라서 시변적 변동에 따른 신호 에너지의 변동은 선택적 합성법의 결정 값 오류를 유발한다. 이러한 SC 기법의 결정 값 변동에 대한 확률적 분석을 통해 결정 값을 추출하기 위한 MLE를 적용하였다.

정규 분포 MLE는 모수가 미지의 μ인 확률분포에서 뽑은 표본 x 들을 바탕으로 μ를 추정하는 기법으로 Eq. (5)와 같다.^[11]

여기서 x는 정규화 과정에서 추출한 신호 세기의 표본값, μ는 평균, σ2은 분산이다.

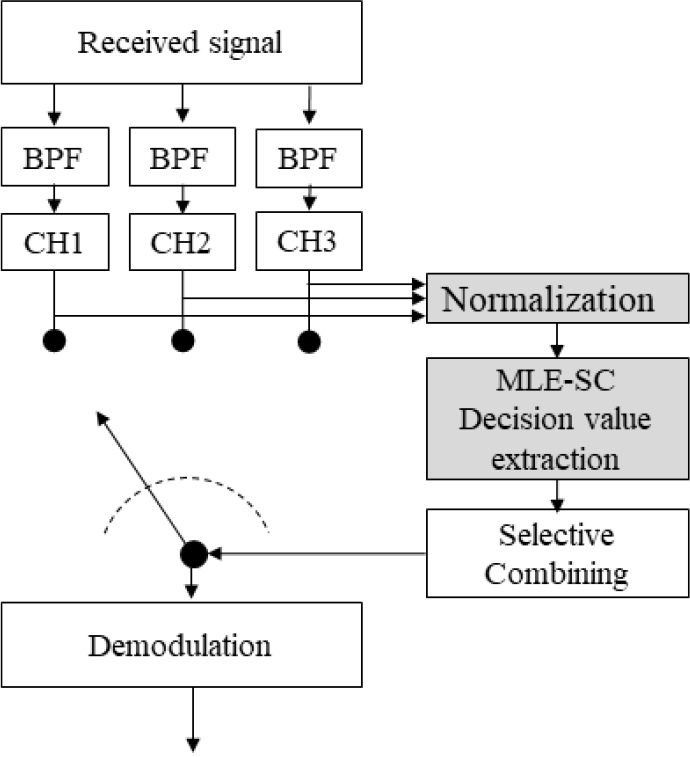
MLE에서 추출한 기여도가 높은 세기의 신호 값을 SC 기법의 판정 기준으로 적용하는 MLE-SC 주파수 다이버시티의 구성도는 Fig. 3과 같다. 수신 신호는 대역통과 필터를 통해 각 채널로 분리되고, FFT 분석을 통해 신호의 에너지를 추출한다. 추출된 에너지는 정규화되어, MLE의 표본 값으로 입력된다. 입력된 표본 값은 Eq. (5)를 통해 MLE분석되고, 최대 우도를 가지는 값을 결정 값으로 선택 후 SC 기법에 적용한다. 선택된 채널은 복조 과정과 복호화 과정을 통해 정보를 복원한다.

Fig. 3.

Block diagram of frequency diversity applying MLE-SC.

III. 실험 및 결과

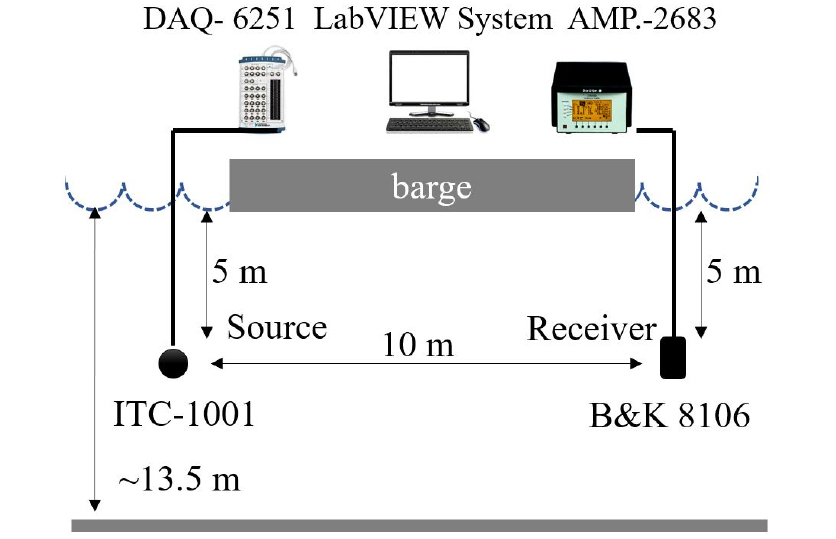
MLE-SC 주파수 다이버시티 성능평가는 거제도 탑포리 연안의 바지선에서 수행하였다. 수심은 13.5 m, 실험 당일의 유효파고는 약 0.3 m로, 산란 특성이 우세한 해면 경계면 특성과 진흙과 모래의 해저 면으로 구성되어 있다. Fig. 4의 구성도와 같이 송·수신기의 거리는 10 m, 송신기 수심은 5 m, 수신기의 수심은 5 m로 하였다. Table 1은 실험 파라메타로, 3채널 주파수 다이버시티로 구성하였다. 각 채널은 4-FSK 방식으로 변조하였으며, 보호대역은 1 kHz, 0.5 kHz로 선택하였다.

Fig. 4.

Experimental configuration.

전송률은 실험 해역의 송·수신거리 및 수심에 대한 수치모의 실험결과를 바탕으로 결정하였다. 최대초과지연에 따른 RMS 지연확산은 2.78 ms로 확인되었으며, 채널의 코히어런스 대역은 상관성이 0.5이하로 지연확산과의 역상관계에 따라 71.9 Hz로 확인되었다. 수치모의 실험을 바탕으로 오류 감소 성능평가를 위해 오류가 발생되는 100 bps의 전송률로 전송하였다.

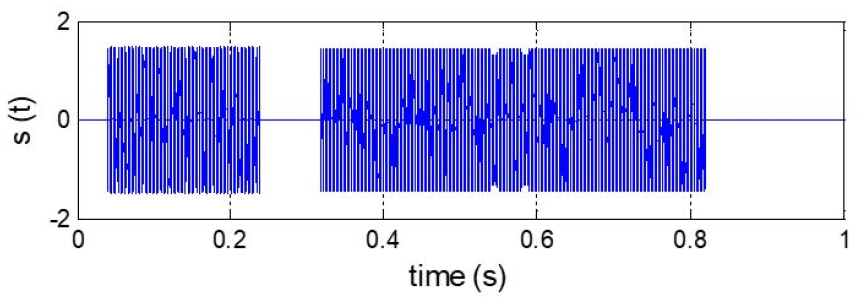
송신 신호 프레임 구성은 Fig. 5와 같다. 신호의 동기 확보를 위한 Pseudo Noise(PN) 신호는 200 ms이며, PN신호의 상호상관정합을 통해 동기 포인터를 추출한다. 데이터는 silence 구간 이후 500 ms로 1 s 단위의 프레임으로 구성하였다.

Fig. 5.

(Color available online) Transmission signal 3CH MLE-SC frequency diversity.

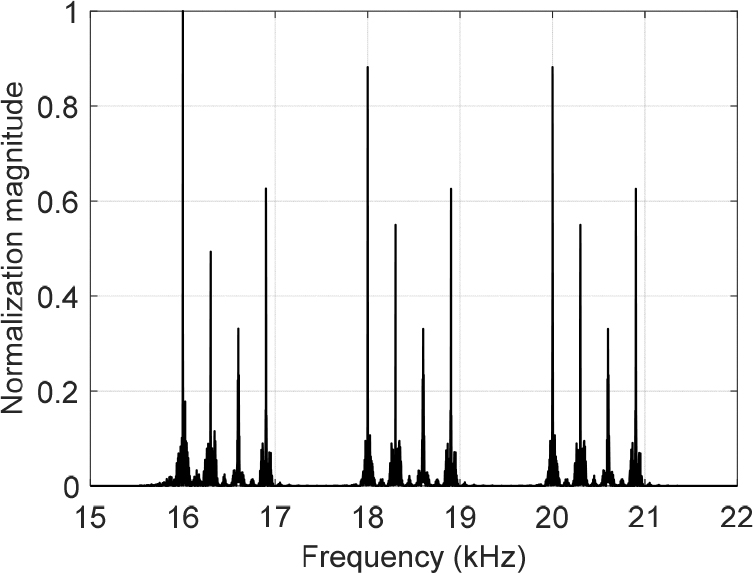
MLE-SC 주파수 다이버시티 성능평가에 사용된 3채널 송신 신호의 스펙트럼은 Fig. 6과 같다. 전송률에 따른 1개 채널의 대역폭은 900 Hz로 채널 간섭을 최소화하기 위해 2 kHz 간격의 마크 주파수 16 kHz, 18 kHz, 20 kHz을 설정 후 4-FSK 변조하였다.

Fig. 6.

Transmission signal spectrum of 3-channel frequency diversity.

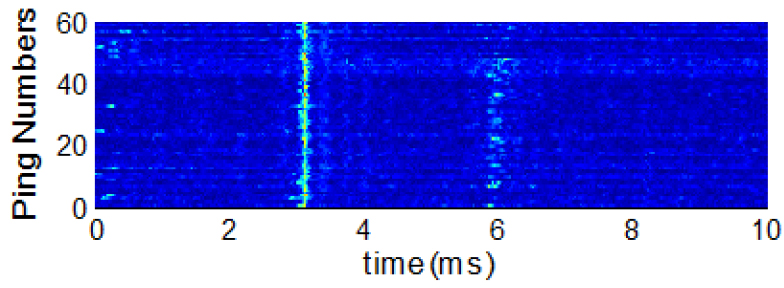
Fig. 7은 실험 해역의 LFM 신호 60회 전송에 대한 지연확산 특성으로 직접파 도달 후 3 ms 지연을 가지는 반사파가 수신된다. 하지만 해면의 파고에 의한 산란과 진흙과 모래로 구성도 해저면 흡수손실로 인해 반사파의 세기는 상대적으로 낮게 나타났다.

Fig. 7.

(Color available online) Multipath intensity profile.

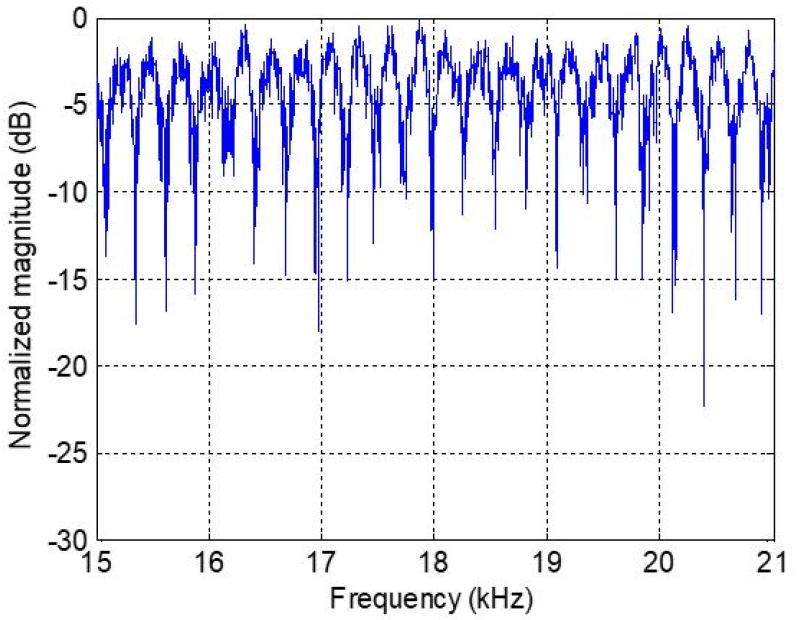
수중 다중경로 채널의 주파수 선택성은 Fig. 8과 같이 분석되었다. 1개 채널 사용되는 1 kHz 구간에 상쇄 간섭에 의한 깊은 페이딩이 4개의 주파수에서 나타났다. 따라서 단일 채널 통신에서 주파수 선택성이 증가되면 정보 오류는 필연적으로 발생되며, 이러한 주파수 선택성 채널에서 다이버시티 기법은 필수적이라고 할 수 있다.

Fig. 8.

(Color available online) Frequency selective of the experimental channel.

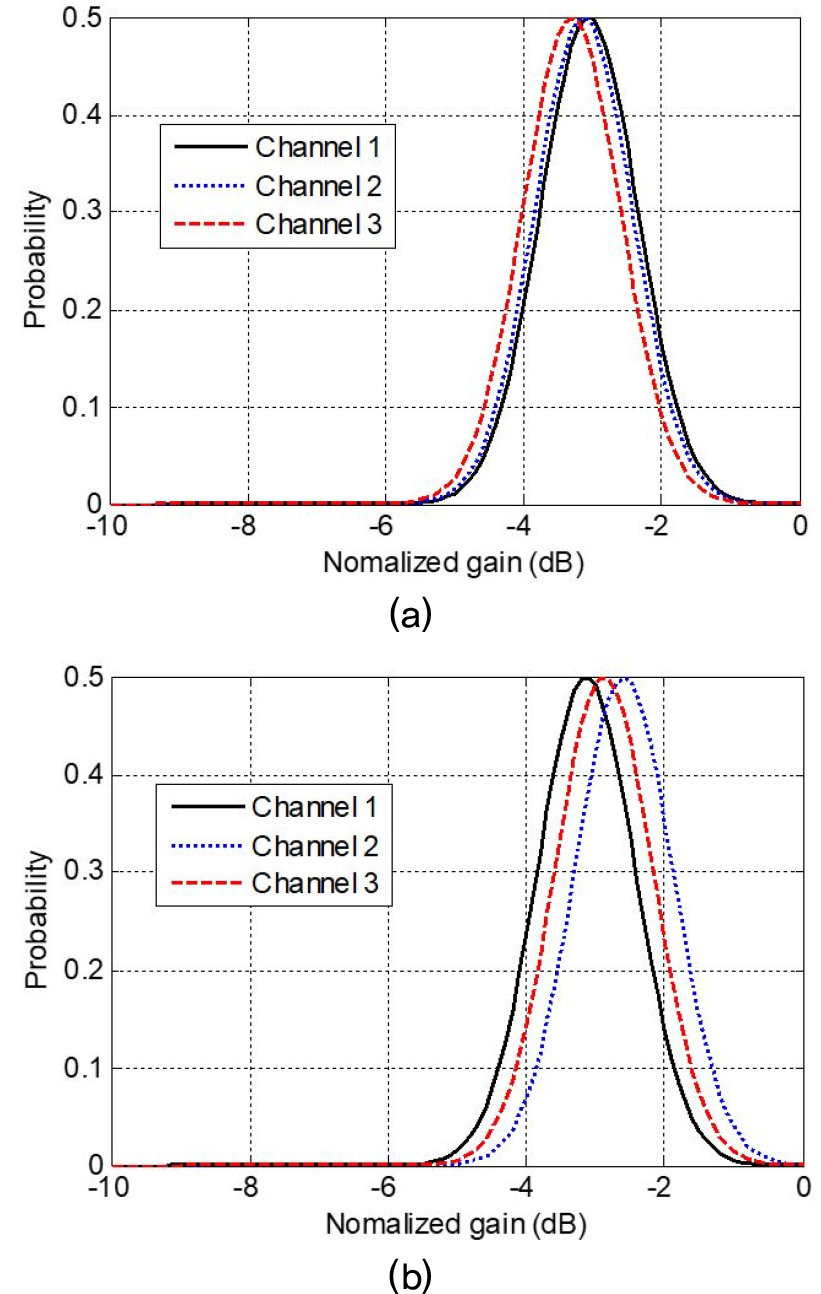
SC의 판정을 위한 MLE값 추출은 Eq. (5)의 수식을 적용하였다. Fig. 9(a)는 실험 1(EXP1)로 채널 보호구간이 1 kHz인 경우 각 채널의 정규화된 표본 값을 이용하여 MLE 값을 추출하였다. 채널 1 ~ 채널 3의 기여도 이득 값은 –3.2 dB로 나타났다. Fig. 9(b)는 실험 2(EXP2)로 채널 보호구간이 0.5 kHz인 경우이다. 실험 2에서 채널 1의 기여도 이득 값은 –2.6 dB로 나타났으며, 채널 2와 채널 3은 –3 dB로 나타났다.

Fig. 9.

(Color available online) Extraction of MLE decision value for each channel: (a) experiment 1 (guard band 1 kHz), (b) experiment 2 (guard band 0.5 kHz).

Table 2는 SC에 MLE 값 미적용 시 보호대역에 따른 실험 1과 실험 2의 각 채널 별 복원된 이미지와 BER을 나타내고 있다. 실험 1에서 채널 1은 0.032, 채널 2는 0.035, 채널 3은 0.043으로 확인되었으며, 실험 2에서 채널 1은 0.056, 채널 2는 0.052, 채널 3은 0.05로 BER 확인되었다. 1 kHz 보호대역을 가지는 실험 1이 0.5 kHz 보호대역을 가지는 실험 2에 비해 상대적으로 보호구간이 넓으며, 주파수 다이버시티의 채널 간 간섭(Inter Channel Interference, ICI)이 낮아 BER이 낮게 나타난 것으로 판단된다.

Table 2.

Image transmission performance without MLE value applied in experimental 1 and 2.

EXP	Channel 1	Channel 2	Channel 3
EXP1
	BER : 0.032	BER : 0.035	BER : 0.043
EXP2
	BER : 0.056	BER : 0.052	BER : 0.05

Table 3은 SC에 MLE 값을 적용한 실험으로 실험 1의 MLE 적용 후 채널 1은 0.0026, 채널 2는 0.029, 채널 3은 0.037로 BER이 감소하였다. 실험 2에서도 MLE 적용 후 채널 1은 0.044, 채널 2는 0.039, 채널 3은 0.037로 BER이 감소하였다. 이 실험을 통해 MLE 결정 값을 적용한 SC 기법이 단일 채널 전송에서도 효과적임을 확인하였다.

Table 3.

Image transmission performance with MLE value applied in experimental 1 and 2.

EXP	Channel 1	Channel 2	Channel 3
EXP1
	BER : 0.006	BER : 0.006	BER : 0.006
EXP2
	BER : 0.012	BER : 0.013	BER : 0.013

MLE-SC를 적용한 주파수 다이버시티 합성 이미지 전송성능은 Table 4에서 보는 바와 같다. 실험 1의 결과에서 최대 에너지를 가지는 신호를 선택하는 기법을 적용할 경우 실험 1과 실험 2의 BER은 0.091, 0.05로 확인되었으며, MLE-SC 미적용 시 BER은 0.022, 0.034로 확인되었다. MLE-SC 적용 후 실험 1의 BER은 0.006으로, 최대 에너지 선택 기법에 비해 15배, MLE-SC 미적용 시에 비해 3.6배의 성능향상을 보였다. MLE-SC 적용 후 실험 2의 BER은 0.012로, 최대 에너지 선택 기법에 비해 4.2배, MLE-SC 미적용 시에 비해 2.8배의 성능향상을 보였다.

Table 4.

Image transmission performance with MLE- SC in experimental 1 and 2.

EXP	Frequency diversity using max value	Frequency diversity without MLE-SC	Frequency diversity with MLE-SC
EXP1
	BER 0.091	BER : 0.022	BER : 0.006
EXP2
	BER : 0.05	BER : 0.034	BER : 0.012

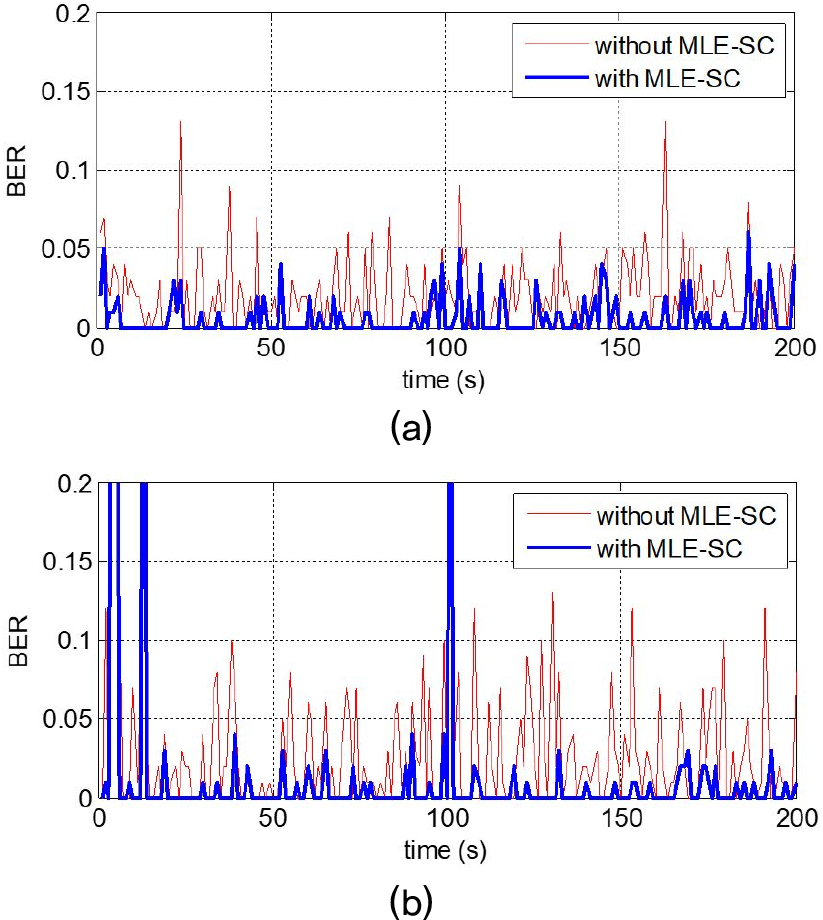
MLE-SC 미적용 시와 MLE-SC 적용 시 총 200 프레임에 대한 BER 변동 특성은 Fig. 10과 같다. Fig. 10(a)는 보호대역 1 kHz에 대한 실험 1이며, MLE-SC 적용 후 BER이 감소되는 것을 확인할 수 있다. Fig. 10(b)는 보호대역 0.5 kHz에 대한 실험 2이며, 실험 1에 비해 상대적으로 높은 BER 특성을 가진다. 프레임에 대한 BER 변동 특성에서도 MLE-SC 기법의 적용이 BER 감소에 효과적임을 확인하였다. 하지만 Fig. 10(b)의 높은 BER 가지는 3개의 프레임 구간에서는 MLE-SC 적용 후에도 오류 발생하였으며, 차후 분석을 통해 문제점을 분석할 계획이다.

Fig. 10.

(Color available online) BER per frame: (a) experiment 1 (guard band 1 kHz), (b) experiment 2 (guard band 0.5 kHz).

IV. 결 론

수중 다중경로 주파수 선택적 채널에서 MLE-SC 기법의 주파수 다이버시티의 성능을 평가하였다. 성능평가 결과 1 kHz의 보호대역을 가지는 주파수 다이버시티에 MLE-SC 적용 시 최대 에너지 선택 기법에 비해 15배, MLE-SC 미적용 시에 비해 3.6배의 성능향상을 보였다. 0.5 kHz의 보호대역에서는 MLE-SC 적용 후 최대 에너지 선택 기법에 비해 4.2배, MLE-SC 미적용 시에 비해 2.8배의 성능향상을 보였다.

수중 다중경로의 경계면 반사에 의해 형성되는 주파수 선택성은 수중 음향 통신에서 필연적으로 발생되는 성능감소 요인이다. 이러한 채널에서 MLE-SC를 적용한 주파수 다이버시티는 수중 음향 통신 성능을 향상시킬 수 있는 방법임을 확인하였다. 또한, 단일 센서를 적용한 수중 음향 통신에 효율적인 통신방법임을 확인하였다. 또한, 수중로봇 및 수중 무선 이동통신에서 시변적 변동 요인에 따른 무선 통신의 성능을 향상시킬 수 있을 것으로 기대한다.