I. 서 론

소나 탐지확률을 계산하기 위한 방법에는 결정론적 방법과 확률적 방법이 있다. 결정론적 방법은 수직 음속구조, 지음향 인자와 같은 해양환경 정보를 반영한 음파 전달 모델링을 통해 전달손실을 계산하고 Eq. (1)의 소나방정식을 통해 신호초과(Signal Excess, SE)를 산출한다.^[1,2]

Eq. (1)에서 SE_R은 잔향음 제한환경에서의 신호초과, SE_N은 소음 제한환경에서의 신호초과를 의미하며, SL은 음원 준위(Source Level), TL은 전달손실(Transmission Loss), RL은 잔향음 준위(Reverberation Level), NL은 소음 준위(Noise Level), TS는 표적 강도(Target Strength), DI 는 지향 지수(Directivity Index), DT는 탐지 문턱(Detection Threshold)을 의미한다. 기존의 결정론적 방법은 신호초과가 정규분포를 따른다고 가정하고 Eq. (2)을 통해 탐지확률, P_d를 계산한다.^[2]

여기서 𝜎는 수중음향 불확정성에 의한 신호초과의 표준편차를 의미한다. 기존의 결정론적 방법은 Eq. (2)의 𝜎에 8 dB ~ 9 dB의 고정된 상수를 대입하여 탐지확률을 계산한다.^[3] 하지만, 실험해역, 해양환경의 시․공간적 변동성에 따라 탐지성능이 변화하기 때문에 소나성능분석 결과의 오차가 발생할 가능성이 크다. 반면에, 확률적 방법은 해상실험을 통해 측정된 전달손실, 소음준위 자료의 확률밀도함수를 기반으로 수중음향 불확정성을 추정하여 예상탐지확률을 계산하는 방법이다.^[4,5,6]

본 연구에서는 Eq. (1)의 소나 방정식에서 SE_N을 고려하였으며, 표적에 의한 오차(표적 강도)와 소나 기계적 특성(음원 준위, 지향 지수, 탐지문턱)은 고려하지 않았기 때문에, 전달손실과 소음준위 합의 불확정성을 신호초과의 불확정성으로 가정하였다. 두 파라미터 측정 결과의 확률밀도함수를 반영한 몬테카를로 역변환 샘플링(Monte Carlo inverse transform sampling)^[7]을 수행하여 신호초과의 확률밀도함수를 모의하였다. 마지막으로 신호초과의 확률밀도함수에서 신호초과가 0 dB 이상인 구간에 대해 적분하여 예상탐지확률을 산출하였다.

본 논문의 구성은 다음과 같다. 제II장에서는 해상실험 및 환경에 대해 설명하고 제III장에서는 해상실험 데이터 기반의 수중음향 불확정성을 산출하였으며, 제IV장에서는 예상탐지확률 기반 탐지성능 분석에 대해 다룬다. 마지막으로 제V장에서는 본 연구의 결론 및 고찰에 대해 기술하였다.

II. 해상실험 및 환경

2020년 7월, 국방과학연구소 주관으로 동해 수심 50 m ~ 60 m의 천해환경에서 중주파수 전달손실 측정 실험이 수행되었다. 음원은 조사선에 의해 수심 약 25 m에서 예인되었으며, 송신 신호는 연속파(Continuous Wave, CW) 신호와 선형 주파수 변조(Linear Frequency Modulation, LFM) 신호가 사용되었으며, 송신된 신호는 해상에 계류되어 있는 수직 선배열에서 수신되었다. 수직 선배열은 13개의 수중청음기로 구성되었으며, 수심 약 9 m 부터 약 49 m 까지 약 3.3 m 간격으로 배치되었다. 조사선이 수직 선배열 위치로부터 멀어지는 구간에서는 중심주파수 3 kHz, 밴드폭 1 kHz, 신호 길이 1 s의 LFM 신호(T1), 수직 선배열 위치로 근접하는 구간에서는 주파수 2.3 kHz, 신호 길이 0.1 s의 CW 신호(T2)와 중심주파수 2.3 kHz, 밴드폭 1 kHz, 신호 길이 0.1 s의 LFM 신호(T3)가 20 s 간격으로 송․수신되었다(Fig. 1). 해양환경 정보를 반영한 고유음선 추적 결과를 통해 음파가 하향 굴절하는 환경이며, 해수면 보다 해저면과의 상호작용이 큰 환경임을 알 수 있었다.^[8]

Fig. 1.

(Color available online) Topographic map of the experimental site including ship track (black solid line) and the mooring location of VLA (black triangle).

III. 수중음향 불확정성 추정

수중음향 불확정성을 추정하기 위해 전달손실과 소음준위의 불확정성 산출이 수행되었다. 전달손실의 불확정성의 경우, Lee et al.^[8]의 전달손실 분석 결과를 바탕으로 산출되었다. Fig. 2(a)는 수직 선배열 중 수심 9 m, 26 m, 49 m에 위치한 3개 수신기에 수신된 신호(T1, T2, T3)의 거리에 따른 전달손실 측정 결과를 나타낸다. 3개 수심에서의 전달손실 측정 결과는 22.5log(r)+0.0033r과 16log(r)+0.0033r의 범위 내에서 나타났으며, 18.5log(r)+0.0033r의 회귀분석 결과를 나타냈다. 본 실험 환경은 음파의 하향굴절이 우세한 환경이었으나, 전달손실 분석 결과에서 수신기 수심에 따른 전달손실 경향의 차이는 확인하기 어려웠다. 또한 음원이 예인되면서 송․수신된 음향신호에 대해 전달손실 분석을 수행했기 때문에 본 논문에서는 3개 수신기 수심 및 송신기와 수직 선배열 간 거리에 따른 구분 없이 각 전달손실 측정값과 전달손실 측정값 기반 회귀분석 결과와의 에러를 확률밀도함수로 구성하여 전달손실의 불확정성으로 가정하였다. Fig. 2(b)는 측정된 전달손실의 확률밀도함수를 나타내고, 빨간색 실선은 Eq. (3)의 커널 밀도 추정(Kernel Density Estimation, KDE) 방법^[9]을 통해 피팅된 전달손실의 불확정성을 나타낸다.

여기서 n은 데이터의 개수로 총 558개이며, h는 커널 함수의 밴드폭 파라미터이며, 1.06σn-1/5으로 적용되었다.^[9] Eq. (4)의 K(u)는 정규분포 형태의 커널 함수를 나타낸다.

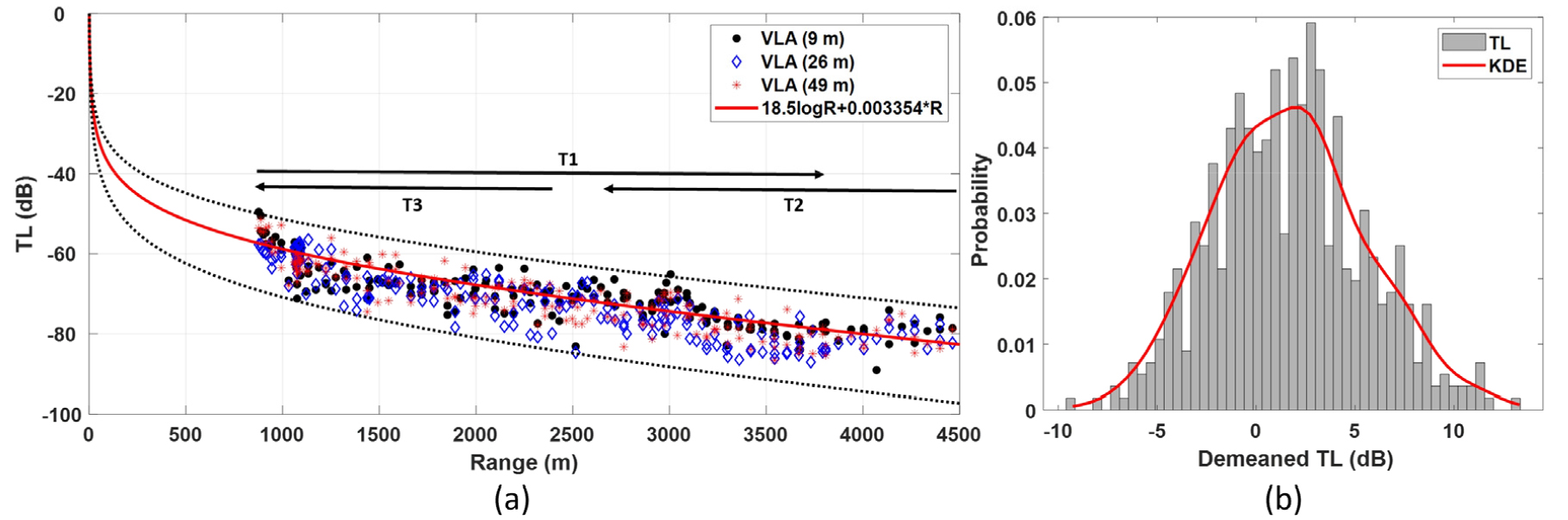
Fig. 2.

(Color available online) (a) Comparison of TL measurements versus range (T1, T2, T3) and regression curve (red solid line). The black circles, blue diamonds, and red stars show the individual measured TL at the water depths of 9 m, 26 m, 49 m, respectively. The upper black dashed line represents 16log(r)+0.0033r, while the lower one represents 22.5log(r)+0.0033r. Black arrows shows the direction of movement of the sound source. (b) The histogram of demeaned TL. Red solid line indicates the kernel density estimation result.

소음준위의 경우, 배경소음만 존재하는 구간에서 측정된 연속적인 1 s 길이의 음향 신호를 추출하여 파워 스펙트럼 밀도 분석을 수행한 후, 가장 근접한 시간에 해당하는 송신 신호의 중심주파수를 기준으로 1 kHz의 밴드폭을 고려한 소음준위가 산출되었다. Fig. 3(a)는 수심 26 m에 위치한 수신기에 측정된 소음준위 결과를 나타내며, 파란색 점은 배경소음만 존재하는 구간에서 측정된 소음준위를 나타낸다. 데이터 개수는 6,000개로 충분하였기 때문에 수심 26 m에서 측정된 자료만 사용되었다. Fig. 3(b)는 추출된 소음준위의 확률밀도함수를 나타내고, 빨간색 실선은 KDE를 통해 추정된 소음준위의 불확정성 분포를 나타낸다.

Fig. 3.

(Color available online) (a) Noise level measurements versus range. Blue circles show the individual measured ambient NL at the water depths of 26 m while the black solid line represents the noise level measurements during the experiment. (b) The histogram of demeaned noise level. Red solid line indicates the kernel density estimation result.

전달손실과 소음준위의 불확정성을 기반으로 신호초과의 불확정성을 모의하기 위해 전달손실과 소음준위의 확률밀도함수를 누적분포함수로 변환하였다. 전달손실 측정 결과의 경우, 단방향 결과이기 때문에, 전달손실 측정값의 2배를 하여 누적분포함수로 변환되었다. 두 파라미터의 누적분포함수를 기반으로 각각의 몬테카를로 역변환 샘플링을 결과를 합하여 신호초과를 모의하였으며, 이 샘플링 과정은 2,000번 반복하여 전달손실과 소음준위의 불확정성을 반영한 신호초과를 모의하였다(Fig. 4). 모의된 신호초과 불확정성은 정규분포에 가까운 형태를 나타냈으며, 표준편차는 약 8.9 dB로 나타났다. 마지막으로, 신호초과의 확률밀도함수에서 신호초과의 크기가 0 dB 이상인 구간에 대하여 적분하여 예상탐지확률을 구하였다.

Fig. 4.

(Color available online) Example of Monte Carlo inverse transform sampling for simulating ASE based on the probability distribution of two-way TL and NL.

IV. 예상탐지확률 모의

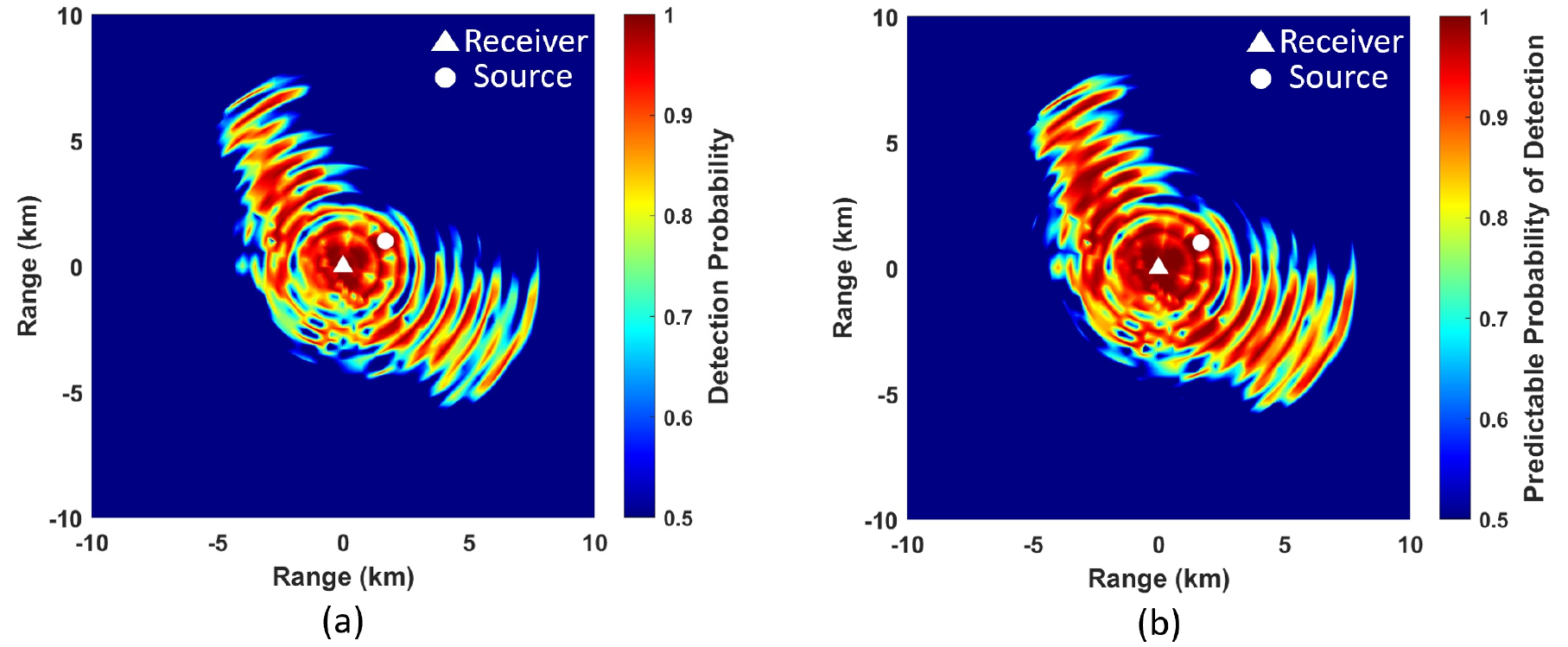
확률적 방법을 기반으로 소나 탐지성능 분석을 수행하기 위해 국방과학연구소와 한양대학교가 공동으로 개발한 Bistatic Sonar Performance Analysis System (BiSPAS) 모델이 사용되었다.^[10,11] BiSPAS는 음선이론 기반의 소나 성능분석 모델이며, 거리 종속의 해양환경 정보와 소나 파라미터 정보, 표적 정보를 반영할 수 있다. Fig. 5는 Fig. 1의 해상실험 환경에서 결정론적 방법으로 모의한 탐지성능 분석 결과와 확률론적 방법으로 모의한 예상탐지확률 분석 결과를 나타낸다. 중심주파수는 3 kHz, 밴드폭은 1 kHz, 음원준위는 205 dB, 신호길이는 1 s로 설정되었으며, 송․수신기간의 거리는 2 km, 송신기 수심은 25 m, 수신기 수심은 9 m, 표적 수심은 25 m, 표적 강도는 6 dB로 설정되었다. 결정론적 방법에서 신호초과의 수중음향 불확정성의 표준편차는 9 dB로 고려되었다.

Fig. 5.

(Color available online) (a) Predicted detection probability in experimental site and (b) their predictable probability detection(source depth: 25 m, receiver depth 25 m, target depth : 25 m, source to receiver range : 2 km).

해상실험 환경에서 음파는 하향 굴절이 우세한 환경이기 때문에 탐지확률이 띠의 형태로 반복되며 나타났다(Fig. 5). 수신기 위치를 기준으로 북동쪽 방향으로 거리가 증가할수록 수심이 깊어지는 형태의 해저지형이기 때문에 음파가 표적수심 보다 깊은 수심에서 전파된다. 반면에 수신기 위치에서 남서쪽 방 향으로 거리가 증가할수록 수심이 얕아지는 해저지형으로 인해 해저면 반사, 산란 등에 영향으로 탐지성능이 제한되었다. 실험해역에서 전달손실, 소음준위 측정값을 기반으로 추정된 수중음향 불확정성의 분포는 표준편차 약 8.9 dB를 가지는 정규분포에 가까운 형태로 나타났기 때문에 기존의 결정론적 탐지성능 예측 결과와 확률적 기반의 예상탐지확률 결과의 탐지영역 차이는 거의 없는 것으로 확인되었다(Fig. 5). 하지만, 신호초과 불확정성 분포의 중심이 0 dB를 기준으로 오른쪽으로 치우친 형태가 반영되어 신호초과가 0 dB 이상인 영역에서 결정론적 탐지확률결과보다 예상탐지확률이 높게 나타났다.

본 논문에서는 신호초과의 불확정성이 정규분포가 아닌 경우에 탐지확률 결과가 어떻게 나타나는지 추가로 확인하였다. 추가로 고려된 신호초과의 불확정성 분포는 최빈값이 0이 아니며 비대칭적인 확률분포를 가정하였으며, 최빈값이 0보다 작은 레일리 분포와 0보다 큰 음으로 치우친 분포가 고려되었다. Fig. 6은 신호초과의 불확정성의 분포를 레일리 분포, 음으로 치우친 분포와 각 분포가 고려된 예상탐지확률 결과를 나타낸다. 레일리 분포의 경우, 신호초과가 0 dB일 때, 불확정성 분포의 최빈값이 –5 dB가 되는 형태로 모의하였다. 불확정성 분포의 최빈값이 신호초과 0 dB 보다 큰 경우, 결정론적 탐지확률 결과보다 예상탐지확률이 크게 예측되었으며 반대로 최빈값이 0 dB 보다 작은 경우, 결정론적 탐지확률 결과보다 예상탐지확률이 작게 나타났다. 반면에 음으로 치우친 분포의 경우, 신호초과가 0 dB일 때, 불확정성 분포의 최빈값이 5 dB가 되는 형태로 모의하였다. 불확정성의 분포가 신호초과 0 dB 이상인 구간에 집중되었기 때문에 불확정성 분포의 최빈값이 0 dB 보다 큰 경우, 전체적으로 예상탐지확률이 결정론적 탐지확률 결과와 해상실험 데이터 기반의 보다 높게 나타나는 것이 확인되었다. 반대로 최빈값이 0 dB 보다 작은 경우에는 결정론적 탐지확률 결과보다 예상탐지확률이 작게 나타났다.

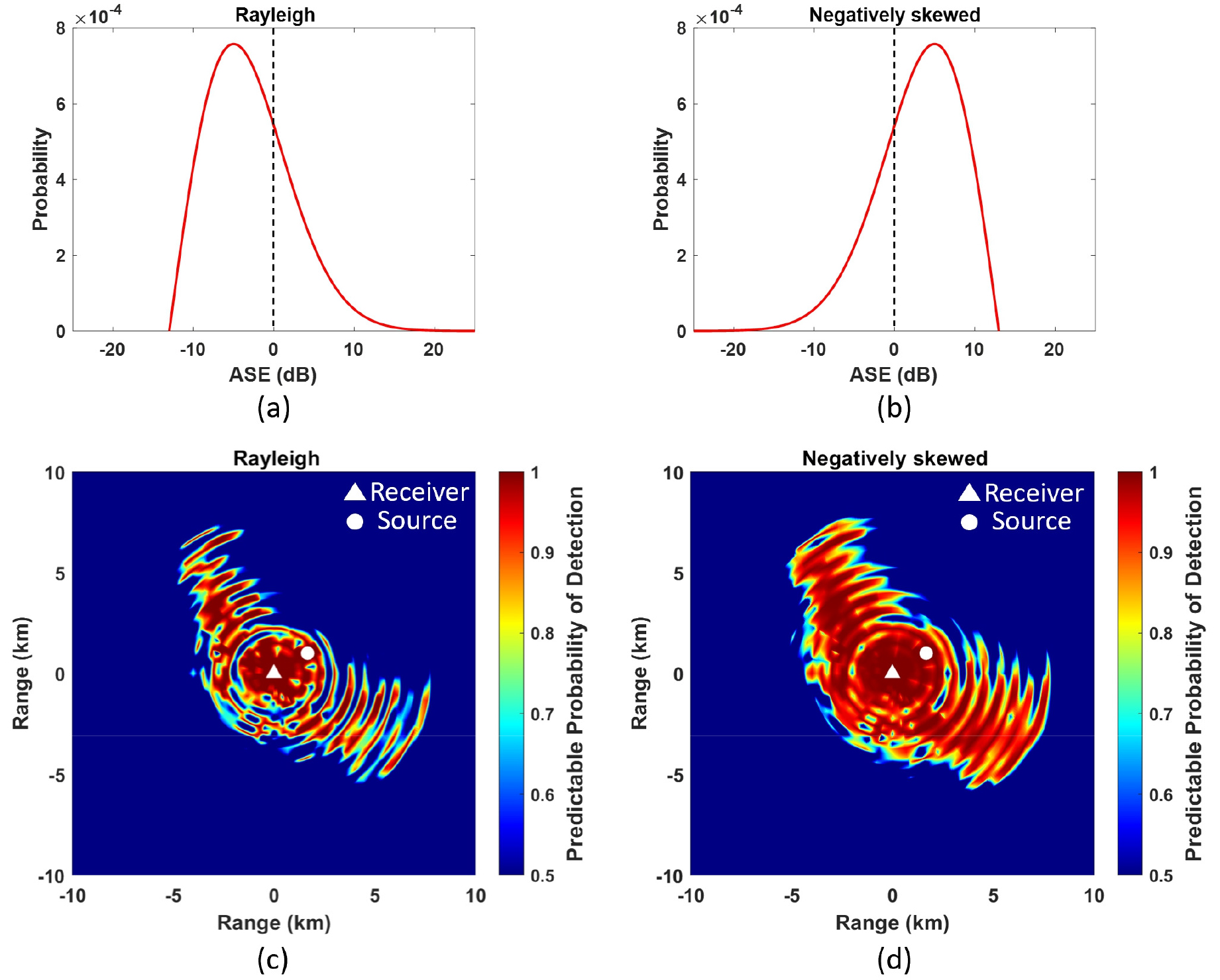
Fig. 6.

(Color available online) (a) Simulated Rayleigh distribution and (b) negatively skewed distribution. The predictive detection probability considering the (c) Rayleigh distribution and (d) negatively skewed distribution for underwater acoustic uncertainty (source depth: 25 m, receiver depth: 25 m, target depth : 25 m, source to receiver range : 2 km).

V. 요약 및 결론

선행연구에서는 실험값을 기반으로 수중음향 불확정성을 산출하였으나, 그 결과가 소나 성능분석 모델에 반영된 바 없다. 본 논문에서는 동해 해역에서 측정된 중주파수 전달손실과 소음준위 자료를 기반으로 수중음향 불확정성을 산출하고, 이를 소나 탐지성능 분석 모델에 반영하여 탐지성능 예측을 수행하였다. 결론적으로 해상실험 데이터 기반으로 추정된 신호초과의 불확정성은 표준편차 8.9 dB의 정규분포의 형태로 나타났기 때문에, 결정론적 방법의 결과와 큰 성능의 차이를 보이지 않았다. 하지만 추정된 불확정성의 분포가 정규분포가 아닌 경우에는 기존의 결정론적 방법의 탐지확률 결과와 탐지영역, 탐지확률의 결과의 차이가 발생하기 때문에 예상탐지확률 결과 기반의 탐지성능 분석이 수행되어야 할 것으로 판단된다.

본 논문에서는 조사선이 이동하면서 송․수신된 신호에 대해 분석했기 때문에 수중음향 불확정성의 송․수신기 거리에 따른 종속성은 고려되지 않았다. 그러나 수중음향 불확정성의 송․수신기 거리에 따른 종속성을 반영하기 위해서는 고정된 송․수신기 위치에서 수십 개 이상의 핑 신호를 반복 송․수신해야 하며, 이를 다양한 거리, 위치에서 반복 수행해야 한다. 또한 소나 파라미터 중에 기계적 특성과 표적에 의한 오차에 영향을 받는 파라미터의 불확정성과 잔향음의 불확정성이 고려되지 않았다. 따라서 본 논문의 방법을 수중음향 불확정성을 고려한 탐지성능 모델링 방법으로 일반화하기는 어려울 것으로 판단된다. 잔향음 제한환경에서 수중음향 불확정성을 고려한 탐지성능을 예측하기 위해서는 잔향음의 수중음향 불확정성을 고려하기 위한 추가 연구가 필요하다. 복잡한 해양환경 변동성을 고려한 수중음향 불확정성을 추정하고 이를 탐지성능 모델링에 반영하기 위해서는 다양한 해양환경 조건에서의 음향 실험 및 해양환경정보 측정을 통한 검증연구가 수행되어야 한다.