I. 서 론

수중방사소음이란 해양무기체계에서 수중으로 방사되는 소음으로써, 기계류 소음과 추진기 소음, 유체소음 등이 포함되어 있으며, 수동소나의 탐지대상이 된다. 수중방사소음을 저감하여 피탐 확률을 낮추어야 해양무기체계의 생존성을 높일 수 있으므로 수중방사소음의 측정과 분석이 중요하다. 수상함의 수중방사소음의 측정 방법은 이미 많은 연구가 이루어져 표준으로 정립되었다.^[1] 이를 바탕으로 해양환경에 소음이 미치는 영향을 줄이기 위하여 해양무기체계 뿐만 아니라 일반 상선의 수중방사소음을 대상으로 하는 연구 또한 널리 진행되고 있다. Grelowska et al.^[2]은 천해에 소형 선박에서 발생하는 수중방사소음을 분석하여 100 Hz 이하 주파수대역에서 추진기와 기계류 성분이 주요소음원임을 확인하였다. Arveson과 Vendittis^[3]은 대형 화물선에서 발생하는 수중방사소음을 분석하였는데 방사소음의 지향성에 관심을 갖고 연구하였다. Brooker와 Humphrey^[4]은 연구용 선박의 수중방사소음을 측정 및 분석하여 속력별 방사소음 수준을 비교하였다.

수중방사소음은 해수를 통하여 전파되므로 거리 감쇠, 투과손실, 굴절, 표면간섭 등에 의해 음향신호의 전달에 영향을 받게 된다. 또한, 매질인 해수의 온도, 해류, 배경소음과 같은 해양환경의 특성과 파고, 수심, 해저지질의 종류 등 경계조건 등이 고려되어야 수중방사소음을 측정하고 분석할 수 있다. 고려되어야 하는 환경의 영향 중 하나로써 해수면에 의한 표면간섭 현상인 로이드 미러 효과는 Ainslie,^[5] Ross,^[6] Kinsler et al.^[7]의 저서를 통해 알려져 있다. Audoly와 Meyer^[8]은 로이드 미러 효과의 수학적 모델을 비교하여 수중방사소음 측정에 영향을 미치고 있음을 밝혔고, Kapolka^[9]는 천해에서 음파 전달 경로 2개가 형성되어 로이드 미러 효과가 나타날 때 Closet Point of Approach(CPA) 거리를 추정할 수 있음을 확인하였다. 로이드 미러 효과는 본 연구의 대상인 수중운동체의 수중방사소음 측정에도 영향을 미칠 것으로 추정된다.

본 연구에서는 소형의 해양무기체계 중 하나인 수중운동체가 수중에서 기동하는 동안 발생하는 수중방사소음을 측정하고, 수중운동체의 수중방사소음 측정결과에 나타나는 로이드 미러 효과의 영향을 확인하고자 한다. 이를 위하여 수중운동체의 수중방사소음 측정결과와 이론식으로부터 예측한 로이드 미러 패턴을 비교하고, CPA 거리를 추정하며, 로이드 미러 효과로 인한 음향신호의 음원준위 변동이 방사소음에 미치는 영향을 분석하였다.

II. 수중방사소음 측정

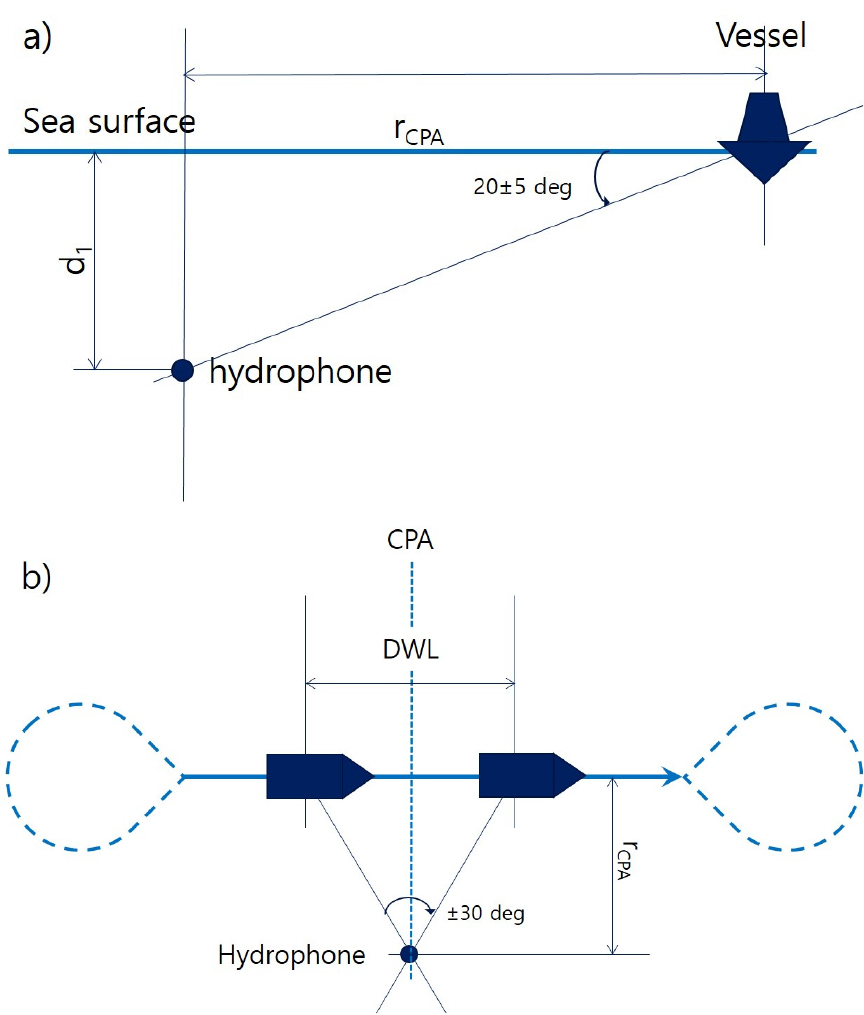
수중운동체의 수중방사소음 측정 시험 구성은 ANSI/ASA S12.64-2009/Part.1^[1] 수중방사소음 측정 절차에 관한 표준을 참고하였다. S12.64는 수상함에서 발생하여 수중으로 방사되는 소음을 측정 및 분석하는 방법에 대한 표준이다. Fig. 1a)에 도시한 것과 같이 Grade C에서는 1개의 하이드로폰을 측정대상과의 각도가 각각 20 ± 5°를 이루는 심도에 설치한다. 하이드로폰을 중심으로 최근접점 거리인 r_cpa는 100 m 이상 또는 전장 이상으로 유지하면서 Fig. 1b)와 같은 S자 기동을 수행하여 4회 이상 반복 측정한다. 각 하이드로폰에서 측정한 음원 준위를 CPA ± 30°에 해당하는 구간(Data Windowing Length, DWL)에 대해 분석한다. 센서 감도를 보정하고 1m 거리로 환산한 하이드로폰 신호의 4회 이상 측정 결과를 산술평균하여 1/3 옥타브 밴드로 평가한다.

Fig. 1.

(Color available online) Diagrams for measurement of underwater radiated noise a) hydrophone geometry b) test approach according to ANSI/ASA S12.64-2009.

본 연구에서는 Grade C 수준으로 수중운동체의 기동 특성을 고려하여 시험 방법을 Fig. 2와 같이 구성하였다. 시험해역은 수심 1,500 m 이상인 곳으로 선정하여 해저면 반사에 의한 영향을 피하였다. 해상 시험 수행을 위한 측정지원선의 선미에서 하이드로폰 1개를 심도 20 m에 설치하였고, 수중운동체는 심도 30 m에서 기동하여 하이드로폰 하부를 지나가도록 하였다. 수중에서 기동하기 때문에 수중운동체의 정확한 위치는 확인이 불가능하므로 음향신호를 활용하여 CPA 거리를 추정하였다. 본 연구에서는 수중운동체의 소음수준을 평가하기 위한 목적이 아니므로 1회 측정 결과를 대상으로 분석하였다. 측정 시 해상상태는 SeaState 2 수준이었다.

Fig. 2.

(Color available online) Configuration for the measurement of underwater radiated noise of an underwater vehicle.

한편, S12.64는 하이드로폰에서 얻은 음향 신호를 DWL을 통과하는 동안의 시간 길이인 Data Window Period(DWP)만큼 평균하고, 1 m 거리에서의 음압으로 환산하여 1/3 옥타브 밴드 음압 레벨로 측정결과를 나타낸다. 이 과정을 통해 시간적 변동이나 거리에 의한 효과들이 상쇄되므로 S12.64에서는 로이드 미러 효과를 별도로 고려하지 않는다. 하지만 수중방사소음 신호는 음원에 대한 다양한 정보를 포함하고 있기 때문에 스펙트럼 분석, Low Frequency Analyzing and Recording(LOFAR) 분석 등의 옥타브 레벨 평가 이외의 다른 분석 기법에서는 해수면에 의해 로이드 미러 효과가 나타난다면 음향신호가 왜곡될 수 있고 결과 분석에 영향을 주게 된다. 그러므로 수중운동체의 수중방사소음 신호 분석 시 로이드 미러 효과가 나타나는지 확인할 필요가 있다.

III. 로이드 미러 효과 이론

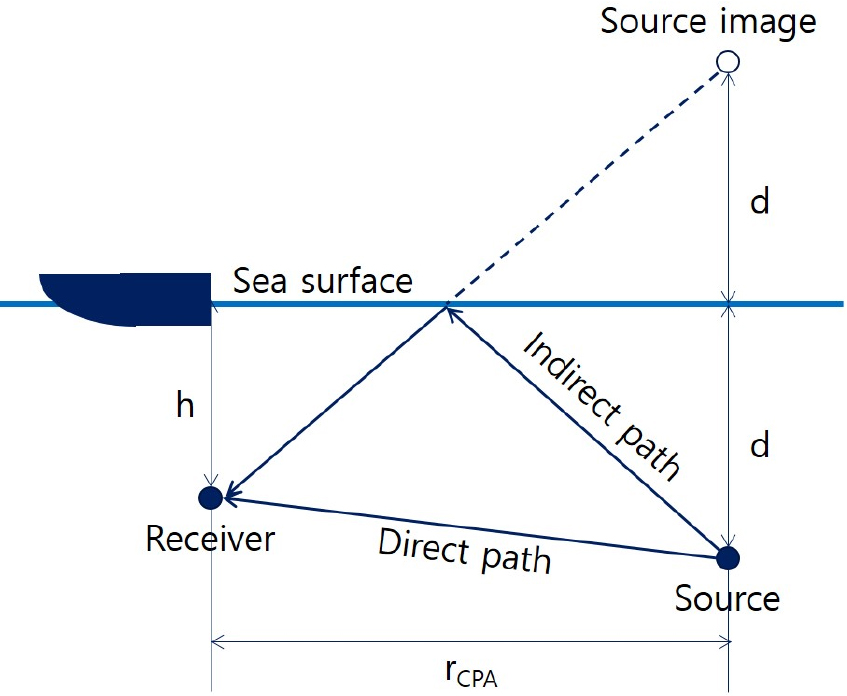
로이드 미러 효과는 표면에 의한 간섭효과로, 해수면이 아주 잔잔할 때 마치 거울역할을 하게 되어 음파가 전달되는 경로차를 형성하여 발생한다. 서로 다른 경로로 하이드로폰에 도달한 음파는 해수면 위 같은 거리의 반대위상을 가진 가상의 음원에서 방사되는 음파가 존재하듯이 거동하게 된다. 직접경로와 간접경로 간의 경로 차에 따라 위상차가 발생하고 서로 보강-상쇄 간섭이 반복적으로 일어난 결과로 간섭 패턴이 나타난다.

음원의 수심을 d, 하이드로폰의 수심을 h, 음원과 하이드로폰 간의 수평거리를 r, 파수를 k, 음원에서 1 m 떨어진 거리에서의 음압진폭을 A라고 할 때, 음압 P는

과 같다.^[9] 로이드 미러 효과로 인한 로이드 미러 간섭 패턴은 다음과 같이 나타난다.^[7]

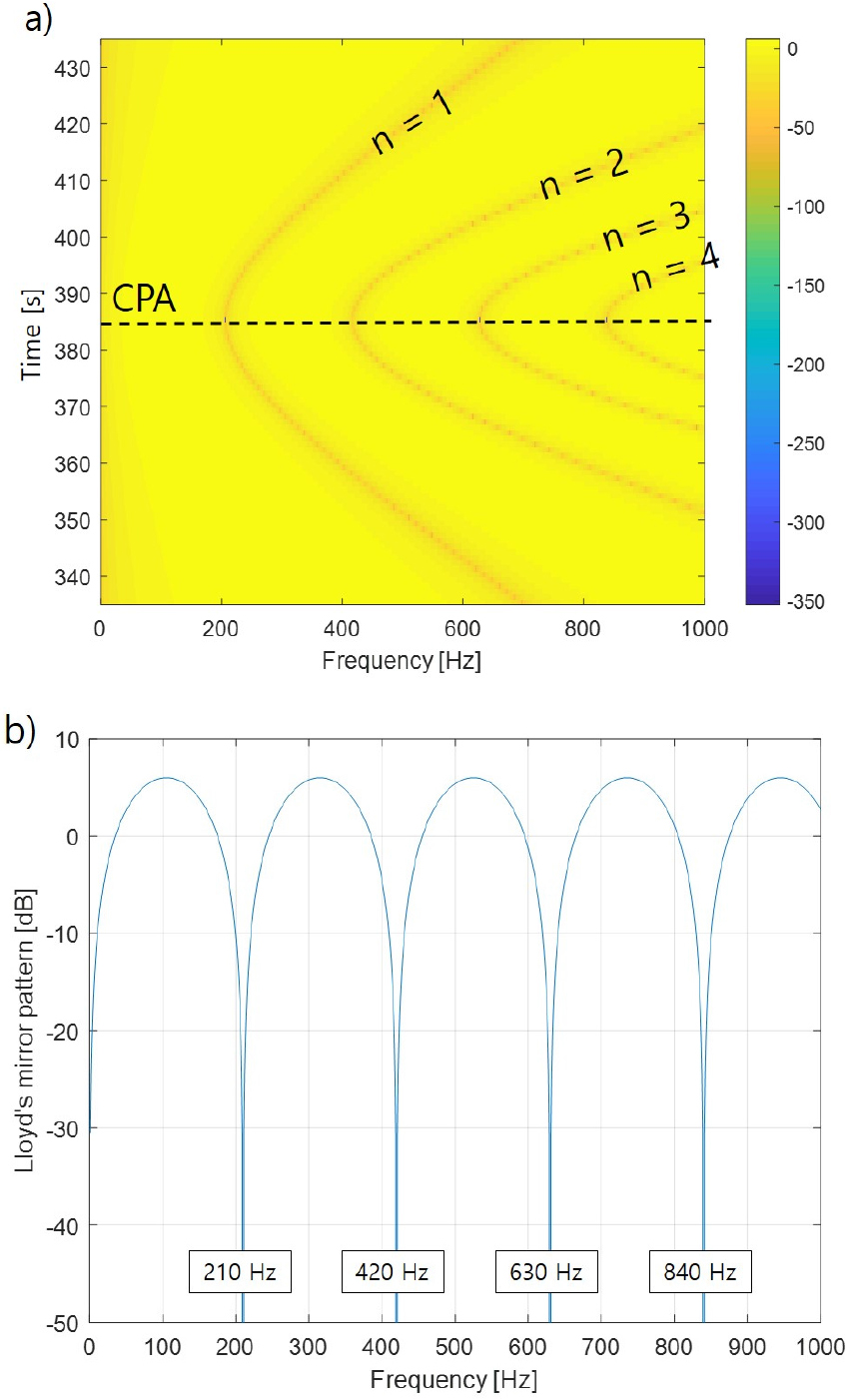
0≤k≤4.2,d=30m,h=20m,r=168m일 때 , Eq. (2)에 따른 로이드 미러 패턴은 Fig. 3과 같다. Fig. 3a)에서 로이드 미러 패턴은 시간에 따라 여러 포물선이 차례로 쌓인 듯한 형태로 나타나는데, 포물선의 대칭축에 해당하는 시점이 CPA를 통과하는 시점이고, CPA 시점의 로이드 미러 패턴은 Fig. 3b)와 같이 나타난다. 이론적인 값이기 때문에 보강간섭이 강하게 나타난다.

Fig. 3.

(Color available online) Theoretical Lloyd’s mirror interference pattern (d=30m,h=20m,r=168m) a) during 100 s and b) at CPA point.

CPA 시점에 나타난 포물선의 꼭짓점에 해당하는 주파수는 Eq. (3)와 같다.^[9]

여기서 n은 포물선의 순서이고 c는 음속(1,500 m/s)이고 r은 거리이다. Eq. (3)에 의하여 로이드 미러 패턴을 이용하여 CPA 거리를 추정할 수 있다. 또한, Eq. (3)으로부터 거리가 멀수록 로이드 미러 패턴은 고주파수에서 나타나고, 측정대상과 하이드로폰 심도가 깊을수록 저주파수에서 나타난다는 것을 알 수 있다. 즉, 로이드 미러 효과는 CPA 거리를 가깝게 설정할수록, 심도가 깊은 곳에서 기동할수록 낮은 주파수에서 나타나게 된다. 수중운동체의 수중방사소음을 분석할 때 기계류 토널 성분이나 추진기 성분이 주로 나타나는 관심 주파수대역(1 kHz 이하)에서 로이드 미러 효과의 영향을 받을 가능성이 있음을 추측할 수 있다.

IV. 수중방사소음 측정결과 분석

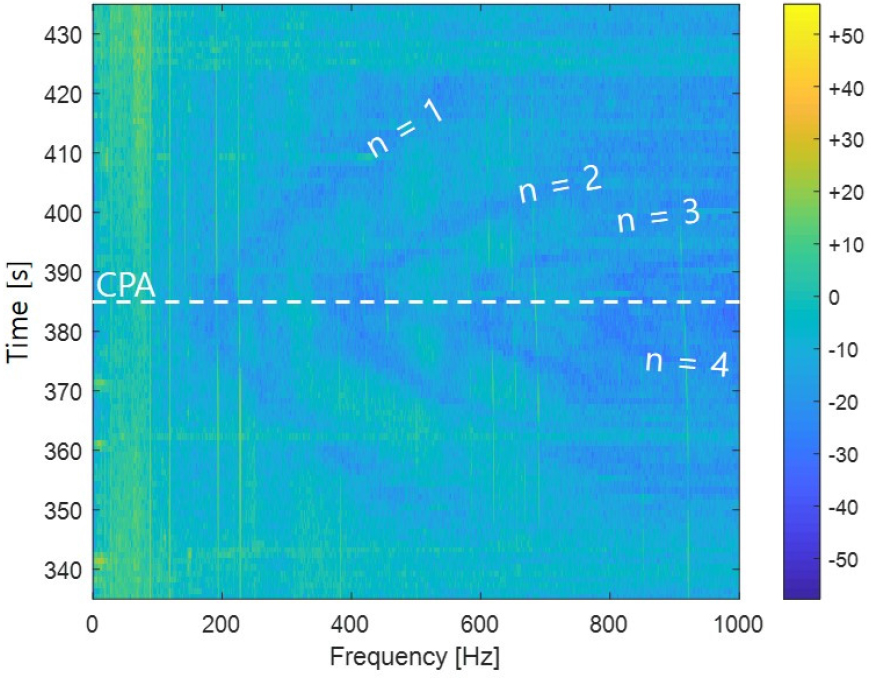
Fig. 4의 스펙트로그램은 수중운동체의 방사소음 측정결과를 나타낸 것이다. 이론식을 통해 구한 것과 같은 로이드 미러 효과에 의한 포물선 형태의 간섭 패턴이 확인된다. 그러나 이론적으로 구한 로이드 미러 패턴의 골은 아주 작은 값으로 나타나고 형상 또한 매우 날카로운 반면 측정 결과에서는 상대적으로 넓은 대역의 음영으로 확인되어 스펙트로그램 상 포물선의 초점을 정확하게 판단하기 어렵다.

Fig. 4.

(Color available online) Spectrogram of underwater radiated noise for an underwater vehicle.

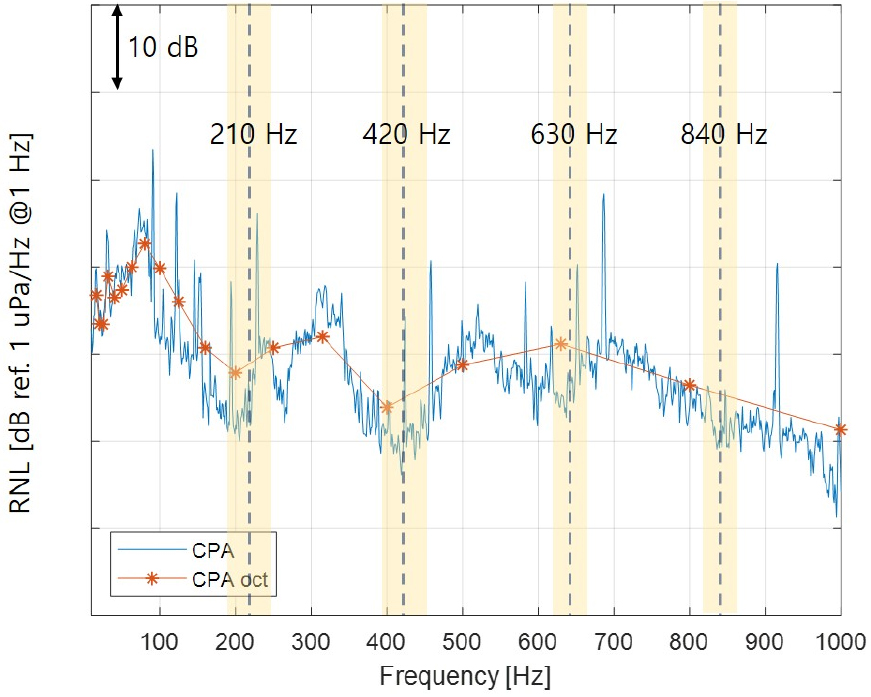
첫 번째 포물선 꼭짓점의 주파수를 판단하기 위하여 CPA 시점에서 7 s 간 평균한 스펙트럼을 Fig. 5에 나타내었다. 수중방사소음 신호에는 토널 성분, 광대역 성분 등의 소음 성분과 배경소음이 함께 나타나므로 하나의 최소 주파수가 아니라 광대역 변동으로 로이드 미러 효과를 확인할 수 있다. 1 Hz 밴드 스펙트럼 레벨의 광대역 변동이 나타나기 때문에 1/3 옥타브밴드 레벨도 Fig. 4에서 확인하였듯이 1 kHz 이하에 4개의 포물선이 나타나고 각각의 초점의 주파수는 약 210 Hz, 420 Hz, 630 Hz, 840 Hz이다. Eq. (3)에 대입하면 수중운동체의 CPA 거리는 168 m으로 추정할 수 있다.

Fig. 5.

(Color available online) Spectrum level of an underwater vehicle at CPA.

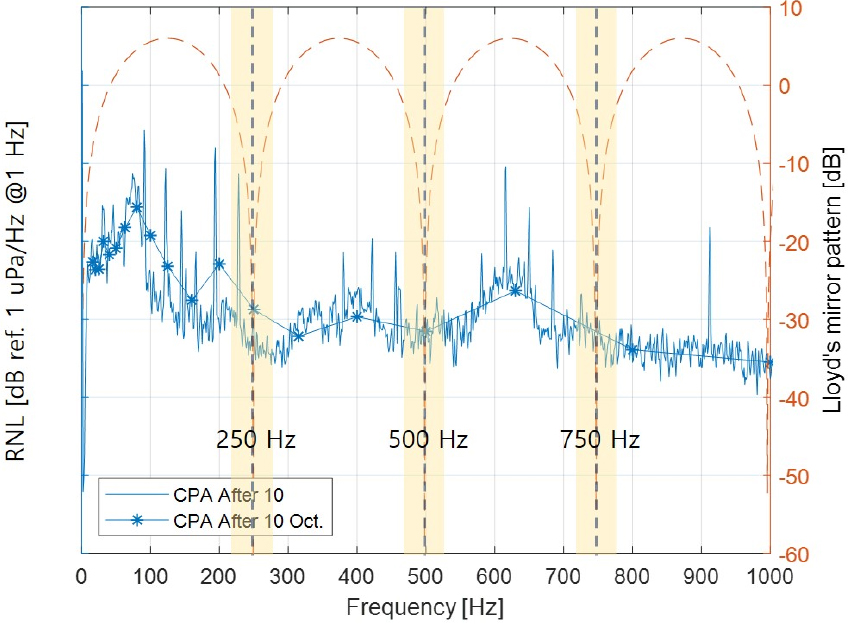
로이드 미러 효과가 수중방사소음 측정 결과에 어떤 영향을 주고 있는지 비교하기 위하여 CPA 시점과 CPA 통과 후의 방사소음 수준을 비교하였다. 본 연구를 위한 측정 설계에 따른 DWP는 18 s이고, 수중운동체의 주요 소음원이 추진부일 것으로 가정한다면 CPA통과 전에 비해 통과후의 소음수준이 높을 것으로 예상되므로 CPA 통과 후 10 s 후의 이론적 로이드 미러 패턴과 스펙트럼 레벨을 확인하기 위하여 Fig. 6에 나타내었다. 시간이 증가한 만큼 수중운동체가 이동하여 하이드로폰과 수중운동체 간 거리가 증가하였고, 이로 인해 로이드 미러 패턴의 골에 해당하는 주파수가 상승하였다. 로이드 미러 패턴의 변화에 따라 Fig. 6의 스펙트럼 레벨의 변동이 나타나는 주파수 대역 또한 상승한 것을 확인할 수 있다. 스펙트럼 레벨 변동의 변화로 인해 옥타브 밴드 레벨의 경향이 변화하였는데, Fig. 5의 200 Hz 밴드는 골에 해당하였으나 Fig. 6 의 200 Hz 밴드는 피크에 해당하는 것으로 변화하였다. 400 Hz 밴드를 비교하여도 로이드 미러 효과로 인해 경향이 변화하였음을 알 수 있다.

Fig. 6.

(Color available online) Comparison results at 10 s after CPA of theoretical Lloyd’s mirror interference pattern and spectrum level.

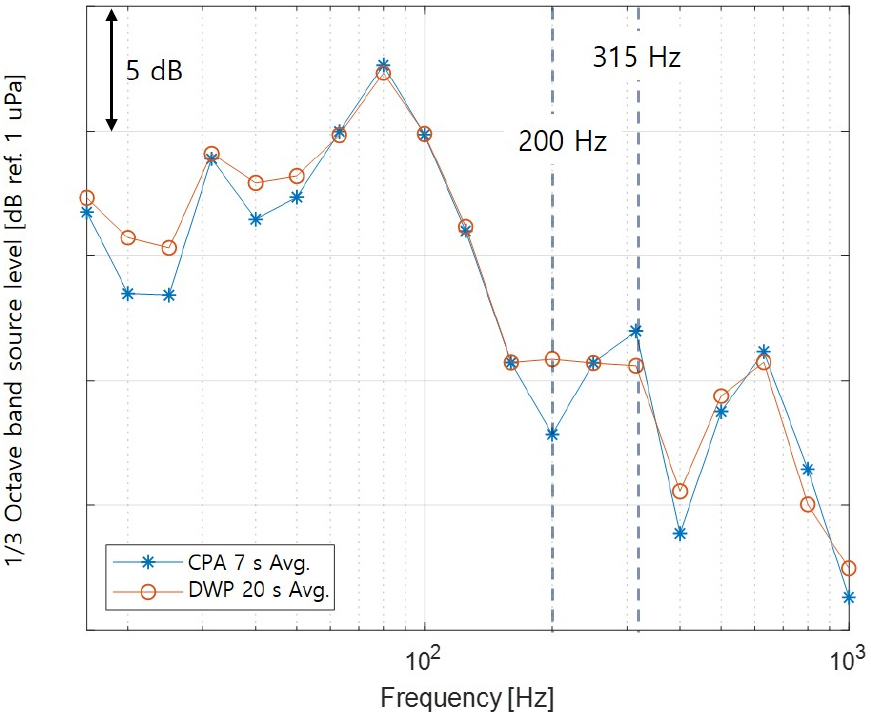
수중방사소음 레벨에 나타나는 로이드 미러 효과의 영향을 확인하기 위하여 로이드 미러 패턴으로 인한 레벨 변동이 상쇄되는 DWP를 포함하는 20 s 간 평균한 방사소음 수준과 CPA 통과 시점의 7 s 간 평균한 방사소음 수준을 Fig. 7에 비교하여 나타내었다. DWP 평균은 CPA 7 s 평균에 비하여 1/3 옥타브 밴드로 나타낸 결과에서도 피크와 골의 변동이 저감되거나 사라지는 것이 확인된다. 즉, DWP 구간을 평균함으로써 주파수에 따른 방사소음 레벨의 변동 폭이 감소하는 것을 알 수 있다. 이로부터 DWP 구간을 평균하지 않고 수중방사소음을 분석하는 경우에는 로이드 미러 효과로 인한 음압 레벨의 변동을 고려해야 할 필요가 있다.

Fig. 7.

(Color available online) Comparison of an 7 s average at CPA and an 20 s (DWP) average.

V. 결 론

본 연구에서는 수중운동체의 수중방사소음 측정 결과에 나타나는 해수면에 의한 로이드 미러 효과를 확인하였다. 이론적으로 알려진 로이드 미러 패턴을 구하여 예측하였고, 수중방사소음 측정결과와 비교하였다. 그 결과, 이론과 측정에서 로이드 미러 효과에 의한 스펙트럼 변동이 일치하였다. 또한, 측정결과에서 확인된 로이드 미러 패턴으로부터 수중운동체의 CPA 거리를 예측하였다. 로이드 미러 효과는 수중방사소음 측정결과의 협대역 스펙트럼에도 변동이 나타나게 하고, 광대역 스펙트럼에도 영향을 준다. 그러므로 방사소음 측정결과 분석 시 로이드 미러 효과에 의한 영향을 고려할 수 있도록 로이드 미러 효과의 실용적인 보정 방법에 대한 연구가 앞으로 더 필요하다.