A study on the active sonar reverberation suppression method based on non-negative matrix factorization with beta-divergence function

Seokjin Lee; Geunhwan Kim

doi:10.7776/ASK.2024.43.4.369

Preview

Research Article

The Journal of the Acoustical Society of Korea. 31 July 2024. 369-382
https://doi.org/10.7776/ASK.2024.43.4.369

A study on the active sonar reverberation suppression method based on non-negative matrix factorization with beta-divergence function

베타-발산 함수를 활용한 비음수 행렬 분해 기반의 능동 소나 잔향 제거 기법에 대한 연구

Seokjin Lee¹²

Geunhwan Kim ³^*

이 석진¹²

김 근환³^*

¹경북대학교 전자공학부

²경북대학교 전자전기공학부

³세종대학교 해양시스템융합공학과

^{*Corresponding Author}

License (open-access, http://creativecommons.org/licenses/by-nc/4.0/):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

To suppress the reverberation in the active sonar system, the non-negative matrix factorization-based reverberation suppression methods have been researched recently. An estimation loss function, which makes the multiplication of basis matrices same as the input signals, has to be considered to design the non-negative matrix factorization methods, but the conventional method simply chooses the Kullback-Leibler divergence as the loss function without any considerations. In this paper, we examined that the Kullback-Leibler divergence is the best loss function or there is the other loss function enhancing the performance. First, we derived a modified reverberation suppression algorithm using the generalized beta-divergence function, which includes the Kullback-Leibler divergence. Then, we performed Monte-Carlo simulations using synthesized reverberation for the modified reverberation suppression method. The results showed that the Kullback-Leibler divergence function (β = 1) has good performances in the high signal-to-reverberation environments, but the intermediate function (β = 1.25) between Kullback-Leibler divergence and Euclidean distance has better performance in the low signal-to-reverberation environments.

Keywords

Reverberation suppression

Non-negative matrix factorization

Loss function

Beta-divergence

능동 소나 시스템에서 잔향을 제거하기 위하여 최근 비음수 행렬 분해 기법을 활용한 잔향 제거 알고리즘이 고안된 바 있다. 비음수 행렬 분해 알고리즘을 설계하기 위해서는 분해된 기저 행렬의 곱이 원본 신호와 같도록 유도하는 추정 비용 함수가 필요한데, 기존의 연구에서는 이에 대한 고찰이 없이 쿨백-라이블러 발산 함수를 활용하였다. 본 논문에서는 쿨백-라이블러 발산 함수의 선택이 좋은 선택이었는지, 혹은 성능을 개선할 수 있는 다른 추정 비용 함수가 있는지 연구하고자 하였다. 이를 위하여, 먼저 쿨백-라이블러 함수를 포함하여 일반화된 베타-발산 함수를 활용하여 수정된 잔향 제거 알고리즘을 제안하였다. 그리고 수정된 잔향 제거 알고리즘에 대해 합성된 잔향 신호를 활용한 몬테-카를로 시뮬레이션을 수행하였다. 그 결과 높은 신호대잔향비 환경에서는 쿨백-라이블러 발산 함수(β = 1)가 좋은 성능을 보이지만, 낮은 신호대잔향비 환경에서는 쿨백-라이블러 발산 함수와 유클리드 거리의 중간 특성을 가지는 함수(β = 1.25)가 더 좋은 성능을 보이는 것을 확인하였다.

키워드

잔향 제거

비음수 행렬 분해

비용 함수

베타-발산

MAIN

I. 서 론
II. 비음수 행렬 분해 기반의 잔향 제거 알고리즘
2.1 비음수 행렬 분해
2.2 잔향 제거 알고리즘
III. 베타-발산 함수 비음수 행렬 분해 및 잔향 제거 기법
3.1 잔향 그룹의 주파수 및 시간 기저 추정
3.2 표적 반향 그룹의 시간 기저 행렬 추정
IV. 시뮬레이션
4.1 시뮬레이션 환경
4.2 시뮬레이션 결과
V. 결 론

I. 서 론

능동 소나 시스템은 수중에서 표적을 탐지하기 위하여 음향 신호를 방사한 후 그 반향을 수신하여 분석하는 시스템이다. 수중에서 음향 신호를 방사하지 않고 표적이 내는 소음을 수신하여 분석하는 수동소나와 달리, 능동 소나는 음향신호를 직접 방사하여 그 반향을 탐지하기 때문에, 표적을 탐지하기 위한 신호대잡음비를 원하는 대로 조절할 수 있다는 장점이 있다. 수동 소나의 경우 표적이 스스로의 소음을 제어하면 이를 수신하기가 어렵지만, 능동 소나는 방사하는 음향 신호의 세기를 강하게 하면 되기 때문이다.

하지만 실제 음향 환경에서 이를 운용하는 경우 방사 음향 신호의 세기를 크게 하는 것이 항상 도움이 되는 것은 아닌데, 이는 표적에서의 반향 외에도 수면, 바닥면, 그리고 물고기 떼 등의 주변 산란체에서 반사되는 잔향 신호가 함께 수신되기 때문이다. 따라서, 많은 경우 잔향 신호가 능동 소나의 성능을 제한하는 주요 요소가 된다.

능동 소나 시스템을 연구하고 개발하는 많은 학자들은 이와 같이 잔향으로 인한 성능 저하를 극복하고자 많은 노력을 기울여 왔으며, 그 중 한 가지는 송신 파형을 잔향에 강인하게 만드는 방법이다. 예를 들어, 표적의 도플러를 잘 판별할 수 있지만 잔향에 취약한 지속파 파형의 단점을 보완하여, 잔향에 강인한 선형 주파수 변조 파형을 사용하는 방법 등이 있을 수 있다.^[1] 이 외에도 정현파 주파수 변조 파형 및 이를 발전시킨 일반화된 정현파 주파수 변조 파형 등이 연구된 바 있다.^[2] 그럼에도 불구하고 여전히 능동 소나시스템에서는 지속파 송신파형을 주요하게 활용하고 있고, 이 경우 잔향에 의한 문제를 해결할 필요가 있다.

이를 위하여 신호처리 알고리즘을 활용해 잔향을 제거하는 기법이 연구되고 있다. 대표적으로 자기회귀 모델을 기반으로 하는 백색화 기법이 연구된 바 있다.^[3] 이는 고전적인 신호처리 기법을 활용하여 잔향을 제거하는 방안을 제시하였다는 의미가 있지만, 낮은 도플러의 표적에서 성능이 저하되는 단점이 있다. 신호를 분석하고 처리하는 기법이 발전함에 따라 주성분 역산(principal component inverse)^[4] 및 신호 부공간 추출(signal subspace extraction)^[5] 등의 기법이 고안되었으며, 이와 같은 기법들은 신호 및 자기상관 행렬의 고유값 분해를 활용하는 주성분 분석와 연관된 기술이라고 볼 수 있다.

최근 신호처리 분야에서는 주성분 분석과 다른 관점에서 신호를 분석 및 분해할 수 있는 다른 기법이 고안되었는데, 이는 비음수 행렬 분해(Non-negative Matrix Factorization, NMF)라고 불리는 기술이다.^[6] NMF 기법은 앞서 언급한 주성분 분석 및 벡터양자화 기술과 동일하게 신호를 여러 요소로 분해하는 기법이지만, 비음수 행렬로 이루어진 신호를 두 비음수 행렬의 곱으로 분해한다는 점에서 차이점을 가지며, 이를 처음 고안한 연구팀에서는 인간의 인지적 특성과의 유사성에 주목한 연구 결과를 발표하기도 하였다.^[7]

NMF 기법으로 분석된 신호가 의미론적 특성을 가질 수 있다는 결과가 보고되면서, 음향 신호를 다루는 여러 분야에서도 이를 활용하기 시작하였다. 예를 들어, 음향 신호의 크기 스펙트로그램에 NMF 기법을 적용하면 각 음악적 이벤트의 음고 및 활성 시간 정보를 얻을 수 있다는 점이 밝혀지면서, 음악 신호의 자동채보 알고리즘에 활용되기도 하였다.^[8]

후술할 바와 같이, NMF 알고리즘은 음향 신호의 크기 스펙트로그램(입력 데이터)과 주파수 기저 행렬과 시간 기저 행렬의 곱(복원된 입력)의 비용 함수를 최적화함으로써 신호를 분석한다. 따라서, 주어진 입력 데이터와 복원된 입력 사이의 거리 함수를 무엇으로 설정하느냐에 따라 주파수 및 시간 기저 행렬을 추정하는 양상이 달라진다.

기존에 연구되었던 NMF 기반음향 신호처리 시스템은 각각 정보 분석, 잡음 제거 등 다양한 목적을 위해 개발되었으며, 각 목적에 적합하도록 비용함수도 다양하게 선택되어 사용되고 있다. 그 중에서도 유클리드 거리^[9]와 쿨백-라이블러 발산^[10]이 가장 널리 사용되며, 과업에 따라 이타쿠라-사이토 발산이 활용되는 경우도 있다.^[11]

한편, 본 논문에서 다루고 있는 수중음향 능동소나 잔향 제거 알고리즘에서도 NMF 기법을 기반으로 한 알고리즘이 개발된 바 있다.^[12] 이는 NMF 기법을 응용하여 능동소나 수신 신호의 시간-주파수 영역 신호, 즉 크기 스펙트로그램을 주파수 기저 행렬과 시간 기저 행렬의 곱으로 분해하는 것으로, 이 때 각 기저 행렬을 표적 반향 기저와 잔향 기저로 구분하여 추정함으로써 잔향을 제거하는 기법이다. NMF 기반의 지속파 능동소나 잔향 제거 기법이 기존의 주성분 역산 혹은 신호 부공간 추출 기법에 비해 향상된 성능을 보였으며, 이후 추가적인 전/후처리를 통해 선형 주파수 변조 신호에도 사용될 수 있도록 하거나,^[13] 양상태 소나에 적용되는 등의 확장 연구가 진행된 바 있다.^[14]

Reference [12]의 연구는 기존의 기법에 비해 좋은 성능을 보여주었지만, 적절한 비용 함수에 대한 고민 없이 쿨백-라이블러 발산 함수를 임의로 선택하여 연구를 진행하였다는 한계점이 있다. 앞서 언급한 바와 같이, NMF 기반의 능동소나 잔향 제거 알고리즘은 입력 신호 스펙트로그램에서 추정한 주파수 기저 행렬과 시간 기저 행렬을 그대로 사용하는 것이 아니라 표적 반향 기저와 잔향 기저를 분리하여 제거하기 때문에, 비용 함수에 따라 추정 양상이 달라지면 잔향 제거 성능 또한 크게 달라질 수 있다.

본 논문에서는, 비용 함수의 선택에 따른 NMF 기반 잔향 제거 기법의 성능에 대해 분석하는 것을 목표로 한다. 이를 위하여 베타-발산 함수를 활용하여 Reference [12]에서 제안하는 NMF 기반 능동소나 잔향 제거 알고리즘을 확장한다. 베타-발산 함수는 NMF에서 주로 사용하는 세 가지의 비용 함수, 즉 유클리드 거리, 쿨백-라이블러 발산, 이타쿠라-사이토 발산을 일반화한 함수로, 상수 값을 조절하여 세 비용 함수를 모두 표현할 수 있을 뿐만 아니라 그 사이의 성질을 가지는 함수도 만들 수 있다. 본 논문에서는 이와 같이 베타-발산 함수를 통해 확장된 알고리즘을 활용, 몬테카를로 시뮬레이션을 통하여 비용함수에 따른 성능의 변화에 대해 살펴보고자 한다.

II. 비음수 행렬 분해 기반의 잔향 제거 알고리즘

2.1 비음수 행렬 분해

비음수 행렬 분해 기법은 비음수 원소로 이루어진 임의의 행렬 $V \in ℝ_{+}^{K \times N}$ 을 다음과 같이 두 행렬 $W \in ℝ_{+}^{K \times R}$ 과 $H \in ℝ_{+}^{R \times N}$ 의 곱으로 분해하는 기법이다.^[6]

(1)

V = WH + E,

여기서 $E \in ℝ^{K \times N}$ 은 잔여 행렬을 나타낸다.

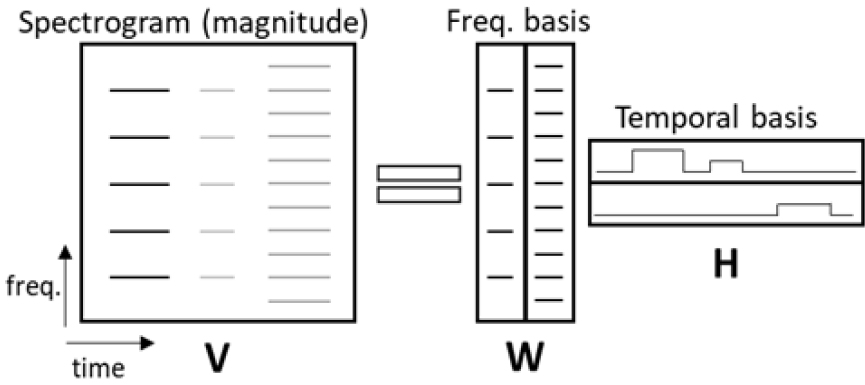
비음수 행렬 분해 기법을 기반으로 한 음향 신호 처리 알고리즘은 입력 신호의 크기 스펙트로그램을 분해 대상 행렬 $V$ 로 활용하며, 이 때 $K$ 와 $N$ 은 각각 주파수 빈의 개수와 시간 프레임의 개수가 된다. Fig. 1에서 보는 바와 같이 기저 벡터의 개수 $R$ 을 적절하게 선택하여 크기 스펙트로그램을 분해하면, 행렬 $W$ 와 $H$ 는 각각 음향 이벤트의 주파수 축 특성과 시간축 활성 정보를 나타내는 결과를 얻을 수 있다.^[8]

https://cdn.apub.kr/journalsite/sites/ask/2024-043-04/N0660430401/images/ASK_43_04_01_F1.jpg

Fig. 1.

An illustrative diagram for NMF method.

2.2 잔향 제거 알고리즘

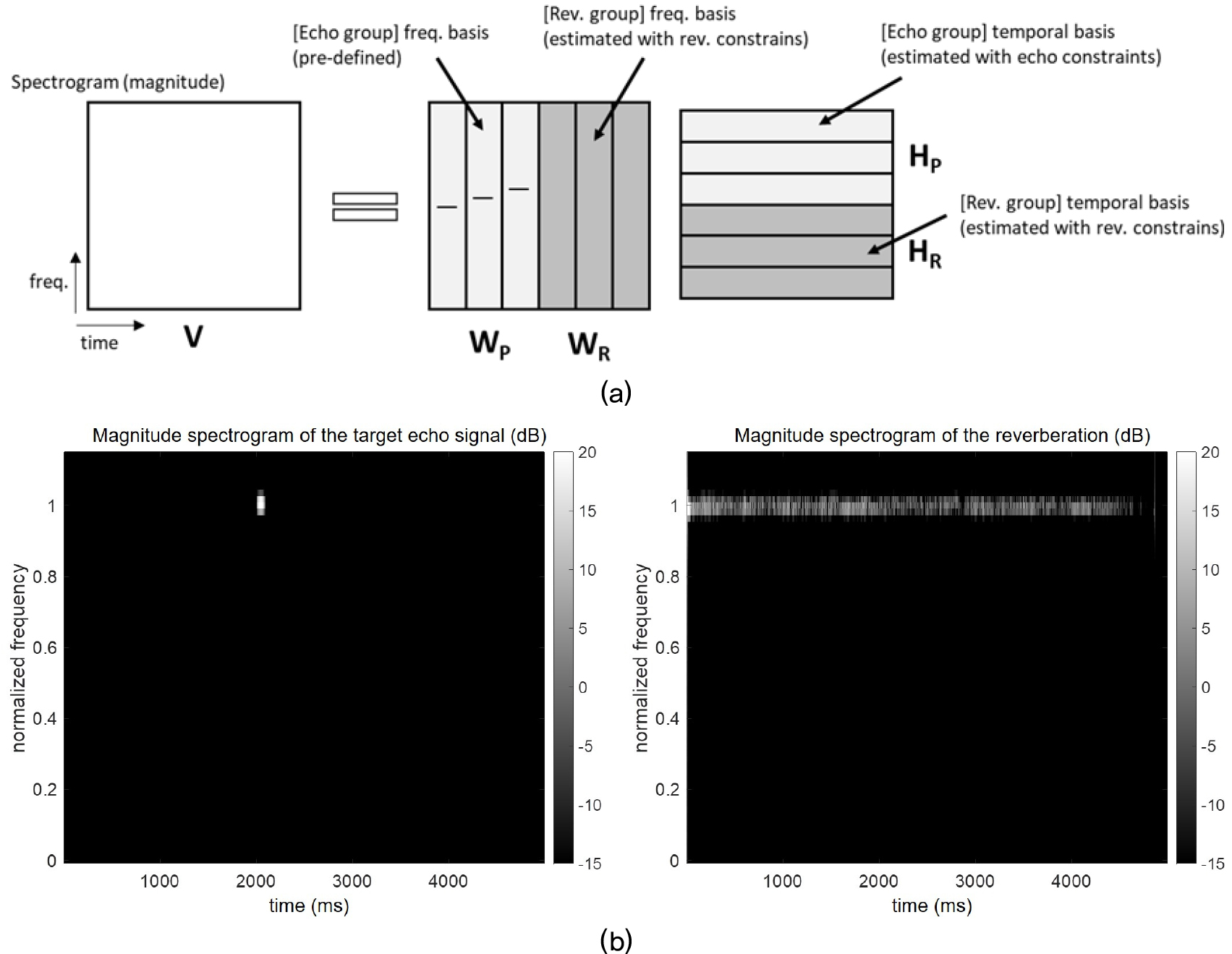
앞서 살펴본 비음수 행렬 분해 기법의 특성을 활용하여 능동 소나의 잔향 제거 기법이 개발된 바 있다.^[12] 이는 Fig. 1과 같이 비음수 행렬 분해 기법이 음향 이벤트의 주파수 기저와 시간 활성 기저를 분석할 수 있다는 특성을 이용하되, 음향 이벤트를 두 그룹 – 표적 반향 그룹과 잔향 그룹 – 으로 나눌 수 있도록 제약 조건을 추가하여 추정하는 기법이다. Fig. 2(a)에서 보는 바와 같이 주파수 기저 행렬 $W$ 와 시간 기저 행렬 $H$ 을 두 그룹으로 나눈다.

(2)

W = [W_{P} | W_{R}],

(3)

H = [H_{P}^{T} | {H_{R}}^{T}]^{T},

여기서 $W_{P}$ 와 $W_{R}$ 은 각각 표적 반향 그룹과 잔향 그룹의 주파수 기저 행렬을, $H_{P}$ 와 $H_{R}$ 은 표적 반향그룹과 잔향 그룹의 시간 기저 행렬을 나타낸다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-04/N0660430401/images/ASK_43_04_01_F2.jpg

Fig. 2.

(a) An illustrative diagram for NMF-based active sonar reverberation method, and (b) examples for magnitude spectrogram of simulated target echo and reverberation, respectively.

각 기저 그룹을 서로 다르게 추정하기 위해서, Reference [12]에서는 다음과 같이 표적 반향 신호와 잔향 신호의 크기 스펙트로그램이 서로 다른 특징을 가지고 있다고 가정한다. 1) 표적 반향 신호는 송신된 신호가 도플러 주파수 이동된 레플리카의 형태를 가진다(여기서 도플러 주파수 변화로 인한 신호 길이의 변화는 무시한다). 2) 잔향 신호의 포락선이 시간축에서 무작위로 요동치는 반면 표적 반향 신호의 포락선은 상대적으로 연속적이다. 3) 표적 반향 신호는 잔향 신호에 비해 시간 길이가 한정적이다.

위 가정은 Fig. 2(b)에 나타난 시뮬레이션 예시에서도 살펴볼 수 있다. Fig. 2(b)의 좌측 그래프는 시뮬레이션에 의해 생성된 표적 반향, 우측 그래프는 생성된 잔향 신호의 크기 스펙트로그램을 도시하고 있으며, 해당 그래프를 보면 표적 반향 신호는 짧고 일정한 포락선을 가지고 있는 반면, 잔향 신호는 길고 요동치는 포락선을 가지고 있음을 볼 수 있다. Reference [12]에서는 실측 데이터에서도 이와 같은 경향을 확인할 수 있다. 이와 같은 가정을 바탕으로 각 그룹에 적합한 목적함수를 설정한 후, 이를 최적화하여 각 기저 그룹을 추정하게 된다.

표적 반향 신호의 경우, 위의 가정을 만족하면서 크기 스펙트로그램을 잘 복원하는 신호 성분을 추정하도록 한다. 먼저, $W_{P}$ 행렬을 송신된 신호의 주파수 특성의 도플러-이동된 레플리카 형태로 구성한다. 지속파 능동 소나의 경우 송신 신호가 단일 주파수 형태로 나타나기 때문에, $W_{P}$ 행렬은 Fig. 2에서 보는 바와 같이 주파수-이동된 델타함수 형태로 구성된다. 선형 주파수 변조 신호를 활용하는 경우에는 디처핑 과정을 통해 단일주파수와 유사한 형태로 변형한 후 활용할 수 있다.^[13] $W_{P}$ 행렬은 이와 같이 구성된 후 추정 과정에서 값이 변하지 않고 고정된다.

$H_{P}$ 행렬을 추정하기 위해서, Reference [12]에서는 다음과 같은 비용 함수를 사용한다.

(4)

C (H_{P}) = C_{E} (W, H) + α C_{T} (H_{P}) + γ C_{L} (H_{P}),

여기서 $C_{E} (H_{P})$ , $C_{T} (H_{P})$ 및 $C_{L} (H_{P})$ 은 각각 추정 비용 함수, 시간 연속성 함수, 그리고 시간 길이 제한 함수를 나타내며, 각 함수는 다음과 같이 정의된다.^[12]

(5)

C_{E} (W, H) = \sum_{k, n} ([V]_{k, n} \log \frac{[V]_{k, n}}{[WH]_{k, n}} - [V]_{k, n} + [WH]_{k, n}),

(6)

C_{T} (H_{P}) = \sum_{r = 1}^{R} \frac{\sum_{n = 2}^{N} {({[H_{P}]}_{r, n} - {[H_{P}]}_{r, n - 1})}^{2}}{\frac{1}{N} \sum_{n = 1}^{N} {({[H_{P}]}_{r, n})}^{2}},

(7)

C_{L} (H_{P}) = \sum_{r = 1}^{R} (1 - \sum_{m = n}^{n + l_{n} - 1} {[{\hat{H}}_{P}]}_{r, m}),

여기서 $[A]_{k, n}$ 은 행렬 $A$ 의 $(k, n)$ 번째 원소를 의미한다. Eq. (5)는 복원 대상인 행렬 $V$ 와 추정 값인 $WH$ 의 쿨백-라이블러 발산이고, Eq. (6)은 시간 축에서 인접한 두 원소의 차이가 클수록 비용이 커지는 시간 연속성 함수이다.

Eq. (7)은 시간 축에서 $l_{n}$ 길이 단위로 최대 에너지를 가지는 구간의 비용을 줄여주는 함수이며, 이를 통해서 추정된 값이 $l_{n}$ 길이 단위로 집중된 에너지를 가질 수 있도록 하는 비용 함수이다. Eq. (7)의 ${\hat{H}}_{P}$ 는 최대값 지시 함수로, 다음과 같이 계산된다.^[12]

(8)

[{\hat{H}}_{P}]_{r, n} = \frac{\exp ([H_{P}]_{r, n})}{\sum_{m = 1}^{N} \exp ([{\bar{H}}_{P}]_{r, m})},

여기서 ${\bar{H}}_{P}$ 는 다음과 같이 $H_{P}$ 행렬의 값을 $l_{n}$ 길이로 시간 축에서 이동합산을 취한 값이다.^[12]

(9)

[{\bar{H}}_{P}]_{r, n} = \sum_{m = n - l_{n} + 1}^{n} [H_{P}]_{r, m} .

Eq. (8)은 softmax 함수로, 최대값을 가리키는 함수와 유사한 역할을 하면서 미분이 가능하도록 하기 위하여 사용되었다.

앞서 언급한 바와 같이, 표적 반향 그룹의 주파수 기저 $W_{P}$ 행렬은 송신 신호의 도플러-이동 레플리카로 구성되어 고정되고, 시간 기저 $H_{P}$ 행렬은 Eq. (4)를 최적화하여 얻어진다. 잔향 기저인 $W_{R}$ 과 $H_{R}$ 행렬은 표적 반향 가정에 포함되지 않으면서 크기 스펙트로그램 $V$ 를 잘 추정할 수 있는 값이기 때문에, 별도의 비용함수 없이 추정 비용 함수만 사용하여 추정하며, 이 추정 비용 함수는 Eq. (5)와 동일하다.

반복적인 추정 과정을 통해 각 기저들의 추정이 완료되면, 표적 반향 기저 행렬의 곱으로 잔향이 제거된 신호의 크기 스펙트로그램을 추정한다. 표적 반향의 시간 축 파형이 필요한 경우 역 푸리에 변환을 통하여 시간 축 파형을 획득할 수 있으며, 이 때 필요한 위상 정보는 입력 신호의 위상 정보를 활용한다.

III. 베타-발산 함수 비음수 행렬 분해 및 잔향 제거 기법

3.1 잔향 그룹의 주파수 및 시간 기저 추정

2.2절에서 언급한 바와 같이, 잔향 그룹의 주파수 기저 $W_{R}$ 및 시간 기저 $H_{R}$ 행렬은 입력 스펙트로그램 $V$ 와 기저의 곱 $WH$ 사이의 비용 함수를 최적화하는 방법으로 추정된다. 기존의 잔향 제거 기법에서는 이와 같은 비용 함수로 Eq. (5)와 같은 쿨백-라이블러 발산 함수를 활용하였으나, 본 논문에서는 추정 비용 함수에 대한 성능 분석을 위하여 주요 비용 함수가 일반화된 베타-발산 함수를 활용한다. 베타-발산 함수는 다음과 같이 정의된다.^[15]

(10)

D_{β} (x | y) = \{\begin{cases} x \log \frac{x}{y} - x + y if β = 1 \\ \frac{x}{y} - \log \frac{x}{y} - 1 if β = 0 . \\ \frac{x^{β}}{β (β - 1)} + \frac{y^{β}}{β} - \frac{x y^{β - 1}}{β - 1} o . w . \end{cases}

Eq. (10)은 𝛽=0인 경우 이타쿠라-사이토 발산과 같고, 𝛽=1인 경우 쿨백-라이블러 발산과 같으며, 𝛽=2 인 경우 유클리드 거리와 같은 함수가 된다.

잔향 그룹의 주파수 및 시간 기저를 추정하기 위해서는 Eq. (10)의 추정 비용 함수를 최적화하도록 각 기저 행렬을 추정하면 되며, 휴리스틱 곱셈 갱신(heuristic multiplicative update) 방법에 따르면 다음과 같이 추정할 수 있다. 먼저, $W$ 및 $H$ 에 대한 비용함수의 미분이 $\nabla_{W} C = \nabla_{W}^{+} C - \nabla_{W}^{-} C$ 혹은 $\nabla_{H} C = \nabla_{H}^{+} C - \nabla_{H}^{-} C$ 와 같이 두 비음수 값의 차이로 나타낼 수 있다고 가정하자. 여기서 + 기호가 붙은 항과 - 기호가 붙은 항은 각각 뺄셈 기호를 기준으로 앞과 뒤에 위치하는 비음수 항을 나타낸다. 예를 들어, $\nabla_{W} C = W^{T} WH - W^{T} V$ 인 경우, $\nabla_{W}^{+} C = W^{T} WH$ , $\nabla_{W}^{-} C = W^{T} V$ 를 의미한다. 이 경우, 다음의 연산을 반복적으로 수행하여 이를 추정할 수 있다.^[6,15]

(11)

W \leftarrow W \otimes \frac{\nabla_{W}^{-} C (W, H)}{\nabla_{W}^{+} C (W, H)},

(12)

H \leftarrow H \otimes \frac{\nabla_{H}^{-} C (W, H)}{\nabla_{H}^{+} C (W, H)},

여기서 ⊗는 원소 단위의 곱셈을, 분수 표기는 원소 단위의 나눗셈을 의미한다.

앞서 언급한 바와 같이, 잔향 기저 추정을 위해서는 다른 제약 조건 없이 추정 비용 함수만을 활용한다. 따라서, 잔향 기저 추정을 위한 비용 함수는 다음과 같이 정의될 수 있다.

(13)

C_{R} (W, H) = \sum_{k, n} D_{β} ([V]_{k, n} | [WH]_{k, n}) .

Eq. (10)에서 정의된 베타-발산 함수를 활용하면, Eq. (13)에 대한 $W_{R}$ 및 $H_{R}$ 에 대한 미분은 다음과 같다.

(14)

\nabla_{W_{R}} C_{R} (W, H) = (WH)^{\cdot (β - 1)} H_{R}^{T} - \{V \otimes (WH)^{\cdot (β - 2)}\} H_{R}^{T},

(15)

\nabla_{H_{R}} C_{R} (W, H) = W_{R}^{T} (WH)^{\cdot (β - 1)} - W_{R}^{T} \{V \otimes (WH)^{\cdot (β - 2)}\},

여기서 $A^{. β}$ 는 행렬 $A$ 에 대한 원소 단위의 𝛽 거듭제곱을 의미한다. Eqs. (11) 및 (12)에 Eqs. (14) 및 (15)를 적용하면 다음과 같은 곱셈 갱신 식을 얻을 수 있다.

(16)

W_{R} \leftarrow W_{R} \otimes \frac{{V \otimes (WH)^{. (β - 2)}} H_{R}^{T}}{(WH)^{. (β - 1)} H_{R}^{T}},

(17)

H_{R} \leftarrow H_{R} \otimes \frac{W_{R}^{T} {V \otimes (WH)^{. (β - 2)}}}{W_{R}^{T} (WH)^{. (β - 1)}},

3.2 표적 반향 그룹의 시간 기저 행렬 추정

Reference [12]에서 보는 바와 같이, 표적 반향 신호는 시간 축에서 길이가 제한적이며 변화가 적다는 특성을 가진다는 가정을 활용한다. 이 경우, 표적 반향 그룹의 시간 기저 행렬은 추정 비용 함수 외에 Eq. (6)의 시간 연속성 비용 함수와 Eq. (7)의 시간 길이 제한 비용 함수를 추가로 활용한다. 따라서, 표적 반향 그룹의 시간 기저 행렬을 추정하기 위한 비용 함수는 다음과 같이 정의된다.

(18)

C_{P} (H_{P}) = C_{E, β} (W, H) + α C_{T} (H_{P}) + γ C_{L} (H_{P}),

여기서 $C_{E, β} (W, H)$ 는 베타-함수에 의한 추정 비용 함수로, $C_{E, β} (W, H) = \sum_{k, n} D_{β} ([V]_{k, n} [WH]_{k, n})$ 와 같이 정의된다. 시간 연속성 비용 함수 $C_{T} (H_{P})$ 및 시간 길이 제한 비용 함수 $C_{L} (H_{P})$ 는 각각 Eq. (6) 및 Eq. (7) 로 정의된다.

앞서 설명한 바와 같이, 시간 연속성 비용 함수 $C_{T} (H_{P})$ 는 추정된 $H_{P}$ 함수의 시간축 인접값의 차이가 클수록 비용이 증가하는 비용 함수이다[Eq. (6) 참고]. 그리고 시간 길이 제한 비용 함수 $C_{L} (H_{P})$ 는 시간축에서 $l_{n}$ 길이 만큼의 이동-평균을 취한 뒤[Eq. (9)], 이에 대한 최대값을 찾아서[Eq. (8)], 최대값 근처의 $l_{n}$ 길이 만큼의 비용을 0으로 만들고 나머지를 1로 만들어[Eq. (7)] 추정 결과의 시간축 길이를 제한하는 비용 함수이다. 각 비용함수에 의한 최적화 갱신은 수렴이 보장되지 않기 때문에 𝛼 및 𝛾 값이 큰 경우 수렴하지 않고 발산할 위험이 있으며, Reference [12]의 분석에 따르면 두 값 모두 100 보다 작은 값을 사용하는 것이 바람직하다.

Eq. (12)에 기술된 휴리스틱 곱셈 갱신 방법을 활용하기 위해서는 Eq. (18)의 비용 함수에 대한 미분을 계산하여 이를 두 비음수 값의 차이로 표현하여야 한다. 먼저, 추정 비용 함수를 미분하면 다음과 같다.

(19)

\nabla_{H_{P}} C_{E, β} (W, H) = \underset{\nabla_{H_{p}}^{+} C_{E, 3} (W, H)}{\underset{⏟}{W_{P}^{T} (WH)^{. (β - 1)}}} - \underset{\nabla_{{\bar{H}}_{P}} C_{E, 3} (W, H)}{\underset{⏟}{W_{P}^{T {} {V \otimes (WH)^{(β - 2)}}}} .

다음으로, 시간 연속성 비용 함수에 대한 미분은 다음과 같이 얻어진다.^[12]

(20)

\nabla_{H_{P}} C_{T} (H_{P}) = \frac{4 N H_{P}}{\underset{\nabla_{H_{P}}^{+} C_{T} (H_{P})}{\underset{⏟}{H_{P}^{. 2} 1_{N \times N}}}} - \underset{\nabla_{H_{P}}^{-} C_{T} (H_{P})}{\underset{⏟}{[2 N \frac{Δ_{2} H_{P}}{H_{P}^{. 2} 1_{N \times N}} + \frac{2 N H_{P} \otimes {{(Δ H_{P})}^{. 2} 1_{N \times N}}}{{(H_{P}^{. 2} 1_{N \times N})}^{. 2}}]}},

여기서 $Δ H_{P} = H_{P} - H_{P, \to 1}$ , $Δ_{2} H_{P} = H_{P, \leftarrow 1} - H_{P, \to 1}$ 이며, $H_{P, \to 1}$ 와 $H_{P, \leftarrow 1}$ 는 각각 행렬의 원소를 우측 혹은 좌측으로 한칸 이동시킨 행렬을 의미한다. 마지막으로, 시간 길이 제한 비용 함수의 미분을 원소 단위로 표현하면 다음과 같다.^[12]

(21)

{[\nabla_{H_{P}} C_{L} (H_{P})]}_{r, n} = \underset{{[\nabla_{H_{P}}^{+} C_{L} (H_{P})]}_{r, n}}{\underset{⏟}{\sum_{m = n}^{n + l_{n} - 1} {\{\frac{\exp ({[{\bar{H}}_{P}]}_{r, m})}{\sum_{i = 1}^{N} \exp ({[{\bar{H}}_{P}]}_{r, i})}\}}^{2}}} \underset{{[\nabla_{H_{P}}^{-} C_{L} (H_{P})]}_{r, n}}{- \underset{⏟}{\sum_{m = n}^{n + l_{n} - 1} \frac{\exp ({[{\bar{H}}_{P}]}_{r, m})}{\sum_{i = 1}^{N} \exp ({[{\bar{H}}_{P}]}_{r, i})}} \cdot}

Eqs. (19), (20) 및 (21)이 모두 두 비음수 성분의 차이 형태로 기술되었기 때문에, 휴리스틱 곱셈 갱신 방법을 활용하면 다음과 같이 추정할 수 있다.

(22)

H_{P} \leftarrow H_{P} \otimes \frac{\{\nabla_{H_{P}}^{-} C_{E, β} (W, H) + α \nabla_{H_{P}}^{-} C_{T} (H_{P}) + γ \nabla_{H_{P}}^{-} C_{L} (H_{P})\}}{\{\nabla_{H_{P}}^{+} C_{E, β} (W, H) + α \nabla_{H_{P}}^{+} C_{T} (H_{P}) + γ \nabla_{H_{P}}^{+} C_{L} (H_{P})\}} .

Eqs. (16), (17), 그리고 (22)의 연산을 반복수행하면 $W_{R}$ , $H_{R}$ , 그리고 $H_{P}$ 를 추정할 수 있다. 이를 이용하여 표적 반향 신호의 크기 스펙트럼을 다음과 같이 추정한다.

(23)

\hat{V} = W_{P} H_{P} .

본 논문에서 도출된 베타-발산 함수 기반의 알고리즘은 Table 1과 같이 요약된다.

Table 1.

Summary of the proposed algorithm.

NMF-based reverberation suppression algorithm
with Beta-Divergence

Initialization:

W_{P}

is initialized with frequency structures of transmitted ping and its Doppler-shifted replicas.

W_{R}

H_{P}

, and

H_{R}

are initialized by absolute values of Gaussian random numbers.

Iterations:
1)

W_{R}

is updated using Eq. (16);
2)

W

is updated by Eq. (2);
3)

\nabla_{H_{P}}^{+} C_{E, β} (W, H)

and

\nabla_{H_{P}}^{-} C_{E, β} (W, H)

are updated using Eq. (19);
4)

\nabla_{H_{P}}^{+} C_{T} (W, H)

and

\nabla_{H_{P}}^{-} C_{T} (W, H)

are updated using Eq. (20);
5)

\nabla_{H_{P}}^{+} C_{L} (W, H)

and

\nabla_{H_{P}}^{-} C_{L} (W, H)

are updated using Eq. (21);
6)

H_{P}

is updated using Eq. (22); 7)

H_{R}

is updated using Eq. (17);
8)

H

is updated by Eq. (3).

After convergence: magnitude spectrogram

\hat{V}

of the output signal is reconstructed by Eq. (23).

IV. 시뮬레이션

4.1 시뮬레이션 환경

앞에서 고안한 베타-발산 함수 비음수 행렬분해 기반의 잔향 제거 기법을 활용, 추정 비용 함수의 선택에 대한 잔향 제거 성능을 분석하기 위하여 PC 환경에서의 시뮬레이션을 진행하였다. 본 시뮬레이션에서 가정한 시뮬레이션 환경은 Reference [12]과 유사하며, 소나 시스템은 100 ms 길이의 지속파 핑을 방사하면서 $2 V / c = 0.033$ 이 되는 속력 $V$ 로 이동하는 것을 가정하였다. 잔향 신호는 비-레일레이 수중 잔향 모델^[16]을 활용하여 합성하였다. 표적 신호는 수신 시작 시점 기준 2 s 후에 수신되며, 표적의 도플러 주파수 $f_{d}$ 는 $f_{d} / f_{0} = 0.005$ 가 되도록 설정하였다. 표적의 도플러 주파수를 작게 설정한 이유는, 낮은 도플러의 표적을 가정하여 표적 반향의 수신이 잔향에 의해 방해받는 상황을 가정하려고 하였기 때문이다.

본 논문에서 도출된 알고리즘을 적용하기 위한 환경 설정은 다음과 같다. 먼저, 8 kHz의 샘플링 주파수로 수신된 신호에서 단시간 푸리에 변환을 활용하여 크기 스펙트로그램을 획득하였으며, 75 % 중첩된 16 ms 길이의 해밍 윈도우를 활용, 128-포인트 고속 푸리에 변환을 수행하였다. 비음수 행렬 분해 알고리즘에서의 전체 기저 개수 $R$ 은 77 으로 설정하였으며, 이 중 표적 반향 기저의 개수는 17, 잔향 기저의 개수는 60으로 설정하였다. 시간 연속성 제약 조건의 가중치 𝛼와 시간 길이 제약 조건의 가중치 𝛾는 각각 0.01과 1로 설정하였으며, 시간 길이 제약 조건의 $l_{n}$ 은 100 ms로 설정하였다. 잔향 기저의 개수 및 각 제약 조건의 가중치는 Reference [12]의 실험을 참고하여 설정하였으며, 각 파라미터의 영향에 대한 부분은 후속 실험에서 분석하였다. Table 1에서 나타내는 바와 같이 비음수 행렬 분해 알고리즘은 반복적인 추정 과정을 필요로 하는데, 본 시뮬레이션에서 평균적으로 100회 이하의 반복을 통해 비용함수가 충분히 수렴하는 것을 확인하였으며, 본 시뮬레이션 결과는 모두 200회의 반복을 통해 비음수 기저 행렬을 추정한 결과이다.

다양한 입력 신호대잔향비 환경에서의 각 알고리즘의 잔향 제거 성능을 분석하기 위하여, –24 dB ~ –9 dB 범위에 대한 3 dB 간격의 입력 신호대잔향비 환경에서 각 100회의 몬테-카를로 시뮬레이션을 수행하여 성능지표의 평균값을 획득하였다. 성능지표로는 다음과 같이 출력 신호대잡음비를 활용하였다.

(24)

S N R = \frac{\sum_{n} | s_{e} (n) |^{2}}{\sum_{n} | s_{e} (n) - {\hat{s}}_{e} (n) |^{2}},

여기서 $s_{e} (n)$ 는 잔향이 없는 이상적인 핑 신호를, ${\hat{s}}_{e} (n)$ 는 알고리즘의 출력 신호를 나타낸다. 추정 비용 함수를 결정하는 𝛽는 0 ~ 2 사이의 값을 0.25 간격으로 바꾸어 실험을 수행하였는데, 이는 𝛽=0, 𝛽=1, 𝛽=2 가 각각 이타쿠라-사이토 발산, 쿨백-라이블러 발산, 그리고 유클리드 거리를 나타내기 때문이다.

4.2 시뮬레이션 결과

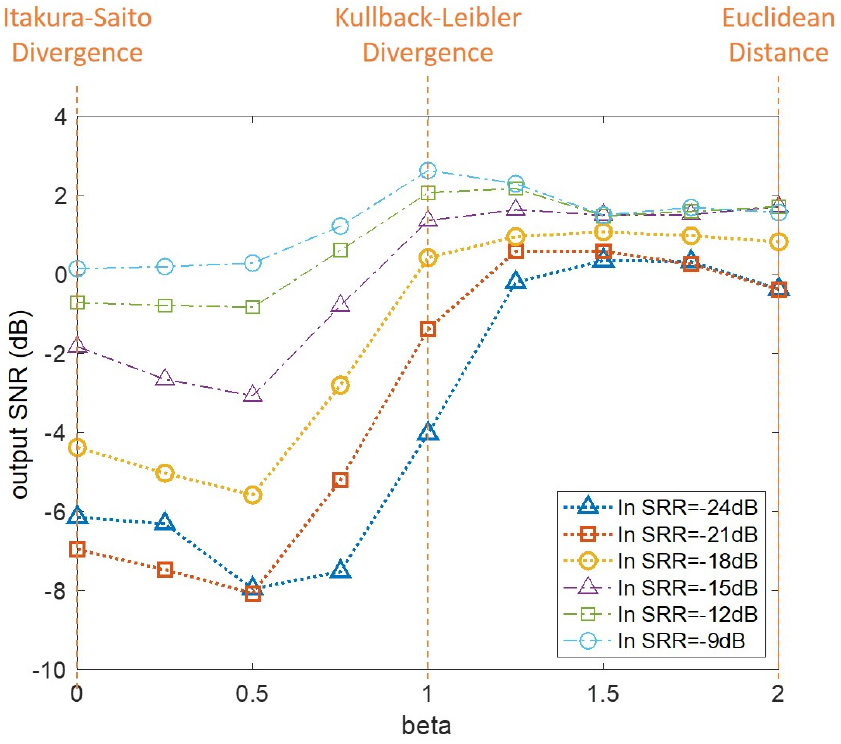
Fig. 3은 각 입력 신호대잔향비 환경에서의 𝛽에 따른 성능 지표의 결과를 보여주고 있다. Fig. 3의 가로축은 𝛽값을, 세로축은 각 입력 신호대잔향비의 출력 SNR 성능을 나타낸다. 𝛽=0, 𝛽=1, 𝛽=2의 결과를 살펴보면, 기존 알고리즘이 선택했던 쿨백-라이블러 발산(𝛽=1)과 유클리드 거리(𝛽=2)가 전반적으로 좋은 성능을 보이는 것을 확인할 수 있다. –9 dB 및 –12 dB의 높은 신호대잔향비의 경우는 쿨백-라이블러 발산이 좋은 성능을 보이고, –18 dB 및 –21 dB의 낮은 신호대잔향비의 경우는 유클리드 거리가 좋은 성능을 보이는 특성을 가진다. 반면 이타쿠라-사이토 발산함수의 경우(𝛽=0), 모든 입력 신호대잔향비 환경에서 저하된 성능을 보여 잔향 제거 과업에는 적절하지 않은 선택임을 보여준다. 𝛽가 0에서 0.5로 증가하는 경우 성능이 저하되는 경향을 보이는데, 이에 대한 원인은 현 단계에서 확실히 분석하기는 어렵다. 다만, 해당 구간에서 𝛽가 증가할수록 전반적으로 잔향의 제거 정도가 저하되는 경향이 확인되었다. 이와 같은 결과를 보았을 때, 기존의 방법에서 추정 비용 함수로 쿨백-라이블러 발산을 선택한 것은 나쁘지 않은 선택으로 보인다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-04/N0660430401/images/ASK_43_04_01_F3.jpg

Fig. 3.

(Color available online) Performance comparisons for 𝛽 in various input SRR conditions.

𝛽에 따른 결과를 좀 더 세부적으로 살펴보면, –21 dB ~ –9 dB 범위의 입력 신호대잔향비에 대해 𝛽=1.5 인 베타-발산 함수가 가장 적은 성능 변화를 보이며, 특히 낮은 입력 신호대잔향비(–21 dB 이하)에서 쿨백-라이블러 발산에 비해 좋은 성능을 보이는 것을 확인할 수 있다. Fig. 3의 결과로 보았을 때, 가장 좋은 결과는 𝛽=1.25의 비용 함수의 경우라고 볼 수 있는데, 낮은 입력 신호대잔향비(–21 dB 이하)에서 성능 열화가 가장 적으면서도 높은 입력 신호대 잔향비(–9 dB)에서도 좋은 성능을 보이고 있기 때문이다.

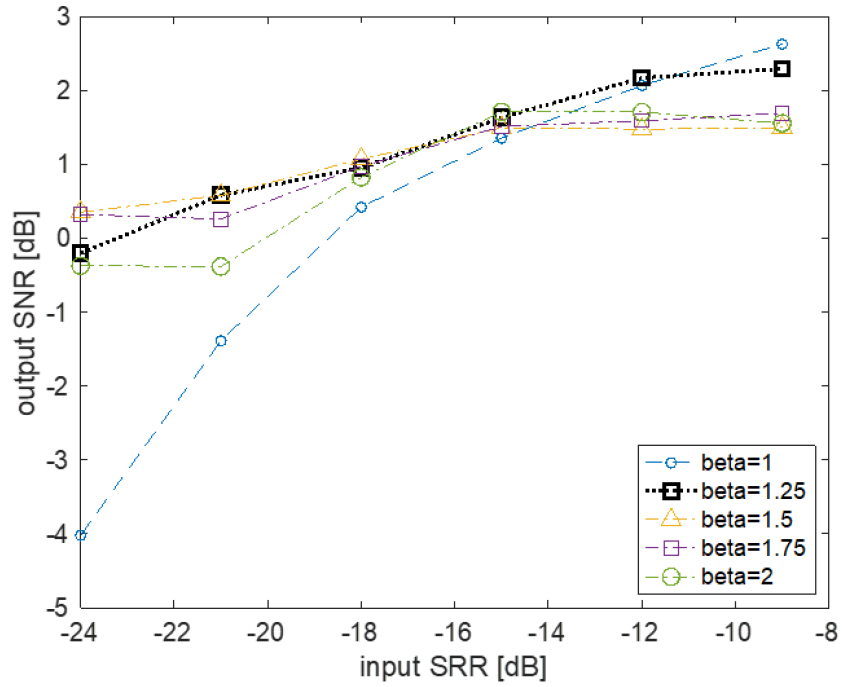
Fig. 4의 결과를 보면 입력 신호대잔향비에 대한 각 베타-발산 함수의 효과를 잘 살펴볼 수 있다. Fig. 4의 가로축은 입력 신호대잔향비를, 세로축은 각 𝛽 값의 출력 SNR 지표를 보여주고 있다. 1보다 작은 𝛽의 경우는 모든 경우에서 성능이 저하되었기 때문에 본 그래프에 표시하지 않았다. 𝛽=1(청색파선)의 경우 높은 입력 신호대잔향비에서 좋은 성능을 보이지만 낮은 입력 신호대잔향비 환경에서 성능이 저하되는 경향을 보이는 것을 쉽게 확인할 수 있으며, 특히 –21 dB 이하의 낮은 입력신호대잔향비 환경에서도 성능 저하가 커지는 경향을 뚜렷하게 보이는 것을 확인할 수 있다. 반면 𝛽=1.25인 경우의 성능이 여러 입력신호대잔향비 환경에서 좋은 성능을 보이는 것을 확인할 수 있다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-04/N0660430401/images/ASK_43_04_01_F4.jpg

Fig. 4.

(Color available online) Performance comparisons for input SRR conditions.

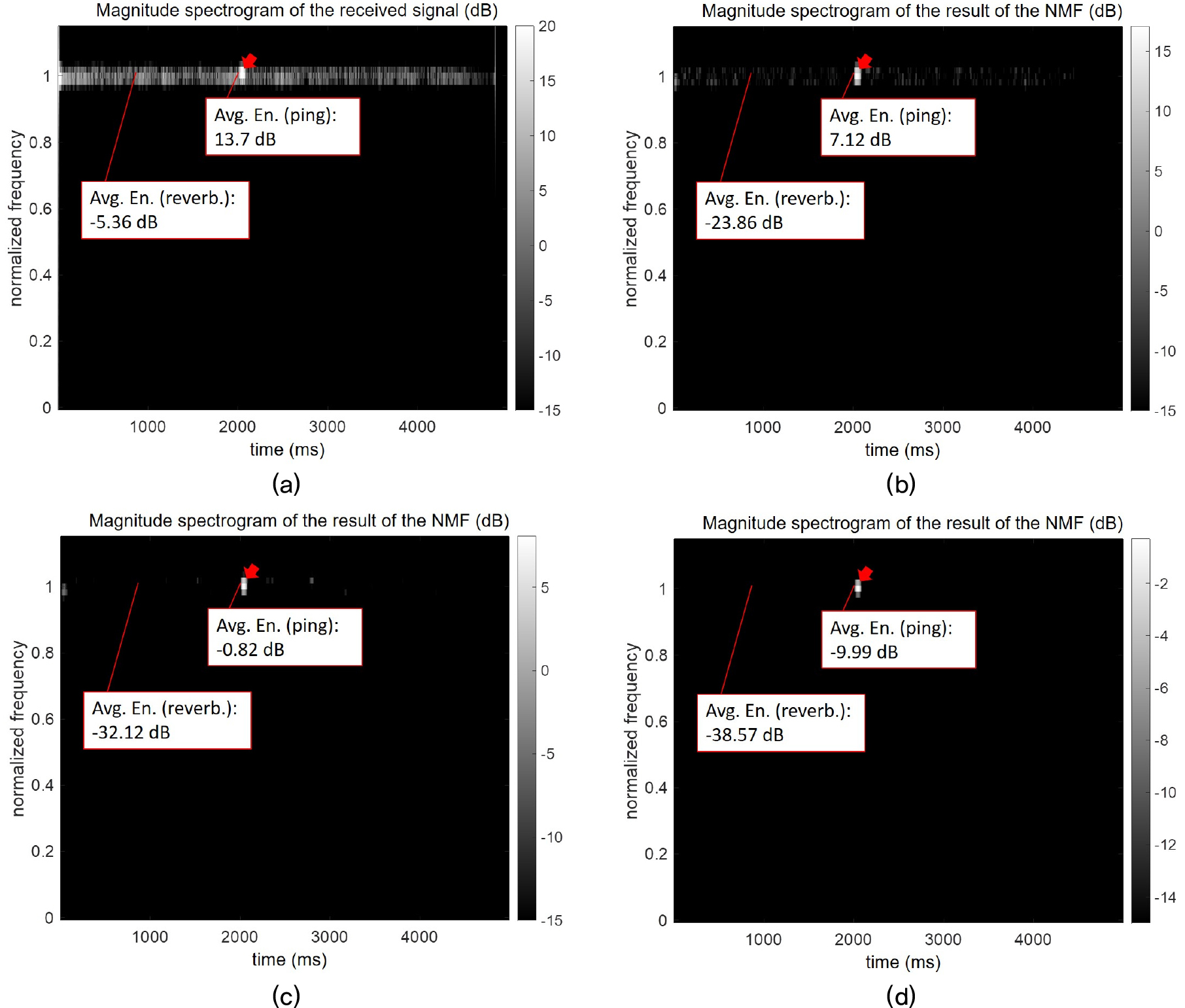
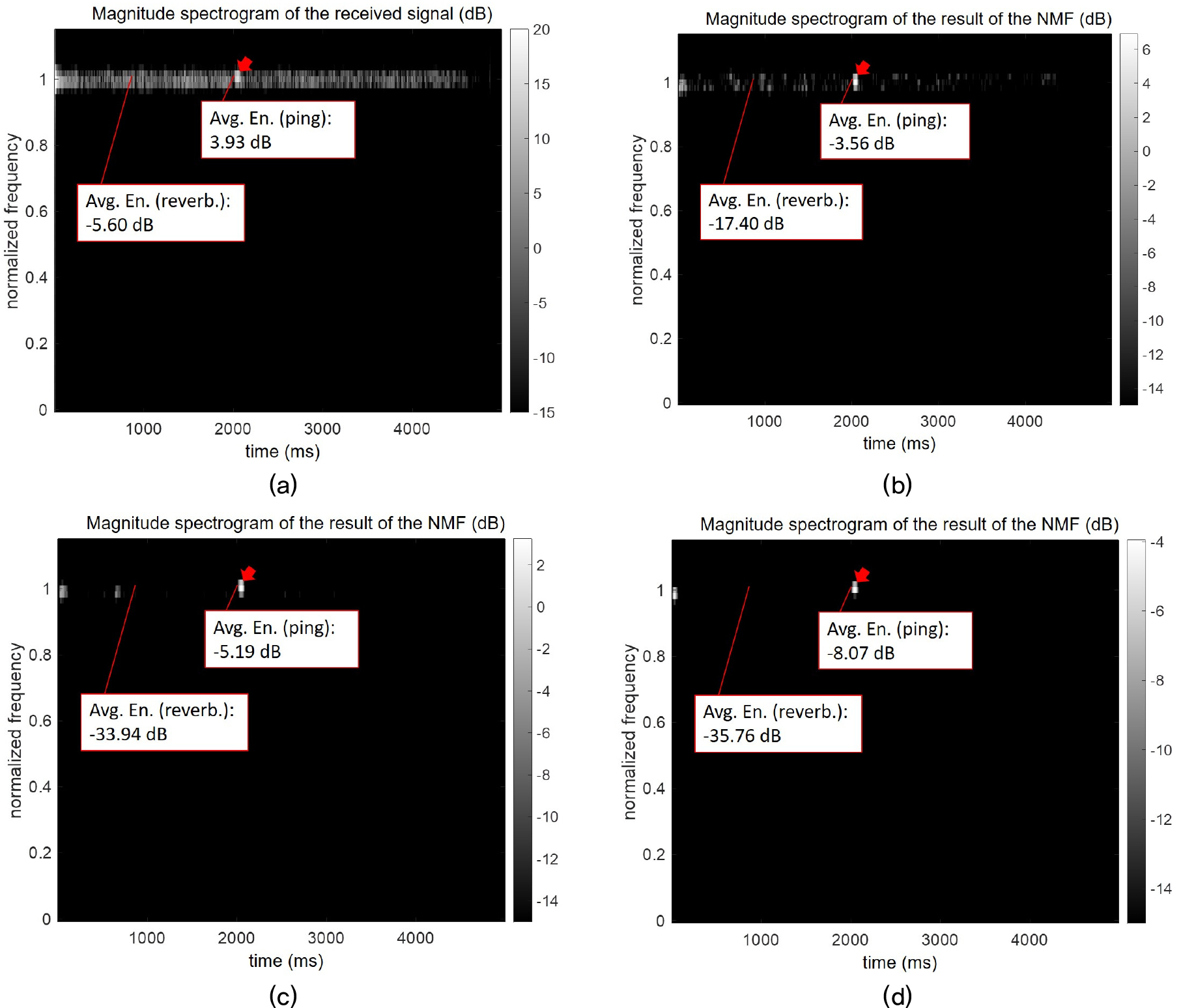
Figs. 5와 6은 𝛽=1.0, 𝛽=1.25, 𝛽=1.5 인 경우에 대한 출력 신호의 크기 스펙트럼을 도시하고 있다. 각 그래프들을 살펴보면 신호대잔향비 환경에서 𝛽 값이 클수록 잔향의 제거 정도가 큰 장점이 있지만, 표적 반향의 복원 성능도 떨어지는 단점이 있음을 확인할 수 있다. Fig. 5(b) ~ (d) 그래프에서 살펴볼 수 있는 바와 같이, 높은 신호대잔향비 환경에서는 𝛽=1 인 경우에도 잔향이 효과적으로 제거 된 것을 확인할 수 있으며, 𝛽=1.25 및 𝛽=1.5의 경우에는 잔향 에너지가 더 줄어들었지만 표적 반향의 에너지 또한 같이 감소되어 이득이 크지 않음을 확인할 수 있다. 반면 Fig. 6(b) ~ (d) 그래프에서 확인할 수 있는 낮은 신호대잔향비 환경에서는 𝛽=1의 경우 잔향 제거 성능이 제한적임을 확인할 수 있으며, 𝛽=1.25 및 𝛽=1.5의 경우에는 표적 반향의 에너지가 감소된 것에 비해 잔향 에너지의 감소 정도가 더욱 두드러져서 성능이 향상되는 것임을 확인할 수 있다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-04/N0660430401/images/ASK_43_04_01_F5.jpg

Fig. 5.

(Color available online) Magnitude spectrograms of (a) input signal and output signals when (b) 𝛽=1.0, (c) 𝛽=1.25, and (d) 𝛽=1.5 in high input SRR condition (–9 dB). Red arrow indicates target echo.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-04/N0660430401/images/ASK_43_04_01_F6.jpg

Fig. 6.

(Color available online) Magnitude spectrograms of (a) input signal and output signals when (b) 𝛽=1.0, (c) 𝛽=1.25, and (d) 𝛽=1.5 in low input SRR condition (–18 dB). Red arrow indicates target echo.

위의 시뮬레이션 결과를 통해서, 높은 신호대잔향비 환경에서는 기존과 같은 쿨백-라이블러 발산 함수가 좋은 선택이 될 수 있지만, 낮은 신호대잔향비 환경에서는 1.0 ~ 1.5의 𝛽 값이 좋은 선택이 될 수 있음을 확인할 수 있다. 일반적으로 높은 신호대잔향비 환경보다는 낮은 신호대잔향비의 환경에서 잔향 제거 알고리즘이 더 효과를 발휘하기 좋다는 점을 감안하였을 때, 쿨백-라이블러 발산(𝛽=1.0)보다 더 큰 𝛽 값이 더 유용할 것으로 판단된다.

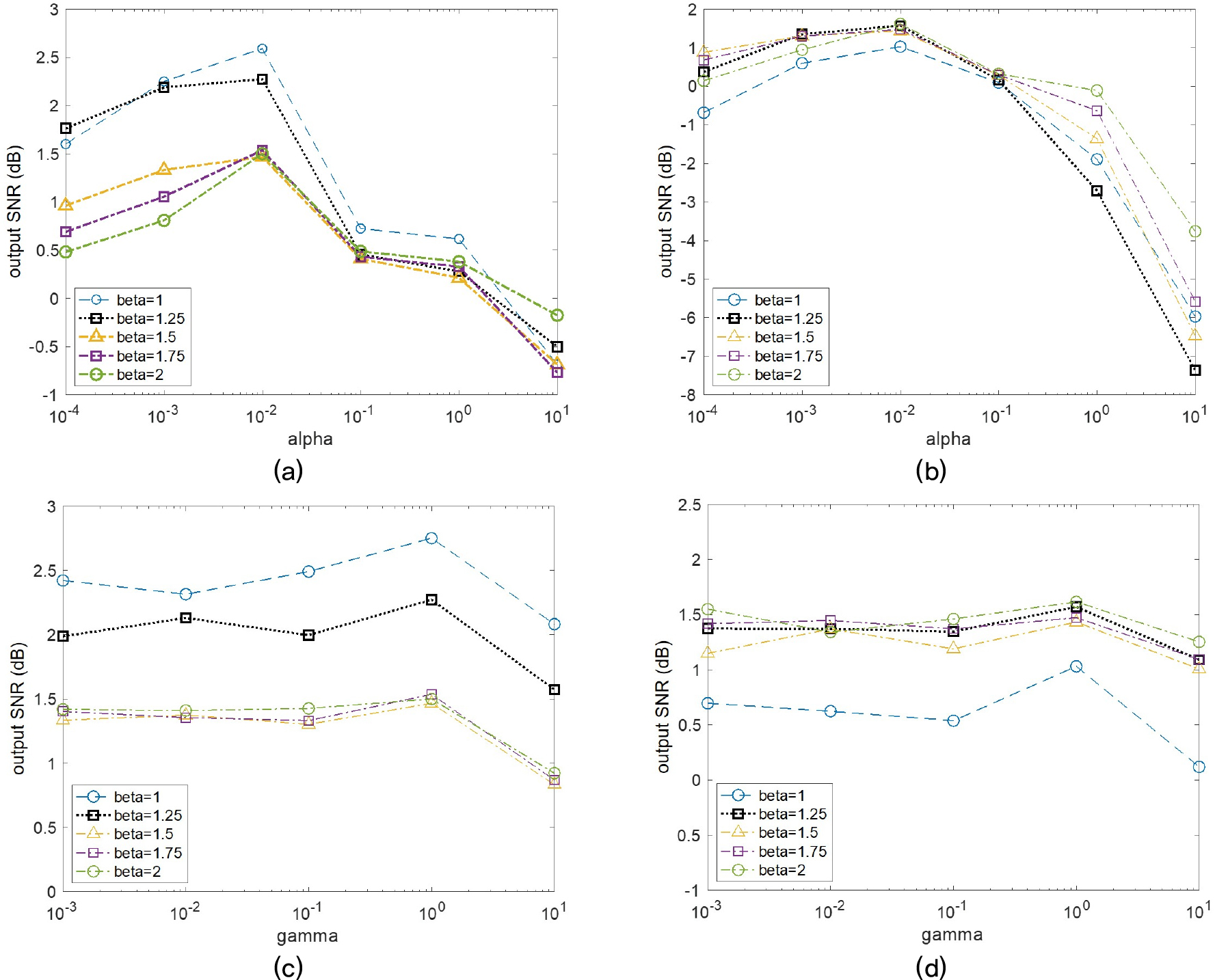
Fig. 7은 다양한 제약조건 가중치(𝛼 및 𝛾)에 대한 성능 변화를 보여주고 있다. Fig. 7(a)와 Fig. 7(b)는 각각 높은 신호대잔향비 및 낮은 신호대잔향비 환경에서 𝛼의 값을 0.0001부터 10까지 10배 단위로 바꾸어 값을 도시한 결과이다. 모든 𝛽에 대해 0.01에서 가장 높은 성능을 얻을 수 있는 것을 확인할 수 있으며, 0.1 보다 큰 𝛼에서는 성능이 저하되는 것을 확인할 수 있다. Fig. 7(c) 및 Fig. 7(d)는 𝛾의 값을 0.001부터 10까지 10배 단위로 바꾸어 값을 도시한 결과이다. 𝛾=1에서 가장 좋은 성능을 얻을 수 있으나, 비교적 그 값의 변화가 크지 않은 것을 확인할 수 있다. 다만 𝛾=10인 경우에는 성능 저하가 두드러지게 나타나므로, 𝛾는 1 이하의 값이 권장된다고 판단된다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-04/N0660430401/images/ASK_43_04_01_F7.jpg

Fig. 7.

(Color available online) Performance evaluation results depending on alpha [(a) for high input SRR (–9 dB) and (b) for low SRR (–18 dB)] and gamma [(c) for high input SRR (–9 dB) and (d) low input SRR (–18 dB)].

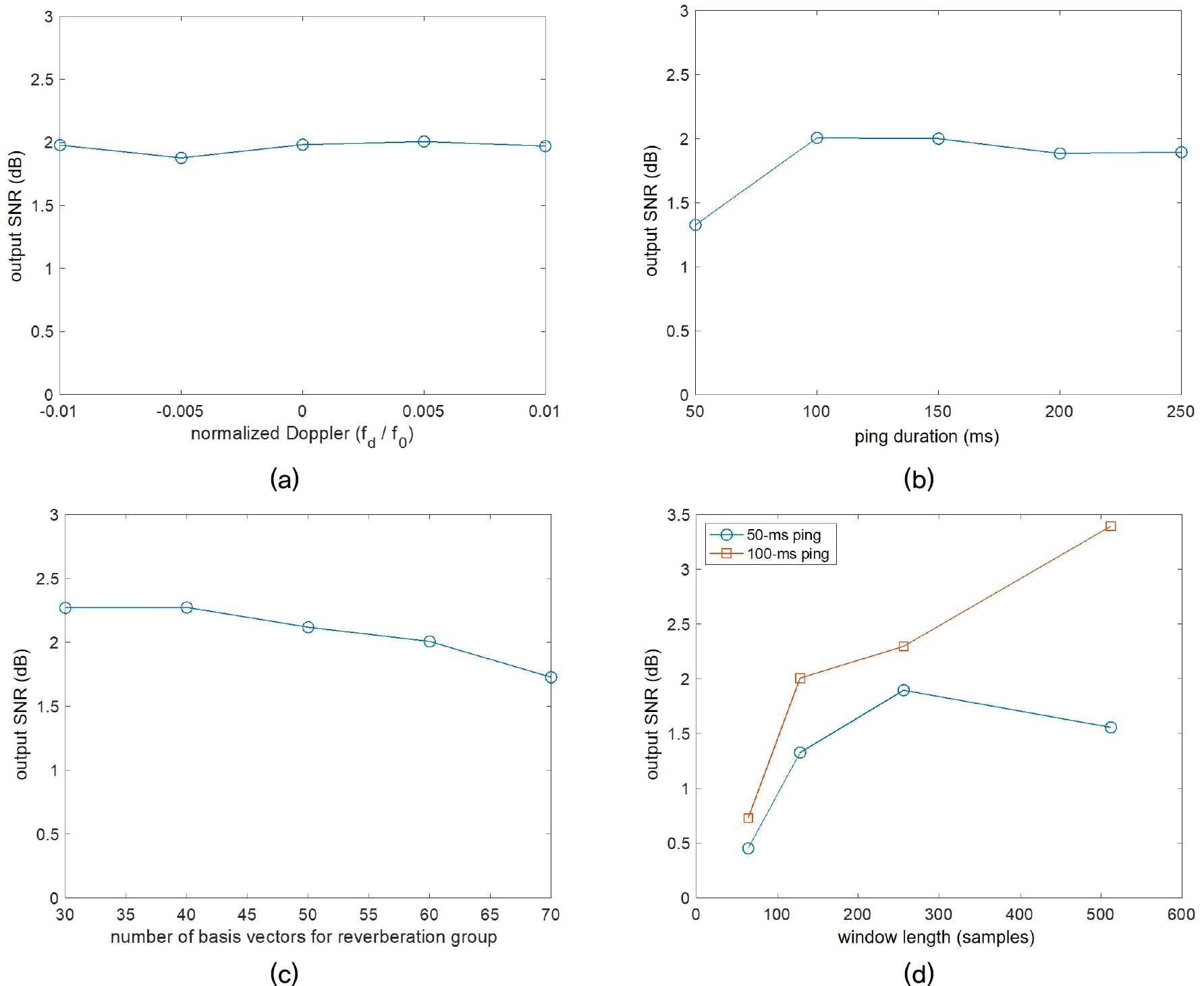
Fig. 8은 –12 dB의 입력 신호대잔향비 환경에서 여러 시나리오 환경 및 시스템 설정값에 따른 성능 변화를 도시한 그래프이다. Fig. 8(a)는 $- 0.01 f_{0} \leq f_{d} \leq 0.01 f_{0}$ 의 범위에서 표적 도플러의 변화에 따른 성능 변화를 보여주고 있으며, 해당 도플러 주파수 범위는 잔향의 주파수 대역 내에 표적 반향이 존재하는 저속 표적을 시뮬레이션 할 수 있는 범위로 설정되었다. Fig. 8(a)의 결과를 보면 저속 표적에 대한 알고리즘의 성능이 일정하게 확보되는 것을 확인할 수 있다. Fig. 8(b)는 송신 핑의 길이에 따른 성능의 변화를 도시하고 있으며, 대부분의 송신 핑에 대해 일정한 성능을 확보하는 것을 확인할 수 있다. 다만, 50 ms의 짧은 송신 핑에 대해서는 성능이 저하되는 것을 관찰할 수 있는데, 이는 푸리에 변환 윈도우의 길이에 비해 송신 핑의 길이가 충분히 길지 않아서, 시간 연속성 제약조건을 활용하는 이득이 감소되어 나타나는 현상으로 판단된다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-04/N0660430401/images/ASK_43_04_01_F8.jpg

Fig. 8.

(Color available online) Performance changes for (a) target Doppler frequencies, (b) ping durations, (c) number of basis vectors for reverberation group, and (d) window length with –12 dB input SRR condition.

Fig. 8(c)는 알고리즘의 설정 값인 기저 벡터의 개수에 따른 성능 변화를 도시하고 있다. 표적 반향 그룹의 기저 개수는 분석하고자 하는 도플러 범위에 따라 결정되는 값이기 때문에, 본 실험에서는 잔향 그룹의 기저 개수를 변화시켜 그 성능의 변화를 살펴보았다. 알고리즘의 성능이 기저 개수에 따라 크게 변하는 것은 아니지만, 전반적으로 기저 개수가 클수록 성능이 감소하는 경향을 보였다. 이는 기저 개수가 과도하게 커질 경우 표적 반향의 에너지가 감소되어 나타나는 현상으로 판단된다.

Fig. 8(d)는 푸리에 변환에 사용되는 해밍윈도우의 길이에 따른 성능 변화를 도시하고 있다. 75 % 중첩의 동일한 조건 하에 64샘플, 128샘플, 256샘플, 512샘플의 윈도우 길이에 대해 성능을 살펴보았으며, 전반적으로 윈도우의 길이가 증가할수록 성능이 증가하는 경향을 보인다. 이는 윈도우의 길이 증가에 따른 주파수 분해능의 향상에 의한 것으로 판단된다. 다만, 50 ms 핑을 사용한 경우 512샘플의 윈도우 사용 시 성능이 저하되는 현상을 보이는데, 이는 핑 길이보다 더 긴 윈도우를 사용하게 되어 주파수 분해능 증가에 따른 이득보다 시간 분해능 감소에 따른 손실이 더 큰 상황으로 판단된다.

V. 결 론

본 논문에서는 비음수 행렬 분해 기반의 잔향 제거 기법의 추정 비용 함수의 선택에 따른 성능의 변화에 대해 연구하여 알고리즘 설계에 대한 가이드를 제시하고 성능의 향상을 도모하고자 하였다. 기존의 연구에서는 추정 비용 함수로 쿨백-라이블러 발산 함수를 사용하여 알고리즘을 고안하였으나, 본 연구에서는 일반적으로 주로 사용되는 유클리드 거리, 쿨백-라이블러 발산, 이타쿠라-사이토 발산 함수를 모두 포괄할 수 있는 베타-발산 함수를 활용하여 알고리즘을 도출하였다. 도출된 알고리즘은 𝛽=0의 값에서 이타쿠라-사이토 발산과, 𝛽=1의 값에서 쿨백-라이블러 발산과, 그리고 𝛽=2에서 유클리드 거리와 동일하며, 𝛽 값의 선택에 따라 그 중간의 성질을 가지게 할 수도 있다.

본 논문에서는 합성된 잔향 신호를 활용한 몬테-카를로 시뮬레이션을 통하여 𝛽에 따른 성능 분석을 진행하였다. –21 dB ~ –9 dB의 입력 신호대잔향비 환경에 대하여 3 dB 간격으로 100회의 반복실험을 진행하여 그 성능의 평균을 산출하였으며, 출력 신호대잡음비로 성능을 측정하였다. 그 결과 높은 신호대잔향비에서는 기존과 같은 쿨백-라이블러 발산 함수(𝛽=1)가 유용하지만, 낮은 신호대잔향비에서는 1.25의 𝛽 값이 더 유용함을 확인할 수 있었다.

Acknowledgements

이 논문은 2024년 정부(방위사업청)의 재원으로 국방기술진흥연구소의 지원을 받아 수행된 물리데이터 기반 지능형 소나 신호 탐지 기술 연구임(No. KRIT-CT-22-052, 물리데이터 기반 지능형 소나 신호 탐지 기술 연구).

References

T. Collins and P. Atkins, "Doppler-sensitive active sonar pulse designs for reverberation processing," IEE Proceedings of Radar, Sonar, and Navigation, 145, 347-353 (1998).

10.1049/ip-rsn:19982434

G. Kim, K. Lee, K. Yoon, and S. Lee, "A study on pulse train waveforms for high duty cycle sonar systems: optimization scheme and relationship between orthogonality and bandwidth," IEEE Access, 9, 119800-119817 (2021).

10.1109/ACCESS.2021.3107907

S. Kay and J. Salisbury, "Improved active sonar detection using autoregressive prewhiteners," J. Acoust. Soc. Am. 87, 1603-1611 (1990).

10.1121/1.399408

G. Ginolhac and G. Jourdain, "Principal component inverse algorithm for detection in the presence of reverberation," IEEE J. Oean. Eng. 27, 310-321 (2002).

10.1109/JOE.2002.1002486

W. Li, Q. Zhang, X. Ma, and C. Hou, "Active sonar detection in reverberation via signal subspace extraction algorithm," EURASIP J. Wirel. Commun. Netw. 2010, 1-10 (2010).

10.1155/2010/981045

D. D. Lee and H. S. Seung, "Algorithms for non-negative matrix factorization," Proc. NeurIPS, 556-562 (2001).

D. D. Lee and H. S. Seung, "Learning the parts of objects by non-negative matrix factorization," Nature, 401, 788-791 (1999).

10.1038/4456510548103

P. Smaragdis and J. C. Brown, "Non-negative matrix factorization for polyphonic music transcription," Proc. IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, 177-180 (2003).

W. Wang, Y. Luo, J. A. Chambers, and S. Sanei, "Non-negative matrix factorization for note onset detection of audio signals," Proc. 16^th IEEE Signal Processing Society Workshop on Machine Learning for Signal Processing, 447-452 (2006).

10.1109/MLSP.2006.275592PMC1626491

M. Sun, Y. Li, J. F. Gemmeke, and X. Zhang, "Speech enhancement under low SNR conditions via noise estimation using sparse and low-rank NMF with Kullback-Leibler divergence," IEEE/ACM Trans. on Audio, Speech, and Lang. Process. 23, 1233-1242 (2015).

10.1109/TASLP.2015.2427520

A. Ozerov and C. Févotte, "Multichannel nonnegative matrix factorization in convolutive mixtures for audio source separation," IEEE Trans. on Audio, Speech, and Lang. Process. 18, 55-563 (2009).

10.1109/TASL.2009.2031510

S. Lee and J.-S. Lim, "Reverberation suppression using non-negative matrix factorization to detect low-doppler target with continuous wave active sonar," EURASIP J. Adv. Signal Process. 2019, 1-18 (2019).

10.1186/s13634-019-0608-6

G. Kim, K. Lee, and S. Lee, "Linear frequency modulated reverberation suppression using non-negative matrix factorization methods, dechirping transformation, and modulo operation," IEEE Access, 8, 110720-110737 (2020).

10.1109/ACCESS.2020.3001865

S. Lee and Y. Lee, "Improvement for non-negative matrix factorization-based reverberation suppression for bistatic active sonar" (in Korean), The J. Acoust. Soc. Kr. 41, 468-479 (2022).

A. Marmin, J. H. de Morais Goulart, and C. Fevotte, "Joint majorization-minimization for nonnegative matrix factorization with the beta-divergence," Signal Processing, 209, 109048 (2023).

10.1016/j.sigpro.2023.109048

D. Abaham and A. Lyons, "Simulation of non-rayleigh reverberation and clutter," IEEE J. Oceanic Eng. 29, 347-362 (2004).

10.1109/JOE.2004.828202

The Journal of the Acoustical Society of KoreaISSN:1225-4428(Print) 2287-3775(Online)한국음향학회

Preview

A study on the active sonar reverberation suppression method based on non-negative matrix factorization with beta-divergence function

ABSTRACT

MAIN

(1)

Fig. 1.

An illustrative diagram for NMF method.

(2)

(3)

Fig. 2.

(a) An illustrative diagram for NMF-based active sonar reverberation method, and (b) examples for magnitude spectrogram of simulated target echo and reverberation, respectively.

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

Table 1.

Summary of the proposed algorithm.

(24)

Fig. 3.

(Color available online) Performance comparisons for 𝛽 in various input SRR conditions.

Fig. 4.

(Color available online) Performance comparisons for input SRR conditions.

Fig. 5.

(Color available online) Magnitude spectrograms of (a) input signal and output signals when (b) 𝛽=1.0, (c) 𝛽=1.25, and (d) 𝛽=1.5 in high input SRR condition (–9 dB). Red arrow indicates target echo.

Fig. 6.

(Color available online) Magnitude spectrograms of (a) input signal and output signals when (b) 𝛽=1.0, (c) 𝛽=1.25, and (d) 𝛽=1.5 in low input SRR condition (–18 dB). Red arrow indicates target echo.

Fig. 7.

(Color available online) Performance evaluation results depending on alpha [(a) for high input SRR (–9 dB) and (b) for low SRR (–18 dB)] and gamma [(c) for high input SRR (–9 dB) and (d) low input SRR (–18 dB)].

Fig. 8.

(Color available online) Performance changes for (a) target Doppler frequencies, (b) ping durations, (c) number of basis vectors for reverberation group, and (d) window length with –12 dB input SRR condition.

Acknowledgements

References