I. Introduction
II. Related works
2.1 Sequence-to-sequence models
2.2 Attention mechanism
III. Double-attention mechanism
IV. Experiments
V. Conclusions
I. Introduction
Recently, sequence-to-sequence Deep Neural Networks (DNN) have been widely used in various tasks such as machine translation,[1,2] image captioning,[3] and speech recognition.[4,5,6,7] Attention mechanisms[8,9,10] are critical in the successful application of the sequence-to-sequence models to those tasks, because the models learn the mapping between differently sized input and output sequences by using the attention mechanisms, thus enabling the models to focus on the relevant portion of the input sequence for each output token.
For domains where the size of the input sequence is much larger than that of the output sequence, the attention mechanisms should be capable of handling a large area of the input focus for each output token. Particularly, in speech recognition, the input sequences (speech signals) are much longer than the corresponding output sequences (phoneme or word labels). Furthermore, the characteristic of the input speech signals often changes within a single phoneme segment due to the coarticulation effect, implying that a single context vector computed as a weighted average of the high-level representation of the input sequence is insufficient to cover the wide range of a varying input sequence.
In this work, we propose a double-attention mechanism that can handle a large area of the input focus with a varying characteristic caused by the left and the right context in the input. It uses two context vectors that cover the left and the right parts of the input focus separately. The experimental results of speech recognition on the TIMIT corpus show that the proposed method is effective in enhancing the speech recognition performance.
II. Related works
2.1 Sequence-to-sequence models
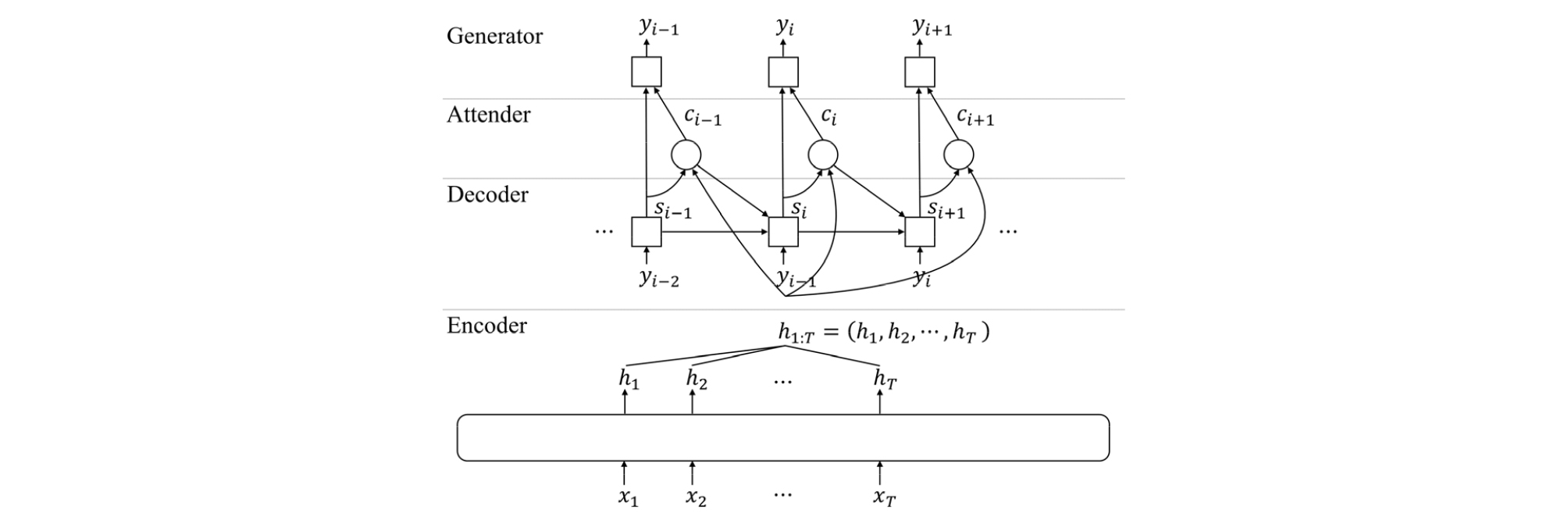
A sequence-to-sequence model uses the input vector sequence and produces the output token sequence , whose length may differ from that of the input sequence. As shown in Fig. 1, a sequence-to-sequence model typically consists of four modules: encoder, decoder, attender, and generator.
The encoder uses the input vector sequence and transforms the input into a high-level representation as follows:
| $$h_{1:T}=\mathrm{Encode}(x_{1:T}).$$ | (1) |
Long Short-Term Memory (LSTM)[11,12] networks or Convolutional Neural Networks (CNNs)[13,14] are typically used for the encoder. Depending on the architecture of the encoder, the length of may be shorter than that of .
The decoder computes its output at each output token time step by using the previous decoder’s output , the previous context vector , and the previous output token as follows:
| $$s_i=\mathrm{Decode}(s_{i-1},c_{i-1},y_{i-1}).$$ | (2) |
In this work, we used LSTM networks for the decoder.
The attender creates the context vector from the encoder’s output and the decoder’s output as follows:
| $$c_i=\mathrm{Attend}(h_{1:T},s_i).$$ | (3) |
The context vector can be considered as a relevant summary of that is useful in the prediction of the output token at each time step. Additionally, the attender may utilize the previous alignment vector, which will be explained in the following sections in detail.
The context vector and the decoder’s output are fed into the generator to produce the conditional probability distribution of the output token as follows:
| $$P(y_i│\;x_{i:T},y_{1:i-1})=\mathrm{Generate}(s_i,c_i).$$ | (4) |
The generator is typically implemented as a MultiLayer Perceptron (MLP) network with a softmax output layer.
2.2 Attention mechanism
The context vector at the output token time step is defined as a weighted sum of the encoder’s outputs ’s as follows:
| $$c_i=\sum_t^{}a_{i,t}h_t,$$ | (5) |
where the alignment vector is the probability distribution of the weights over . That is, represents the contribution of for the context vector , which is computed as follows:
| $$e_{i,t}=\mathrm{Score}(s_i,h_t),$$ | (6) |
| $$a_{i,t}=\exp(e_{i,t})/\sum_{t'}^{}\exp(e_{i,t'}).$$ | (7) |
Typical choice for the score function, , includes an additive score function and a multiplicative score function defined as follows:
| $$e_{i,t}=w^T\tanh(\phi(s_i)+\psi(h_t)),\;(\mathrm{additive})$$ | (8) |
| $$e_{i,t}=\phi(s_i)\bullet\psi(h_t),\;(\mathrm{multiplicative})$$ | (9) |
where is a dot product. and are typically implemented using MLPs. These score functions are said to be content-based because each element, , is computed from the content of the decoder’s output and the encoder’s output .
The hybrid attention mechanism suggested by Chorowski et al.[8] extends the content-based attention mechanism by utilizing the previous alignment vector . At each output token time step , the location-aware feature is calculated from the previous alignment vector as follows:
| $$f_i=F\otimes\;a_{i-1},$$ | (10) |
where is a learnable convolution matrix, and is a convolution operator. The location-aware feature is expected to facilitate the sequence-to-sequence model to learn the alignment better, as the current alignment between the speech signal and its corresponding text is dependent on the previous alignment information. It can be fed into the additive score function as follows:
| $$e_{i,t}=w^T\tanh(\phi(s_i)+\psi(h_t)+\theta(f_{i,t})),$$ | (11) |
where is another MLP.
III. Double-attention mechanism
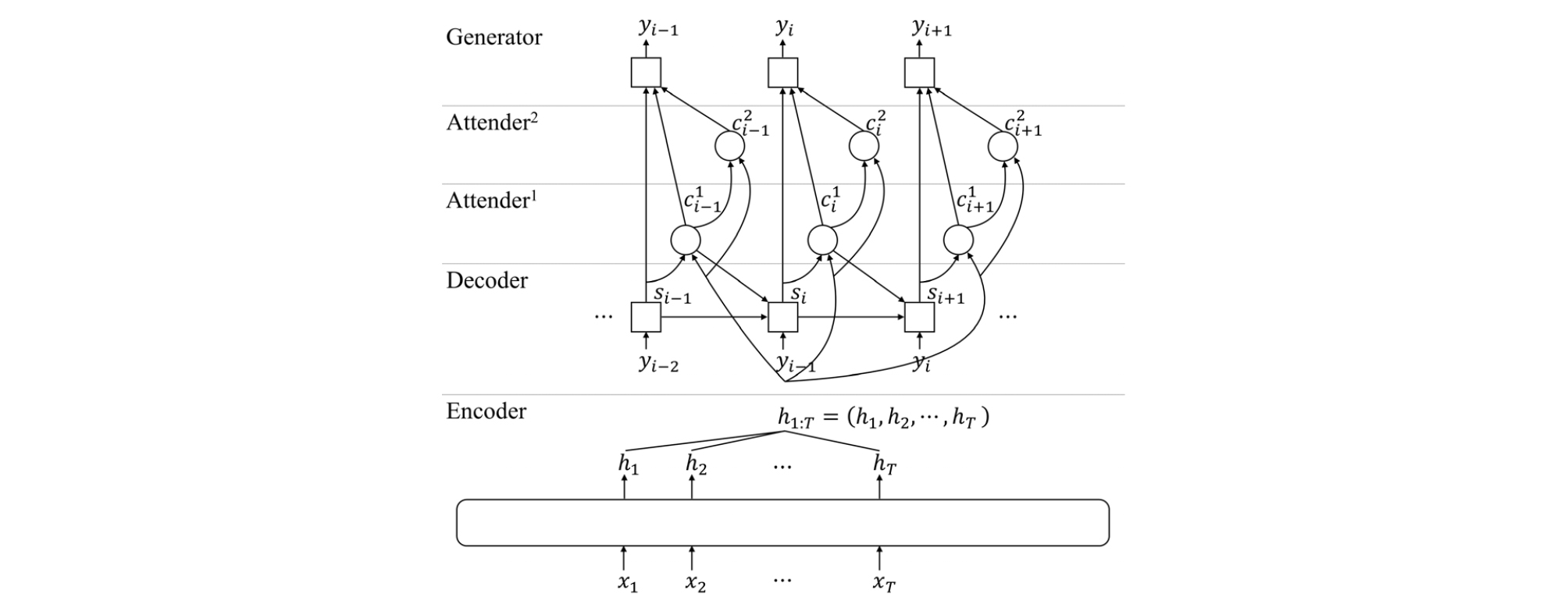
In speech recognition, the size of the encoder’s output sequence is much larger than that of its corresponding output token sequence. Furthermore, the left and the right speech contexts may affect the current phoneme to be pronounced, owing to the coarticulation effect as shown in Fig. 2. Therefore, a single context vector may not be sufficient to capture the relevant information in detail, because the single context vector represents the entire relevant information for each output token as a weighted sum of the long encoded sequence. A method to mitigate this problem is to use two separate context vectors computed by two attenders: one for the left context and the other for the right context,[15] as shown in Fig. 3.
The first context vector focusing on the left part of a phoneme is obtained using the attention vector which is computed from , , and as follows:
| $$f_i^1=F^1\otimes\;a_{i-1}^1,$$ | (12) |
| $$e_{i,t}^1=w^T\tanh(\phi^1(s_i)+\psi^1(h_t)+\theta^1(f_{i,t}^1)),$$ | (13) |
| $$a_{i,t}^1=\exp(e_{i,t}^1)/\sum_{t'}^{}\exp(e_{i,t'}^1),$$ | (14) |
| $$c_i^1=\sum_t^{}a_{i,t}^1h_t.$$ | (15) |
Similarly, the second attention vector and the second context vector are computed as follows to focus on the right part of the phoneme:
| $$f`_i^2=F^2\otimes\;a_i^1,$$ | (16) |
| $$e_{i,t}^2=v^T\tanh(\phi^2(c_i^1)+\psi^2(h_t)+\theta^2(f_{i,t}^2)),$$ | (17) |
| $$a_{i,t}^2=\exp(e_{i,t}^2)/\sum_{t'}^{}\exp(e_{i,t'}^2),$$ | (18) |
| $$c_i^2=\sum_t^{}a_{i,t}^2h_t.$$ | (19) |
It is worth noting that utilizes instead of , and is used instead of in computing . Hence, the second attention vector is expected to attend to different parts of the input sequence in contrast to the first attention vector , because it considers the first context vector and its alignment information .
As the multiplicative score function generally exhibits better performance than the additive score function, further improvements can be achieved by modifying Eqs. (13) and (17) to use the multiplicative score functions that utilize the location-aware feature as follows:
| $$e_{i,t}^1=\phi^1(s_i)\bullet\;\psi^1(h_t)+w^T\tanh(\theta^1(f_{i,t}^1)),$$ | (20) |
| $$e_{i,t}^2=\phi^2(c_i^1)\bullet\;\psi^2(h_t)+v^T\tanh(\theta^2(f_{i,t}^2)).$$ | (21) |
Finally, the generator is modified to use both and as well as to compute the posterior probability as follows:
| $$P(y_i│\;x_{i:T},y_{1:i-1})=\geq\;\neq\;\mathrm{rate}(s_i,c_i^1,c_i^2).$$ | (22) |
The multi-head attention method[10] is similar to the proposed double-attention method in that it inhibits a single averaged context vector. In the multi-head attention method, the input is linearly projected into several subspaces, and the attention is computed in each subspace differently to form multiple attentions. However, it does not care which position to attend to and the order of the multiple attentions. The proposed double-attention mechanism is designed to specifically attend to different parts with an order, i.e., the left and the right parts of a phoneme, to cope with the coarticulation effect. The first context vector is computed using the information available at the previous time ( and ), while the second context vector is computed using the information available at the current time ( and ). Therefore, the two context vectors are expected to attend to different parts of the phoneme.
IV. Experiments
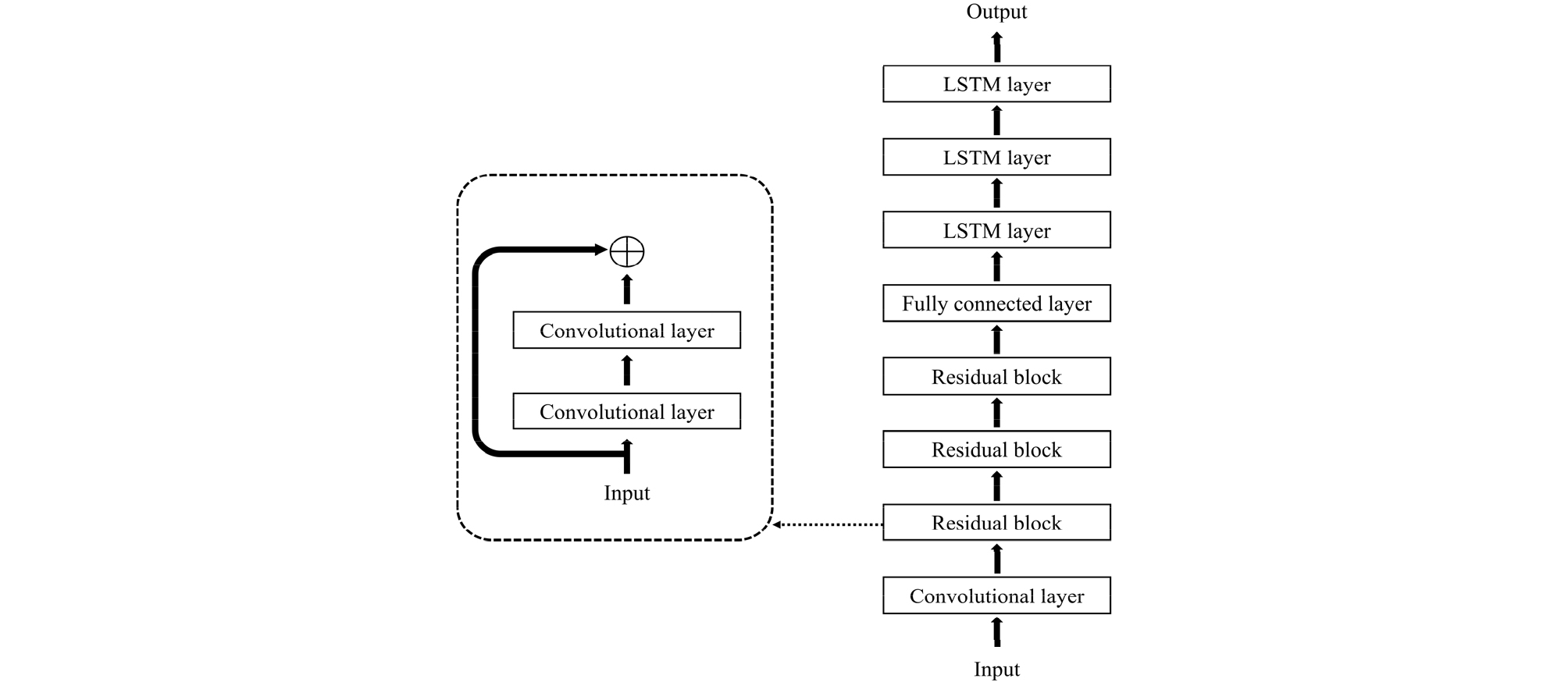
To evaluate the effectiveness of the proposed method, speech recognition experiments were conducted using the TIMIT corpus. 40-dimensional Mel-scaled log filter banks with their first and second order temporal derivatives were used as the input feature vectors. The decoder was a single-layer unidirectional LSTM network, whereas the encoder was a deep architecture consisting of seven CNN layers followed by a fully connected layer and three bidirectional LSTM layers as shown in Fig. 4. The first convolutional layer used 256 filters, and the rest of the convolutional layers used 128 filters. The CNN layers used residual connections and batch normalization.[16] The fully connected layer had 1,024 nodes. Each bidirectional LSTM layer had 256 nodes for each direction. To train the model, the Adam algorithm with a learning rate of 10–3, a batch size of 32, and gradient clipping of 1 was used. A dropout with a probability of 0.5 was used across every neural network layer.
Fig. 5 shows example attention vectors for the conventional single-attention mechanism and the proposed double-attention mechanism. As shown in the figure, the area of the single-attention focus (solid lines) is split into two regions (dotted lines for the left context and dashed lines for the right context) using the proposed double- attention mechanism.
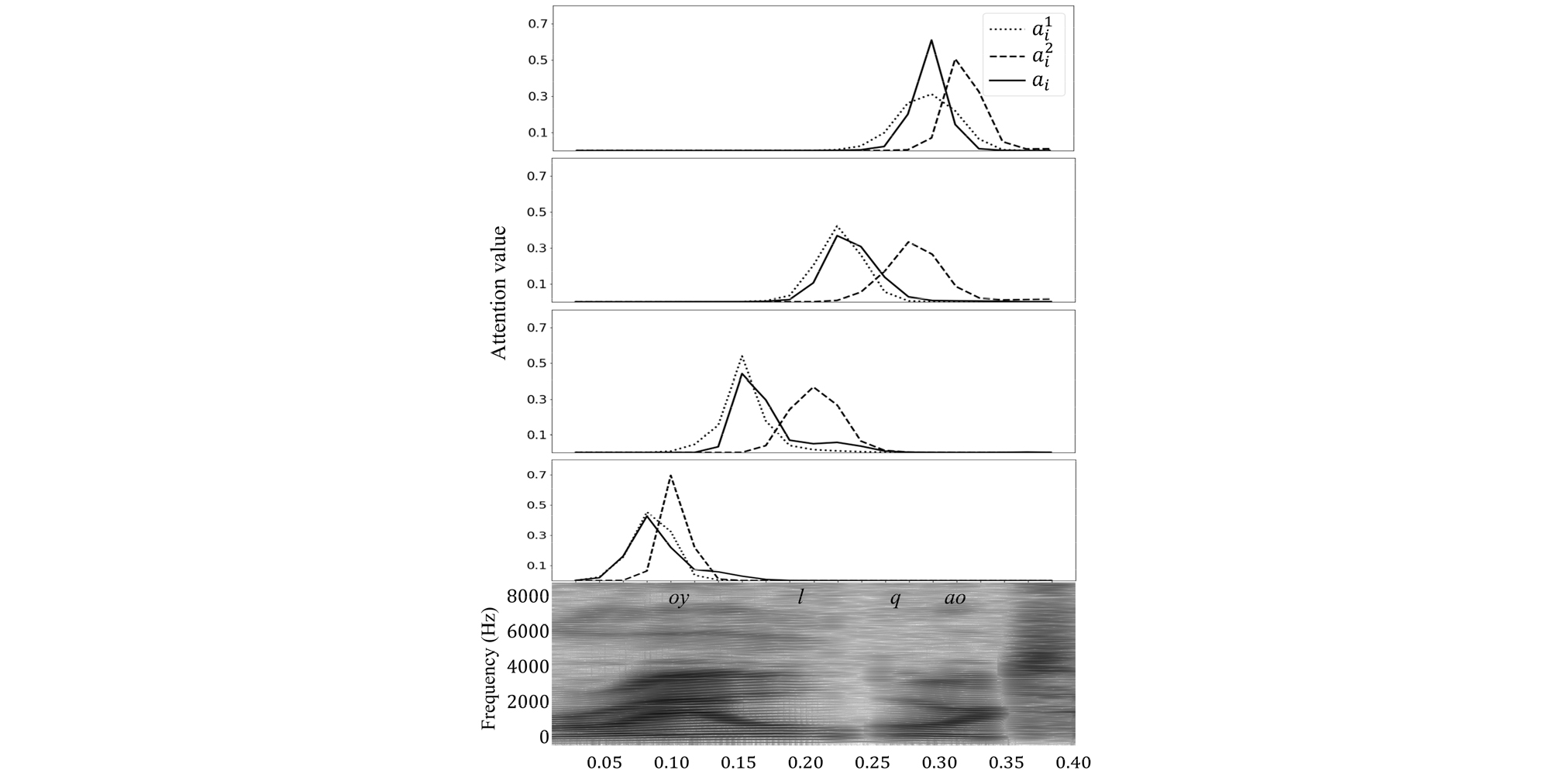
Fig. 5.
Alignment examples of four phonemes “oy”, “l”, “q” (glottal stop), and “ao” in the middle of words “broil or”. Solid lines () represent the alignment vector produced by the conventional single-attention mechanism. Dotted lines () and dashed lines () represent the left and the right alignment vectors produced by the proposed double-attention mechanism.
Table 1 shows the Phone Error Rate (PER) of the speech recognition systems using various attention mechanisms of the sequence-to-sequence models. As shown in the table, the proposed double-attention mechanism with the multiplicative score function reduces the PER by 4 % relatively compared to the baseline system, which uses the conventional single-attention mechanism. When the attention mechanism is replaced with the multi-head attention method,[10] the PER rises to 17.3 %.
V. Conclusions
We herein proposed a double-attention mechanism for the sequence-to-sequence deep neural networks to handle large input focuses with changing characteristics. Furthermore, the multiplicative score function with the location- aware feature was proposed to better utilize the left and the right contexts of the input. The experimental results of the speech recognition task on the TIMIT corpus verified that the proposed double-attention mechanism indeed attended to the left and the right contexts of the input focus and reduced the speech recognition error rates.
The conventional speech recognition systems with Hidden Markov Models (HMM) typically uses three states for a phone model. This corresponds to a triple-attention mechanism in the sequence-to-sequence deep neural networks, which will be our future research direction.