I. 서 론
군사적 목적의 수중 음향 통신은 수중에서 적의 도청을 방지하기 위해 Low Probability Detection(LPD) 또는 Low Probability Intercept(LPI) 통신 시스템을 이용한다.[1,2,3,4,5] 최근에는 수중 생물의 소리를 모방한 생체 모방 음향 통신 기법이 활발히 연구되고 있다.[6,7,8,9,10,11,12,13,14]
생체 모방 음향 통신 기법은 통신 신호를 수중 생물의 소리와 유사하게 생성하여 아군에게 통신 신호를 전송하는 것으로, 적이 통신 신호를 탐지하더라도 수중 생물의 소리로 오인하게 함으로써 은밀히 아군에게 통신 신호를 전송할 수 있다.
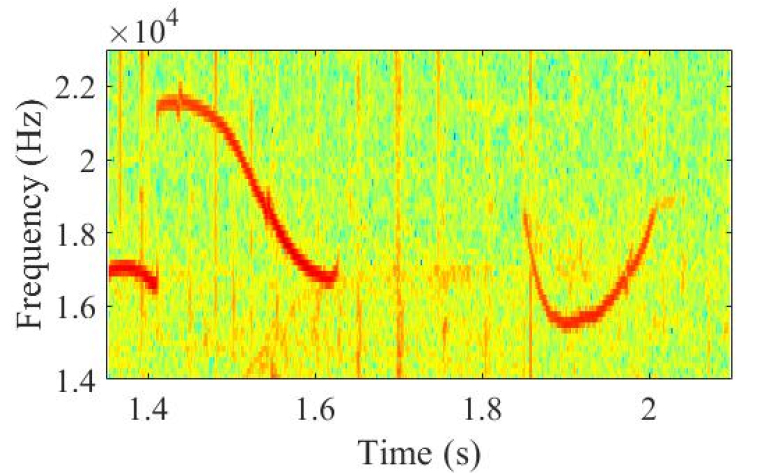
돌고래 휘슬음은 시간 및 주파수 영역에서의 특정한 패턴을 가지고 있으며 이 패턴을 주파수 윤곽(frequency contour)이라 하는데 이와 유사한 패턴을 갖도록 신호를 생성하면 사람이 듣게 되는 소리가 원래의 돌고래 휘슬음과 유사해진다.[6,7,8,13,14]
Reference [6]에서는 Chirp Spread Spectrum(CSS) 기반으로 돌고래 휘슬음을 모방하는 방법을 제안하였다. 본래의 돌고래 휘슬음과 유사한 주파수 윤곽을 갖는 통신 신호를 생성하기 위해서, CSS 변조기법은 모방하고자 하는 돌고래 휘슬음을 시간 영역에서 여러 개의 슬롯으로 나눈다. 나눠진 매 시간 슬롯마다 존재하는 돌고래 휘슬음의 중심 주파수들을 추출한 후, 매 슬롯에 전송하고자 하는 비트에 따라 상향 또는 하향 처프(chirp)를 추출한 중심주파수를 갖도록 할당하여 변조한다. CSS 기반 생체 모방 변조 기법은 처프율(chirp rate)과 시간 슬롯 길이가 작은 경우에는 돌고래 휘슬음의 주파수 윤곽에 왜곡이 적지만, 복조 시에 상향 및 하향 처프 간의 유사 직교성(quasi-orthogonality)을 이용하기 때문에 처프율과 시간 슬롯 길이가 작을수록 신호 복호 성능이 저하된다.[7,14] 이와 반대로 처프율과 시간 슬롯 길이가 큰 경우에는 복호성능은 향상되지만 주파수 윤곽에 왜곡이 커져서 모방성능이 저하된다.[7,8,14]
Reference [7]에서는 CSS 변조기법의 복호 성능을 개선하기 위해 Frequency Shift Keying(FSK) 기반 돌고래 휘슬음 모방 변조 기법을 제안하였다. FSK 변조기법은 CSS 변조기법과 유사하게 모방하고자하는 휘슬음을 시간 영역에서 여러 개의 슬롯으로 나눈 후 매 슬롯의 중심 주파수에 따라 FSK로 변조하여 모방 신호를 생성한다. CSS 변조기법은 상향 및 하향 처프들 간의 유사 직교성을 이용하지만 FSK는 주파수 상에서 심볼 간의 직교성을 이용하기 때문에, CSS 변조기법에 비해 비트오류율(Bit Error Rate, BER) 성능이 3 dB 만큼 Signal-to-Noise power Ratio (SNR) 이득을 갖는다. 그러나 CSS와 FSK 기반 생체 음향 모방 통신 기법들은 원래의 돌고래 휘슬음과 유사한 주파수 윤곽을 갖지만 주파수 윤곽이 불연속적이다는 단점이 있다. 또한, CSS의 경우에는 변조 차수가 2로 고정적이며, FSK의 경우 변조 차수를 증가시키면 모방 통신 신호의 주파수 대역이 변조 차수의 배수만큼 증가하게 되며, 모방 성능의 열화량이 커진다.
본 논문에서는 기존 CSS 및 FSK 모방 변조 기법들의 문제들을 해결하기 위해 Orthogonal Frequency Division Multiplexing(OFDM) 기반 생체 모방 변조 기법을 제안한다. OFDM은 할당된 주파수 대역폭을 Fast Fourier Transform(FFT) 및 Inverse FFT(IFFT)를 이용하여 여러 개의 부반송파(subcarrier)로 나누어 통신 신호를 전송하는 방법이다. OFDM 기반 생체 모방 음향 통신 기법은 실제 돌고래 휘슬음을 모방하기 위해서, 모방하고자 하는 휘슬음을 시간 영역에서 OFDM 심볼 할당이 가능한 여러 개의 시간 슬롯으로 나눈 후, 매 시간 슬롯에서 돌고래 휘슬음이 위치한 부반송파에 통신 심볼을 매핑하여 변조한다. 변조 방식의 특성상 통신 심볼이 매핑된 각 자원요소들은 주파수 윤곽에 따라 시간에 따른 주파수 대역이 달라지며 채널 추정을 위한 파일럿을 할당할 수 있는 자원 요소가 한정적이기 때문에 채널 추정이 필요 없는 Differential Phase Shift Keying(DPSK)로 변조한다.
본 논문에서 제안한 방법은 기존의 CSS와 FSK 변조기법들과는 달리 OFDM 각 심볼의 부반송파에 에너지가 있기 때문에 주파수 윤곽 상의 불연속성이 감소하여 모방 성능이 증가한다. 또한 각 OFDM 심볼은 DPSK로 변조하기 때문에 BER 성능도 FSK와 CSS 변조기법들에 비해 우수하다.[8] 그리고 FSK 변조 기법과는 달리 변조 차수가 증가하여도 모방 통신 신호의 시간 주파수 영역의 변화가 발생하지 않기 때문에 모방 성능의 열화량이 적다는 장점도 있다. 따라서, 제안 방법을 사용 시 채널 환경에 따라 적응적으로 변조차수를 조정하여 전송률을 높일 수 있다. 제안 기법과 기존의 CSS 그리고 FSK 변조 방식의 성능을 비교 분석하기 위해 전산 모의실험을 수행하였으며 제안 방법의 BER 성능이 우수함을 보였다. 그리고 모방 신호와 변조 신호 간의 상호 상관도를 측정하여 모방 성능을 분석하였으며 기존 기법들에 비해 제안 방법의 모방 성능이 우수함을 보였다.
본 논문의 구성은 다음과 같다. 2절에서 본 논문에서 제안한 방법에 대해 설명한 후 3절의 전산 모의실험을 통해 제안한 방법과 기존의 방법들의 BER과 모방성능을 보인다. 그리고 4절에서 결론을 맺는다.
II. 제안 방법
돌고래 휘슬음은 Fig. 1에 나타낸 스펙트로그램과 같이 시간에 따라 주파수가 변화한다. 통신 신호의 시간 및 주파수 패턴을 돌고래 휘슬음의 주파수 윤곽과 유사한 형태를 갖도록 생성하게 되면 사람이 듣게 되는 소리가 모방한 휘슬음과 유사해 진다. 본 절에서는 본 논문에서 제안한 OFDM 기반 돌고래 휘슬음 모방 변조 기법에 대해 설명한다.
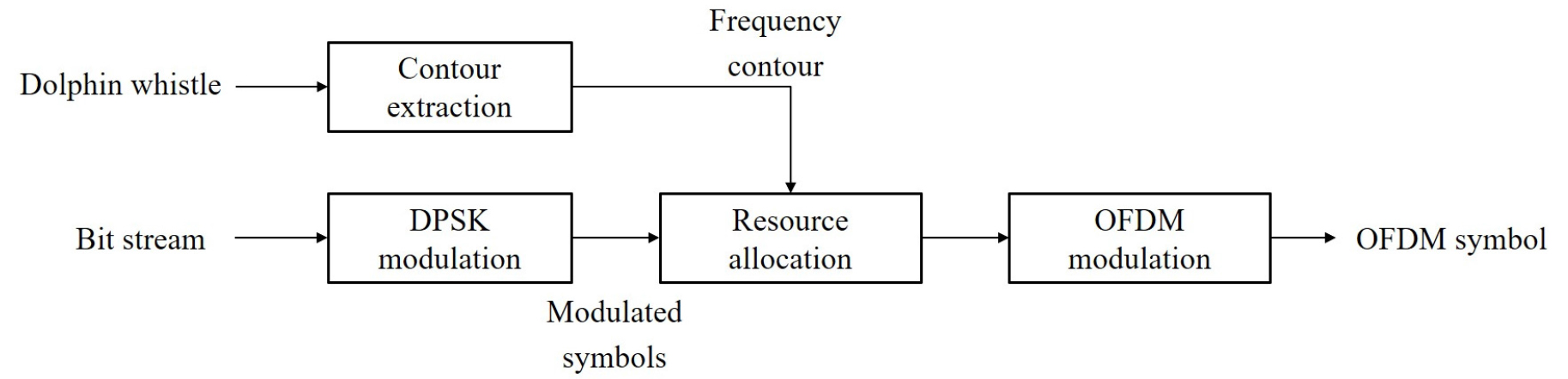
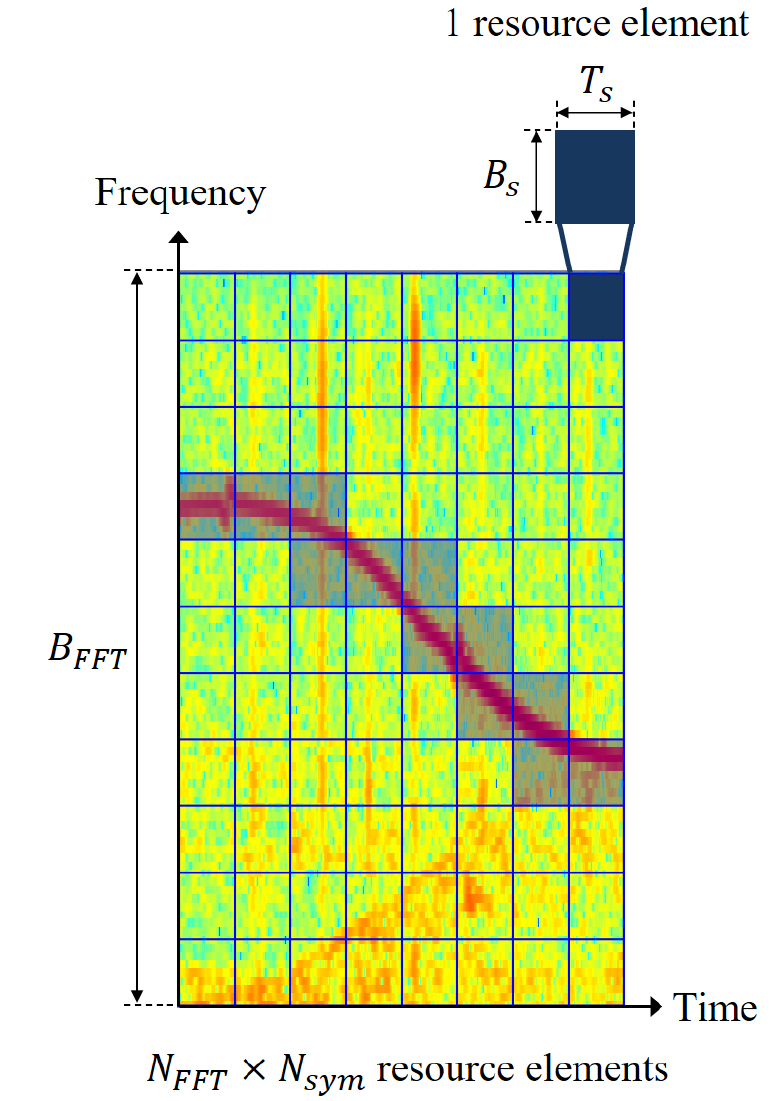
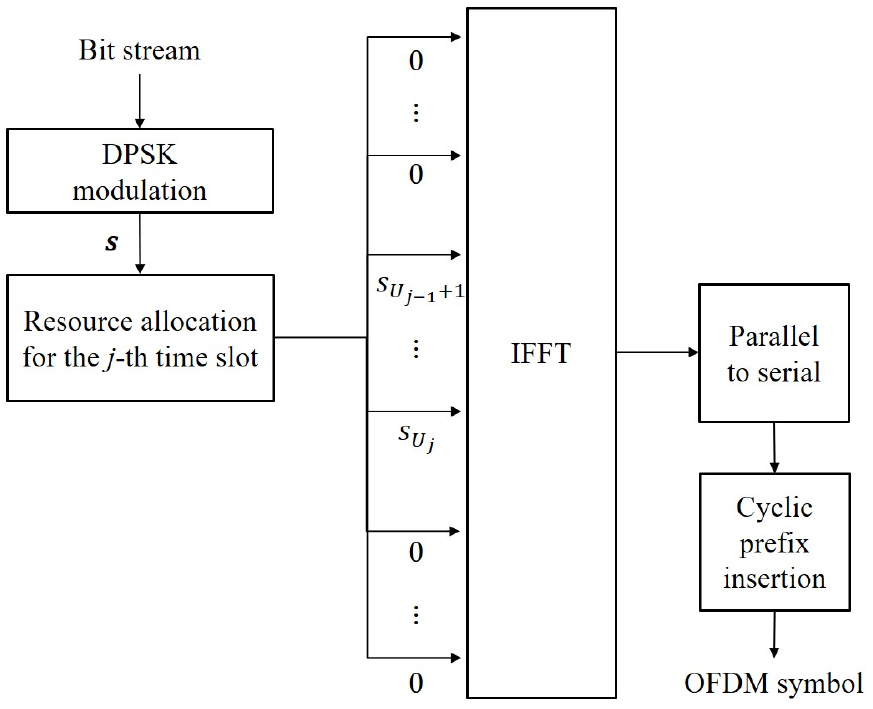
제안한 OFDM 기반 돌고래 휘슬음 모방 변조 기법의 블록도를 Fig. 2 나타내었다. 모방하고자 하는 돌고래 휘슬음을 OFDM의 자원 요소의 크기에 따라 Fig. 3에서 보는 바와 같이 시간 및 주파수 영역에서 여러 슬롯으로 나눈다. Fig. 3에서 는 FFT를 위한 OFDM의 주파수 대역폭이고 는 하나의 부반송파의 주파수 대역폭이다. 그리고 는 OFDM 한 심볼 길이이며 와 은 각각 FFT 크기와 OFDM 심볼의 수이다. 개로 나눠진 슬롯에서 돌고래 휘슬음이 위치하는 자원 요소들을 추출하여 돌고래 휘슬음의 주파수 윤곽을 얻는다. 얻어진 주파수 윤곽에 해당하는 자원 요소들에 통신 심볼을 매핑하여 모방 신호를 생성한다.
돌고래 휘슬음의 주파수 윤곽은 Short Time Fourier Transform(STFT)로 얻을 수 있다. 샘플링된 돌고래 휘슬음을 이라 하고 을 윈도우라 한다. 샘플링 레이트를 라 할 때, STFT의 변수인 윈도우 길이와 FFT 크기를 각각 와 로 하면, 번째 시간 슬롯에서의 번째 주파수 슬롯에서의 에 대한 STFT ( )는 다음과 같이 얻어진다.
위 Eq. (1)에서 이며, 돌고래 휘슬음의 시간 길이를 라 할 때, 이다. 그리고 이고 이다.
Eq.(1)로부터 얻어진 STFT 결과의 시간-주파수 해상도는 OFDM의 자원 요소들의 시간-주파수 위치와 일치하므로 돌고래 휘슬음을 모방할 수 있다. 따라서 돌고래 휘슬음이 위치한 시간-주파수 위치를 추출하고 해당 위치에 통신 심볼을 매핑하면 모방하고자 하는 돌고래 휘슬음과 유사한 주파수 윤곽을 갖는 통신 신호를 생성할 수 있다.
실제 돌고래 휘슬음은 해양 잡음 등에 의해 오염된 신호이기 때문에 돌고래 휘슬음의 시간-주파수 위치를 추정하기 위해서 잡음 하에 존재하는 신호 성분을 검출할 때 널리 사용하는 기법인 Constant False Alarm Rate(CFAR) 검출기를 이용한다.[15,16,17,18,19,20]
CFAR 검출기는 고정된 오경보율(false alarm rate, )에 대한 임계 값을 계산하고, 수신 신호에서 임계 값 이상인 성분을 검출하는 기법으로 본 논문에서는 Cell Average(CA) CFAR 검출기를 이용한다. CA-CFAR 검출기는 수신 신호의 연속적인 데이터를 훈련 셀과 보호 셀 그리고 테스트 셀에 대해 한 샘플씩 이동시켜가며 입력한다. 훈련 셀과 보호 셀은 테스트 셀의 양방향에 구성되어 있으며, 훈련 셀을 통해 테스트 셀의 주변 신호 전력을 추정한다. 추정된 주변 신호 전력으로부터 오경보율에 따른 임계 값을 계산하고, 임계 값과 테스트 셀의 전력을 비교하여 임계 값 이상의 신호를 검출한다.
STFT 결과에서 돌고래 휘슬음의 시간-주파수 위치를 추정하기 위해서 각 시간 영역 슬롯에서의 주파수 성분들을 CA-CFAR의 입력으로 한다. 임의의 번째 시간 영역 슬롯의 임의의 번째 주파수 성분이 테스트 셀인 경우, 훈련 셀의 크기가 이고 보호 셀의 크기가 이면 ,훈련 셀로부터 추정된 주변 신호 전력, 는 다음 식으로 표현된다.
번째 시간 영역 슬롯의 번째 주파수 성분에 대한 CA- CFAR의 임계 값()은 다음 식으로 계산된다.[16]
Eq. (3)으로부터 계산된 임계 값을 이용하여 돌고래 휘슬음의 주파수 윤곽을 추출하며, 돌고래 휘슬음과 유사한 주파수 윤곽을 갖도록 매핑할 수 있는 시간 및 주파수 영역에서의 자원 요소 위치, 은 Fig. 3에서 휘슬음이 위치한 부분이며 반투명 회색으로 표시한 영역을 의미한다. 그리고 은 다음 식으로 표현된다.
위 Eq. (4)에서 계산된 은 이며, 는 CA-CFAR로부터 추출된 할당 가능한 자원요소의 수이다. 즉, 개의 통신 심볼을 휘슬음 모방 통신 신호로 전송할 수 있다. 그러나 돌고래 휘슬음의 주파수 윤곽에 따라 주파수 대역이 달라져 채널이 서로 다르고, 채널 추정을 위한 파일럿을 할당할 수 있는 자원 요소가 한정적이다. 따라서 본 논문에서는 채널 추정이 필요하지 않는 DPSK로 변조된 심볼을 이용한다.
DPSK로 변조된 개의 심볼 을 추출된 자원 요소 위치 에 OFDM을 이용하여 매핑하기 위해서, 을 각 시간 영역 슬롯에 따라 재 정렬한다. 임의의 번째 시간 영역 슬롯에 대하여 재 정렬된 주파수 좌표 집합을 라 하면, 는 다음과 같이 표현된다.
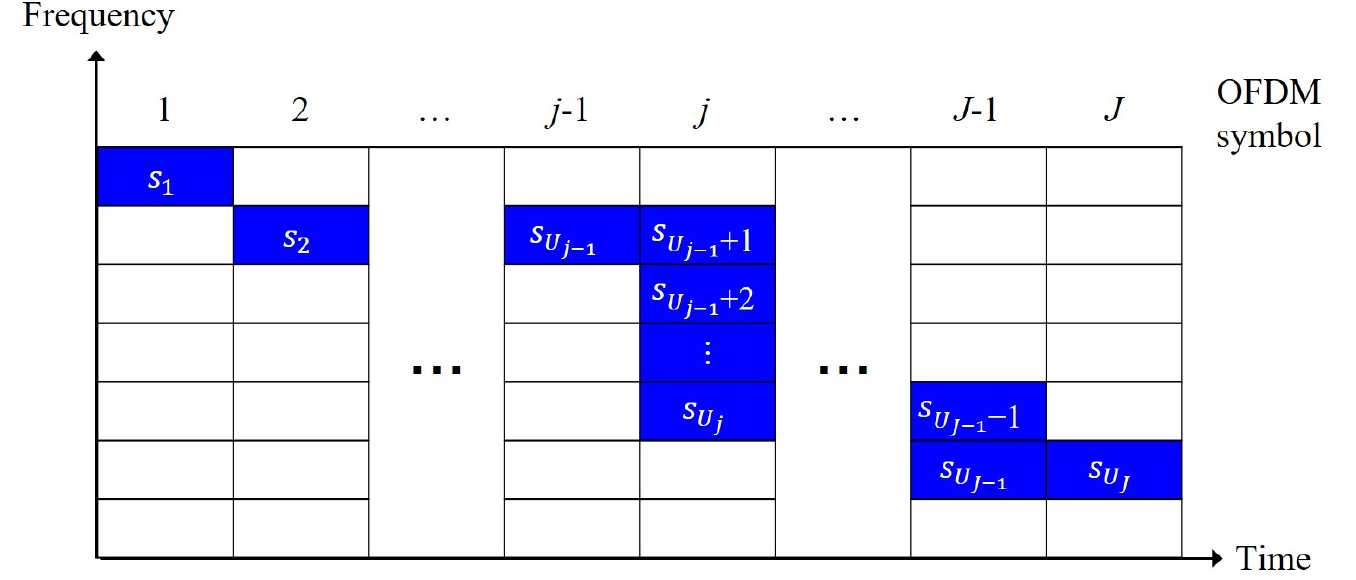
첫 번째 시간 슬롯에서 임의의 번째 시간 슬롯까지 매핑된 DPSK 심볼 수의 총 합을 라 하면, 번째 시간 슬롯에 할당할 수 있는 DPSK 심볼은 이고 , 자원요소에 매핑된 DPSK 심볼의 예를 Fig. 4에 나타내었다. DPSK 심볼을 의 OFDM의 자원 요소에 매핑하기 위해 IFFT를 수행하는데, 에 해당하지 않는 자원 요소에는 0을 입력으로 한다. 이러한 자원 할당 방식을 Fig. 5에 블록도로 나타내었다. 번째 시간 슬롯의 OFDM 심볼 은 다음 식으로 표현된다.
위 Eq. (6)에서 은 의 번째 원소이다. Eq. (6)을 이용하여 OFDM을 기반으로 하는 돌고래 휘슬음 모방 통신 신호를 생성하며 이 신호는 실제 돌고래 휘슬음의 주파수 윤곽과 유사한 패턴을 갖게 되어 사람에게 들리는 소리가 유사해진다.
III. 전산 모의실험
본 절에서는 본 논문에서 제안한 OFDM 기반 돌고래 휘슬음 모방 변조 기법의 BER 및 모방 성능을 전산 모의실험을 통해 기존의 CSS 및 FSK 기반 변조 기법들과 비교 분석한다. BER 성능은 가산 백색 가우스 잡음(Additive White Gaussian Noise, AWGN)과 Rician 채널에 대하여 분석한다. 그리고 모방 성능은 References [7]과 [8]에서 사용한 상호 상관을 통해 분석한다.
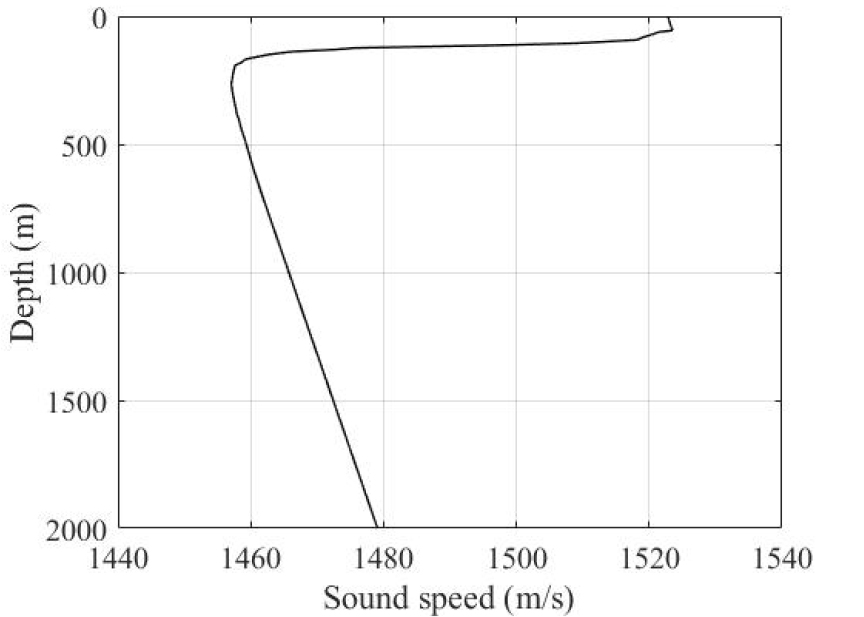
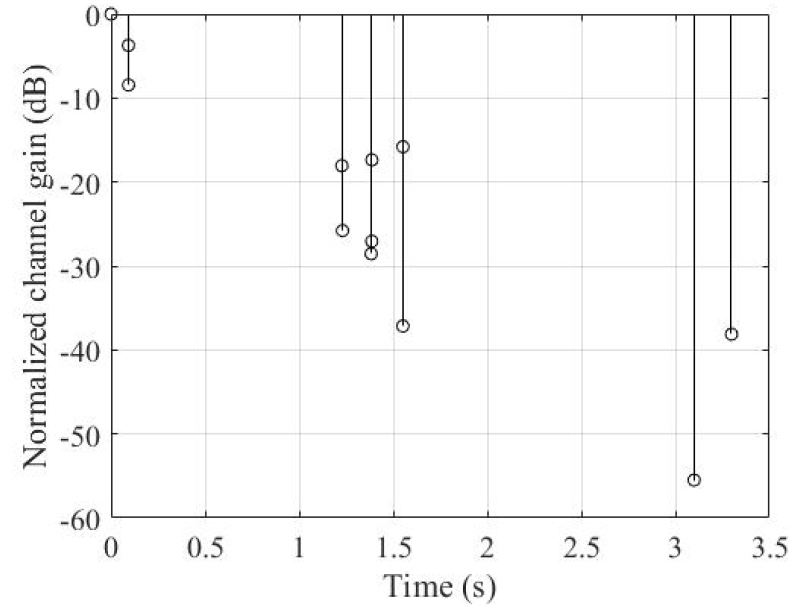
전산 모의실험의 모방 대상 돌고래 종은 낫돌고래로써, 한국 연안에 서식하는 돌고래 종이며 주로 동해에서 발견된다.[21] 돌고래가 주로 서식하는 환경에서 해당 돌고래의 모방 통신 신호를 사용하는 것이 적합하므로, 동해 수중 음향 채널을 모델링하여 BER 성능을 분석하였다. Fig. 6의 동해 정점의 수직음속구조(Sound Speed Profile, SSP)를 이용하여 수중 음향 채널을 Bellhop을 통해 생성하였으며, 환경 변수들을 Table 1에 나타내었다. Table 1에서 감쇠 계수와 해저 밀도는 Reference [22]에서 동해 수중 음향 채널 모델링에 사용한 값을 이용하였으며, 해저면은 평평한 것으로 가정하였다. Bellhop을 통해 생성된 동해 수중 음향 채널의 채널 임펄스 응답(Channel Impulse Response, CIR)을 Fig. 7에 나타내었다.
Table 1.
Underwater channel parameters.
| Parameters | Values |
| Transmitter depth | 200 m |
| Receiver depth | 200 m |
| Distance | 10 km |
| Sound speed at bottom | 1457 m/s |
| Bottom density | 1.48 g/cm3 |
| Attenuation coefficient | 0.1 dB/λ |
Fig. 7에서 보는 바와 같이 두 번째 경로는 정규화된 채널 이득이 -3.7 dB인 93 ms의 긴 지연시간을 갖는다. 이 CIR을 이용하여 Rician 채널을 생성하였고, 이때 모든 경로의 K-factor는 20 dB 그리고 도플러 천이(Doppler shift)는 4 Hz로 설정하였다.
전산 모의실험에 사용된 각 기법들의 변조 파라미터들을 Table 2에 나타내었다. CSS의 처프율은 심볼 길이인 4 ms와 심볼 대역폭인 250 Hz 간의 비율로 62.5 Hz/ms 이다.
Table 2.
Modulation parameters.
| Scheme | Proposed | CSS | FSK |
| FFT size | 192 | - | - |
| Symbol duration | 4 ms | ||
| Symbol bandwidth | 250 Hz | ||
| Whistle duration | 200 ms | ||
| Sampling rate | 192 kHz | ||
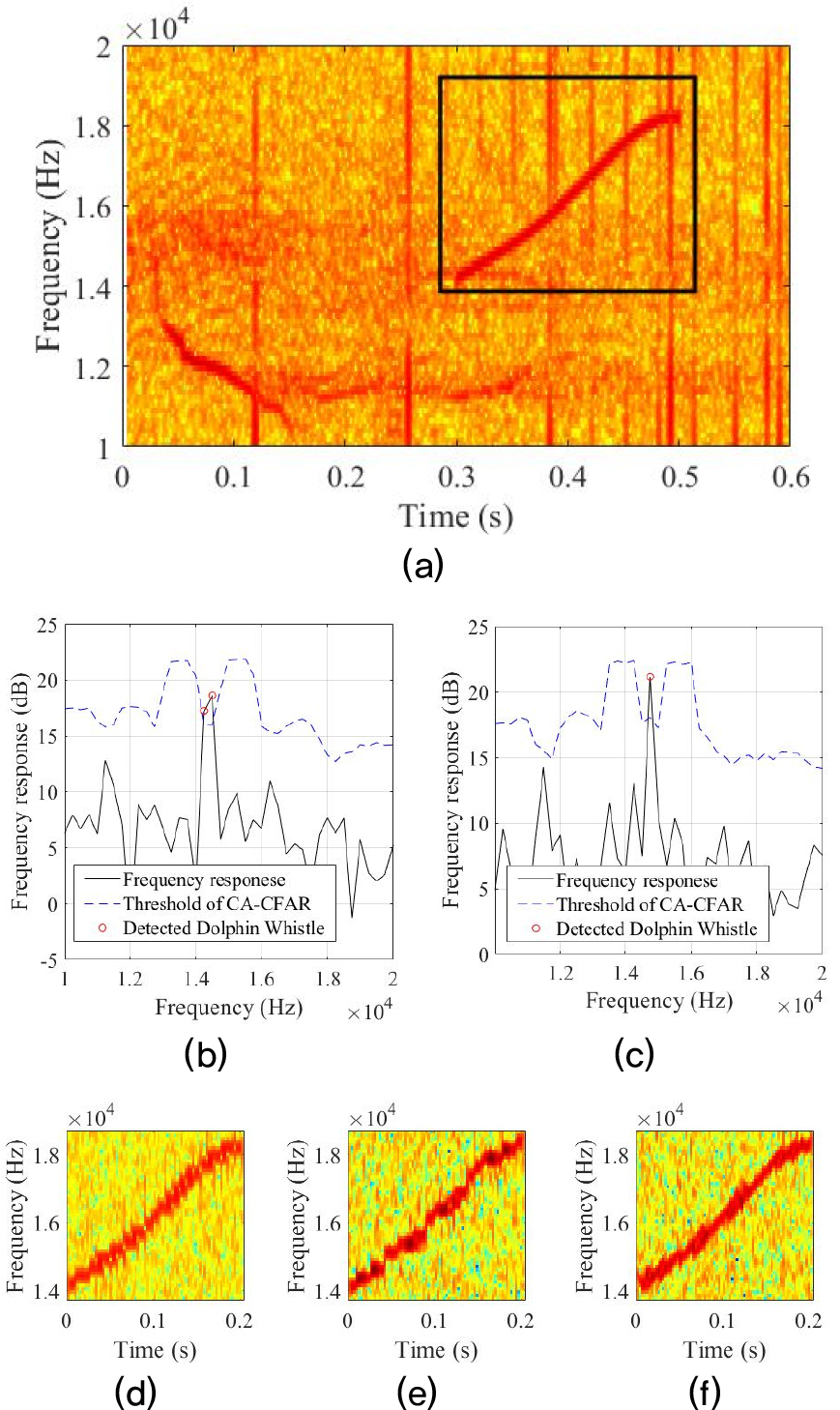
실험에 사용된 돌고래 휘슬음과 주파수 윤곽 추출 과정 그리고 모방 신호의 스펙트로그램을 Fig. 8에 나타내었다. Fig. 8(a)는 본래의 돌고래 휘슬음이고 모방하고자 하는 신호를 검은색 박스로 표시하였다. 돌고래 휘슬음의 주파수 윤곽을 추출하기 위해 CA-CFAR의 를 0.005로 설정하였으며 훈련 셀과 보호 셀의 크기는 각각 8과 2로 설정하였다. 이를 통해 추출된 주파수 윤곽을 Fig. 8(a), (c)에 나타내었다. 검은색 실선은 실제 휘슬음의 주파수 응답이고 파란색 파선은 CA-CFAR의 임계 값, 그리고 빨간색 원형 마커는 검출된 돌고래 휘슬음이다. 그리고 Fig. 8(a)~(f)에 제안 방법, FSK, 그리고 CSS로 모방 변조된 통신 신호의 스펙트로그램을 각각 나타내었다. Fig. 8에서 보는바와 같이 돌고래 휘슬음의 주파수 윤곽을 추출하고, 이를 통해 모방된 변조 신호들의 주파수 윤곽이 원래의 돌고래 휘슬음의 주파수 윤곽과 유사함을 알 수 있다.
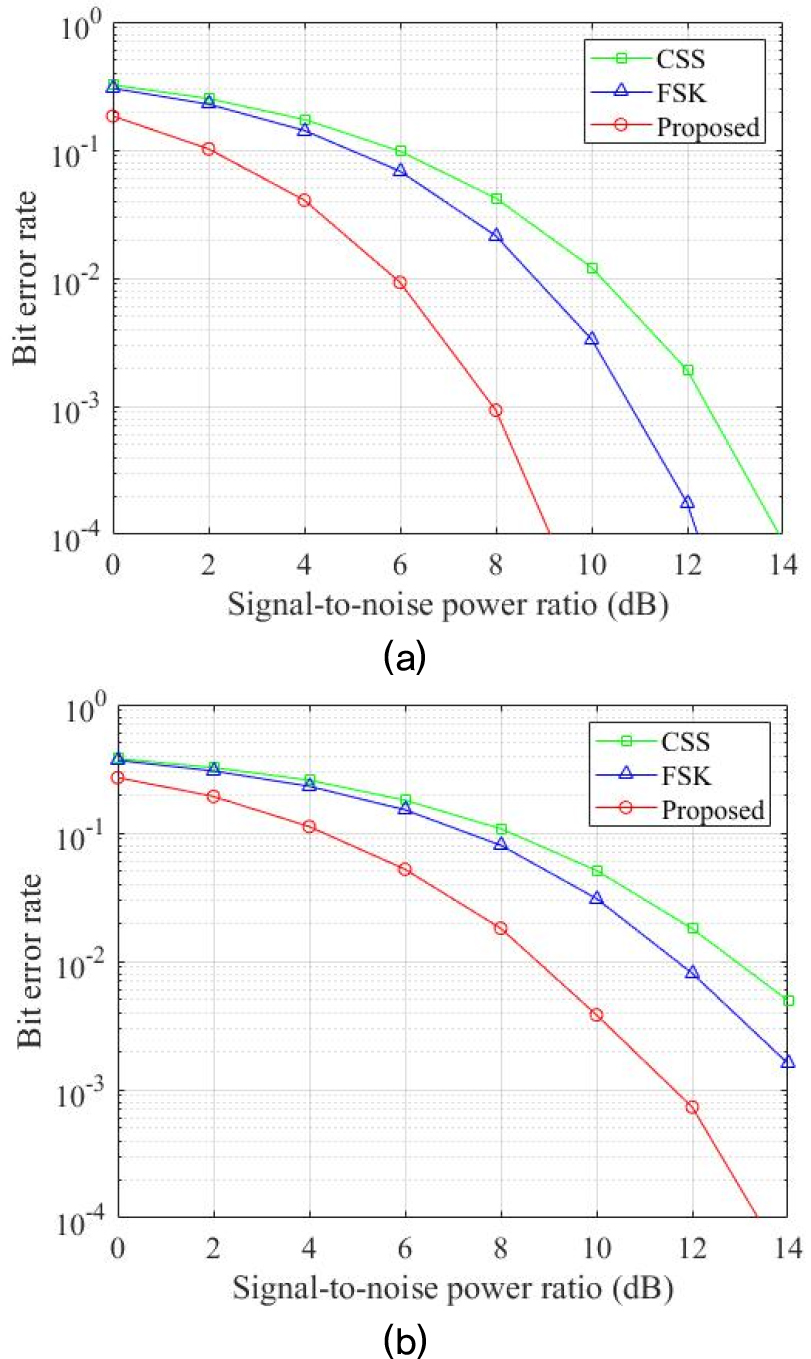
Fig. 9에 제안 방법과 기존의 기법들의 AWGN과 Rician 채널에서의 BER 결과들을 나타내었다. CSS와 FSK의 BER은 각각 녹색 사각형 마커와 파란색 삼각형 마커로 나타내었고 제안 방법은 빨간색 원형 마커로 나타내었다.
Fig. 9(a)의 AWGN에서의 BER 결과에서 알 수 있듯이, 심볼 간의 유사직교성을 이용하는 CSS에 비해 심볼 간의 주파수 직교성을 이용하는 FSK의 BER이 우수한 것을 알 수 있다. 그리고 이론적으로 DPSK기반 OFDM은 비상관(noncoherent) FSK에 비해 BER 성능이 SNR에서 3 dB 우수하다. Fig. 9(a)에서도 제안 방법의 BER 성능이 FSK에 비해 SNR에서 3 dB 우수한 것을 볼 수 있다.
Fig. 9(b)의 Rician 채널의 BER 결과도 AWGN에서의 결과와 같이 제안방법의 FSK의 성능이 CSS보다 우수한 것을 알 수 있다. 시간에 따라 주파수의 변화율이 큰 휘슬음을 모방한 통신 신호의 경우, 동일한 주파수에서 연속된 시간에 자원요소들이 위치하지 않기 때문에 심볼 길이보다 지연시간이 긴 경우에는 심볼간 간섭(Inter-Symbol Interference, ISI)이 발생하지 않는다. 본 전산 모의실험에서도 시간에 따른 주파수 변화가 큰 휘슬음을 모방하였고, OFDM 심볼 길이보다 두 번째 경로의 지연시간이 93 ms로 길기 때문에 ISI 발생하지 않는다. 그러나 다중 경로로 인해 발생하는 주파수 선택적 페이딩의 영향으로 일부 자원요소들의 채널 이득이 낮아져 오류가 증가하게 된다. 따라서, Rician 채널에 대한 세 기법들의 BER들은 AWGN에 비해 4 dB 만큼씩 성능 감소가 발생하였다.
제안한 방법과 기존 기법들의 모방 성능을 Table 3에 나타내었다. 모방 성능은 References [7]과 [8]에서 사용한 상호 상관도를 이용하였다. 상호 상관도의 평균이 1에 가까울수록, 그리고 분산이 0에 가까울수록 모방 성능이 우수한 것을 의미한다. Table 3에서 보는바와 같이 변조 차수가 2일 때 제안 방법의 상호 상관도의 평균이 0.97로 기존의 CSS와 FSK에 비해 우수한 모방 성능을 가지며, 변조 차수가 2, 4, 그리고 8로 증가함에 따라, 제안 방법의 모방 성능은 0.97, 0.97, 그리고 0.96으로 변화가 작지만 FSK의 경우에는 0.91, 0.88, 그리고 0.82로 열화량이 큰 것을 알 수 있다.
IV. 결 론
기존의 CSS와 FSK 기반 생체 음향 모방 통신 기법들은 주파수 윤곽이 불연속성이 크고 변조 차수를 조정함에 따라 모방 성능의 차이가 크다. 본 논문에서는 이러한 문제 들을 해결하기위해 OFDM을 기반으로 하는 돌고래 휘슬음 모방 통신 기법을 제안하였다. 제안한 방법은 돌고래 휘슬음을 여러 개의 OFDM 심볼과 대응되는 시간 슬롯들로 나눈 후, 매 슬롯에서 돌고래 휘슬음이 위치한 주파수 대역을 갖는 부반송파에 DPSK 심볼을 매핑하여 변조한다. 부반송파의 주파수 대역폭에 의해 기존 기법과는 달리 불연속성이 줄어들고 변조 차수를 증가시켜도 모방 성능에 변화가 작다. 전산 모의실험을 통해 제안 방법의 BER과 모방 성능이 기존의 CSS와 FSK에 비해 우수함을 보였다.