I. 서 론
동조질량감쇠기(Tuned Mass Damper, TMD)는 구조물에 가해지는 가진 주파수와 감쇠기의 고유진동수의 관계를 이용해 구조물에 발생하는 진동을 흡수하는 장치로 구조물 자체에서 진동을 감쇠할 수 없을 경우 이용하여 진동을 제어한다. TMD를 이용할 경우 본래의 구조물에 일정한 진동수를 가지는 구조를 추가하면 구조물에 발생하는 특정 주파수의 진동이 TMD로 전달된다. 대부분의 경우 TMD의 질량이나 강성 등의 물성치는 유한요소법(Finite Element Method, FEM)을 통한 해석으로 얻지만, 등가 전기 회로를 구성하여 찾아내는 방법을 사용하기도 한다.[1] 가장 보편적인 구조는 TMD를 하나만 사용하는 단일 TMD(Single TMD)지만, 이전에 진행되었던 TMD 연구를 살펴보면 다중 TMD(Multiple Tuned Mass Dampers, MTMD)를 이용한 연구나, 압전·전자기 등 전기적인 원리를 이용한 TMD, 마찰식 TMD(Frictional Tuned Mass Damper) 등 다양한 연구 결과가 있다.
우선 다중 TMD의 경우에는 전체 구조물에 적절한 TMD를 다중으로 설치하여 구조물의 진동을 제어하는 방법이다. 이 구조는 건축토목 분야에서 주로 사용되는데, 다른 층의 하중을 건물의 MTMD로 사용하는 방법을 고안한 사례와[2] 지반과 건물의 결합에 이상이 있어서 발생하는 진동을 MTMD로 제어할 수 있는지 그 가능성에대한 사례도 있다.[3] 공작 기계를 공구 떨림에 대한 저항을 증가시키기 위해 MTMD를 설계하고 최적화 한 사례도 있으며[4] 그리고 해안 풍력 터빈에 이 MTMD를 설치하여 파도, 지진 등의 위험에 대한 안전성을 향상 시킨 사례도 있다.[5] 고속 열차용 교량에 전달되는 진동을 MTMD를 통해 제어한 사례도 있으며,[6] 전기적인 원리를 이용한 TMD의 연구 사례도 있다.
압전 원리를 이용해 저비용으로 효과적인 TMD를 설계한 사례도 존재하는데,[7] 이 방식은 구조물에 가해지는 진동에너지가 압전 소자를 통해 압전 효과를 일으켜 전기 에너지로 변환되고 이 에너지가 구조물에 부착된 TMD에 기계적 에너지로 변환, 작용하여 구조물의 진동을 흡수하는 원리이다.
마찰식 TMD의 경우에는 구조물의 진동이 감쇠기에 일정한 마찰을 일으켜 이에 의한 열에너지 형태로 진동의 기계적 에너지를 소산시키는 원리를 이용한 TMD의 원리이다. 플랜지에 장착된 볼 베어링과 고정된 축 사이의 마찰을 이용하여 최적의 감쇠 성능을 보인 사례가 있다.[8]
Pounding Tuned Mass Damper(PTMD)는 TMD와 마찬가지로 일정한 질량과 강성을 가진 강체를 설치하고 강체가 주변에 부딪히며 그 운동에너지를 흡수하여 진동을 감쇠시키는 원리이다. 이 원리를 적용시켜 천장에 매달린 배관을 진동으로부터 보호한 사례가 있으며,[9] 수치적으로 최적화시키고 점탄성 재료를 덮은 구조물로 구성하여 교량에 유도되는 진동을 완화시킨 사례도 있다.[10] 그리고 이 PTMD 구조에 진자를 추가하여 자유진동과 강제진동 모두를 실험한 사례도 있다.[11]
최적화를 진행한 연구도 상당 수 진행되어있다. 1자유도 점성 감쇠계에 TMD를 부착해 수치적으로 응답 변위가 최소화되는 주파수에서의 감쇠비와 주파수 비를 산출한 사례가 있다.[12] 핵발전소 배관시스템의 내진 성능을 TMD를 이용해 향상시키고자 주파수 응답 분석에 기반을 둔 최적 설계 방법을 새로 제안하고 기존의 TMD에 비해 개선된 효과를 얻은 연구도 있고,[13] 수치적 기법을 이용하여 MTMD의 감쇠 비, 진동수 비, 주파수 대역폭을 최적화시켜 최적의 TMD를 설계한 연구 결과 또한 있다.[14] 그리고 강성과 감쇠계수를 최적화하기 위해 Root-Mean-Square를 이용한 경우도 있으며,[15] 최적화된 MTMD를 설계하여 이것이 단일 TMD보다 더 효과적임을 확인한 사례도 있다.[16]
이전까지 진행되었던 TMD 관련 연구는 위에 언급된 사례들보다 오래도록 진행되어왔고 그에 따른 결과도 상당수 존재한다. 그러나 많은 경우 특정 주파수의 진폭 줄이는 데 집중되어 있는데, 유동의 흐름에 의해 진동이 발생하는 배관의 경우에는 영향을 받는 주파수의 영역대가 넓고 고르게 분포되어 있는 경우가 있다. 따라서 이 연구에서는 배관 시스템 전체의 진동에너지를 낮추기 위한 TMD의 최적 위치를 찾는 방법을 중점으로 진행하였다. 그리고 이 최적 위치에서 측정되는 주파수에 맞춰 감쇠기의 무게 추를 조절해 주파수를 조절할 수 있는 구조로 TMD를 설계했다.
배관 시스템에 적용할 수 있는 TMD의 최적화 설계방법의 개발을 위해 대리 모델을 MATLAB을 이용하여 설계하였고, 이를 바탕으로 고안된 최적화 방법을 ANSYS Workbench를 이용한 수식적 해석과 시뮬레이션으로 검증하였다. 검증된 설계를 바탕으로 실제 TMD를 제작하여 Fig. 1과 같이 실제 산업체에 쓰이는 압축기-배관 시스템에 설치하고 실측을 통해 해석과 시뮬레이션을 검증하였다.
II. TMD 최적화 설계
2.1 배관 시스템 모델링
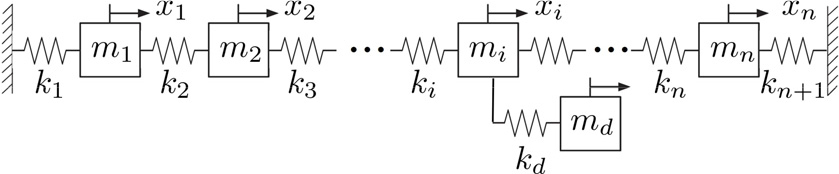
TMD의 설계는 질량과 강성 같은 물리적인 특성뿐만 아니라 TMD가 설치될 구조물의 특정한 위치 선정이 요구된다. TMD 설계변수 최적화 방법을 제안하고 이를 검증하기 위해 TMD가 설치된 배관시스템의 집중 변수 모델을 Fig. 2와 같이 구성하였다. 이 모델은 연속적인 시스템을 개의 구성요소를 가진 분산된 시스템 즉, 무한한 차원의 문제를 유한한 차원의 문제로 바꾸어 나타내는 모델이다. 따라서 이 모델을 이용해 연속적인 배관시스템의 구성요소를 제한하여 해석하며 압축기를 제외한 배관의 문제만을 다룬다. 이 모델에서 배관은 고정 구속조건이 부여된 1차원 모델이며 배관의 길이 방향에 대한 거동을 해석한다. 그리고 감쇠기가 부착되는 위치 역시 배관과 같은 방향으로 운동한다.
TMD가 설치되지 않은 상태에서 배관시스템의 응답특성을 구하기 위한 지배방정식(ℝ)은 아래와 같이 나타낼 수 있다.
는 배관시스템의 질량, 댐핑, 강성 매트릭스를 뜻하며 N은 시스템의 자유도이다. 정상 상태에서 배관시스템에 주어지는 외력 는 조화 가진으로 가정하고 이에 대한 응답 를 구할 수 있다.
TMD를 추가했을 때의 변위 벡터는 는 Eq. (2)에서처럼 지배방정식 ℝ에서의 변위벡터 에 TMD 자유도 를 추가함으로써 구성할 수 있다. Eq. (1)에 주어진 지배방정식을 바탕으로 TMD가 설치된 배관시스템의 state-space 식을 나타내면 Eq. (3)과 같다.
Eq. (4)의 , , 는 TMD를 포함하여 새로 정의된 질량, 댐핑, 강성 매트릭스를 나타내고, TMD를 포함하는 배관시스템에 가해지는 조화 가진은 로 정의된다. 변위 벡터 와 조화가진 벡터 사이의 주파수 응답 매트릭스 는 Eq. (6)과 같이 유도되며
와 는 j번째 고윳값과 고유벡터를 의미하고 와 는 이에 상응하는 켤레 복소수를 의미한다.
2.2 TMD 최적 설계
TMD 최적 설계를 위해서는 질량, 강성과 함께 TMD를 설치할 위치를 선정하여야 한다. 이는 원래의 배관시스템 ℝ의 모델에 질량과 강성 매트릭스가 추가되는 것으로 다음과 같이 표현할 수 있다.
Eq. (8)에 나와 있는 는 j 번째 노드에 추가된 TMD 스프링 상수를 전체 강성 매트릭스에 더해주기 위한 연산자이다. , 매트릭스를 구성하는 요소 성분 , 는 배관시스템 전체 질량과 감쇠기 질량의 비 를 이용하여 하나의 변수로 표현할 수 있다.
Eq. (10)에서 p, q는 질량 매트릭스 의 행과 열의 번호를 의미한다.
TMD가 설치되지 않은 기존 배관 시스템의 가진 주파수 에 대한 주파수 응답을 라 하고, 번째 노드에 TMD가 추가된 배관시스템의 주파수 응답을 이라고 할 때, TMD의 성능을 지표화하기 위해 효율 를 다음과 같이 정의한다.
Eq. (11)에 표현된 효율 는 TMD의 질량비 과 TMD가 추가되는 노드 위치 의 함수로 표현이 되는데, 아래와 같이 최적화 문제를 통해서 가장 효율적인 TMD를 설계할 수 있다.
maximize
subject to
and
는 질량비의 상한을 나타내는데, 현실적인 문제로 TMD의 질량을 무한히 크게 할 수 없기 때문에 실질적으로 TMD를 제작할 때에는 설계자의 의도대로 이 값을 정의해 주어야 한다.
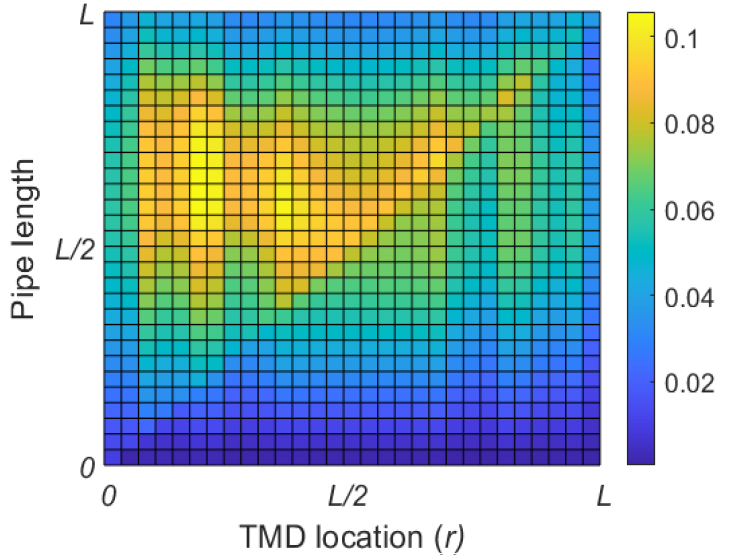
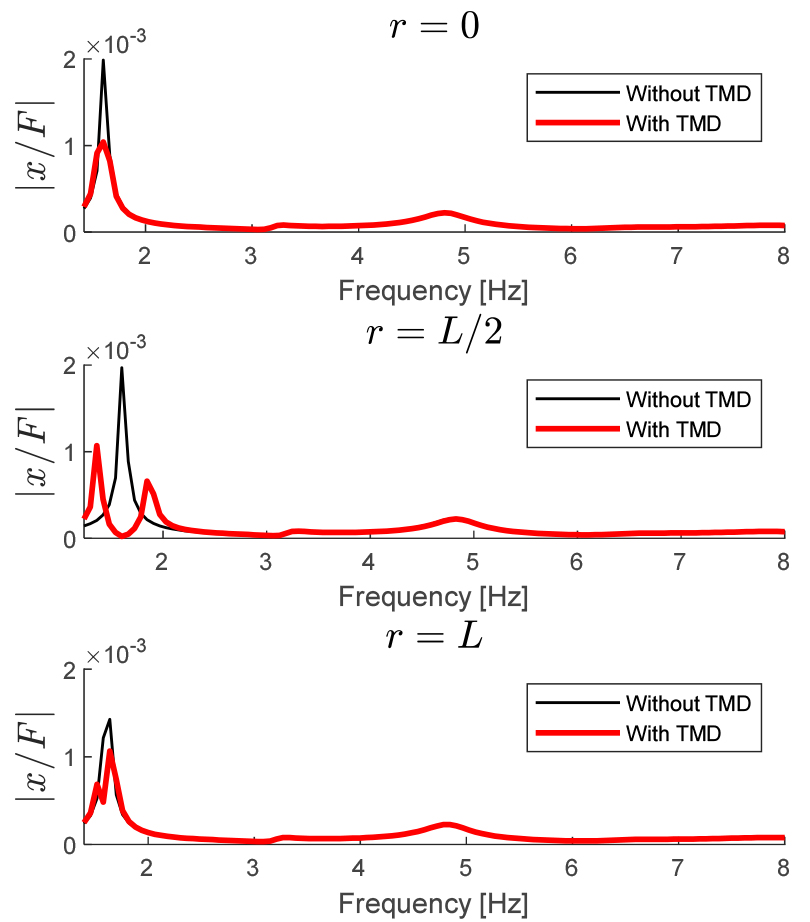
감쇠 계수는 레일리 댐핑(Rayleigh damping)을 이용하여 에서 , 를 대입해 강성 의 1 %에 해당하는 감쇠를 갖도록 했으며, Fig. 3에는 질량비 이 5 %로 고정되어 있을 때 TMD 위치 에 따른 효율 를 배관길이 에 대하여 나타내었다. TMD를 배관 모델의 첫 번째 굽힘 모드에 맞추어 설계하였고, 압축기의 가동에 따른 정현파 형태의 힘이 외력으로 작용한다. 첫 번째 bending mode이기 때문에 배관 길이의 중심에서 변위가 가장 많이 발생하고, TMD에 의한 진동저감 효과를 가장 많이 확인할 수 있다. 또한, TMD의 위치가 진원으로부터 멀어질수록 TMD의 성능이 저하되는데, 이를 통해서 TMD를 설치해야하는 최적의 위치를 확인할 수 있다. Fig. 4에는 배관의 중심에서의 주파수 응답을 TMD위치에 따라 나타냈다.
TMD가 배관의 중심()에 위치할 때 첫 번째 모드를 가장 효과적으로 줄여 주지만 모드 분리가 발생하여 의도치 않은 주파수에서 응답을 발생시키는 것을 확인할 수 있다. 따라서 이 수치적 결과를 다음 ANSYS Workbench를 이용한 시뮬레이션에서 그 감쇠 효과를 검증해 감쇠기를 설치하기 위한 적절한 위치를 확정한다.
2.3 감쇠 효과 검증을 위한 유한요소 해석
최적화 과정을 통해 얻은 댐퍼 위치 과 질량비 값을 검증하기 위해 실제 측정된 배관시스템을 바탕으로 유한요소모델을 만들고 ANSYS Workbench를 통해 조화 응답 시뮬레이션을 진행했다.
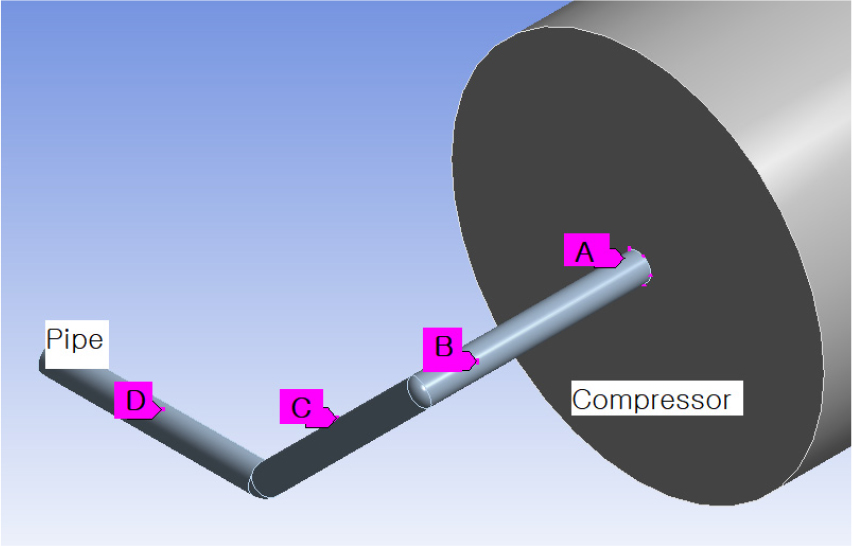
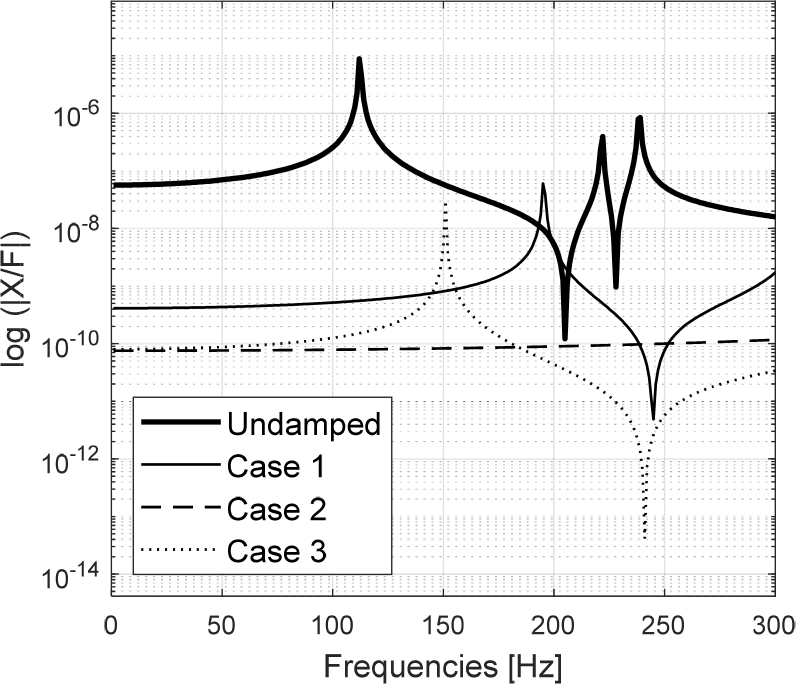
감쇠기를 설치하지 않은 압축기 모델의 조화 응답 해석 결과 해당 시스템에서 증폭이 가장 큰 1st mode는 112 Hz의 진동수를 갖는 것으로 나타났다. 따라서 이 진동수의 진폭을 감소시키고 최적화를 검증하는 시뮬레이션을 구성했다. 이 검증에서는 TMD를 세 위치에 설치한 는 각각 Table 1과 같으며 세 부분은 최적화 과정에서 알아낸 중앙 부분()과 사례 연구를 위해 추가적으로 입구부()와 배관의 끝 단()두 위치를 사용하기로 했다.
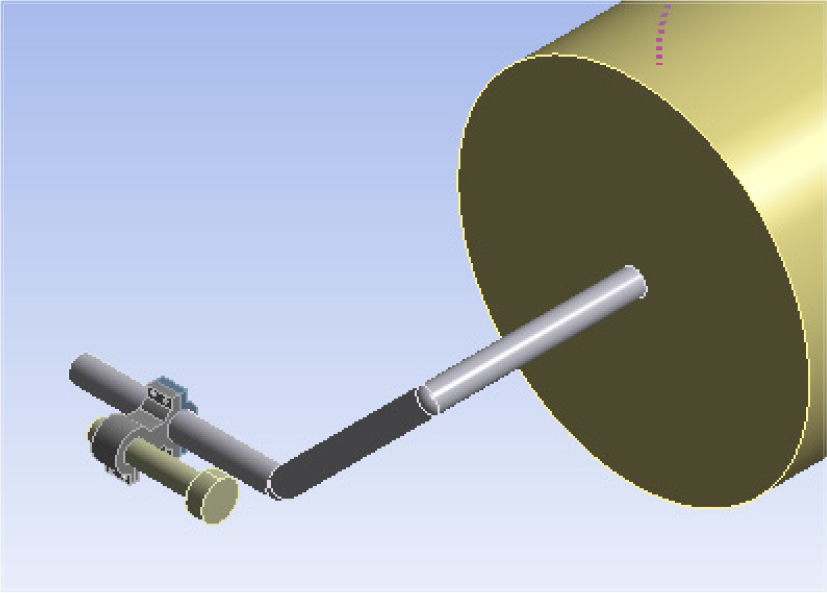
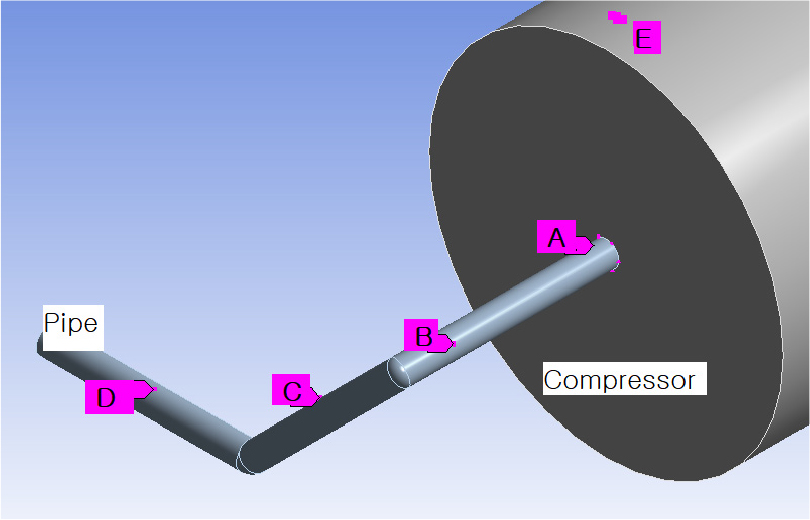
Case 1은 인 배관 입구부, Case 2는 인 중앙부, Case 3은 인 끝단에 각각 감쇠기를 설치한 것을 말하며 해당 세 부위는 각각 Fig. 5의 B, C, D 위치에 해당한다. Fig. 5는 시뮬레이션을 위해 압축기와 배관 시스템을 모델링한 것으로, 압축기는 지면에 고정되어있고 배관의 한쪽은 압축기에 연결되어있다. 배관의 반대편 끝은 질량이 매우 큰 구조물로 유입되는 부분이므로 고정 구속조건을 적용했으며, 메쉬는 SOLID187 타입의 구성요소로 형성되었다. 그리고 A 지점에 가동 최대 압력인 900 psi에 상당하는 외력을 정현파의 형태로 가중했다. 압축기와 배관의 재질은 스테인리스 스틸로 설정하고 구조 감쇠 계수 β= 0.01을 적용해 모델링했다.
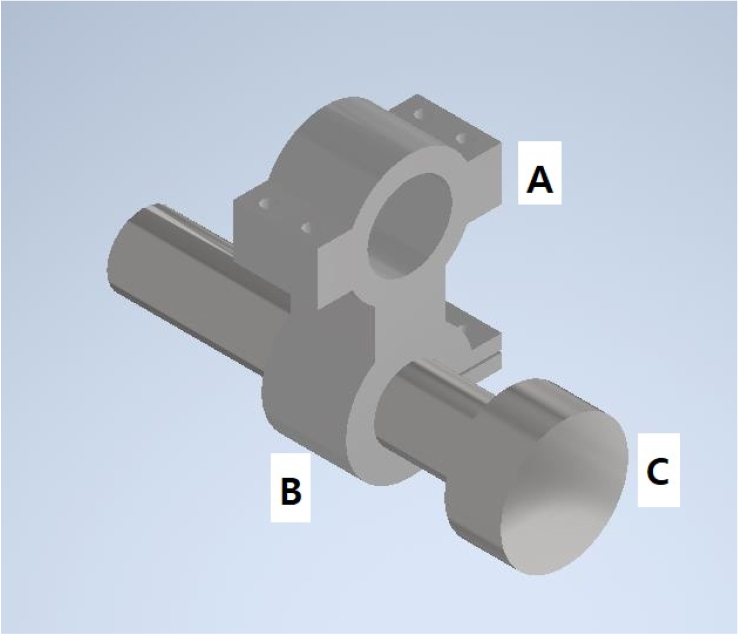
Fig. 6은 시뮬레이션을 위해 설계한 감쇠기의 유한요소 모델로, 소재는 스테인리스 스틸이며 1st mode인 121 Hz에 맞춰 설계했다. 그리고 실제 배관 시스템의 측정 오차를 보정하고 설계공차를 고려해 무게 추의 고정 위치를 움직여 유동적으로 TMD의 고유진동수를 수정할 수 있도록 설계했다. 이렇게 조절되는 TMD는 외팔보로 가정할 수 있고, 그 등가 강성을 계산하는 식에 따라 고유진동수가 결정된다.
Fig. 7은 Fig. 6의 감쇠기를 Fig. 5의 D 지점에 설치한 예시를 모델링 한 것으로, Fig. 5의 B, C, D 세 지점에 설치한 유한요소 모델을 이용해 각각의 조화 응답 시뮬레이션을 진행하고 그 결과를 얻었다.
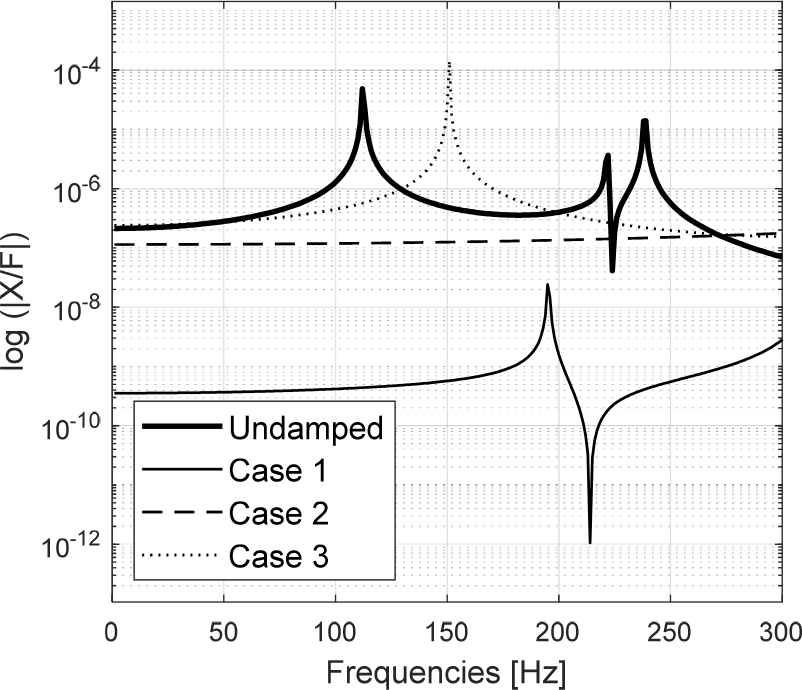
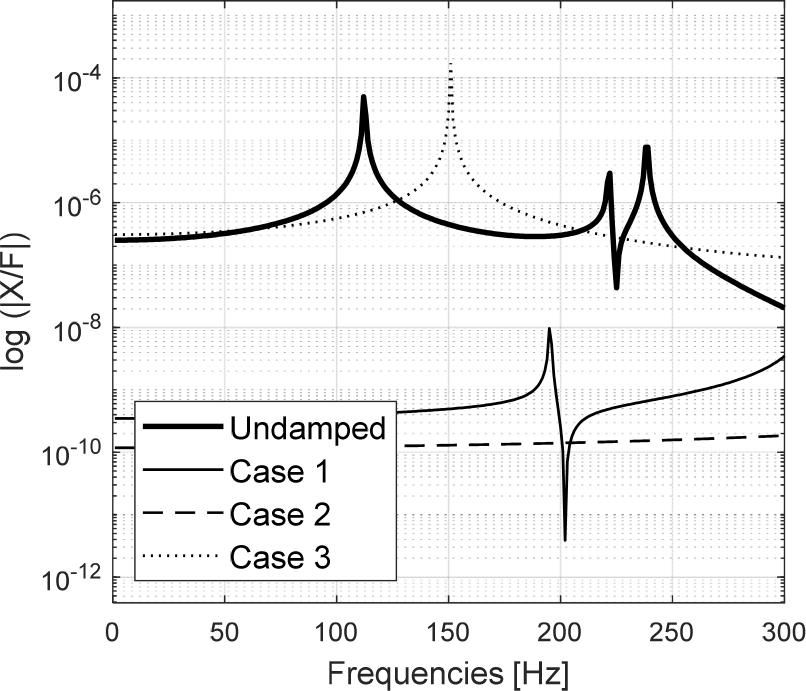
Figs. 8, 9, 10까지는 B, C, D 각 지점의 Case 1, 2, 3번에 따른 진폭의 값을 외력에 대해 정규화()하고 그래프를 1st mode 중심으로 도식한 것이다. Case 1과 Case 2는 1st mode의 주파수에서 응답이 사라졌지만, Case 3의 경우 감쇠기를 지나기 전인 B 지점과 C 지점에서 새로운 peak가 약 150 Hz에서 생기는 것을 확인할 수 있다. 하지만 감쇠 대상이었던 112 Hz에서는 세 경우 모두 충분한 감쇠 성능을 보이는 것을 확인할 수 있다.
그래프에 나타난 결과로는 감쇠기가 설치된 위치를 지나야 감쇠 효과가 확실하게 나타남을 알 수 있다. 따라서 이에 해당하는 경우는 Case 1 즉, 외력이 발생한 지점에 감쇠기를 설치한 경우인 것을 확인하고 해당 지점으로 확정했다.
이 시뮬레이션 결과까지 종합하여 실제 압축기에서 진동 측정을 위해 감쇠기를 설치할 위치 그리고 감쇠기 형태를 최종적으로 확정했다.
III. 측정 결과 분석
최적화와 조화 응답 시뮬레이션을 통해 확인한 결과로 감쇠기의 위치를 정했고, 여기에 실제 감쇠기를 제작하여 설치한 뒤 실제 진동 응답을 측정했다. 그리고 설계한 감쇠기의 감쇠 효과를 실측하기에 앞서 원래 시스템이 어떤 진동 응답을 보이는지 알기위한 진동 측정이 선행되었다. 이 측정은 압축기와 배관 시스템에 Brűel & Kjᴂr사의 Type 4326A 미니어처 3축 압전 가속도계를 부착해 진행했다. 가속도계는 압축기, 압축기와 배관의 연결 부위, 배관이 굴절되는 부분 그리고 굴절 이후의 부분에 부착하여 측정을 하였고, 각 측정 부위의 위치는 Fig. 11에 도식화 하였다. 그림에 표시된 A, B, C, E 위치에 3축 가속도계를 설치하고 압축기 가동 회전수의 70 cycle ~ 80 cycle에 해당하는 30 s 동안 데이터를 수집, 진동 응답을 분석했다. 측정은 150 r/min으로 작동되는 시스템에서 별도의 인위적인 가진 없이 시스템의 작동에 의한 가진을 측정했다.
제작된 TMD의 실물은 Fig. 12와 같다. 압축기의 사양과 배관에 가해지는 정확한 진원에 대한 정보가 없고, TMD와 배관이 서로 클램프로 연결되어있어 이상적인 고정 구속조건이 아니라는 점 등을 고려하여 무게 추의 고정점을 움직여 고유진동수를 조절할 수 있도록 하였다. TMD가 실제 배관에 설치된 모습은 Fig. 13과 같다.
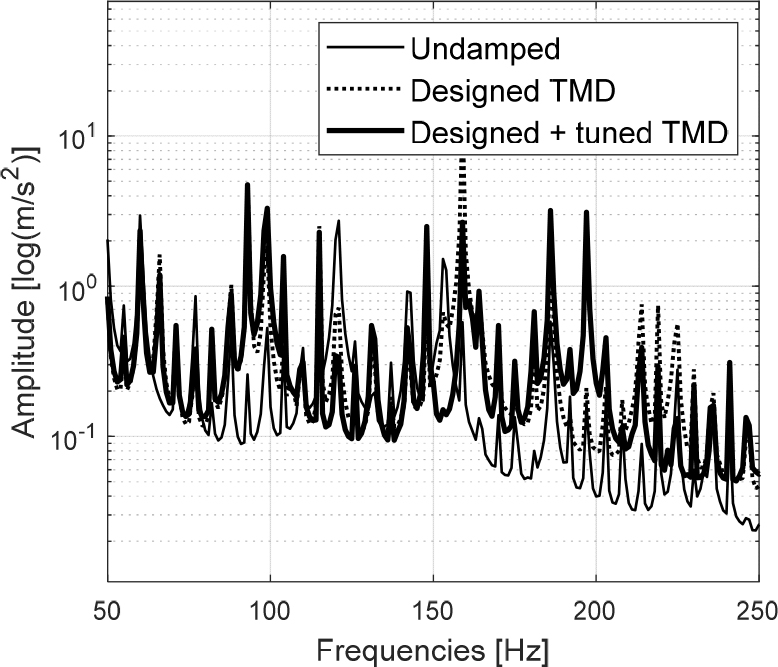
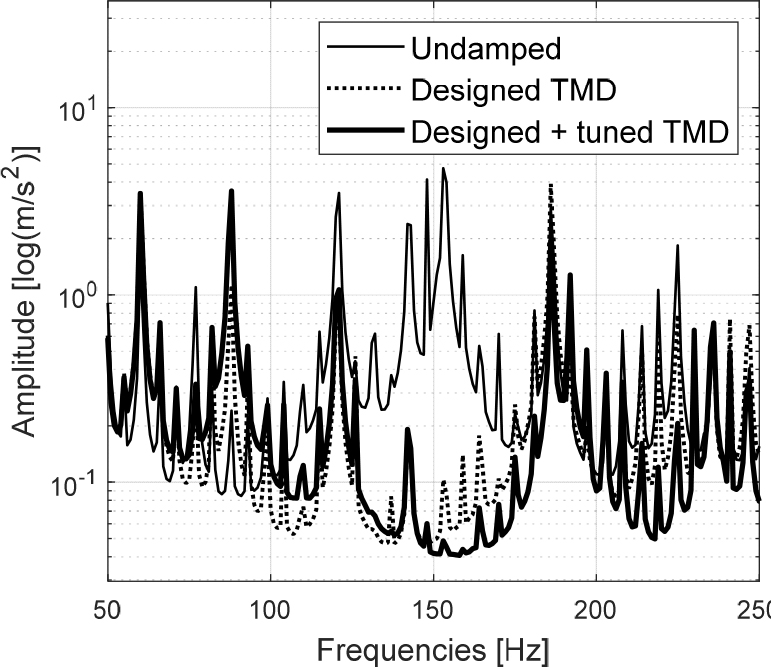
TMD의 설치위치를 선정하기 위해 배관 시스템의 A, B, C, E 4개 위치의 진동 응답을 측정했다. 측정한 결과, 압축기(E)에서의 진동은 크지 않았으나, 압축기와 배관의 연결부위(A) 지점에서 진동이 발생하기 시작했다. 배관의 방향이 바뀌기 전(B)보다 방향이 바뀐 직후에(C) 진동의 진폭이 큰 것으로 측정되었다. 이에 따라, 시뮬레이션과 실측 결과를 고려해 진동 응답이 크고 진원에 가까운 C 지점에 TMD를 설치하고, TMD 설치 전과 후의 B, C 지점에서의 응답 변화를 측정 및 비교했다. TMD가 설치되지 않은 배관 시스템(Undamped)의 반응과 시뮬레이션으로만 검증된 설계값 그대로의 TMD(designed TMD)의 반응 그리고 고유진동수를 조절하여 성능 보정이 된 TMD(designed + tuned TMD)의 결과를 Figs. 14와 15에 각각 비교하였다. Fig. 14에 나타난 바와 같이 B 지점에서는 TMD의 유의미한 효과가 나타나지 않는다. 하지만 TMD가 설치된 C지점에서는 1st mode가 나타나는 150 Hz 부근에서 진폭이 최대 95 % 감소하였다. 특히나 TMD 고유진동수의 보정을 통해서 TMD의 감쇠 성능을 최대 1.8 % 증대시킬 수 있음을 확인하였다.
IV. 결 론
본 연구에서는 동조질량감쇠기의 원리를 이용해 배관 시스템의 진동 응답을 감소시키고, 시스템에 맞는 감쇠기를 설계하기 위한 최적화 방법을 개발했다. 수학적인 모델링을 통해 TMD의 물성치와 설치할 위치를 계산하고 이를 바탕으로 만든 유한요소 모델을 조화 응답 시뮬레이션으로 검증했다. 검증 결과를 바탕으로 감쇠기를 제작하고 실제 배관 시스템에 적용함으로써 최적화가 적절하게 진행되었는지 확인하는 과정을 거쳐 다음의 결과를 얻었다.
1. 본 연구에서는 감쇠기와 전체 시스템의 질량비를 정하고, 설계변수 최적화 방법을 이용해 감쇠기의 최적화 위치를 찾는 방법을 보였다.
2. TMD는 진원에 가깝게 위치하는 것이 효과적임을 확인하였고, 반대로 TMD 설치 위치를 통해 진원을 확인하는 것도 가능함을 보였다.
3. 배관 설비의 구체적인 사양과 정확한 진원에 대한 정보가 없는 상태에서도 TMD설계가 가능하며 측정 오차, 가공 공차 그리고 현실적인 제약 등을 반영하여 TMD를 설치 후 보정할 수 있는 설계를 제시하였고, 설계된 TMD의 이론값 보다 효율을 1.8 %정도 향상시킬 수 있음을 보였다.