I. 서 론

수중음향통신 채널은 시간에 따라 채널 특성이 변화하는 시변 채널로, 수심 및 수온에 따른 음속구조, 수표면의 변화, 전송 거리에 따른 감쇠, 다중 경로와 도플러 등 다양한 성능 저하 요소를 가지고 있어 이와 같은 요소에 대한 보정이 필수적이다.^[1] 이러한 성능의 한계를 극복하기 위하여 다중 밴드 통신 기법을 활용하는데 이 방식은 동일한 데이터를 여러 개의 주파수 대역으로 보내 수중에서의 선택적 페이딩을 극복할 수 있어 성능 및 전송효율 측면에서 효과적이다.^[2] 수중에서 다중 밴드 통신을 할 때 주파수 선택적 페이딩에 의해 일부 밴드에서 성능 저하가 일어나는데 이를 극복하기 위하여 밴드별로 가중치를 부여하는 방법을 사용할 수 있다. 가중치 설정에는 다양한 방법을 이용할 수 있으며, 대표적인 방법으로는 수신 Signal to Noise Ratio(SNR) 및 사전 신호 데이터의 오류율을 이용하는 방법이 있다.^[3,4] 수신 SNR을 이용하는 방법은 패킷 전송 시 데이터 구간과 침묵 구간의 잡음을 이용한 수신 SNR 측정을 통해 각 밴드에서의 수신 품질을 예측하는 방법이며, 사전 신호 오류율을 이용하는 방법은 송·수신자가 서로 알고 있는 사전 신호의 성능을 이용해 각 밴드에서의 데이터 부분의 성능을 예측하여 가중치를 할당하는 방법이다. 그러나 시변 수중통신 채널에서 사전 신호 데이터의 수신 SNR 또는 오류율이 데이터 부분의 성능과 일치한다는 보장이 없다. 따라서 본 논문에서는 추정 Bit Error Rate(BER)을 이용한 다중 밴드 전송 기법의 가중치 설정 방법에 대해 제안한다. 추정 BER은 복조된 데이터와 복호 후 재 부호화 시킨 데이터의 오류 개수를 산정하는 방식으로 복조된 데이터가 신뢰성이 있으면 추정 BER은 낮게 나오며, 반대로 복조된 데이터가 신뢰성이 없으면 추정 BER이 높게 나오므로 이에 따라 각 밴드에서 가중치를 설정하는 방식이다. 본 논문에서는 제안한 추정 BER 기법을 통한 가중치 설정 방식을 적용하기 위해 부호화율 1/3을 가지는 터보 부호^[5]를 적용하였으며, 수신부에는 추가적으로 도플러 및 위상 오프셋을 보상하고 다중 경로 효과를 제거하기 위한 결정 궤환 등화기 Decision Feedback Equalizer(DFE)를 이용하였다.^[6] 또한 등화기와 복호기가 역-인터리버를 통해 연결되어 서로의 정보를 반복적으로 업데이트하여 반복횟수 증가에 따라 성능이 향상되는 터보 등화 기법^[7,8]을 적용하였다. 본 논문에서 제시된 추정 BER을 이용한 가중치 설정이 효율적임을 나타내기 위해 시뮬레이션을 이용하여 추정 BER과 가중치 값의 설정하였으며, 해상 실험을 통해 효율성을 증명하였다.

II. 다중 밴드 통신 기법

2.1 시스템 모델

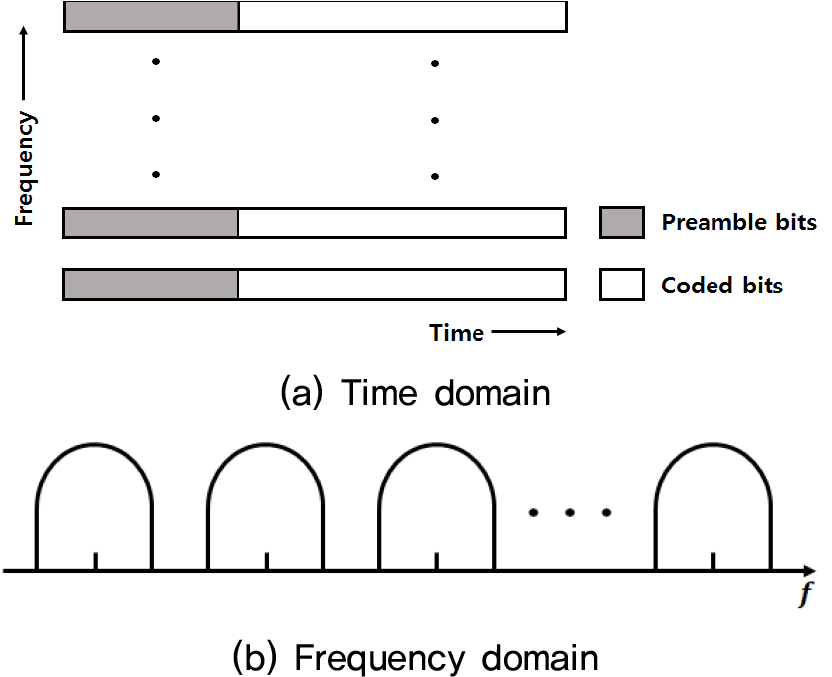
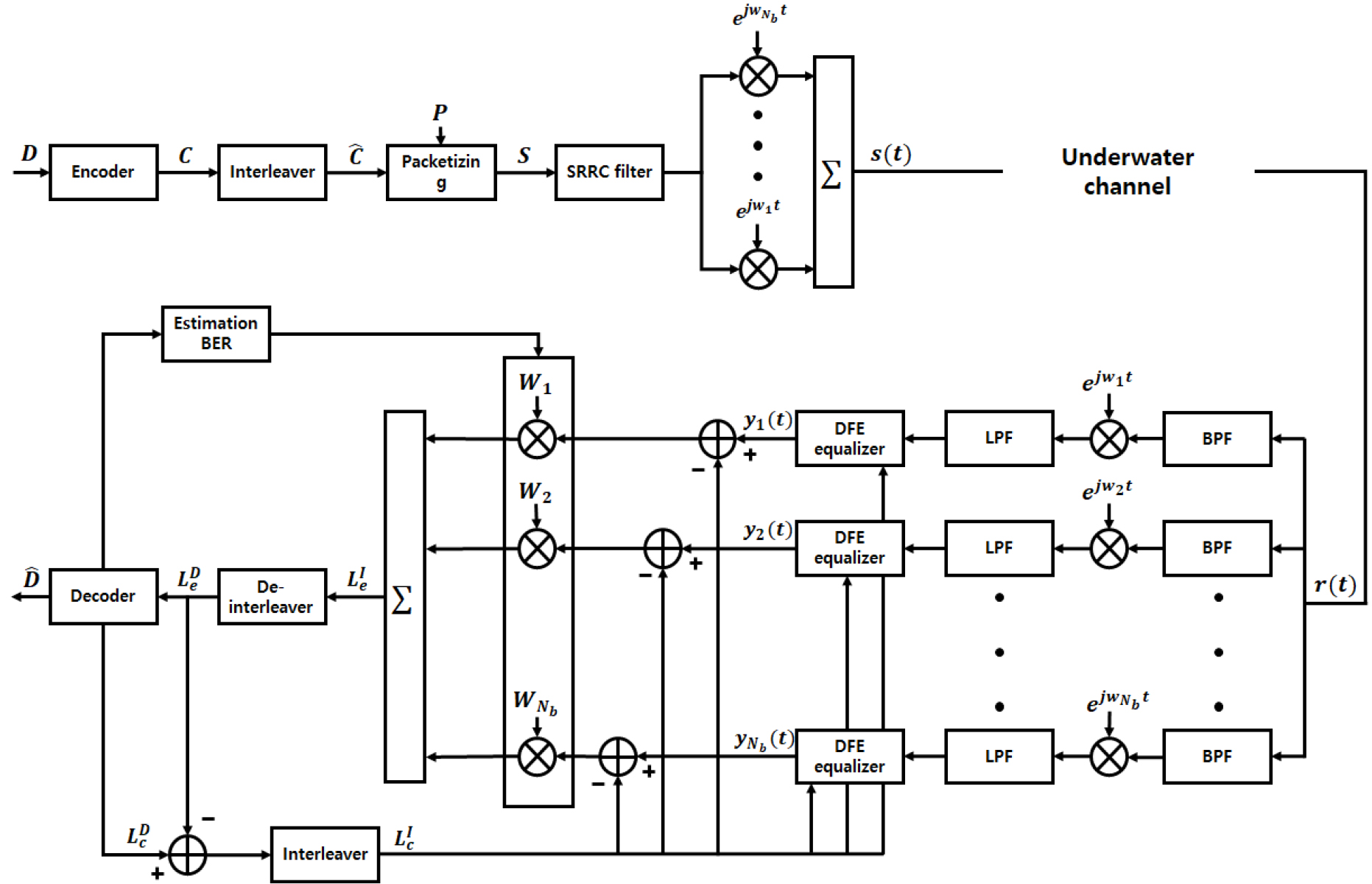
다중 밴드 전송 기법은 전체 대역폭 채널을 여러 개의 작은 대역폭을 갖는 부채널로 분할하여 다수의 협대역 부반송파를 각 부채널로 다중 전송하는 방법이다. 수중음향통신의 채널은 사용되는 주파수에 따라 특성이 다른 페이딩 채널이며 다중 밴드 전송 기법은 인접 심벌간의 간섭과 주파수 페이딩 현상을 극복하면서 신뢰성을 향상시킬 수 있다. Fig. 1(a)는 다중 밴드 전송 기법의 패킷구조이며, Fig. 1(b)는 주파수 영역에서의 파형을 나타낸다. 다중 밴드 전송 기법은 Fig. 1과 같이 동일하게 부호화된 비트열을 서로 다른 주파수로 변조하여 전송하는 방식으로 각각의 주파수 선택 시 부반송파간의 보호 대역(guard band)을 사용하여 도플러 확산과 같은 환경에서도 인접 반송파간의 간섭 Inter-Carrier Interference(ICI)을 받지 않게 된다. Fig. 2는 수중음향통신에서 다중 밴드 전송 기법을 적용한 송·수신 구조의 블록도이다. 송신부에서 채널부호화 후 연집 오류를 산발 오류로 만들어 복호 성능을 향상시킬 수 있도록 부호화 된 비트의 순서를 다르게 하고(인터리버) 패킷화 한 후 Nb개의 서로 다른 주파수에 대해 변조한 뒤 합하여 전송한다.

Fig. 1.

Packet structure and frequency band for multi-band transmission.

Fig. 2.

Transceiver structure of multi-band communication.

송신부에서 입력되는 K개의 비트를 dk라고 할 때 입력신호의 집합은 Eq. (1)과 같이 D로 나타낼 수 있다.

입력신호 D는 (n,k) 채널부호화를 한 뒤, Eq. (2)와 같이 나타낼 수 있다.

이 때, N은 부호어의 길이를 나타낸다. 부호어 C는 군집 오류를 산발 오류로 바꾸기 위하여 인터리버를 통과한다. C^은 인터리버를 수행한 후의 데이터를 나타내며 Eq. (3)와 같이 나타내어진다.

인터리버를 수행한 데이터 C^은 송신부와 수신부에서 서로 알고 있는 n개의 Pseudo Noise(PN) 코드를 데이터의 앞단에 위치시켜 하나의 패킷으로 구성한다. 이 때, PN 코드의 비트열 P는 Eq. (4)와 같이 나타낼 수 있으며, 패킷으로 구성된 비트열 S는 Eq. (5)와 같이 나타낼 수 있다.

패킷화 된 비트열 S는 Nb개의 서로 다른 주파수에 대해 변조되며 다중 밴드 통신의 송신신호 s(t)는 Eq. (6)과 같다.

송신신호 s(t)는 Nb개의 서로 다른 밴드에 대해 ejωkt를 곱해줌으로써 각각의 밴드에 대해 변조과정을 거친 후, Nb개의 밴드에 대한 각각의 변조된 신호들을 합하여 전송한다. 송신신호는 다중 채널과 같은 수중 채널을 통과하게 되는데 다중 경로 전달에 의해 수신된 신호는 수중음향통신 시스템에서 인접 심벌 간 간섭을 발생시키고, 통신 시스템의 성능 저하를 일으키는 주요 원인 중 하나이다. 이러한 다중 경로는 음향 신호가 전달되는 과정에서 반사되거나 산란되어 발생하는 잔향 현상 및 수심에 따라 달라지는 수온에 의해 음파의 전파 경로가 달라지는 ray bending 현상으로 인해 발생된다. 이 때, 수신신호 r(t)는 Eq. (7)과 같다.

L은 전체 다중 경로의 수를 나타내며 l은 다중 경로의 인덱스이다. hl(t)는 l번째 경로에 있는 채널 응답 계수를 나타내며, η(t)는 가우시안 잡음을 나타낸다. 수신부에서 수신신호는 각 밴드에 대하여 신호를 얻기 위해 Nb개의 서로 다른 신호에 대해 Band Pass Filter(BPF)를 각각 통과하여 다른 대역의 신호를 제거한다. 그리고 Nb개의 각 밴드에 대하여 복조와 Low Pass Filter(LPF)를 통과하여 다중 경로 효과를 제거하기 위해 등화기에 입력한다. 이 때, 등화기를 통과한 k번째 밴드의 출력신호를 yk(t)라고 하였을 때 복호기 입력신호 L(t)는 Eq. (8)과 같이 나타낼 수 있다.

각 대역에 대하여 등화기 출력 신호는 서로 동일하게 합해져 역-인터리버를 수행한 후 복호기에 입력되어 데이터를 복원한다. 이러한 다중 밴드 전송 기법을 적용한 모델은 밴드 수의 증가에 따라 성능을 향상시킬 수 있다.

2.2 터보 등화 기법

수신된 신호는 각 주파수를 분할하기 위해 정합 필터를 사용하여 각 채널의 정보를 획득하고 난 후 등화기에서 다중 경로 간섭을 각 밴드에서 제거하고 복호기의 성능을 판단하는 임계값 설정을 하여 복호기의 오류 복호 성능 한계에 접근하는 밴드에 해당되는 데이터를 복호한다. 등화기의 출력 값 L(t)는 결정 궤환 등화기의 출력 값으로 수신 신호로부터 등화기에서 추정되어진 외부정보(extrinsic) 값이다. LeI와 LcI의 차를 임계값 결정 파라미터에 적용하여 각 밴드에 대한 신호를 합한 뒤 역-인터리빙 하여 계산되어져 복호기에 입력된다. 복호기에서 추정된 외부입력 값 LcD은 Eq. (9)과 같이 구할 수 있다.

외부입력 값 LcD는 복호기의 출력 값으로써 사후 확률 값을 계산하여 0 또는 1의 오류 값을 보정할 수 있는 값이다. 이러한 LcD와 LeD의 차이 값을 다시 인터리빙하여 LcI를 계산하여 Least Mean Square – DFE (LMS-DFE) 등화기에 입력한다. LcI를 업데이트 하여 오류 값을 보정하게 되는데, 반복 횟수가 늘어남에 따라 업데이트 하는 오류 보정 값이 송신하고자 하는 원 신호에 가깝게 되어 성능이 향상된다. 이러한 수신부 전체를 반복하는 터보 등화 방식은 복호된 데이터의 외부 정보를 등화기에 피드백 하는 터보 등화기를 구성함으로써 성능을 향상시킬 수 있는 방식이다.

2.3 가중치 할당 방법

기존의 다중 밴드 전송 기법에서 수신부는 밴드별로 복조한 후, 등화기 출력 값을 동일한 비중으로 합하여 복호기에 입력한다. 하지만 특정 대역의 상태가 열악할 때에도 다른 밴드와 동일한 비중으로 합하여 복호기에 입력할 경우 단일밴드 전송 기법을 적용하였을 때보다 열악한 성능을 나타낼 수 있다. 이러한 문제는 각 대역의 오류율을 분석하고 임계값에 따라 가중치를 할당함으로써 해결할 수 있다. Fig. 2에서 등화기를 통과한 신호에서 각 밴드별로 가중치 값을 설정하기 전에 기존의 두 가지 방법으로 가중치를 설정하는 방식이 있다.^[9] 첫 번째는 Effective SNR(ESNR) 추정 방식이다. ESNR 추정 방식은 Received SNR(RSNR)을 추정하기 위해 송신부와 수신부에서 서로 알고 있는 보조 신호 또는 사전 신호와 침묵 구간에서의 잡음 성분을 활용한다. 두 번째 방법은 사전 신호 비트의 오류율을 이용하여 데이터 부분의 오류율을 예측해 가중치를 할당하는 방법이다.

데이터 부분의 앞에 존재하는 사전 신호는 송·수신 간에 서로 알고 있는 데이터를 이용하여 동기를 획득하는 기능을 하고 있으므로 채널 부호화를 하지 않고 전송된다. 이러한 비부호화 된 사전 신호 데이터는 대부분의 연구에서는 동기 획득을 위해 활용되지만 이의 성능을 이용하여 데이터 부분의 성능 또한 예측할 수 있어 데이터 부분의 복호부에 정보를 제공할 수 있다. 따라서 비부호화 된 사전 신호의 오류율을 이용해 데이터 부분의 오류율을 예측하여 데이터 부분에 가중치를 설정할 수 있다. 그러나 위의 두 가지 방식은 사전 신호 데이터의 수신 SNR 및 오류율이 수중 시변 채널 특성으로 인해 데이터 부분에서 변하여 추정된 값의 정확도가 떨어질 수가 있으므로 새로운 방법의 가중치 할당 방식이 요구된다.

III. 추정 BER을 이용한 가중치 설정

기존의 다중 밴드 수신 구조에서는 밴드별로 복조 및 등화를 거친 수신 신호 값을 합해 복호기에 입력한다. 그러나 이 방식은 특정 주파수 대역의 성능이 열악할 경우에도 다른 주파수 대역의 신호와 동일한 비중으로 입력되기 때문에 일부 채널 환경에서는 단일밴드 전송 기법을 적용하였을 때보다 열악한 성능을 나타내는 경우가 있다. 이를 극복하기 위해 II장에서 언급한 바와 같이 가중화된 다중 밴드 통신을 한다. 그러나 기존의 가중치 설정 방식들인 ESNR 추정 방식이나 사전 신호 오류율 방식은 실제로 데이터 부분에서 도플러 변화 등으로 인하여 성능이 급격하게 떨어지는 경우 정확도가 떨어질 수 있다. 따라서 본 논문에서는 II장에서 Fig. 2의 추정 BER을 이용한 다중 밴드 전송 기법의 가중치 설정 방법에 대해 제안한다. 추정 BER은 복호된 데이터와 복조 후 데이터의 성능 차이를 이용하여 수신된 데이터의 신뢰도를 측정하는 방법이다. 사전 신호 데이터는 송·수신자간에 서로 알고 있는 데이터를 이용하기 때문에 성능 분석이 가능하지만 부호화된 데이터는 수신 측에서 성능을 알 수 있는 척도가 없으므로 다른 방법으로 성능을 추정해야 한다. 이 때, 부호화된 데이터 부분의 성능을 분석하기 위해 추정 BER을 이용하고 그 값을 바탕으로 적절한 가중치를 부여할 수 있다.

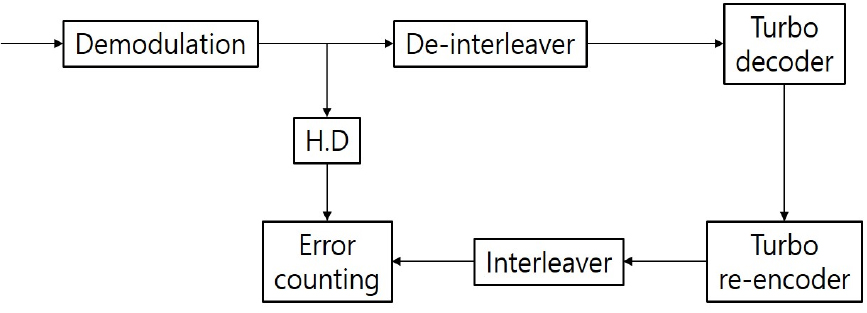
본 논문에서 제안하는 추정 BER을 이용하여 가중치를 설정하는 수신부 모델에서는 밴드별로 복조 및 등화를 거친 신호를 합하지 않고 각각 복호한 후 Fig. 3과 같은 과정을 통해 각 밴드의 추정 BER 값을 얻는다. 추정 BER을 이용하여 밴드별 가중치를 재설정하여 다시 복조 및 등화 과정을 거치고 가중치를 적용하여 합한 신호를 복호기에 입력해 더 나은 성능을 얻을 수 있다.

Fig. 3.

Block diagram of estimation BER.

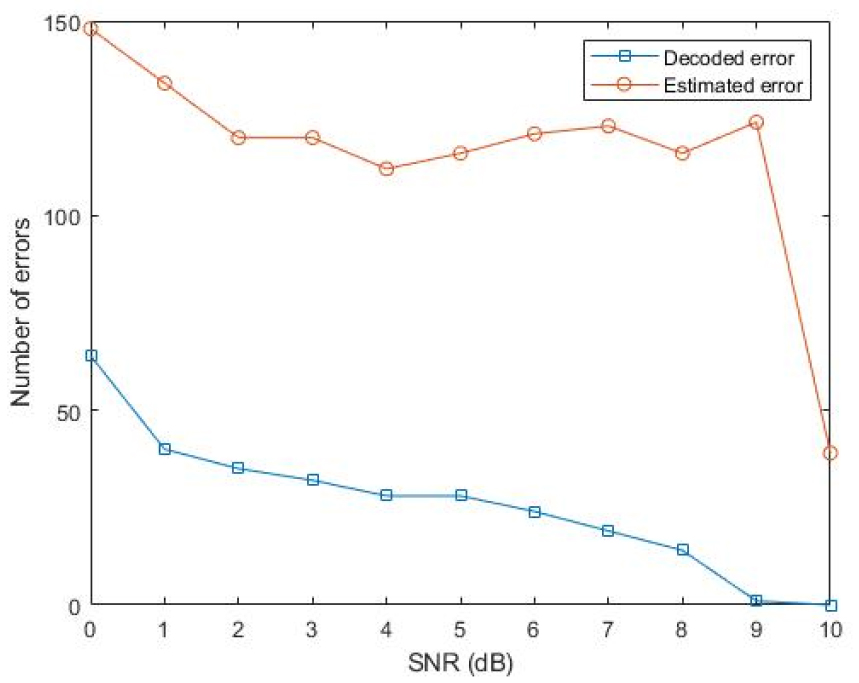
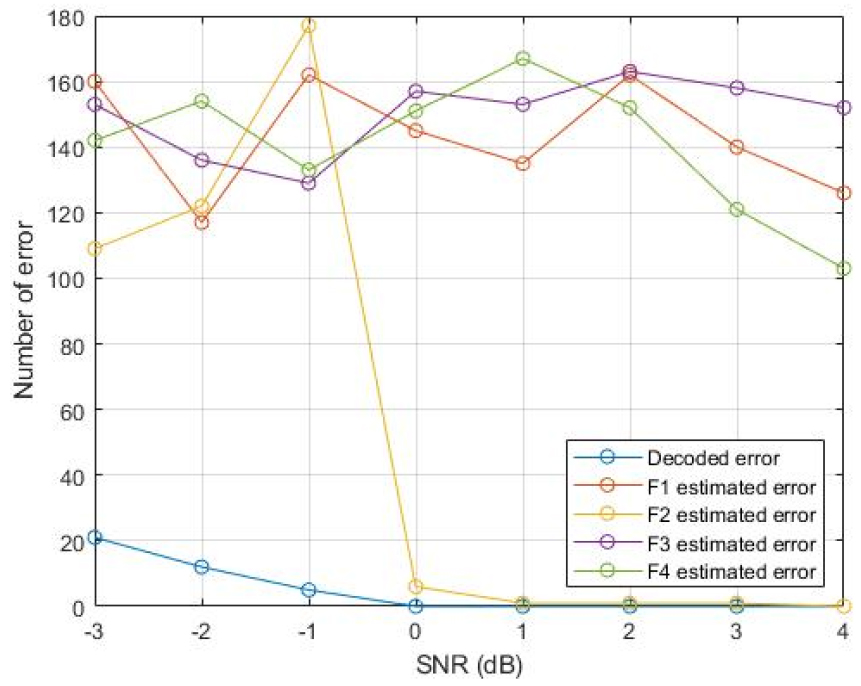
Fig. 3은 Fig. 2에서 추정 BER 블록의 상세 블록도이다. 추정 BER 블록에서는 터보 복호화기를 통해 출력된 비트를 재 부호화시켜 수신된 신호를 강판정 Hard Decision(HD) 한 비트와의 오류 갯수를 산정해 추정 BER을 구하며 이는 복호 후 성능과 밀접한 관계가 있다. 만일 복조된 데이터의 오류가 적다면 복호기에 입력되는 심볼의 오류가 적다는 의미이므로 추정 BER은 낮게 나올 것이다. 부호화율 1/3을 가지는 터보 부호의 부호화 비트 336비트를 이용해 시뮬레이션 한 결과인 Fig. 4는 단일 밴드에서 복호 에러와 추정 에러의 관계를 나타낸 그래프이다. 이 때, 가로축은 SNR을 나타내며 세로축은 오류 개수를 나타낸다. SNR이 증가하면서 단일 밴드에서 복호 오류가 점차 줄어드는 것을 확인할 수 있으며 복호 오류가 0이 되는 지점에서 추정 오류의 개수 또한 급격히 감소함을 알 수 있다. Fig. 4의 결과에 따라 복호 오류가 작을 때에는 이에 따른 추정 BER 또한 작으며 이는 복호가 제대로 동작하는지에 대한 기준이 될 수 있음을 알 수 있다. 따라서 각 밴드에서 추정 BER을 구하면 데이터 부분의 오류율을 예측하여 각 밴드의 가중치를 할당할 수 있다.

Fig. 4.

(Color available online) Relation of decoding and estimation errors.

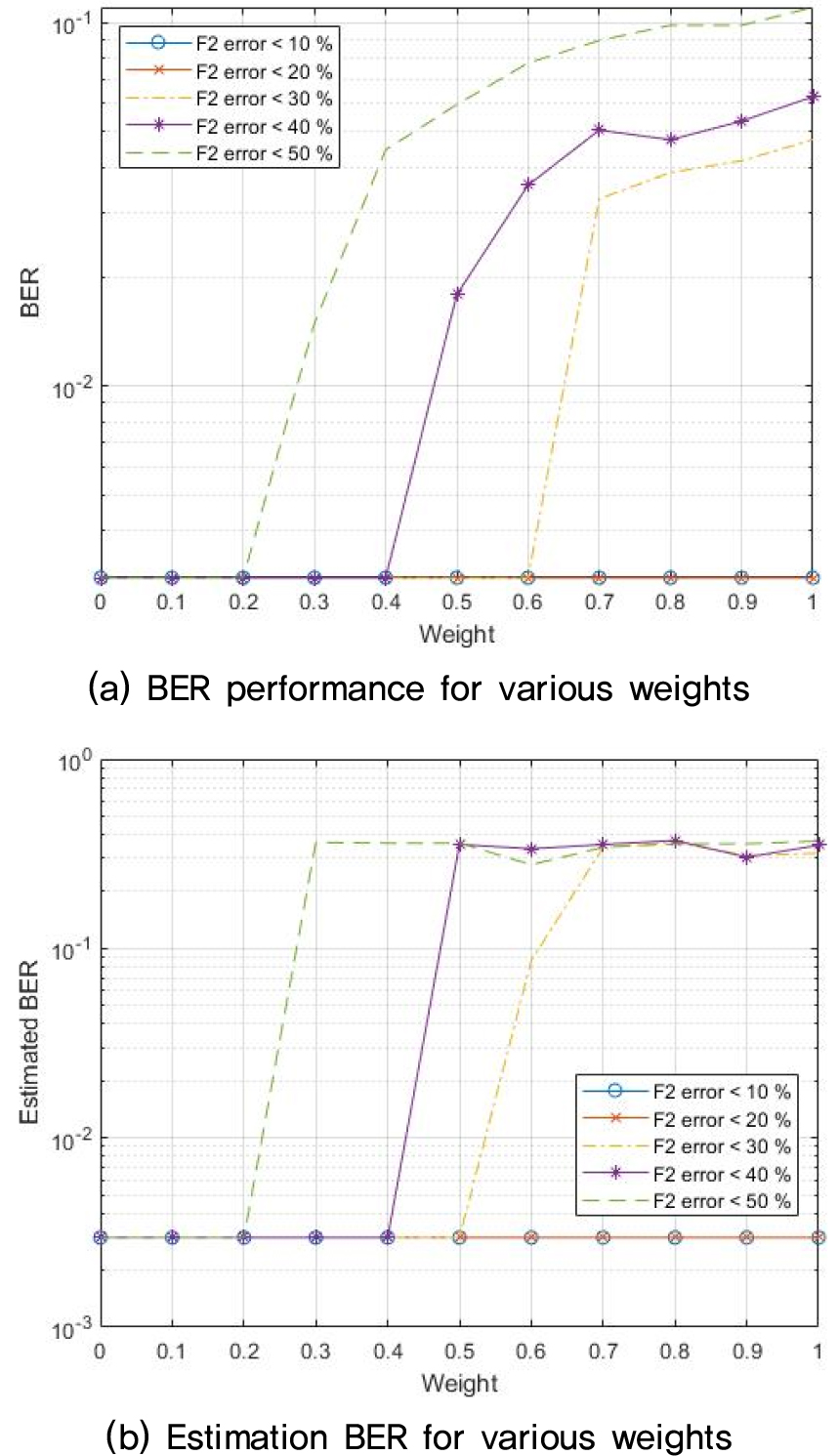
Fig. 5는 오류율 및 추정 BER에 따른 적절한 가중치 값을 알아보기 위해 시뮬레이션을 진행한 결과이다. 2 개의 밴드 F1, F2에서 임의로 F2 밴드의 잡음을 크게 주고 F1의 복조 오류율을 10 % 이내로 조절하였을 때 Fig. 5와 같은 결과를 얻었다. Fig. 5(a)는 위와 같은 시뮬레이션을 진행하였을 때 F2 밴드의 오류율과 가중치에 따른 복호 오류율의 그래프이다. F2 밴드의 오류율이 10 %, 20 %인 경우에는 F2 밴드의 가중치에 상관없이 모두 에러를 정정하였다. F2 밴드의 오류율이 30 %인 경우에는 가중치가 0.6 이하일 때만 에러를 모두 정정하였다. F2 밴드의 오류율이 40 %인 경우와 50 %인 경우에는 각각 가중치가 0.4, 0.2이하일 때만 에러가 완전히 정정되었다. Fig. 5(b)는 위와 같은 시뮬레이션을 진행하였을 때 F2 밴드의 오류율과 가중치에 따른 추정 BER의 그래프이다. 이 때, 추정 BER은 각 밴드별로 구한 것이 아니라 가중치를 적용하여 합해진 신호와 복호 후 재 부호화 시킨 데이터를 비교한 추정 BER이다. Fig. 5(a)와 (b)를 비교하면 두 번째 주파수의 복조 오류율이 30 %인 경우를 제외하고는 복호 오류율이 증가하는 지점과 추정 BER이 증가하는 지점이 일치함을 알 수 있다.

Fig. 5.

(Color available online) BER performance for various weighting values.

시뮬레이션을 통해 다중 밴드에서 각 밴드의 오류율에 따른 추정 BER 및 복조 오류율에 따른 적절한 가중치에 대해 알 수 있다. 이 결과를 바탕으로 추정 BER에 따른 최적의 가중치를 결정하고 Table 1에 나타내었다.

IV. 시뮬레이션 결과

추정 BER을 이용한 가중치 결정의 효과에 대해 알아보기 위해 시뮬레이션을 진행하였다. 이 때, 시뮬레이션 파라미터는 Table 2와 같다. 부호화율 1/3의 터보 부호를 사용하였으며 255 비트의 사전 신호와 112 비트의 입력 비트를 사용하였다. 터보 부호화기의 부호화 길이는 336 비트이며, 수중 채널의 다중 경로, 도플러 확산 등의 성능 감소 요인을 최소화 하기 위해 짧은 부호화 비트 및 낮은 부호화율을 가지는 터보 부호화 방식을 선택하였다.^[10] 터보 등화의 반복 횟수는 5 회이며, 등화기로는 LMS-DFE를 사용하였다. 15 k, 17 k, 19 k, 21 k 총 네 개의 밴드를 사용하였으며 변조 방식은 BPSK이다. 전송율은 100 bps로 가정하였으며 샘플링 주파수가 192 kHz이기 때문에 심볼 당 샘플 수는 1920 개다.

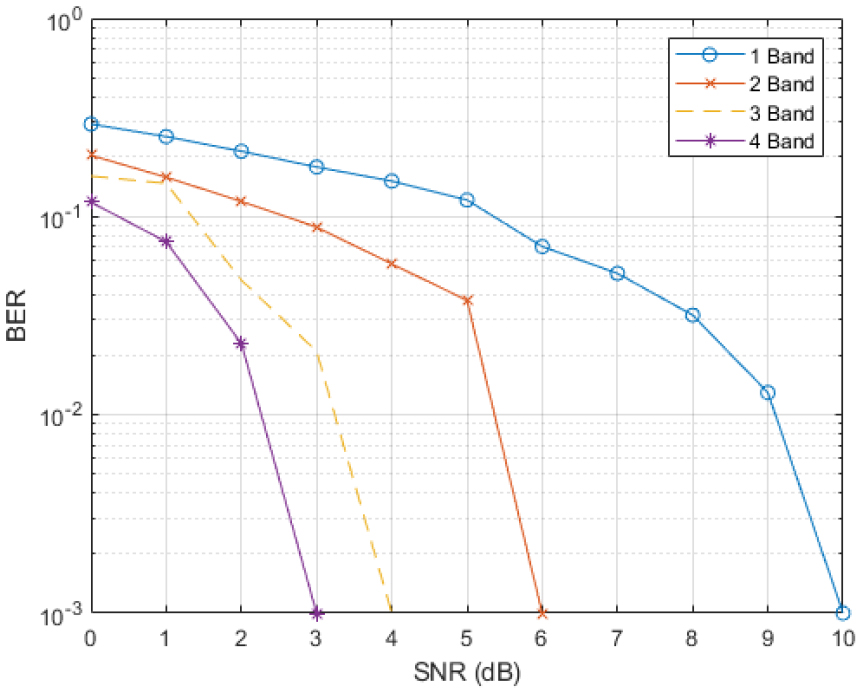
Fig. 6는 밴드 수에 따른 시뮬레이션 결과이다. 밴드 수를 각 1, 2, 3, 4 개로 하여 일정한 다중 경로 및 잡음을 주었을 때의 성능을 비교하였다. 이와 같은 시뮬레이션 결과, 밴드 수의 증가에 따라 성능이 향상됨을 알 수 있었다.

Fig. 6.

(Color available online) Performance according to the number of band.

밴드 수가 1 개일 경우 수신 SNR이 10 dB일 때 완벽히 복호가 되었으며 밴드 수가 2 개일 경우 수신 SNR이 6 dB일 때 완벽히 복호가 되어 밴드 수가 1 개일 경우보다 약 4 dB 성능이 향상되었다. 밴드 수를 3 개로 증가시킨 경우 수신 SNR이 4 dB일 때 완벽히 복호가 되어 밴드 수가 2개일 경우보다 약 2 dB의 성능이 향상됨을 확인할 수 있다. 또한 밴드 수가 4 개일 경우 3 dB의 성능을 보였으며 밴드 수가 3 개에서 4 개로 증가 시 약 1 dB의 성능이 향상됨을 확인할 수 있었다.

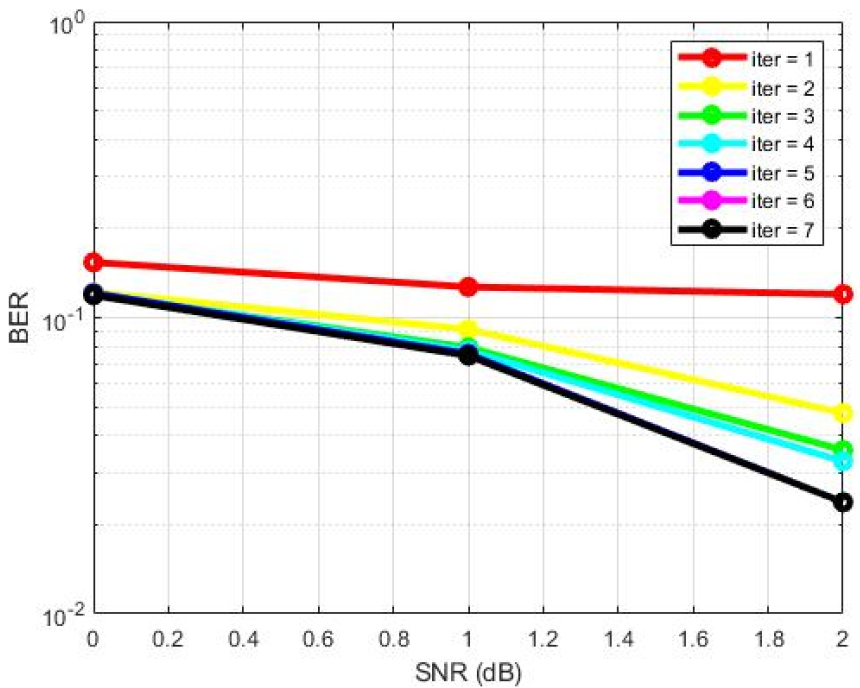
Fig. 7은 4 개의 밴드에서 반복 횟수에 따른 성능 분석 결과이다. 반복 횟수가 많아질수록 성능은 향상되나 반복 횟수가 5 회 이상일 때는 성능이 거의 동일하게 나타나기 때문에 반복 횟수에 따른 계산량을 고려했을 때, 최적의 반복 횟수는 5 회임을 알 수 있었다.

Fig. 7.

(Color available online) Performance according to number of iterations of turbo equalizer.

Fig. 8은 III장에서 구한 추정 BER에 따른 최적의 가중치 및 반복 횟수를 적용해 4 밴드에서 시뮬레이션 한 결과이다. 이 때, 주파수 F2 밴드에만 임의적으로 낮은 잡음을 주어 다른 밴드에 비해 높은 SNR을 가지도록 하였다.

이 때, 상대적으로 높은 SNR을 가지는 F2 밴드의 추정 에러가 급격히 감소하는 0 dB 지점에서 가중치의 적용을 통해 에러를 모두 정정하는 것을 확인할 수 있었다.

Fig. 8.

(Color available online) Estimation BER for seperate frequency band.

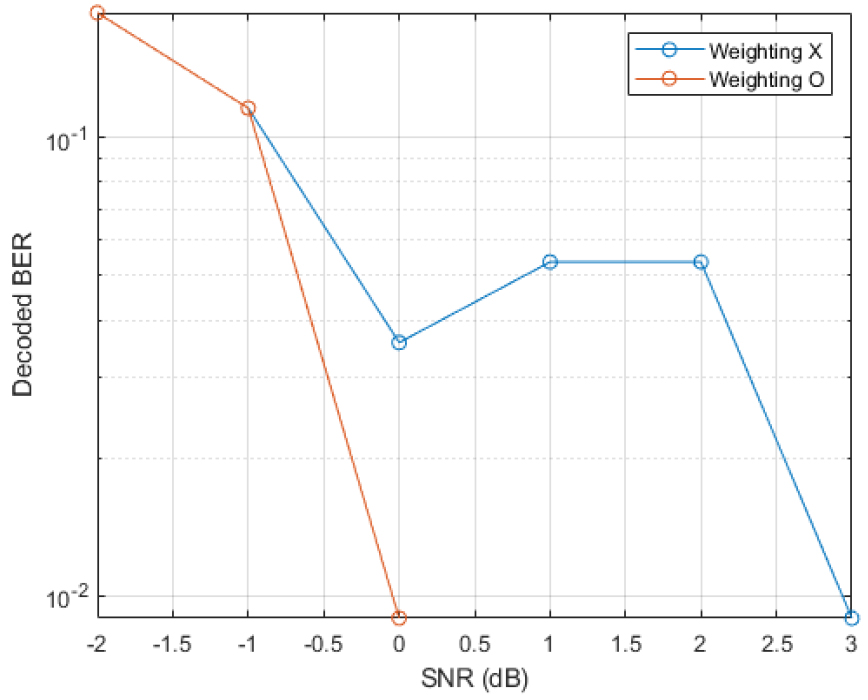
Fig. 9는 다중 밴드 시뮬레이션에서 가중치를 적용한 경우와 가중치를 적용하지 않은 경우의 오류율 곡선을 나타낸 것이다.

Fig. 9.

(Color available online) Multi-band simulation result of estimation BER technique.

가중치를 적용하지 않은 경우, 3 dB에서 오류를 완전히 정정하였으나 가중치를 적용한 경우 0 dB에서 오류를 완전히 정정하였다. 따라서 가중치를 적용하지 않은 경우에 비해 성능이 3 dB 향상되었다. 이와 같은 시뮬레이션을 통해 추정 BER에 따른 가중치 적용이 시스템의 성능 향상에 효과가 있음을 확인하였다.

V. 해상 실험 결과

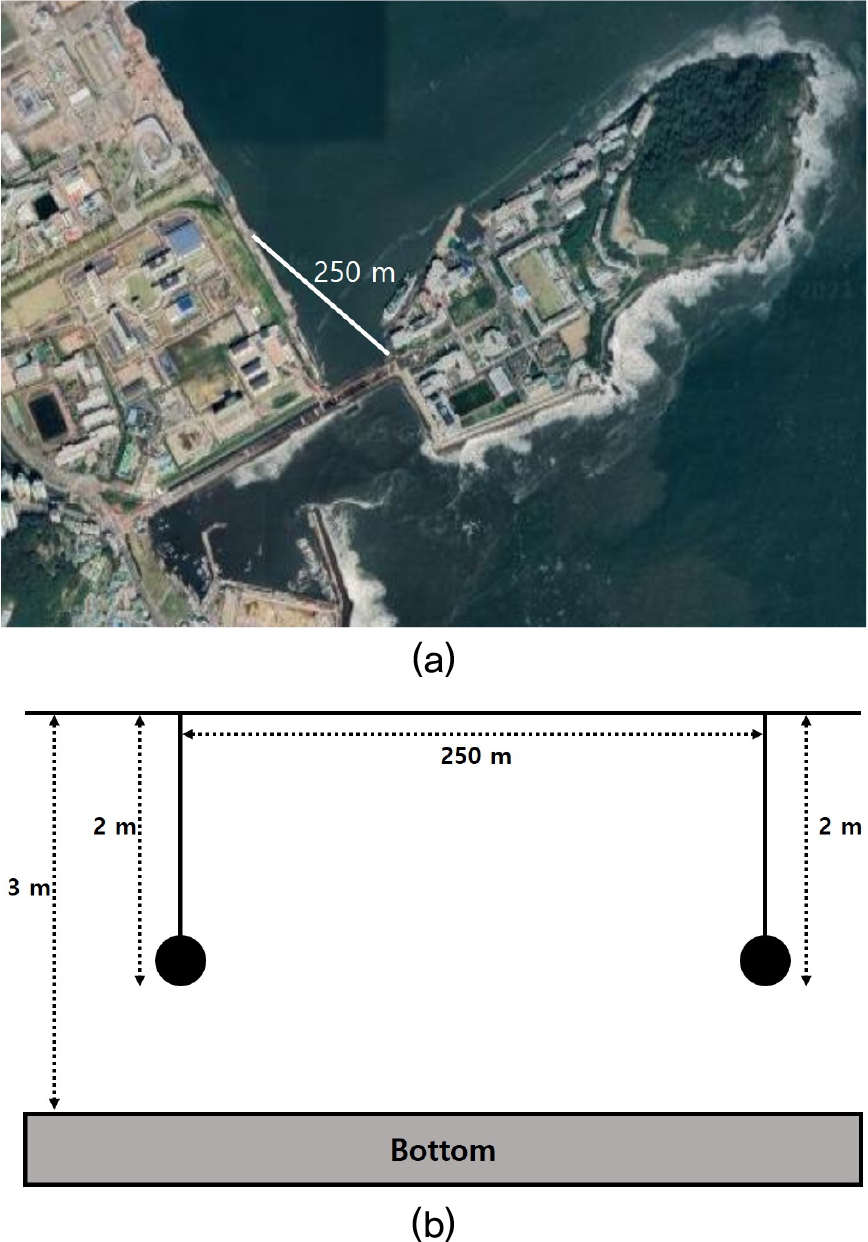
IV장의 시뮬레이션 파라미터 및 결과를 바탕으로 설정된 최적의 실험 파라미터 값을 이용하여 Fig. 10과 같은 환경에서 실제 수중음향통신 실험을 수행하였다. 실험은 II장에서 제시된 네 개의 밴드를 갖는 다중 밴드 PSK 변조 방식을 적용하였다. 송신기로는 Neptune 사의 D/17 모델을 사용하였고, 수신기로는 TC 4032를 사용하였다. 실험은 한국해양대학교 앞 해역에서 수행되었다. 실험 시기는 2020년 10월이었으며, 송·수신기 사이의 거리는 약 250 m였다. 실험 파라미터는 IV장의 Table 2와 동일하게 하였으며, 송신기와 수신기는 수면 아래 2 m에 위치하였다.

Fig. 10.

(Color available online) Illustration of the sea trial experiment.

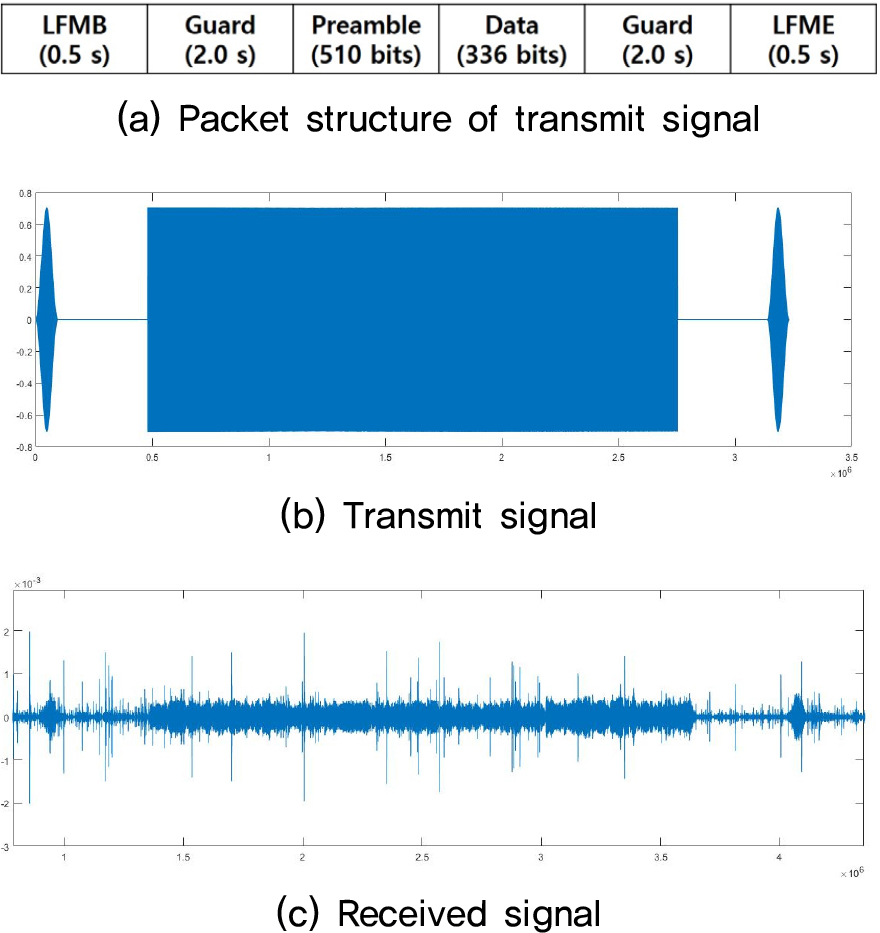
본 실험에서, 원 데이터인 112 비트를 부호화율 1/3을 가지는 터보 부호화 하여 336 비트의 부호화 비트를 생성하였다. 따라서 전체 송신 신호는 사전 신호 255 비트, 부호화 비트(N) 336 비트를 합한 846 비트이다. 이의 패킷 구조는 Fig. 11(a)와 같으며, Fig. 11(b)는 송신 신호, Fig. 11(c)는 수신 신호이다.

Fig. 11.

(Color available online) Packet structure and waveform of transmit and received signals.

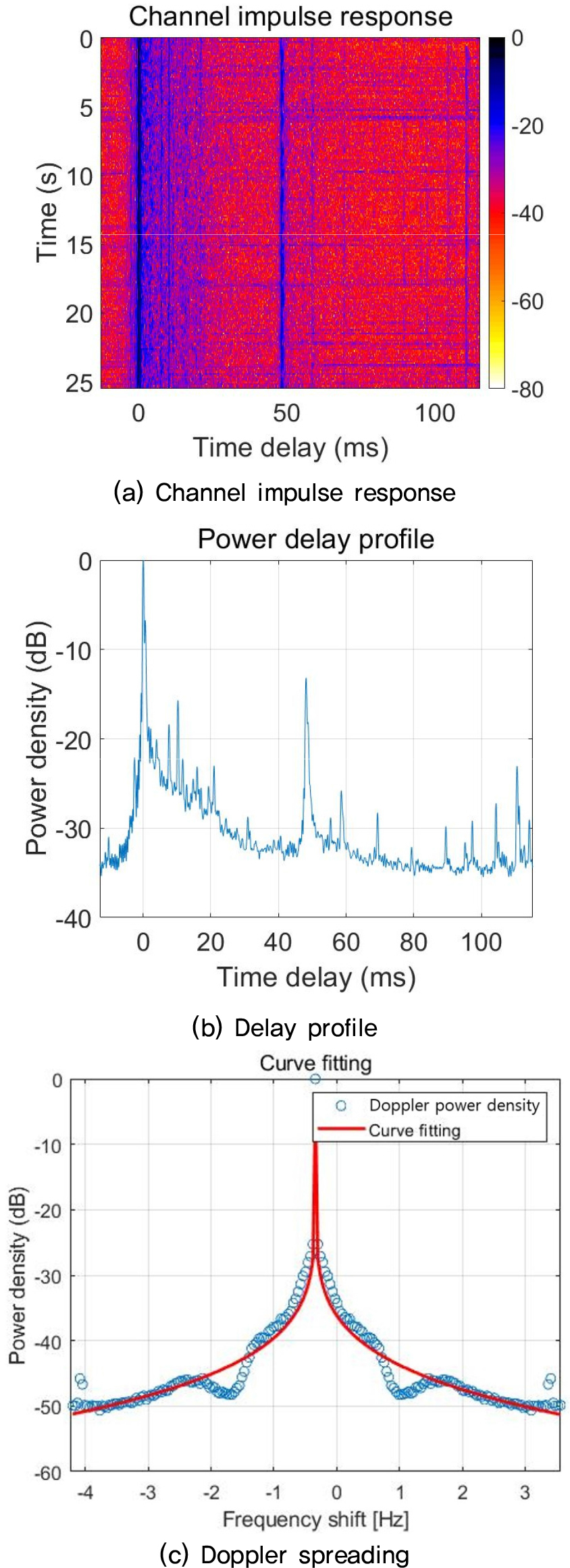
샘플링 주파수는 192 kHz로 하였으며, 전송률은 100 bps로 하였다. Fig. 12는 실험 해역에서 측정한 전달 특성이다. 측정을 위해 약 2 kHz 대역폭을 갖는 0.2 s 길이의 Linear Frequency Modulation(LFM) 신호를 주기적으로 약 1000 회 가량 송신하였다. Fig. 12(a)에서 다중 경로에 따른 영향을 확인할 수 있다. 이는 수면에 반사되어지는 반사파, 그리고 바닥에서 들어오는 신호들이 있다는 것을 의미한다. Fig. 12(b)는 수중 채널의 지연 프로파일을 나타내며, Fig. 12(a)와 같이 아주 큰 다중 경로가 2 개 있음을 알 수 있다. 또한 LFM을 이용하여 도플러 확산을 측정한 결과 약 2 Hz 정도의 확산이 있음을 Fig. 12(c)에서 알 수 있다.

Fig. 12.

(Color available online) Underwater channel characteristic.

Table 3은 다중 밴드 실험 결과로 동일한 데이터를 4 개의 밴드를 이용하여 전송하였으며, 총 5 번을 반복하여 실험하였다. 터보 등화 반복 복호 횟수는 시뮬레이션에서 제시된 최적의 값인 5 회로 설정하였다. 실험 결과는 4 개의 밴드에서 각각의 오류 개수에 대한 백분율로 나타내었으며, 이 경우 부호화된 비트 336비트에 대해 오류 개수에 대한 백분율 표시이다. 각 밴드에서의 추정 BER을 기반으로 III장에서 제시한 최적의 가중치 값을 적용한 경우와 적용하지 않은 경우를 비교하였다. 가중치를 적용하지 않은 경우, 즉 모든 밴드에 대해 동일하게 가중치 값을 1 로 놓고 합하여 터보 복호기 입력한 경우 오류를 완전히 정정하지 못했으나 추정 BER에 따른 최적의 가중치를 적용한 결과 오류를 모두 정정할 수 있었다. 예를 들어 2 회차 실험에서 추정 BER이 네 개의 밴드 각각에서 48.2 %, 8 %, 36.6 %, 47.3 %이고 가중치를 적용하지 않은 경우, 복호 오류율이 12.5 %로 오류를 모두 정정하지 못한 반면 가중치를 Table 1과 같이 적용한 경우 오류가 모두 정정됨을 알 수 있다. 따라서 데이터 부분의 복조 오류율은 알 수 없으나 추정 BER을 이용한 오류율은 계산 가능하므로 본 논문에서 제안한 방식이 다중 밴드 수중통신에서 성능 향상에 효과적임을 알 수 있다.

VI. 결 론

수중통신 환경에서 발생하는 다양한 성능 저하 요소를 극복하기 위해 다중 밴드 통신 기법을 이용하는데, 주파수 선택적 페이딩 현상에 의해 일부 밴드에서 성능 저하가 일어날 수 있다. 이 때, 전체 밴드의 신호를 합산해 복호기에 입력하기 때문에 일부 성능이 떨어지는 밴드가 전체 신호에 영향을 줘 성능이 단일 밴드를 이용한 경우보다 열화될 수 있다. 이를 극복하기 위하여 각 밴드의 오류율에 따른 가중치를 줄 수 있는데, 기존의 방법에서는 각 밴드의 오류율을 산출하는 방식이 사전 신호에 의존적이기 때문에 급격한 도플러 변화 등으로 인해 사전 신호와 부호화 데이터 부분에서의 오류율이 달라질 경우 이 차이를 반영하지 못해 최적의 성능을 얻지 못할 수 있다. 하지만 본 논문에서 제시하는 추정 BER을 이용한 가중치 설정 방식은 복호된 데이터와 복조 후 데이터의 성능 차이를 이용하여 수신된 데이터의 신뢰도를 측정하기 때문에 기존 방식에서는 분석할 수 없었던 부호화된 비트의 성능을 알 수 있다. 이 방식의 효과를 확인하기 위해 시뮬레이션 및 해상 실험을 한 결과 추정 BER을 이용한 가중치 설정을 통해 오류를 모두 정정할 수 있었다. 본 논문의 결과를 바탕으로 향후에는 장거리 해상 실험을 통해 본 논문에서 제안한 추정 BER을 이용한 다중 밴드 전송 기법의 가중치 알고리즘을 적용할 것이며, 도플러 추정 등에도 응용할 수 있다.