I. 서 론
II. 흡음형 소음기
2.1 Biot 모델과 Biot-Allard 모델
2.2 흡음형 소음기 구성 및 환경
III. 음향성능 해석
3.1 물성치 변화에 따른 해석 결과
3.2 단층 흡음형 소음기 해석 결과
3.3 다층 흡음형 소음기 해석 결과
IV. 흡음재 배치 최적화
4.1 최적화 설계
4.2 흡음재 배치 최적화 결과
V. 결 론
I. 서 론
함정 내부에는 다수의 배관이 존재하며, 배관 내부에 물과 같은 유체가 흐르면서 소음이 발생하게 된다. 이와 같은 소음은 함정의 생존성과도 직결되기 때문에 배관 소음을 줄일 수 있는 유체소음기의 설치 및 운용은 필수적이다. 그러나 함정 내부의 협소한 공간을 고려했을 때 소음기의 크기는 제한적일 수밖에 없으며, 이때 음향성능이 우수한 흡음형 소음기가 주로 사용된다.
소음기의 음향성능은 주로 투과손실로 판단하며, 과거 많은 연구에서 실험 및 계산, 수치해석 방법 등을 통해 비교, 검증된 바 있다. Selamet et al.[1,2]은 다공성 흡음재가 포함된 단층 및 2층 흡음형 소음기에서 경계조건을 이용하여 투과손실을 계산하였으며, 경계요소법 및 실험 결과와 비교하여 계산 결과가 타당함을 입증하였다. Seo et al.[3]은 함정의 해수 배관소음을 저감하기 위해 탄성 흡음재를 이용한 흡음형 소음기를 연구하였으며, 흡음재 두께, 길이 및 재질특성에 따른 투과손실 이론값을 구하여 실험 결과와 비교하였다. Lee와 Yang[4]은 팽창형 소음기의 투과손실을 실험 및 수치해석 방법을 통해 비교, 검증하였으며, 다공성 흡음재가 채워진 흡음형 소음기의 투과손실을 수치해석 방법을 통해 검증 및 예측하였다. Nenning et al.[5]은 Biot 모델이 적용된 다공탄성 흡음재로 이루어진 단층 흡음형 소음기의 투과손실을 모드매칭법을 이용하여 계산하였다. 이를 발전시켜 Lee et al.[6]은 다층 다공탄성 흡음형 소음기의 투과손실을 모드매칭법을 이용하여 계산하였으며, 수치해석 결과와 비교하여 그 유효성을 입증하였다. Gupta et al.[7]은 팽창형 소음기의 음향성능을 향상시키기 위해 소음기의 입/출구 위치를 최적 설계하였다.
본 연구에서는 흡음형 소음기 배관 내부에 물이 흐르는 상황을 가정하여 투과손실에 영향을 주는 다공탄성 흡음재의 물성을 확인하였다. 투과손실을 계산하기 위해 유한요소법 기반 수치해석 프로그램인 COMSOL Multiphysics를 사용하였으며, 2 kHz 대역까지 관심주파수 영역으로 설정하였다. 단층 및 다층 흡음재를 가진 소음기에서 투과손실을 확인한 뒤 소음기의 흡음재 배치 순서를 최적화하여 소음기의 투과손실을 향상시키고자 하였다.
II. 흡음형 소음기
2.1 Biot 모델과 Biot-Allard 모델
이번 연구에서 흡음재는 흡음형 소음기에서 많이 사용되는 폴리우레탄을 사용하였으며, 다공탄성 물질로 가정하였다. 이때 수치해석 프로그램에서는 Biot 이론을 기반으로 한 Biot 모델과 Biot-Allard 모델을 선택할 수 있다. 먼저, Biot 모델은 물질 내부의 유체가 물이나 기름과 같은 액체일 때 주로 사용하고 점성 손실만을 고려한다. 반면, Biot-Allard 모델은 물질 내부에 공기와 같은 기체가 채워져 있을 때 주로 사용하며, 점성 손실 뿐만 아니라 열에 의한 손실을 고려한다.[8]
Biot 이론을 적용한 Biot 모델은 아래와 같다. 다공성 물질의 변위를 u, 다공성 물질 내 유체의 변위를 w, 유체와 다공성 물질의 총 응력 텐서를 𝜎라 할 때 Biot의 다공탄성 물질에 대한 파동방정식은 아래와 같이 표현할 수 있다.[9,10,11]
이때 와 는 유체의 밀도와 점성계수, 𝜏는 뒤틀림도, 는 공극률, 는 다공성 물질 내 유체의 압력, 𝜘는 투과성, 는 다공성 물질의 밀도, 는 평균 밀도를 각각 나타낸다. 평균 밀도는 다공성 물질과 유체를 모두 포함한 전체 밀도를 의미한다.
Biot-Allard 모델의 파동방정식은 점성계수와 유체 압축률을 주파수에 종속된 식으로 대체함으로써 표현할 수 있다. 주파수 종속 점성계수 𝜇(𝜔) 및 유체 압축률 는 아래 Eqs. (3), (4)와 같이 표현되며, 이때, 는 점특성 길이, 는 열특성 길이, 는 흐름저항률, 는 정압비열, 는 정적비열, 는 주변 압력, Pr는 프란틀 수를 의미한다.[12]
본 연구에서는 흡음재인 폴리우레탄 내부에 공기가 채워진 상황을 가정하므로 Biot-Allard 모델을 적용하였다.
2.2 흡음형 소음기 구성 및 환경
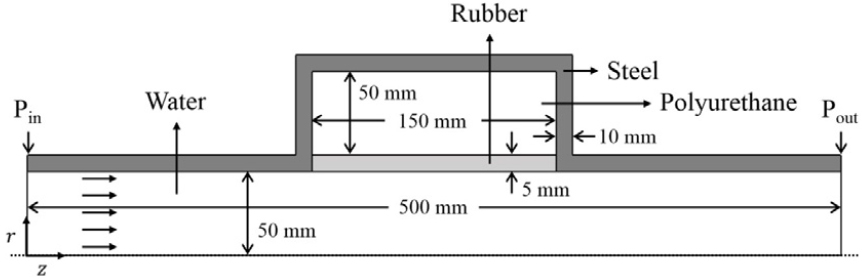
이번 연구에서 흡음형 소음기는 원통형 소음기를 가정하기 때문에 2D 축 대칭 차원에서 설계하였으며, 흡음형 소음기의 구조 및 크기는 Fig. 1과 같다.
해석 환경은 상온(20 °C), 상압(1atm)을 가정하여 배관 내 음속은 1481.4 m/s, 밀도는 998.2 kg/m3를 적용하였으며, 공기의 밀도는 1.204 kg/m3를 적용하였다. 흡음재인 폴리우레탄의 물성치 중 밀도, 전단계수, 손실계수는 독일 KRAIBURG Co.의 물성치[13]를 적용하였으며, 나머지 물성치는 일반적인 폴리우레탄에서 보여지는 범위 내에서 임의로 지정하였다. 세부 물성치는 Table 1과 같으며, 밀도, 전단계수, 손실계수에 따라 각각 폴리우레탄 A, B, C, D, E로 구분하였다. 배관 및 소음기를 감싸는 케이싱 부분은 강철, 배관과 소음기 사이를 물리적으로 분리하는 라이너는 고무로 가정하였으며, 세부 물성치는 Table 2와 같다.
Table 1.
Polyurethane properties.
III. 음향성능 해석
3.1 물성치 변화에 따른 해석 결과
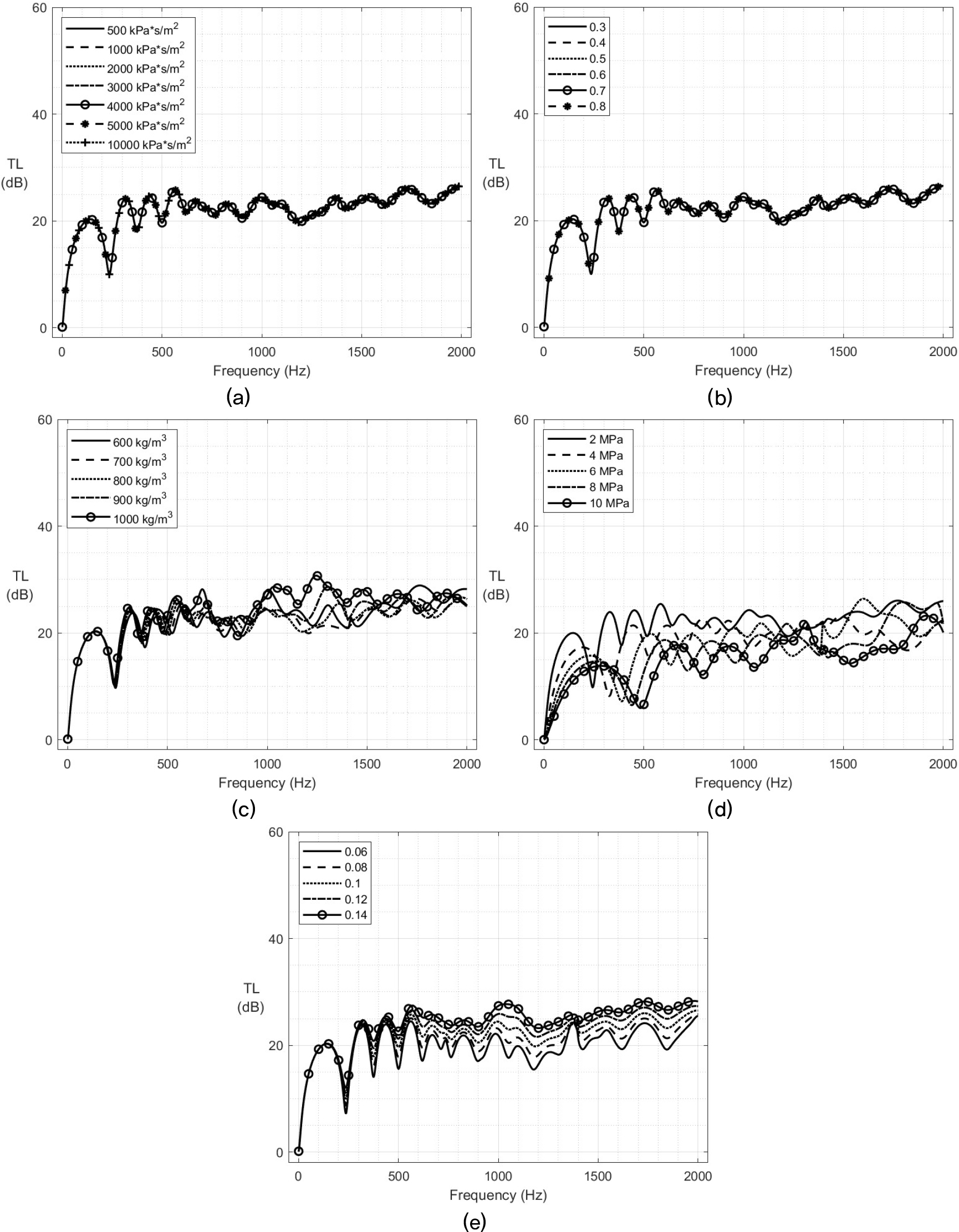
흡음형 소음기 해석에 앞서 폴리우레탄 각각의 물성치 중 어떤 물성치가 소음기 투과손실에 주요한 영향을 주는지 파악하기 위해 물성치 변화에 따른 해석을 수행하였다. Table 1에서 보여지는 각각의 물성치에 따른 투과손실 변화를 살펴보기 위해 폴리우레탄의 밀도, 전단계수, 손실계수, 공극률, 흐름저항률의 물성치를 일반적인 범위 내에서 비교하였다. 세부적으로 밀도는 600 kg/m3 ~ 1,000 kg/m3, 손실계수는 0.06 ~ 0.14, 전단계수는 2 MPa ~ 10 MPa, 흐름저항률은 500 kPa·s/m2 ~ 10,000 kPa·s/m2, 공극률은 0.3 ~ 0.8 범위에서 투과손실 변화를 관찰하였으며, 이때 밀도, 전단계수, 손실계수물성치 변화에 따른 투과손실을 관찰할 때 비교대상이 아닌 나머지 물성치는 폴리우레탄 B의 물성치를 공통 적용하였다.
Fig. 2에서 볼 수 있듯이 (a)흐름저항률과 (b)공극률 변화에 따른 영향은 전혀 없는 것으로 확인하였다. Fig. 2(c) 밀도의 경우 대체로 비슷한 음향성능을 보였으나, 고주파수 대역에서는 밀도가 높을 때 대체로 음향성능이 높은 것을 확인하였다. Fig. 2(d) 전단계수의 경우 그 값이 증가하면서 첫 번째 공진주파수가 증가하는 반면 흡음재의 탄성이 줄어들면서 음향성능은 전반적으로 감소하는 경향을 보여주었다. Fig. 2(e) 손실계수는 그 값이 증가함에 따라 공진에 의한 영향이 줄어들면서 음향성능이 전 주파수 대역에서 전반적으로 증가하는 결과를 확인하였다. 본 논문에서는 폴리우레탄 B의 물성치를 대표적으로 선택하여 그에 따른 결과를 보여주지만 나머지 폴리우레탄 물성치를 적용하였을 때에도 비슷한 경향을 확인한 바 있다.
흡음형 소음기 음향성능에 영향을 주는 물성치는 그 영향성에 따라 크게 전단계수, 손실계수, 밀도 순으로 정리할 수 있으며, 이 세 가지 물성치는 폴리우레탄 종류에 따라 구분되는 물성치이다. Fig. 2의 폴리우레탄 물성치별 음향성능 해석결과를 바탕으로 단층 흡음형 소음기에서 흡음재 각 층에 폴리우레탄 물성치를 적용하여 음향성능을 확인해 보았다.
3.2 단층 흡음형 소음기 해석 결과
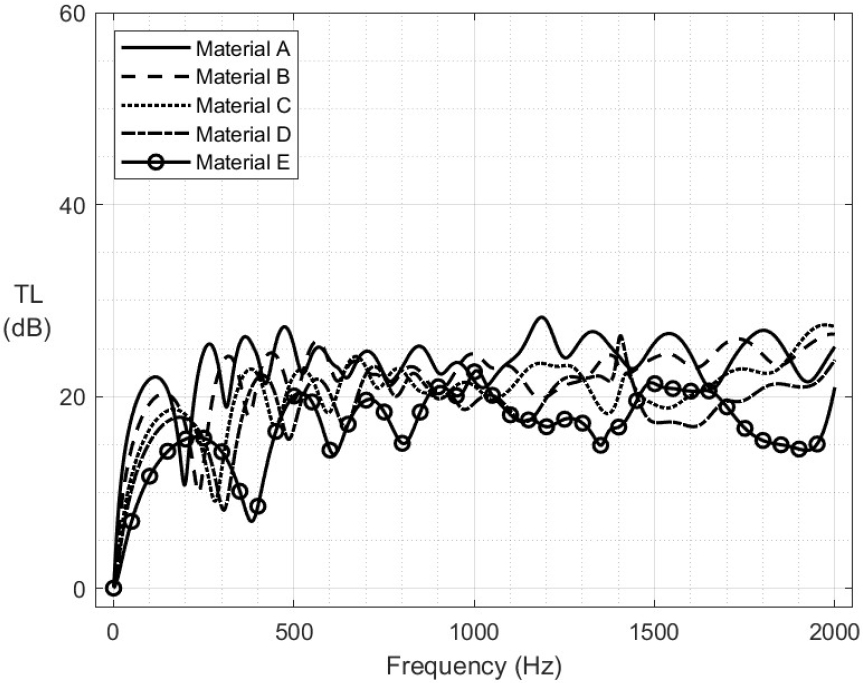
단층 흡음형 소음기의 흡음재에 폴리우레탄 물성치 A, B, C, D, E를 적용했을 때의 투과손실은 Fig. 3과 같다. 물성치 A의 경우 밀도는 가장 낮지만, 손실계수가 높고 전단계수가 낮기 때문에 첫 번째 공진주파수는 낮은 값을 보이면서 상대적으로 좋은 음향성능을 보여주었다. 하지만 물성치 B, C, D로 갈수록 전단계수의 영향 등으로 음향성능은 점차 감소하였고, 물성치 E를 적용했을 때 밀도는 가장 높지만, 손실계수가 낮고 전단계수가 가장 높기 때문에 물성치 중 가장 낮은 음향성능을 보여주었다.
3.3 다층 흡음형 소음기 해석 결과
다층 흡음형 소음기는 Fig. 1의 구조에서 N개의 동일한 두께의 흡음재로 구성하였으며, 이때 흡음재 전체 두께는 50 mm로 고정하였다. 다층 흡음형 소음기의 형상은 Fig. 4와 같으며, 배관에 가까운 순서대로 1층, 2층, … , N층을 의미한다.
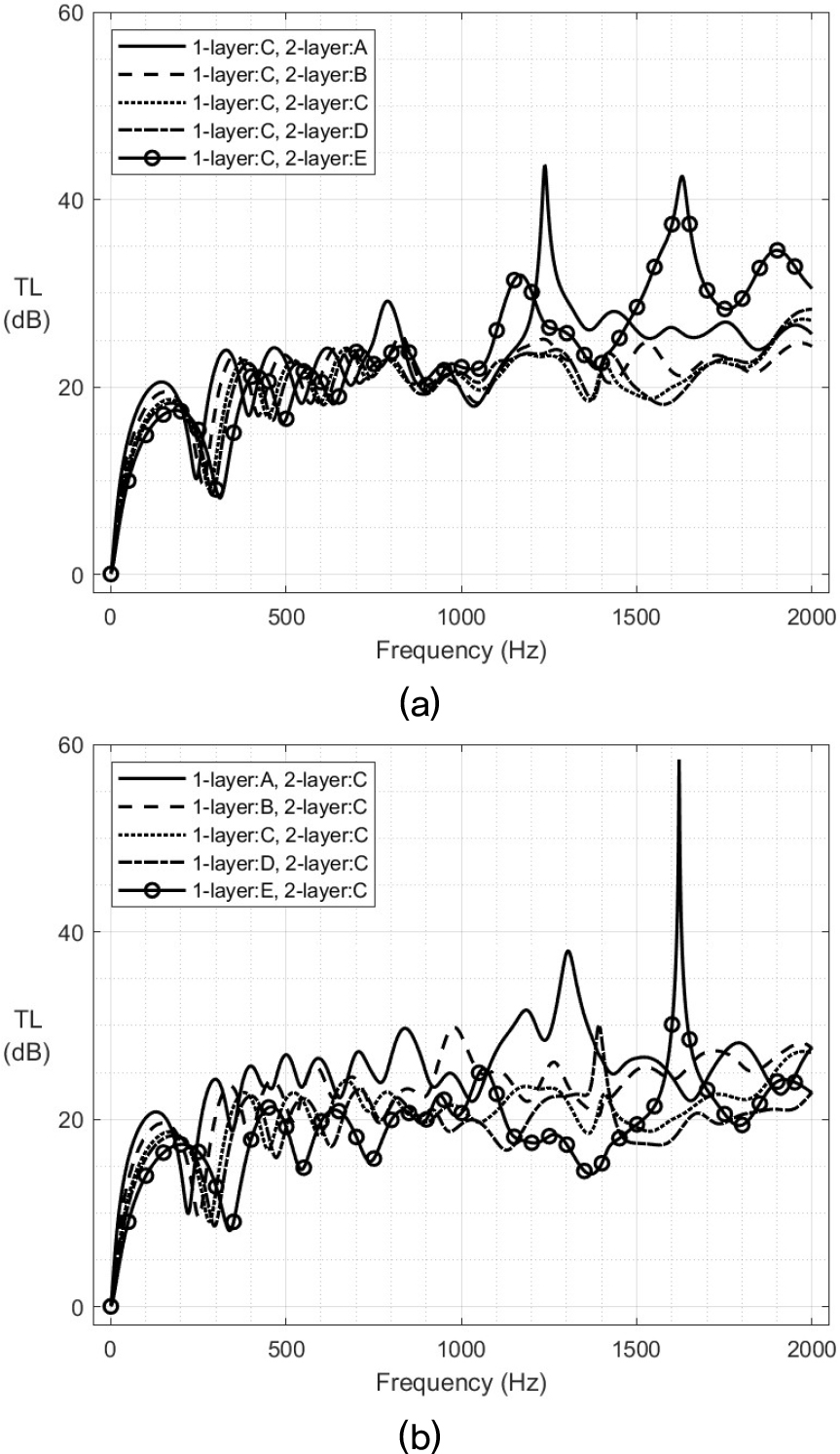
Fig. 5는 두 층의 흡음재를 포함하는 소음기에서 흡음재 각 층의 물성치 변화에 따른 투과손실을 계산한 결과이다. Fig. 5(a)는 흡음재 1층에 물성치 C를 고정한 상태에서 흡음재 2층에 다섯 종류의 물성치를 각각 적용한 결과이며, 700 Hz 이하 주파수 대역에서 전반적으로 비슷한 음향성능을 보여주었다. 하지만 그 이상 대역에서는 흡음재 2층에 물성치 A와 E를 적용하였을 때 상대적으로 높은 음향성능을 확인하였다. Fig. 5(b)는 흡음재 2층에 물성치 C를 고정한 상태에서 1층의 물성치 변화를 준 결과이며, 물성치 A에서 E로 바뀔수록 첫 번째 공진주파수가 높아지면서 전반적으로 음향성능은 낮아지는 것을 확인하였다. 앞서 Fig. 5(a)와 비교했을 때 중고주파 영역에서는 물성치 변화에 따른 영향이 비슷한 수준으로 볼 수 있다. 그러나 저주파 대역을 포함하여 관심주파수 영역 전반에 걸쳐 평가하였을 때 배관에 가까운 흡음재의 물성치 변화가 소음기의 음향성능에 더 많은 영향을 끼친다는 사실을 확인할 수 있었다.
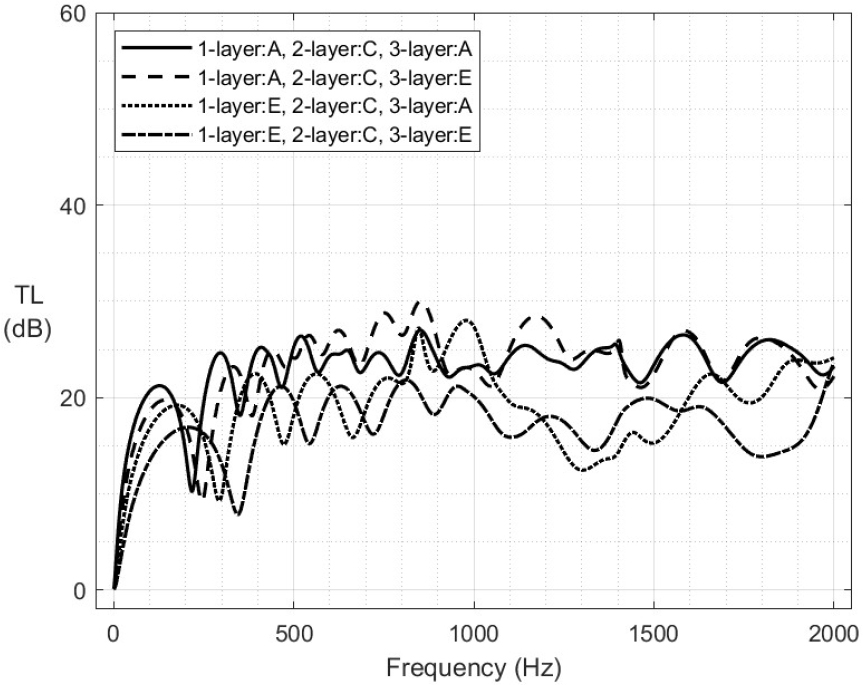
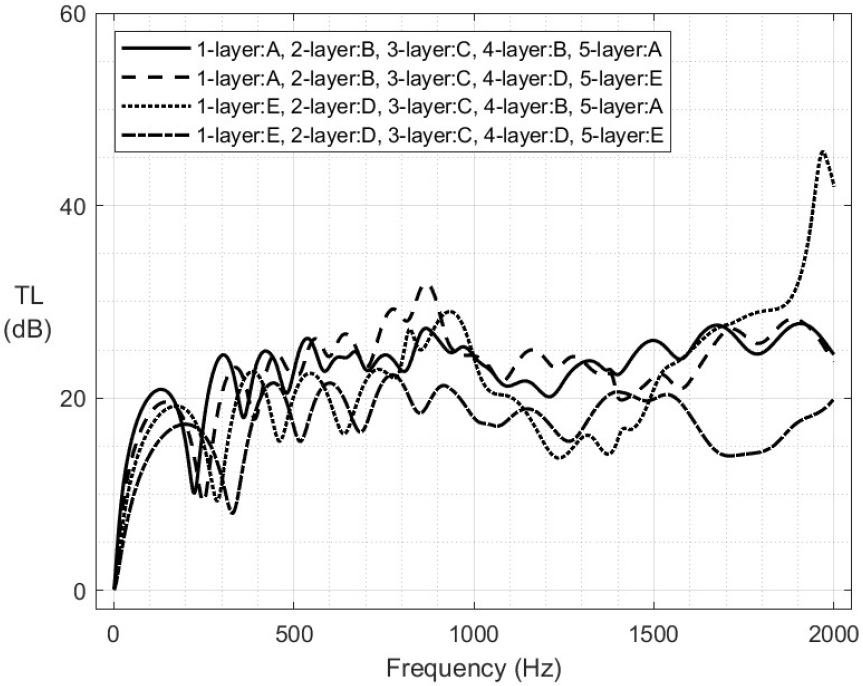
Figs. 6과 7은 흡음재를 3층 또는 5층으로 구성한 소음기에서 물성치 변화에 따른 투과손실을 계산한 결과이다. 앞서 2층 흡음형 소음기에서 분석한 결과와 같이 배관에 가까운 층에 적용된 물성치가 음향성능에 지배적인 영향을 끼치는 사실을 확인하였다.
IV. 흡음재 배치 최적화
4.1 최적화 설계
이번 연구에서 흡음재 배치 순서를 최적화하기 위해 초기 조건에 민감하지 않고 수렴에 빠르게 도달할 수 있는 Nelder-Mead 방법[14]을 최적화 기법으로 사용하였다.
최적화 목표를 효과적으로 달성하기 위해서는 목적함수를 적절하게 설정하는 것이 중요하며, 이번 연구에서는 아래의 두 가지 목적함수를 적용하였다. 먼저, 전반적으로 음향성능을 향상시키기 위해 Eq. (5)와 같이 첫 번째 목적함수를 설정하였다.
이때 특정 주파수 대역에서만 투과손실 값이 급격히 증가하고, 나머지 대역에서는 평균에 미치지 못할 것을 우려하여 두 번째 목적함수는 음향성능이 균일하게 나올 수 있도록 Eq. (6)과 같이 평균 투과손실을 기준으로 평균보다 작은 값을 모두 더한 총합을 목적함수로 설정하였다. 이때 평균 투과손실은 최적화 과정에서 한 번의 계산이 종료되었을 때 결괏값인 투과손실의 평균을 의미한다.
설계변수는 흡음재 종류인 폴리우레탄을 구분하여 적용하기 위해 밀도, 전단계수, 손실계수를 고려하였는데, Table 1에 의하면 폴리우레탄의 밀도가 바뀌면 전단계수와 손실계수가 함께 바뀌기 때문에 밀도 하나만을 설계변수로 적용하였다. 나머지 물성치는 음향성능에 큰 영향을 주지 않기 때문에 Table 1과 같이 적용하였다.
4.2 흡음재 배치 최적화 결과
최적화는 흡음재를 3층 또는 5층으로 구성한 소음기에 대해 각각의 목적함수를 구분하여 적용하였으며, 전 주파수 대역을 최적화 구간으로 설정하여 진행하였다.
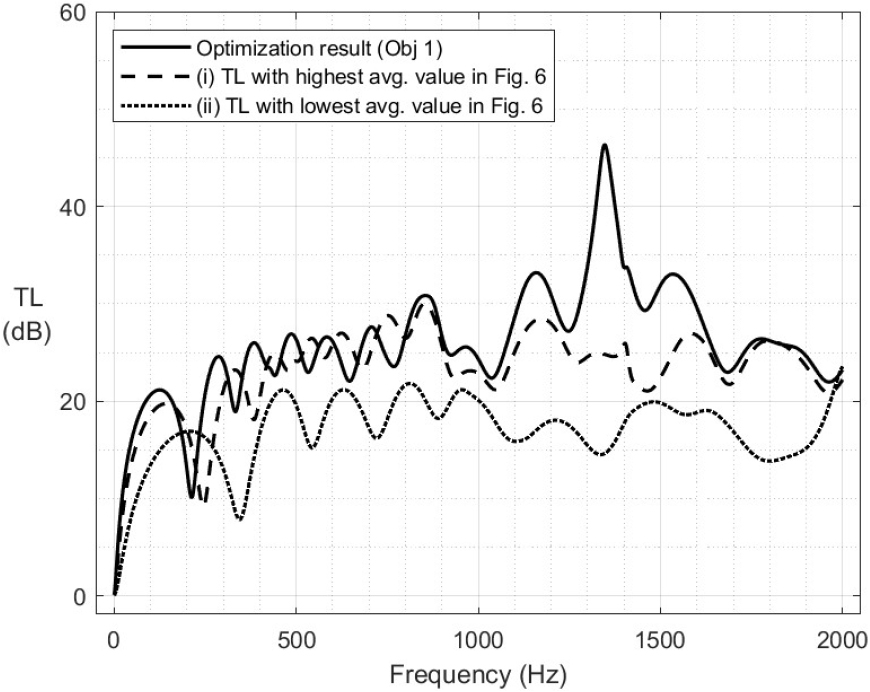
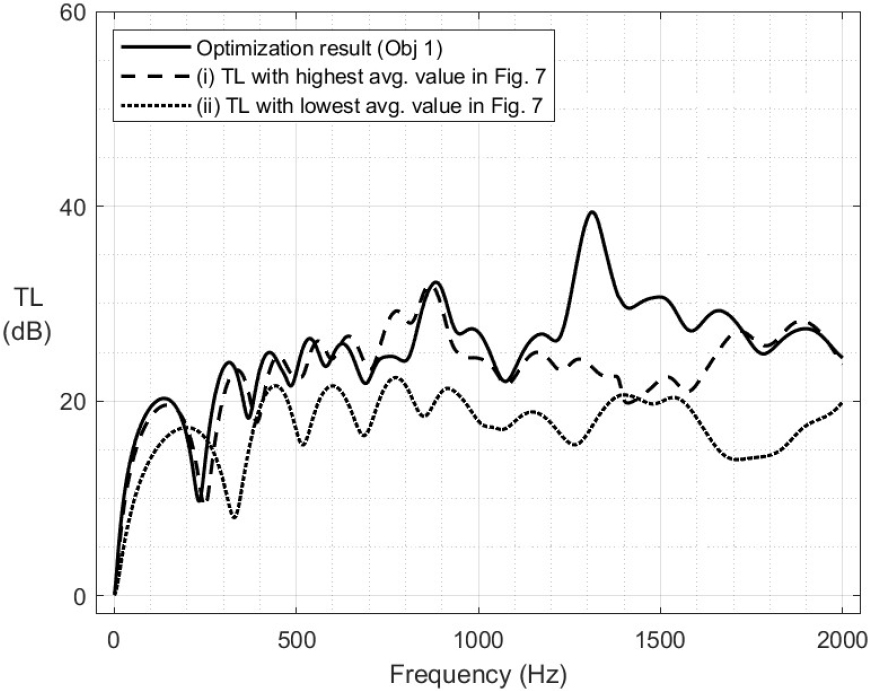
3층 흡음형 소음기에 첫 번째 목적함수를 적용한 최적화 결과는 Fig. 8과 같다. 앞서 Fig. 6에서 3층 흡음형 소음기의 평균 투과손실이 가장 큰 경우와 가장 작은 경우를 함께 비교하였으며, 흡음재 배치 순서 및 세부 결과는 Table 3과 같다. 이때 흡음재 배치 순서는 좌측부터 1층, 2층, … , N층을 의미한다. 최적화 결과 약 1,000 Hz ~ 1,700 Hz 주파수 대역에서 투과손실이 상당히 증가하였으며, 평균 투과손실은 기존 해석 결과 대비 약 3 dB ~ 9 dB 증가하면서, 음향성능 향상이라는 목표를 달성하였다.
Table 3.
Optimization result of 3-layer absorptive silencer (Objective function 1).
| Case |
Objective function 1 | Random arrangement | |
| (i) | (ii) | ||
| Arrangement | AAD | ACE | ECE |
| Avg. TL [dB] | 25.91 | 23.19 | 16.95 |
| Increased TL [dB] | 2.72 ~ 8.96 | - | - |
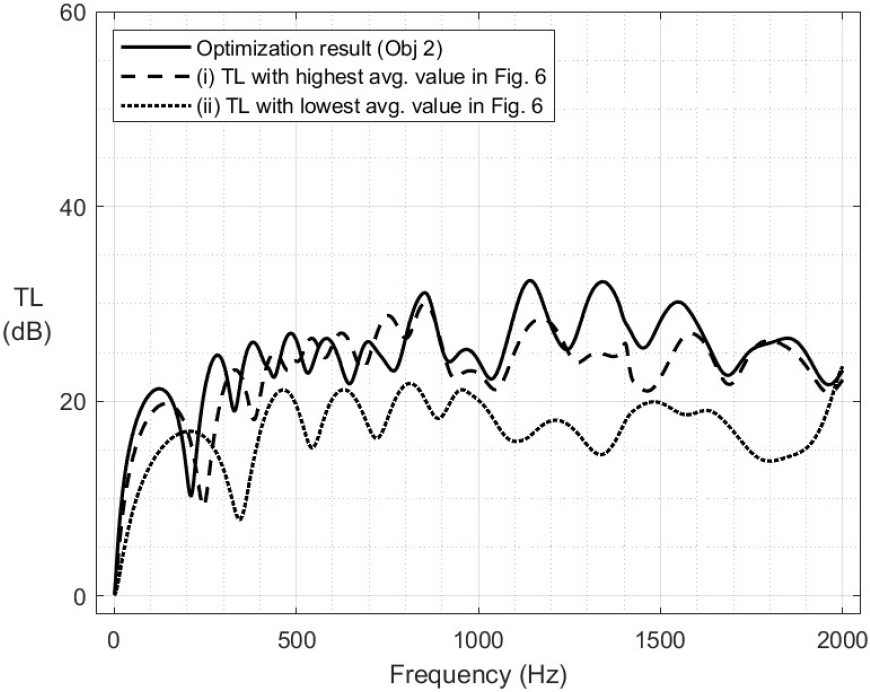
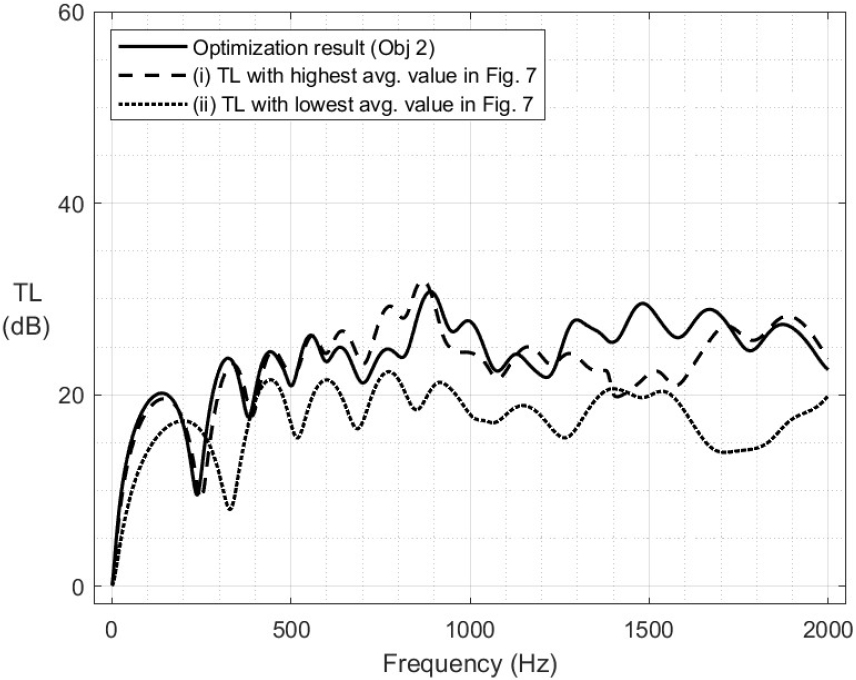
이어서 두 번째 목적함수를 적용한 결과는 Fig. 9 및 Table 4와 같다. 기존 해석 결과 대비 전반적으로 균일한 음향성능을 보여주었으며, 평균 투과손실이 약 2 dB ~ 8 dB 증가하면서 최적화 목표를 달성하였다. 다만, 두 번째 목적함수를 적용한 최적화 결과가 첫 번째 목적함수를 적용한 최적화 결과 대비 상대적으로 낮은 증가량을 보이는 것은 평균 투과손실보다 큰 값을 모두 0으로 처리하면서 최적화 구간이 축소되었기 때문으로 판단된다.
Table 4.
Optimization result of 3-layer absorptive silencer (Objective function 2).
| Case |
Objective function 2 | Random arrangement | |
| (i) | (ii) | ||
| Arrangement | AAC | ACE | ECE |
| Avg. TL [dB] | 24.80 | 23.19 | 16.95 |
| Increased TL [dB] | 1.61 ~ 7.85 | - | - |
Fig. 10 및 Table 5는 5층 흡음형 소음기에 첫 번째 목적함수를 적용한 최적화 결과이다. 앞서 Fig. 7에서 5층 흡음형 소음기에서 물성치를 임의 적용한 경우보다 약 2 dB ~ 8 dB 높은 평균 투과손실을 보여주었으며, 약 1,100 Hz ~ 1,700 Hz 주파수 대역에서 높은 투과손실을 보이면서 음향성능 향상이라는 최적화 목표를 달성하였다.
Table 5.
Optimization result of 5-layer absorptive silencer (Objective function 1).
| Case |
Objective function 1 | Random arrangement | |
| (i) | (ii) | ||
| Arrangement | ABBCC | ABCDE | EDCDE |
| Avg. TL [dB] | 25.32 | 23.13 | 17.33 |
| Increased TL [dB] | 2.19 ~ 7.99 | - | - |
마지막으로 5층 흡음형 소음기에서 두 번째 목적함수를 적용한 결과는 Fig. 11 및 Table 6과 같다. 전 주파수 대역에서 균일한 음향성능을 보여주면서 기존 해석 결과 대비 평균 투과손실이 약 1 dB ~ 7 dB 증가하면서 최적화 목표를 달성하였다. 마찬가지로 두 번째 목적함수는 평균에 미치지 못하는 구간만을 최적화 구간으로 삼았기 때문에 최적화 구간이 축소되면서 첫 번째 목적함수를 적용했을 때 대비 낮은 증가량을 보여주는 것으로 판단된다.
Table 6.
Optimization result of 5-layer absorptive silencer (Objective function 2).
| Case |
Objective function 2 | Random arrangement | |
| (i) | (ii) | ||
| Arrangement | ABDCB | ABCDE | EDCDE |
| Avg. TL [dB] | 23.93 | 23.13 | 17.33 |
| Increased TL [dB] | 0.8 ~ 6.6 | - | - |
전반적으로 최적화된 흡음재 배치 순서를 살펴보면 두 층이 연속적으로 같은 종류의 폴리우레탄으로 배치된 경우를 볼 수 있다. Table 3에서 최적의 흡음재 배치 순서는 AAD이며, Table 5에서는 ABBCC이다. 이처럼 두 층이 연속적으로 같은 종류의 폴리우레탄으로 구성될 경우 흡음재 두께를 고려하지 않는다면 AD 혹은 ABC와 같이 2층 혹은 3층의 구조로 볼 수 있을 것이다. 다만, 실제 폴리우레탄을 제작하는 단계에서는 규격화된 두께로 폴리우레탄을 제작하기 때문에 본 논문에서는 일정한 두께로 구성되는 폴리우레탄을 가정하여 각각 3층 및 5층 구조로 제시하였다.
V. 결 론
본 연구에서는 흡음형 소음기의 음향성능 향상을 목표로 수치해석 방법을 이용하여 다층 흡음형 소음기에서 흡음재 배치 순서를 최적화하였다. 그 과정에서 흡음형 소음기 안에 들어가는 흡음재의 물성치에 따른 음향성능 경향을 파악하였으며, 단층 및 다층 흡음형 소음기에서 음향성능을 확인하였다.
단층 흡음형 소음기에서 다섯 종류의 폴리우레탄 물성치를 적용해 본 결과 전단계수가 낮고 손실계수가 높은 물성치를 가진 흡음재가 전반적으로 더 높은 음향성능을 보여주었다. 또한 다층 소음기에서 물성치를 임의 적용하였을 때 배관에 가까운 흡음재가 음향성능에 더 지배적인 영향을 끼친다는 사실을 확인할 수 있었다. 더 나아가 최적화 과정을 통해 음향성능을 향상시키고자 하였다. 최적화 기법은 Nelder-Mead 방법을 사용하였으며, 3층 및 5층 흡음형 소음기에서 흡음재 배치 순서를 최적화하였다. 그 결과 전반적으로 평균 투과손실의 향상을 확인하였으며, 만약 특정 주파수 대역에서의 음향성능 향상을 목표로 한다면 본 연구에서의 최적화 방법을 적용해 볼 수 있을 것이다.