I. 서 론

에어컨의 실외기는 에어컨의 냉방 성능뿐만 아니라 에어컨의 소음 성능을 결정 짓는 중요한 요소이다. 실외기 압축기, 축류팬, 열교환기와 구성 요소를 연결하는 배관계로 이루어져 있다. 이 중 압축기의 진동 소음은 실외기의 주 소음원으로 알려져 있다. 에어컨의 성능과 효율을 증가를 위하여 압축기의 작동 속도를 증가시키면서, 압축기 냉매의 유속이 증가하였으며, 이는 배관계의 유동 기인 진동 소음의 상대적 기여도를 증가시켰다. 냉매 유동에 의한 배관계 진동을 유발하는 가진원은 냉매의 난류 유동에 의하여 벽면에 형성되는 압력장이다. 이러한 압력장은 두가지 성분으로 구분할 수 있다. 먼저, 난류에 의해 발생한 와류가 배관의 벽면에 직접적으로 부딪힘으로서 형성되는 압력섭동이 있으며, 이러한 압력성분을 비압축성 압력성분이라고 할 수 있다. 비압축성 압력성분은 와류가 발생한 지점 근처에서 배관을 가진하게 되며, 유속과 같은 속도로 전파되게 된다. 두번째 성분으로는 압축성 압력성분이 있다. 압축성 압력성분은 와류의 압력 섭동에 의하여 발생한 음향파가 배관의 길이 방향으로 전파하며 배관을 가진하면서 형성되는 압력섭동이며, 음속의 속도로 먼거리까지 전파되게 된다.

유체의 유동에 의한 구조 진동과 방사 소음을 예측하기 위해선 소음의 발생 메커니즘을 고려하여 총 3단계의 수치 해석을 진행해야 한다. 먼저 유동 해석을 통하여 난류 유동을 정확하게 예측하고, 이후 유동 해석을 통한 압력을 가진력으로 적용하여 구조 진동해석을 진행해야 된다. 최종적으로, 구조 표면의 속도 응답을 이용하여 소음의 전파를 예측해야 된다.

배관계 유동에 의한 소음의 상대적 기여도가 증가함에 따라 유동 소음을 저감시키고자 하는 연구가 활발하게 진행 중에 있다. Zhang et al.^[1]은 곡관에서 발생하는 유동 소음을 저감시키기 위하여 난류 강도를 평가 지표로 선정하였다. 그는 가이드 판을 이용하여 곡관에서의 난류 강도를 완화시킴으로써 소음을 저감 시켰다. 또한, Kim et al.^[2]은 압축성 압렵성분으로 구분할 수 있는 와류 소음원을 이용하여 오리피스에서 발생하는 소음원을 평가하였으며, 오리피스 형상을 변경함으로써 소음을 저감하였다. 이러한 평가 지표는 소음의 상대적 비교를 하는데 있어서 좋은 상관성을 보였으나, 정확한 소음 측정값을 예측하는 데는 어려움이 있었다. Kottapalli^[3]는 Reynolds Averaged Navier-Stokes(RANS) 방정식을 기반으로한 2-equation 난류 모델인 k-ω 또는 k-ε 난류 모델이 표면 압력섭동을 실제보다 과소예측 한다고 보고 하였다.그는 벽면 압력 섭동의 예측 정확도를 높이기 위하여, 난류 운동에너지와 난류 소산율을 이용하여 압력 값을 보정하였다. Kottapalli et al.^[4]은 추가적으로 비압축성 대와류 모사기법(Large Eddy Simulation, LES)을 이용하여 벽면 압력 섭동을 계산하였으며, 실험을 통하여 그 유효성을 확인하였다.하지만, 실험에서 발생하는 고주파의 압축성 압력성분에 의한 소음을 예측하는데 어려움이 있었다.

고주파 영역에서는 압축성 압렵 성분과 비압축성 압력성분이 발생하는데, 두 성분에 의한 가진력의 기여도를 분석하기 위해선 두 가지의 압력성분을 분리해야 한다. 압축성 압력성분과 비압축성 압력성분을 분리하기 위한 방법으로서, 앞서 설명한 전파속도의 차이를 이용하여 두가지의 성분을 분리하는 파수-주파수 분석을 적용할 수 있다.^[5,6,7]

하지만, 실제 압축기 배관에서 소음을 유발하는 가진원은 난류에 의한 비압축성 압력성분과 압축성 압력성분 뿐만 아니라, 압축기 토출부의 서어징효과와 압축기 진동에의 구조 진동에너지의 전파 등 다양한 가진원이 존재한다. 따라서, 본 논문에서는 냉매의 난류 유동에 의한 소음뿐만 아니라, 다양한 가진원에 대한 배관 방사 소음의 기여도를 분석하였다.

앞서 설명한바와 같이 배관계 유동에 의한 소음 발생 메커니즘을 고려하여 3단계의 수치해석을 진행하였다. 먼저 압축성 대와류 모사 기법을 이용하여 배관계 벽면의 압력장을 계산하였다. 이후, 유동 해석을 통하여 계산된 압력장을 입력 하중으로 하여 구조 진동해석을 진행하였다. 마지막으로, 배관계 표면 속도 응답을 소음원으로 하여 방사소음을 예측하였다. 실험과의 비교를 통하여 해석의 유효성을 검증하였다. 이후, 냉매 유동에 대하여, 압축기 토출부의 서어징 효과에 의한 소음 영향을 주파수 대역별로 확인하였으며, 추가적으로 압축기 진동에 의한 구조파 형태의 전파를 고려하여 소음의 영향을 주파수 대역별로 분석하였다.

II. 수치해석 기법

2.1 전산 유체 역학(Computational Fluid Dynamics, CFD)

앞절에서 설명한 바와 같이 배관 벽면의 압력장을 예측하기 위해선 압축성 압력성분과 비압축성 압력성분을 포함한 압력장을 예측할 수 있는 해석 기법이 필요하다. 따라서, 본 논문에서는 압축성 대와류모사기법을 이용하여 유동 해석을 진행하였다. 대와류모사기법의 지배 방정식은 다음과 같다.

Eq. (1), Eq. (2) 그리고 Eq. (3)은 각각 연속방정식, 운동량 방정식 그리고 에너지 방정식이다. 여기서, Eq. (2)의 σij와 τij는 전단 응력 텐서와 아격자 응력 텐서이며 다음과 같이 정의된다.

Eq. (5)의 S¯kk는 변형률 텐서이며, 다음과 같이 정의된다.

대와류 모사 기법은 매우 작은 크기의 와류 또는 격자의 크기보다 작아 해상이 어려운 와류(subgrid scale eddy)에 대하여 모델링을 통하여 계산하며, 이보다 큰 와류에 대하여 모델링 없이 계산을 하기 때문에 RANS에 비해 고정밀한 결과를 도출한다고 알려져 있다. Eq. (5)의 난류 점성항을 계산하기 위한 아격자 모델로는 Smagorinsky-Lilly 모델을 적용하였으며, 다음과 같이 정의된다.

Eq. (7)의 CS는 Smagorinsky상수이며, Eq. (9)의 V는 격자의 부피이며, 다음과 같이 정의된다.

해석 시 압력-속도 연성기법으로 coupled를 적용하였으며, 압력, 운동량 그리고 에너지 차분은 2차 upwind를 적용하였다. 해석의 시간 간격은 5e-6 s (1/200,000 s)이며, 상용 해석 프로그램인 ANSYS Fluent 20.0을 사용하였다.

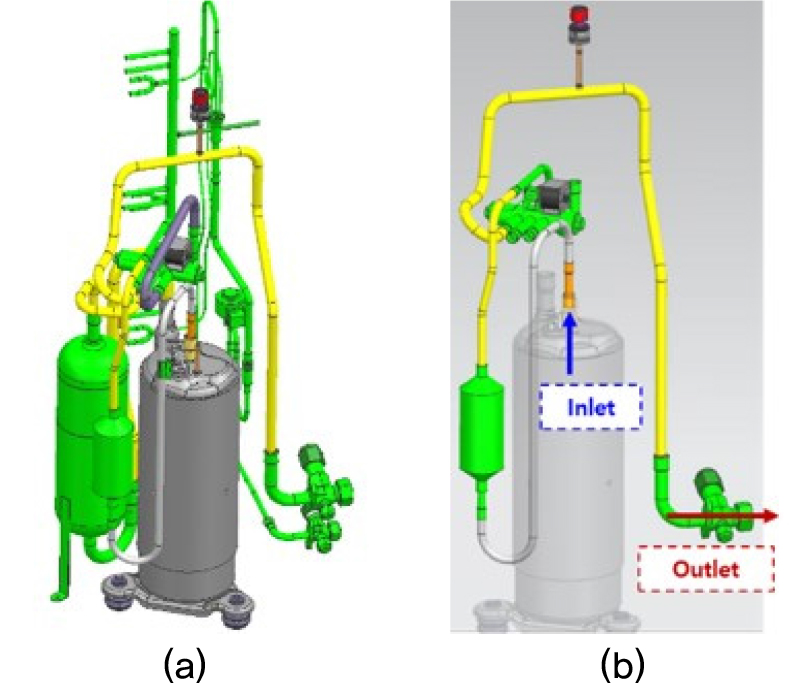
Fig. 1(a)는 에어컨 실외기 배관계의 전체 형상을 나타내었다. 배관계는 흡기배관 과 배기배관으로 구성되어 있으며, 머플러, 팽창 밸브, 4-way 밸브와 같은 요소로 구성되어 있다. 압축기의 배기배관은 압축기의 토출부에 연결되어 있으며, 고온 고압의 냉매 유동이 흐른다. 본 논문에서는 Fig. 1(b)와 같이 해석영역을 구성하여 배기배관의 냉매 유동만 고려하였다.

Fig. 1.

(Color available online) Geometry of (a) piping system in air-conditioner outdoor unit and (b) computational domain.

Fig. 2에서는 주요 배관 요소에서의 격자 구성을 나타내었다. Fig. 2(a), (b)와 (c)는 각각 배관, 머플러 그리고 4-way 밸브에서의 격자 구성을 나타내었다. 체적 격자의 크기는 배관의 직경이 8 mm임을 고려하여 20개 이상의 격자가 구성될 수 있도록 0.4 mm로 설정하였으며, 벽면에서의 난류 경계층을 정확하게 모사하기 위해, 17층의 프리즘격자를 구성하였다. 프리즘의 첫번째 층의 두께는 y+가 1이하를 유지할 수 있도록 구성하였으며, 프리즘 격자간의 성장률을 1.3으로 설정하였다.

Fig. 2.

(Color available online) Section view of mesh configuration at the (a) pipe, (b) muffler and (c) 4-way valve.

작동 유체는 냉매 R-410A를 적용하였다. 압축기 토출부에서 냉매의 상태는 고온, 고압의 과열 증기 상태임으로 냉매의 거동을 확인하기 위하여 압축성 인자를 평가 지표로 적용하였으며, 다음과 같이 정의된다.

압축기 토출부에서의 냉매 압축성 인자는 0.8의 값을 가지게 되며, 이는 냉매의 거동이 이상 기체에서 벗어났음을 의미한다. 따라서, 기체상태의 냉매 거동예측 하기 위하여 실제 가스 모델 인 Aungier-Redlich-Kwong(ARK)모델을 적용하였으며 다음과 같이 정의된다.

여기서

아래 첨자 C는 임계점을 의미하며, R, T, P, v 그리고 ω는 각각 가스상수, 온도, 압력, 체적부피 그리고 acentric 수를 의미한다. 이외의 비열, 열 전도 계수 및 점성은 실험값을 참고하여 적용하였다.^[8]

해석의 경계조건으로 Fig. 1(b)에 나타낸 위치에 적용하였다. 압축기 토출부의 입구단에는 압력 경계조건을 적용하였으며, 출구단에는 질량 유량 경계조건을 적용하였다.

Fig. 3은 유동 기인 진동(Flow Induced Vibration, FIV)의 영향을 확인하기 위해 서어징 현상으로 발생하는 압력 맥동을 적용한 압력과 적용하지 않은 압력을 나타내었으며, 해석의 입구단 경계조건에 적용하였다.

Fig. 3.

(Color available online) Comparison of surging and non-surging pressure boundary condition.

2.2 유한요소기법을 이용한 진동 및 방사소음 해석

배관의 진동을 유발하는 난류의 성분으로서 와류에 의한 정압의 섭동과 전단응력에 의한 섭동으로 구분할 수 있다. 하지만, 전단 응력에 의한 배관의 진동의 매우 작음으로 진동 해석에서는 정압의 섭동만을 고려하였다.^[9]

Fig. 4는 진동해석의 영역을 나타내었다. 유동해석에서는 전체 형상에 대하여 작동 유로만을 고려하였지만, 진동해석에서는 구조파의 전파로 인하여 모든 요소들이 전달경로가 되기 때문에 모든 형상을 고려하였다. 또한, 실제 실외기에 연결 방식을 고려하여 구속 경계조건을 적용하였으며, 빨간색 원으로 그 위치를 표시하였다. Fig. 5에는 진동 해석 영역을 둘러싸는 음향 해석 영역을 나타내었다.

Fig. 4.

(Color available online) Computational domain for vibrational analysis and position of fixed boundary condition.

Fig. 5.

(Color available online) Measured acceleration signal applied as the structural wave to the junction between compressor and discharging pipe.

진동해석을 위한 경계조건으로서 냉매의 유동 해석을 통하여 획득한 압력장을 입력 가진으로 적용하였다. 또한, 배관 연결된 기기에 의한 진동(Machinery Induced Vibration, MIV)의 영향을 분석하기 위해 압축기의 작동으로 발생하는 진동의 가속도 신호를 실험을 통하여 계측하였다. 계측된 신호는 압축기가 연결된 파이프에 적용하였으며, 가속도 신호를 Fig. 5에 나타내었다. 압축기의 진동 신호와 압축기 작동에 의한 맥동 압력의 신호의 위상을 일치시켜, 실제 압축기에서 발생하는 현상을 모사하였다.

구조물의 진동에 의해 발생하는 속도 응답은 주 소음원으로 작용함으로, 구조물 격자 주위의 음향 격자를 구성하여 해석을 해야 된다. 이를 위해 Fig. 6과 같이 소음해석 영역을 구성하였다. Fig. 6(a)는 구조물 주위의 근접 소음장을 예측하기 위한 유한요소를 나타내었으며, Fig. 6(b)는 원거리 소음장을 예측하기 위한 경계요소를 나타내었다. 여기서, 유한요소의 경계면에 Automatically Matched Layer(AML) 경계조건을 적용하여 비 반사 경계조건을 적용하였다.

Fig. 6.

(Color available online) Mech configuration using (a)Finite Element (FE) and (b) Boundary Element (BE) for acoustic analysis.

진동 및 소음 해석을 위한 지배방정식으로 구조물 및 음향 공간을 연성하여 진동 해석에 널리 사용되는 운동방정식을 적용하였으며, 아래와 같다.

여기서

Eq. (18)의 [M], [B] 그리고 [K]는 각각 질량 행렬, 감쇠 행렬 및 강성 행렬이며, {Q}와 {F}는 각각 응답 행렬과 가진 행렬이다. Eqs. (18), (19), (20), (21), (22), (23), (24)의 첨자 s는 구조물을 의미하며, a는 음향공간을 의미한다. Eq. (22)는 형상 행렬을 의미이다. Eq. (24)에서 X_s는 구조물에서의 변위이며, P_a는 음향공간에서의 음압이다.

Eq. (18)을 계산하기위해 좌변의 행렬의 역함수를 이용하여 각 주파수 별로 계산하는 직접계산법을 사용하였다. 입력 하중을 위해 500개의 유동해석 데이터를 사용하였으며, 각 노드 별 신호에 대하여 푸리에 변환을 통하여 시간영역에서의 압력신호를 주파수 영역에서의 신호로 변환하였다. 관심 주파수 대역으로 0 Hz ~ 5,000 Hz까지를 고려하였으며, 주파수 간격을 50 Hz가 되도록 구성하였다. 진동 및 소음의 계산을 위한 솔버로서 SIMCENTER 3D를 사용하였다.

III. 수치해석 결과

3.1 해석 기법의 검증

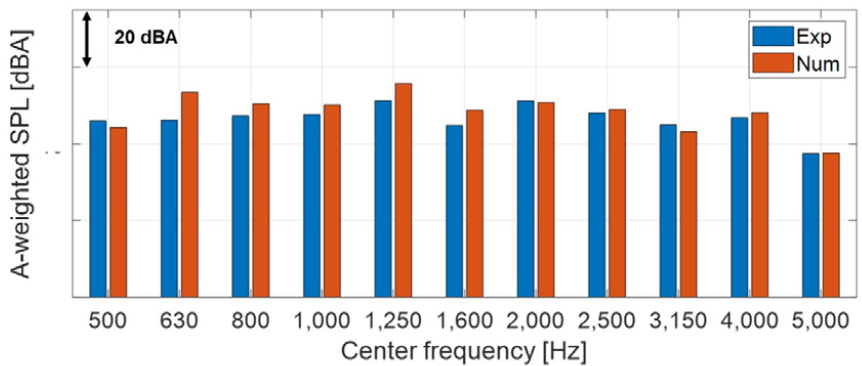
해석 기법의 검증을 위하여 소음의 계측 결과와 유동 및 진동-소음 해석결과를 비교하였으며, Fig. 7에 A 청감 보정이 적용된 음압 레벨(Sound Pressure Level, SPL)을 1/3 옥타브 밴드 그래프로 나타내었다. 해석의 주파수 간격이 50 Hz이며, 주파수 밴드 당 3개 이상의 소음 해석 결과를 반영 할 수 있는 500 Hz 이상의 주파수 대역에서 결과를 비교하였다. 해석 결과는 저주파 대역에서 편차를 보이고 있다. 이는 기존의 실외기의 주 소음원으로 알려진 압축기의 진동소음과 축류팬의 소음으로 판단된다.^[10,11,12]하지만 유동 소음의 영향이 크다고 알려진 고주파수 대역에서는 실험과 높은 상관성을 보이고 있으며, 이를 통하여 해석기법의 유효성 확인하였다.

Fig. 7.

(Color available online) SPL comparison of experimental and numerical results in 1/3 octave band spectrum.

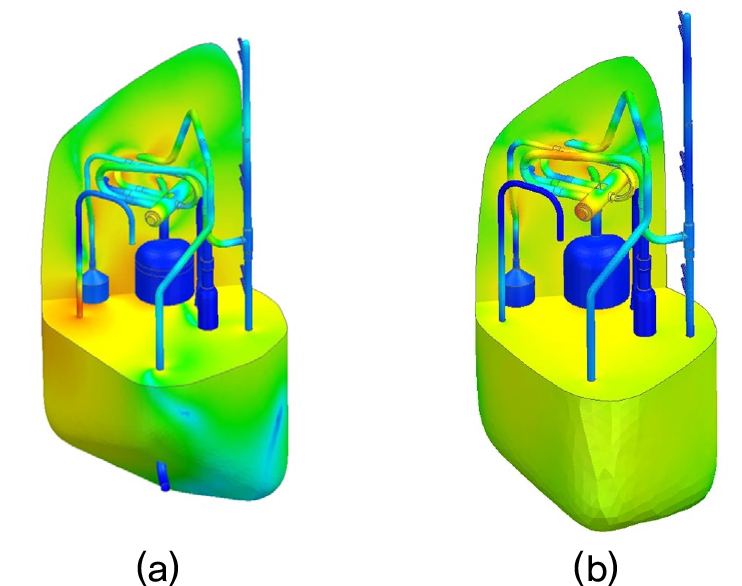
Fig. 8에는 1,000 Hz에서 2,000 Hz 대역 사이에서 소음의 기여도가 큰 진동 및 음향장을 나타내었다. 대부분의 주파수 진동 형상에서 4-way 밸브의 기여도가 크게 발생하는 것을 확인 할 수 있다.

Fig. 8.

(Color available online) Vibrational response and pressure field at (a) 1,550 Hz, (b) 1,700 Hz and (c) 1,850 Hz.

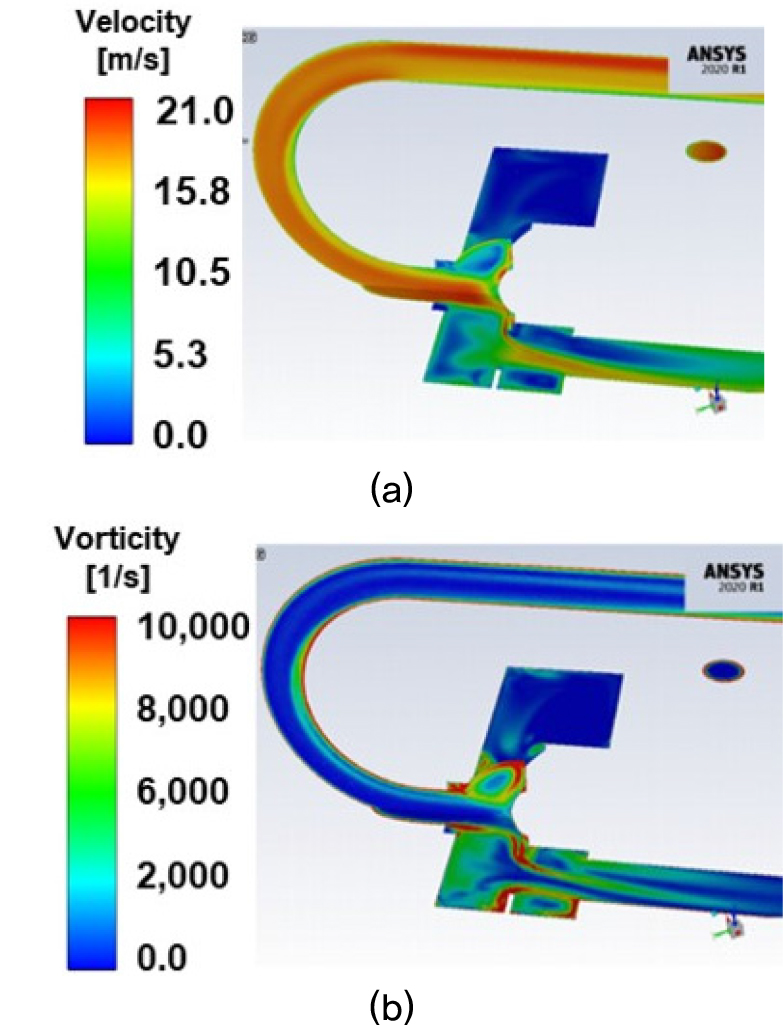
Fig. 9에서는 4-way 밸브 내의 속도장과 와도장을 나타내었다. 4-way 밸브에서는 급격한 유로 변화가 발생하게 되며, 이로 인하여 복잡한 형상의 난류 유동이 발생하게 된다. Fig. 9(b)에서 확인할 수 있듯이 밸브 내의 공동에서 회전하는 유동이 발생하게 되며, 이러한 유동은 벽면에 강한 압력 섭동을 발생시키게 되어, 주 소음원으로 작용하게 됨을 확인할 수 있다.

Fig. 9.

(Color available online) Snapshot of (a) velocity and (b) vorticity contour at the 4-way valve section plane.

3.2 유동 기인 진동 및 기기 기인 진동에 의한 유동 및 소음의 영향 분석

유동 기인 진동 및 기기 기인 진동의 영향을 분석하기 위하여 3개의 조건에 대하여 유동 및 진동해석을 수행하였으며, 각각의 조건을 Table 1에 정리하였다.

CP는 압축기의 서어징 효과와 압축기의 진동을 고려하지 않고 배관의 입출구의 압력차를 일정하게 적용하였다. 반면에, CP-A는 CP의 조건에서 압축기 결합부의 가속도 신호를 추가한 조건이다. 마지막 조건인 OP-A에서는 압축기의 진동과 압축기의 맥동 압 모두를 고려한 조건이다.

Fig. 10(a)에서는 CP와 OP에 대한 소음을 비교하였으며, Fig. 10(b)에서는 CP와 CP-A에서의 소음을 비교하였다.

Fig. 10(a)에서 확인할 수 있듯이 압축기의 진동은 1,000 Hz 이하의 저주파 영역에서 기여도가 있음을 확인 할 수 있으며, 고주파로 갈수록 그 영향도가 작음을 확인할 수 있다. Fig. 10(b)의 결과에서는 압축기의 맥동 압에 의하여 1,600 Hz 이상의 주파수 대역에서 소음이 증가하는 경향을 확인할 수 있다.

Fig. 10.

(Color available online) SPL comparison of (a) CP and CP-A conditions and (b) CP-A and OP-A conditions in 1/3 octave band spectrum.

Fig. 11은 Fig. 10(a)에서 소음의 차이가 가장 크게 발생하는 800 Hz대역에서의 진동모드와 음향장을 확인한 결과이다. 압축기의 진동에 의한 구조파는 배기배관의 입구부의 진동을 유발하며, 이로 인해 입구부의 배관과 4-way 밸브에서의 소음을 유발하는 것을 확인 할 수 있다.

Fig. 11.

(Color available online) Vibrational and acoustic pressure contour under (a) CP and (b) CP-A conditions.

Fig. 12은 Fig. 10(b)에서 소음이 가장 큰 차이를 보이는 1,600 Hz 이상의 대역에서의 진동 모드를 확인한 결과이다. 압축기의 맥동 압은 배관을 따라 전파하며, 머플러의 진동을 유발함을 확인할 수 있다. 머플러를 통과하며, 맥동 압의 진폭은 크게 감소하며, 사방 변 밸브에서는 기여도가 작음을 확인하였다.

Fig. 12.

(Color available online) Vibrational and acoustic pressure contour under (a) CP-A and (b) OP-A conditions.

IV. 결 론

본 연구에서는 에어컨 실외기 압축기의 배기배관에서의 냉매 유동에 의한 배관 방사소음을 예측하기 위하여 유동 해석 및 진동-소음해석을 수행하였다. 압축기의 기기 작동에 의한 진동과 압축기의 맥동 압에 의한 진동에 의한 소음의 영향을 분석하였다. 이를 위해 진동 시 압축기의 진동 계측 값을 배관의 연결부에 적용하였으며, 유동 해석 시 압축기의 맥동 압을 경계조건으로 적용하였다.

실외기 압축기 배기 배관에서 소음에 가장 큰 기여를 하는 요소는 4-way 밸브임을 확인하였다. 유동장을 확인하였을 때, 공동영역에서 회전하는 유동이 발생하였으며, 강한 난류 성분이 발생함을 확인하였다.

추가적으로 압축기 기기 작동에 의한 진동의 영향과 맥동 압의 영향을 비교하였을 때, 압축기의 진동에 의한 구조파는 1,000 Hz 이하의 저주파 영역대에서 기여도가 큼을 확인하였으며, 맥동 압은 2,000 Hz 이상의 고주파 대역에서 기여도가 큼을 확인하였다. 본 연구를 통하여 에어컨 실외기의 압축기 배기배관계에서 가장 큰 소음 기여도를 가지는 요소로가 4-way 밸브임을 확인하였으며, 진동 가진원으로서 급격한 유로 변화로 인한 난류 유동 즉 비압축성 압력 성분임을 확인하였다. 또한, 압축기의 서어징 효과에 의한 압력섭동은 음향 기인 진동에 의한 소음으로서 고주파 대역에서의 머플러의 진동 소음을 유발하지만, 머플러가 소음기 역할을 수행함에 따라 4-way 밸브의 소음에 영향을 거의 주지 않음을 확인하였다. 이를 통하여, 압축기 배기 배관시스템에서의 소은은 큰 진동이 발생하는 4-way 밸브에 추가 구속을 하거나 4-way밸브 내부의 유로를 최적화하여 저감 시킬 수 있을 것으로 기대된다.