I. 서 론

소노부이는 소나와 부이의 합성어로 음탐부표를 말한다. 해상 초계기에 의해 목표지점에 투하되어 수중표적의 탐지신호를 해상초계기로 RF통신을 통해 전송하여 해상초계기의 전술컴퓨터에서 수중표적을 탐지하는 방식으로 운용되며 항공기의 신속성을 이용하여 표적의 탐지·추적이 가능하므로 대잠전(Anti-Submarine Warfare, ASW)에 효과적인 무기체계로 알려져 있다.

소노부이는 목적에 따라 수동형, 능동형, 특수목적형 등 다양한 종류가 있다.^[1] 수동형 소노부이는 능동형 소노부이 또는 음원과 함께 다중상태 음향탐지를 위한 수신기로 활용된다. 그 중 DIrectional Frequency Analysis and Recording(DIFAR) 소노부이는 기존의 Low Frequency Analysis and Recording(LOFAR) 소노부이의 방향성 분석 제한 요소를 극복한 소노부이로 국내외에서 활발히 연구되고 있다.^[2,3,4,5]

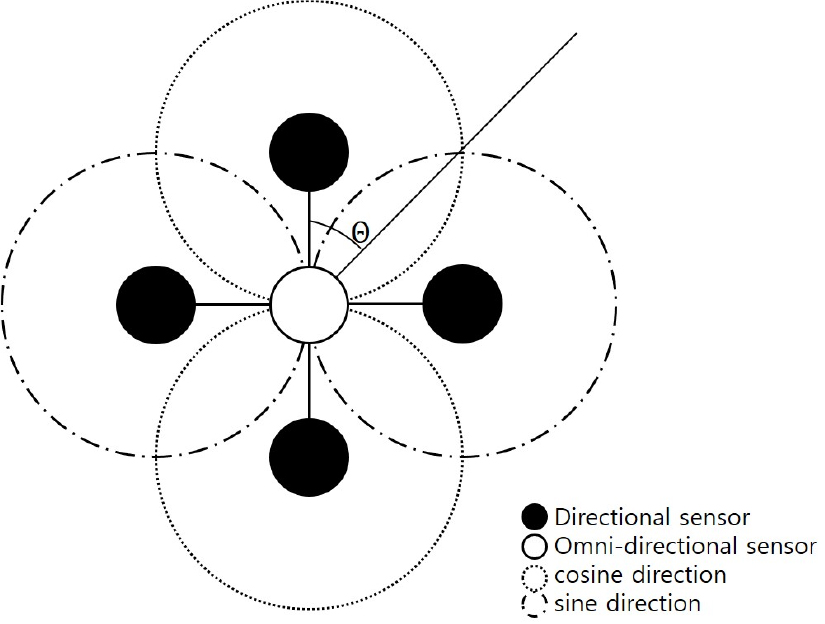
DIFAR 소노부이는 Fig. 1과 같이 하나의 무지향성 센서와 두 개의 지향성 센서로 구성되어 있으며, 신호의 크기 및 주파수 성분을 감지하는 무지향채널, 수직방위(North-South, NS)를 감지하는 쌍극자 센서를 코사인 채널, 수평방위(East-West, EW)를 감지하는 쌍극자 센서를 사인 채널이라 한다.

Fig. 1.

Structure of DIFAR sonobuoy.

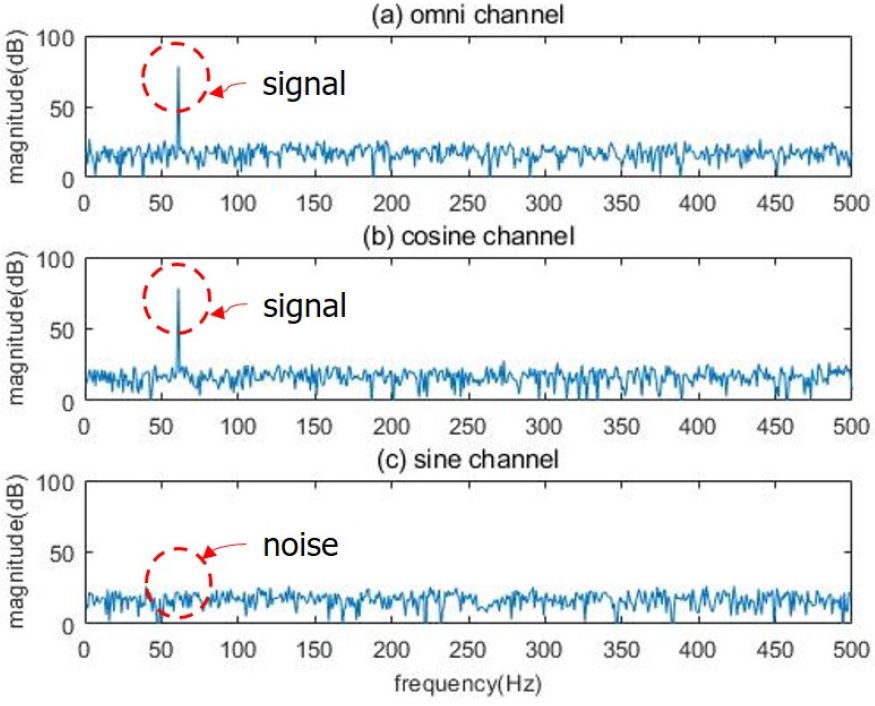
이러한 DIFAR 소노부이의 방위 추정 원리는 직교하는 두 개의 지향성 센서의 크기 비에 아크탄젠트를 취하는 것이다. 하지만 주변 소음의 영향으로 표적 탐지 오차로 인한 DIFAR 소노부이의 표적탐지 성능이 저하된다. 특히 표적이 소노부이 기준 0°, 90°, 180°, 270°에 위치할 경우 두 개의 지향성 센서 중 하나는 0 dB의 값을 가져야 하지만 주변소음의 영향으로 그렇지 못하고 이로 인해 방위각 추정 오차가 발생한다.^[5] Fig. 2는 표적이 0°에 위치할 경우, DIFAR 소노부이의 3채널 FFT 결과를 비교한 것이다. 무지향 채널과 코사인 채널에는 신호가 탐지되고 사인채널에는 신호가 탐지되지 않지만 주변소음의 영향으로 부정확한 값이 존재하는 것을 확인할 수 있다.

Fig. 2.

(Color available online) FFT results of three channels of DIFAR sonobuoy.

DIFAR소노부이를 이용한 탐지성능 향상을 위한 선행연구는 다음과 같다. D. Derocher가 DIFAR 빔형성의 적은 채널 수에서 기인하는 넓은 빔폭을 개선하기 위해 적응빔형성 기반의 고해상도 빔형성 기법을 DIFAR 소노부이에 적용하는 것을 제안하였다.^[2] 제안한 최소분산과 고유벡터 빔형성 기법은 기존 일반빔형성 대비 좁은 빔폭과 낮은 부엽준위를 만족하였지만 낮은 신호대잡음비에서의 탐지성능 저하는 여전히 해결해야 할 문제로 남았다. 국내에서도 이와 유사한 연구가 수행되었고, 실제 해상 실험데이터를 통해 일관적인 결과를 얻을 수 있었다.^[3] 그 외 Chang et al.^[4]은 카디오이드 빔형성을 사용하여 DIFAR 시스템의 방위를 추정하는 방법을 제안하였지만 낮은 신호대잡음비에서 방위 추정 성능 저하는 여전한 문제점으로 남아 있다.

이와 같이 위 언급한 주변소음에 의한 문제점을 직접적으로 다루거나 해결한 방법은 없었다. 따라서 본 논문에서는 DIFAR 소노부이의 주변소음을 추정 및 제거하기 위한 방법을 제안하고 주변소음을 제거하면 DIFAR 소노부이의 탐지성능이 향상되는지 확인하고자 한다.

II. DIFAR 소노부이 표적탐지기법

DIFAR 소노부이의 표적 탐지는 빔형성기법을 사용한다.^[2,3] 빔형성을 위해 사용하는 가중치 벡터에 입력신호의 사용 여부에 따라 일반 빔형성과 적응빔형성으로 나뉜다. 일반적으로 적응빔형성이 일반빔형성보다 좁은 주엽폭과 낮은 부엽준위를 가지므로 탐지성능이 더 높다고 알려져 있다. 본 연구에서는 주변소음 추정 및 제거가 DIFAR 소노부이 표적탐지에 미치는 영향을 분석하는 목적이 있기 때문에 가중치 벡터가 결정적인 일반 빔형성을 사용하였다.

주파수가 f이고 θ 각도로 입사하는 DIFAR 소노부이의 무지향, 코사인, 사인채널의 시계열 입력신호는

과 같다.^[4,5] 여기서 no(t), nc(t), ns(t)는 각각 무지향, 코사인, 사인 채널의 주변 소음을 의미한다. 위 신호들을 이산 푸리에 변환을 통해 입력신호 스펙트럼 벡터로 변환하여 나타내면

로 나타낼 수 있다. 여기서 T는 전치를 의미한다.

또한, 일반 빔형성 출력을 구하기 위한 가중치 벡터는

와 같다.

일반 빔형성 출력은 Eq. (4)의 입력신호 스펙트럼 벡터와 Eq. (5)의 가중치 벡터와의 내적의 제곱을 의미하며 다음과 같이 나타낼 수 있다.

여기서

는 3 × 3 크기의 교차 스펙트럼 밀도 행렬(Cross Spectral Density Matrix, CSDM)을 말하고, *는 복소공액을, H는 Hermitian transpose를 의미한다. 최종적으로 Eq. (6)에서 모든 θ 중에서 빔형성 출력이 최댓값을 갖는 θ를 표적 방위로 추정한다.

III. 제안한 방법

주변 소음 제거를 위해 본 논문에서는 위너필터 기반의 잡음제거 기법을 사용한다. 위너필터는 신호 추정 평균 제곱 오차를 최소화시키는 필터로 음성신호강화 분야에 많이 활용된다.^[6,7] 변수 내장형 위너필터는 위너필터의 일반화된 형태이며 전체 추정 오차를 잔여잡음과 음성왜곡의 합으로 정의하고 평균 제곱 잔여 잡음과 평균 음성왜곡과의 constrained optimization 문제를 해결함으로써 얻을 수 있다.

DIFAR 소노부이 입력신호에 적용할 위너필터 벡터는

이고, 여기서 무지향 채널에 인가되는 변수내장형 위너필터[7]는

와 같이 표현될 수 있다. 여기서 So^(t,f)와 No^(t,f)는 각각 추정된 신호와 잡음의 스펙트럼을 의미하고, |∙|기호는 절대값을 나타낸다. 위 Eq. (9)의 변수내장형 위너필터는 추정된 신호대 잡음비에 의해 동작한다. 또한, μ는 잡음제거도를 조절하는 변수로 값이 1일 때 일반적인 위너필터와 같고 값이 클수록 잔여잡음이 줄어들지만 신호왜곡이 커지고 값이 작을수록 잔여잡음이 커지고 신호왜곡이 작아지는 특성이 있다.

신호와 잡음이 무상관이므로 입력신호 스펙트럼과 추정된 잡음 스펙트럼을 이용하여 신호 스펙트럼을 나타내면

과 같이 표현된다. Eq. (10)의 주변소음 추정을 위해 소나신호처리 분야에서 널리쓰이는 Order Truncate Average(OTA) 방식을 사용하였다.^[8,9] OTA를 이용하여 추정된 주변소음은

로 표현될 수 있다. 여기서 i∈Rk이고 Rk는 해당 주파수 f의 주변 주파수 빈 값 인덱스를 의미한다. 또한, I는 가장 작은 값들과 가장 큰 값들을 제외한 OTA에 사용될 인덱스 들의 총 개수, |Xo(sort)(t,f)|2는 오름차순으로 정렬된 무지향 채널 입력 스펙트럼 파워를 의미한다.

최종적으로 Eq. (10)을 Eq. (9)에 적용하여 정리하면

를 얻을 수 있다. 이와 같이 Eqs. (9), (10), (11), (12)와 같은 원리로 코사인, 사인 채널에 인가되는 변수 내장형 위너필터는

와 같이 도출된다. Eqs. (12), (13), (14)를 이용하여 Eq. (8)을 구성할 수 있고 Eq. (4)와 Eq. (8)을 이용하여 위너필터링된 DIFAR소노부이 입력신호를 다음과 같이 얻을 수 있다.

여기서 ∘는 아다마르 곱(Hadamard product)을 나타낸다. Eq. (15)를 이용하여 Eq. (7)과 같이 표현하면

과 같이 주변소음이 줄어든 교차 스펙트럼 밀도 행렬을 구할 수 있다. 여기서 Xo~(t,f),Xc~(t,f),Xs~(t,f) 는 각각 주변소음이 줄어든 무지향, 코사인, 사인 채널의 스펙트럼을 의미한다. Eq. (16)을 이용하여 Eq. (6)과 같이 표현하면

과 같이 주변소음이 제거된 일반빔형성 출력을 얻을 수 있고, 최종적으로 Eq. (17)에서 모든 θ 중에서 빔형성 출력이 최댓값을 갖는 θ를 표적 방위로 추정한다.

IV. 실험 및 결과

4.1 모의실험 환경

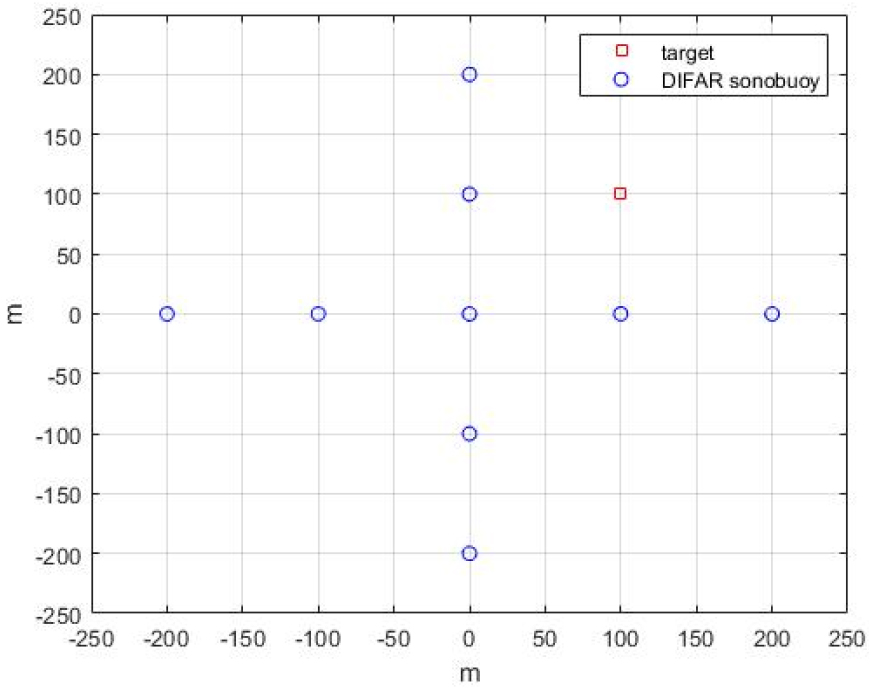
제안한 방법을 검증하기 위해 DIFAR 소노부이 탐지 모의실험을 수행하였다. Fig. 3과 같이 정지된 하나의 표적이 10 s 동안 60 Hz의 토날 신호를 방사하고 9개의 DIFAR소노부이를 열십자 형태로 배치하였다.^[5]

Fig. 3.

(Color available online) Arrangement of DIFAR sonobuoys and a target.

DIFAR 센서에 입력되는 신호는 각각 Eqs. (1), (2), (3)과 같이 모사하여 생성되었다. 각 채널의 잡음은 정규분포를 갖는 Additive White Gaussian Noise(AWGN)을 각 채널마다 독립적으로 생성하였고 설정된 신호대잡음비에 따라 크기 조정치를 산출하여 곱함으로써 잡음의 크기를 조정하였다. 잡음 생성에 사용된 신호대잡음비의 정의와 산출된 크기조정치를 나타내면

와 같다. 여기서, Ps는 사인파이므로 1/2로 설정하였다. 또한, 각 소노부이에 설정된 신호대잡음비는 전달손실, 음원크기 등은 고려되지 않은 각각의 소노부이에 입사하는 신호와 잡음의 크기비를 나타낸다.

잡음제거를 위해 음성신호처리 분야에서 널리쓰이는 파라미터내장형 위너필터를 사용하였고,^[6,7]주변소음 추정을 위해 소나신호처리 분야에서 널리쓰이는 Order Truncate Average(OTA)방식을 사용하였다.^[8,9] 샘플율과 FFT크기는 각각16384 Hz와 16384포인트로 주파수 해상도를 1 Hz로 설정하였다. 각 채널에 OTA를 이용한 잡음 추정을 위해 0 Hz ~ 59 Hz, 61 Hz ~ 120 Hz에 해당하는 신호주변 주파수 빈의 크기 값을 오름차순으로 정렬한 후 하위 20개, 상위 20개를 제외하고 평균하였다.

4.2 모의실험 결과

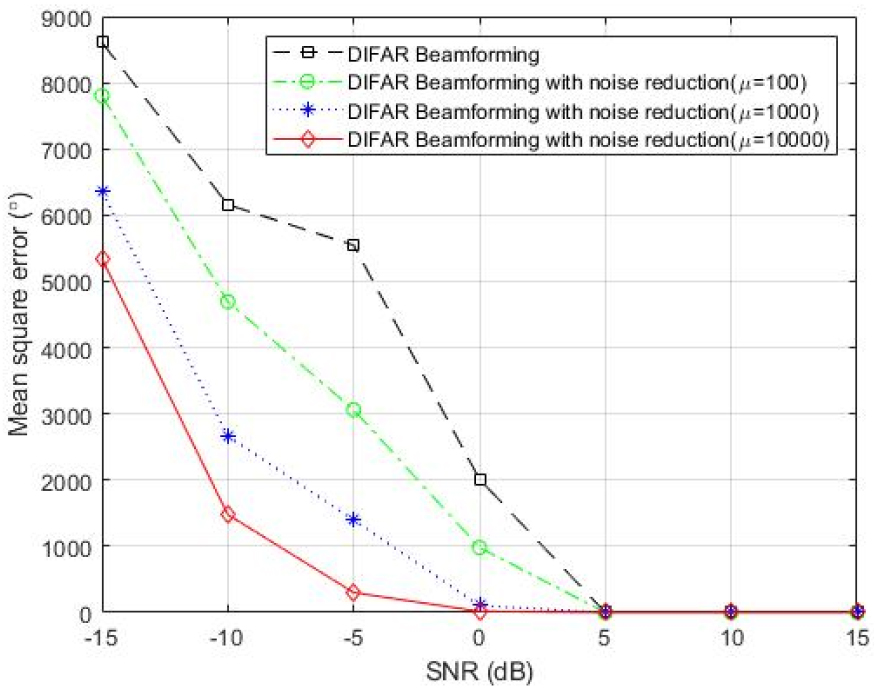
Fig. 4는 위너필터링을 이용한 잡음제거 적용여부에 따른 DIFAR 소노부이 표적 탐지 결과를 평가하기 위하여 9개의 소노부이 방위각 추정 평균제곱오차(Mean square error, MSE)의 평균 값을 도시한 것이다. 신호대잡음비(Signal-to-Noise Ratio, SNR)는 –15 dB에서 15 dB까지 5 dB간격으로 총 7가지 경우를 고려하였으며 위너필터링을 위한 잡음제거도 조절 변수는 100, 1000, 10000의 세가지 경우를 실험하였다. 또한, Fig. 4에 도시된 각각의 비교 방법 및 신호대잡음비에 해당하는 마커 값은 몬테카를로 시뮬레이션을 통해 총 100번 반복 수행된 값들의 평균이다. Fig. 4에서 확인할 수 있듯이 제안한 위너필터링기반 주변잡음제거를 적용한 DIFAR 빔형성의 방위각 추정 평균제곱오차가 주변잡음제거를 적용하지 않은 DIFAR빔형성의 방위각 추정 평균제곱 오차보다 월등히 줄어들었고, 잡음제거도 조절 변수가 커질수록 잡음제거도가 높아져 방위각 추정 평균제곱오차가 줄어드는 것을 확인할 수 있었다. 또한, 제안한 방법이 소음의 크기가 신호의 크기보다 크거나 같은 신호대잡음비 0 dB 이상에서 효과적임을 알 수 있었다.

Fig. 4.

(Color available online) DIFAR beamforming with noise reduction with respect to μ.

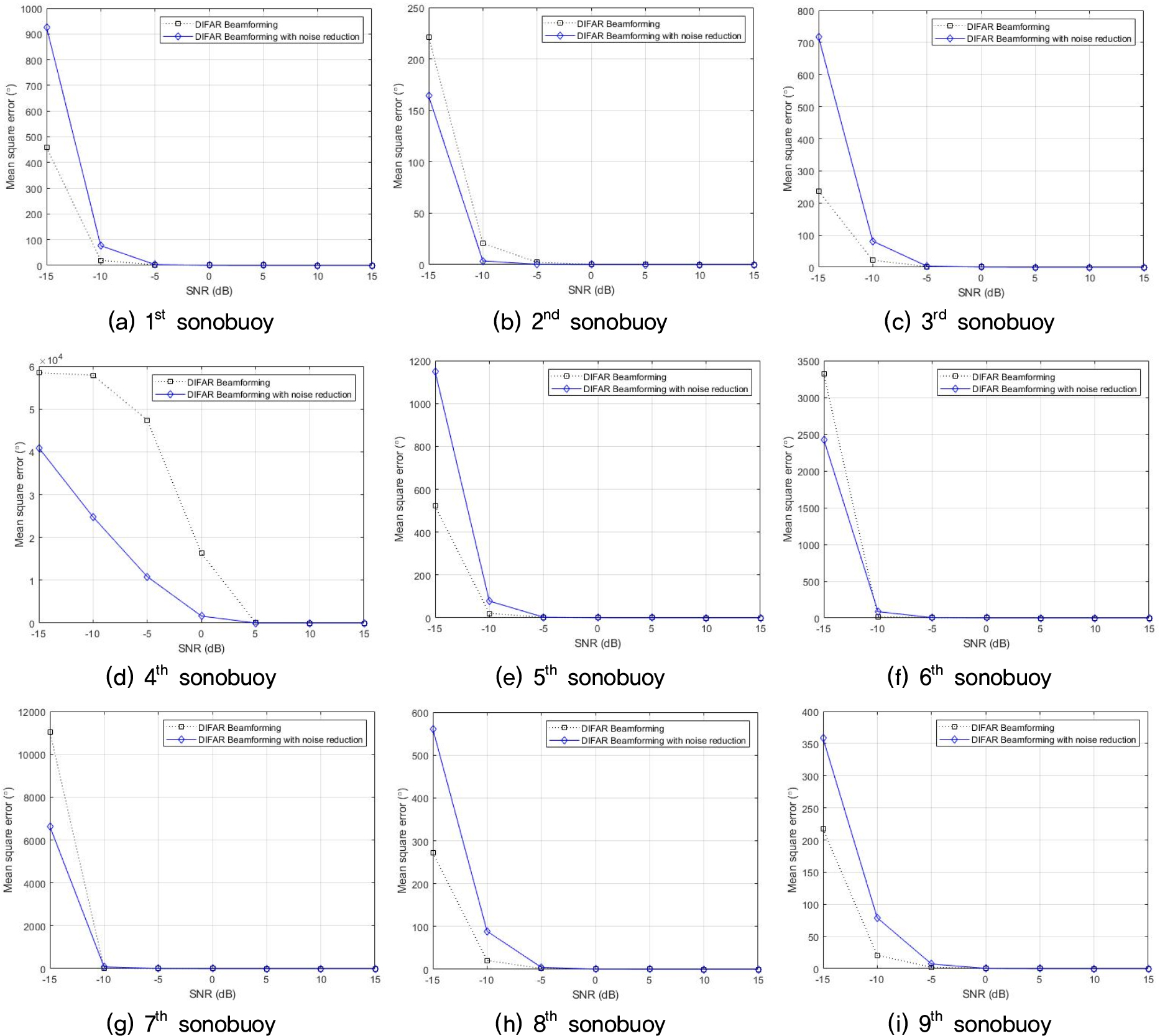
Fig. 5는 9개의 소노부이의 표적 탐지 결과를 개별적으로 분석한 결과(μ = 1000)이다. 개별 소노부이의 순서는 Fig. 3에 표기되어 있다. 2, 4, 6, 7번째 소노부이는 방위각 추정 평균 제곱 오차가 개선된 반면에 1, 3, 5, 8, 9번째 소노부이는 방위각 추정 평균 제곱 오차가 증가하는 결과를 보였다. 이것은 주변잡음제거가 항상 방위각 추정 결과를 개선하는 것은 아니라는 것을 의미한다. 소노부이 2, 4의 경우는 주변 잡음의 영향으로 성능 저하가 급격한 90°와 0°로 잡음제거를 적용하였을 때 성공적으로 탐지 오차가 줄어드는 경우에 해당한다. 다만 소노부이 4의 경우 0°와 359°의 경계(360° = 0° 이므로 359°(-1°)와 0°의 차이는 1° 이지만 따로 보정하지 않음)로 인해 탐지 오차가 크게 나타난다. 위와 같은 에러 과장 현상을 보정 하기 위해 경험적인 방법을 적용하진 않았다. 만약 적절한 경험적인 방법으로 위 현상이 보정된다면 소노부이 2와 유사한 결과를 얻을 것으로 판단된다. 소노부이 6, 7과 8, 9 간의 모의실험 조건은 유사하나 차이 나는 이유는 소노부이 4에서 나타나는 현상과 관계가 있는 것으로 보인다. 소노부이 6, 7 이 소노부이 8, 9 보다 0°에 가깝기 때문에 0° 보다 좌측으로 오탐지 되던 경우가 소노부이 6, 7에서는 잡음제거를 통해 줄어들기 때문에 성능 향상이 있는 것으로 보인다. 하지만, 이는 일반적인 경우는 아니고 적절한 보정 방법을 적용한다면 소노부이 8, 9와 같은 경향성을 보일 것으로 판단된다.

Fig. 5.

(Color available online) Comparison between DIFAR beafmorming and DIFAR beamfomring with noise reduction for individual sonobuoy.

추가적으로 실행한 자체 실험에서 타겟이 2사분면(-100, 100), 3사분면(-100, -100), 4사분면(100, -100)에 위치할 경우에 대해 실험한 결과 Fig. 5의 결과와 유사하게 타겟이 2사분면(-100, 100)에 위치할 때 소노부이 #2, #8에서, 타겟이 3사분면(-100, -100)에 위치할 때 소노부이 #6, #8에서, 타겟이 4사분면(100, -100)에 위치할 때 소노부이 #4, #6에서 성능향상을 확인할 수 있었다. 또한, 타겟이 2사분면에 위치할 때 소노부이 #8에서 타겟이 1사분면에 위치할 때의 현상과 같은 현상이 발생함을 확인할 수 있었다.

따라서, 종합적으로 제안한 방법은 0°, 90°, 180°, 270°의 경우에 잡음제거를 통한 탐지성능오차를 줄일 수 있고 해당 경우에만 선택적으로 잡음제거를 적용할 필요성이 있다.

V. 결 론

본 논문에서는 DIFAR 소노부이의 표적탐지성능을 향상시키기 위해 OTA기반의 주변소음 추정 기법 및 변수내장형 위너필터기반의 주변소음 제거기법을 제안하였다. 실험을 통해 주변소음을 제거하면 DIFAR 소노부이의 탐지성능이 향상됨을 확인하였다. 하지만, 주변소음제거는 항상 표적 방위각 탐지 오차를 개선하지는 않기 때문에 0°, 90°, 180°, 270°의경우에 따라 선택적으로 적용할 필요가 있다. 따라서, 향후 주변 소음 제거를 적용할 소노부이 선택 알고리즘에 대한 연구가 필요하다.