I. 서 론

수중 무선통신의 경우, 기존 지상에서의 무선통신처럼 전자기파를 사용하지 못하고, 음파로만 제한적인 통신을 할 수 있고 가용 가능한 주파수 자원이 지상 무선통신과는 달리 한정적이다. 따라서 지상에서의 무선통신 기술을 그대로 적용하기에는 어려움이 많다. 수중 음향통신에서는 해양 채널 환경에 의해 발생하는 다중 경로, 시간 지연 등과 송수신부 시스템 자체의 잡음, 이동성 등, 다양한 문제점으로 인해 수신된 신호를 바로 이용하기에는 많은 문제가 발생한다.^[1,2,3,4] 특히 데이터의 에러와 버스트 에러를 제거하기 위해서는 가장 먼저 수신된 신호 중에서 수신하고자 하는 데이터의 시작지점을 찾는 것이 가장 중요하다. Reference [4]에서는 Linear Frequency Modulation(LFM), Hyperbolic Frequency Modulation(HFM) 신호를 이용한 프레임 동기를 제안하였는데, 본 논문에서는 프리앰블을 Pseudo Noise(PN) 시퀀스로 사용하여 상호상관을 통한 프레임 동기를 제안하였다. 또한 도플러 주파수가 존재할 때의 비동기 방식^[5]과 고속 푸리에 변환(Fast Fourier Transform, FFT)를 통해 도플러 주파수를 획득하는 방식^[6]과 도플러 주파수 보상 이후의 동기 방식을 이용한다.

따라서 본 논문에서는 수중 음향통신의 채널 특성에서 프리앰블 상관 방식으로 수신신호 중 데이터의 시작지점을 찾는데, 비동기 방식 상관으로 대략적인 프레임의 시작지점을 확인하고 Sliding 고속 푸리에 변환으로 주파수 옵셋을 확인한다. 하지만 비동기 방식 상관과 Sliding FFT은 신호 전력이 약한 경우의 한계를 확인하고, 동기 방식 상관으로 신호 전력이 약한 경우에도 강인한 프레임 동기 방식의 성능을 실험 결과로 확인할 수 있었다.

본 논문은 우선 II장에서 프레임 동기 구조에 대한 개념적 구조에 대해 설명하며, III장에서는 해상실험 결과를 제시하였다. 최종적으로 IV장에서는 본 논문의 결론을 제시하였다.

II. 프레임 동기 구조 설계

송신기에서 생성한 신호 u(t)는 다음과 같다.

여기서 d()는 데이터, p(t)는 제곱근 상승 여현펄스정형 필터 특성을 갖는 펄스정형신호, T는 비트의 길이를 나타낸다.

송신기 최종단에서 전송되는 신호 s(t)는 다음과 같다.

여기서 At는 송신기의 이득, fc는 반송파 주파수를 나타낸다.

송수신기에서 사용한 반송파 주파수가 일치한다고 가정하면, 수중 환경을 통과한 수신신호는 다음과 같다.

여기서 밑줄(_)은 복소 신호를 나타내며, At은 수신신호의 크기, L은 다중 경로의 수, αl(t)는 l-번째 경로 신호의 진폭 변화, τl(t)은 L-번째 경로 신호의 시간 지연, θl(t)은 l-번째 경로 신호의 위상 변화를 나타낸다.

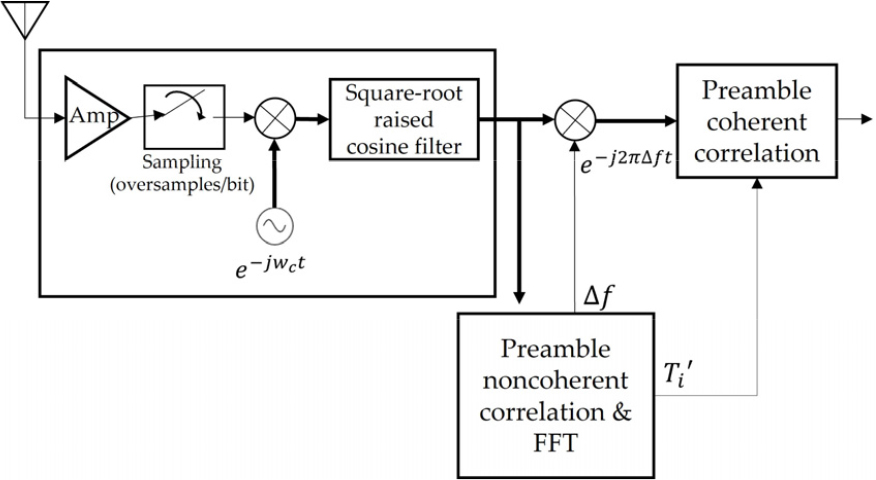
Fig. 1은 제안하는 수신기 및 프레임 동기 구조를 나타낸다. 이때 프레임 동기 구조에서는 수신신호를 하향변환하고 상승 여현 펄스정형 필터로 필터링한 이후의 기저대역 신호를 사용한다.^[1]

Fig. 1.

Frame synchronization diagram.

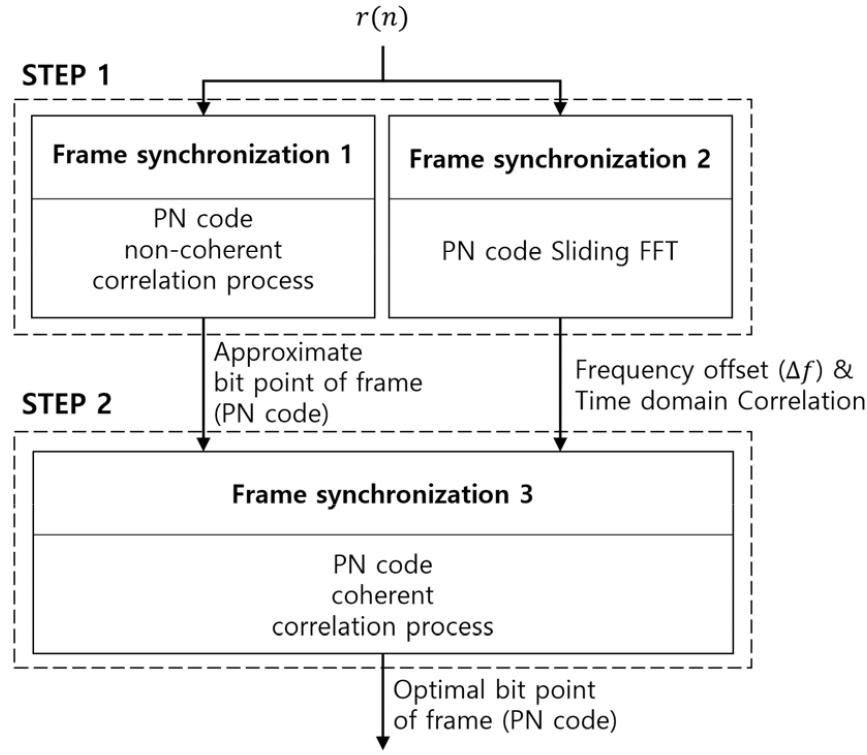
Fig. 2는 프레임 동기 알고리즘을 나타낸다. 본 논문에서 프레임 동기는 2 STEP으로 진행된다. 프레임 동기 과정은 미리 알고 있는 프리앰블의 상관값을 이용하여 프레임의 시작지점을 획득한다. 이때의 프레임의 시작지점은 Fig. 1의 Ti'와 같다.

Fig. 2.

The process of frame synchronization.

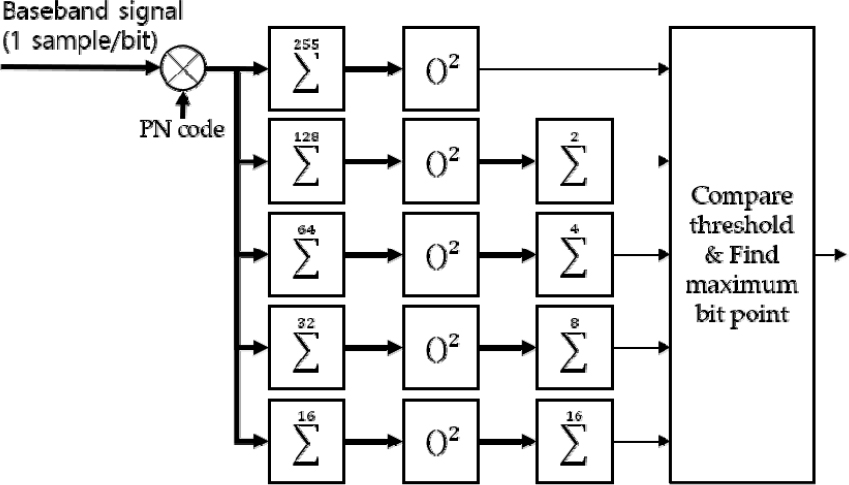
STEP 1 에서는 Frame Synchronization 1 ~ 2 과정인 프리앰블의 비동기 방식 상관과 Sliding FFT을 동시에 진행한다. 수중 통신 환경에서 송수신기의 이동에 의해 발생하는 도플러 효과(Doppler Effect)로 인해 주파수 오차가 발생한다. 주파수 오차로 인해 동기 방식 상관(Coherent Correlation)의 결과는 프레임의 시작점을 찾는데 사용할 수 없게 된다. 이러한 결과는 주파수 오차로 인해 동기 누적과정에서 상관 값이 감소하기 때문이다. 따라서 이를 보완하여 Fig. 3과 같은 비동기 방식 상관을 사용함과 동시에 Fig. 4와 같이 Sliding FFT를 통해 시간 축에서의 결과를 사용한다. 그러나 이러한 결과는 명확한 프레임의 시작점을 얻기에는 모호함이 존재하여 다소 부족한 점이 있다.

Fig. 3.

Frame frame synchronization.

Fig. 4.

Sliding FFT.

따라서 대략적인 프레임의 시작점을 찾는 과정은 비동기 방식 상관과 Sliding FFT의 시간 축에서의 결과를 활용한다. 그러나 보다 정확한 프레임 위치를 얻기 위해, FFT의 결과에서 얻은 주파수 옵셋을 보상하여 동기 방식 상관을 진행한다. 이중으로 상관 값을 확인함으로써 신뢰성 또한 높아지게 된다.

Frame Synchronization1과정의 비동기 방식 상관에서는 기저대역 신호와 이미 알고 있는 프리앰블의 상호상관을 사용한다. 이때 자기상관 특성에 따라 프리앰블의 타이밍이 맞지 않게 되는 경우에 상관 값이 모두 0에 가까운 값이 나온다. 이론적으로, 타이밍이 맞은 경우에는 타이밍이 맞은 비트의 상관 값이 최대가 되고, 그 이외의 상관 값은 0에 가까운 값이 된다. Eq. (4)는 상호상관을 확인하는 수식을 나타낸다.

여기서 xn과 yn은 상호상관을 확인하고자 하는 두 신호이며, R은 상호상관 시퀀스이다.

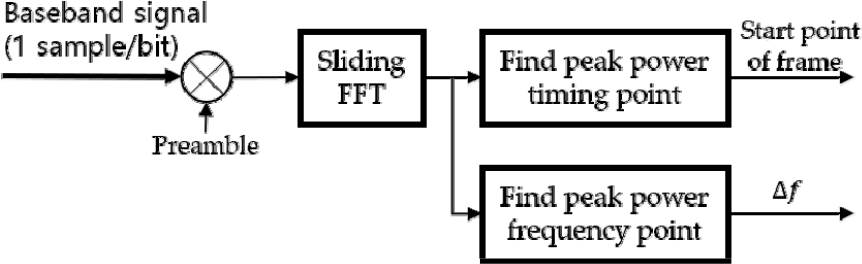
Frame Synchronization2 과정에서는 Frame Synchronization1과정이 진행되는 동시에 프리앰블의 Sliding FFT를 진행하게 된다. Fig. 4는 Sliding FFT의 블럭도를 나타낸다.

Sliding FFT 방식에서는 비트단위로 Sliding 하면서 FFT를 진행하고, 시간 축과 주파수 축에서의 결과를 모두 확인할 수 있다. 시간 축에서의 결과에서는 프레임의 시작지점을 확인할 수 있는데, FFT로 확인한 결과로는 확인하고자 하는 결과 외의 사이드의 파워가 상대적으로 많이 올라와서 정확한 프레임의 시작지점이라고 보기 어려움이 있다. 따라서 STEP 1의 Frame Synchronization 1 ~ 2에서 얻은 프레임의 시작지점은 STEP 2의 동기 방식 상관을 진행하기 위한 프레임의 대략적인 위치를 파악하는 용도로 이용하게 된다. 또한, Sliding FFT 결과의 주파수축에서 검출한 주파수 옵셋을 기저대역 신호에 보상하여 STEP2 과정을 진행한다.

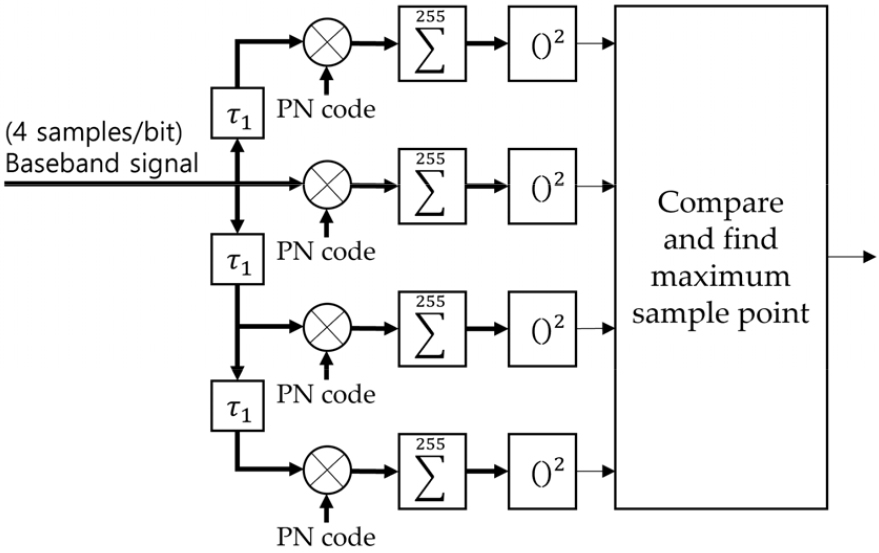
STEP 2에서는 Frame Synchronization 3 과정인 동기 방식 상관을 진행한다. STEP 1에서 검출한 주파수 옵셋이 보상된 비트당 4샘플로 다운 샘플링 된 기저대역 신호를 이용하여 동기 방식 상관을 진행하게 된다. Fig. 5는 동기 방식 상관을 나타낸다.

Fig. 5.

Sliding FFT.

동기 방식 상관에서는 STEP 1에서 확인한 프레임의 시작 비트를 기준으로 앞뒤로 4샘플을 각각 동기 방식 상관을 진행한다. 이때 가장 상관 값이 높은 샘플을 프레임의 시작지점으로 결정한다. 이때 1τ를 1샘플을 나타낸다.

III. 해상 실험 결과

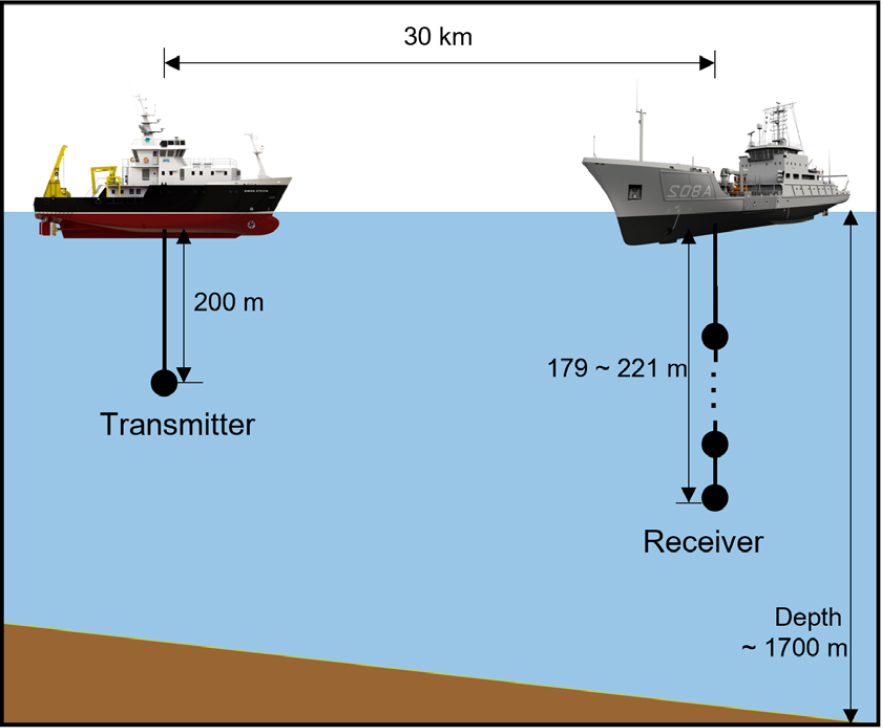
수중 음향 통신에서의 제안한 프레임 동기 구조의 성능을 확인하기 위하여 해상 실험을 진행하였다. Fig. 6은 해상실험의 환경을 보여준다.

Fig. 6.

(Color available online) Experiment environment.

Table 1과 Fig. 7에서 확인할 수 있듯이, 샘플링 주파수는 16384 Hz, 반송파 주파수는 1800 Hz, 송수신기간 거리는 약 30 km, 송신기의 깊이는 200 m, 수신기는 총 16개의 수신기를 사용하여 179 m ~ 221 m 깊이에서 실험을 진행하였다. 데이터는 Binary Phase Shift Keying(BPSK) 변조방식, 데이터율은 100 bps, Guard Interval은 200 bit, 프리앰블은 510 bit, 데이터는 336 bit로 하여 실험을 진행하였다.

Fig. 7.

Frame structure.

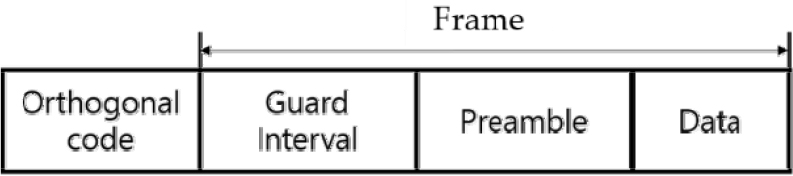
송신 신호는 신호의 위치를 파악하기 위해 Orthogonal code를 사용하였다. 그리고 프레임간 인접 심볼 사이의 간섭을 방지하기 위한 Guard Interval, 프레임의 시작지점을 검출하기 위한 프리앰블과 데이터로 구성되어 있다. 실제 실험에서는 Fig. 7의 프레임 구조를 5번 이어 붙여서 송신신호를 구성하였다. Guard Interval은 첫번째 프레임에서 200 bit, 이후 두번째 프레임에서 다섯번째 프레임에서는 100 bit를 사용하였고, 데이터 전송 속도를 100 bps로 하여 송신신호를 구성하여 실험하였다. 본 논문에서는 신호의 전력이 가장 큰 13번 수신기의 결과를 이용하였다.

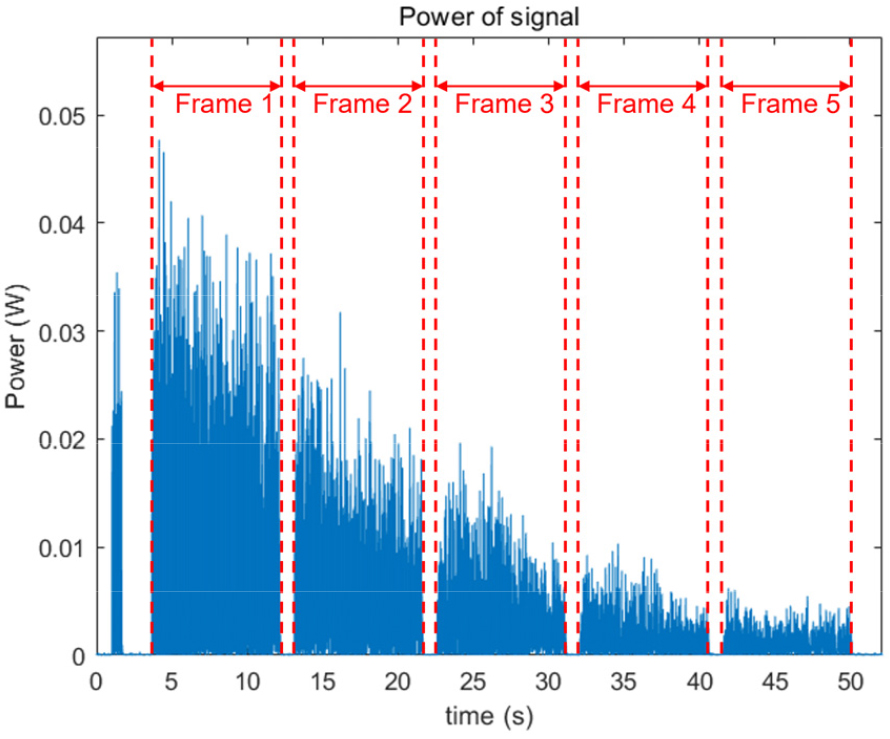
Fig. 8은 해상실험에서 수신신호의 전력을 나타낸다. Fig. 8의 결과에서 각 프레임의 전력이 감소하는 것을 볼 수 있다. 이는 실험을 수행한 수중 채널특성으로 인한 현상이다. 수중 채널특성으로 인해 수신 신호의 전력이 감소하는 현상은 각 프레임마다 달라지는 것으로 볼 수 있다. 따라서 이는 거리에 따른 채널특성으로 보고, 본 논문에서는 수신 신호에서 전력이 가장 큰 첫 번째 프레임과 전력이 가장 작은 다섯 번째 프레임의 결과를 확인하였다.

Fig. 8.

(Color available online) Received signal power (100 bps).

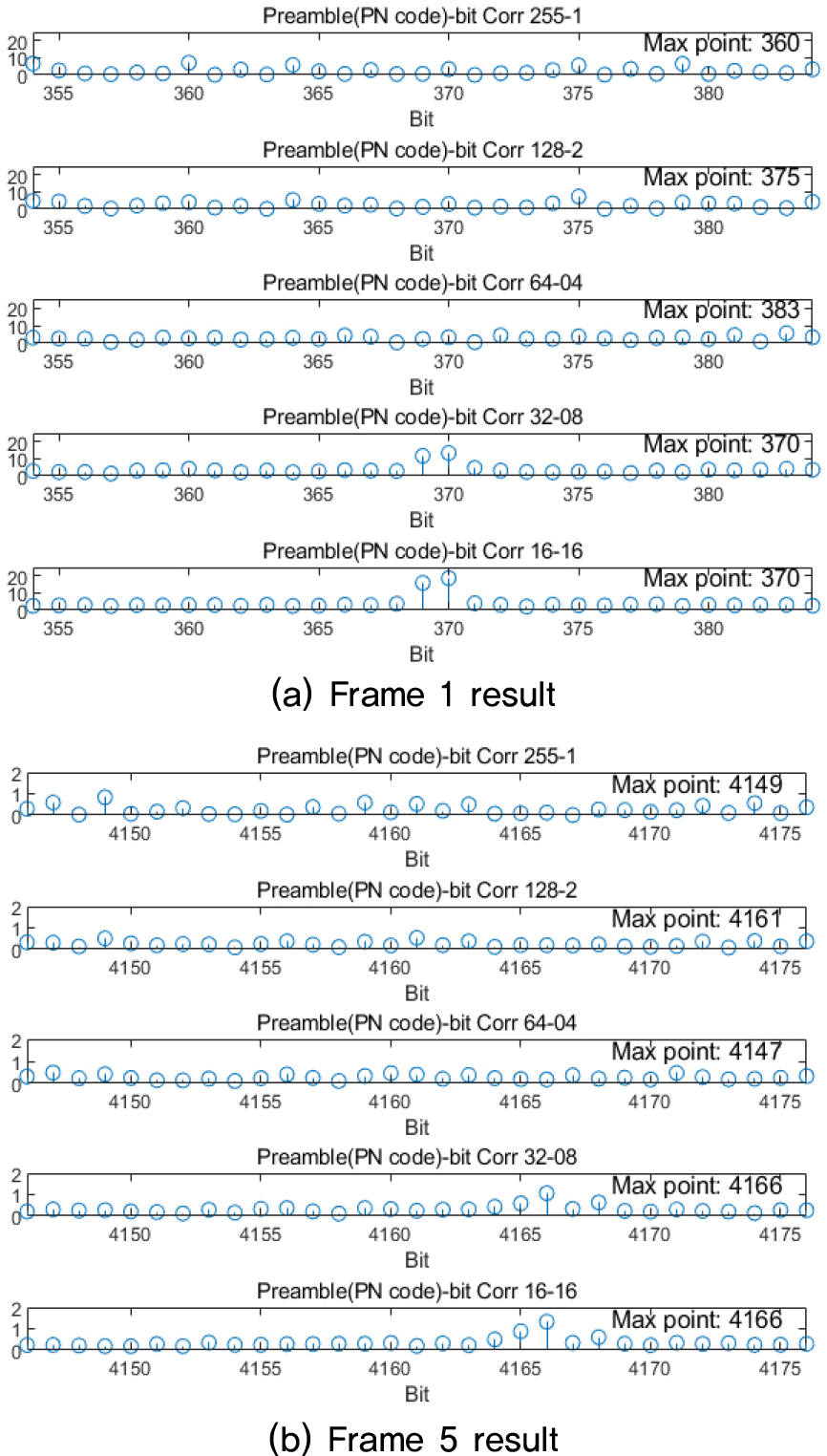
Fig. 9의 (a), (b)는 각각 수신 신호의 첫 번째 프레임과 다섯 번째 프레임의 STEP 1 과정에서Frame Synchronization 1 결과를 보여준다.

Fig. 9.

(Color available online) STEP1 Synchronization1 result: Noncoherent correlation.

두 결과 모두 주파수 옵셋이 존재하므로 동기누적 계수가 255, 128, 64인 경우에서는 상관 값을 확인할 수 없고, 동기누적 계수가 32, 16인 경우에서만 상관 값을 확인할 수 있다. 특히 동기 누적 계수가 16인 경우에 각각 370 bit, 4166 bit에서 최고 상관 값이 확인되었다. 하지만 최고 상관 값 이외의 값에서 최고 상관 값과 비슷한 크기를 갖는 비트가 존재하므로 정확한 프레임의 시작지점이라고 하기에는 어려움이 있다. 따라서 STEP 1 Synchronization 2의 Sliding FFT를 진행하여 주파수 옵셋을 검출하여 보상하여 정확한 결과를 확인한다.

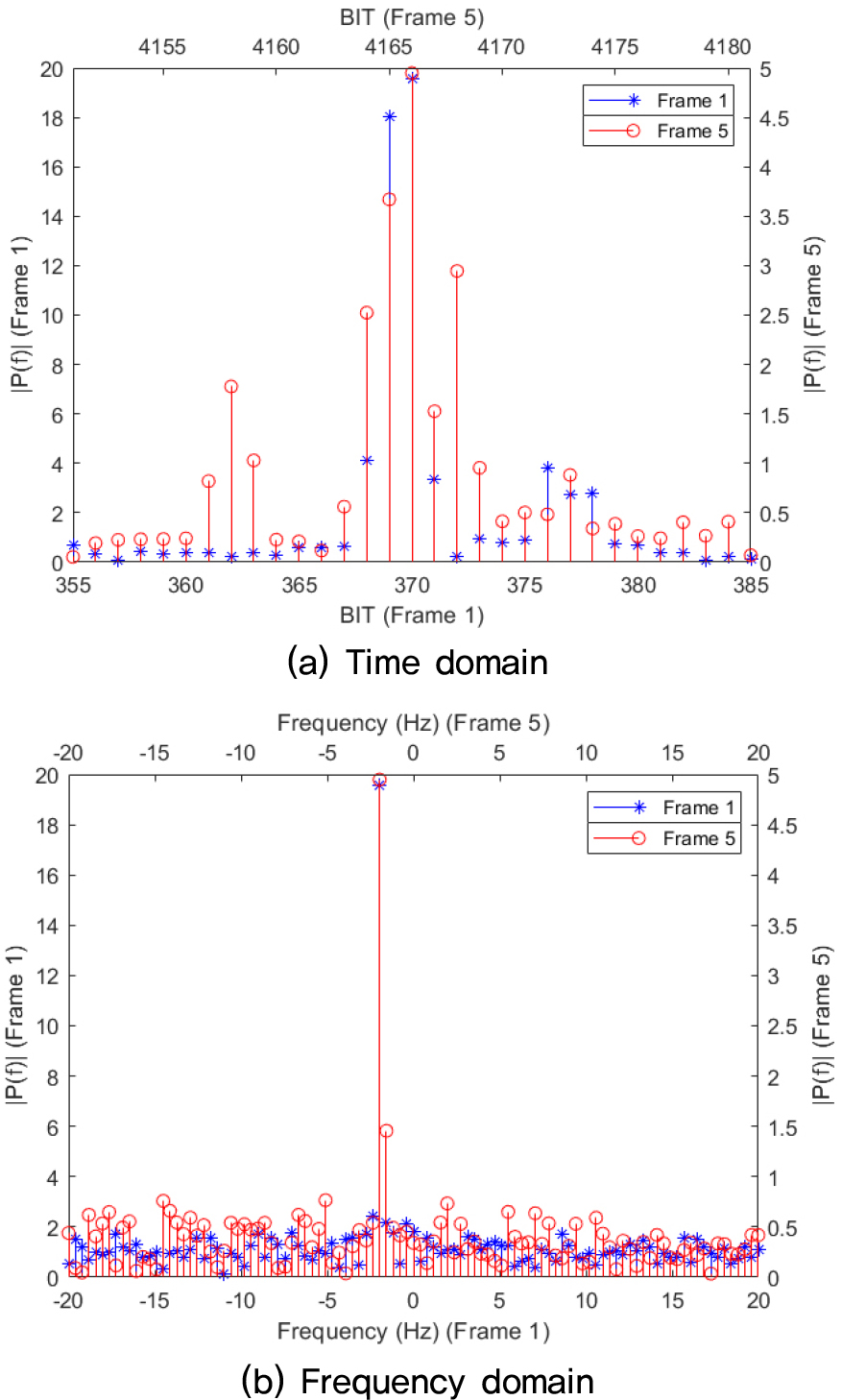
Fig. 10은 첫 번째, 다섯 번째 프레임 수신신호 STEP 1과정의 Synchronization 2 결과를 보여준다. (a)와 (b) 결과는 각각 Fig. 4 Sliding FFT의 알고리즘으로 각각 시간 축과 주파수 축에서의 Sliding FFT의 결과를 나타낸다. 이때 파란색으로 보여주는 아래쪽, 왼쪽 축은 첫 번째 프레임의 결과를 나타내고, 빨간색으로 보여주는 오른쪽, 위쪽 축은 다섯 번째 프레임의 결과를 보여준다. 첫 번째 프레임의 신호의 파워는 다섯 번째 프레임의 신호의 파워에 비해 스케일이 크고, 잡음의 파워보다 눈에 띄게 높다. 즉, 수신 신호의 전력 이 높은 상황이다. 따라서 Sliding FFT 결과에서는 대략적인 결과를 확인할 수 있지만, 다섯 번째 프레임의 결과에서는 최고 상관 값 이외의 비트 지점에서 비슷한 크기의 상관 값을 갖는다는 것을 확인할 수 있다. 따라서 이를 보완하기 위해 주파수 축에서의 결과로 약 –1.96 Hz의 주파수 옵셋이 발생하는 것을 알 수 있고, 이를 신호에 보상하여 STEP 2 과정을 진행한다.

Fig. 10.

(Color available online) STEP1 Synchronization2 result: Sliding FFT result.

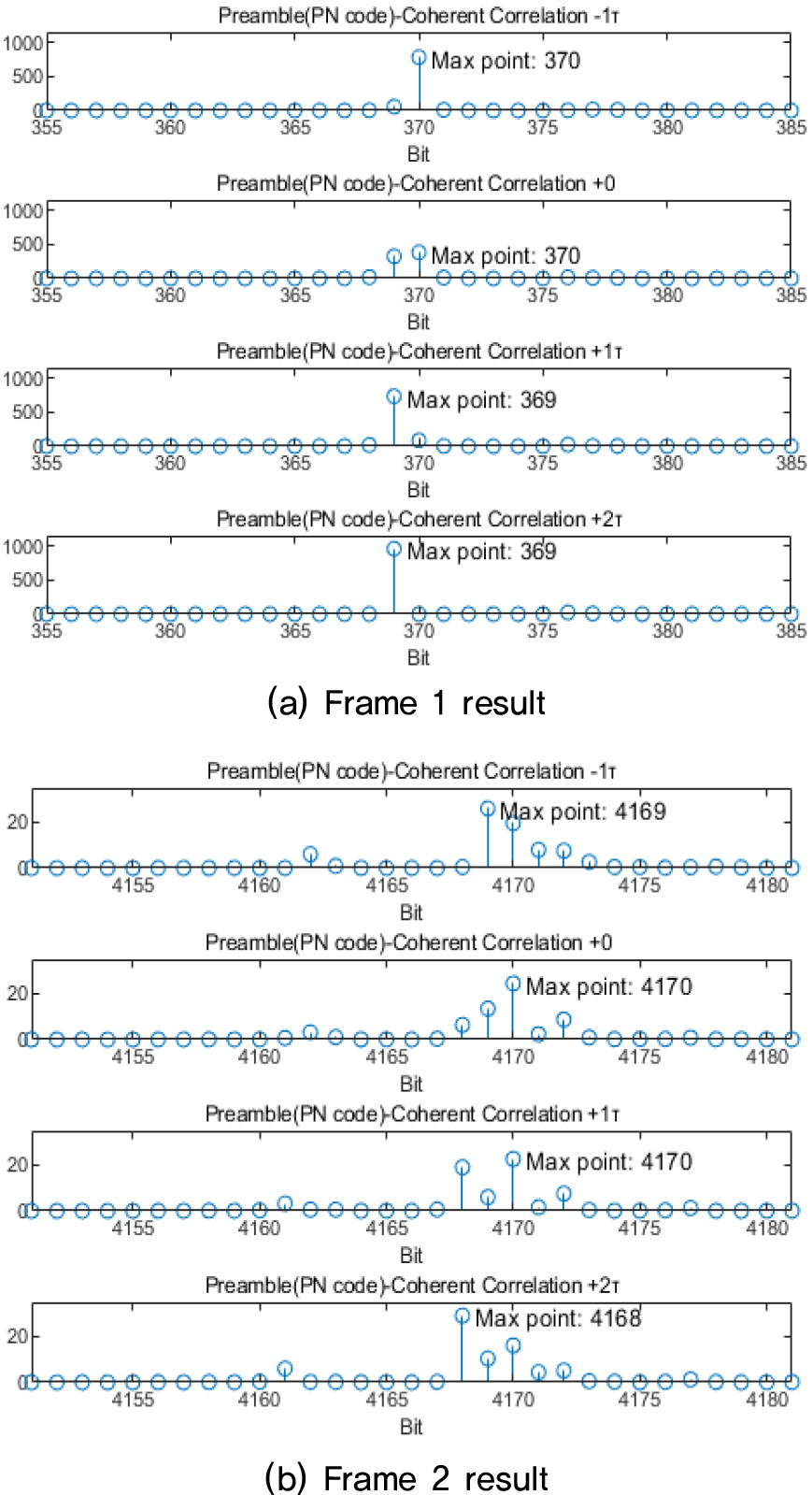
Fig. 11은 STEP 2 Synchronization 3의 결과를 나타낸다. Synchronization 3 과정에서는 Fig. 5에서 볼 수 있듯이 STEP 1의 결과인 주파수 옵셋을 보상한 1비트당 4샘플의 기저대역신호를 STEP 1에서 얻은 프레임의 시작점을 기준으로 동기방식 상관을 진행한다. 이때 1τ는 1 샘플을 의미한다.

Fig. 11.

(Color available online) STEP2 Synchronization3 result: Coherent correlation.

첫 번째 프레임의 STEP 1 결과에서는 370비트가 프레임의 시작지점이지만, 동기방식 상관 결과에서는 370 비트에서 2샘플 이전의 위치가 정확한 프레임의 시작지점임을 확인할 수 있고, 369 비트의 최고 상관 값 이외의 상관 값은 잡음과 같은 상관 값을 확인할 수 있다. 다섯 번째 프레임의 STEP 1 결과에서는 4166 비트가 프레임의 시작지점이지만, 동기방식 상관 결과에서는 4168 비트가 프레임의 시작지점임을 확인할 수 있다. 이때 Fig. 8에서 볼 수 있듯이, 첫 번째 프레임과 다섯 번째 프레임에서 신호의 전력 차이가 나는 것을 확인할 수 있는데, 신호의 전력 차이로 인하여 동기방식 상관 값의 차이가 생긴다. STEP 1의 다섯 번째 프레임에서 보이지 않았던 수중 음향 채널의 다중경로가 STEP 2의 동기 상관에서는 확인이 되며, 이외의 값은 0에 가까운 값으로 나타나기 때문에 최종적으로 정확한 프레임의 시작지점을 확인할 수 있다.

IV. 결 론

본 논문에서는 수중 통신환경에서BPSK 변조방식 데이터의 프레임 동기 구조를 제안하였다. 제안한 프레임 동기 구조를 검증하기 위하여 해상 실험을 수행하였다. 프레임 동기는 총 2 STEP으로 진행된다. STEP 1과정에서는 비동기 방식 상관을 통한 최대 상관 값 검출과 Sliding FFT를 통한 시간 축에서 최대 값을 이용하여 레임의 대략적인 시작지점을 확인했다. 하지만 수신신호 전력이 높은 상황에서는 프레임의 시작지점을 확인할 수 있지만, 수신신호 전력이 낮은 상황에서의 프레임 동기의 결과에서는 최대 상관 값과 비슷한 값이 다른 비트지점에서 확인되었고, 이는 정확한 프레임의 시작지점이라고 할 수는 없다. 따라서 STEP 2과정에서는 STEP 1과정에서 확인한 주파수 옵셋을 보상한 비트당 4샘플의 신호를 동기 방식 상관을 통해 프레임 동기의 결과를 확인할 수 있었다.