I. 서 론

해양플랜트에서는 채굴 및 정제과정에서 고온/고압의 가스가 발생하며, 이를 처리하기 위한 배관 및 밸브 시스템은 안정적인 가스 이송과 이를 통한 플랜트 안전을 위해 필수적이다. 감압밸브는 이러한 고압가스의 압력을 낮추어 안전하게 가스를 이송하기 위하여 설치되지만, 감압밸브를 지나면서 발생하는 급격한 압력저하는 높은 난류 섭동과 이로 인한 유동소음의 주요 원인이 된다. 강한 음향에너지는 하류 방향으로 전파하면서 배관 진동 및 손상을 유발하며, 고주파 진동으로 인해 수 분 내로 큰 소음과 함께 배관의 피로파괴를 유발한다고 알려져 있다. 이러한 현상을 음향유기진동(Acoustic Induced Vibration, AIV)이라 하며, 1980년대에 음향유기진동에 의한 배관의 파손이 보고된 이후 많은 연구들이 수행되었고 이를 기초로 배관 설계기준들이 마련되었다.

Carucci와 Mueller^[1]는 당시까지의 배관 파손 사례들을 모두 조사하여 AIV에 의한 피로파괴 사례를 분류하고 배관 파손을 예방하기 위해 배관 직경을 이용한 설계 기준을 제시하였다. Eisinger와 Joseph^[2,3]은 배관 직경과 배관의 두께를 고려한 설계 기준을 제시하였으며, Veritas^[4]는 배관 설계를 위한 기준식을 제시한 바 있다. 이러한 설계 기준의 대부분은 단순 경험식에 의해 제시된 것으로서 사용이 용이하다는 장점이 있으나, 경험식의 특성상 AIV에 대한 물리적 발생 메커니즘 특성을 반영하기 어려우므로 문제 발생이 예상될 때 효율적인 저감대책 마련에 한계가 있다. 최근에 Ku et al.^[5,6]과 Kim et al.^[7]은 고정밀 압축성 대와류모사(Large Eddy Simulation, LES) 기법을 이용해서 밸브를 모사한 노즐 형상에 대해서 배관 내 유동과 유동소음을 직접 모사하였으며, 배관 AIV의 원인이 되는 벽면 압축성 압력섭동을 파수-주파수 변환을 이용해서 성공적으로 추출하여 정량적으로 평가할 수 있음을 보였다.

본 논문에서는 이러한 기존 연구를 확장하여 고압가스 배관 내 실제 밸브 형상에 대하여 유동 소음을 평가할 수 있는 수치적 방법론을 제시하고, 이를 이용하여 밸브 유동 소음 저감을 위한 다공성 판의 영향을 정량적으로 분석하였다. 먼저, 고정확도의 비정상 압축성 LES 기법을 이용하여 고압가스 배관의 밸브 유동과 이로 인한 유동소음을 예측하였으며, 예측한 벽면 압력 스펙트럼을 측정값과 비교함으로써 수치해석결과의 유효성을 검증하였다. 다음으로 배관 내에서 평균 유동장과 중첩되어 전파해가는 음향장의 음향파워를 예측하였으며, 다공성 판의 설치 전후 음향 파워를 비교함으로써 다공성 판의 소음저감 효과를 확인하였다.

II. 배관 내 밸브 유동 소음 실험

2.1 실험 방법

실제 현장에서 사용되는 밸브와 배관을 대상으로 실제 작동조건을 반영하여 실험을 진행하였으며, 배관 내 밸브 유동에 의한 압력섭동을 측정하기 위하여 한국표준과학연구원(Korea Research Institute of Standards and Science, KRISS)의 고압 가스 유동 표준 시스템을 사용하였다^[6].

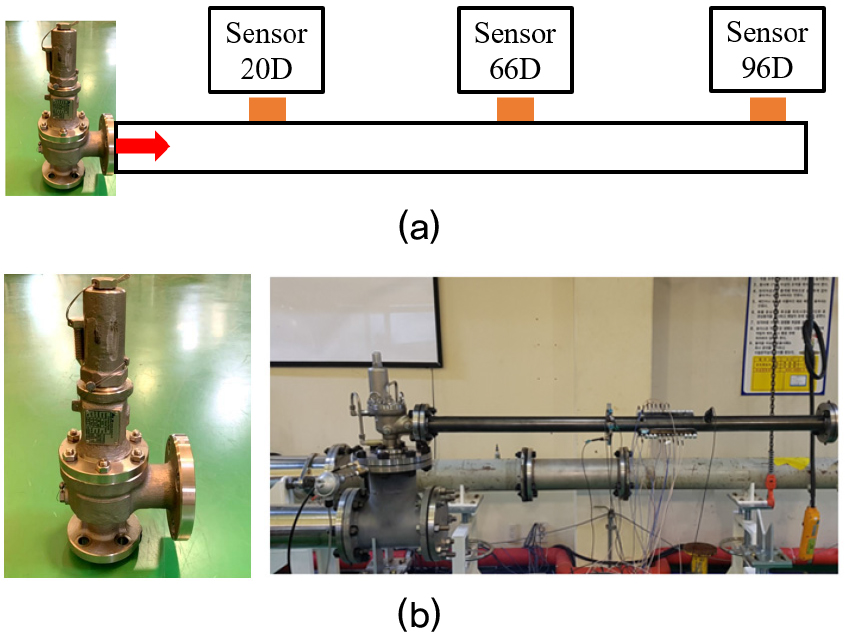
Fig. 1에서 배관 내 밸브유동소음을 측정하기 위한 전체 실험에 대한 개념도와 대상 밸브와 배관시스템 압력측정 사진을 나타내었다. 밸브 출구 직경(D = 50 mm)을 기준으로 하류방향으로 20D, 66D, 96D위치에 압력센서를 부착하고 배관 내 밸브 유동에 의한 압력을 측정하였다. 압력 측정을 위하여 PCB Piezotronic 102B15 동압력센서와 NI PXI 5922 디지털 신호변환기, PCB conditioner 482C05 파워 공급장치를 사용하였으며, PXI 5922는 NI PXI 1033-Chassis에 장착하고 LabVIEW 프로그램을 이용하여 신호 분석을 수행하였다.

Fig. 1

(Color available online) Experimental set-up for measurement of valve flow noise for a piping system: (a) schematic diagram and (b) photograph for target valve and piping system.

2.2 실험 결과

고압 탱크를 이용하여 밸브 상류방향에서의 절대 압력을 12기압으로 유지하였으며, ISO 9300 규격에 따라 압력 센서와 온도 센서를 부착하였다. 유량, 온도, 벽면 압력 섭동을 측정하였으며, 배관 내 측정 유량 및 온도는 각각 0.2 kg/s, 288 K이다.

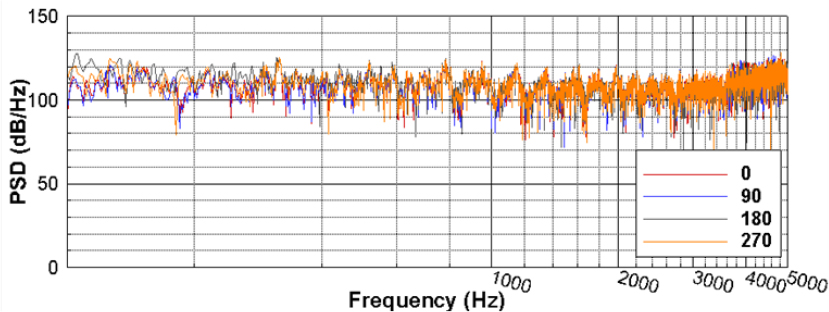
Fig. 2에서 밸브 출구로부터 하류 방향으로 20D 떨어진 위치에서 파이프 원형 절단면을 따라 0°, 90°, 180°, 270°의 네 지점에서 측정한 압력 스펙트럼을 나타낸 그림이다. 여기서 D는 밸브 출구 배관의 직경이며, 50 mm이다. 측정 시 샘플링 주파수는 20 kHz 이며, 주파수 해상도는 3.125 Hz이다. 측정결과의 신뢰성을 위하여 나이키스트의 반인 5 kHz까지 제시하였다. 원형 절단면을 따라 측정 위치 차이에 따른 소음 변화는 미미한 수준이며, 전 주파수 영역대에서 100 dB 이상의 강한 압력섭동이 발생하는 것을 확인할 수 있다.

Fig. 2

(Color available online) Spectral density levels of pressure measured on inner surface of pipe at 20D downstream of valve outlet.

III. 수치해석 방법

3.1 지배방정식과 이산화기법

배관 내 밸브유동에 대한 지배방정식으로 3차원 압축성 Navier-Stokes 방정식을 사용하였다.

여기서 ρ는 밀도, v→는 속도, p는 정압, τ¯는 점성응력텐서, F→는 외부 체적힘을 나타낸다. 점성응력텐서는 다음식과 같이 나타낼 수 있다.

여기서 μ는 동점성계수, I는 단위텐서이다. 에너지 보존 방정식은 다음과 같이 나타낼 수 있다.

여기서 E는 단위질량당 에너지, h는 열전달계수, J→와 Sh는 각각 확산 플럭스와 열원이다. 압축성 배관 내 밸브 유동과 유동소음 해석을 위해 먼저 정상상태 Reynolds-Averaged Navier-Stokes(RANS) 방정식 기반의 수치해석을 수행하였으며, 수렴해를 압축성 LES 해석의 초기조건으로 활용함으로써 고정확도 비정상 유동해석의 효율성을 높였다.

본 연구에서는 상용 코드인 Ansys Fluent v.19.1을 사용하였으며, 먼저 압력 기반 압축성 RANS 해석을 수행하였다. 배관 내 유체는 이상기체로 가정하였으며, 지배방정식은 내재적 방법을 통해 연속 방정식과 운동량 방정식을 동시에 푸는 연성 해석기법을 적용하였다. 유동의 차분화 방법은 충격파와 같은 급격한 유동 특성의 변화를 안정적으로 모사하기 위하여 풍상차분법을 적용하였으며, 난류 유동을 모사하기 위하여 k-ω SST 난류 모델을 적용하였다.

LES 기법은 지배방정식에 공간적인 평균화 조작을 행하고, 유동장을 격자보다 큰 난류 성분과 그 이하의 작은 성분으로 분리하여 전자는 직접 계산하고 후자는 모델링을 하는 해석방법이다. 격자 크기를 충분히 작게 구성할 경우, 격자 크기 이하의 난류 구조는 등방성이라고 간주할 수 있어 보편적인 모델을 구성하기 쉬운 특징을 갖고 있다. 또한 시간평균을 이용하는 RANS 방정식과는 달리 공간필터링만을 사용하기 때문에 시간 변동에 따른 비정상 유동을 풀기에 적합하다. 격자 크기보다 작은 난류 구조를 모사하기 위하여 LES 해석 시 많이 사용되는 Smagorinsky-Lilly 모델을 적용하였으며, 난류 동점성 계수는 다음 식을 이용하여 계산한다.

여기서 Sij는 유동의 텐서변형률을 의미하며, Ls는 격자보다 작은 크기의 난류 성분을 고려하기 위한 혼합거리이다.

3.2 계산 영역과 격자

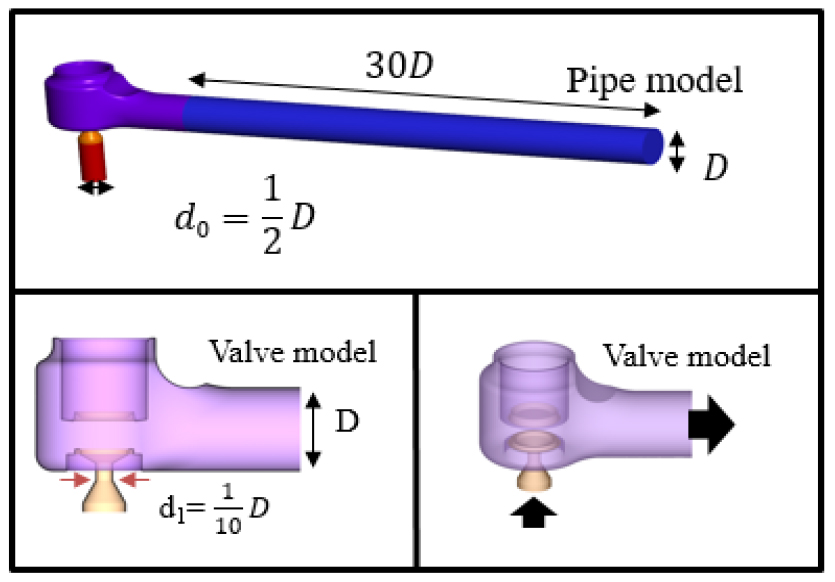
Fig. 3에서 전체 계산영역과 관련치수를 나타내었다. 계산 비용을 고려하여 20D 압력 측정위치를 포함하면서 밸브에서 발생한 유동섭동이 감쇠되고 음향파가 전파되는 영역을 포함하도록 하류 방향 배관의 길이는 30D로 설정하였다. 감압 밸브의 경우 감압 상태의 밸브를 모사하기 위해 밸브가 완전히 열린 형태로 모델을 구현하였다. 해석 시 경계조건으로 밸브 입구단에는 측정 유량 0.2 kg/s를 적용하였으며, 출구단에는 대기압 조건을 주었다. 또한 배관 끝에서 음향파의 반사를 최소화하기 위하여 비반사조건을 적용하였다.

Fig. 3

(Color available online) Numerical modeling of pipe and valve.

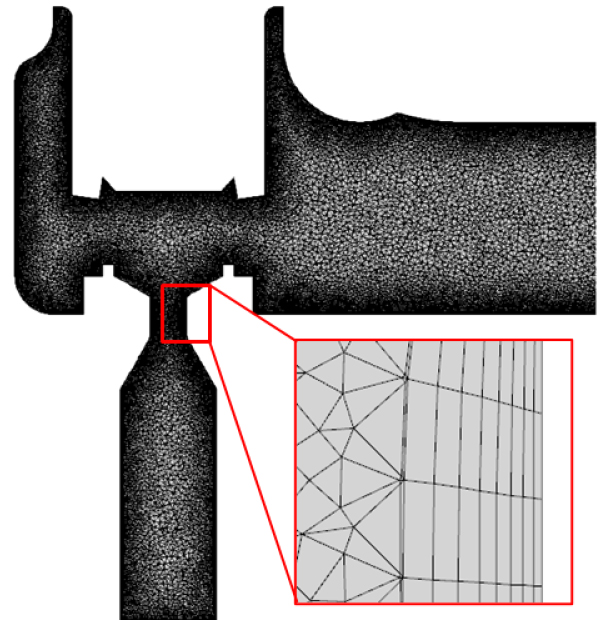
Fig. 4에서 Fig. 3의 계산영역을 반영하여 구성한 격자를 나타내었다. 격자 크기는 음향파의 정밀한 계산을 위하여 5 kHz에 해당하는 한 파장에 격자가 20개 이상 들어가도록 구성하였으며, 총 약 3천만 개의 격자를 사용하였다. 또한, 밸브 내 난류 및 충격파와 같은 주요 유동소음원의 정밀한 모사를 위하여 밸브 내부에 15M개의 격자를 적용하였으며, 벽면 경계층 유동을 정밀하기 모사하기 위하여 배관 내부 벽면에 8개의 프리즘 격자를 구성하였다.

Fig. 4

(Color available online) Simulation geometry part on valve and grid of valve wall.

3.3 배관 내 음향 파워

배관 유동처럼 평균 유동이 존재하는 음향장에서 단위 면적 당 음향 파워인 음향 강도는 다음과 같다.

여기서, H'와 m'는 각각 정체 엔탈피 섭동량과 질량 플럭스 섭동량이며, 다음과 같이 표현할 수 있다.

따라서 배관 단면을 통과하는 순간 음향 파워는 다음 식과 같이 표현할 수 있다.

Eq. (9)를 이용해서 배관 내 단면을 통과하는 음향파워를 계산하였다. Eq. (9)를 적용할 때, 주의해야 할 점은 섭동량이 음향파에 의한 것일 때 음향파워를 나타내지만, 섭동량에 난류에 의한 와류파가 같이 포함될 때는 유동전체 섭동량에 의한 파워를 나타낸다는 것이다.

3.4 와류 음원(Vortex sound source)

Lighthill^[8]은 당시 상업용 제트항공기의 운항과 더불어 문제가 된 공력소음원을 수학적으로 처음으로 유도하고 다음과 같이 공력소음원을 정의하였다.

여기서 Tij은 Lighthill의 응력텐서로 다음과 같이 정의된다.

Howe^[9]는 Lighthill의 공력소음원을 다음과 같이 근사할 수 있음을 보였다.

여기서 ω→는 유동의 와류벡터를 나타낸다. 본 절에서는 배관 내 밸브유동에 의한 유동소음원의 정량적 분석을 위해 Eq. (12)에서 나타낸 와류소음원을 사용하였다.

IV. 수치해석 결과

본 절에서 제시하는 결과는 모두, 정상상태의 RANS 해석을 수행하여 유량과 압력을 기준으로 실험과 동일조건이 되도록 수렴시킨 후, 이를 초기 조건으로 LES 해석을 수행한 결과이다. 해석 시간 간격은 10 μs이며, 배관 출구에서 유량이 실험과 동일하게 수렴된 시점으로부터 0.01 s까지의 시변 자료를 활용하였다.

4.1 유동 해석 결과

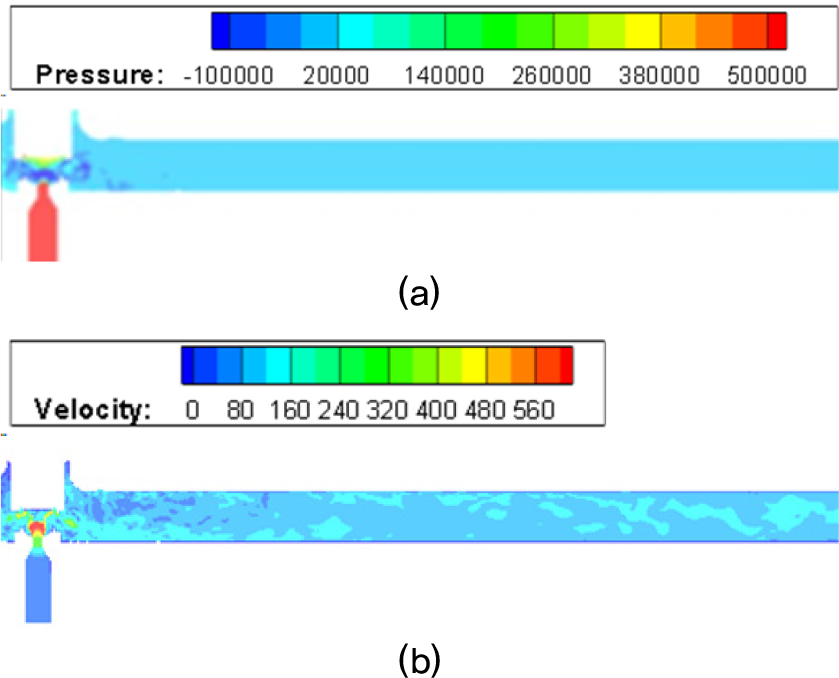
먼저 Fig. 5에서 배관 전체의 유동해석결과를 나타내었다. Fig. 5(a)의 압력장으로부터 유동이 밸브를 지나면서 압력이 급격하게 저하되는 것을 확인할 수 있으며, Fig. 5(b)의 속도장으로부터 밸브를 지나는 유동이 초음속으로 가속되어 충격파와 함께 복잡한 난류 구조가 발생하는 것을 확인할 수 있다. 또한 하류로 흘러가면서 이러한 난류에 의한 섭동은 급격히 감소하고 유동 소음에 의한 음향파가 하류로 전파되고 있음을 알 수 있다.

Fig. 5

(Color available online) Pressure and velocity contour flow on pipe. (a) Pressure contour. (b) Velocity contour.

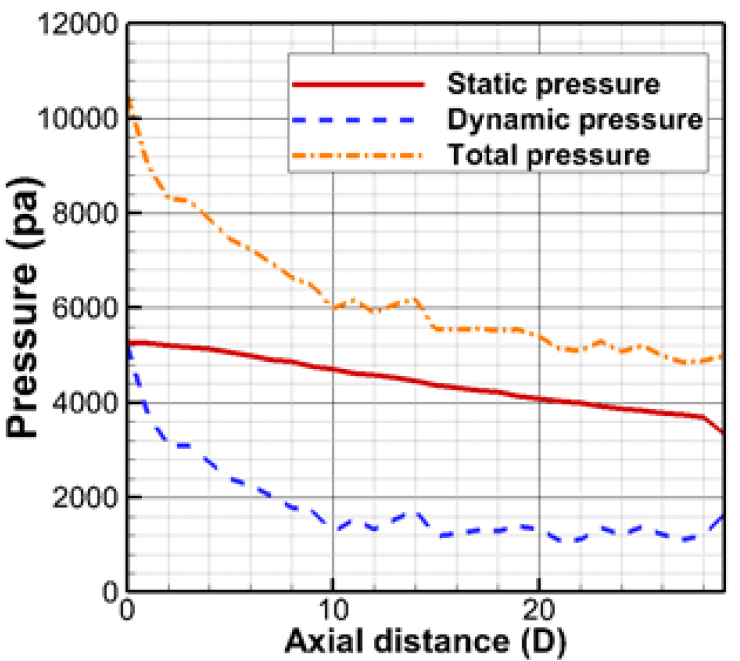
보다 정량적인 분석을 위하여 밸브 출구에서 하류 방향으로 배관을 따라 계산한 평균 압력장을 Fig. 6에 도시하였다. 밸브 근처 후류 영역에서 동압력감소에 따라 전압력이 급격히 감소하고 10D 부근부터는 배관 벽면 손실에 따른 정압력 손실에 비례하여 전압력 감소량이 급격히 줄어들고 있음을 알 수 있다.

Fig. 6

(Color available online) Variation of total pressure, dynamic pressure, and static pressure along with downstream direction.

4.2 소음 해석 결과

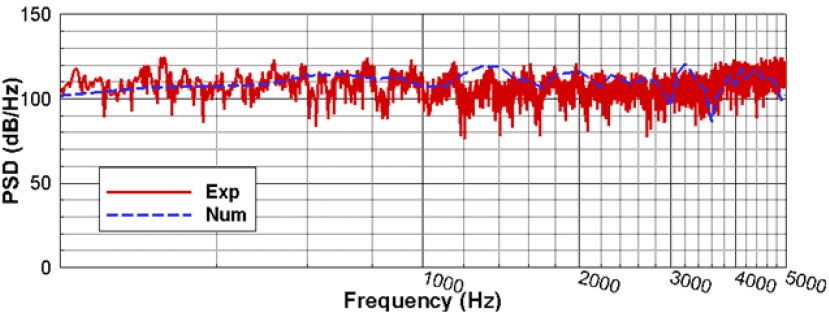
Fig. 7은 밸브 하류 20D 위치에서 예측한 음압 스펙트럼을 Fig. 2의 측정값과 비교한 그림이다. 전 주파수대역에서 두 결과가 잘 일치함을 확인할 수 있다.

Fig. 7

(Color available online) Validation on Numerical calculation & experiment result.

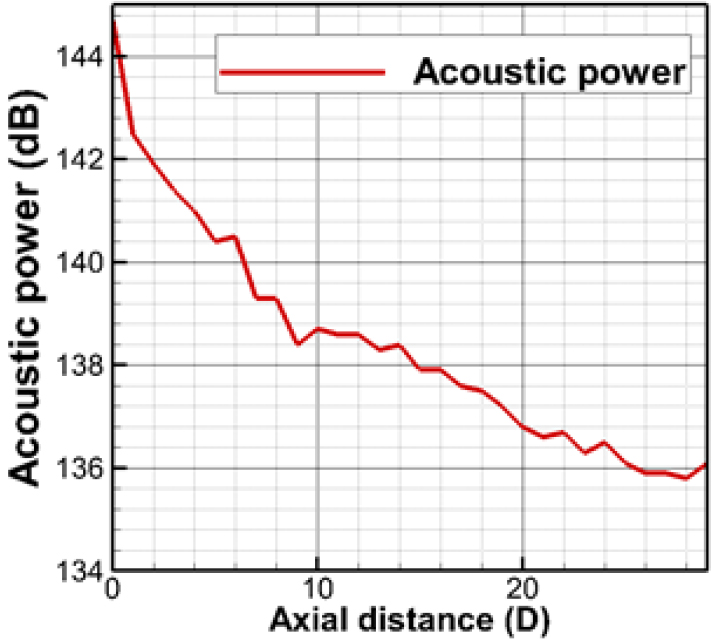
Fig. 8에서 Eq. (9)에서 정의한 음향 파워식을 이용하여 계산한 음향 파워를 나타낸 그림이며, 배관 하류 방향을 따라 음향 파워의 변화를 나타내었다. 10D 근처까지는 급격히 감소하다가 하류 방향을 따라 점차 수렴하고 있으며, 배관 끝에서 136 dB에 이르는 것을 알 수 있다. Eq. (9)에서 언급한 바와 같이 음향파워를 계산할 때 섭동량들이 밸브 근처에서는 난류섭동과 연관된 비압축성 섭동값들이 포함되므로 급격히 감소하고 이후 거리가 멀어지면서 음향 섭동값들만 관여하면서 거리에 따른 감쇠량이 작아짐을 알 수 있다.

Fig. 8

(Color available online) Variation of acoustic powers along with downstream direction.

Fig. 9

(Color available online) Iso-contours of vortex sound sources in flow downstream of valve.

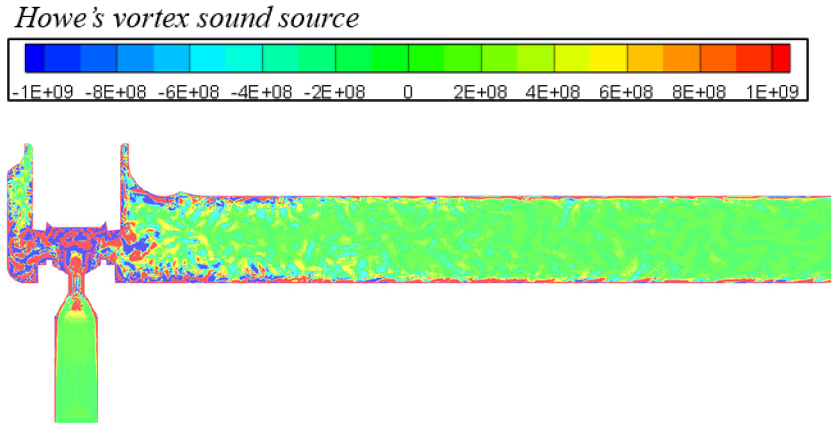
Fig. 9는 Eq. (12)에서 정의한 와류소음원을 도시한 그림이다. 앞서 언급한바와 같이 밸브 내 유동 전단층을 중심으로 강한 섭동을 가지는 것을 알 수 있고, 점차 후류로 멀어지면서 그 크기가 급격히 작아지는 것을 알 수 있다.

V. 밸브 소음 저감장치 분석

배관 내부 유동에서 소음 저감을 위하여 사용되는 장치는 크게 세 가지로 구분할 수 있다. 첫째는 일반적인 기계장치에 가장 많이 사용하는 소음기이며, 둘째는 항공기 엔진과 같이 유동 저항을 최소화 하는 벽면 흡음 장치, 마지막은 산업 현장에서 고압 배관 내에 가장 많이 사용하는 다공성 판이다. 본 논문에서는 현장에서 가장 많이 사용하는 다공성 판을 설계하고 배관에 부착하여 그 성능을 평가하였다.

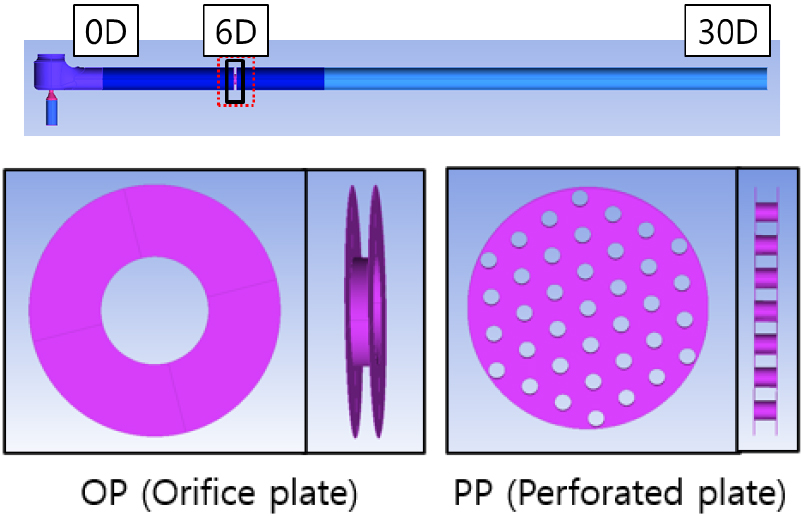
Fig. 10은 본 논문에서 대상인 다공성 판(Perforated Plate, PP)과 비교 대상으로 단일 구멍을 가지는 오리피스 판(Orifice Plate, OP)을 나타낸 그림이다. OP의 경우 단일 유로면적을 지니며, PP의 경우 37개의 구멍으로 이루어져 있고, 전체 유로면적은 OP의 유로 면적과 동일하다. PP의 경우 Laffay et al.^[10]이 고려하였던 형상 중 자체 소음을 가장 작게 발생시키는 PP형상을 참고해서 설계하였다.

Fig. 10

(Color available online) Geometries of perforated plate designed as a valve-noise suppression device and single hole orifice plate with the same open area as perforated plate.

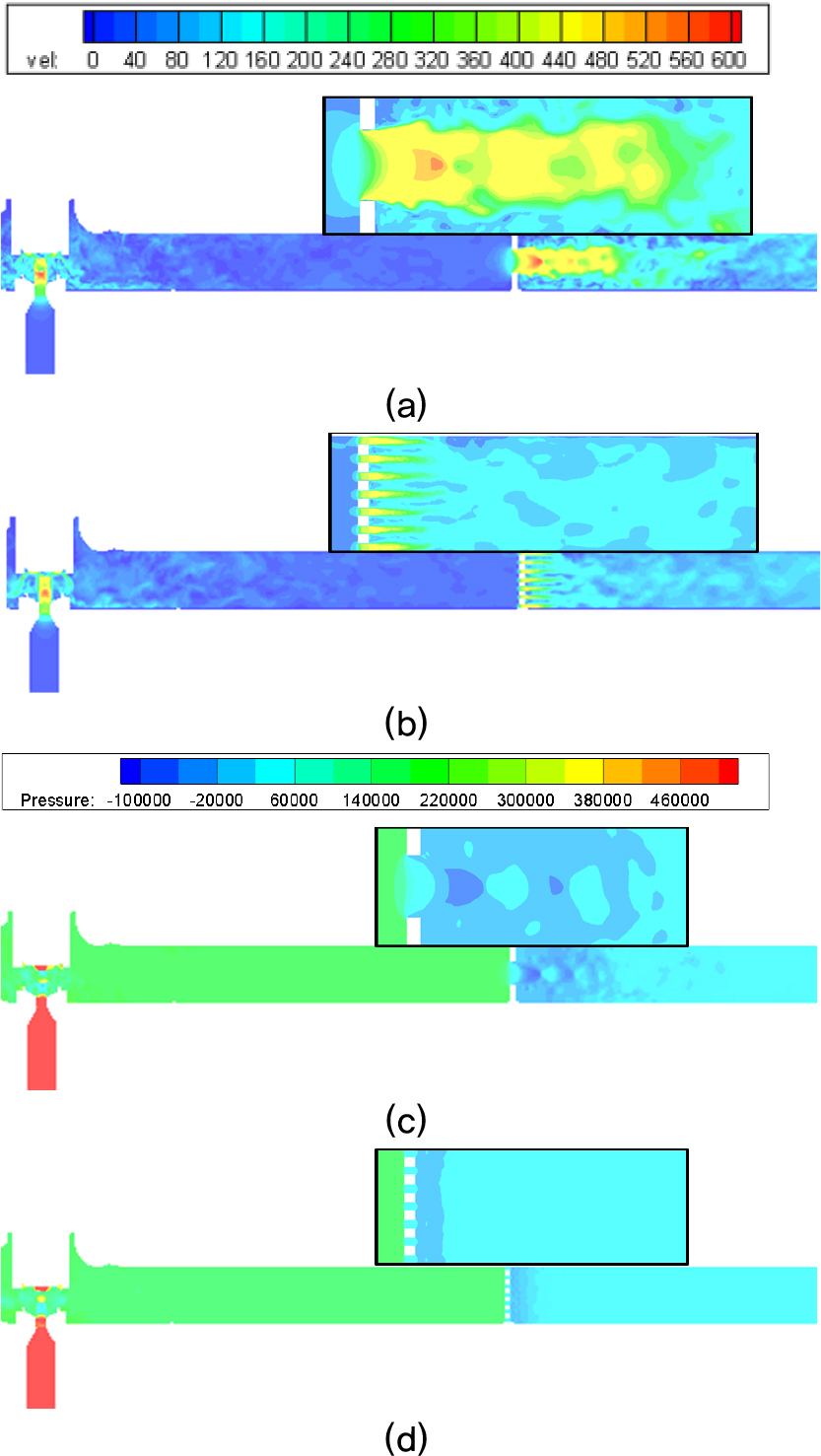
Fig. 11에서 OP와 PP를 밸브 하류 방향 6D 지점에 부착하고 각각 수치해석한 결과를 비교한 그림이다. OP의 경우 또 다른 밸브 역할을 하여 OP 후류에서 강한 와류와 충격파가 형성되고 있는 것을 알 수 있다. PP의 경우 각각의 구멍에서 와류가 발생하고 있으나 그 크기가 작고 또한 와류가 소음원으로 작용할 때, 위상차로 서로 상쇄되는 영향이 발생하여 소음이 작게 발생할 것으로 판단되며, 상류 밸브에서 오는 음향파를 임피던스 차이와 와류파로의 에너지로 전환을 통하여 일부 감쇠시킬 수 있을 것으로 사료된다.

Fig. 11

(Color available online) Iso-contours of predicted velocity and pressure on centered vertical plane: (a) velocity for OP, (b) velocity for PP, (c) pressure for OP, and (d) pressure for PP.

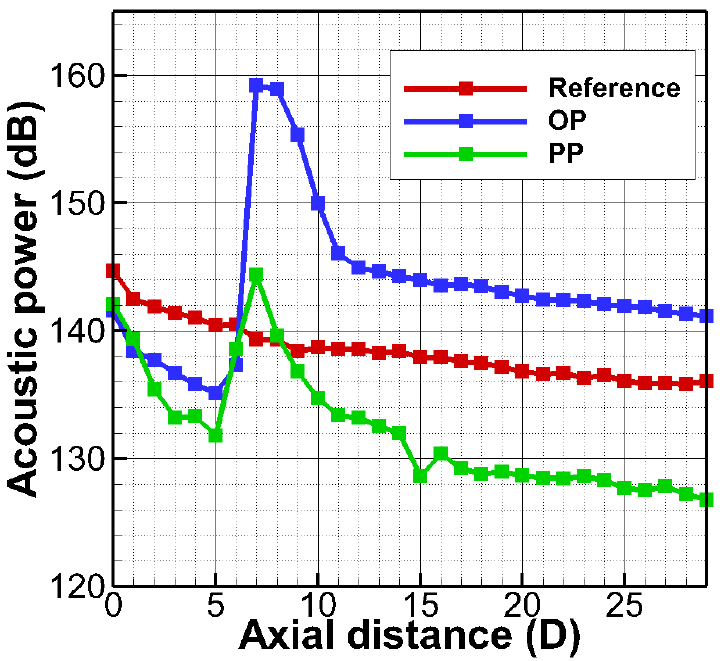
이러한 OP와 PP의 밸브 소음에 대한 영향을 정량적으로 확인하기 위하여 밸브 후류 방향을 따라 계산한 음향파워를 Fig. 12에 나타내었다. 밸브출구인 0D 위치에서는 밸브 후류에 설치한 다공성 판에 의한 저항으로 인해 밸브 입출구 압력차가 감소하므로 OP와 PP 경우 모두 섭동량이 다공성 판을 설치하지 않은 기존 밸브보다 2.5 dB ~ 4 dB정도 감소하였다. OP의 경우 자체에서 발생한 난류섭동의 영향으로 배관 끝단에서 기존 시스템보다 4.6 dB 증가하였지만, PP의 경우 자체 소음을 최대한 억제하고 밸브 소음을 저감하여 배관 끝단에서 9.5 dB 감소하였다.

Fig. 12

(Color available online) Comparison of acoustic power predicted along with downstream direction between original, OP- and PP-installed systems.

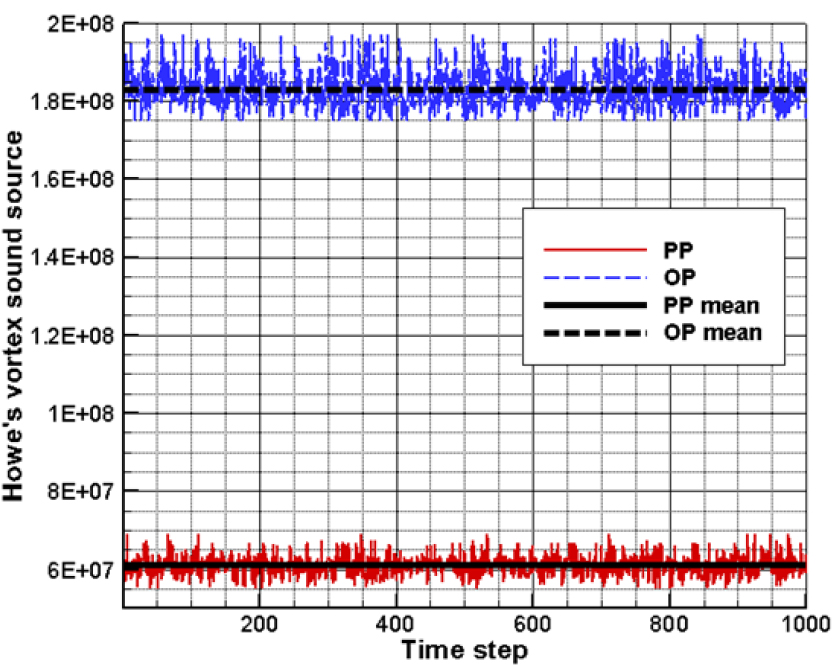
PP의 소음저감 메커니즘을 정량적으로 분석하기 위하여 다음식과 같이 와류소음원을 점음원으로 가정하고 소음원의 크기 S를 정의하였다.

Fig. 12의 결과를 참고하여 6D에서 11D 사이의 배관내 유동장을 대상으로 Eq. (13)을 사용하여 계산한 결과를 Fig. 13에 나타내었다. 그림에서 알 수 있는 바와 같이 PP 하류 유동소음원의 섭동크기가 OP와 비교하여 작다는 것을 알 수 있다.

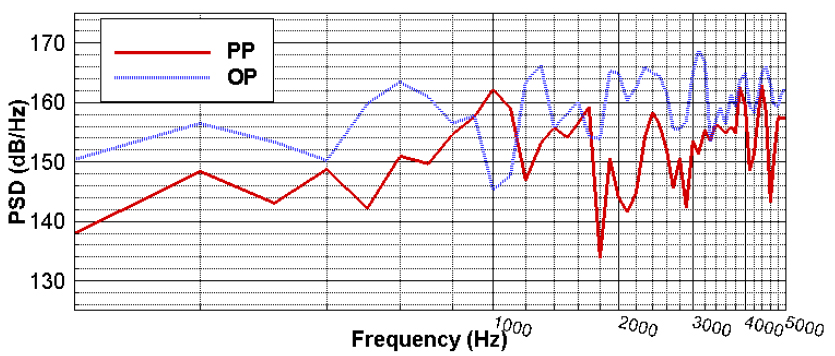
보다 정량적인 비교를 위하여 Fig. 14는 Fig. 13에서 계산한 와류소음원에 대한 스펙트럼 밀도를 나타내었다. 거의 모든 주파수 대역에서 PP를 설치한 배관에서 소음원 레벨이 작다는 것을 알 수 있다. Fig. 14의 결과를 기초로 계산한 OP와 PP의 Overall 값은 각각 179 dB와 173 dB로서 PP의 경우 OP와 비교하여 6 dB 작다는 것을 확인할 수 있다.

Fig. 13

(Color available online) Time-variation of vortex sound source integrated over pipe flow between 6D and 11D dowstream of OP and PP.

Fig. 14

(Color available online) Comparison of power spectral density of vortex sound sources between downstream flow of PP and OP.

VI. 결 론

본 논문에서는 고압가스 배관의 밸브 유동 소음을 평가할 수 있는 수치적 방법론을 제시하고 이를 이용하여 다공성 판이 밸브 유동 소음 저감에 미치는 영향을 정량적으로 분석하였다. 먼저, 고정확도의 비정상 압축성 LES 기법을 이용하여 고압가스 배관의 밸브 유동과 이로 인한 유동소음을 예측하였으며, 예측한 벽면 압력 스펙트럼을 측정값과 비교하여 해석 결과의 유효성을 검증하였다. 다음으로 배관 내에서 평균 유동장과 중첩되어 전파하는 음향장의 음향파워를 계산하였으며, 다공성 판에 의한 밸브 유동 소음 저감 효과를 확인하였다. PP에 의한 음향 파워 예측 결과를 다공성 판이 설치되지 않은 기존 배관 밸브 결과와 비교하여 9.5 dB 감소함을 확인하였으며, 와류소음원을 이용하여 PP의 후류에서 발생하는 유동소음원이 OP보다 6 dB 작다는 것을 확인하였다. 결국 OP와 PP 모두 밸브 후류에서 발생한 음향파를 판을 지나면서 발생하는 와류파로 전환하여 소음을 저감시키지만 OP의 경우 다시 이러한 와류파에 의하여 발생하는 음향파가 저감량보다 큰 반면 PP의 경우는 저감량이 발생량보다 커서 전체적으로 소음을 저감하는 것으로 판단된다.

이러한 결과를 바탕으로 본 연구에서 제시한 수치방법론은 고압가스 배관의 밸브 유동 소음을 설계단계에서부터 평가할 수 있을 뿐만 아니라 기존 시스템에서 발생하는 밸브 유동 소음을 효율적으로 저감할 수 있는 저소음 설계에도 활용할 수 있을 것으로 기대한다. 추후 좀 더 다양한 형상의 다공평판에 대해서 비교분석하고 관련 샘플을 제작하여 실험 검증할 예정이다.