Measurement and simulation of high-frequency bistatic sea surface scattering channel in shallow water of Geoje bay

Kang-Hoon Choi; Yongbin Kim; Sea-Moon Kim; Jee Woong Choi

doi:10.7776/ASK.2021.40.1.001

Preview

Research Article

The Journal of the Acoustical Society of Korea. 31 January 2021. 1-9
https://doi.org/10.7776/ASK.2021.40.1.001

Measurement and simulation of high-frequency bistatic sea surface scattering channel in shallow water of Geoje bay

거제 내만해역에서의 고주파 양상태 해수면 음파산란 채널 측정 및 모의

Kang-Hoon Choi¹

Yongbin Kim¹

Sea-Moon Kim²

Jee Woong Choi³^*

최 강훈¹

김 용빈¹

김 시문²

최 지웅³^*

¹한양대학교 해양융합과학과

²선박해양플랜트연구소

³한양대학교 ERICA 해양융합공학과

^{*Corresponding Author}

ABSTRACT

High-frequency bistatic sea surface scattering channels according to sea state were measured at an experimental site of Geoje bay in April 2020, and compared with predictions based on scattering theory. A linear frequency-modulated signal with a center frequency of 128 kHz and a bandwidth of 32 kHz was used for the acoustic measurements. Sea surface wavenumber spectrum was calculated from surface roughness data measured by a wave buoy, and bistatic scattering cross-section of Small Slope Approximation (SSA) based on the wavenumber spectrum was estimated. In addition, scattering from near-surface bubbles using wind speed measured during experiments was considered. Surface scattering channel intensity impulse responses were simulated using the scattering cross-section and the simulation results were compared and analyzed with the field data.

Keywords

High-frequency bistatic sea surface scattering

Sea surface roughness

Sea surface wavenumber spectrum

Sea surface bubble scattering

해수면 상태에 따른 고주파 양상태 해수면 음파산란 채널 측정 실험은 2020년 4월 거제 내만해역에서 수행되었으며 산란이론을 기반으로 한 모의결과와 비교하였다. 신호는 중심주파수 128 kHz, 대역폭 32 kHz의 선형 주파수 변조 신호를 이용하였다. 파고부이를 통해 측정된 해수면 거칠기로부터 해수면 파수 스펙트럼을 계산하였고 산란이론인 Small Slope Approximation(SSA)에 적용하여 해수면 거칠기에 의한 산란강도를 추정하였다. 또한 실험 당시 풍속을 이용하여 해수면 부근 공기방울층 음파산란을 고려하여 산란강도를 계산하였다. 모의된 산란강도를 이용하여 해수면 산란 채널 세기 임펄스 응답을 모의하였고, 해수면 파수 스펙트럼과 공기방울층 산란에 따른 모의결과를 측정치와 비교, 분석하였다.

키워드

고주파 양상태 해수면 음파산란

해수면 거칠기

해수면 파수 스펙트럼

공기방울층 산란

MAIN

I. 서 론
II. 이 론
2.1 양상태 해수면 음파 산란단면적
2.2 양상태 해수면 음파산란 신호 모의
III. 해상실험 및 환경
IV. 모의 결과와 비교
V. 요약 및 결론

I. 서 론

천해 해양환경에서 음파는 해수면, 해저면과 같은 해양경계면에서 반사 및 산란되면서 전파된다. 특히 시공간적인 변동성을 갖는 해수면의 경우 해수면 거칠기와 해수면 하부에 존재하는 공기방울층에 의해 전방향으로 음파가 산란되며 고주파일수록 그 영향이 크게 나타난다. 이러한 해수면에 의한 음향채널은 직접경로, 해저면 반사경로와 더불어 다중경로의 주된 요소로서 소나 시스템을 운용하는데 제한 요소로 작용한다. 해저 자원개발 및 해양환경의 실시간 관측 등에 대한 필요성이 증가하면서 수중음향통신 연구가 활발히 수행되고 있으며 이에 따라 통신 주파수 대역인 고주파수의 해수면 음파산란 채널 특성을 파악하는 것이 중요해지고 있다.

고주파수 대역에서 해수면 음파산란 특성을 파악하기 위해 국내외에서 다양한 연구가 수행되어 왔다.^[1,2,3,4] Choi et al.^[1]은 천해환경에서 주파수 126 kHz의 전방산란강도를 수평입사각에 따라 측정하여 Kirchhoff Approximation(KA) 및 Small Slope Approximation(SSA)로 모의한 산란강도와 비교하였고, Dahl^[2,3]은 20 kHz ~ 50 kHz 주파수 대역 내에서 해수면 음파산란 신호를 모의하였으며 거칠기에 따른 산란신호의 시간 확산 및 각도 확산 특성을 연구하였다. Zapevalov^[4]은 해수면 파고형태가 등방성을 갖지 않을 때의 입사각에 따른 해수면 음파산란 특성을 분석하였다. 본 논문에서는 외해와 다른 기작을 갖는 내만해역에서의 고주파 양상태 해수면 음파산란 특성 연구를 수행하였다. 128 kHz를 중심주파수로 갖는 신호를 이용하여 음파산란 측정 해상실험을 수행하였으며, 해수면 거칠기 및 공기방울층 영향을 반영한 모델과 비교, 분석하였다. 분석 결과는 외해 환경 기준으로 개발된 해수면 스펙트럼 확장방법과 공기방울층 산란모델을 적용하였기 때문에 모의결과가 실측값과 차이를 보였다.

본 논문의 구성은 아래와 같다. II장에서는 양상태 해수면 음파 산란이론 및 이를 이용한 해수면 산란신호 모의과정에 대해 설명한다. III장에서는 해수면 음파산란 해상 실험결과 및 실험환경에 따른 해수면 산란채널 추정 결과를 제시한다. IV장에서는 측정된 해수면 거칠기 스펙트럼과 해수면 부근 공기방울층의 산란을 고려한 해수면 산란신호 모의 결과와 실측값을 비교 분석하며 V장에서는 요약 및 결론을 맺는다.

II. 이 론

2.1 양상태 해수면 음파 산란단면적

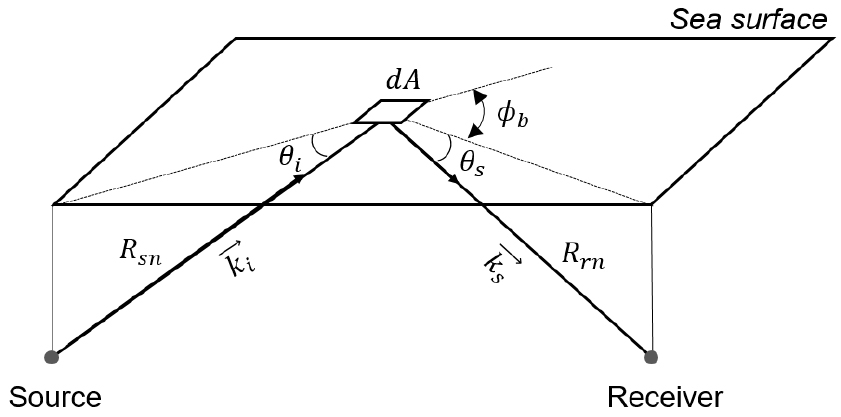
양상태 해수면 음파산란은 해수면의 거칠기와 해수면 부근의 공기방울층에 의해 영향을 받는다. 해수면 양상태 산란강도는 아래 식으로 정의할 수 있다.^[5]

(1)

S s = 10 \log σ_{s} (θ_{i}, θ_{s}, ϕ_{b}),

여기서 $σ_{s}$ 는 양상태 해수면 산란단면적이고, $θ_{i}$ , $θ_{s}$ 와 $ϕ_{b}$ 는 각각 입사각, 산란각 그리고 양상태방위각이다(Fig. 1). 양상태 해수면 산란단면적은 다음 식과 같이 정의할 수 있으며,^[6]

https://static.apub.kr/journalsite/sites/ask/2021-040-01/N0660400101/images/ASK_40_01_01_F1.jpg

Fig. 1

Definition of bistatic angle for sea surface scattering ( $θ_{i}$ : incident grazing angle, $θ_{s}$ : scattered grazing angle, $ϕ_{b}$ : bistatic angle).

(2)

σ_{s} = σ_{r} α_{b} + σ_{b},

여기서 $σ_{r}$ 과 $σ_{b}$ 는 각각 해수면 거칠기와 해수면 부근 공기방울에 의한 산란단면적이고 $α_{b}$ 는 음파가 공기방울층을 통과할 때 발생하는 에너지 감쇠계수이다.

본 논문에서는 해수면 거칠기에 의한 음파산란은 SSA를 이용해 모의하였고, SSA에 의한 산란단면적( $σ_{S S A}$ )은 반사각 부근의 산란 예측에 우수한 성능을 보이는 KA 산란단면적( $σ_{K A}$ )과 아래와 같은 관계를 갖는다.^[2,7]

(3)

σ_{S S A} = σ_{K A} / g^{2},

여기서 $g$ 는 반사각과 먼 산란각 범위에서의 산란단면적 값을 보정해주는 파라미터로 반사각에 가까울수록 $σ_{S S A}$ 은 $σ_{K A}$ 으로 수렴한다.^[7] KA에 의한 산란단면적인 $σ_{K A}$ 는 아래 식으로 표현할 수 있다.^[8,9]

(4)

σ_{K A} = k^{2} \frac{F^{2}}{2 π} \int_{0}^{\infty} ρ J_{0} (2 κ ρ) e^{- χ^{2 [1 - C (ρ)]}} d ρ,

여기서 $k$ 는 파수이고 $χ$ 는 해수면 거칠기와 파수와의 관계를 나타내는 레일리(Rayleigh) 파라미터[ $χ = k H (\sin θ_{i} + \sin θ_{s})$ , $H$ 는 rms 해수면 파고임]로 $χ$ 가 1보다 작으면 반사가 우세한 환경, 1보다 크면 산란이 우세한 환경이다. $F$ 는 $(α^{2} + β^{2} + γ^{2}) / γ$ 로 표현되고, $α$ , $β$ , $γ$ 는 해수면으로 입사하는 음파의 파수벡터 $\vec{k_{i}}$ 와 해수면으로부터 산란되어 나오는 파수벡터 $\vec{k_{s}}$ 의 차 벡터인 $(\vec{k_{i}} - \vec{k_{s}}) / k$ 의 ( $x, y, z$ ) 성분으로, 수평입사각, 산란각 및 방위각의 함수이다.^[2] 또한 $κ$ 는 $k \sqrt{α^{2} + β^{2}}$ 로 표현된다. $C (ρ)$ 는 해수면 거칠기의 공간 변동성이 반영된 등방성 자기상관함수(isotropic autocorrelation function)로 지향 평균 파수 스펙트럼( $W (K)$ , directionally averaged wavenumber spectrum)을 통해 계산할 수 있으며,^[2] 본 논문에서는 파고부이를 통해 측정된 해수면 거칠기 주파수 스펙트럼을 이용하여 계산하였다. 또한 음파산란에 적용되는 해수면 파수 스펙트럼의 파수 범위인 브래그 파수(Bragg wavenumber)는 Eq. (5)와 같이 계산할 수 있다.

(5)

\begin{matrix} K_{b r a g g} = \sqrt{K_{x}^{2} + K_{y}^{2}}, \\ where K_{x} = k (\cos θ_{s} \cos ϕ_{b} - \cos θ_{i}) \\ K_{y} = k (\cos θ_{s} \sin ϕ_{b} - \cos θ_{i}) . \end{matrix}

해수면 음파산란은 주파수가 높아질수록 공기방울층에 의한 음파산란 영향 또한 증가한다. Eq. (2)의 공기방울에 의한 감쇠( $α_{b}$ )와 산란단면적( $σ_{b}$ )은 해수면 부근 공기방울의 밀도 및 개수 등에 대한 식으로 표현할 수 있고, 일반적으로 공기방울층에 의한 음파특성은 취송제한 환경에서 풍속을 변수로 갖는 경험식을 사용하여 예측할 수 있다.^[2,10] 하지만 기존의 공기방울 특성에 대한 경험식은 외해를 기준으로 하기 때문에 선박 통행량이 많은 내만에서의 공기방울 특성을 해석하는 데에는 한계가 있을 수 있다.

2.2 양상태 해수면 음파산란 신호 모의

양상태 해수면 음파산란 신호를 모의하기 위해 해수면 경로의 채널 세기 임펄스 응답을 모의하였고, 채널 세기 임펄스 응답은 다음 식과 같이 해수면 반사 신호의 음의 세기 $I_{c ο h} (t)$ 와 산란 신호의 음의 세기 $I_{incoh} (t)$ 의 합으로 표현할 수 있다.^[11]

(6)

I (t) = I_{c ο h} (t) \exp (- χ^{2}) + I_{incoh} (t) .

Eq. (6)에서 우변의 첫 번째 항은 코히어런트 부분으로 반사 영역, 두 번째 항은 인코히어런트 부분으로 산란 영역을 의미하고, 레일리 파라미터 $χ$ 가 1보다 작을 경우에는 반사 영역이 우세하나 1보다 굉장히 큰 경우에는 산란 영역이 우세하게 된다. $I_{incoh} (t)$ 은 해수면을 여러 격자로 나눈 후 아래 식을 이용하여 계산할 수 있다.^[3,11]

(7)

I_{i n c o h_{n}} = \frac{I_{0} σ_{n} 10^{- α_{w} (R_{s n} + R_{r n}) / 10}}{(R_{s n} R_{r n})^{2}} d A,

여기서 $I_{0}$ 는 음원으로부터 1 m 떨어진 지점에서의 음의 세기, $d A$ 는 해수면 격자들의 산란면적, $σ_{n}$ 는 n 번째 산란면적에서의 단위면적당 해수면 산란단면적, $α_{w}$ 는 수층의 감쇠계수(attenuation coefficient, dB/m), $R_{s n}$ 은 음원으로부터 산란면적까지의 거리, $R_{s n}$ 은 수신기로부터 산란면적까지의 거리이다. 본 논문에서는 해수면 산란면적 $d A$ 를 0.0625 m²로 설정하여 각 산란면적에서의 $θ_{i}, θ_{s}, ϕ_{b}, R_{s n}, R_{r n}$ 값을 계산하였고, 산란면적에 따른 해수면 산란단면적, 전달손실 및 도달시간을 계산한 후 시간에 따른 해수면 음파산란 채널 세기 임펄스 응답(Channel Intensity Impulse Response, CIIR)을 모의하여 해수면 산란신호 모의에 이용하였다(자세한 모의과정은 Reference [11] 참조).

III. 해상실험 및 환경

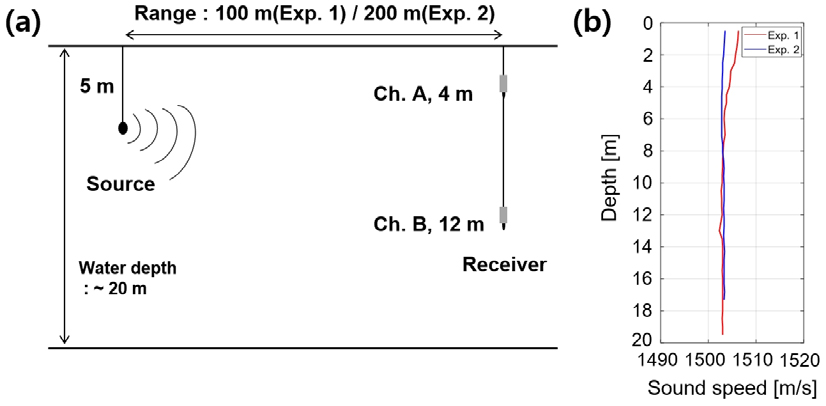
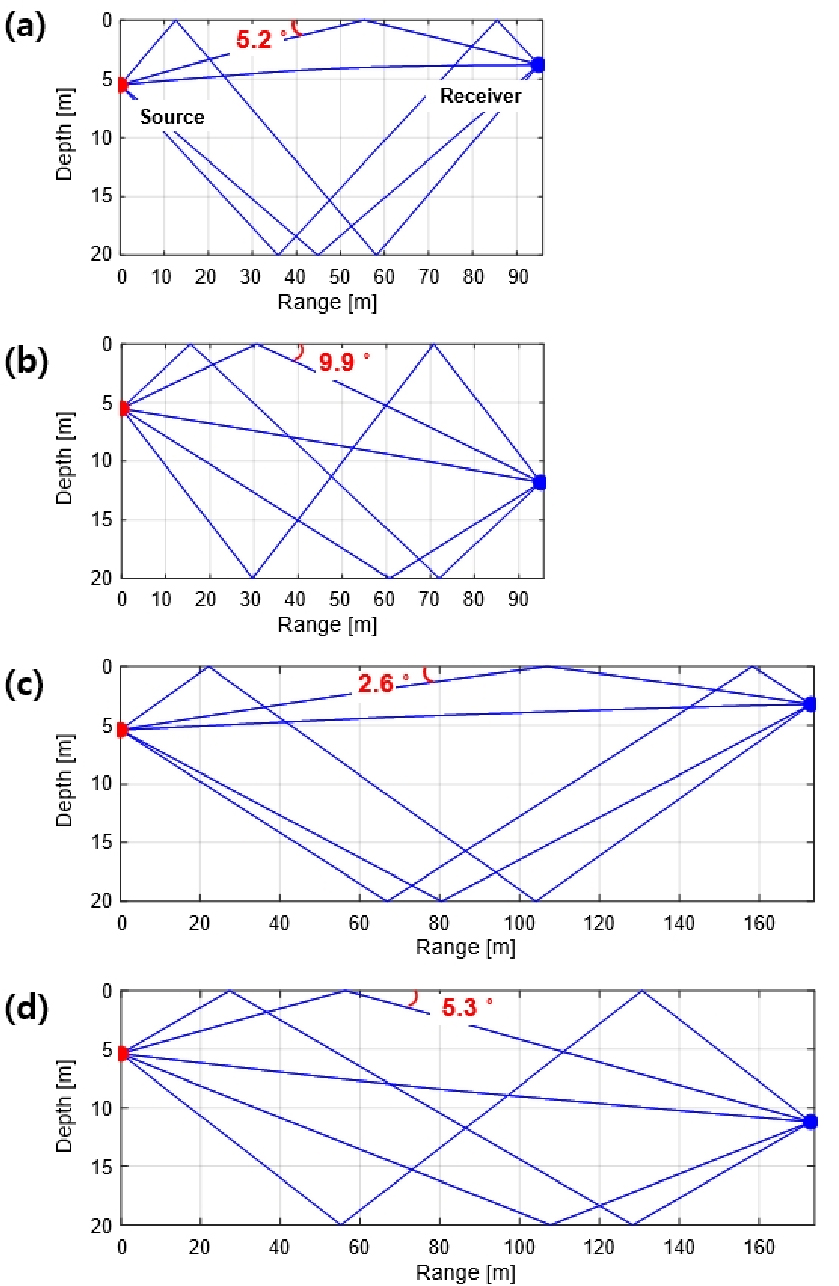
고주파 양상태 해수면 음파산란 신호 측정 실험은 2020년 4월 29일부터 2일 간 거제 내만 해역(35° 2‘ N, 128° 35.8’ E)에서 선박해양플랜트연구소 주관으로 수행되었다(Fig. 2). 실험 해역의 수심은 약 20 m로 평탄하였고, 양상태 시스템을 구성하기 위해 2대의 조사선에 음원과 수신기를 분리하여 설치하였다[Fig. 3(a)]. 음원(TC-4033, Reson)은 수심 5 m에 위치하였고, 수신기(TC-4014, Reson)는 총 2개로 수심 4 m와 12 m에 수직 배열하여 위치하였으며 실험당시 정확한 수심변화를 측정하기 위해 음원과 수신기 상단에 심도기록계(HOBO water level logger, Onset)를 설치하였다. 또한 음원과 수신기 간 수평거리는 29일(Exp. 1)에 100 m, 30일(Exp. 2)에 200 m로 설정하였으나 조류로 인해 설정한 거리와 차이가 발생하였기 때문에 이를 보상하기 위해 각 조사선의 GPS 정보를 이용하여 음향실험 동안의 음원과 수신기간 수평거리를 계산하였다. Fig. 3(b)는 CTD(SVP-15, Reson)를 이용하여 측정한 수온, 염분 및 수심으로부터 계산된 수직 음속구조로 수심에 따른 음속 변화가 약 3 m/s 이내였다.

https://static.apub.kr/journalsite/sites/ask/2021-040-01/N0660400101/images/ASK_40_01_01_F2.jpg

Fig. 2

(Color available online) Location of the experimental site.

https://static.apub.kr/journalsite/sites/ask/2021-040-01/N0660400101/images/ASK_40_01_01_F3.jpg

Fig. 3

(Color available online) (a) Experimental layout of acoustic measurements and (b) the sound speed profiles.

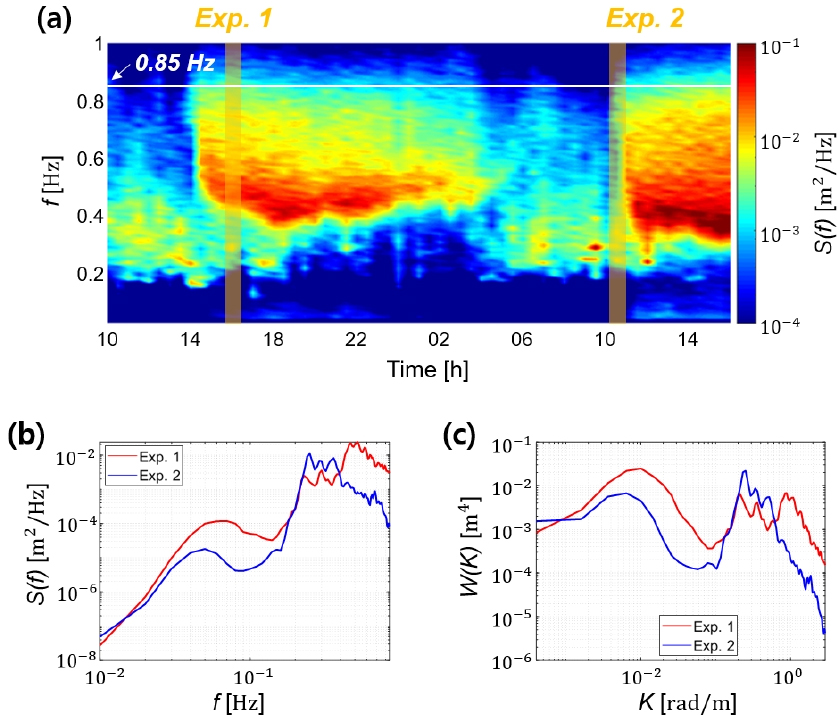
해수면 상태를 파악하기 위해 수신 조사선으로부터 약 100 m 떨어진 거리에 파고 부이(DWR4/ACM Bouy, DATAWELL)를 설치하여 2.56 Hz의 샘플링 주파수로 해수면 파고를 측정하였다. 측정된 해수면 파고 데이터는 고속 푸리에 변환을 통해 해수면 주파수 스펙트럼[ $S (f)$ ]을 구하고, 해수면 공간 주파수 $ω$ 와 파수 $K$ 의 관계식인 dispersion relationship( $ω^{2} = g K$ , 여기서 $g$ 는 중력가속도)을 통해 해수면 파수 스펙트럼[ $W (K)$ ]을 계산하였다.^[12] Fig. 4(a)는 2일 간의 시간에 따른 해수면 주파수 스펙트럼으로 약 0.85 Hz 부근에서부터 주파수가 높아짐에 따라 스펙트럼 에너지가 현저히 작아짐을 확인하였고 부이응답의 롤오프(Roll-off) 구간으로 판단되어 해수면 파수 스펙트럼 계산 시 0.85 Hz이하의 주파수 스펙트럼만을 이용하였다. Fig. 4(b)와 (c)는 각 실험 환경(Exp. 1 and 2)의 해수면 주파수 스펙트럼과 파수 스펙트럼 계산 결과이고 Exp. 1의 환경이 Exp. 2의 환경보다 약 0.2 Hz ~　0.4 Hz의 주파수 범위를 제외한 대부분의 주파수에서 스펙트럼 에너지가 높게 나타났다. 이렇게 계산한 해수면 파수 스펙트럼은 해수면 산란채널과 수신신호 모의에 이용되었다.

https://static.apub.kr/journalsite/sites/ask/2021-040-01/N0660400101/images/ASK_40_01_01_F4.jpg

Fig. 4

(Color available online) (a) Sea surface frequency spectrum estimated by surface roughness data measured during experiments, (b) frequency spectrum and (c) wavenumber spectrum for Exp. 1 and 2.

Table 1은 실험 케이스별 실험 환경 및 레일리 파라미터를 보여준다. 음선기반 음향채널 모델에 측정 음속구조를 적용하여 계산된 고유음선(eigenrays, Fig. 5)으로 해수면 반사각을 추정하여 레일리 파라미터를 계산하였다. 또한 실험당시 측정된 해수면 파고를 이용하여 rms 해수면 파고를 계산하였다. Exp. 1과 2 모두 World Meteorological Organization(WMO) 기준으로 해상상태(sea state) 1에 해당하여 잔잔한 해수면 상태를 보이나 레일리 파라미터를 통해 Exp. 2보다 Exp. 1의 환경에서 해수면에 의한 음파산란이 더 우세하게 발생할 것으로 예상할 수 있다.

Table 1.

Scattering geometry, conditions and Rayleigh parameters for Exp. 1 and 2.

Exp #	Ch #	Source depth (m)	Receiver depth (m)	Range (m)	Specular angle (°)	Rayleigh parameter χ	Wind speed (m/s)	rms wave height (cm)
1	A	5.5	3.8	95	5.2	6.8	4.8	7.2
1	B	5.5	11.8	95	9.9	12.9	4.8	7.2
2	A	5.4	3.2	173	2.6	1.9	< 1	3.7
2	B	5.4	11.2	173	5.3	4.0	< 1	3.7

https://static.apub.kr/journalsite/sites/ask/2021-040-01/N0660400101/images/ASK_40_01_01_F5.jpg

Fig. 5

(Color available online) Eigenrays based on the measured sound speed profiles using ray-based channel model, and specular grazing angles for single surface bounce (a) Ch. A and (b) Ch. B in Exp. 1, (c) Ch. A and (d) Ch. B in Exp. 2.

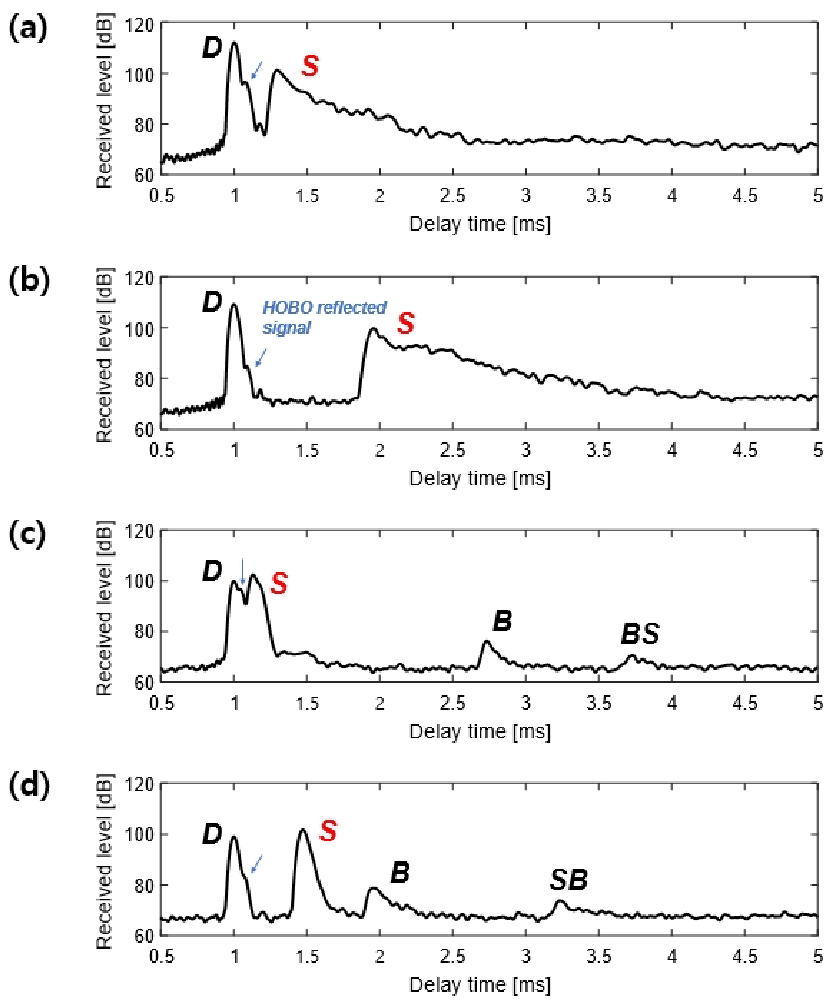
해수면 산란채널 측정을 위한 송신신호는 신호 길이 5 ms, 중심주파수 128 kHz(32 kHz 대역폭)의 선형 주파수 변조 신호이며, 각 실험환경에서 0.4 s 간격으로 총 50핑을 반복 송·수신하였다. 수신된 50핑의 신호는 각각 정합필터링을 수행하였고 에너지 영역에서 앙상블 평균하여 평균 CIIR을 추정하였다. Fig. 6은 실험 환경별 평균 CIIR로 같은 거리에서 수심이 깊어질수록 직접 경로(D)와 해수면 경로(S)의 도달 시간 차이가 커졌고, Exp. 1[Fig. 6(a), (b)]의 경우가 Exp. 2[Fig. 6(c), (d)]보다 해수면 음파산란이 더 발생함을 확인할 수 있다.

https://static.apub.kr/journalsite/sites/ask/2021-040-01/N0660400101/images/ASK_40_01_01_F6.jpg

Fig. 6

(Color available online) Ensemble-averaged intensity of the matched filter envelop over 50 pulses (averaging performed in intensity domain) (a) Ch. A and (b) Ch. B in Exp. 1, (c) Ch. A and (d) Ch. B in Exp. 2.

IV. 모의 결과와 비교

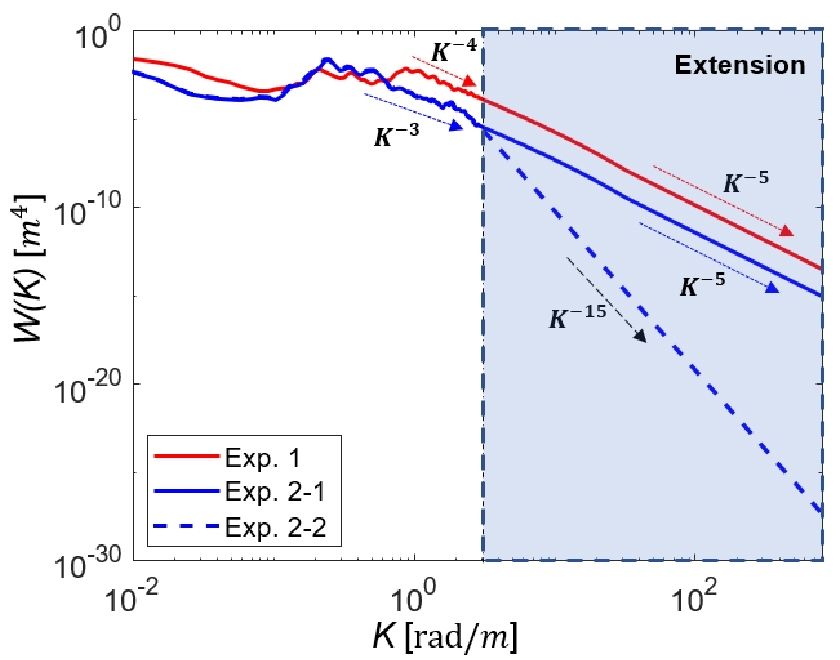
실험이 진행되는 동안 파고 부이를 통해 해수면 파고를 측정하여 해수면 산란신호 모의에 필요한 해수면 파수 스펙트럼을 추정하였다. 해수면 파수 스펙트럼을 이용하여 해수면 산란강도를 추정하기 위해 고려해야 할 부분은 중심주파수에 해당하는 브래그 파수 영역범위이다. 브래그 파수는 특정 주파수의 음파가 경계면을 맞고 산란될 때 우세하게 작용하는 경계면의 공간적 파수를 의미한다. 본 실험 환경에서의 브래그 파수를 계산한 결과 약 800 rad/m까지의 범위를 보였으나 파고 부이를 통해 추정된 해수면 파수 스펙트럼의 파수 범위는 약 2.9 rad/m까지의 값만을 갖기 때문에 스펙트럼의 확장이 필요하였다. 따라서 취송제한 환경 하에 적용 가능한 Banner^[13]의 확장방법을 이용하여 파수 스펙트럼을 확장하였다. 먼저 해수면 주파수 스펙트럼은 확장방법에 따라 멱법칙(power law, $S (ω) ~ ω^{- n}$ )의 형태로 해수면 공간 주파수를 2.8 Hz까지 확장하고, 확장 경향은 멱법칙 지수 $n$ 의 초기 값과 종료 값에 의해 결정한다. 초기 $n$ 값은 측정 주파수 스펙트럼의 기울기로 계산하였고, 종료 $n$ 값은 피크 주파수(peak frequency)의 0.5배부터 1.5배까지의 스펙트럼 적분 값( $A$ )과 피크 파수(peak wavenumber, $K_{p}$ )의 곱으로 설정하였다. 또한 $n$ 의 초기 값에서 종료 값으로 주파수에 따라 선형적으로 변화하는 $n (f)$ 을 산정하여 2.8 Hz까지 주파수 스펙트럼을 확장하였고, 그 이후의 파수 800 rad/m에 해당하는 공간 주파수 14 Hz까지의 주파수 스펙트럼은 종료 $n$ 값을 이용하여 확장하였다. 다음 식은 실험 환경별로 0.85 Hz부터 2.8 Hz까지의 $n (f)$ 로 Exp. 1의 경우는 4에서 5로, Exp. 2의 경우 3에서 5로 변화하였다.^[2,13]

(8)

n (f) = \begin{array}{l} 0.5128 f + 3.5642 for Exp . 1 \\ 1.0256 f + 2.1283 for Exp . 2 . \end{array}

이렇게 확장된 주파수 스펙트럼으로부터 Fig. 7과 같이 파수 스펙트럼을 계산하였다. Exp. 2의 경우 파수 스펙트럼에서 끝 파수 부분의 기울기가 전반적인 기울기 경향과 달랐기 때문에, Banner의 확장방법(Exp. 2-1)과 더불어 끝 파수 부분의 기울기인 $ω^{- 15}$ 로 파수 스펙트럼을 확장(Exp. 2-2)하여 2가지 파수 스펙트럼에 의한 해수면 산란을 모의하였다.

https://static.apub.kr/journalsite/sites/ask/2021-040-01/N0660400101/images/ASK_40_01_01_F7.jpg

Fig. 7

(Color available online) Extended surface wavenumber spectrum (Exp. 1 : using Banner method for Exp. 1, Exp. 2-1 : using Banner method for Exp. 2, Exp. 2-2 : using the end slope of spectrum for Exp. 2).

Figs. 8과 9는 실험환경 별 해수면 음파산란 모의결과이다. 해수면 음파산란 신호[Figs. 8과 9, (a)와 (b)]는 각 실험 환경에서 모의된 해수면 산란 CIIR와 LFM 음원신호 정합필터링 결과를 음의 세기 단위에서 컨볼루션하여 모의하였고,^[12] 해수면 산란강도[Figs. 8과 9, (c)와 (d)]는 Exp. 1의 경우 수신기 Ch. A, Exp. 2의 경우 Ch. B의 해수면 거칠기와 공기방울층 영향을 고려하여 각각 2가지의 방법에 대해 모의하였다.

https://static.apub.kr/journalsite/sites/ask/2021-040-01/N0660400101/images/ASK_40_01_01_F8.jpg

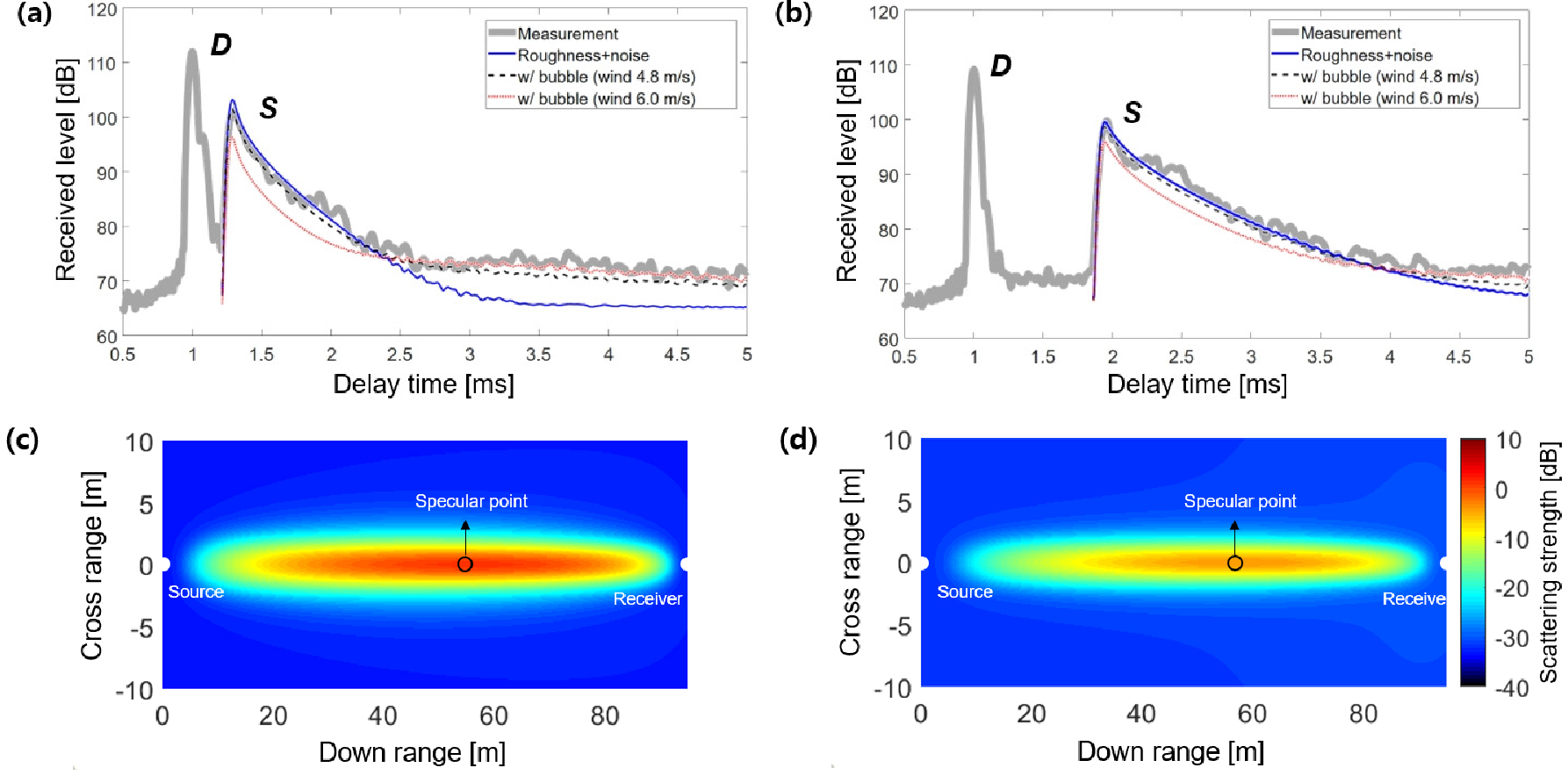
Fig. 8

(Color available online) Ensemble-averaged intensity of LFM matched filter and simulated sea surface scattering signals for (a) Ch. A and (b) Ch. B of Exp. 1, and the sea surface bistatic scattering strength considering wavenumber spectrum and near-surface bubbles for Ch. A of Exp. 1 (c) by wind speed of 4.8 m/s, (d) by wind speed of 6.0 m/s.

https://static.apub.kr/journalsite/sites/ask/2021-040-01/N0660400101/images/ASK_40_01_01_F9.jpg

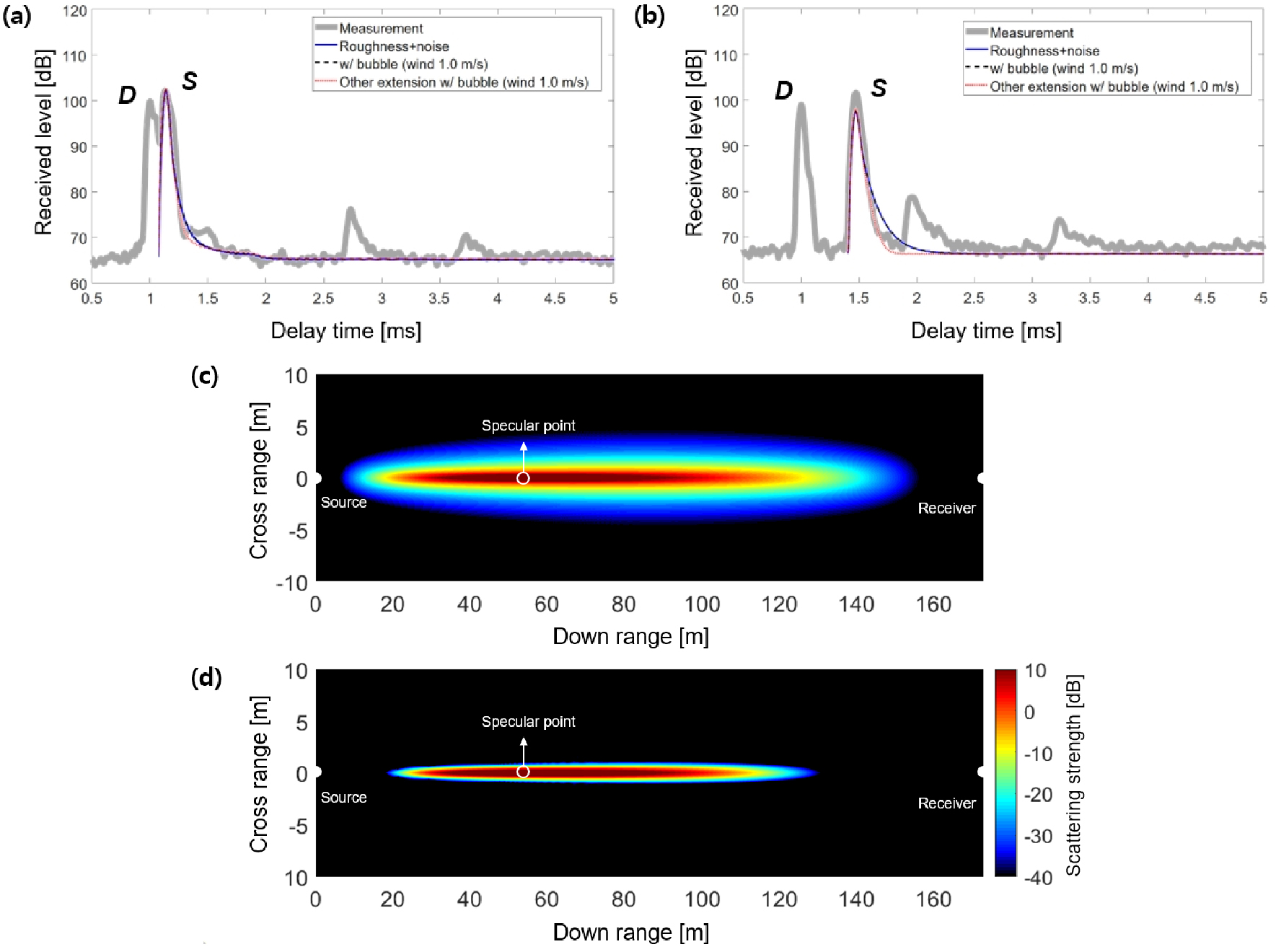
Fig. 9

(Color available online) Ensemble-averaged intensity of LFM matched filter over 50 pulses and the simulated sea surface scattering signals for (a) Ch. A and (b) Ch. B of Exp. 2, and the sea surface bistatic scattering strength considering wavenumber spectrum and near-surface bubbles for Ch. B of Exp. 2 (c) by Banner extension method, (d) by end slope of spectrum (Exp. 2-2 of Fig. 7).

Exp. 1의 경우에서는 해수면 거칠기 산란만을 고려하여 모의하였을 경우 반사각도에 해당하는 첫 번째 해수면 임펄스 응답 도달시간을 기준으로 수신기 Ch. A의 경우 약 2.4 ms[Fig. 8(a)], Ch. B의 경우 약 4 ms [Fig. 8(b)]까지만 측정된 수신준위와 거의 일치하였고 그 이후는 실측값에 비해 낮은 준위를 보였다. 이러한 해수면 산란신호 꼬리(tail) 부분에서 실측값과 모델값의 차이는 해수면 하부 공기방울층에 의한 영향일 수 있다. 측정 당시의 풍속인 4.8 m/s 기준으로 공기방울층 산란 영향을 포함하여 모의한 경우에는 산란신호 꼬리 부분에서 2 dB ~ 3 dB 낮게 모의되기는 하였으나 오차범위 내에서 비교적 실측치와 유사하였다. 풍속에 의한 CIIR 차이를 확인하기 위하여 측정 당시 풍속보다 높은 6.0 m/s을 적용하여 해수면 산란신호를 모의하여 보았다. 결과적으로 꼬리 부분의 에너지가 실측치와 더 근접하게 모의되었으나 반사부근에서 약 5 dB 내외로 차이가 발생하였다. 수신기 Ch. A의 해수면 산란강도 모의결과를 확인했을 때 풍속 4.8 m/s 기준의 공기방울층 산란을 고려한 결과[Fig. 8(c)]보다 풍속 6.0 m/s의 공기방울층 산란을 고려한 결과[Fig. 8(d)]가 반사지점에서 멀어질수록 산란강도가 증가하나 반사부근의 산란에너지는 공기방울층에 의한 감쇠로 인해 반대로 감소하는 것을 확인할 수 있다. 본 결과는 공기방울층에서의 감쇠와 산란 효과가 외해를 기준으로 개발된 모델을 사용하였기 때문에 실험이 실시된 내만은 바람에 의한 해수면 거칠기 발달 과정이 외해와 다를 수 있고 외해에 비해 높은 선박 통행량 등의 영향에 의해 신호가 실측 신호와 다르게 모의될 수 있다. 그렇기 때문에 본 논문에서 사용된 공기방울 산란모델이 내만에서도 적합한지는 추가 연구가 필요하다.

Exp. 2 실험에서는 풍속이 1 m/s 미만이었고, 산란에 큰 영향을 미치는 고주파 성분의 해수면 거칠기 에너지가 Exp. 1보다 낮았다(Fig. 4). 이러한 영향으로 해수면 산란신호가 Exp. 1의 경우에 비해 급격히 줄어들어 전체적으로 0.5 ms 이내에서 주변소음 준위로 수렴되는 것으로 모의되었다(Fig. 9). 또한 풍속이 1 m/s 미만인 해상상태였기 때문에 해수면 공기방울층에 의한 산란 에너지는 거의 존재하지 않는 것으로 모의되었다. 측정 준위와의 비교에서는 Ch. A의 경우 비교적 잘 일치하게 모의되었으나 Ch. B의 경우 해수면 산란신호 약 0.2 ms 이후부터 모델 예측치가 측정 준위보다 조금 더 완만하게 떨어지는 경향을 보였다. 이는 해수면 파수 스펙트럼을 확장함에 있어 Exp. 1의 경우 파수 스펙트럼에서 큰 파수로의 스펙트럼 에너지 감소 경향이 유사하게 연장되었으나 Exp. 2의 경우 실측 스펙트럼에서 최대 파수 부근의 기울기에 비해 더 완만하게 확장되어 꼬리 부분의 산란에너지가 실측값보다 크게 모의된 것으로 보인다. Banner의 확장방법에 의한 Exp. 2의 확장 스펙트럼이 천해환경이었던 실험해역의 실제 해수면 스펙트럼과 상이할 수 있으므로 실측 스펙트럼의 최대 파수 부근 순간 기울기 $ω^{- 15}$ 로 확장한 값으로 해수면 산란신호를 추가 모의하였다. 모의한 결과 Banner 확장방법에 의해 추정된 스펙트럼의 모의신호보다 순간 기울기의 확장 스펙트럼으로 모의한 신호가 실측값과 유사하게 모의됨을 확인할 수 있다. 또한 Ch. B의 해수면 산란강도 모의결과를 확인했을 때 Banner 확장방법에 의한 결과[Fig. 8(c)]보다 순간 기울기로 확장한 결과[Fig. 8(d)]가 반사지점 근방 이외의 영역에서 산란강도가 급격히 떨어짐을 확인할 수 있다. 이 결과는 참고 문헌에 따른 스펙트럼 확장방법이 외해의 취송제한 환경을 가정한 모델이며 Exp. 2와 같이 바람과 해수면 거칠기의 상관성이 적은 내만의 경우에서는 고주파수 부분의 스펙트럼 특성이 다를 수 있기 때문에 그에 따른 산란신호 모의결과와 측정치의 차이가 발생할 수 있음을 의미한다. 따라서 추후 천해에서 고주파 영역의 해수면 거칠기에 대한 연구 또한 필요하다.

V. 요약 및 결론

본 논문에서는 고주파 양상태 해수면 음파산란 채널을 분석하고 모의하기 위해 약 20 m 수심의 거제 인근해역에서 128 kHz(32 kHz 대역폭)의 LFM 신호를 이용하여 음향실험을 수행하였다. 실험당시 측정된 해수면 파고를 이용하여 해수면 파수 스펙트럼을 계산하였고 산란에 큰 영향을 미치는 브래그 파수를 고려하기 위해 스펙트럼 주파수를 확장하였으며, 측정 당시 풍속 기준으로 해수면 공기방울층의 산란 영향을 포함하여 산란신호를 모의하였다. Exp. 1의 경우 전반적으로 모의된 CIIR이 측정치와 유사하게 모의되었으나 산란신호의 꼬리 부분에서 실측치보다 2 dB ~ 3 dB 낮게 모의되었다. 이는 공기방울층 산란모델이 외해가 기준인 모델이기 때문일 수 있다. Exp. 2의 경우 풍속이 1 m/s 미만인 환경으로 Exp. 1보다 고주파 성분의 해수면 거칠기 스펙트럼 에너지가 낮았기 때문에 산란신호가 짧은 시간 내 존재하는 임펄스 형태로 수신되었다. 따라서 공기방울층에 의한 산란에너지가 거의 존재하지 않았던 것으로 모의되었다. 또한 모의신호가 산란신호 꼬리 부분에서 측정치보다 다소 크게 모의되는 경향을 보였고, 이는 취송제한 환경이 기준인 외해에서의 해수면 파수 스펙트럼 확장방법을 적용하였기 때문으로 판단된다.

본 논문에서 사용한 해수면 스펙트럼 확장방법과 공기방울층 산란모델은 외해 환경을 기준으로 개발된 모델이기 때문에 내만 환경을 모사하기에 적합하지 않을 수 있다. 따라서 육지 효과와 잦은 선박통행량 등과 같은 내만에서의 기작에 의한 공기방울 밀도 및 분포 특성이 반영된 공기방울층 특성과 내만의 해상상태 기준에 따른 해수면 스펙트럼 특성 연구가 향 후 진행된다면 더욱 정확한 천해에서의 해수면 산란신호 특성 파악이 가능할 것이다.

Acknowledgements

본 연구는 한국해양과학기술진흥원 국가R&D사업“수중 광역 이동통신 시스템 기술개발(PMS4110)” 과제의 지원에 의해 수행되었습니다.

References

J. W. Choi, J. Na, and Y. N. Na, "Measurements of bistatic sea surface scattering signals" (in Korean), J. Acoust. Soc. Kr. 20, 81-86 (2001).

P. H. Dahl, "On bistatic sea surface scattering: Field measurements and modeling," J. Acoust. Soc. Am. 105, 2155-2169 (1999). 10.1121/1.426820

P. H. Dahl, "High-frequency forward scattering from the sea surface: The characteristic scales of time and angle spreading," IEEE J. Ocean. Eng. 26, 141-151 (2001). 10.1109/48.917951

A. S. Zapevalov, "Evaluation of the scattering coefficient for high-frequency sound scattered from the sea surface," Acoustical Physics. 53, 603-610 (2007). 10.1134/S1063771007050119

E. I. Thorsos, "Acoustic scattering from a ' Pierson- Moskowitz ' sea surface," J. Acoust. Soc. Am. 88, 335-349 (1990). 10.1121/1.399909

P. H. Dahl, "On the spatial coherence and angular spreading of sound forward scattered from the sea surface: Measurements and interpretive model," J. Acoust. Soc. Am. 100, 748-758 (1996). 10.1121/1.416237

A. G. Voronovich, Wave Scattering from Rough Surfaces (Springer-Verlag, New York, 2013), pp. 148-163.

P. Beckmann and A. Spizzichino, The Scattering of Electromagnetic Waves from Rough Surfaces (Pergamon, Oxford, 1963), pp. 17-33.

A. Ishimaru, Wave Propagation and Scattering in Random Media Vol. II (Academic, New York, 1978), pp. 463-492. 10.1016/B978-0-12-374702-0.50014-5

J. W. Choi, J. Na, K. J. Park, K.-S. Yoon, J.-S. Park, and Y. N. Na, "Measurements of high-frequency sea surface backscattering signals" (in Korean), J. Acoust. Soc. Kr. 21, 421-429 (2002). 10.12671/jksf.2002.15.1.21

J. W. Choi and P. H. Dahl, "Measurement and simulation of the channel intensity impulse response for a site in the East China Sea," J. Acoust. Soc. Am. 119, 2677- 2685 (2006). 10.1121/1.2189449

W. J. Plant, "The ocean wave height variance spectrum: Wavenumber peak versus frequency peak," J phys. Oceanogr. 39, 2382-2383 (2009). 10.1175/2009JPO4268.1

M. L. Banner, "Equilibrium spectra of wind waves," J. Phys. Oceanogr. 20, 966-984 (1990). 10.1175/1520-0485(1990)020<0966:ESOWW>2.0.CO;2

The Journal of the Acoustical Society of KoreaISSN:1225-4428(Print) 2287-3775(Online)한국음향학회

Preview

Measurement and simulation of high-frequency bistatic sea surface scattering channel in shallow water of Geoje bay

ABSTRACT

MAIN

(1)

Fig. 1

Definition of bistatic angle for sea surface scattering (θi : incident grazing angle, θs : scattered grazing angle, ϕb : bistatic angle).

(2)

(3)

(4)

(5)

(6)

(7)

Fig. 2

(Color available online) Location of the experimental site.

Fig. 3

(Color available online) (a) Experimental layout of acoustic measurements and (b) the sound speed profiles.

Fig. 4

(Color available online) (a) Sea surface frequency spectrum estimated by surface roughness data measured during experiments, (b) frequency spectrum and (c) wavenumber spectrum for Exp. 1 and 2.

Table 1.

Scattering geometry, conditions and Rayleigh parameters for Exp. 1 and 2.

Fig. 5

(Color available online) Eigenrays based on the measured sound speed profiles using ray-based channel model, and specular grazing angles for single surface bounce (a) Ch. A and (b) Ch. B in Exp. 1, (c) Ch. A and (d) Ch. B in Exp. 2.

Fig. 6

(Color available online) Ensemble-averaged intensity of the matched filter envelop over 50 pulses (averaging performed in intensity domain) (a) Ch. A and (b) Ch. B in Exp. 1, (c) Ch. A and (d) Ch. B in Exp. 2.

(8)

Fig. 7

(Color available online) Extended surface wavenumber spectrum (Exp. 1 : using Banner method for Exp. 1, Exp. 2-1 : using Banner method for Exp. 2, Exp. 2-2 : using the end slope of spectrum for Exp. 2).

Fig. 8

Fig. 9

Acknowledgements

References

Definition of bistatic angle for sea surface scattering ( $θ_{i}$ : incident grazing angle, $θ_{s}$ : scattered grazing angle, $ϕ_{b}$ : bistatic angle).