Application of ray-based blind deconvolution to long-range acoustic communication in deep water

Donghyeon Kim; Heejin Park; J. S. Kim; Joo Young Hahn

doi:10.7776/ASK.2022.41.2.242

Preview

Research Article

The Journal of the Acoustical Society of Korea. 31 March 2022. 242-253
https://doi.org/10.7776/ASK.2022.41.2.242

Application of ray-based blind deconvolution to long-range acoustic communication in deep water

음선 기반 블라인드 디컨볼루션의 장거리 심해 환경으로의 적용

Donghyeon Kim¹

Heejin Park²

J. S. Kim³^*

Joo Young Hahn⁴

김 동현¹

박 희진²

김 재수³^*

한 주영⁴

¹한국해양과학기술원-한국해양대학교 해양과학기술전문대학원

²한화시스템 해양연구소

³한국해양대학교 해양공학과

⁴국방과학연구소

^{*Corresponding Author}

ABSTRACT

When the source waveform is unknown, the Green’s function can be estimated by Ray-based Blind Deconvolution (RBD) based on the simple array signal processing. In previous papers, RBD was successfully demonstrated using simulation and experiments in shallow water environment. In this paper, we investigate the applicability of RBD for a long-range communication (e.g., 30 km, 60 km, and 90 km) in a deep water environment (1,000 m ~), using experimental data conducted in the east of Pohang, South Korea, in October 2018. Data results are presented to demonstrate Green’s function estimation of a communication signal (2.2 kHz ~ 2.9 kHz) using a 16-element, 42-m long vertical array. The results show that the Green’s function estimated from RBD is comparable to that of matched filter result. Additional communication performance at a maximum range of 90 km will be also presented.

Keywords

Long-range communication

Ray-based blind deconvolution

Green’s function

Deep water

송신 신호를 알지 못하는 경우에 대해 그린 함수는 간단한 배열 신호 처리 기반의 음선 기반 블라인드 디컨볼루션을 이용해 추정될 수 있다. 근거리 천해 환경에서의 음선 기반 블라인드 디컨볼루션은 선행 연구들에 의해 시뮬레이션 및 데이터를 기반으로 검증되었다. 본 논문에서는 30 km부터 90 km까지의 장거리 심해(1,000 m 이상의 깊이) 환경에서의 음선 기반 블라인드 디컨볼루션 기법의 가능성을 확인하였다. 이를 위해 2018년 포항 동방 해역에서 수행된 해상실험을 활용하였으며, 데이터 결과는 16개 수신기로 구성된 42 m 길이의 수직 선 배열 센서를 통해 수신된 통신 신호(2.2 kHz ~ 2.9 kHz) 의 그린 함수 추정을 입증하기 위해 도시하였다. 분석 결과로부터 정합 필터와 음선 기반 블라인드 디컨볼루션으로 추정한 그린 함수가 유사함을 확인하였다. 또한, 음선 기반 블라인드 디컨볼루션을 이용하여 최대 90 km 거리의 장거리 통신 신호의 성능 분석 결과를 제시하였다.

키워드

장거리 통신

음선 기반 블라인드 디컨볼루션

그린 함수

심해

MAIN

I. 서 론
II. 음선 기반 블라인드 디컨볼루션
III. BLAC18
IV. 해상실험 분석 결과
4.1 빔형성
4.2 그린 함수 추정
4.3 통신 성능 분석
V. 결 론

I. 서 론

수중 도파관을 통해 전파되는 음파는 수신기에 도달했을 때 다중경로에 의해 왜곡되고 시간 영역에서의 지연 확산이 발생한다. 이러한 도파관에서의 전파 특성을 나타내는 그린 함수는 음속구조, 송 ‧ 수신기 사이의 거리, 송 ‧ 수신기의 깊이, 그리고 수심 등에 의해 결정되며, 수중음원 탐지 또는 수중통신과 같은 분야에서 활용될 수 있다.^{[1,2,3,4,5,6,7]} 그린 함수는 채널 임펄스 응답과는 푸리에 변환 관계이며, 송신 신호가 임펄스 신호일 때의 수신 신호라고도 할 수 있다. 하지만, 실제 해상실험 데이터를 통해 그린 함수를 얻기 위해서는 정확한 임펄스 신호를 송신하거나 수중통신 분야에서의 탐침 신호와 같이 알고 있는 신호를 송신해야 한다는 조건이 필요하다. 장비의 한계로 인해 정확한 임펄스 신호의 송신은 불가능에 가까우므로, 궁극적으로는 송신 신호의 존재가 필요하다.

송신 신호의 정보가 없는 상황에서 수신 신호로부터 송신 신호와 그린 함수를 분리하는 기법을 블라인드 디컨볼루션이라고 한다. 일반적으로 블라인드 디컨볼루션 기법은 추가적인 정보나 가정이 없다면 불량조건문제이지만, 최근 Sabra et al.^[8]는 최소한의 해양환경 정보와 간단한 신호 처리를 통해 그린 함수의 파형을 추정할 수 있는 음선 기반 블라인드 디컨볼루션 기법을 제안하였다. Abadi et al.^[9]는 송신 신호의 추정 결과와 위치 추정으로의 활용 사례 등과 같이 좀 더 상세한 내용을 추가로 발표하였다. 음선 기반 블라인드 디컨볼루션 기법을 통해 추정한 그린 함수는 정확한 진폭과 시지연 정보를 추정하지 못하지만, 간단한 신호 처리인 빔형성 기법과 상호 상관을 이용하여 정확한 도달 음선 구조와 음선들 사이의 상대적인 위상 변화가 반영된 그린 함수를 추정할 수 있다는 장점이 있다. 음선 기반 블라인드 디컨볼루션 기법은 주로 임의의 신호라고 할 수 있는 선박 소음의 그린 함수를 추정하기 위해 사용되고 있으며,^{[10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]} 선박의 거리 및 깊이(또는 두 가지 모두)를 추정하기 위해 추정된 그린 함수가 활용되었다.^{[13,14,15,16,17,18,20,23,24,25]} 또한, 추정된 그린 함수를 활용하여 지음향 정보 역산 연구^[26]와 채널 변동성이 존재하는 환경에서의 수중통신 성능 분석 연구가 발표되었다.^[27] 수동형 시역전 처리 기반의 수중통신 분석 시 탐침 신호가 없어도 된다는 점은 데이터 전송률 측면에서 장점이라 할 수 있다. 하지만, 음선 기반 블라인드 디컨볼루션 기법을 이용한 모든 문헌은 근거리 천해 환경에만 국한하여 검증되어왔다.

본 논문에서는 최대 90 km 거리의 장거리 심해 환경에서 음선 기반 블라인드 디컨볼루션 기법을 검증함과 동시에 90 km까지의 통신 성능 분석 결과를 제시하였다. 분석에 활용된 통신 신호는 Binary Phase Shift Keying(BPSK)로 변조된 신호이며, 90 km 거리는 국내에서 수행된 수중통신 실험 중 최대 거리이다. 본 논문에서 활용할 예정인 동일 해상실험 데이터를 이용하여 90 km 거리에서의 Frequency Shift Keying (FSK)나 Chirp Shift Keying(CSK) 계열로 설계된 신호의 통신 분석 결과는 발표된 바가 있으나^[28] Phase Shift Keying(PSK) 계열 통신 성능 분석 결과 제시는 전무하므로, 90 km 거리에서의 PSK 변조 신호의 가능성 검증 또한 이 논문의 기여라고 할 수 있다.

본 논문의 구성은 다음과 같다. II장에서는 음선 기반 블라인드 디컨볼루션 기법의 배경 이론을 정리하고, III장에서는 본 논문에서 활용한 해상실험인 Biomimetic Long-range Acoustic Communication experiment 2018(BLAC18)과 설계한 송신 신호의 구조를 소개한다. IV장에서는 해상실험 데이터를 기반으로 장거리 심해 환경에서의 음선 기반 블라인드 디컨볼루션 결과와 통신 성능 분석 결과를 제시한다. 마지막으로 V장에서는 결론을 맺는다.

II. 음선 기반 블라인드 디컨볼루션

음선 기반 블라인드 디컨볼루션 기법은 배열 센서에 수신된 신호만을 이용하여 채널 임펄스 응답을 추정하는 기법이다. 관련 연구는 활발하게 진행되고 있으며, 본 장에서는 음선 기반 블라인드 디컨볼루션 기법의 수식들을 정리하기로 한다.^[8,9,15]

해양 도파관에서 송신 신호 $S (ω)$ 가 음원으로부터 수직 선 배열 센서의 $j$ 번째 수신기로 전파된다고 가정할 때, $j$ 번째 수신기에 수신되는 신호 $R_{j} (ω)$ 는 Eq. (1)과 같이 표현된다.

(1)

R_{j} (ω) = S (ω) G ({\vec{r}}_{j}, {\vec{r}}_{s}, ω) = S (ω) \sum_{k = 1}^{K} A_{k} e^{i ω \{τ_{j} (θ_{k}) - T (θ_{k})\}} .

(2)

τ_{j} (θ_{k}) = d (j - 1) \sin θ_{k} / c,

여기서 $G ({\vec{r}}_{j}, {\vec{r}}_{s}, ω)$ 는 음원의 위치 ${\vec{r}}_{s}$ 로부터 수신기 배열단 $j$ 번째 수신기 위치 ${\vec{r}}_{j}$ 로의 그린 함수를 의미하며, Eq. (1)의 마지막 식에서 송신 신호를 제외한 성분은 그린 함수를 음선 관점에서 표현한 식이다. $θ_{k}$ 는 $k$ 번째 음선 방향의 각도를 의미한다. $τ_{j} (θ_{k})$ 는 $k$ 번째 음선 방향에 대한 첫 번째 채널과 $j$ 번째 채널 사이의 시지연으로 Eq. (2)와 같이 센서간 간격 ( $d$ )과 음속 ( $c$ ) 등으로 구성되며, $T (θ_{k})$ 는 $k$ 번째 음선의 시지연을 나타낸다.

$R_{j} (ω)$ 로부터 그린 함수를 추정하기 위해 우선적으로 수신된 신호의 정규화 과정이 수행되어야 하며, 이는 Eq. (3)으로 표현할 수 있다.

(3)

{\tilde{R}}_{j} (ω) = \frac{R_{j} (ω)}{\sqrt{\sum_{j = 1}^{N} | R_{j} (ω) |^{2}}} = \frac{G ({\vec{r}}_{j}, {\vec{r}}_{s}, ω)}{\sqrt{\sum_{j = 1}^{N} | G ({\vec{r}}_{j}, {\vec{r}}_{s}, ω) |^{2}}} e^{i ϕ_{s} (ω)},

여기서 ${\tilde{R}}_{j} (ω)$ 는 정규화된 수신 신호를, 그리고 $ϕ_{s} (ω)$ 는 송신 신호의 위상을 나타낸다.

Eq. (3)과 같이 수신 신호를 정규화하게 된다면, 각 채널 별 송신 신호의 크기는 같다고 가정할 수 있으므로 정규화된 그린 함수와 송신 신호의 위상 성분만 남게 된다. 그린 함수 추정을 위해서는 송신 신호의 위상을 제거할 필요성이 있으며, 이를 제거하기 위해 빔형성 기반의 위상 보정 인자를 적용한다. 수신 신호를 특정 방향으로 빔형성한다면 출력은 Eq. (4)와 같다.

(4)

B (ω, θ_{k}) = \sum_{j = 1}^{N} e^{- i ω τ_{j} (θ_{k})} R_{j} (ω) \approx e^{i ϕ_{s} (ω) - i ω T (θ_{k})} = e^{i ψ (ω, θ_{k})},

여기서 $B (ω, θ_{k})$ 는 $θ_{k}$ 방향으로의 빔형성한 출력을 의미한다. 이 조향 각도는 먼저 전 방향에 대하여 빔형성한 후 일반적으로 빔형성 결과가 최대가 되는 각도로 선택된다.

음선 기반 블라인드 디컨볼루션 기법에서 빔형성 결과의 위상 성분인 $ψ (ω, θ_{k})$ 을 위상 보정 인자라고 정의한다. 음선들의 방향들의 차이가 배열의 길이와 주파수 등에 의해 계산되는 빔 분해능보다 클 경우, 특정 방향으로 빔형성했을 때 선택되지 않은 다른 각도들에 의한 신호들은 완화된다. 이에 따라 위상 보정 인자는 송신 신호의 위상과 임의의 시지연으로 근사 된다.

Eq. (4)을 통해 계산된 위상 보정 인자와 Eq. (3)의 정규화된 수신 신호의 곱을 통해 그린 함수를 추정할 수 있으며 이는 Eq. (5)와 같이 나타낼 수 있다.

(5)

G_{e} ({\vec{r}}_{j}, {\vec{r}}_{s}, ω) = {\tilde{R}}_{j} (ω) e^{- i ψ (ω, θ_{k})} = \frac{G ({\vec{r}}_{j}, {\vec{r}}_{s}, ω)}{\sqrt{\sum_{j = 1}^{N} | G ({\vec{r}}_{j}, {\vec{r}}_{s}, ω) |^{2}}} e^{i ω T (θ_{k})} .

음선 기반 블라인드 디컨볼루션 기법은 수신 신호와 배열의 깊이 정보만을 통해 실제 그린 함수의 파형과 음선별 상대적인 시지연 정보가 포함된 그린 함수를 추정할 수 있는 기법이며, 최소한의 해양환경 정보만 필요하다는 점과 효율적인 연산이 가능하다는 점에서 매우 효율적인 그린 함수 추정 기법이다. 최종적으로는 이러한 과정을 통해 송신 신호의 정보 없이 수신 신호로부터 그린 함수의 파형을 추정할 수 있으며, 본 논문에서는 장거리 심해 환경에서의 음선 기반 블라인드 디컨볼루션 기법 적용 가능성을 보이고자 한다. 또한, 음선 기반 블라인드 디컨볼루션 기법의 응용으로, 음선 기반 블라인드 디컨볼루션을 이용하여 국내에서 가장 먼 거리의 장거리 통신 데이터를 탐침 신호 없이 분석하여 얻은 통신 성능 결과를 제시한다.

III. BLAC18

2018년 10월 포항 동방 해역에서 생체모방 장거리 수중음향통신 해상실험인 BLAC18이 수행되었다.^{[28,29,30,31]} Fig. 1(a)는 해상실험이 수행된 해역을 나타내는 그림으로, 해상실험이 수행된 해역은 최대 1,700 m 깊이의 심해 해역이며 수신기를 기준으로 30 km, 60 km, 90 km에서 통신 신호를 송신하였다. Fig. 1(b)는 해상실험의 모식도를 나타내며, 해상실험 동안 16개의 수신기가 2.8 m 간격으로 구성된 수직 선 배열 센서가 사용되었다. 수직 선 배열 센서가 설치된 위치에서 측정한 음속 구조를 Fig. 1(b)에 나타냈으며, 최소음속이 위치한 깊이를 나타내는 음향축은 250 m에 형성되었다. 효율적인 장거리 전파를 위해 음향축은 매우 중요한 요소이며, 음원은 음향축 주변에 설치해야 한다. 본 연구팀은 해상실험 당시 현장에서 음속 구조를 측정 후, 케이블 길이와 같은 장비의 사양과 해상상황을 고려하여 음원의 깊이를 200 m 부근으로 결정하였다.

https://static.apub.kr/journalsite/sites/ask/2022-041-02/N0660410216/images/ASK_41_02_16_F1.jpg

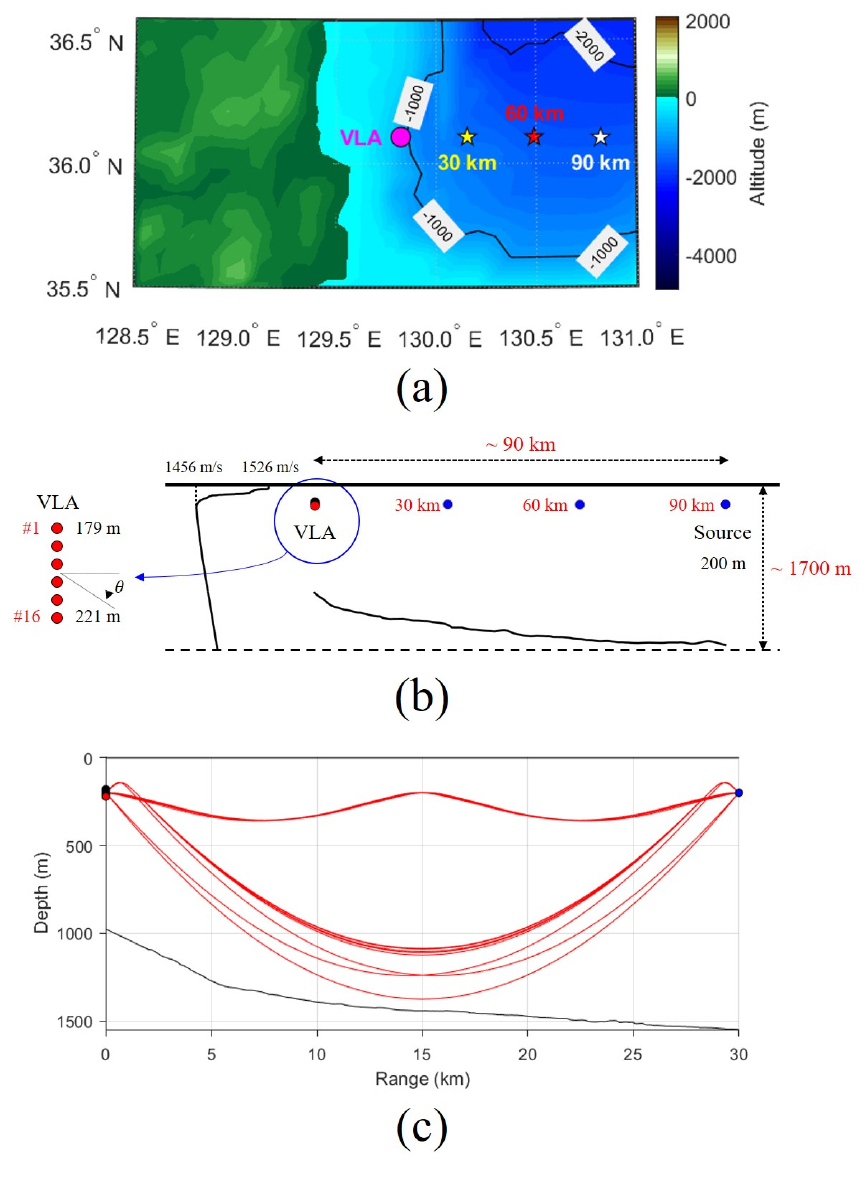
Fig. 1.

(Color available online) (a) Experimetal site, (b) schematic of BLAC18. On the left side of (b), the sound speed profile is shown, and the sound axis, which is the depth at which the lowest sound speed exists, is formed at 250 m. The horizontal solid line on the right side of (b) shows the depth of water, and it can be noticed that the depth increases up to 1,700 m as the distance from the receiver increases. (c) Ray diagram for the source/receiver geometry depicted in (b) at a 30 km range.

Fig. 1(c)는 음원과 수신기 사이의 고유음선으로 대표적으로 30 km 거리 환경에 관한 결과를 나타냈다. 4장에서 표현될 데이터 분석으로부터 도출되는 음선들에 대응되는 음선들만을 나타냈으며, 실제 해수면 또는 해저면 반사파가 존재할 수 있지만 음원이 음향축 부근에 위치하여 굴절파가 지배적임을 알 수 있다. 반사 손실이 발생하는 반사파와 달리 굴절파는 반사 손실이 존재하지 않으므로 전달 손실이 최소화되어 음원을 음향축 주변에 설치할 경우 효율적인 장거리 전파가 가능하다.

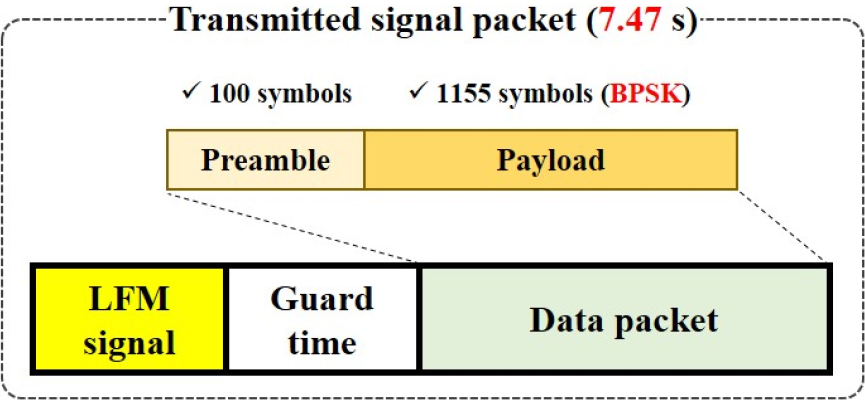
Fig. 2는 해상실험을 위해 설계된 통신 신호의 구조를 나타내는 그림으로, chirp 신호로 설계된 탐침 신호와 BPSK으로 변조된 통신 신호로 구성되어있다. 탐침 신호와 통신 신호의 길이는 각각 3 s, 2.47 s이며, 두 신호는 중심 주파수와 밴드폭이 각각 2,560 Hz, 640 Hz인 주파수 대역으로 설계되었다. 다중경로에 의한 간섭을 피하고자 두 신호 사이에는 2 s의 가드 타임이 포함되어있다. 통신 신호는 512 bps의 전송률로 roll-off factor가 0.25인 Root-Raised Cosine (RRC) 필터를 이용하여 설계되었으며, 동기화, 위상추적, 그리고 등화기 내부에서의 훈련을 위한 심볼 100개와 1,155개의 페이로드로 구성되어있다.

https://static.apub.kr/journalsite/sites/ask/2022-041-02/N0660410216/images/ASK_41_02_16_F2.jpg

Fig. 2.

(Color available online) Structure of the transmitted signal packet, which consists of a 3 s long chirp signal, 2 s silence period, followed by a data packet.

본 논문에서는 탐침 신호로부터 정합 필터를 이용하여 추정한 채널 임펄스 응답과 통신 신호에서 음선 기반 블라인드 디컨볼루션을 이용하여 추정한 채널 임펄스 응답을 비교할 예정이며, 두 결과의 비교를 통해 장거리 심해 환경에서도 음선 기반 블라인드 디컨볼루션이 가능할 수 있음을 보여주고자 한다.

IV. 해상실험 분석 결과

4.1 빔형성

음선 기반 블라인드 디컨볼루션 기법에서 가장 중요한 요소는 빔형성을 통해 위상 보정 인자를 추정하여 송신 신호의 위상을 제거하는 것이다. 구체적으로는 빔형성을 통해 신호의 각도를 추정하여, 해당 각도로 조향함으로써 위상 보정 인자를 추정하는 것이다. 빔형성 과정은 Eq. (6)과 같이 나타낼 수 있다.

(6)

B (ω, θ) = \sum_{j = 1}^{N} R_{j} (ω) e^{- i ω (j - 1) (\frac{d \sin θ}{c})},

여기서 $B (ω, θ)$ 는 전 방향에 대한 빔형성 결과를 의미하며, 지배적인 음선의 각도를 추정하기 위해 활용된다. 특정 방향에 대한 빔형성 결과를 나타내는 Eq. (4)와 구분하고 Fig. 4에 나타낼 예정인 그림을 위해, 모든 방향에 대한 식인 Eq. (6)을 추가로 표기하였다.

https://static.apub.kr/journalsite/sites/ask/2022-041-02/N0660410216/images/ASK_41_02_16_F3.jpg

Fig. 3.

(Color available online) Waterfall plot of 9-s data received on the vertical line array.

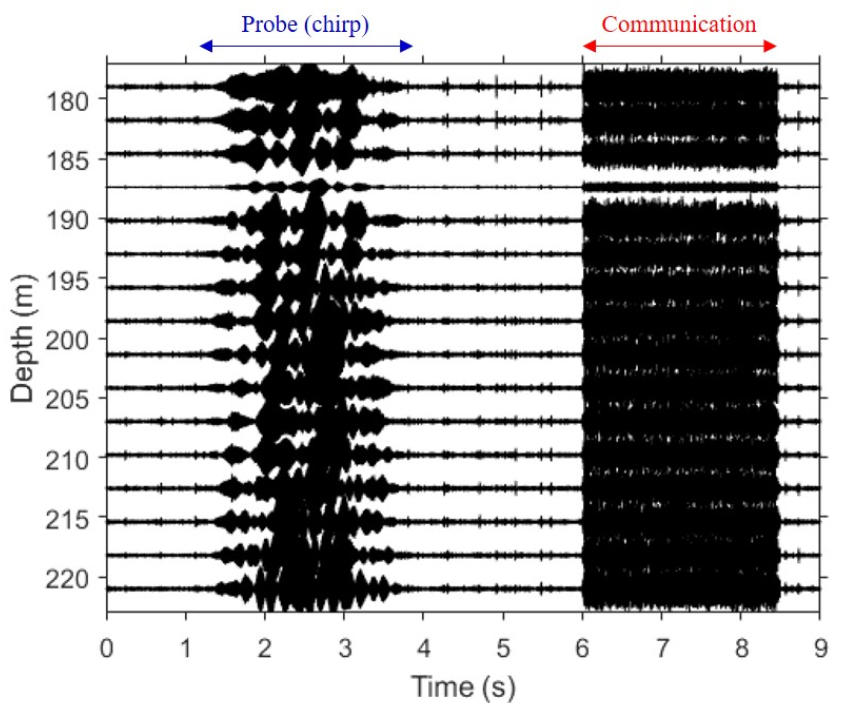
Fig. 3은 수직 선 배열 센서로부터 30 km 떨어진 음원에 의한 수신 신호를 나타내며, 앞서 언급한 바와 같이 chirp 신호와 통신 신호 순서대로 수신되었다. 빔형성 과정은 모든 거리에 대해서 동일한 과정으로 수행하므로, 본 논문에서는 세 가지 거리 중 30 km 거리의 데이터를 대표적으로 자세하게 설명하기로 한다.

https://static.apub.kr/journalsite/sites/ask/2022-041-02/N0660410216/images/ASK_41_02_16_F4.jpg

Fig. 4.

(Color available online) (a) Conventional beamforming result as functions of the frequency and the angle, (b) version with a zoom range of -15 to 15 degrees of (a), (c) beamforming result incoherently summed over the frequency band for (b).

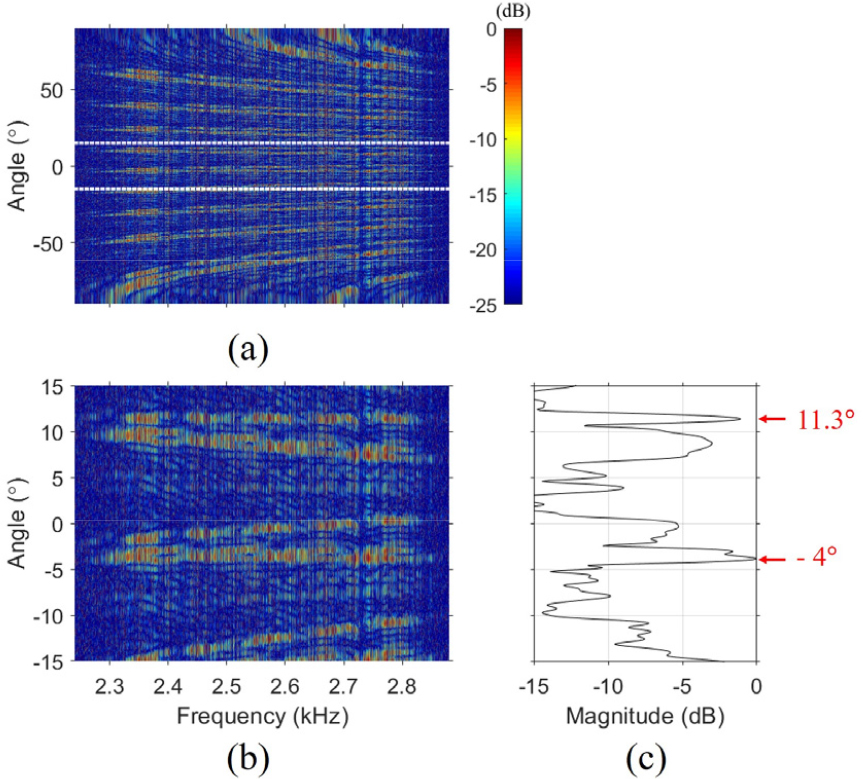
Eq. (6)의 결과인 $B (ω, θ)$ 는 주파수와 각도 변화에 따른 빔형성 결과를 나타내며, 30 km 거리의 해상실험 데이터에 Eq. (6)과 같은 빔형성을 수행하면 Fig. 4(a)와 같이 도출된다. 빔형성 각도는 –90°부터 90°까지 설정하였으며, 이 각도 범위에서의 빔형성 결과에는 여러 줄무늬가 나타난다. 이는 신호의 주파수와 설계 주파수의 차이에 의해 발생하는 공간 에일리어싱에 의한 문제이다. 수직 선 배열 센서의 간격은 2.8 m이므로 설계 주파수는 약 268 Hz이다. 이에 비해, 송신 신호의 주파수 범위(2.2 kHz ~ 2.9 kHz)가 설계 주파수보다 최소 8배 이상이므로 공간 에일리어싱으로 인해 그레이팅 로브라고 하는 부엽이 발생한다. 이러한 공간 에일리어싱으로 인해 부엽의 크기가 증가하게 되며, 여러 다중경로 중 세기가 낮은 일부의 각도는 부엽의 영향을 받아 빔형성을 통해 모든 다중경로에 대응하는 각도들을 추정하는 것은 어렵다. 하지만, 공간 에일리어싱으로 인해 발생하는 그레이팅 로브의 실제 음선 각도를 기준으로한 간격은 Reference [32]에 따르면 주파수에 따라 발생 각도가 달라지며, 실제 음선의 각도는 변하지 않은 채 유지된다.^[32] 즉, 그레이팅 로브에 의한 줄무늬는 주파수 축을 따라 평행하지 않는다. 따라서 실제 각도의 경우만 모든 주파수에서도 해당 각도 성분이 있으므로, Fig. 4(a)와 같이 공간 에일리어싱으로 인해 여러 줄무늬가 나타나는 상황에서도 주파수 축을 따라 가로로 평행하게 나타나야 한다. 이를 확인하기 위해 –15°부터 15° 범위를 확대한 그림을 Fig. 4(b)에 나타냈다. Fig. 4(b)에서 11.3°와 –4° 부근에 가로 선의 형태로 줄무늬가 나타나고 있으며, 이 두 각도는 음선이 도달하는 다중경로 중 일부임을 알 수 있다. 또한, 모든 주파수 성분에 대해 큰 세기를 갖는다는 특징을 활용하여 주파수에 따라 빔형성 결과의 파워를 적분한다면 해당 각도 값을 추정할 수 있다.

Fig. 4(c)는 Fig. 4(b)의 결과를 주파수에 따라 적분한 결과이며, 예상한 바와 같이 11.3°와 –4°에서 큰 세기가 나타난다. 본 논문에서는 음선 기반 블라인드 디컨볼루션 기법에서 중요한 요소인 위상 보정 인자를 추정하기 위해 두 각도 중 가장 큰 세기를 나타내는 각도인 –4°를 선택하였으며, 4.2절에서는 이러한 빔형성 결과에서 가장 큰 세기를 갖는 각도 정보를 활용하여 음선 기반 블라인드 디컨볼루션 기법의 목적인 그린 함수 추정 결과를 나타낸다. 또한, 60 km와 90 km 거리 데이터에 대해 동일한 과정을 통해 그린 함수 추정 결과를 나타낸다.

4.2 그린 함수 추정

2장에서 설명한 바와 같이 음선 기반 블라인드 디컨볼루션 기법의 궁극적인 목적은 수신 신호로부터 위상 보정 인자를 추정하고, 이를 정규화된 수신 신호에 적용함으로써 그린 함수를 추정하는 것이다. 본 절에서는 음선 기반 블라인드 디컨볼루션의 결과들을 제시하고자 하며, 크게 두 가지 흐름으로 구성되어있다. 첫 번째는 음선 기반 블라인드 디컨볼루션 기법의 가장 중요한 요소인 위상 보정 인자의 추정 가능성을 탐침 신호를 활용하여 확인하는 것이다. 두 번째는 위상 보정 인자 추정의 가능성을 확인한 후, 통신 신호에 대해 동일한 위상 보정 인자 추정 과정을 적용하여 그린 함수를 추정하고 이를 탐침 신호에 정합 필터를 적용하여 얻은 그린 함수와 비교하는 것이다. 통신 신호만을 활용하여 추정한 음선 기반 블라인드 디컨볼루션 기반 그린 함수는 통신 성능 분석을 위해 활용될 수 있으며, 이는 4.3절에서 다시 설명하기로 한다.

Abadi는 음선 기반 블라인드 디컨볼루션 기법의 가장 중요한 요소인 위상 보정 인자 추정 가능성을 확인하기 위해 빔형성 신호와 송신 신호의 상관도를 활용하였으며, 본 논문에서도 선행 연구에서 수행된 방식을 그대로 활용하였다.^[9]

Fig. 5(a)는 Fig. 3에서 보이는 수신 신호에 Fig. 4(c)로부터 추정한 각도 방향으로 시지연을 보상하여 모든 수신기에 대해서 더한 결과를 나타낸다. Fig. 5(b)는 비교를 위해 나타낸 설계한 탐침 신호를 나타낸다. 두 결과의 유사도를 정량적으로 비교하기 위해 상관 계수라는 지표를 활용하였으며, 이는 Eq. (7)과 같다.

(7)

C_{\max} = \max (\frac{\int_{- \infty}^{\infty} S_{b} (ω) S (ω) e^{i ω t} d ω}{\sqrt{\int_{- \infty}^{\infty} | S_{b} (ω) |^{2} d ω} \sqrt{\int_{- \infty}^{\infty} | S (ω) |^{2} d ω}}),

여기서 $S (ω)$ 와 $S_{b} (ω)$ 는 비교하고자 하는 두 대상으로써, 본 논문에서는 $S (ω)$ 에 설계한 탐침 신호를, $S_{b} (ω)$ 에 빔형성된 신호를 적용하였다.

https://static.apub.kr/journalsite/sites/ask/2022-041-02/N0660410216/images/ASK_41_02_16_F5.jpg

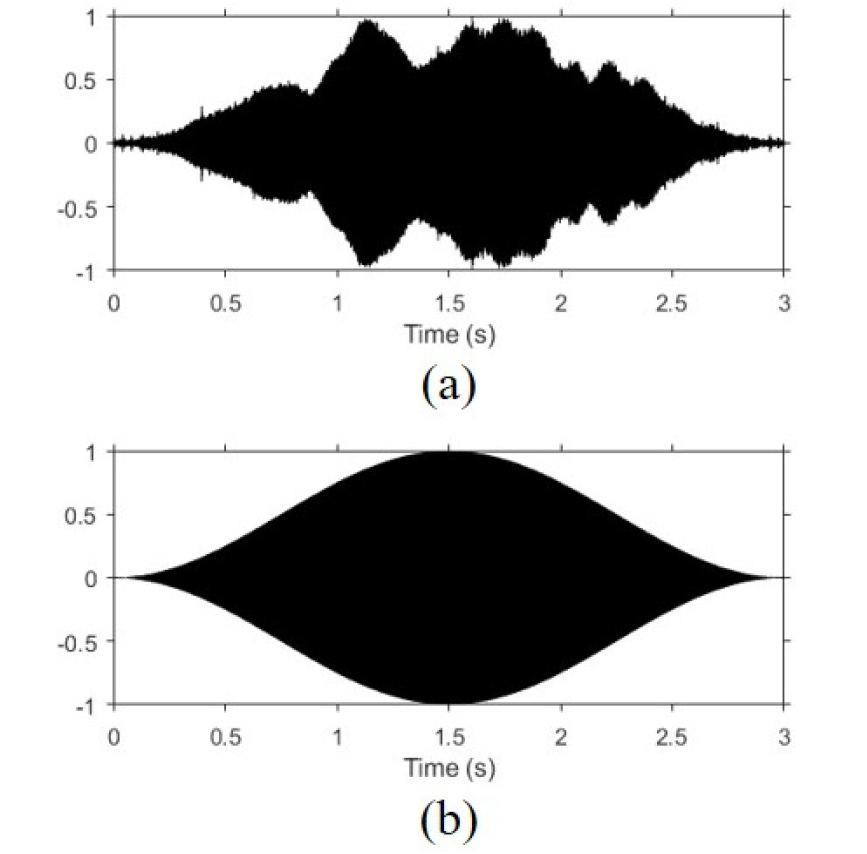
Fig. 5.

(a) Beamformed chirp signal with the -4°, which corresponds to the maximum-intensity arrival in Fig. 4(c), (b) the original chirp signal.

두 신호에 대한 상관 계수는 약 94.4 %였으며, 이러한 수치는 공간 에일리어싱이 존재하는 BLAC18 환경에서도 다중경로의 영향이 효과적으로 완화되어 위상 보정 인자를 원활하게 추정할 수 있음을 보여준다. 좀 더 확장한다면 장거리 심해 환경에서도 음선 기반 블라인드 디컨볼루션 기법이 가능할 수 있음을 즉, 그린 함수가 잘 추정될 수 있음을 보여주는 지표라고 할 수 있다.

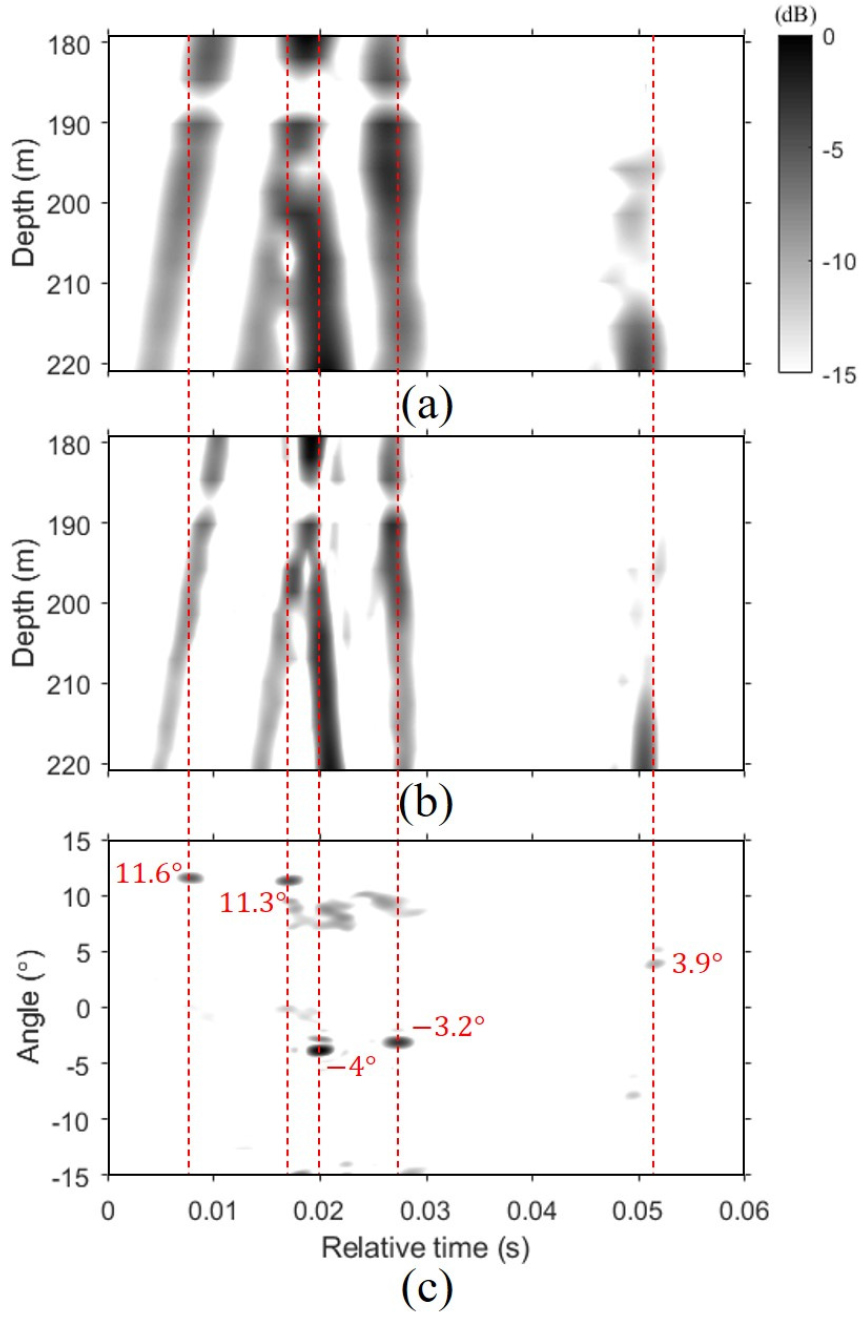
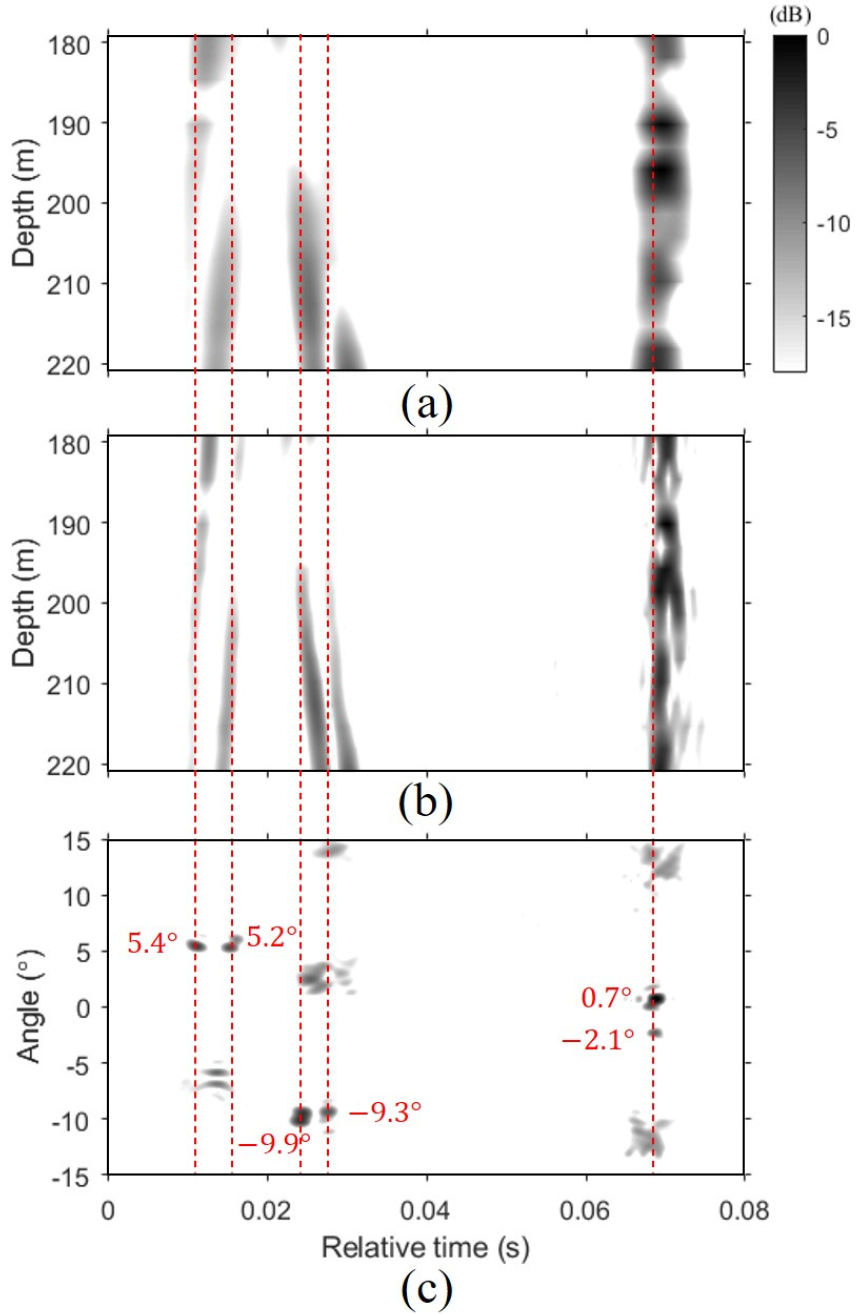
Eq. (3)과 같이 배열 센서를 통해 수신된 신호를 정규화한다면, 정규화된 그린 함수와 송신 신호 위상의 조합으로 표현된다. 빔형성을 통해 위상 보정 인자를 추정하여 정규화된 수신 신호에 보상하게 되면 임의의 시지연이 포함된 정규화된 그린 함수를 추정할 수 있다. 송신 신호의 파형을 추정하는 것이 주목적인 수중통신의 관점에서 임의의 시지연의 영향은 무시할 수 있다. Fig. 6(a)와 (b)에 두 종류의 추정된 시간 영역에서의 그린 함수를 나타냈다. 음선 기반 블라인드 디컨볼루션 결과와의 비교를 위해 탐침 신호에 대해 정합 필터를 이용하여 추정한 시간 영역에서의 그린 함수를 Fig. 6(a)에 나타냈다. Fig. 6(b)는 통신 신호에 음선 기반 블라인드 디컨볼루션을 적용하여 추정한 시간 영역에서의 그린 함수이다. 두 결과 [Fig. 6(a)와 (b)]를 비교했을 때, 패턴이 매우 유사한 것을 알 수 있으며 해상도에서만 차이점이 나타난다. 구체적으로 음선 기반 블라인드 디컨볼루션 기반 결과가 정합 필터 기반 결과에 비해 해상도가 향상되었다. 이는 Eqs. (3)과 (5)의 분모에 표현되는 정규화의 영향이다. 주파수 영역에서 평탄(flat)하게 신호를 설계하더라도 해상실험 데이터를 통해 신호를 수신하게 되면, 송신 장비 자체의 구동 원리에 의해 주파수 영역에서 해닝창이 적용된 것과 같이 나타난다. RRC 필터를 이용하여 설계된 통신 신호 또한 마찬가지이다. 이와 달리 백색화 과정이라고 할 수 있는 주파수 영역에서의 정규화를 하게 되면 주파수 영역에서 평탄한 출력을 얻을 수 있다. 스펙트럼의 주엽의 폭은 시간 영역에서의 주엽의 폭(또는 해상도)과 반비례하므로, 정규화 과정을 포함하고 있는 음선 기반 블라인드 디컨볼루션 결과의 해상도가 정합 필터 결과보다 향상된다.

https://static.apub.kr/journalsite/sites/ask/2022-041-02/N0660410216/images/ASK_41_02_16_F6.jpg

Fig. 6.

(Color available online) Green’s function estimated at 30 km range from: (a) chirp signal after matched-filtering and (b) communication signal using ray-based blind deconvolution, (c) beam-time migration of the Green’s function estimated from ray- based blind deconvolution.

음선들의 각도 정보는 시간 영역에서의 그린 함수에 시간 영역 빔형성 기법을 적용하여 얻어지는 빔-시간 그래프를 통해 추정될 수 있다. 빔형성은 수직 선 배열 센서의 중심 깊이인 200 m를 기준으로 수행되었으며, Fig. 6(c)에 빔-시간 그래프 결과를 도시하였다. 추정한 시간 영역 그린 함수에는 다섯 개의 음선이 나타나고 있으며, 200 m 깊이에서의 시간 정보들을 활용했을 때 빔-시간 그래프에서도 다섯 개의 각도 정보가 나타남을 알 수 있다. 빨간색 선을 통해 빔-시간 그래프에서 다섯 개의 시간 및 각도 정보를 확인할 수 있게 하였으며, 이외의 부엽은 공간 에일리어싱에 의해 생긴 결과이다. 반사파와 굴절파를 모두 포함한 고유음선 중 이러한 다섯 개 음선들의 각도와 대응하는 고유음선들을 Fig. 1(c)에 나타냈으며, 고유음선으로부터 다섯 개의 음선 모두 굴절파인 것을 알 수 있다.

빔-시간 그래프를 이용하여 추정한 각도 정보들은 다중경로 완화와 관련된 중요한 정보를 담고 있다. 선 배열 센서에 대한 빔 분해능( $∆ θ$ )은 파장과 배열 길이 정보를 이용하여 다음과 같이 나타낼 수 있다.

(8)

∆ θ = 0.89 \frac{λ}{L} [r a d],

여기서 $λ$ 는 파장을 의미하며, $L$ 은 배열의 길이를 의미한다.

해상실험에 사용된 신호의 중심 주파수(2,560 Hz)와 배열의 길이(42 m)를 적용한다면 분석하고자 하는 환경에서의 빔 분해능은 약 0.71°(= 0.012 rad)이다. Fig. 4(c)에 표현된 빔형성 결과의 최대값이 나타나는 각도(–4°)와 Fig. 6(c)로부터 추정한 다른 각도들의 차이는 최소 0.8° 이상으로 빔 분해능보다 크다. –4°를 기준 각도라고 정의할 때, 빔형성 결과와 송신 신호 사이의 높은 상관 계수는 다중경로들의 입사각과 기준 각도 사이의 간격으로 인한 결과다. 또한, 더 나아가 이러한 간격은 성공적인 음선 기반 블라인드 디컨볼루션 기반 그린 함수 추정의 요인이다.

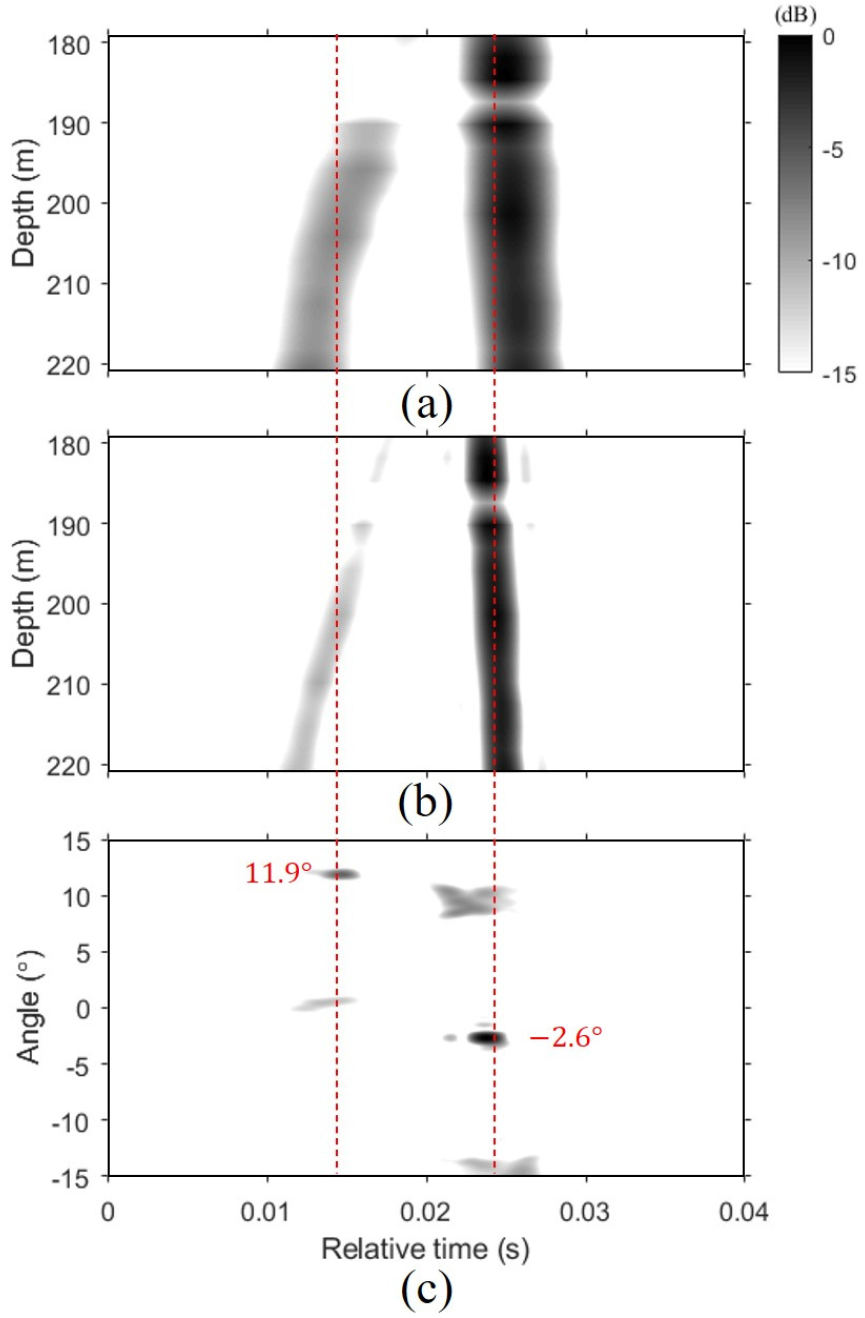
지금까지 30 km에 관한 결과를 도시하였으며, 60 km와 90 km 거리의 데이터에 대해서도 동일한 과정을 거쳐 시간 영역에서의 그린 함수를 추정하였으며, 이를 각각 Figs. 7과 8에 도시하였다. Figs. 7과 8에서 (a)와 (b)는 각각 정합 필터와 음선 기반 블라인드 디컨볼루션 결과이며, (c)는 음선 기반 블라인드 디컨볼루션 결과에 대한 빔-시간 그래프이다. 위상 보정 인자의 추정을 위해 빔형성의 최대값 각도(60 km : 0.7°, 90 km : -2.6°)를 활용하였다. 30 km의 결과와 마찬가지로 60 km와 90 km의 결과에서도 동일한 특징들(유사한 패턴과 해상도 향상)이 나타나는 것을 알 수 있었으며, 또한, 본 논문에서는 생략했지만 고유음선과 비교할 때 나머지 두 거리에서 수신되는 모든 음선들이 굴절파임을 알 수 있었다. 결론적으로 세 가지 거리(30 km, 60 km, 그리고 90 km)의 데이터를 이용한 결과로부터 장거리 심해 환경에서도 음선 기반 블라인드 디컨볼루션 기법이 검증되었다.

https://static.apub.kr/journalsite/sites/ask/2022-041-02/N0660410216/images/ASK_41_02_16_F7.jpg

Fig. 7.

(Color available online) Green’s function estimated at 60 km range from: (a) chirp signal after matched-filtering and (b) communication signal using ray-based blind deconvolution, (c) beam-time migration of the Green’s function estimated from ray- based blind deconvolution.

https://static.apub.kr/journalsite/sites/ask/2022-041-02/N0660410216/images/ASK_41_02_16_F8.jpg

Fig. 8.

(Color available online) Green’s function estimated at 90 km range from: (a) chirp signal after matched-filtering and (b) communication signal using ray-based blind deconvolution, (c) beam-time migration of the Green’s function estimated from ray- based blind deconvolution.

4.3 통신 성능 분석

수동형 시역전 처리 기반의 통신 성능 분석을 위해 흔히 사용하는 방법은 탐침 신호로부터 그린 함수를 추정하여 활용하는 것이다. 하지만, 4.2절에서 설명한 바와 같이 음선 기반 블라인드 디컨볼루션을 이용하면 탐침 신호 없이 통신 신호로부터 그린 함수 추정이 가능하며, 이를 통해 통신 성능을 분석이 가능하다. 본 절에서는 음선 기반 블라인드 디컨볼루션 기법의 응용으로써 4.2절에서 통신 신호로부터 추정한 그린 함수를 이용하여 통신 성능 분석 결과를 제시한다.

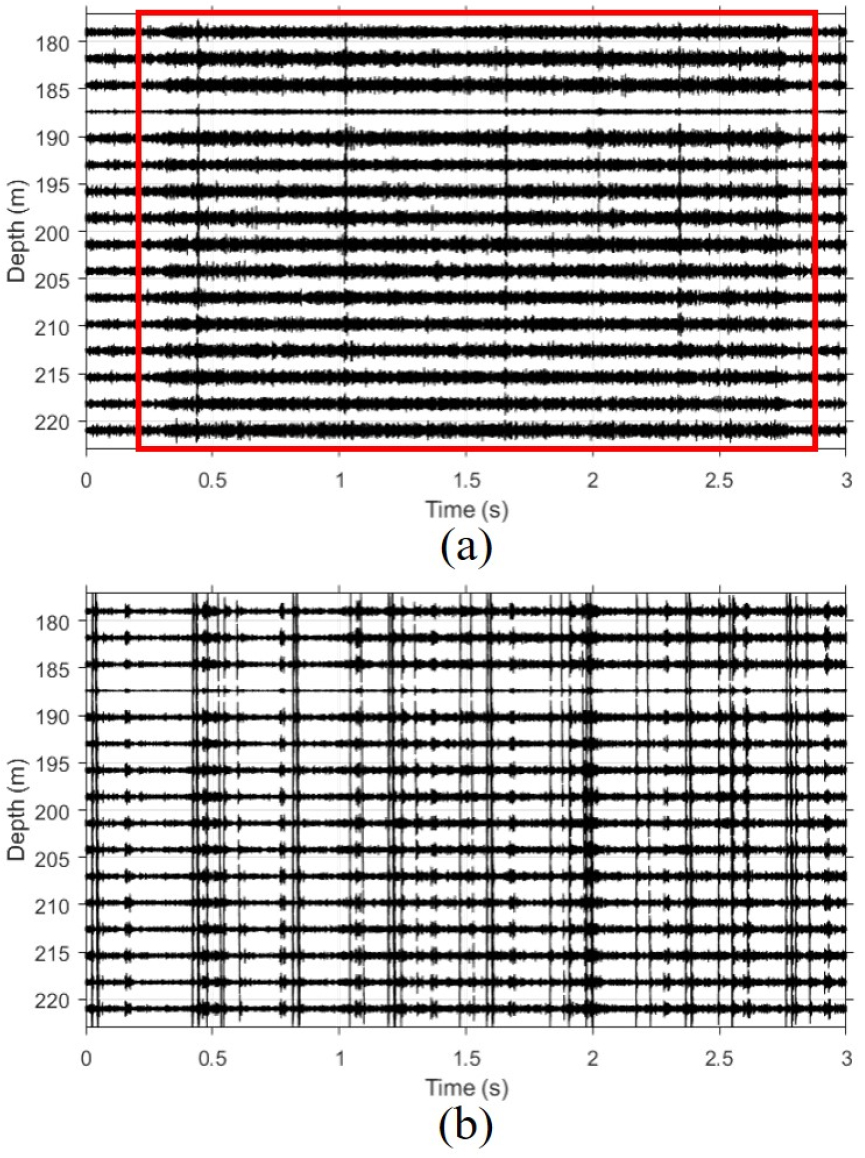
3장의 Fig. 2에서 보여준 송신 신호는 해상실험 동안 각 거리에서 총 18번 송신하였다. 하지만, 데이터에는 임펄스성 신호인 돌고래 클릭음이 다수 잡혔으며,^[33,34] 60 km와 90 km 데이터 중 일부 데이터가 다수의 돌고래 클릭음에 의해 오염되어 복조에 실패하여 결과에 포함하지 않았다. 구체적으로 60 km 데이터에는 18개 데이터 중 두 개의 데이터가 오염되었으며, 90 km 데이터에는 16개의 데이터가 오염되었다. 시각적으로 보여주기 위해 복조에 성공한 경우의 데이터와 실패한 경우의 데이터를 각각 Fig. 9(a)와 (b)에 나타냈다. 두 데이터 모두 90 km 데이터이다. 복조에 성공한 데이터[Fig. 9(a)]의 경우, 90 km 거리이지만 Fig. 9(a)의 빨간 박스 내에서와같이 신호가 육안으로도 확인되고 있다. 이와 달리 복조의 실패한 데이터의 경우 육안으로 확인할 수 없었으나, 송신 시간과 복조에 성공한 데이터의 수신 시간 등의 정보를 활용하여 도달 예상 시간대의 데이터를 출력하였다. Fig. 9(b)에서는 수십 개의 클릭음이 보인다. 클릭음은 임펄스성 신호이므로 시간 또는 주파수 영역에서 제거할 수 없으며, 이로 인해 PSK 방식의 신호는 위상이 왜곡되어 복조에 실패하였다.

https://static.apub.kr/journalsite/sites/ask/2022-041-02/N0660410216/images/ASK_41_02_16_F9.jpg

Fig. 9.

(Color available online) Waterfall plot of communication data received on the vertical line array in the event of (a) the successful decoding and (b) failure.

세 가지 거리에서의 통신 신호 데이터에 음선 기반 블라인드 디컨볼루션 기법을 적용하여 송신한 통신 신호를 추정하여 복조한 결과를 보여준다. 음선 기반 블라인드 디컨볼루션을 통해 그린 함수를 추정할 수 있으며, 수신 신호와 추정된 그린 함수를 이용하면 송신 신호를 추정할 수 있다. 이는 수동형 시역전 처리 과정과 동일하며, Eq. (9)와 같이 나타낼 수 있다.

(9)

S (ω) = \sum_{j = 1}^{N} R_{j} (ω) G_{e}^{*} ({\vec{r}}_{j}, {\vec{r}}_{s}, ω),

https://static.apub.kr/journalsite/sites/ask/2022-041-02/N0660410216/images/ASK_41_02_16_F10.jpg

Fig. 10.

(Color available online) Scatter plots based on ray-based blind deconvolution at (a) 30 km, (b) 60 km, and (c) 90km ranges.

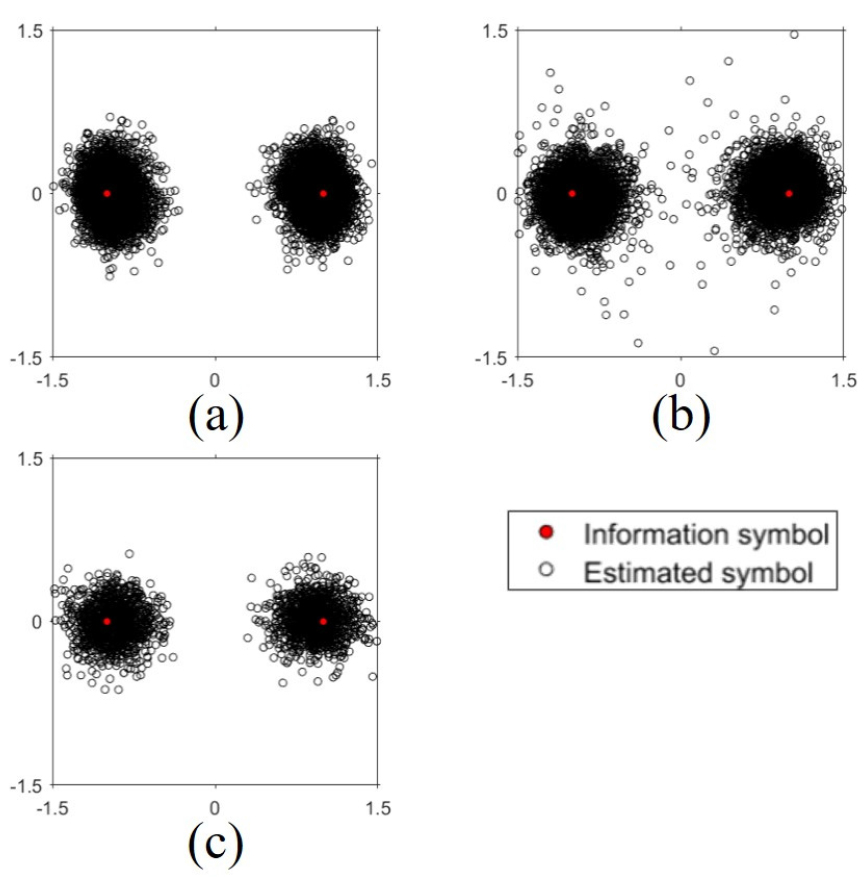
Fig. 10(a)부터 (c)까지 차례대로 30 km, 60 km, 그리고 90 km 거리에 대한 통신 성능 분석 결과를 나타내고, Table 1에 거리별 통신 성능 결과를 정리하였다. 세 가지 거리 데이터에 대해 모두 0 %에 가까운 비트 오류율과 11.5 dB 이상의 출력 신호 대 잡음비가 도출되었으며, 이는 음선 기반 블라인드 디컨볼루션 기법에 의해 송신 신호가 성공적으로 추정됨을 보여주는 결과이다. 비록 돌고래 클릭음과 같은 외부적인 요인으로 인해 90 km 데이터의 경우 데이터 대부분이 복조에 실패하였지만, 외부적인 요인의 영향이 적었던 두 개의 데이터에서 성공적인 복조 결과를 획득하였다. 이는 외부적인 요인을 제외하고 물리적으로 동해 해역에서 90 km 거리의 PSK 계열 기반 장거리 통신이 가능함을 보인 첫 번째 사례로 매우 유의미한 결과이다. 특히, 90 km의 거리는 PSK 계열 신호 기준으로 국내에서 최장 거리의 데이터 분석 결과이다. 또한, 음선 기반 블라인드 디컨볼루션 기법을 활용할 경우 수동형 시역전 처리를 위해 필요한 탐침 신호가 없어도 되므로, 이는 데이터 전송률 관점에서도 장점이다.

Table 1.

BER and output SNR according to the range.

Range	BER	Output SNR
30 km	0/20790 (0 %)	14.5 dB
60 km	9/18480 (0.05 %)	12.8 dB
90 km	0/2310 (0 %)	11.5 dB

V. 결 론

음선 기반 블라인드 디컨볼루션 기법은 송신 신호 정보 없이 수신 신호로부터 그린 함수와 송신 신호를 추정할 수 있는 기법이며, 선행 연구들에서는 근거리 천해 환경에서만 검증되었다. 본 논문에서는 장거리 심해 환경에서의 음선 기반 블라인드 디컨볼루션 기법의 활용 가능성을 검증하였다. 2018년 장거리(30 km, 60 km, 그리고 90 km) 수중통신 해상실험이 수행되었으며, 해상실험 동안 chirp 신호와 BPSK로 변조된 통신 신호를 송신하였다.

30 km 데이터에 대해 그린 함수를 추정하기에 앞서 빔형성 신호와 송신 신호의 유사도는 94.4 %였으며, 이는 음선 기반 블라인드 디컨볼루션의 가장 중요한 요소인 위상 보정 인자 추정이 성공적임을 의미한다. 이러한 결과들을 기반으로 통신 신호에 대해 음선 기반 블라인드 디컨볼루션을 이용하여 추정한 그린 함수와 chirp 신호의 정합 필터로 추정된 그린 함수와 비교했을 때, 두 기법에 의한 그린 함수가 매우 유사하게 도출되었으며 이는 60 km와 90 km 거리에서도 동일하였다. 즉, 장거리 심해 환경에서도 음선 기반 블라인드 디컨볼루션이 가능함을 해상실험 데이터를 기반으로 검증하였다.

추가적으로 수신 신호와 음선 기반 블라인드 디컨볼루션에 의해 추정된 그린 함수를 이용한 수동형 시역전 처리를 수행하였으며, 그린 함수는 통신 신호에서 자체적으로 추정되었다. 통신 성능 분석 결과 모든 거리에서 0 %에 가까운 비트 오류율과 11.5 dB 이상의 높은 출력 신호 대 잡음비가 도출되어 탐침 신호 없이 성공적으로 복조가 됨을 확인하였다. 특히, 90 km 거리에서의 분석 결과는 국내에서 수행된 PSK 계열 분석 결과 중 가장 먼 거리의 결과이므로 매우 의미 있으며, 탐침 신호가 없어도 된다는 사실은 데이터 전송률 관점에서 장점이라 할 수 있다.

Acknowledgements

본 논문은 국방과학연구소의 지원으로 수행되었습니다(UD200010DD).

References

A. B. Baggeroer, W. A. Kuperman, and P. N. Mikhalevsky, "An overview of matched field methods in ocean acoustics," IEEE J. Oceanic Eng. 18, 401-424 (1993). 10.1109/48.262292

H. C. Song, "An overview of underwater time-reversal communication," IEEE J. Oceanic Eng. 41, 644-655 (2016). 10.1109/JOE.2015.2461712

S. Lee and N. C. Makris, "The array invariant," J. Acoust. Soc. Am. 119, 336-351 (2006). 10.1121/1.213907416454289

C. Cho, H. C. Song, and W. S. Hodgkiss, "Robust source-range estimation using the array/waveguide invariant and a vertical array," J. Acoust. Soc. Am. 139, 63-69 (2016). 10.1121/1.493912126827005

H. C. Song and C. Cho, "Array invariant-based source localization in shallow water using a sparse vertical array," J. Acoust. Soc. Am. 141, 183-188 (2017). 10.1121/1.497381228147576

C. Cho, H. C. Song, P. Hursky, and S. M. Jesus, "Iterative range estimation in a sloping-bottom shallow- water waveguide using the generalized array invariant," J. Acoust. Soc. Am. 142, 55-60 (2017). 10.1121/1.499067028764451

G. Byun, H. C. Song, and C. Cho, "Adaptive array invariant in range-dependent environments with variable bathymetry," J. Acoust. Soc. Am. 149, 1363-1370 (2021). 10.1121/10.000356233639832

K. G. Sabra, H. C. Song, and D. R. Dowling, "Ray- based blind deconvolution in ocean sound channels," J. Acoust. Soc. Am. 127, EL42-EL47 (2010). 10.1121/1.328454820136177

S. H. Abadi, D. Rouseff, and D. R. Dowling, "Blind deconvolution for robust signal estimation and approximate source localization," J. Acoust. Soc. Am. 131, 2599-2610 (2010). 10.1121/1.368850222501041

S. Byun, C. M. A. Verlinder, and K. G. Sabra, "Blind deconvolution of shipping sources in an ocean waveguide," J. Acoust. Soc. Am. 141, 797-807 (2017). 10.1121/1.497604628253650

S. Byun, G. Byun, and K. G. Sabra, "Ray-based blind deconvolution of shipping sources using multiple beams separated by alternating projection," J. Acoust. Soc. Am. 144, 3525-3532 (2018). 10.1121/1.508383430599679

N. C. Durofchalk and K. G. Sabra, "Analysis of the ray-based blind deconvolution algorithm for shipping sources," J. Acoust. Soc. Am. 147, 1927-1938 (2020). 10.1121/10.000091932237794

G. Byun and H. C. Song, "Adaptive array invariant," J. Acoust. Soc. Am. 148, 925-933 (2020). 10.1121/10.000176832873004

G. Byun, J. S. Kim, C. Cho, H. C. Song, and S. Byun, "Array invariant based ranging of a source of opportunity," J. Acoust. Soc. Am. 142, EL286-EL291 (2017). 10.1121/1.500332728964101

G. Byun, C. Cho, H. C. Song, J. S. Kim, and S. Byun, "Array invariant based calibration of array tilt using a source of opportunity," J. Acoust. Soc. Am. 143, 1318- 1325 (2018). 10.1121/1.502584429604662

G. Byun, H. C. Song, J. S. Kim, and J. Park, "Real- time tracking of a surface ship using a bottom-mounted horizontal array," J. Acoust. Soc. Am. 144, 2375-2382 (2018). 10.1121/1.506479130404486

H. C. Song and G. Byun, "Simultaneous localization of a surface ship and a submerged towed source," J. Acoust. Soc. Am. 144, 2238-2241 (2018). 10.1121/1.506335230404518

G. Byun, H. C. Song, and J. S. Kim, "Performance comparisons of array invariant and matched field processing using broadband ship noise and a tilted vertical array," J. Acoust. Soc. Am. 144, 3067-3074 (2018). 10.1121/1.508060330599643

H. C. Song, G. Byun, and J. S. Kim, "Remote acoustic illumination using time reversal and a surface ship," J. Acoust. Soc. Am. 145, 1565-1568 (2019). 10.1121/1.509536331067953

G. Byun, H. C. Song, and S. Byun, "Localization of multiple ships using a vertical array in shallow water," J. Acoust. Soc. Am. 145, EL528-EL533 (2019). 10.1121/1.511177331255094

H. C. Song and G. Byun, "Extrapolating Green's functions using the waveguide invariant theory," J. Acoust. Soc. Am. 147, 2150-2158 (2020). 10.1121/10.000096932359253

G. Byun and H. C. Song, "Extracting Green's functions between ships of opportunity using a vertical array," J. Acoust. Soc. Am. 148, 1800-1807 (2020). 10.1121/10.000210333138482

H. C. Song and G. Byun, "Localization of a distant ship using a guide ship and a vertical array," J. Acoust. Soc. Am. 149, 2173-2178 (2021). 10.1121/10.000395733940904

S. Cho, G. Byun, S. Byun, and J. S. Kim, "Ray backpropagation-based ship localization" (in Korean), J. Acoust. Soc. Kr. 37, 196-205 (2018).

S. Cho, D. Kim, and J. S. Kim, "Source depth discrimination based on channel impulse response" (in Korean), J. Acoust. Soc. Kr. 38, 120-127 (2019).

X. Zhang, N. C. Durofchalk, H. Niu, L. Wu, R. Zhang, and K. G. Sabra, "Geoacoustic inversion using ray- based blind deconvolution of shipping sources," J. Acoust. Soc. Am. 147, 285-299 (2020). 10.1121/10.000060532006998

S. Oh, G. Byun, and J. S. Kim, "Performance improvement of underwater acoustic communication using ray- based blind deconvolution in passive time reversal mirror" (in Korean), J. Acoust. Soc. Kr. 35, 375-382 (2016). 10.7776/ASK.2016.35.5.375

J. Lee, G. Lee, K. Kim, and W. Kim, "Sea trial results of long range underwater acoustic communication based on frequency modulation in the East Sea" (in Korean), J. Acoust. Soc. Kr. 38, 371-377 (2019). 10.1109/ICUFN.2019.8806162

H. Park, D. Kim, J. S. Kim, J. Hahn, and J. Park, "Performance improvement of long-range underwater acoustic communication in deep water using spatiotemporal diversity" (in Korean), J. Acoust. Soc. Kr. 38, 587-592 (2019).

D. Kim, H. Park, J. S. Kim, J. Park, and J. Hahn, "Performance analysis of underwater acoustic communication based on beam diversity in deep water" (in Korean), J. Acoust. Soc. Kr. 38, 678-686 (2019).

D. Kim, D. Kim, J. S. Kim, and J. Hahn, "Long-range multiple-input-multiple-output underwater communication in deep water" (in Korean), J. Acoust. Soc. Kr. 40, 417-427 (2021).

H. L. van Trees, Optimum Array Processing: Part IV of Detection, Dstimation, and Modulation Theory (John Wiley & Sons, New York, 2004), pp. 50-55.

J. Song, D. Kim, Y. Choi, and J. S. Kim, "Study of acoustic characteristics of east sea dolphin in BLAC18" (in Korean), Proc. J. Acoust. Soc. Kr. Suppl. 1(s) 38, 232 (2019).

Y. Yoon, H. Sohn, K. Park, Y. Choi, S. Kim, and J. Choi, "Study of acoustic characteristics of common dolphins Delphinus delphis in the East Sea" (in Korean), Korean J. Fish. Aquat. Sci. 50, 406-412 (2017).

The Journal of the Acoustical Society of Korea ISSN:1225-4428(Print) 2287-3775(Online) 한국음향학회지

Preview

Application of ray-based blind deconvolution to long-range acoustic communication in deep water

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

Fig. 1.

Fig. 2.

(Color available online) Structure of the transmitted signal packet, which consists of a 3 s long chirp signal, 2 s silence period, followed by a data packet.

(6)

Fig. 3.

(Color available online) Waterfall plot of 9-s data received on the vertical line array.

Fig. 4.

(Color available online) (a) Conventional beamforming result as functions of the frequency and the angle, (b) version with a zoom range of -15 to 15 degrees of (a), (c) beamforming result incoherently summed over the frequency band for (b).

(7)

Fig. 5.

(a) Beamformed chirp signal with the -4°, which corresponds to the maximum-intensity arrival in Fig. 4(c), (b) the original chirp signal.

Fig. 6.

(Color available online) Green’s function estimated at 30 km range from: (a) chirp signal after matched-filtering and (b) communication signal using ray-based blind deconvolution, (c) beam-time migration of the Green’s function estimated from ray- based blind deconvolution.

(8)

Fig. 7.

(Color available online) Green’s function estimated at 60 km range from: (a) chirp signal after matched-filtering and (b) communication signal using ray-based blind deconvolution, (c) beam-time migration of the Green’s function estimated from ray- based blind deconvolution.

Fig. 8.

(Color available online) Green’s function estimated at 90 km range from: (a) chirp signal after matched-filtering and (b) communication signal using ray-based blind deconvolution, (c) beam-time migration of the Green’s function estimated from ray- based blind deconvolution.

Fig. 9.

(Color available online) Waterfall plot of communication data received on the vertical line array in the event of (a) the successful decoding and (b) failure.

(9)

Fig. 10.

(Color available online) Scatter plots based on ray-based blind deconvolution at (a) 30 km, (b) 60 km, and (c) 90km ranges.

Table 1.

BER and output SNR according to the range.

Acknowledgements

References