I. 서 론
II. 가진력 추정 이론
2.1 가진력 추정 이론 및 차수 감소 모델링
2.2 가상 지점 변환
III. 유한요소 해석을 통한 가진력 추정 방법 검증
IV. 실험을 통한 가진력 추정 방법 검증
4.1 실험 절차
4.2 실험 대상 시스템 특성 분석
4.3 실험을 통한 검증 결과
V. 결 론
I. 서 론
동적 시스템의 응답 예측을 위해서는 시스템에 작용하는 가진력을 정확하게 파악하는 것이 필수적이다. 특히, 기계 구조물, 교량, 차량, 가전제품과 같은 복잡한 기계 시스템의 강건 설계를 위해서는 설계 단계에서 신뢰도 높은 응답 및 진동 특성 분석이 필요한데, 이때 가진력에 대한 정확한 정보가 요구된다.[1,2,3] 뿐만 아니라, 가진력 추정은 시스템의 손상 감지 또는 상태 모니터링에도 활용될 수 있다. 외부 가진력의 변화를 추정하고 응답 특성의 변화를 분석함으로써 기계 시스템의 손상 여부를 판단하거나 예방할 수 있으며, 유지보수 계획을 수립할 수 있다.[4] 또한, 가진력 추정은 제어 시스템 설계에도 필수적인 정보를 제공한다. 시스템의 성능을 최적화하기 위한 제어기 설계는 실제 시스템에 작용하고 있는 가진력에 대한 정보가 필수적이다.[5,6] 하지만, 직접적으로 가진력을 측정하는 것은 시스템의 복잡성 및 측정 장비의 한계 등으로 인해 실질적으로 불가능한 경우가 많다. 따라서, 간접적으로 가진력을 추정하는 방법에 대한 연구들이 진행되어왔는데, 주파수 영역과 시간 영역 기반으로 구분할 수 있다.
주파수 영역 방법 중 전달경로 해석(Transfer Path Analysis, TPA) 방법은 주파수 응답 함수를 사용하여 시스템에 작용하는 힘을 추정하고 목표 지점의 응답을 예측하는 방법이다.[7] Classical-TPA 관련 방법들은 가진 부위와 측정 부위 사이의 주파수 응답 함수를 구성하여 측정된 응답과 주파수 응답 함수를 활용하여 가진력을 역산하는 방법이다. 하지만 이 방법은 시스템 전체에 대한 주파수 응답을 구하기 위해 실제 측정 대상이 필요하며, 시스템의 구성이 바뀔 때 마다 매번 측정을 새로 해야 한다는 단점이 있다. 이러한 단점을 보완하기 위해 Component-based TPA 방법은 가진원에서 발생하는 힘을 구성품들 사이에 작용하는 등가 힘으로 치환하여 사용한다. 이 방법은 등가 힘을 가진력이 발생하는 부품만 가지고 측정할 수 있으며, 이때 측정한 등가 힘은 가진력을 포함하는 부품을 제외한 시스템의 다른 부분이 변경되어도 적용 가능하다는 장점이 있다. Moorhouse et al.[8]은 측정을 통해 시스템이 결합된 상태에서 측정된 주파수 응답 함수를 사용하여 가진원을 독립적인 등가 힘으로 특성화하는 in-situ 방법을 제안했다. Parloo et al.[9]은 동작 중 모달 분석을 통해 구조물의 모드 형상을 추정 및 정규화하고, 주파수 응답 함수를 합성하여 실제 작용하는 힘을 추정하는 방법을 제안했다. 하지만, 이 방법 역시도 부품 단위의 주파수 응답에 대한 정보가 필요하다. 실험적으로 주파수 응답을 구할 수 없는 대상의 경우 적용이 불가능하며, 체결 부위에서 발생하는 동역학적 특성이 반영되지 않는 단점이 있다.
시간 영역에서는 시스템의 역학적 상태를 추정하는 재귀적 알고리즘인 칼만 필터를 활용한 방법들이 활발하게 연구되고 있다. Lourens et al.[10]는 상태벡터에 힘 성분을 포함하여 상태와 힘을 동시에 추정하는 확장 칼만 필터 방법을 적용하여 I-빔에 대한 실험을 통해 가진력을 추정하였고, 기존의 결정론적 방법과 성능을 비교하였다. Naets et al.[11]는 더미 측정을 추가로 적용하여 가속도 측정값에서 발생하는 드리프트 현상을 방지함으로써, 필터의 안정성을 향상시키는 방법을 제안하였다.
앞서 열거한 실험 기반의 가진력 측정 방법 뿐 아니라 수식 기반의 가진력 측정 방법에 관한 연구도 다수 진행되었다. 수식 모델 기반 방법은 정밀 가공 분야에서 활발하게 연구되어 왔다. Zhou[12]은 5축 밀링 공정에서 공구와 공작물 움직임 간의 기하학적 관계를 기반으로 절삭 두께와 접촉영역을 계산함으로써 다양한 리드각과 경사각에 따른 절삭력을 추정하였다. Aucejo와 De Smet[13]은 확률론적 방법인 완전한 베이지안 방법을 제안하였고, 모델의 모든 파라미터를 추정하기 위한 하이브리드 깁스 샘플러를 도입하여 추정값의 불확실성을 정량화함으로써 신뢰성을 확보했다.
하지만, 기존의 가진력 추정 방법들은 다음과 같은 한계점들이 있다. 주파수 영역 방법들은 주파수 응답 함수의 정확성에 크게 좌우되며, 시간에 따라 변하는 동적 힘을 추정하기 어렵다. 또한, 시간 영역의 가진력으로 변환하기 위해 추가적인 알고리즘이 필요하며 오차의 원인이 될 수 있다. 시간 영역 기반 방법들은 초기 조건과 노이즈에 민감하고, 고차원의 상태 공간을 다룰 때 연산량이 기하급수적으로 증가해 대규모 시스템에 적용하기 어렵다는 문제점이 있다. 수식 모델 기반 방법은 자유도가 굉장히 많은 실제 시스템을 정확하게 구현하기 어렵기 때문에 정확도가 낮다는 한계점이 존재한다.
이러한 한계점들을 극복하기 위해, 본 연구에서는 전체 시스템에서 측정된 응답과 수식 모델 해석을 결합하여 동적 시스템의 가진력을 간접적으로 추정하는 새로운 방법을 제안한다. 이 방법은 가진원을 집중 질량 모델로 단순화하고, 수신부는 유연체 모델로 가정하여 부분 모드 합성법을 적용하였다. 조립된 상태의 시스템을 대상으로 진동을 측정하고, 측정값과 부분 모드 합성법을 적용한 수식 모델을 기반으로 가진원과 수신부 사이의 인터페이스 힘을 계산하여 가진력을 정량화하였다. 제안된 방법은 유한요소 모델을 통해 모의 검증을 거친 후 실제 압축기-배관 시스템을 대상으로 검증을 추가적으로 진행하였다.
II. 가진력 추정 이론
2.1 가진력 추정 이론 및 차수 감소 모델링
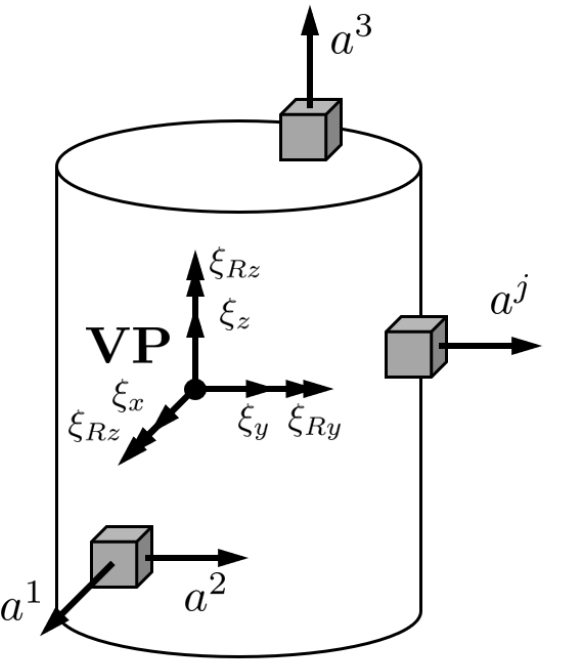
Fig.1과 같이 가진원과 수신부가 결합된 임의의 동적 시스템에서 가진원의 운동방정식은 Eq. (1)과 같이 나타낼 수 있다. 이때, 강성이 𝜆인 연결부에서 발생하는 반력 를 인터페이스 힘이라 정의하고, 하첨자 는 가진원, 은 수신부를 의미한다. , , , 는 각각 가진원의 질량, 댐핑, 강성, 가진력을 의미하며, 𝛽는 구조 댐핑 계수를 나타낸다. Eq. (1)을 가진력에 대해서 정리한 Eq. (2)를 통해 가진력은 관성력, 마운트 힘, 댐핑 힘과 구성 요소 간 인터페이스 힘을 추정함으로써 추정될 수 있음을 알 수 있다.
Fig. 1의 시스템의 운동방정식을 가진원과 수신부 전체로 표현하면, Eq. (3)과 같이 나타낼 수 있다.
여기서 강체인 가진원과 달리 유연체로 고려한 수신부는 N개의 자유도를 가진다고 가정한다. 따라서, 각각에 대한 일반화 좌표는 xs∈ℝ6⨯1, xr∈ℝN⨯1과 같고, 두 좌표의 커플링 요소는 아래 첨자 rs로 표기로 되었다.
유연체 모델의 높은 자유도와 비선형 요소로 인한 긴 해석 시간 문제를 해결하기 위해 Craig-Bampton 방법[14,15,16]을 적용하면 Eq. (4)와 같이 일반화 좌표의 차수를 감소시킬 수 있다.
𝛷와 𝛹는 각각 고정 경계 정규 모드와 구속 모드를 뜻하며, 는 물리적 영역에서의 일반화 좌표, 는 모드 영역의 일반화 좌표를 나타낸다. 이때, 고정 경계 정규 모드를 선별적으로 선택하면 일반화 좌표의 차수를 감소시킬 수 있다. 여기서, 와 는 축소된 성분을 의미한다. Eq. (4)를 통해 경계 자유도 는 좌표계 투영 시에도 물리 영역의 변위와 동일한 것을 알 수 있다. Eq. (4)에 고정 경계 정규 모드와 구속 모드로 구성된 Craig-Bampton 변환행렬 를 이용하여 좌표변환을 하고 Eq. (5)와 같이 에 투영하면 모드 영역의 Eq. (6)을 얻을 수 있다.
Eq. (6)으로부터 얻은, Eqs. (7)과 (8)을 연립하면 가진력은 Eq. (10)과 같이 나타낼 수 있다. Eq. (10)에서 가진력은 Eq. (11)로 계산된 인터페이스 힘을 통해 계산되는 것을 알 수 있다.
추정된 가진력 을 유한요소 모델에 직접 적용하여 특정 노드의 정상 상태 응답 를 계산할 수 있다. 추정된 가진력을 Eq. (11)의 Fast Fourier Trans(FFT) - formation를 적용하여 주파수 성분으로 분해하고, 조화 응답 해석을 통해 모달 진폭 를 계산한다. 이후, Eq. (13)과 같이 모드 벡터와 곱하여 얻어진 물리 영역에서의 응답 에 Eq. (14)와 같이 중첩의 원리를 적용하여 특정 노드에서의 정상상태 응답을 예측한다.
2.2 가상 지점 변환
다자유도 시스템의 운동방정식을 나타낸 Eq. (3)에서 , , 는 질량 중심 위치에서 집중 질량으로 모델링 된 가진원의 변위, 속도, 가속도를 의미한다. 실제 시스템의 경우 질량 중심에서의 응답을 직접적으로 측정하는 것은 현실적으로 불가능한 경우가 많다. 따라서, Fig. 2와 같이 주변에서 얻은 응답들을 기하학적 관계를 기반으로 목표 지점 VP의 응답으로 축소하는 가상 지점 변환(Virtual Point Transformation, VPT) 기법[17,18]을 적용한다. 이때, 센서를 부착하여 응답을 얻는 가상의 위치와 목표 지점이 강체로 구성된 영역에 있다고 가정하면, 측정된 개의 자유도로 구성된 와 가상 위치 VP의 자유도 𝜉간의 관계는 행렬 를 이용하여 Eq. (17)과 같이 나타낼 수 있다.
측정된 자유도 1개와 가상 지점 자유도 간 관계식 Eq. (18)에서 위 첨자 는 측정된 자유도 각각의 인덱스를 의미한다. 측정 지점과 목표 지점 사이의 기하학적인 강체 조건을 나타내는 행렬 는 자유도 방향을 각 좌표계에 투영한 단위 벡터의 방향 별 성분 , 측정된 위치와 단일 목표 지점 사이의 거리의 방향별 성분 로 구성되어 있다. 최종적으로, 가상의 목표 지점으로 축소된 자유도 𝜉는 의 의사 역행렬을 통해 계산될 수 있고, Eq. (19)과 같이 표현된다. 본 연구에서는, Eq. (19)를 통해 압축기의 질량 중심 위치로 축소된 자유도 𝜉를 Eq. (6)의 에 대입하여 집중 질량 위치에서의 가진력을 추정한다.
III. 유한요소 해석을 통한 가진력 추정 방법 검증
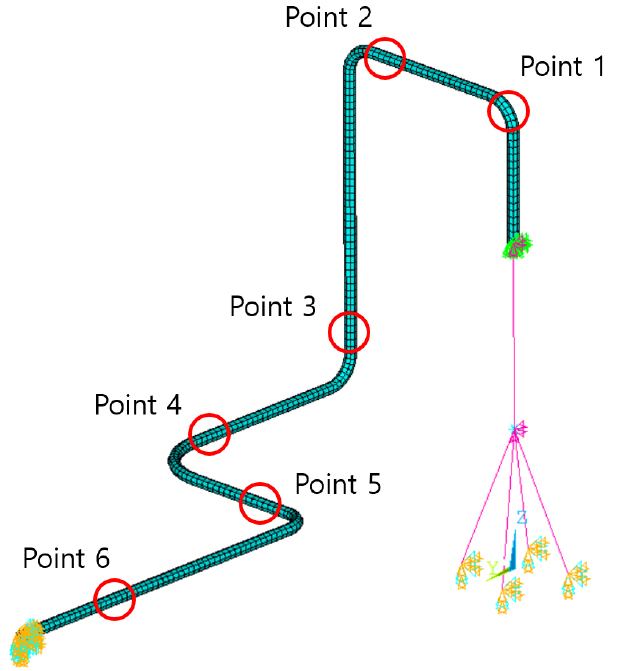
제안된 방법의 유효성을 확인하기 위해 압축기-배관 시스템을 모사한 유한요소 모델을 대상으로 검증을 진행하였다. 가진원인 압축기는 Fig. 3과 같이 집중 질량으로 모델링 되었고, 강체 움직임을 나타내는 요소를 통해 마운트와 연결되었다. Shell 요소로 구성된 배관은 압축기 집중 질량과 연결되었고, 반대쪽 끝은 질량이 매우 큰 구조물에 결합된 것으로 가정하여, 고정 경계 조건을 부여했다. 배관은 효율적인 가진력 추정 및 응답 예측을 위해 Craig-Bampton 방법을 기반으로 차수 감소 모델링하였다.
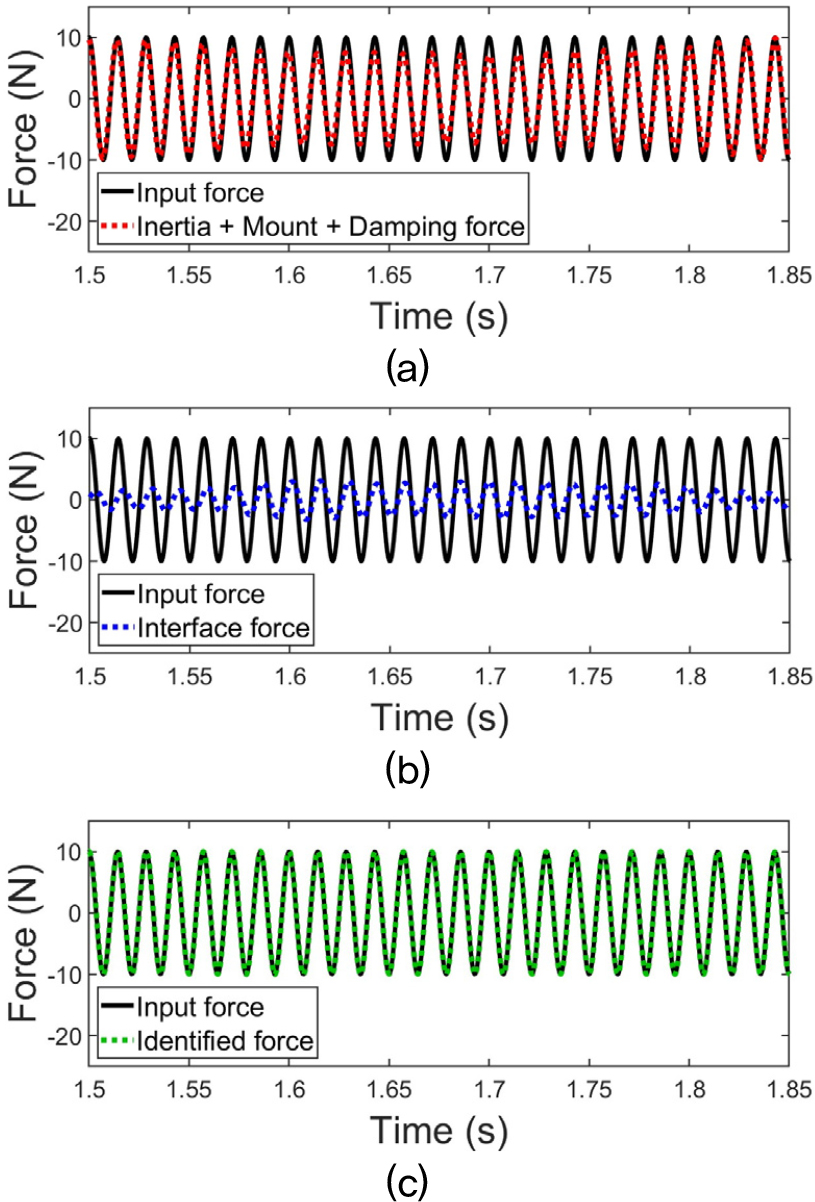
가진원 위치에 임의로 정한 조화 가진력을 입력하고, 시계열 해석(Time Domain Analysis, TDA)을 통해 가진력 추정에 필요한 응답들을 얻었다. 응답을 얻은 위치는 Fig. 3의 Point 1 ~ 6에 해당한다. 해당 모델로부터 차수감소모델 행렬을 구성하고 해석을 통해 얻은 응답과 함께 Eq. (6)에 적용하여 가진력을 추정하였다. Fig. 4(a)는 입력된 가진력과 관성력, 강성 힘, 댐핑 힘의 합을 비교한 결과로 진폭과 주파수 성분이 일치하지 않음을 알 수 있다. 여기에, Eq. (10)을 통해 계산된 가진원과 수신부 사이의 인터페이스 힘 Fig. 4(b)를 Eq. (9)와 같이 고려하여 가진력을 추정한다. 추정된 가진력은 해석 시 입력한 가진력과 정확하게 일치하며, 이는 Fig. 4(c)를 통해 확인할 수 있다. 해당검증 결과는, 제안된 가진력 추정 방법의 유효성을 입증한다.
IV. 실험을 통한 가진력 추정 방법 검증
4.1 실험 절차
제안된 방법이 실제 건조기의 압축기-배관 시스템에서도 유효한지 확인하고, 추정된 가진력이 가진원의 고유한 성분인지 검증하기 위해 두 개의 서로 다른 압축기-배관 시스템을 구성하였다. 두 시스템 모두 동일한 압축기를 가진원으로 하고, 수신부는 서로 다른 특성을 가지는 배관으로 구성된 별도의 시스템이다. 두 시스템은 각각 Fig. 5의 추정 시스템(a)과 검증 시스템(b)에 해당한다. 검증 시스템을 구성하기 위해 Fig. 5(a)의 추정 시스템 배관에 추가 질량을 부착하여 별도의 특성을 가진 수신부를 모사하였다.
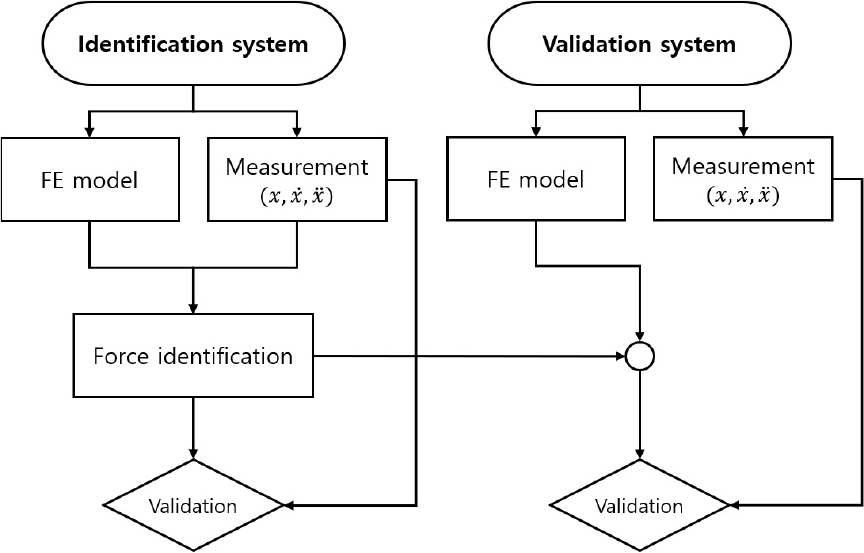
검증 실험 절차는 다음과 같다. 추정 시스템의 압축기 구동 실험에서 얻은 응답 데이터를 기반으로 가진력을 추정하고, 해당 가진력을 유한요소 모델에 적용하여 배관의 특정 위치에서 정상상태 응답을 예측한다. 이후, 예측된 응답을 동일한 위치에서 측정된 응답과 비교함으로써 제안된 방법의 유효성을 검증한다. 또한, 추정 시스템에서 추정된 가진력을 동일한 가진원으로 구성된 검증 시스템 유한요소 모델에 적용하여 특정 위치의 응답을 예측, 측정값과 비교한다. 이를 통해, 추정된 가진력의 독립성을 확인하며, 전체 검증 실험 절차는 Fig. 6의 흐름도와 같다.
4.2 실험 대상 시스템 특성 분석
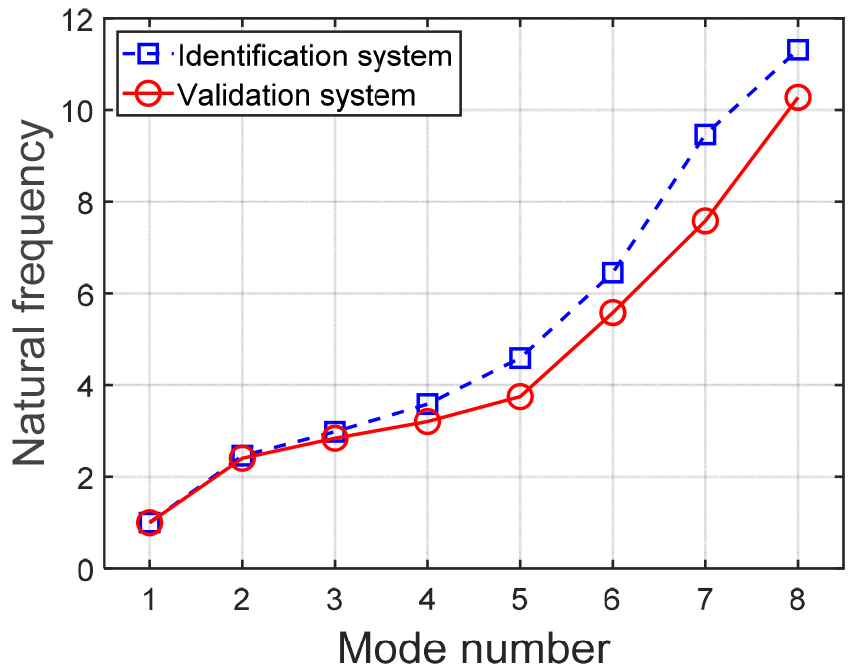
상용 소프트 웨어 ANSYS APDL을 활용하여 추정 및 검증 시스템의 유한요소 모델을 구성하였고, Fig. 7과 같다. 배관에 부착되는 센서의 영향을 고려하기 위해 시뮬레이션 모델에 센서 부착 위치와 동일한 노드에 센서의 무게와 같은 집중 질량을 추가하였다. 해당 모델은 Fig. 3의 대체 모델과 동일한 요소들로 구성되어 있고, 검증 모델의 경우 추가 질량 부착 위치에 점 질량을 추가하여 실제 시스템을 구현하였다. 또한, 실제 시스템에 대한 충격 가진 실험 결과를 기반으로 두 시스템 간 역학적 특성의 차이를 확인하고 유한요소 모델의 정확도를 평가하였으며, 반복적인 실험을 통해 센서 부착의 타당성을 확인하였다. Fig. 8과 Table 1은 충격 가진 실험을 통해 얻은 추정 시스템과 검증 시스템의 고유진동수를 비교한 결과이며 제품 보안상의 이유로 정규화되었다. 해당 결과로부터, 두 시스템은 서로 다른 특성을 나타내는 별개의 시스템임을 알 수 있다.
Table 1.
Relative error of natural frequencies between identification and validation system.
| Mode number | Relative error (%) |
| 1 | 0.68 |
| 2 | 1.65 |
| 3 | 4.16 |
| 4 | 10.02 |
| 5 | 17.76 |
| 6 | 12.88 |
| 7 | 19.35 |
| 8 | 8.55 |
4.3 실험을 통한 검증 결과
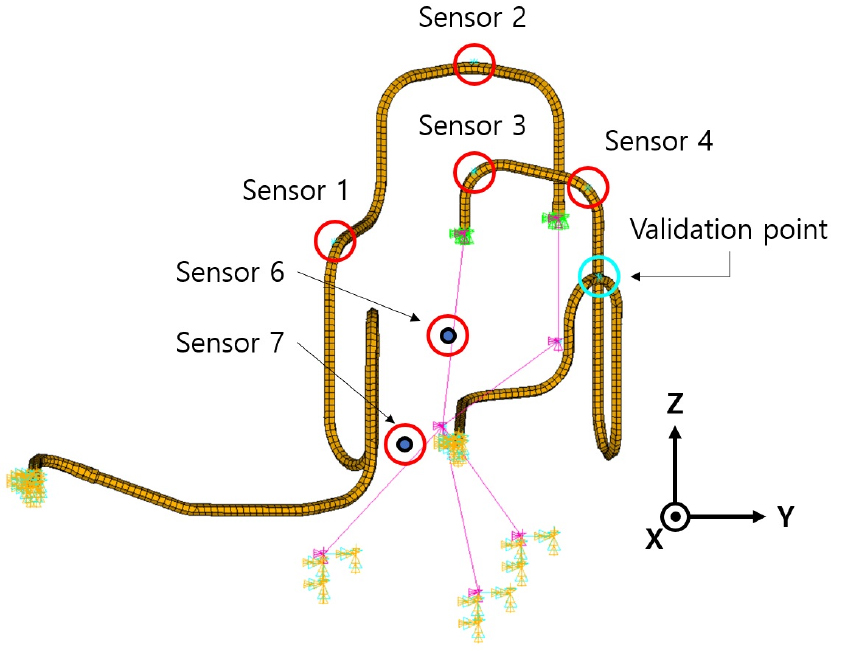
배관 내 유체에 의한 영향을 배제하기 위해 냉매를 제거한 두 압축기-배관 시스템의 압축기 구동 중 응답을 얻기 위해 구동 주파수를 66.13 Hz, 73.04 Hz, 101.8 Hz로 증가시키면서 가속도 응답을 측정했다. 측정은 구동 주파수(~200 Hz)보다 큰 0 kHz ~ 5 kHz의 측정 주파수 범위를 가지는 3축 가속도계와 LMS SCADAS Mobile(SCM05) 데이터 수집 장비를 사용하였고, 센서 부착위치는 Fig. 6에 나타나 있다. 또한, 가진력 추정을 위한 시계열 데이터 연산 및 주파수 영역 분석을 고려하여 Table 2의 정보로 신호를 획득하였다. 측정된 가속도 응답 데이터는 수치 적분 시 발생하는 오차 제거를 위해 차단 주파수 3.5 Hz를 가지는 고역 통과 필터가 적용되었다. 압축기 질량 중심 위치에서의 응답은 직접적으로 측정할 수 없으므로, Fig. 6에 Sensor 6, 7로 표시된 압축기 표면에 부착한 센서들의 측정값들을 가상 지점 변환 기법에 적용하여 계산되었다. 실험을 통해 얻은 배관 응답들과 유한요소 모델을 Eq. (6)에 반영하여 압축기의 가진력을 추정하였다.
Table 2.
Information of signal acquisition and processing used for FFT.
| Measurement time per driving frequency (s) | 47 |
| Frequency resolution (Hz) | 0.02 |
| Sampling frequency (Hz) | 512 |
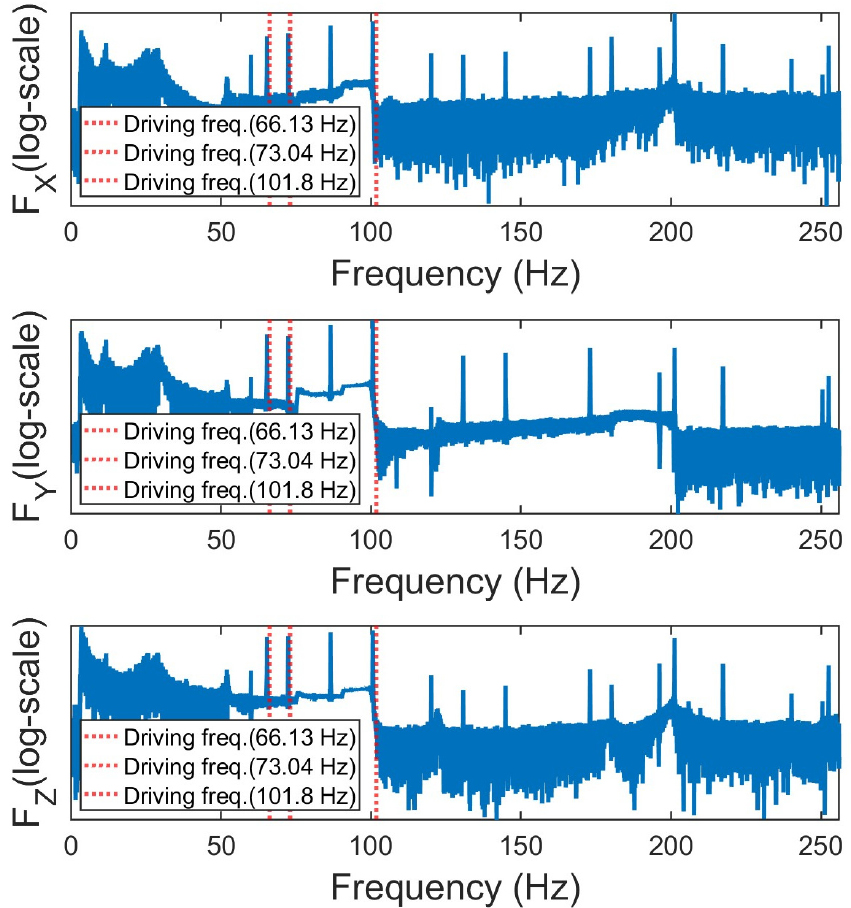
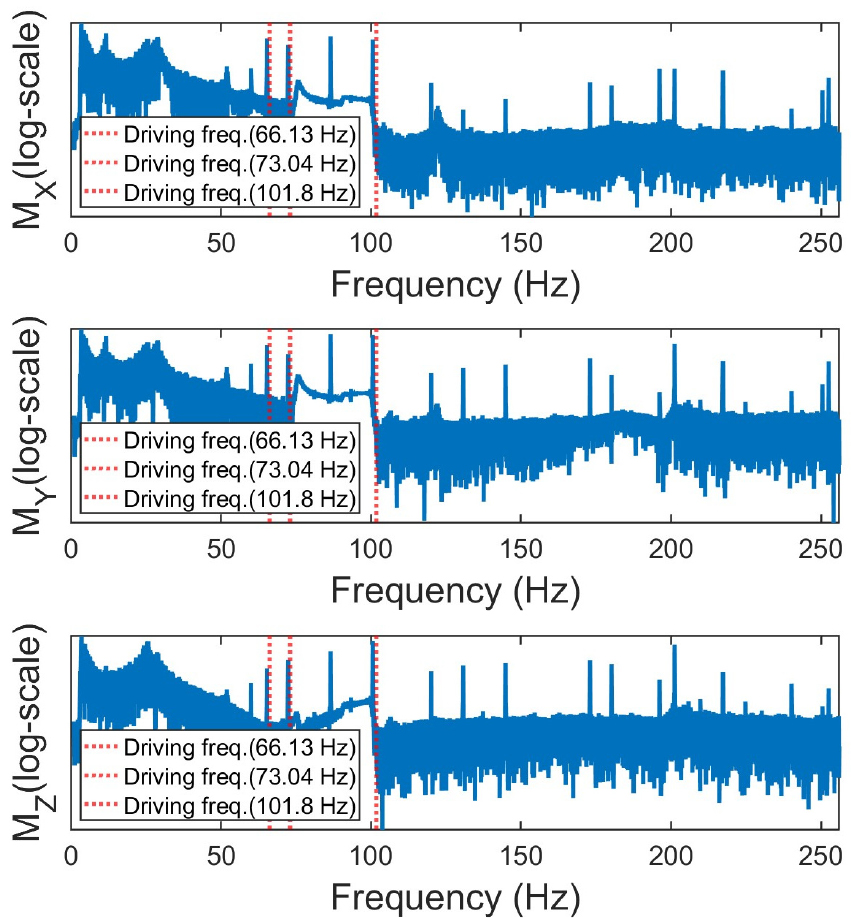
Figs. 9와 10은 압축기 질량 중심에서 발생하는 가진력()과 모멘트()의 방향 별 성분들을 주파수 영역에 나타낸 결과이며, 진폭은 제품 보안상의 이유로 정규화되었다. 가진력은 y축 방향에서 가장 크고 z축 방향에서 가장 작게 추정되었고, 모멘트는 x축 방향에서 가장 크고 y, z방향에서는 비슷한 수준으로 추정되었다.
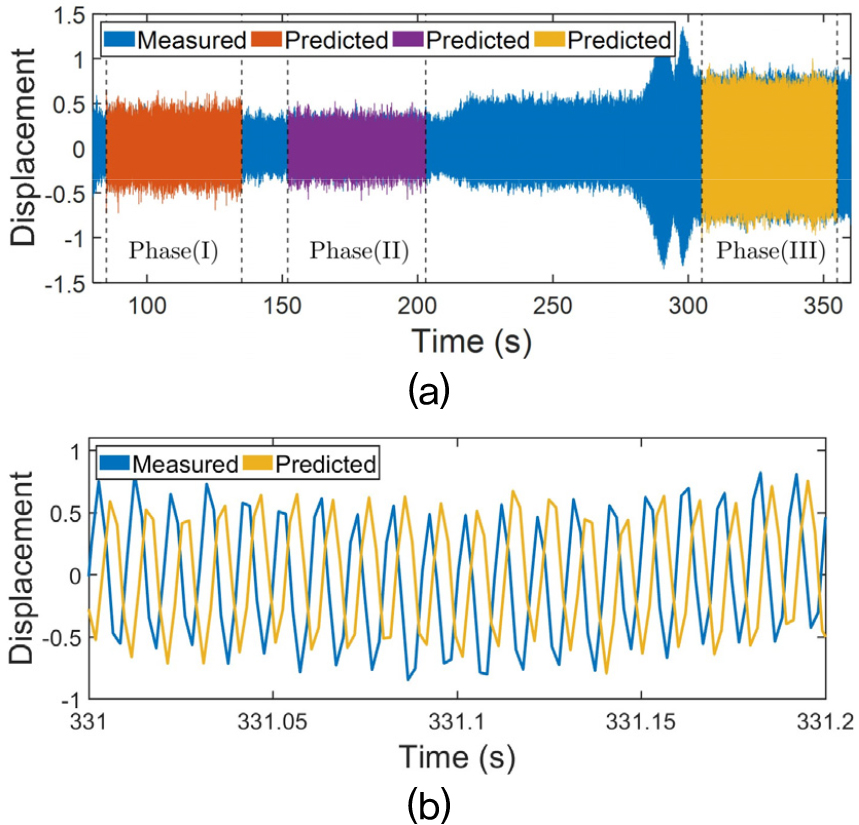
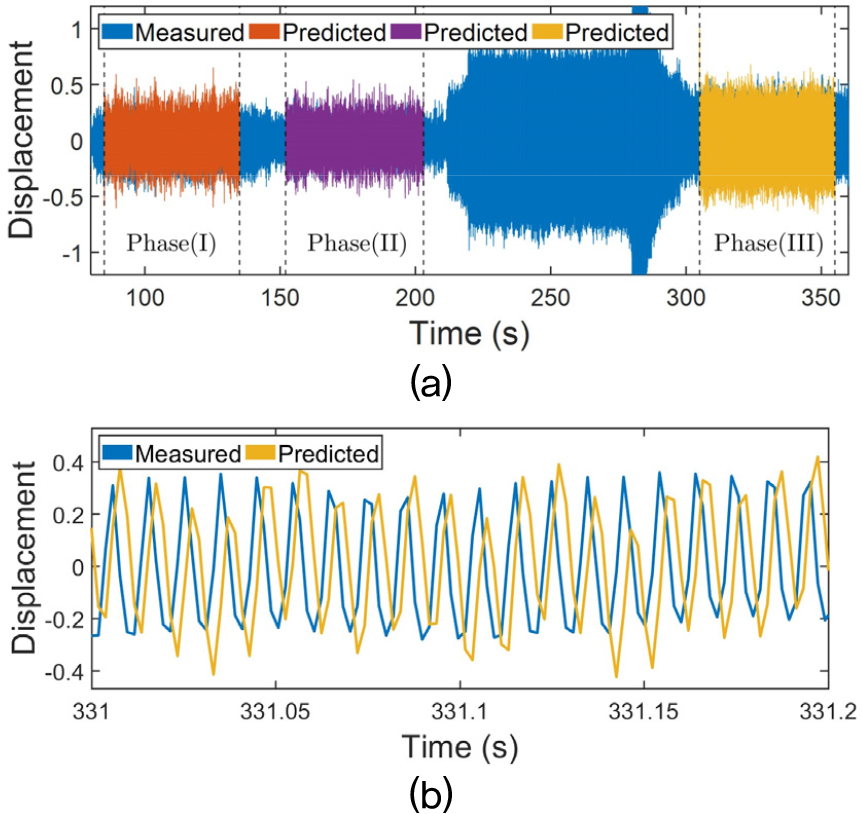
추정된 가진력과 모멘트를 바탕으로 Eqs. (11), (12), (13), (14), (15)를 통해 예측된 추정 시스템과 검증 시스템의 응답 측정값과 정상상태 응답 예측값은 각각 Figs. 11과 12와 같으며, 진폭 값은 제품 보안상 이유로 응답의 최댓값을 기준으로 정규화되었다. 또한, 해당 응답들은 모두 Fig. 6의 validation point에서 예측 및 측정되었다. Figs. 11(a)과 12(a)에 나타난 측정된 응답의 경향성은 수신부 특성의 차이로 인해 구동 주파수 변화에 따라 큰 차이가 있음을 보여준다.
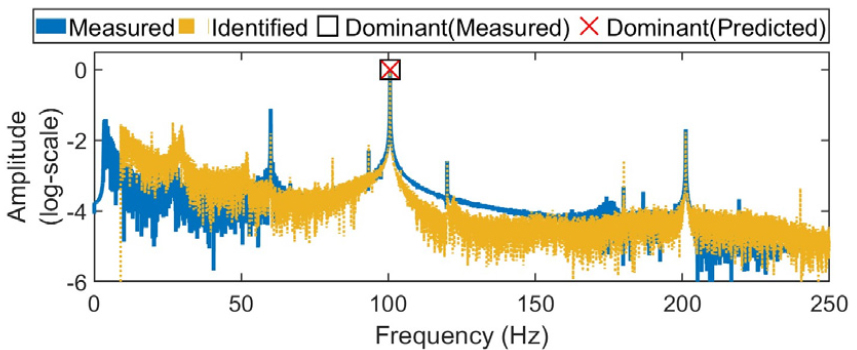
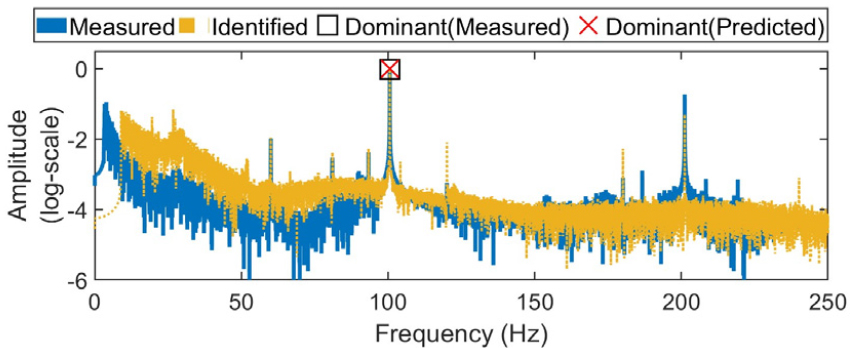
Figs. 11과 12에서 각 구동 주파수에 따른 정상 상태 구간을 Phase (I), (II), (III)으로 구분하였으며, 예측된 정상 상태 응답을 토대로 추정된 가진력의 정확도를 평가하였다. 이를 위해, 시간 영역에서 각 구간별로 예측된 응답과 측정된 응답의 Root Mean Square(RMS) 값 사이의 상대오차를 계산하고, 해당 응답들에 대해 FFT를 수행하여 가장 지배적인 주파수 성분의 진폭 간 상대오차를 분석하였다. Figs. 13과 14는 Phase (III) 구간 응답들의 주파수 성분들을 보여준다. Tables 3과 4는 각각 추정 시스템과 검증 시스템에서 계산된 상대오차이며, RMS 값의 상대 오차 계산 시 노이즈 영향을 줄이기 위해 예측된 응답의 상위 2 %와 하위 2 % 데이터를 제거하여 계산하였다. 또한, FFT 분석에서 사용된 정상 상태 응답 데이터의 길이와 샘플링 주파수로 인해 주파수 해상도는 0.02 Hz로 설정되었으며, 이 조건에서 지배적인 주파수 성분의 피크 위치가 정확히 일치함을 확인하였다.
Table 3.
Relative errors between the RMS values of the identification system responses and the amplitude of the dominant frequency component after FFT for each phase.
| Phase (I) | Phase (II) | Phase (III) | |
|
RMS value relative error (%) | 4.34 | 0.13 | 9.71 |
|
FFT amplitude relative error (%) | 6.29 | 5.84 | 0.16 |
Table 4.
Relative errors between the RMS values of the validation system responses and the amplitude of the dominant frequency component after FFT for each phase.
| Phase (I) | Phase (II) | Phase (III) | |
|
RMS value relative error (%) | 6.96 | 11.34 | 1.2 |
|
FFT amplitude relative error (%) | 8.54 | 9.57 | 3.6 |
서로 다른 수신부를 갖는 두 시스템에 대한 검증 결과를 통해, 제안된 방법이 시스템 레벨에서 측정된 응답과 유한요소 해석을 결합하여 압축기의 가진력을 높은 정확도로 추정할 수 있음을 확인할 수 있으며, 추정된 가진력이 연결된 수신부의 특성을 반영하지 않은 가진원 고유의 성분임을 알 수 있다.
V. 결 론
본 연구에서는 대상 시스템의 분해 과정 없이 시스템 레벨에서 측정된 응답과 유한요소 해석을 통합한 간접적인 가진력 추정 방법을 제안하였다. 이를 검증하기 위해, 동일한 가진원과 각각 서로 다른 특성을 나타내는 수신부를 가진 두 개의 시스템을 구성하고, 추정 시스템에서 식별된 가진력을 두 시스템에 적용하여 수신부의 특정 위치에서의 정상 상태 응답을 예측하였다. 추정 시스템과 검증 시스템에서 예측값과 측정값의 RMS 값 상대오차는 3개의 구간들에 대해 평균 4.73 %, 6.5 %로 나타났으며, 응답의 지배적인 주파수 성분에 대한 상대오차는 평균 4.1 %, 7.23 %로 나타났다. 이를 통해, 제안된 방법이 가진원의 고유한 가진력을 효과적으로 추정할 수 있음을 확인하였다.
하지만, 해당 방법은 유한요소 모델의 정확도와 응답 측정 시 노이즈가 가진력 추정에 큰 영향을 미친다는 한계를 가지고 있다. 이를 보완하기 위해, 예측값과 측정값 간의 오차를 기반으로 유한요소 모델을 최적화하는 알고리즘을 추가하여 추정된 가진력의 정확도를 개선해 나갈 것이다. 또한, 실제 제품의 압축기를 대상으로 한 검증 실험에서 상용 압축기 제어 프로그램(Pulse Generator Module, PGM) 조작 제한으로 인해 정해진 프로그램만 사용 가능하였다. 따라서, 구동 조건에 대한 가진력 추정 및 검증에 제약이 있었다. 향후 연구에서는 보다 다양한 구동 주파수에 대한 검증시험을 통해 제안하는 방법의 검증 범위를 확대하고, 적용 가능한 주파수 범위 도출에 관한 연구를 추가로 진행할 예정이다.