I. 서 론

소나체계는 송․수신기 구성 방법에 따라 단일 플랫폼의 송․수신기로 구성된 단상태, 서로 공간적으로 이격된 송․수신기로 구성된 양상태, 다중 송․수신기 시스템으로 구성된 다중상태로 구분될 수 있다. 최근 잠수함의 저소음화로 인해 수중표적 탐지가 어려워짐에 따라 양상태 및 다중상태 소나 시스템을 고려한 모델링 및 시뮬레이션 연구의 필요성이 증대되고 있다.

공간적으로 분리된 수상함 2척에서 양상태 소나를 운용하는 경우, 직접파에 의해 발생하는 음영구역과 단상태 소나로 탐지하는 영역 외에 추가적으로 탐지할 수 있는 영역이 존재할 수 있다.^[1,2,3,4] 따라서 각 수상함에서 단상태 소나와 양상태 소나를 교차 운용하는 경우, 단상태 소나만을 운용하는 경우보다 수중표적 탐지성능을 향상시킬 수 있다. 하지만 양상태 소나 탐지성능은 해양환경, 송․수신기 위치(위도, 경도)와 수심에 따라 크게 변동하기 때문에 해양환경을 반영한 송․수신기의 위치와 수심 최적화 연구가 필요하다.^[1,2,3,4] 수동소나, 단상태 소나(소노부이, 수상함)를 활용한 소나 배치 연구는 많이 수행되었지만,^[5,6,7,8,9] 양상태 소나 배치 연구는 연산량 증가로 인해 해양환경을 간단하게 고려한 연구만이 진행되었으며,^[2,9] 특히 단상태 소나와 양상태 소나의 교차 운용을 고려한 소나 배치 연구는 수행된 바 없다.

본 논문에서는 서로 이격된 위치에서 정지한 상태의 수상함 2척이 각각 단상태 소나와 양상태 소나를 운용하는 경우를 고려하였다. 단상태․양상태 소나 탐지확률은 국방과학연구소와 한양대학교가 공동으로 개발한 음선이론 기반의 소나 성능분석 모델인 Bistatic Sonar Performance Analysis System(BiSPAS)을 통해 산출되었으며,^[3,4] 산출된 각각의 탐지확률을 융합하여 탐색구역 내의 탐지 가능 면적을 계산하였다. 탐색구역 내 탐지가 가능한 면적을 최대로 하는 송․수신기의 위치와 수심을 탐색하기 위해 입자 군집 최적화(Particle Swarm Optimization, PSO) 알고리즘이 사용되었다. 본 연구에서는 동해 울릉분지 지역의 해양환경을 기반으로 PSO 알고리즘을 이용하여 양상태 소나의 최적 위치를 계산하였다. 또한, 제안하는 배치 알고리즘의 성능을 평가하기 위해 모델 반복 횟수에 따른 탐지면적과 입자들의 수렴성을 확인하였다.

본 논문의 구성은 다음과 같다. 제2장에서는 단상태 소나와 양상태 소나의 융합탐지확률 산출 방법에 대해 설명하고 제3장에서는 양상태 소나 배치 최적화 방안을 기술하였다. 제4장에서는 동해 울릉분지 지역에서 PSO 알고리즘을 적용한 배치 결과를 분석하였다. 마지막으로 제5장에서는 본 연구의 요약 및 결론에 대해 기술하였다.

II. 단상태․양상태 교차 운용에 따른 융합탐지확률 산출

소나 탐지성능을 나타내는 능동 신호초과(Active Signal Excess, ASE)는 Eq. (1)의 소나방정식으로 산출할 수 있다.^[10,11]

Eq. (1)에서 ASER, ASEN은 각각 잔향음 제한환경에서의 능동 신호초과, 주변소음 제한환경에서의 능동 신호초과이며, SL은 음원준위, TL1은 음원에서 표적까지의 전달손실, TL2는 표적에서 수신기까지의 전달손실, RL은 잔향음 준위, NL은 주변소음 준위이며, TS는 표적강도, DI는 지향지수, DT는 탐지문턱이다. Eq. (1)을 통해 계산된 능동 신호초과는 Eq. (2)를 통해 탐지확률 Pd로 계산된다.^[11]

Eq. (2)에서 𝜎는 수중음향 불확정성에 의한 신호초과의 표준편차를 의미하며, 본 논문에서는 9 dB로 적용되었다.^[10] 중주파수 대역의 소나를 가정하였으며, 음원준위는 215 dB, 신호길이는 4 s로 설정되었으며, 송․수신기간의 거리는 30 km, 수상함 1, 수상함 2의 송․수신기 수심과 표적 수심은 동일하게 150 m, 표적강도는 6 dB로 설정되었다.

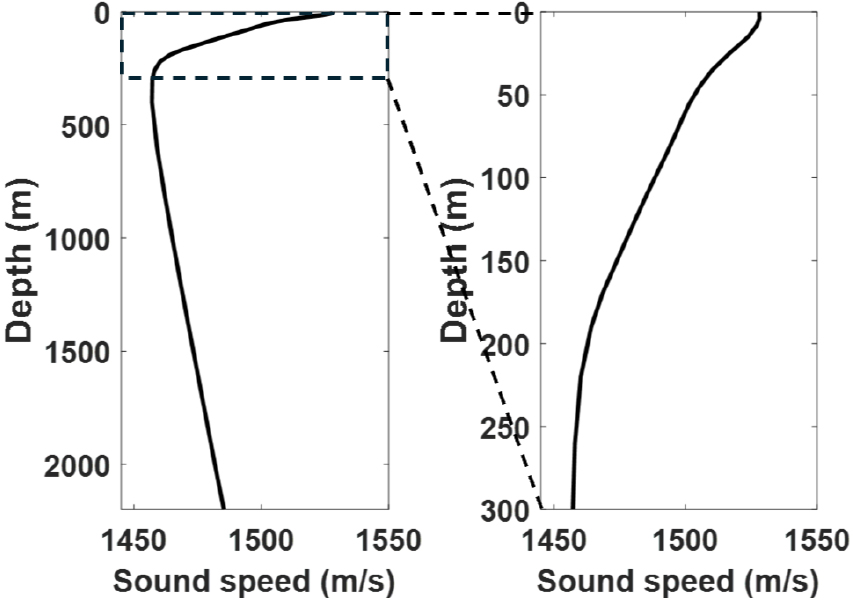
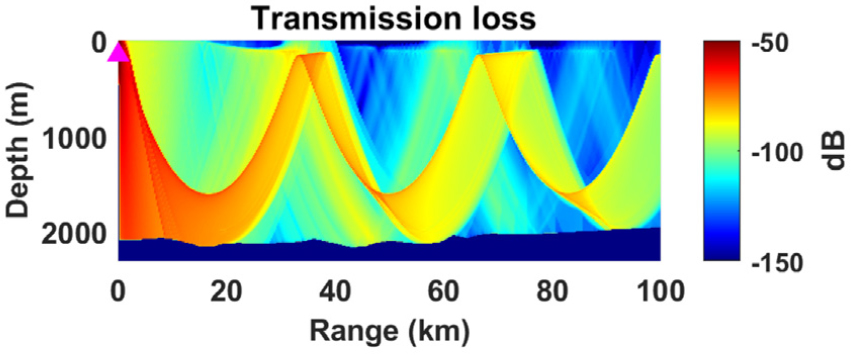
Fig. 1은 동해에서의 여름철 대표적인 음속구조를 나타낸다.^[12] Son et al.^[4]이 심해에서 양상태 소나 탐지환경에 대해 보고한 바와 같이 동해 울릉분지 지역에서 소파(Sound Fixing and Ranging channel, SOFAR) 채널 내에서 방사되는 음파는 최소음속층을 기준으로 하향굴절과 상향굴절을 반복하며 장거리 전파되는 특성을 나타낸다(Fig. 2).

Fig. 1.

Sound speed profile of East sea in summer.

Fig. 2.

(Color available online) Sound propagation at source depth of 150 m in summer. Magenta triangle indicates the sound source.

공간적으로 분리된 수상함 2척(수상함 1, 수상함 2)에서 각각 단상태 소나, 양상태 소나를 교차 운용하는 경우의 탐지확률 결과는 아래 4가지로 구분될 수 있다.

1. 수상함 1에서 산출된 단상태 소나 탐지확률

2. 수상함 1에서 산출된 양상태 소나 탐지확률(수상함 1이 수신기인 경우)

3. 수상함 2에서 산출된 단상태 소나 탐지확률

4. 수상함 2에서 산출된 양상태 소나 탐지확률(수상함 2가 수신기인 경우)

본 연구에서는 위 4가지의 탐지확률 결과 중 각 수상함에서 산출된 소나 탐지확률을 기준으로 1번과 2번, 3번과 4번을 각각 Eq. (3)을 통해 융합하였으며, 두 개 융합탐지확률(Combined Detection Probability, CDP) 결과 중 최댓값을 기준으로 최종 융합탐지확률을 산출하였다.

Fig. 3은 여름철 동해 울릉분지 지역에서 수상함 2척 간의 거리 30 km, 송․수신기 수심과 표적 수심을 150 m로 동일하게 설정하여 모의한 최종 융합탐지확률 산출 예시를 나타낸다. 단상태 소나 탐지영역은 각 수상함을 중심으로 원형 띠 모양의 특징을 나타내며, 두 원형 띠가 겹치는 부분에서 양상태 소나 탐지 가능 영역이 형성되었다. 따라서 최종 융합된 탐지확률 결과는 각 수상함의 단상태 소나 탐지영역이 합쳐진 결과로 나타나게 된다. 본 연구에서는 탐색구역 내 최종 융합탐지확률이 50 % 이상인 부분에 해당하는 면적을 탐지 가능 면적으로 고려하였다.

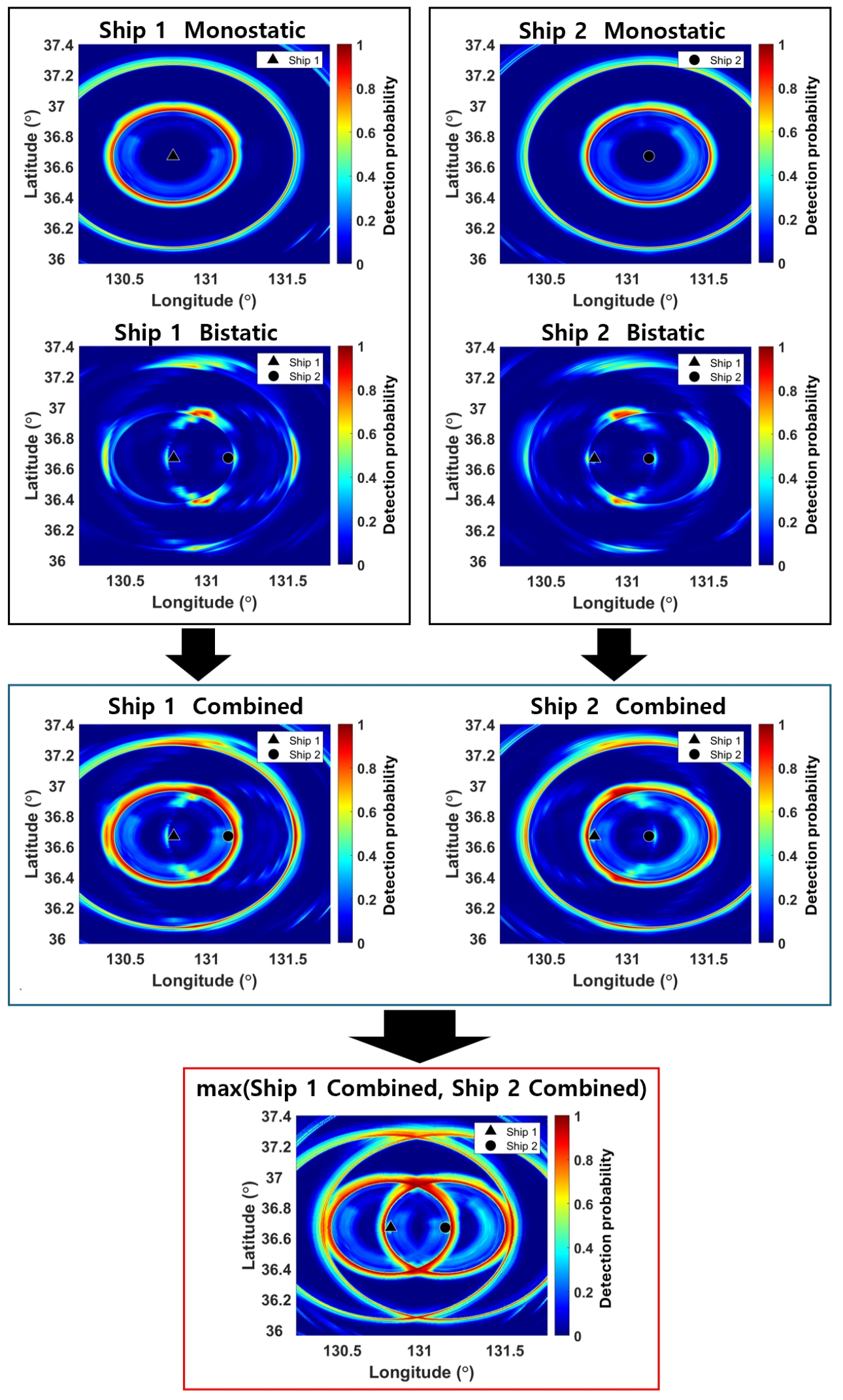
Fig. 3.

(Color available online) Example of the process of combining the monostatic detection probability and bistatic detection probability for each of ship 1 (black triangle) and ship 2 (black circle) simulated in the Ulleung Basin in the East Sea (source depth: 150 m, receiver depth: 150 m, target depth: 150 m, source to receiver range: 30 km).

III. 양상태 소나 배치 최적화

양상태 소나 송․수신기의 위치와 수심 배치 최적화를 위해 입자 군집을 기반으로 문제의 해를 찾는 확률적 최적화 알고리즘인 PSO 알고리즘이 사용되었다. PSO는 광범위한 영역을 효율적으로 빠르게 탐색하며, 안정적으로 최적해를 찾는다는 장점이 있다.^[13,14] 본 연구에서 1개 입자는 수상함 1의 위도(°), 경도(°), 송․수신기 수심(m), 수상함 2의 위도(°), 경도(°), 송․수신기 수심(m), 총 6개 인자로 구성되었다. 본 연구에서는 양상태 성능분석 모델의 연산량과 복잡도를 고려하여 총 20개 입자만을 고려하였다. 초기 20개 입자는 탐색구역 범위 내에서 무작위로 배치되며, 수심은 50 m부터 250 m 사이에 무작위 배치되도록 하였다. 이후 20개 입자들은 Eq. (4)를 통해 탐색구역 내 탐지 가능 면적을 최대로 하는 방향으로 이동하도록 20회 반복 수행되었다.

Eq. (4)에서 vik는 i번째 입자의 k번째 반복 횟수에서의 속도벡터, pi는 i번째 입자가 k번째 반복 횟수까지 탐색했던 최적의 위치, xik는 i번째 입자의 k번째 반복 횟수에서의 위치, g는 군집 전체가 k번째 반복 횟수까지 탐색했던 최적의 위치를 나타낸다. r1과 r2는 각각 단일 입자의 정보 중요도, 군집 전체의 정보 중요도이며, 0부터 1사이의 난수이다. c1과 c2는 가속도 상수이며, 2로 동일하게 설정되었다.^[13,14]W는 속도 항의 가중치이며 0.9로 설정되었다. 각각의 입자들은 Eq. (4)를 k번째 반복하는 동안 vi(k+1)가 최소가 되는 위치로 이동하면서 최적의 위치로 수렴하게 된다.

IV. PSO 알고리즘을 이용한 양상태 최적 배치 결과

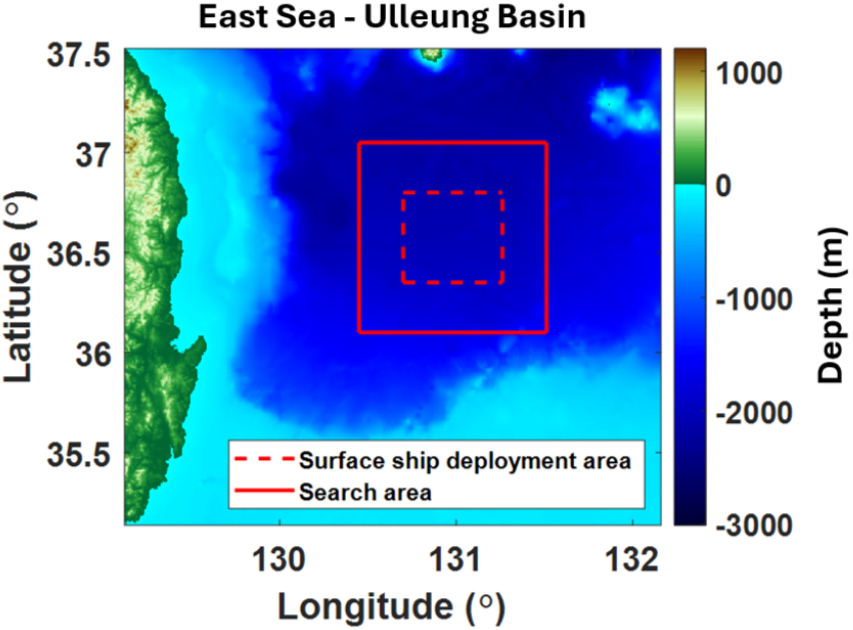
동해 울릉분지 지역에서 PSO 알고리즘을 이용한 양상태 소나 송․수신기의 위치와 수심 배치 최적화가 수행되었다. 탐색구역은 경도 약 130.7°E부터 131.26°E, 위도 36.35°N 부터 36.8°N까지 약 50 km × 50 km의 사각 영역으로 설정하였으며, 수상함 배치 구역은 심해 환경이 원거리 탐지환경임을 고려하여 경도 130.1°E부터 131.5°E, 위도 36.1°N 부터 37.1°N까지 약 100 km × 100 km의 탐색구역을 포함하는 사각 영역으로 설정하였다(Fig. 4). 탐지성능 모의에 사용된 해저 지형 자료는 ETOPO1^[15]가 이용되었으며, 음속구조는 GDEM^[12] 자료가 사용되었다.

Fig. 4.

(Color available online) Bathymetry of East Sea. The solid red square represents the boundary of area where the surface ships can move, and the red dashed square represents the boundary of search area.

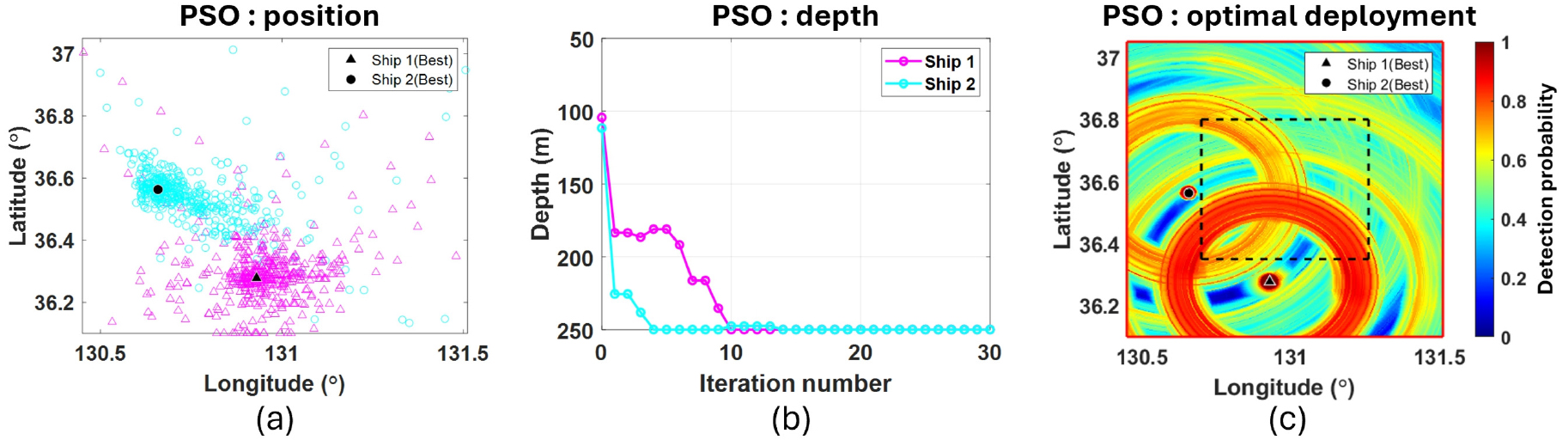
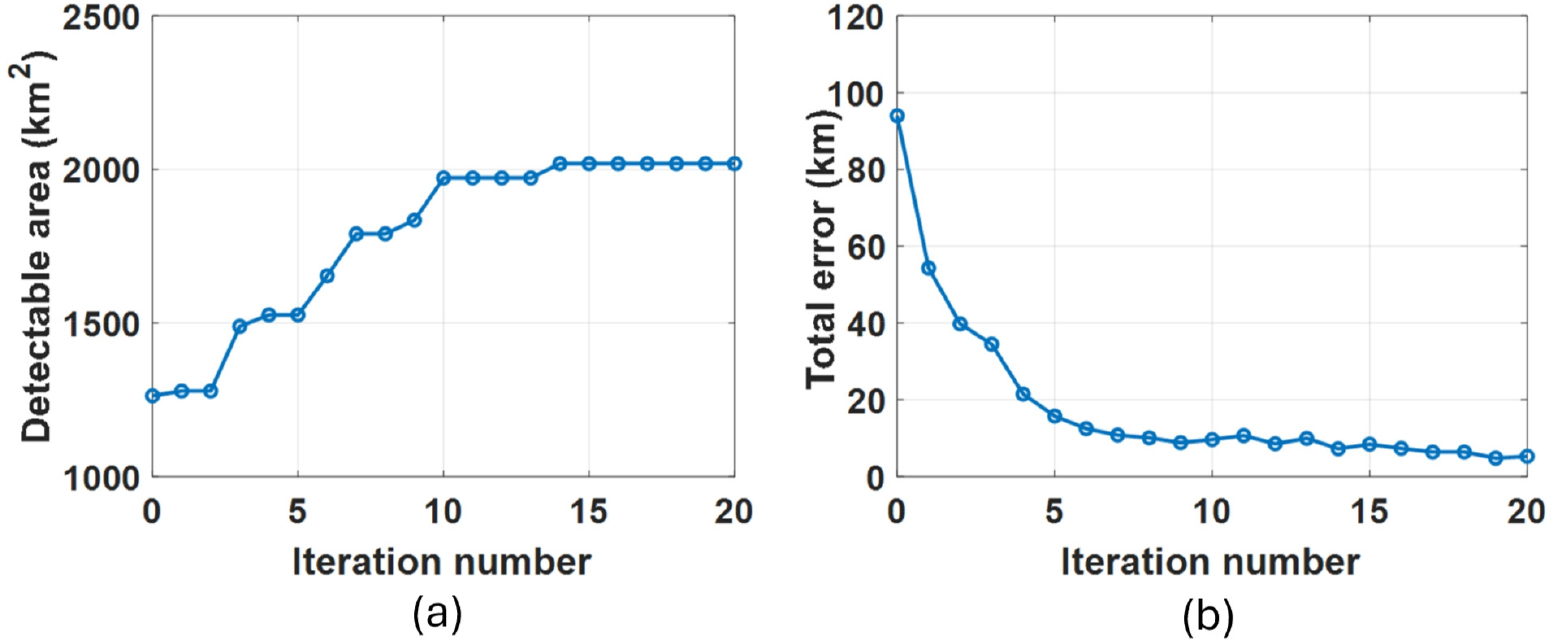
Fig. 5(a)는 PSO 알고리즘을 기반으로 최적화된 수상함 1, 수상함 2의 송․수신기 위치(위도, 경도)를 나타낸다. 분홍색 삼각형과 하늘색 원은 20번째 반복 횟수 동안 수상함 1과 수상함 2 입자의 모든 위치를 나타내며, 검은색 삼각형과 검은색 원은 마지막 반복 횟수에서의 수상함 1, 수상함 2의 최적 위치를 나타낸다. Fig. 5(b)는 PSO 알고리즘을 기반으로 j번째 반복횟수까지 찾은 수상함 1, 수상함 2의 최적화된 송․수신기 수심을 나타내며, 최소음속층 위치에 가까운 250 m로 수렴하는 것이 확인되었다. Fig. 5(c)는 PSO 알고리즘을 기반으로 산출된 송․수신기 위치, 수심에서 산출된 탐지성능 분석 결과를 나타낸다. 마지막으로, 알고리즘 반복 횟수에 따른 입자들의 수렴성을 판단하기 위해 각 수상함의 최적 위치와 각 입자간의 거리 오차의 표준편차를 Eq. (5)을 통해 계산하였다. Eq. (5)로 계산된 각 수상함의 오차는 제곱합의 제곱근을 통해 총 오차로 계산되었다[Eq. (6)].

여기서 Nparticle은 설정한 입자의 개수 20, Xg(j)는 1부터 20번째 중 j번째 반복 횟수까지 찾은 수상함 1, 수상함 2의 최적 위․경도, 수심 벡터이며, Xp(i,j)는 j번째 반복 횟수에서 i번째 입자의 위․경도, 수심 벡터를 의미한다. Fig. 6(a)와 Fig. 6(b)는 알고리즘 반복 횟수에 따른 탐지 면적과 Eq. (6)을 통해 계산된 총 오차를 나타낸다. 그 결과, 반복 횟수의 증가에 따라 더 넓은 탐지면적을 가지며, 오차 또한 빠르게 줄어들며 입자들이 최적 위치에 수렴하는 것이 확인되었다.

Fig. 5.

(Color available online) The results of optimal deployment of ship 1 (black triangle) and ship 2 (black circle). (a) The optimal position and (b) depth, and (c) the simulated detection probability at optimal position and depth using PSO algorithm.

Fig. 6.

(Color available online) The results the detection area and total error according to the number of iteration of simulation for optimal deployment of ship 1 and ship 2 using the PSO algorithm (blue line with circle markers) and Monte Carlo method (black line with circle markers).

V. 요약 및 결론

본 논문에서는 동해 울릉분지 지역에서 수상함 두 척에서 운용되는 양상태 소나의 위치와 심도를 최적 배치하기 위한 연구가 수행되었다. 먼저, 두 척의 수상함에서 산출되는 탐지확률 결과에서 각 수상함을 기준으로 단상태․양상태 융합탐지확률을 계산하고 융합된 두 개의 탐지확률 중 최댓값을 기준으로 최종 융합탐지확률을 산출하였다. 탐색구역 내 최종 융합탐지확률을 최대화하는 양상태 송․수신기의 위치와 수심을 탐색하기 위해 입자 군집 기반의 PSO 알고리즘이 사용되었다. 본 논문에서 제안하는 배치 알고리즘으로 수상함 2척의 송․수신기 위치와 수심 최적화를 수행한 결과, 모델 반복 횟수의 증가에 따라 탐지면적이 증가하였으며 입자들이 최적의 위치와 수심으로 수렴하는 것이 확인되었다.

본 논문에서 제안하는 양상태 소나 배치 알고리즘은 탐색 구역, 수상함 배치 구역, 총 입자의 개수에 따라 다른 배치안이 도출될 수 있다. 본 연구에서는 양상태 소나 성능분석 모델의 복잡도와 연산량을 고려하여 20개 입자만이 고려되었지만, 더 많은 입자 개수를 이용하여 최적화를 수행한다면 기존 결과보다 더 넓은 탐지면적을 가지는 배치안이 도출될 수도 있다. 따라서 본 논문의 제안된 배치안은 제한된 조건에서 도출된 하나의 결과만을 나타낸다.

마지막으로 본 연구에서는 음파가 소파 채널을 통해 장거리 전파되는 해양환경 조건을 기반으로 배치 알고리즘이 구성되었다. 따라서 송․수신기 수심이 최소음속층에 가까이 위치할수록 더 좋은 탐지성능을 나타내기 때문에 송․수신기 수심을 구분하지 않았다. 하지만 동해 대륙사면 지역, 천해환경과 같이 경계면 조건에 의해 복잡한 음파전달 특성이 나타나는 환경^[16]에서는 송․수신기 수심을 구분해야 할 것으로 예상되며, 이에 따른 추가 분석이 필요하다.