I. 서 론

볼트 체결형 란주반 초음파 트랜스듀서는 초음파 용접기 혹은 초음파 균질기 등과 같은 초음파의 동력적인 응용분야에서 매우 널리 사용되고 있다.^[1,2,3] 이러한 란주반형 초음파 트랜스듀서는 시스템에 고정해서 사용되는데 이 때 트랜스듀서의 진동에 영향을 최소로 미치는 부분을 찾아 프렌지를 만들어 고정하는 것이 일반적이다.^[4,5,6] 따라서 프렌지의 설치 위치는 진동속도 혹은 진동 변위 분포에서 절(node)의 위치가 된다. 그러나 면내진동을 하는 란주반형 트랜스듀서의 금속 블럭 표면에서 종진동의 절을 정확히 예측하는 것은 매우 어렵다.^[7,8,9,10] 왜냐하면 물성이 상이한 금속 블록, 금속 볼트 및 압전 세라믹이 혼재되어 있으며 면적이 일정치 않은 구조로 체결되어 있어 등가회로 등을 사용한 이론적 해석으로는 진동분포의 정확한 예측이 어렵기 때문이다. 또한 유한요소 해석을 사용할 경우 구성 물질에 대한 정확한 물성치가 확보되어야만 한다는 제약이 있다.

이러한 문제들을 극복하기 위한 해결책 중의 하나로 본 연구에서는 볼트 체결형 란주반 초음파 트랜스듀서를 고정하기 위한 프렌지의 위치를 최적화하는 실험적 방법을 제안하였다. 본 연구에서는 반원형 쐐기 형태의 지그를 제작하여 란주반형 트랜스듀서의 금속블럭 측면에 부착하고 지그의 띠 형태의 좁은 면적에 일정한 압력을 가하여 프렌지와 유사한 효과를 구현하였다. 압력이 가해지는 위치를 변화시켜가며 트랜스듀서의 전기적 단자에서 측정된 입력 어드미턴스의 변화를 측정하여 분석함으로써 진동에 최소의 영향을 주는 프렌지의 위치를 찾을 수 있었다.

II. 볼트 체결형 란주반 초음파 트랜스듀서에 대한 등가회로 해석

2.1 공진특성 해석

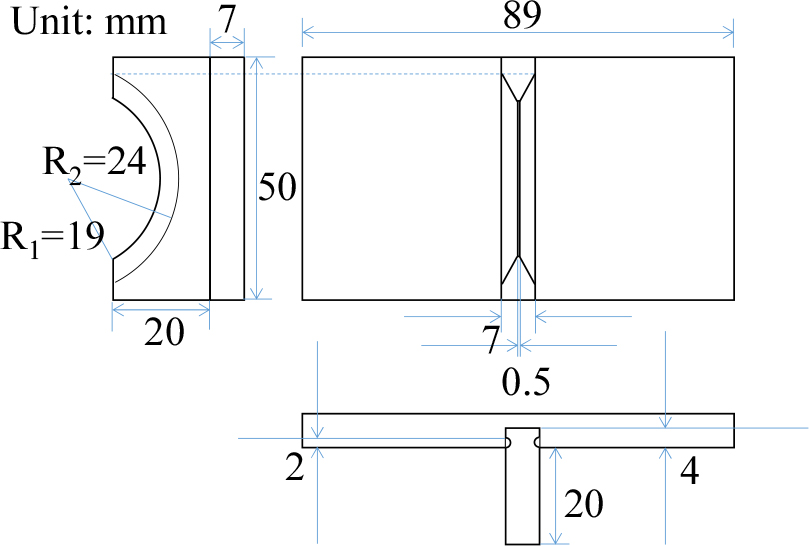
Fig. 1에 나타낸 것과 같은 볼트 체결형 란주반 초음파 트랜스듀서의 공진 특성을 해석하기 위하여 Fig. 2와 같은 Mason의 등가회로를 사용하였다.^[11] Fig. 1의 초음파 트랜스듀서의 구조는 두께가 약 5 mm인 원판형의 압전 진동자 2 장을 분극방향이 서로 마주 보도록 하여 두께가 각각 16.0 mm 및 27.5 mm인 알루미늄 봉 사이에 삽입한 후 스테인리스 스틸제 볼트로 고정되어있다. 등가회로 해석에 있어서, 분극방향을 서로 마주보게 한 고정된 2 장의 압전 진동자는 두께가 2배인 1장의 압전 진동자와 거동이 일치하므로 제동용량이 2배이고 두께가 2배인 한 장의 압전 진동자로 등가 하여 해석할 수 있다. 여기서는 볼트 및 전극판의 영향은 무시하였는데 이는 정확한 공진 주파수의 파악이 목적이 아니라, 두께진동 공진 모드들의 주파수 영역을 파악하기 위한 해석이기 때문이다.

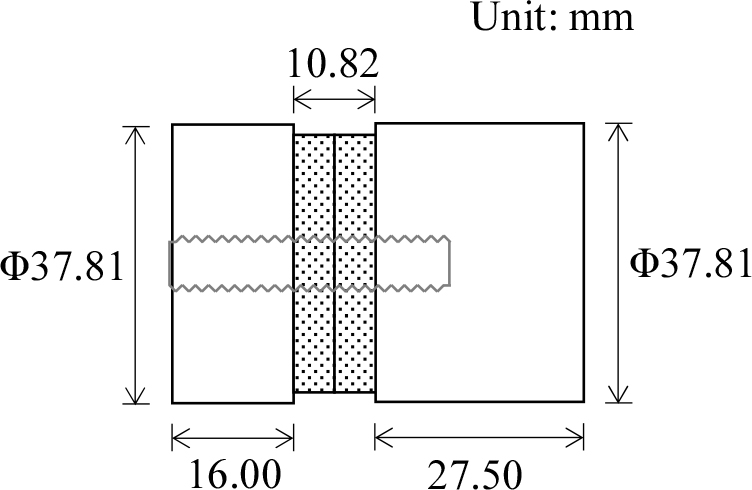
Fig. 1.

Construction of the bolt-clamped Langevin- type ultrasonic transducer. Two disk- shaped piezoelectric ceramics with a thickness of 5 mm were layered that polarization directions faced each other. The layered piezoelectric vibrator is inserted between aluminum rods and it is clamped by a stainless steel bolt.

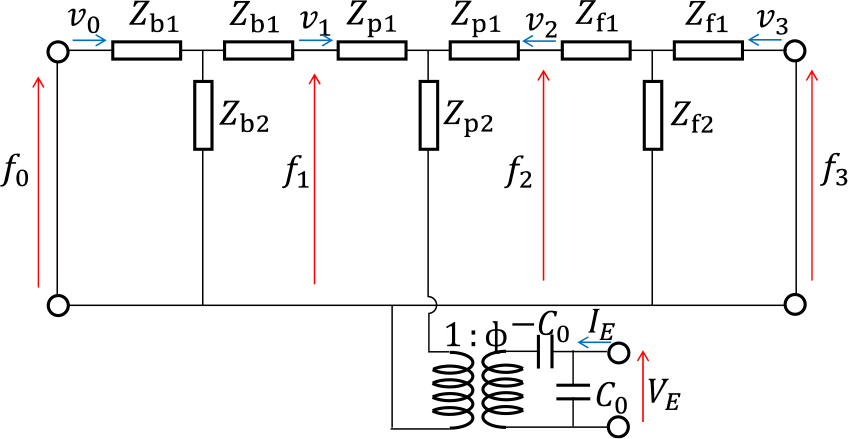
Fig. 2.

(Color available online) Mason’s equivalent circuit for the Langevin-type ultrasonic transducer. Z is the mechanical impedance of each elastic body, v is the particle velocity, and f is the force. V_E and I_E represent the voltage and the current at the electrical terminals, C₀ the clamped capacitance, ϕ the turn ratio of the transformer.

Fig. 2에 나타낸 각 변수는 다음과 같다.

Zb1=jZatankalb2,Zb2=-jZacsckalb,

Zf1=jZatankalf2,Zf2=-jZacsckalf,

Zp1=jZptankplp2,Zp2=-jZpcsckplp,

여기서 Za=ρacaS, Zp=ρpcpS, ka=2πfca, kp=2πfcp이며, ρa 및 ρp는 각각 알루미늄과 압전체의 밀도, ca 및 cp는 각각 알루미늄과 압전체의 음속이다. S는 단면적, lb,lf, 그리고 lp는 각각 뒷부분 알루미늄 봉의 길이, 앞부분 알루미늄 봉의 길이 및 압전진동자의 두께이다. ka 및 kp는 각각 알루미늄과 압전체에서의 파수이다. 전기기계 변환 변압기의 권선비로 나타나는 ϕ 및 제동용량 C0는 각각 다음과 같이 나타낼 수 있다.^[11]

여기서 e33 및 ϵ33S는 압전진동자의 압전 상수 및 유전율을 나타낸다. 또한 Fig. 2의 v0,v1,v2 및 v3와 f0,f1,f2 및 f3는 각 매질의 단면에서의 입자속도 및 힘을 나타내고 있다. 트랜스듀서의 양끝 단면에 음향매질이 없는 경우(자유단), f0 및 f3는 모두 0이 된다. 등가회로에서 전기단의 전류와 전압의 비 IE/VE를 계산하여 입력어드미턴스를 구할 수 있다.

2.2 진동분포 해석

특정 공진 주파수에 대한 트랜스듀서의 진동속도 분포를 계산하기 위하여 다음과 같은 분포정수 행렬을 사용할 수 있다. 각 매질에서의 입자속도 및 힘의 관계는 다음과 같다.^[12]

Eq. (3)에서 첫 번째 식은, 뒷부분의 알루미늄 봉에 대한 진동분포로, 트랜스듀서의 배면에 음향매질이 없다고 가정하므로 단면의 힘 f0는 0으로 두었다. 두 번째 식은 압전진동자에 대한 진동분포이며, 세 번째 식은 앞부분의 알루미늄 봉에 대한 진동분포를 계산하는 식이다. 여기서는 방사면의 입자속도로 규격화된 진동분포를 나타내기 위하여 v2=1로 두고 계산하였다.

위의 세 식을 순차적으로 계산하여 각 탄성매질에서의 입자속도를 구하면 진동속도 분포를 구할 수 있다.

III. 실험방법

란주반 초음파 트랜스듀서를 고정하는 프렌지의 효과를 구현하기 위하여 Fig. 3에 나타낸 것과 같은 반원형 쐐기 형태의 고정 지그를 제작하였다. Fig. 4(a)와 같이, 이러한 지그 1쌍을 바이스에 고정하여 트랜스듀서의 앞부분 알루미늄 봉의 측면에 압력을 가해 고정하도록 하였다. Fig. 4(b)와 같이, 압력을 가하는 부분(d)을 이동해 가며 트랜스듀서의 전기단자에서 입력어드미턴스를 측정하여 공진 특성의 변화를 관찰하였다. 이때 압력이 일정하게 인가되도록 바이스에 토크렌치를 사용하여 일정한 압력을 가하였다. 토크렌치에 의한 회전력과 이로 인해 바이스에 전달되는 축력, F, 사이에는 다음과 같은 관계가 있다.^[13]

여기서 ϕ는 볼트의 직경이고 k는 토크계수로 0.15 ~ 0.2의 값을 가진다. 따라서 지그에 의해 트랜스듀서의 측면에 가해지는 압력 P는 다음과 같이 주어진다.

여기서 A는 트랜스듀서의 측면에 닿는 지그의 면적이다. 본 연구에서는 토크를 T=7.3 Nm로 고정하였으며 바이스의 볼트직경은 ϕ=12.6 mm, 지그와 닿는 면적은 A=38.63 mm², 마찰이 없는 경우로 간주하여 k=0.2가 적용되었다. 따라서 트랜스듀서의 측면에 인가되는 압력은 약 P=75.0 MPa 로 계산될 수 있다.

Fig. 3.

(Color available online) Schematic of the semicircular wedge-shaped jig for fixing the bolt- clamped Langevin-type ultrasonic transducer.

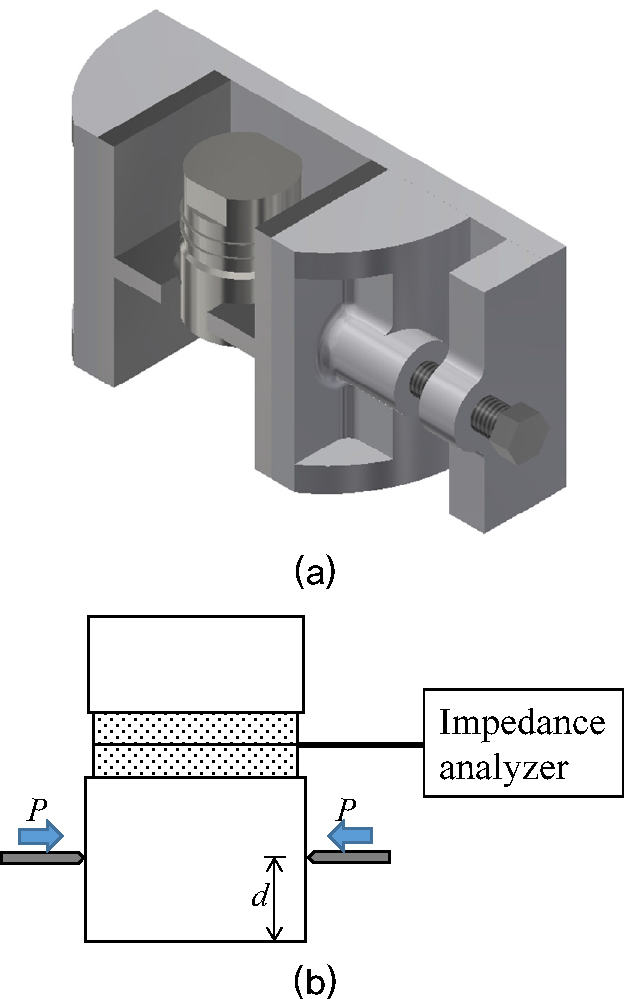
Fig. 4.

(Color available online) Design and schematic of the experimental setup. (a) The head mass of the Langevin-type ultrasonic transducer is fixed with a semicircular wedge-shaped jig. The constant pressure is applied to the jig by rotating the bolt of the right side. (b) The input impedance of the Langevin-type ultrasonic transducer is measured for different position d using the impedance analyzer.

IV. 실험결과 및 분석

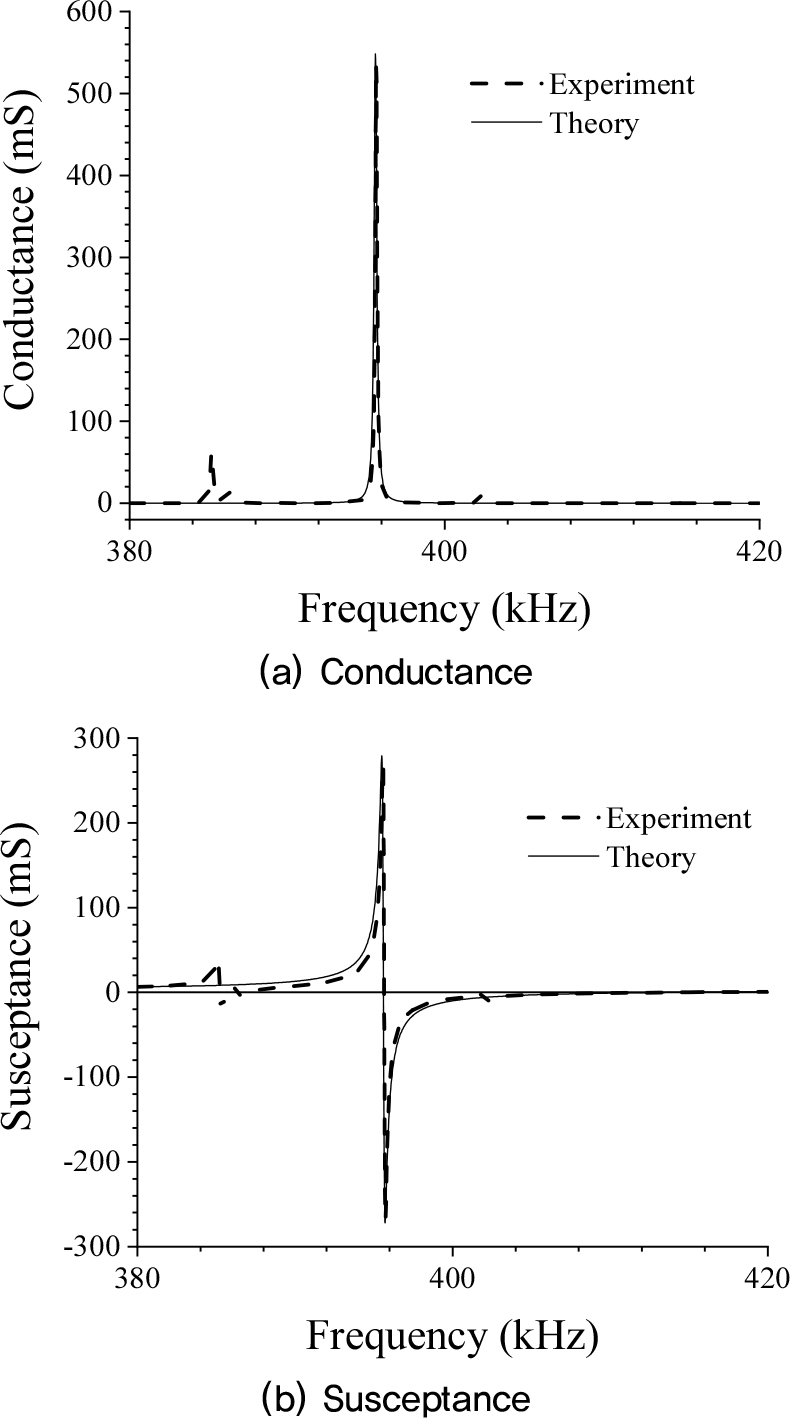
등가회로 계산에 사용할 압전체의 물질상수들을 구하기 위하여 란주반 트랜스듀서를 구성하고 있는 두께 5 mm인 원판형 압전 진동자의 입력어드미턴스를 측정하였고 그 결과를 Fig. 5에 이론계산 결과와 함께 나타내었다. 그림에서 굵은 파선은 측정결과를, 가는 실선은 계산결과를 나타낸다. 이론계산 결과는 등가회로를 이용하여 계산한 것이며 압전 진동자의 감쇠를 결정하기 위하여 계산결과가 측정결과에 근접할 때까지 압전체의 감쇠계수를 변수로 하여 반복계산을 한 후 결정하였다. 또한 란주반 트랜스듀서를 구성하고 있는 알루미늄 봉의 음속 및 밀도를 측정하였다. Fig. 5로부터 도출된 압전진동자의 물질상수와 측정된 알루미늄 봉의 물질상수들을 Table 1에 나타내었다.

Fig. 5.

Input admittance characteristics of piezoelectric vibrator of the bolt-clamped Langevin-type ultrasonic transducer. (a) Conductance that real part of the input admittance and (b) susceptance that imaginary part of the input admittance.

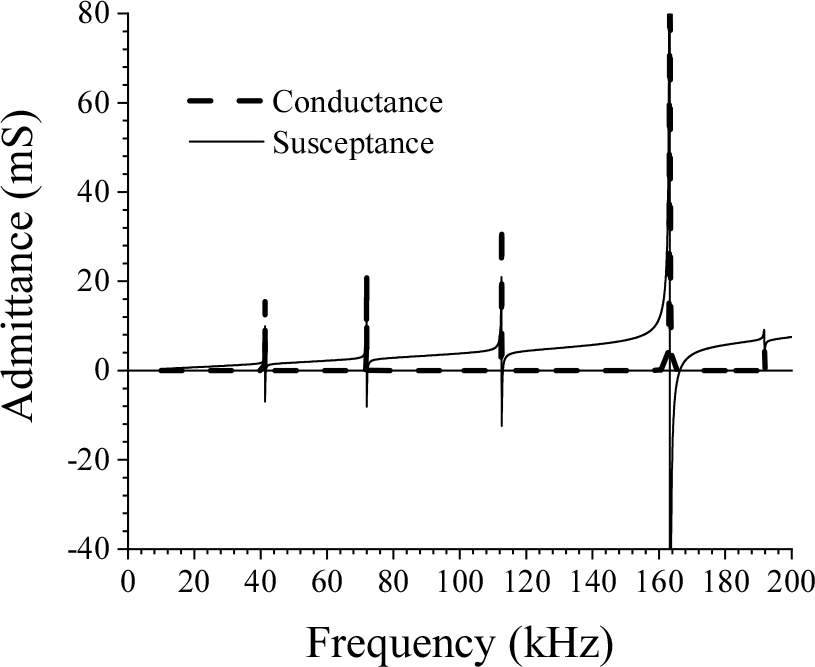
Table 1의 물질상수들을 Fig. 2에 나타낸 란주반 초음파 트랜스듀서의 등가회로의 각 요소에 적용하였다. 이 등가회로에서 란주반 초음파 트랜스듀서의 양 단면이 자유인 조건을 만족하도록 하여 전기단자의 입력어드미턴스를 계산하였고 그 결과를 Fig. 6에 나타내었다. 그림에서 컨덕턴스를 굵은 파선으로, 서셉턴스를 가는 실선으로 나타내었다.

Fig. 6.

Calculation result of the input admittance of the bolt-clamped Langevin-type ultrasonic transducer.

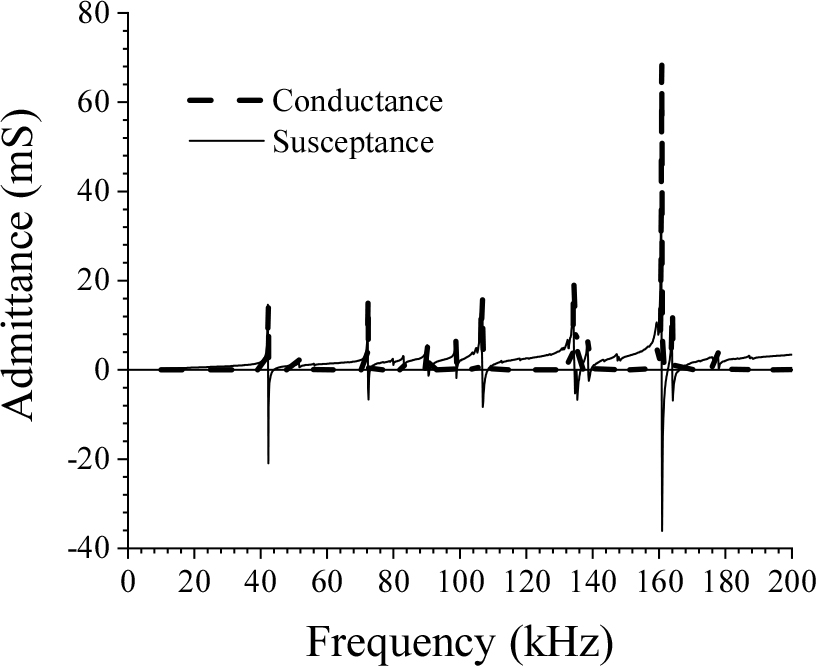
이 결과로부터 약 40 kHz부근의 기본 공진 모드와 75 kHz, 110 kHz부근 등 조화모드가 나타남을 알 수 있다. 한편 Fig. 1의 볼트 체결형 란주반 초음파 트랜스듀서의 양 단면이 자유인 조건을 갖도록 하여 임피던스 아날라이저(Keysight, E4990A)를 이용하여 측정한 입력 어드미턴스의 결과를 Fig. 7에 나타내었다. 이 결과를 보면 등가회로를 사용하여 계산한 결과인 Fig. 6의 결과와 유사하게 약 40 kHz부근에서 기본 공진 모드와 75 kHz, 110 kHz부근에서 조화모드가 나타남을 확인할 수 있다. 측정결과(Fig. 7)에서는 계산결과(Fig. 6)와는 달리 작은 스퓨리어스가 많이 나타나는데, 이들은 알루미늄과 압전 세라믹과의 접합면에서 발생하는 다중반사에 의한 것과 횡방향의 진동모드에 의한 것으로 생각된다. Figs. 6과 7을 비교해 보면, 기본공진모드와 조화모드들의 주파수 영역이 유사함을 알 수 있으며, 두 결과 사이의 약간의 차이는, 상술한 바와 같이, 등가회로 해석 시 금속 볼트 및 전극의 영향을 무시한 것으로부터 기인된 것으로 생각된다. 그럼에도 불구하고 이론계산 결과로부터 길이방향의 유효한 모드는 충분히 확인할 수 있다.

Fig. 7.

Experimental result of the input admittance of the bolt-clamped Langevin-type ultrasonic transducer.

란주반 초음파 트랜스듀서의 진동속도 분포를 해석하기 위하여 Eq. (3)을 사용하여 각 공진 모드에 대한 진동속도를 계산하였고 그 결과를 Fig. 8에 나타내었다. 진동속도 값은 트랜스듀서의 후면에서의 진동속도로 규격화하여 나타낸 것이다. 결과를 보면 기본 공진(실선)인 41.34 kHz에 대해서는 진동의 절 부분이 트랜스듀서의 방사면으로부터 약 24 mm 떨어진 곳에 나타나며 제 2 조화파 모드(파선)에 대해서는 약 5 mm, 제 3 조화파 모드(점선)에 대해서는 약 8.0 mm인 지점에 각각 나타남을 알 수 있다.

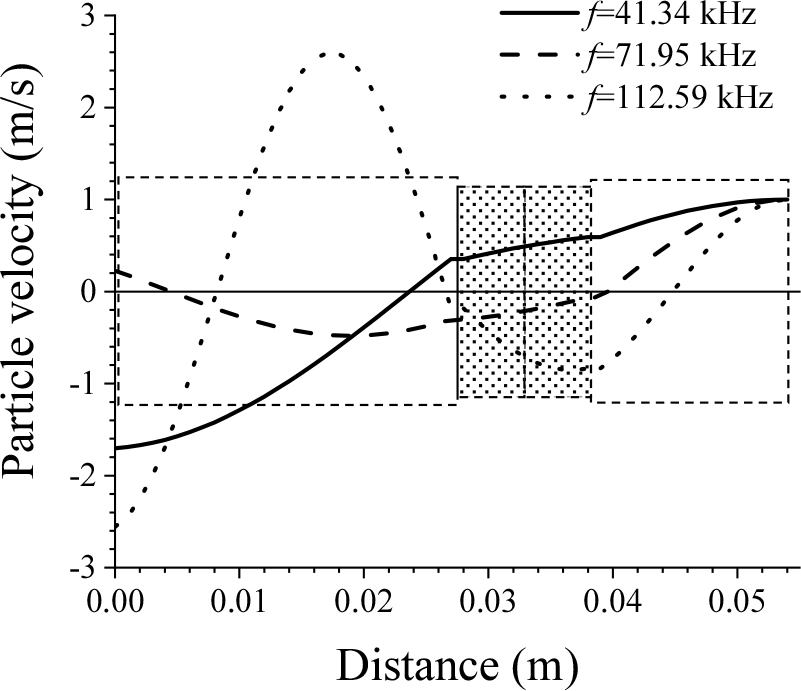
Fig. 8.

Calculation result of the particle velocity distribution for the bolt-clamped Langevin-type ultrasonic transducer under free-ends condition. In the figure, the dotted rectangles refer to the parts of the transducer, the discontinuous distributions appear at the interfaces between the dot pattern part representing the piezoelectric ceramic and the void rectangles representing the aluminum rods.

다음으로 본 연구에서 제안한 방법인 Fig. 4에 나타낸 실험장치를 사용하여 란주반 초음파 트랜스듀서의 측면에 부착한 반원형 쐐기 형태의 지그의 위치를 변화시켜 가며 트랜스듀서의 전기적인 특성 변화를 측정하였고 그 결과를 Fig. 9에 나타내었다. Fig. 9(a)는 기본 공진모드에 대한 입력컨덕턴스의 변화를 압력을 가하는 지점인 d를 변화시켜 가며 측정한 결과이다. 컨덕턴스의 피크의 위치는 공진주파수를 나타내고 있으며 트랜스듀서에 아무런 압력을 가하지 않은 자유상태인 경우의 결과를 파선으로 나타내었다. 이 파선과 피크의 위치가 가장 가까운 경우에 대해 굵은 실선으로 나타내었으며 이 경우 압력을 가한 위치는 트랜스듀서의 방사면으로부터 d=21.96 mm 떨어진 곳임을 알 수 있다. 이 결과는 Fig. 8에 나타낸 진동속도분포에서의 절의 위치와 매우 유사함을 알 수 있다. 같은 방법으로 제 2 조화파 모드에 대한 측정 결과를 Fig. 9(b)에 나타내었다. 파선의 최대값과 가장 가까운 피크를 나타내는 굵은 실선의 결과는 d=6.58 mm로 나타나 Fig. 7의 결과에서 나타난 5 mm의 절의 위치와 대략적으로 잘 대응됨을 알 수 있다. 제 3 조화파 모드에 대해서도 Fig. 9(c)에 나타낸 고정점의 위치는 Fig. 8의 진동속도분포의 절의 위치와도 잘 대응되고 있다.

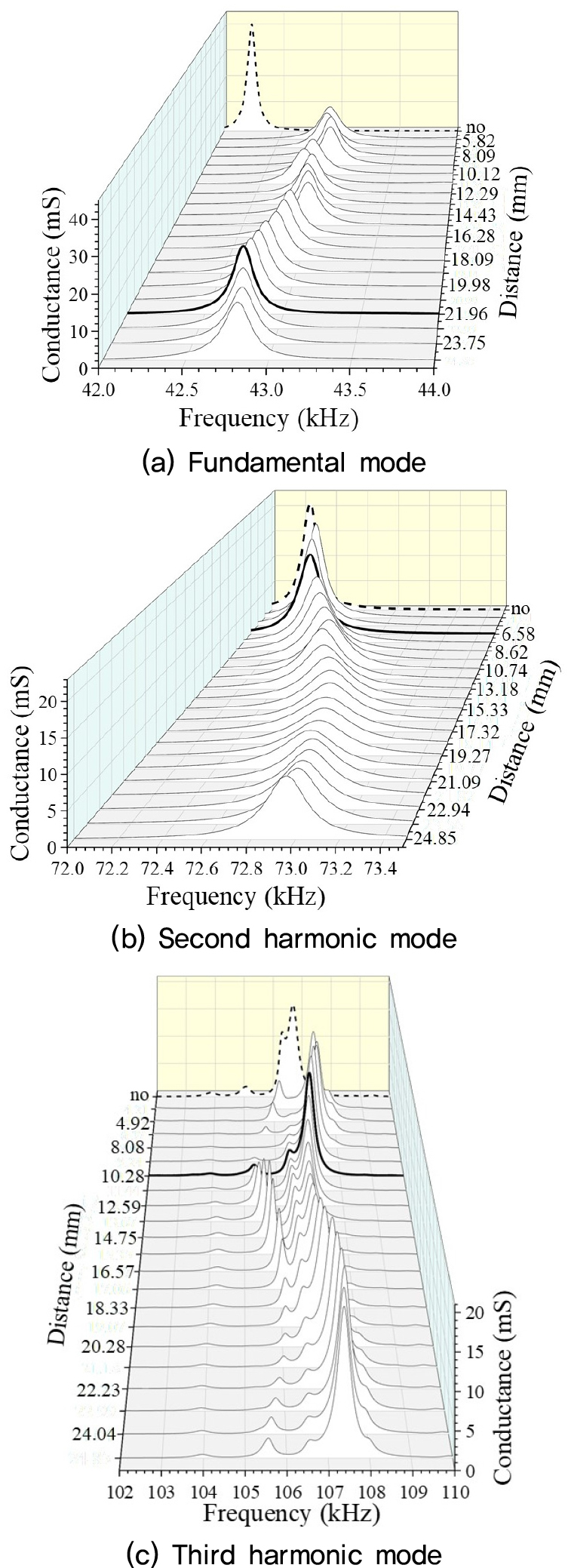
Fig. 9.

(Color available online) Variation of the conductance depending on fixing point on the bolt-clamped Langevin-type ultrasonic transducer. In the figure, the dotted line refers to the conductance for each mode of the transducer without the jig, and the solid lines refer to the conductance when the jig is held at each position of d. (a) In the fundamental mode, the thick solid line shows the conductance when the position of the jig is d = 21.96 mm, and it shows the closest resonant frequency to that of in the case of no jig. (b) In the 2^nd harmonic mode, the closest resonant frequency appears when the position of jig is d = 6.58 mm. (c) In the 3^rd harmonic mode, the closest resonant frequency appears when the position of jig is d = 10.28 mm.

V. 결 론

볼트 체결형 란주반 초음파 트랜스듀서를 고정하기 위한 프렌지의 위치를 최적화하기 위한 실험적 방법을 제안하였다. 반원형 쐐기 형태의 지그를 사용하여 트랜스듀서의 고정점을 변화시켜가며 전기단자에서 측정한 입력 어드미턴스의 특성 변화를 관찰하였다. 그 결과 , 각 공진 모드에 대한 진동 속도분포의 절에 대응하는 위치를 각 모드에 대해 찾을 수 있었고, 이를 이용하여 트랜스듀서를 고정하기 위한 최적의 프렌지 설치위치를 결정할 수 있었다. 본 연구에서 사용한 란주반형 초음파 트랜스듀서의 경우, 기본모드, 제 2 조화파 모드 및 제 3 조화파 모드에 대해 프렌지의 설치 위치는 방사면으로부터 각각 21.96 mm, 6.58 mm, 및 10.28 mm 떨어진 지점으로 나타났다.