I. 서 론

비브라토는 악기음과 보컬음에 대한 주파수의 변조를 의미하며,^[1,2] 음악의 음색을 풍부하게 만들기 위해서 사용되는 대표적인 기법들 중의 하나이다. 비브라토음의 특성 분석은 비브라토와 관련된 음높이의 인지,^[3,4] 감정적인 표현의 분석,^[5] 노래를 위한 보컬음의 합성^[6] 등 다양한 분야에서 필요하다. 또한, 이는 컴퓨터를 이용한 비브라토의 교육 및 평가,^[7] 비서양권 음악의 비브라토 분석^[8] 등에도 활용될 수 있다.

비브라토음의 특성을 분석하기 위해서는 일반적으로 두 단계의 과정을 거친다. 첫 번째는 비브라토 음으로부터 기본주파수 궤적을 추출하는 단계이다. 예를 들어, 비브라토음의 기본주파수 추정을 위해 자기상관법에 근거한 방법^[4,5 혹은 Phase Difference Estimation(PDE)에 근거한 방법^{[3,9,10,11,12]} 등이 사용되고 있다. 두 번째는 기본주파수 궤적으로부터 비브라토 파라미터를 분석하는 단계이다. 비브라토 파라미터는 Intonation, Vibrato Rate, Vibrato Extent 등이 있다.^[1.2]

비브라토음의 기본주파수 궤적은 비브라토 파라미터를 이용하여 정현파로 모델링하는 것이 일반적이며,^[1,2] 이 파라미터들은 천천히 변하는 시변 신호로 간주되어 왔다.^[13] 한편, 최근의 연구 결과에 따르면 비브라토음의 주파수 궤적이 정현파가 아닌 형태들도 존재하는 것을 알 수 있다.^[11] 비브라토음의 기본주파수 궤적이 정현파 형태인 경우 이의 특성을 분석하는 연구는 비교적 많은 수행되었으나, 궤적이 비정현파 형태인 경우에 그 특성을 분석하는 연구는 수행된 바가 거의 없는 상태이다. 따라서, 본 논문에서는 이에 대한 연구를 수행하고자 한다.

본 논문에서는 우선 비브라토음의 기본주파수 궤적이 비정현파 형태일 때 이를 분석하는 방법을 제안한다. 제안된 방법은 주파수 궤적에 대해 Fast Fourier Transform(FFT)를 이용해 배음을 정밀하게 분석하고, 또한 궤적의 정현파 순도 인자를 계산하는 과정으로 이루어진다. 또한, 플루트, 비올라, 색소폰 비브라토음 샘플들을 이용하여 비정현파 형태의 기본주파수 궤적들을 보인다. 마지막으로 이 샘플들에 대해 제안된 방법을 적용하고 실험 결과를 논의한다. 실제의 악기음 비브라토는 주파수 변조 뿐 아니라 진폭 변조도 포함하는 경우가 많지만, 본 논문에서는 주파수 변조만을 대상으로 한다.

II. 비브라토 파라미터 및 Prame’s Method

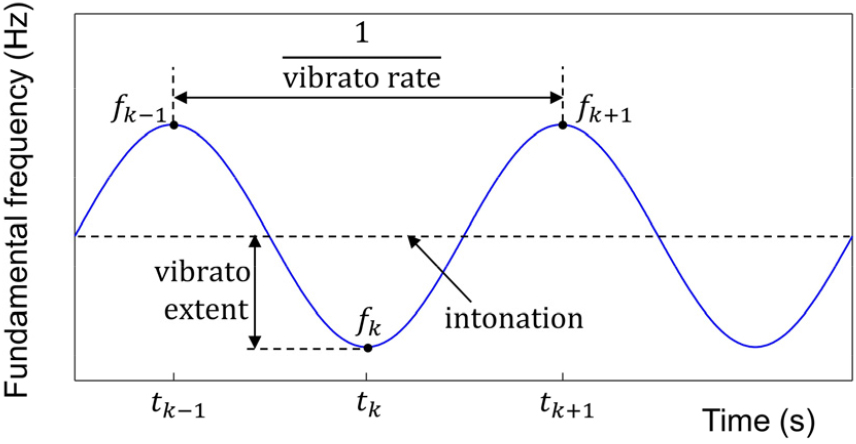
비브라토음에서 비브라토 파라미터가 시간에 따라 천천히 변한다고 가정하자. 그러면 짧은 시간 길이 동안으로 한정했을 때 기본주파수 궤적은 Fig. 1과 같이 정현파 형태로 근사할 수 있다. 이 궤적 f(t)는 다음과 같이 표현 가능하다.^[11]

여기에서 a는 Intonation으로써 음높이를 의미하며, b는 Vibrato Extent로써 주파수 변조의 크기를 의미하며, c는 Vibrato Rate로써 주파수 변조의 진동수를 의미한다. θ는 위상을 의미한다.

Fig. 1.

(Color available online) Fundamental frequency trajectory and vibrato parameters.

Prame’s Method에서는 비브라토 파라미터들을 두 개의 인접한 반주기의 기본주파수 궤적 값들을 이용해 계산한다.^[1,2]Fig. 1과 같이 기본주파수 궤적에서 세 개의 연속적인 피크 혹은 골의 주파수 값들을 f_k−1, f_k, f_{k + 1}라고 하고 이들이 발생하는 시간을 각각 t_k−1, t_k, t_{k + 1}라고 하면, 비브라토 파라미터들은 아래와 같이 구해진다.^[1,2]

시간에 따른 파라미터 값들을 구하기 위해서는 k를 변화시키면서 연속적으로 계산한다. 전체 음 단위로 비브라토 파라미터의 대푯값을 구할 때는 시간별로 구한 값들을 평균하여 사용한다.

III. 제안된 방법

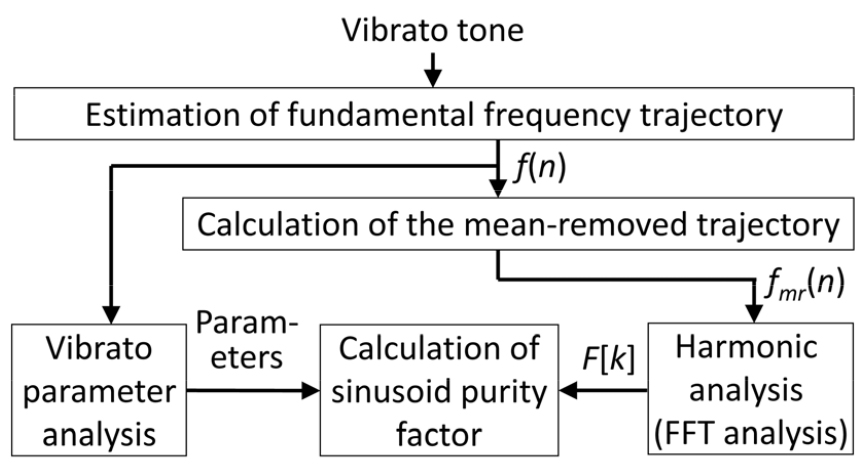
본 논문에서 제안하는 방법은 Fig. 2와 같이 세 가지의 분석 과정으로 이루어진다. 비브라토음으로부터 자기상관법이나 PDE 등을 이용해 추출한 기본주파수 궤적 신호를 f(n) (n = 0,1,...,N ‒ 1)이라고 하자. 첫째로, f(n)에 대해 기존 방법인 Prame’s Method를 이용하여 비브라토 파라미터인 Intonation, Vibrato Rate, Vibrato Extent를 구한다.

Fig. 2.

Basic framework of the proposed method.

둘째로, 궤적 신호에 대해 배음 분석을 수행하고 이의 결과를 분석한다. 우선 신호의 해석을 위해서 Eq. (1)의 신호를 샘플링하여 f(n)를 구하고 이에 윈도우 함수를 곱한 후 Discrete-Time Fourier Transform (DTFT)을 수행한다고 하자. 윈도우 함수의 DTFT를 W(ω)라고 하면, 이의 DTFT는 아래와 같이 표시할 수 있다.

여기에서 ω_c는 ω축에서 c에 대응되는 값이다. Eq. (5)에서 F(ω)는 ω = 0에서 크기가 |a × W(0)|인 피크가 존재하며, Vibrato Rate 위치에 해당되는 ω = ± ω_c에서 크기가 각각 |b × W(0)/2|인 피크들이 존재한다. 일반적으로 Intonation이 Vibrato Extent보다 매우 크기 때문에, ω = 0에서의 피크가 매우 크며 이에 의한 Sidelobe Effect가 심각하게 발생한다. 이 영향을 최소화하기 위해서, 기본주파수 궤적 신호에 대해 전체 평균값을 빼서 Intonation의 영향을 제거하고 이를 이용해 FFT를 수행한다.

f(n)으로부터 평균을 제거한 주파수 궤적 신호를 f_mr(n) (n = 0,1,...,N ‒ 1)라고 할 때, 제안된 방법에서는 이 신호가 아래의 식과 같이 구성된다고 모델링한다.

여기에서 f_s(n)는 정현파 성분이고, f_h(n)는 배음 성분으로써 Vibrato Rate의 2배 이상인 정수배의 진동수를 가지는 주파수 변조 성분을 의미하며, f_r(n)는 잔류 성분으로써 f_mr(n)에서 f_s(n)와 f_h(n)를 뺀 것이다.

배음 분석은 FFT 결과 중에서 f_h(n)에 해당되는 성분을 분석하는 것이다. f_mr(n)의 FFT를 F[k]라고 할 때, f_mr(n)이 정현파로 구성되어 있다면 |F[k]| (k = 0,...,N/2)는 Vibrato Rate의 위치에서 하나의 피크만 관측될 것이다. 만약 |F[k]|에서 여러 개의 피크가 관측된다면 Vibrato Rate의 2배, 3배 등 정수배 위치에 있는 피크들의 위치 및 크기를 구하고, 따라서 f_h(n)이 어떤 배음 구조로 구성되어 있는지 분석할 수 있다. 단, FFT를 수행할 때는 분석의 정확도를 올리기 위해서 적절한 Zero Padding을 병행해주어야 한다. 제안된 방법에서 배음 분석이 FFT에 기반한 이유는 Zero Padding을 병행한 FFT가 기본주파수 궤적의 배음의 주파수와 크기를 정밀하게 측정할 수 있기 때문이다. 추가적으로, Vibrato Rate 및 이의 정수배 위치가 아닌 곳들의 FFT 결과를 분석하여 f_r(n) 신호에 대한 분석을 수행할 수 있다.

셋째로, f_mr(n)이 정현파에 얼마나 가까운지를 추정하기 위해서 Sinusoid Purity Factor(SPF)를 아래와같이 정의하고 계산한다.

Eq. (7)에서 분자는 FFT에 기반하여 구한 Vibrato Extent를 의미하며, f_mr(n)에 대해 Zero Padding 및 FFT를 수행하고 그 결과의 절대치들 중 Vibrato Rate 위치에 있는 피크의 크기로부터 산출한다. 이는 Eq. (6)에서 정현파 성분 f_s(n)에 대해서 구한 Vibrato Extent에 해당된다. 분모는 Prame’s Method로부터 구한 Vibrato Extent 값을 의미하며, 시간에 따른 Vibrato Extent 값들을 평균하여 구한다. 이는 전체 성분인 f_mr(n)에 대해서 구한 Vibrato Extent에 해당된다.

Eq. (7)은 f_mr(n)에 대해서 정현파 성분의 진폭과 전체 성분의 진폭의 비를 계산하는 형태이다. 즉, f_mr(n)이 정현파에 가까우면 1에 가까운 값이 되고, 비정현파의 형태이면 1에서 멀어지게 된다.

IV. 실험 결과

비브라토음 중 비정현파적인 기본주파수 궤적을 가지는 것들의 특성을 분석하기 위해서 비브라토음들을 다수 분석하였고, 이 중 네 개의 음들에 대한 결과를 보인다. 이들은 플루트음 1개, 비올라음 2개, 색소폰음 1개로 구성되어 있으며, 모두 CD(Y. Menuhin, Instruments of the orchestra, EMI Classics, 1995)에서 추출한 것으로써 16 비트, 44.1 kHz의 샘플링 주파수로 되어 있다. 이 음들의 기본주파수 궤적을 추출하기 위해서 PDE를 이용하였는데, 이는 비브라토의 기본주파수 추출에 자주 사용되어 온 방법들 중 하나이다.^{[3,9,10,11,12]} PDE에서는 Hanning Window를 이용하여 2048-point FFT를 사용하였고 Hop Size는 1을 이용하였다. 주파수 궤적 추정 시 연속된 프레임들은 200 샘플 단위로 이동하면서 계산하였으며, 이에 의해 f(n)의 샘플링주파수는 44,100/200 = 220.5 Hz가 된다.

4.1 배음 분석 결과

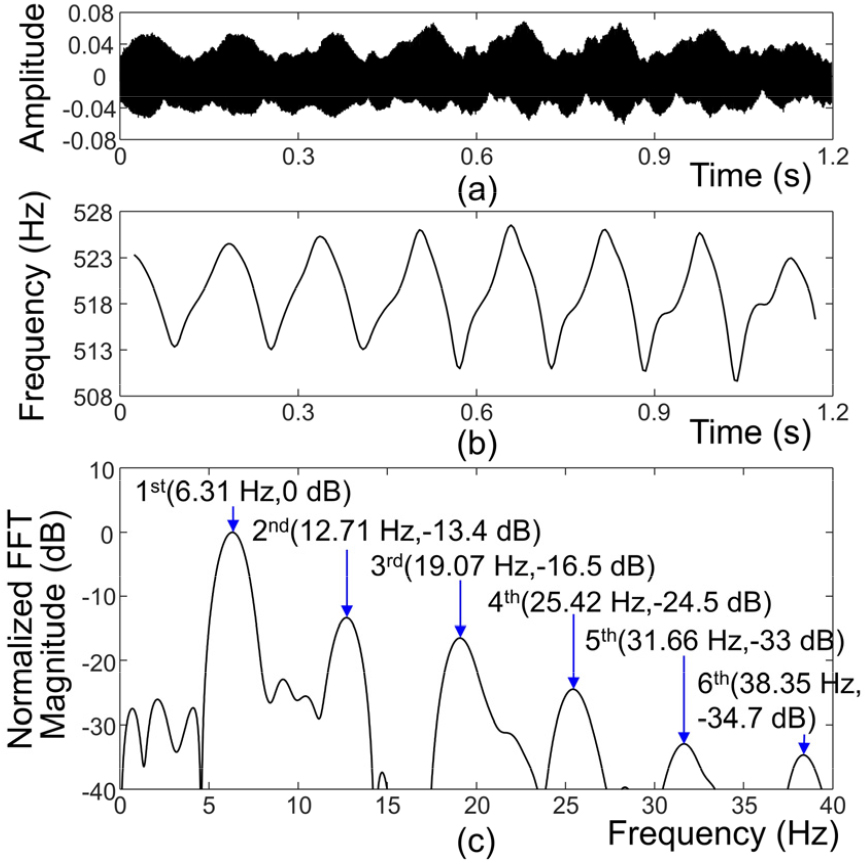
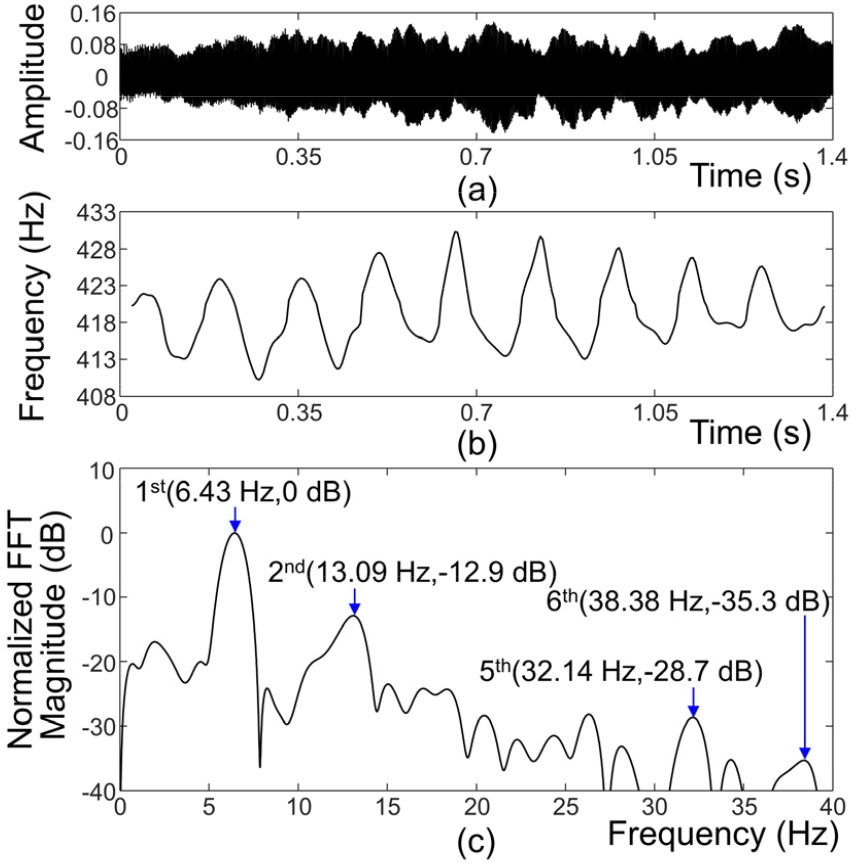
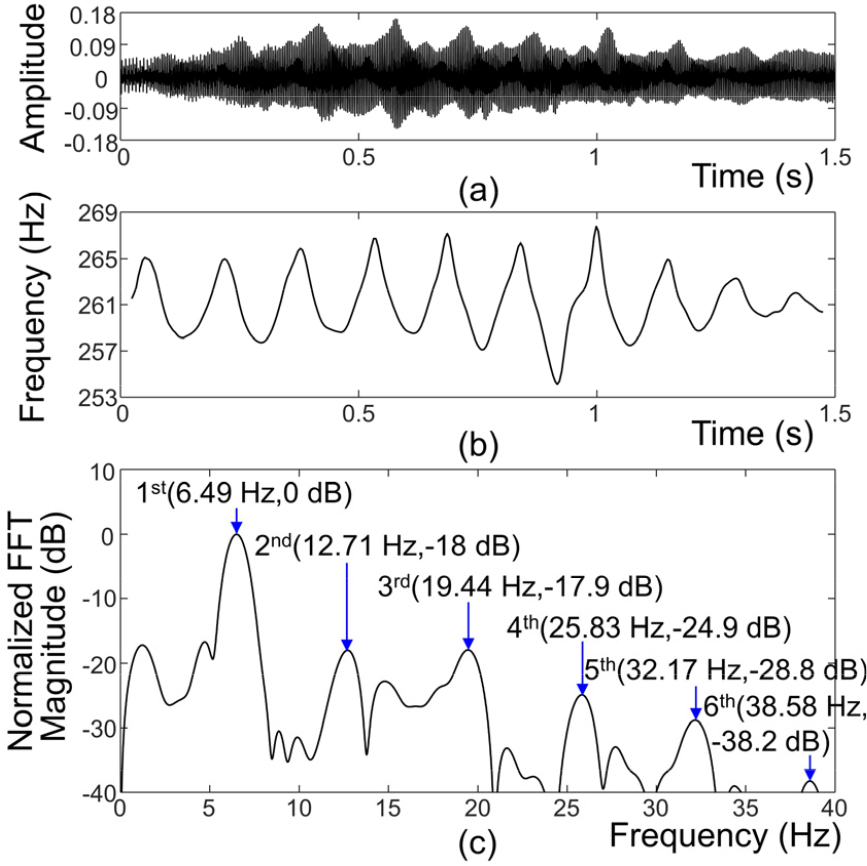
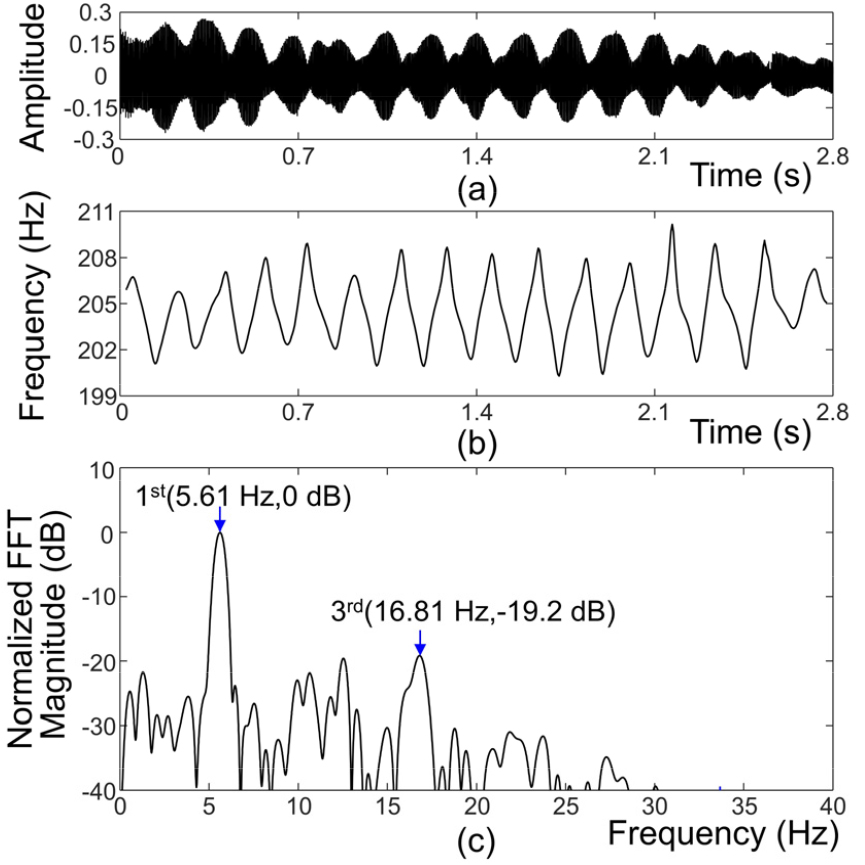
각 비브라토음의 파형은 Fig. 3(a) , 4(a), 5(a), 6(a)에서 보이고 있으며, 이들로부터 추출한 기본주파수 궤적은 Fig. 3(b), 4(b), 5(b), 6(b)에서 보이고 있다. 이 중 Fig. 6(b)의 색소폰의 경우 기본음의 레벨이 매우 낮아서 2배음의 주파수를 구한 후 2로 나눈 것을 사용하였다. 그림들에서 기본주파수 궤적들은 이상적인 정현파 형태와 다른 것을 관측할 수 있다.

Fig. 3(c), 4(c), 5(c), 6(c)에서 각 비브라토음의 평균을 제거한 기본주파수 궤적에 대해 정규화된 FFT 크기값을 보이고 있다. 세밀한 관찰을 위하여 주파수 범위는 0 Hz ~ 40 Hz로 제한하였다. FFT 수행 시 Hanning Window를 사용하였고, 주파수축을 0.01 Hz 단위로 관측할 수 있도록 Zero Padding을 수행하였다. 각 그림에서 첫 번째 피크는 정현파 성분 f_s(n)에 의한 것이며, 피크의 위치는 정현파 성분에 대한 Vibrato Rate에 해당된다. f_h(n)에 의한 배음 성분의 주파수와 크기를 알아보기 위해서 Vibrato Rate의 정수배 위치에 있는 피크들을 그림에서 보인다. 각 그림에서 배음의 주파수가 기본주파수의 정확한 정수배가 아닌 경우를 고려하여, 기본주파수를 f₀라고 할 때 m번째 배음에 대해서 [0.975 × m × f₀, 1.025 × m × f₀] 범위에 피크가 있는 경우 이를 화살표로 표시하였다. 단, 주위의 값들의 레벨에 비해 피크의 레벨이 충분히 크지 않을 때는 수동으로 이를 제외하였다. Fig. 3(c)와 5(c)에서는 배음 성분 중 2배음부터 6배음까지 모두 피크가 관찰되지만, Fig. 4(c)에서는 2, 5, 6배음만 관찰되며 Fig. 6(c)에서는 3배음만 관찰된다.

Fig. 3.

(Color available online) Results for the flute vibrato tone (excerpt: left channel, track 5, 1:13.6- 1:14.8). (a) Waveform. (b) Fundamental frequency trajectory. (c) Normalized FFT magnitude.

Fig. 4.

(Color available online) Results for the viola vibrato tone 1 (excerpt: right channel, track 2, 1:12.0- 1:13.4). (a) Waveform. (b) Fundamental frequency trajectory. (c) Normalized FFT magnitude.

Fig. 5.

(Color available online) Results for the viola vibrato tone 2 (excerpt: right channel, track 2, 1:04.2- 1:05.7). (a) Waveform. (b) Fundamental frequency trajectory. (c) Normalized FFT magnitude.

Fig. 6.

(Color available online) Results for the saxophone vibrato tone (excerpt: left channel, track 17, 0:29.1-0:31.9). (a) Waveform. (b) Fundamental frequency trajectory. (c) Normalized FFT magnitude.

4.2 비브라토 파라미터 분석 결과

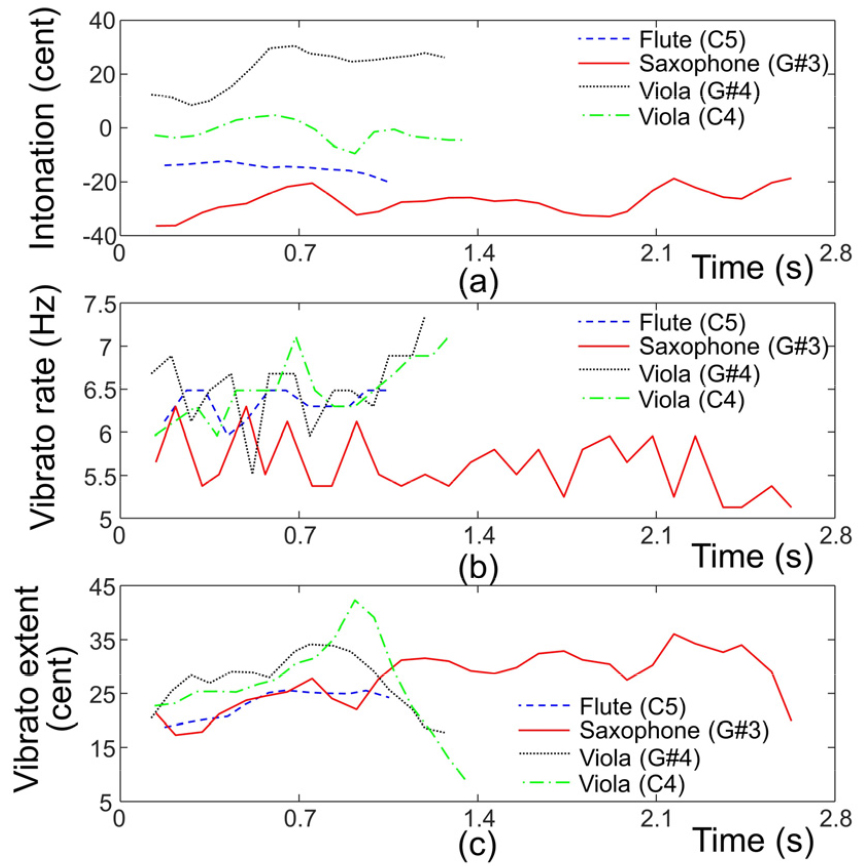
각 악기음의 비브라토 파라미터를 Prame’s Method를 이용하여 산출하였고, 결과들을 Fig. 7에서 보이고 있다. 각 비브라토음의 시간 길이가 다르므로 그림에서도 서로 다른 길이를 가진다. Intonation과 Vibrato Extent는 cent 단위로 변환해서 보인다.

Fig. 7.

(Color available online) Vibrato parameters estimated by Prame’s method. (a) Intonation. (b) Vibrato rate. (c) Vibrato extent.

4.3 SPF 분석 결과

각 비브라토음별로 VE_FFT와 VE_PM를 구하였고, 이들로부터 SPF 값들을 계산하여 Table 1에서 보이고 있다. 이 값들은 1과는 비교적 다른 값을 가지고 있으며, SPF가 Figs. 3, 4, 5, 6의 비브라토음들에 대해 기본주파수 궤적의 비정현파적인 형태 여부를 판단하는데 유용함을 알 수 있다. 단, SPF의 유효성을 일반화하기 위해서는 더 많은 추가 실험이 필요하다. 참고로 Figs. 3, 4, 5, 6의 비브라토음들에 대해 FFT와 Prame’s Method 기반으로 Intonation과 Vibrato Rate도 각각 구한 후 그 비율을 계산하였다. 이 비율들은 모두 1에 매우 근접한 값을 보였으며, 따라서 기본주파수 궤적의 비정현파적인 형태 여부를 판단하는데 유효하지 않았다.

4.4 실험 결과에 대한 논의

이상에서 비브라토음 중 비정현파적인 형태의 기본주파수 궤적을 분석함에 있어 제안된 방법이 유용함을 다양한 관점에서 보였다. 주파수 궤적이 비정현파 형태인 비브라토음의 특성 분석은 기존에 연구된 바가 거의 없다. 따라서, 본 논문에서 제안한 방법 및 실험 결과가 해당 연구의 기초 자료로써 활용되기를 바라며, 또한 이와 관련된 비브라토 연구가 추후 많이 수행되기를 기대한다.

V. 결 론

본 논문에서는 비브라토음이 비정현파적인 기본주파수 궤적을 가질 때 이에 대한 분석 방법을 제안하였다. 플루트, 비올라, 색소폰 등의 악기음에 적용한 결과 제안된 방법이 유용함을 확인할 수 있었다. 본 논문에서 제안된 방법 및 실험 결과를 기반으로 하여 비브라토음의 특성 분석을 위한 연구들이 더 많이 수행되기를 기대한다.