Covariance-based source localization performance improvement for underwater ultra-short baseline systems

Sangman Han; Minhyuk Cha; Haklim Ko; Hojun Lee

doi:10.7776/ASK.2024.43.1.089

Preview

Research Article

The Journal of the Acoustical Society of Korea. 31 January 2024. 89-94
https://doi.org/10.7776/ASK.2024.43.1.089

Covariance-based source localization performance improvement for underwater ultra-short baseline systems

공분산 기반 수중 ultra-short baseline 시스템의 위치 추정 성능 개선 기법

Sangman Han¹

Minhyuk Cha²

Haklim Ko¹

Hojun Lee¹^*

한 상만¹

차 민혁²

고 학림¹

이 호준¹^*

¹호서대학교

²호서대학교 해양IT융합기술 연구소

^{*Corresponding Author}

ABSTRACT

Since Ultra-Short BaseLine (USBL) uses an array with narrow sensor spacing, precise synchronization is required to improve source localization performances. However, in the underwater environment, synchronization errors occur due to relatively strong noise and underwater acoustic channels such as multipath and Doppler, which deteriorates the source localization performances. This paper proposes a covariance-based synchronization compensation method to improve the source localization performances of the underwater USBL systems. The proposed method arranges the received signals through cross-correlation and calculates the covariance of the arranged signals. The synchronization error is related to the phase difference in the covariance. Thus, the phase difference is estimated as the covariance and compensated. Computer simulations demonstrate that the proposed method has better source localization performances than the conventional cross-correlation method.

Keywords

Ultra-Short BaseLine (USBL)

Synchronization

Covariance

Cross-correlation

Source localization

Ultra-Short BaseLine(USBL) 은 센서 간격이 좁은 배열을 사용하기 때문에 위치 추정 성능 향상을 위해서는 정밀한 동기화가 필요하다. 그러나 수중 환경은 비교적 강한 잡음과 다중 경로 및 도플러 등의 수중 음향 채널로 인해 동기화 오류가 발생하여 위치 추정 성능이 저하된다. 본 논문에서는 수중 USBL 시스템의 위치 추정 성능을 향상시키기 위한 공분산 기반 동기 보상 기법을 제안한다. 제안 방법은 상호상관을 통해 신호를 정렬한 후, 정렬된 신호의 공분산을 계산한다. 공분산에서 동기 오차는 위상차와 선형적으로 관련되어 있으므로 위상차를 공분산으로부터 추정하여 동기 오차를 보상한다. 전산 모의실험을 통해 제안 방법이 기존 상호상관 방법보다 우수한 위치 추정 성능을 가지는 것을 보였다.

키워드

Ultra-Short BaseLine (USBL)

동기

공분산

상호상관

신호원 위치 추정

MAIN

I. 서 론
II. 시스템 모델
III. 제안 방법
IV. 전산 모의실험
V. 결 론

I. 서 론

신호원 위치 추정 기법은 레이더, 소나, 무선 통신 등 다양한 연구 분야에서 중요한 역할을 한다.^{[1,2,3,4,5,6,7]} 지상의 Global Navigation Satellite System(GNSS)은 위치 추정을 위해 Radio Frequency(RF) 신호를 사용한다. 반면, 수중에서는 염분과 전해질로 구성된 매질의 특성으로 인해 RF 신호의 투과를 방해한다. 이로 인해 수중 위치 추정 시스템에 GNSS를 활용하기는 어려우며,^[8] 일반적으로 음향 신호를 활용한다.

수중 신호원 위치 추정 기법은 센서 간의 간격에 따라 Long BaseLine(LBL), Short BaseLine(SBL), Ultra Short BaseLine(USBL)로 구분되어 개발되어왔다.^[9,10,11,12] USBL 시스템은 센서 간격이 좁은 센서 배열로 구성되어있어 동작이 간단하고, 선박 등에 설치가 간편하여 효율적인 운용이 가능하다.^[8,9] USBL에서는 각 수신 센서에 도달하는 수신 신호의 전파 지연 차이를 통해 수중 신호원의 위치를 추정한다.^[8] 일반적으로 전파 지연은 처프 신호의 상호상관을 통해 측정된다.^[13,14] 그러나 수중의 강한 잡음과 다중 경로 및 도플러와 같은 수중 통신 환경에서는 전파 지연 추정에 오류가 발생할 수 있다.^[15,16,17] USBL에서는 센서 간격이 좁기 때문에 작은 전파 지연 오류라도 위치 추정 성능에 열화가 발생한다.^[8]

이러한 문제를 동기 오차로 인한 위치 추정 성능 열화를 완화하기 위해 본 논문에서는 USBL 시스템을 위한 공분산 기반 동기 보상 방법을 제안한다. 제안하는 방법은 상호상관을 통해 각 센서로부터 수신된 신호의 대략적인 동기화 지점을 추정한다. 대략적인 동기화 지점을 기준으로 신호를 정렬한 후 정렬된 각 신호 간의 공분산을 계산한다. 공분산의 위상은 시간 지연 오차와 선형적으로 관련되므로, 공분산들의 위상 차이를 계산하여 동기화 지점을 보상한다. 제안된 방법의 위치 추정 성능을 검증하기 위해 전산 모의실험을 수행하였으며, 제안된 방법이 기존 방법에 비해 우수한 위치 추정 성능을 가지는 것을 보였다.

본 논문은 다음과 같이 구성된다. 2장에서 시스템 모델에 대해 설명하고, 3장에서 제안하는 방법에 대하여 설명한다. 그리고 4장에서 전산 모의실험 결과를 분석하고 5장에서 결론을 맺는다.

II. 시스템 모델

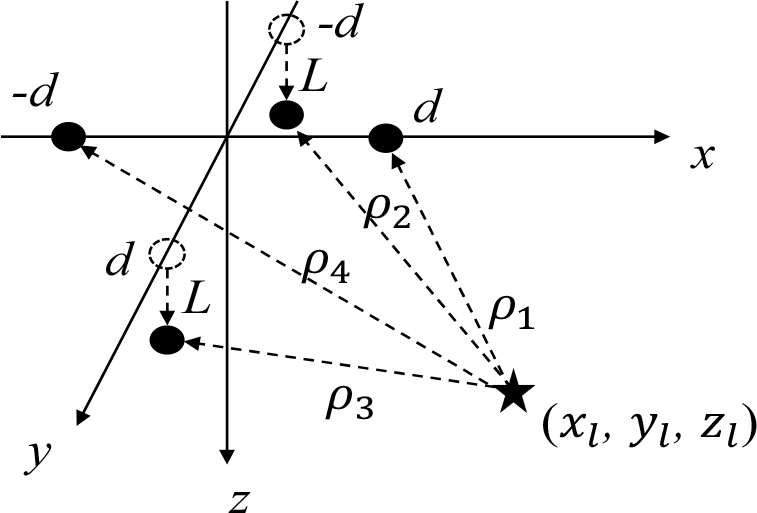
본 논문에서는 수동형 USBL 시스템을 가정하며, USBL의 배열은 반지름이 $d$ 인 원형 배열을 기본 형태로 Fig. 1과 같이 일부 센서는 $z$ 축 방향으로 $L$ 만큼 아래에 위치한다. Fig. 1에서 ( $x_{1}, y_{1}, z_{1}$ )은 $l$ 번째 신호원의 위치를 나타낸다. $ρ_{1}, ρ_{2}, ρ_{3}, ρ_{4}$ 는 각각 $l$ 번째 신호원으로부터 첫 번째부터 네 번째 센서 사이의 거리를 의미한다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-01/N0660430110/images/ASK_43_01_10_F1.jpg

Fig. 1.

Array configuration.

다중 신호원이 존재할 때 각 신호들을 구분하기 위해서 신호원은 처프 신호 및 서로 다른 중심 주파수를 가지는 단일 톤 신호를 발생시킨다. $l$ 번째 신호원에서 발생하는 신호, $s_{l} (t)$ , 는 다음과 같이 표현된다.

(1)

s_{l} (t) = \{\begin{cases} \cos [[2 π (f_{0} t + \frac{α}{2} t^{2})], 0 \leq t \leq T_{c h i r p} \\ \cos (2 π f_{l, c} t), T_{c h i r p} \leq t < T_{c h i r p} + T_{t o n e} \end{cases},

여기서 $f_{0}$ 과 𝛼는 각각 처프의 초기 주파수와 처프율을 의미한다. $T_{c h i r p}$ 및 $T_{t o n e}$ 은 처프와 단일 톤의 시간 길이를 의미한다. $i$ 번째 센서의 수신 신호는 다음과 같이 표현된다.

(2)

r_{i} (t) = h_{i} (t) * s_{l} (t) + n_{i} (t),

여기서 $h_{i} (t)$ 와 $n_{i} (t)$ 는 각각 $i$ 번째 센서의 수중 음향 채널과 잡음을 나타낸다.

수중 USBL 시스템은 신호원에서 발생하는 신호를 센서 어레이를 통해 수신하고, 각 센서에서 수신한 신호의 전파 지연 차이를 통해 신호원의 위치를 추정한다. 일반적으로 전파 지연 시간을 추정하기 위해서는 전송된 처프 신호와 수신된 신호 간의 상호상관을 통해 수행된다. $i$ 번째 센서가 수신한 신호의 상호상관은 다음의 식으로 표현된다.

(3)

R_{i} (μ) = \int_{\infty}^{\infty} \cos [2 π (f_{0} t + \frac{α}{2} t^{2})] r_{i} (t + μ) d t .

기존의 동기화 방법은 상호상관 결과의 최댓값을 찾아 동기화 지점을 구하는데, 이는 다음과 같이 표현된다.

(4)

\hat{τ_{i}} = \max_{μ} | R_{i} (μ) | - T_{c h i r p} .

그러나 수신된 신호가 다중 경로, 도플러, 강한 잡음 등 수중 환경에 의해 오염되면 동기화 성능이 저하된다. 동기화 성능 저하를 완화하기 위해 본 논문에서는 공분산 기반 동기 보상 방법을 제안한다.

III. 제안 방법

본 논문에서는 수중 USBL 시스템의 동기화 및 위치 추정 성능을 향상시키는 방법을 제안한다. USBL 센서 배열은 센서 간격이 좁기 때문에 작은 동기 오차가 발생하더라도 위치 추정 성능이 크게 저하된다. 따라서 위치 추정 성능을 향상시키기 위해서는 정확한 동기화가 중요하다.

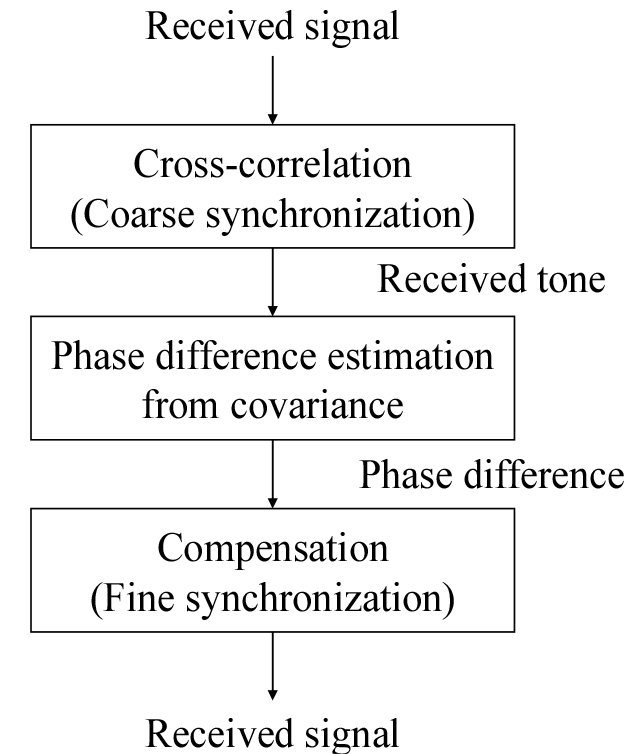
제안 방법은 두 단계의 동기화 과정을 가지며 Fig. 2에 나타내었다. 먼저, Eqs. (3), (4)를 통해 대략적인 동기화를 수행한다 . 그리고 각 센서에 대한 수신 신호를 동기화 지점에 대해서 정렬한다. 그 후 정렬된 단일 톤 신호에 대해서 공분산을 계산하고, 공분산 간의 위상차를 추정 후 동기 오류를 보상한다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-01/N0660430110/images/ASK_43_01_10_F2.jpg

Fig. 2.

Block diagram of the proposed method.

$i$ 번째 센서의 정렬된 단일 톤과 동기화 오류를 각각 $r_{s, i} (t)$ 와 $ϵ_{i}$ 라고 한다. 단일 톤의 경우 동기화 오류는 초기 위상 오류로 간주할 수 있으므로, $r_{s, i} (t)$ 는 다음과 같이 표현할 수 있다.

(5)

r_{s, i} (t) = [h_{i} (t) * s_{s} (t) + n_{i} (t)] \times e^{j 2 π f_{c} ϵ_{i}},

여기서 $h_{i} (t)$ 와 $n_{i} (t)$ 는 $i$ 번째 센서의 수중 음향 채널과 잡음을 의미한다. $s_{s} (t)$ 는 $f_{c}$ 의 중심 주파수로 전송된 단일 톤을 의미한다. USBL에서는 센서 간격이 좁기 때문에 신호원과 배열 사이의 간격이 충분히 멀리 떨어져 있다면, 각 센서에 대한 수중 음향 채널은 동일하다고 가정할 수 있다. 그리고 잡음, $n_{i} (t)$ ,는 $e^{j 2 π f_{c} ϵ_{i}}$ 가 곱해짐에 따라 초기 위상이 변화하더라도 여전히 잡음과 동일하기 때문에 Eq. (5)는 다음과 같이 다시 쓸 수 있다.

(6)

r_{s, t} (t) = [h (t) * s_{s} (t)] \times e^{j 2 π f_{c} ϵ_{i}} + N_{i} (t) .

위상차를 추정하기 위해 $i$ 번째 센서와 $j$ 번째 센서의 정렬된 단일 톤 사이의 공분산 ( $C_{i, j}$ )을 계산하며 다음 식으로 표현된다.^[18]

(7)

C_{i, j} = \frac{1}{T} \int_{T} r_{s, i} (t) r_{s, j}^{*} (t) d t .

Eq. (7)에서 잡음과 신호는 상관관계가 없으므로 다음과 같이 다시 쓸 수 있다.

(8)

C_{i, j} = σ_{h}^{2} σ_{s}^{2} e^{j 2 π f_{c} (ϵ_{i} - ϵ_{j})},

여기서 $σ_{h}^{2}$ 와 $σ_{s}^{2}$ 는 각각 채널과 신호의 전력을 의미한다. Eq. (8)에서 $σ_{h}^{2}$ 및 $σ_{s}^{2}$ 는 서로 상수이므로 위상 추정을 통해 $2 π f_{c} (ϵ_{i} - ϵ_{j})$ 를 얻을 수 있다. 일반적으로 첫 번째 센서의 동기화 에러는 0이 아닐 수 있다. 그러나 USBL 시스템에서의 위치 추정은 시간 차를 활용하기 때문에, 첫 번째 센서를 기준으로 다른 센서들의 지연차이에 의해 위치 추정이 이루어진다. 따라서 첫 번째 센서를 기준으로 다른 센서에 대한 지연시간의 상대적인 동기 오차를 보상하면 위치 추정 성능을 향상시킬수 있다. 따라서 $i$ 번째 센서의 지연시간 보상은 다음 식으로 수행된다.

(9)

{\hat{τ}}_{c, i} = \hat{τ_{i}} - \tan^{- 1} \{\frac{i m a g (C_{1, i})}{r e a l (C_{1, i})}\} / 2 π f_{c} .

Eq. (9)에서 $i m a g (\cdot)$ 과 $r e a l (\cdot)$ 은 각각 허수부와 실수부를 추출하는 함수이다.

본 논문에서 제안한 방법은 공분산 ( $C_{i, j}$ )의 위상을 추정하여 동기오차를 보상한다. 그러나 $C_{i, j}$ 에서 위상은 $1 / f_{c}$ 마다 반복되기 때문에, 제안한 방법의 동기 오차 보상 범위는 $1 / f_{c}$ 이내로 제한된다. 그러나 USBL 시스템에서는 작은 동기화 오차가 큰 위치 추정 오차로 이어지므로, 제안한 방법을 통해 작은 동기 오차를 보상함으로써 위치 추정 성능을 향상시킬 수 있다.

IV. 전산 모의실험

본 절에서는 제안한 방법의 위치 추정 성능을 전산 모의실험을 통해 분석한다. 제안된 방법의 위치 추정 성능은 Root Mean Square Error(RMSE)로 측정되었으며, 기존 상호상관 방법과 비교한다. 전산 모의실험에 사용된 변수는 Table 1에 나타내었다.

Table 1.

Simulation parameters.

Parameters	Values
The number of USBL sensors	4
$d$	15 cm
$L$	15 cm
$T_{t o n e}$	1 s
$T_{c h i r p}$	1 s
𝛼	1 kHz/s
$f_{0}$	32 kHz
Sampling rate, $f_{s}$	1 MHz
Horizontal distance between transmitter and receiver	100 m
Depth of receiver	2 m
Depth of transmitter	35 m

수중 음향 채널은 한국 서해에서 측정된 수직 음속 구조(Sound Speed Profile, SSP)를 사용하여 Bellhop모델에 의해 생생하였고 Rician 채널 모델을 적용하였다. 도플러는 4 Hz를 할당하였으며, K-factor는 10 dB로 설정하였다. SSP와 채널 임펄스 응답은 Figs. 3과 4에 나타내었다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-01/N0660430110/images/ASK_43_01_10_F3.jpg

Fig. 3.

Sound speed profile.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-01/N0660430110/images/ASK_43_01_10_F4.jpg

Fig. 4.

Channel impulse response.

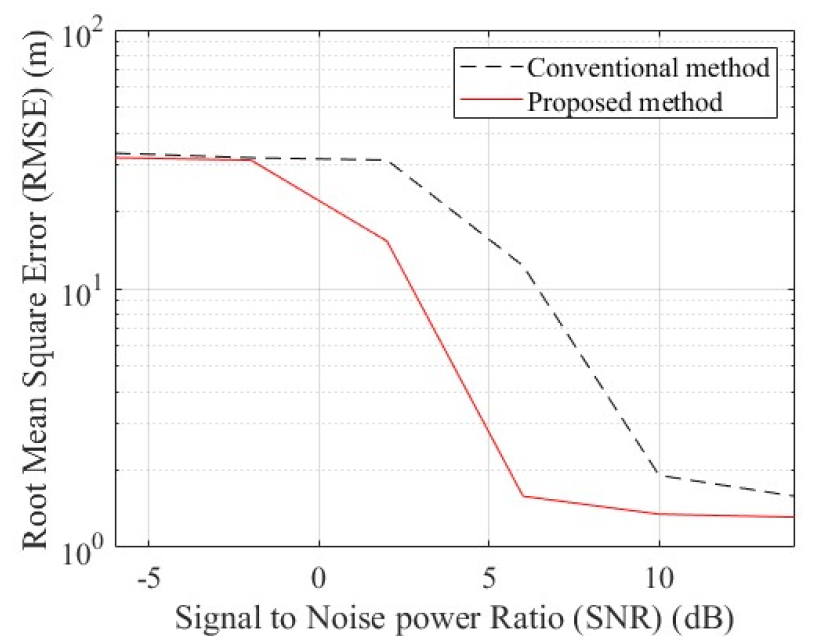
제안 방법과 기존 방법의 신호대잡음비(Signal to Noise Ratio, SNR)에 따른 위치 추정 성능을 Fig. 5에 나타내었다. 붉은색과 검은색 실선은 각각 제안 방법 그리고 기존 방법의 RMSE를 의미한다. Fig. 5에서 보는 바와 같이 제안 방법과 기존 방법은 신호대잡음비가 0 dB 이하에서는 강한 잡음으로 인해 큰 위치 추정 오차를 가지는 것을 알 수 있다. 그러나 신호대잡음비가 0 dB 이상 그리고 10 dB 이하에서는 제안 방법이 상대적인 동기 오차를 보상하여 위치 추정 성능이 향상되었다. 그리고 신호대잡음비가 10 dB 이상에서는 두 기법 모두 약 1.5 m 이내의 위치 추정 오차를 가진다. 따라서 제안한 방법이 기존 기법에 비해 약 4 dB의 신호대잡음비 성능 이득을 가지며 위치 추정 성능이 향상되었음을 보였다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-01/N0660430110/images/ASK_43_01_10_F5.jpg

Fig. 5.

(Color available online) RMSE curve for source localization.

V. 결 론

본 논문에서는 공분산 기반 동기 보상 방법을 제안하였다. 제안하는 방법은 보상할 수 있는 동기화 오차가 $1 / f_{c}$ 이내로 제한되지만, USBL 시스템에서는 작은 동기화 오차로 인해 큰 위치 추정 오차가 발생하므로 제안하는 방법은 제한된 보상 범위에서도 위치 추정 성능을 향상시킬 수 있다. 전산 모의실험 결과를 통하여 제안하는 방법이 기존의 방법보다 신호대잡음비에서 4 dB 우수한 위치 추정 성능을 가졌음을 보였다. 향후 제안 방법의 위치 추정 성능에 대하여 해상 실험을 통한 검증이 필요하며 수중 음향 채널로 인한 영향을 완화할 수 있는 추가적인 연구가 필요하다.

Acknowledgements

본 연구는 소방청 재난현장 긴급대응 기술개발사업(20019290)의 연구비 지원으로 수행되었습니다.

본 연구는 과학기술정보통신부 및 정보통신기획평가원의 대학ICT연구센터육성지원사업의 연구결과로 수행되었음(IITP-2022-2018-0-01417).

References

H. Lee, Y. Kim, S. Seol, and J. Chung, "Deep learning- based near-field source localization without a priori knowledge of the number of sources," IEEE Access, 10, 55360-55368 (2022). 10.1109/ACCESS.2022.3177594

E. Grosicki, K. Abed-Meraim, and Y. Hua, "A weighted linear prediction method for near-field source localization," IEEE Trans. Signal Process. 53, 3651-3660 (2005). 10.1109/TSP.2005.855100

H. Lee, Y. Kim, S. Seol, and J. Chung, "Deep learning-based Direction-of-arrival estimation for far-field sources under correlated near-field interferences," ICT Express, 9, 741-747 (2023). 10.1016/j.icte.2022.06.007

H. Krim and M. Viberg, "Two decades of array signal processing research: The parametric approach," IEEE Signal Process. Mag. 13, 67-94 (1996). 10.1109/79.526899

E. Fisher and B. Rafaely, "Near-field spherical microphone array processing with radial filtering," IEEE Trans. Audio Speech Lang. Process. 19, 256-265 (2011). 10.1109/TASL.2010.2047421

H. Lee, J. Ahn, Y. Kim, and J. Chung, "Direction-of-arrival estimation of far-field sources under near-field interferences in passive sonar array," IEEE Access, 9, 28413-28420 (2021). 10.1109/ACCESS.2021.3059157

L. Kumar and R. M. Hegde, "Near-field acoustic source localization and beamforming in spherical harmonics domain," IEEE Trans. Signal Process. 64, 3351-3361 (2016). 10.1109/TSP.2016.2543201

H. Lee, K. Kim, T. Chung, and H. Ko, "Deep learning-based ultra short baseline underwater positioning," Proc. ICAIIC, 856-859 (2023). 10.1109/ICAIIC57133.2023.10067090

Q. Luo, X. Yan, C. Ju, Y. Chen, and Z. Luo, "An ultra-short baseline underwater positioning system with kalman filtering," Sensors, 21, 143 (2020). 10.3390/s2101014333379311PMC7796008

Y. Yao, X. Xu, D. Yang, and X. Xu, "An IMM-UKF aided SINS/USBL calibration solution for underwater vehicles," IEEE Trans. Veh. Technol. 69, 3740-3747 (2020). 10.1109/TVT.2020.2972526

J. Tong, X. Xiaosu, T. Zhang, Z. Liang, and L. Yao, "Study on installation error analysis and calibration of acoustic transceiver array based on SINS/USBL integrated system," IEEE Access, 6, 66923-66939 (2018). 10.1109/ACCESS.2018.2878756

J. Wang, T. Zhang, B. Jin, Y. Zhu, and J. Tong, "Student's t-based robust kalman filter for a SINS/USBL integration navigation strategy," IEEE Sens. J. 20, 5540-5553 (2020). 10.1109/JSEN.2020.2970766

H. Lee, J. Ahn, Y. Kim, S. Lee, and J. Chung, "A biomimetic communication method based on time shift using dolphin whistle" (in Korean), J. Acoust. Soc. Kr. 38, 580-586 (2019).

Y.-J. Kim, M.-J. Oh, and I.-S. Lee, "Generalized cross correlation with phase transform sound source localization combined with steered response power method" (in Korean), J. Acoust. Soc. Kr. 36, 345-352 (2017).

Y. Kim, H. Lee, J. Ahn, and J. Chung, "Selection of CDMA and OFDM using machine learning in underwater wireless networks," ICT Express, 5, 215-218 (2019). 10.1016/j.icte.2019.09.002

M. Stojanovic and J. Preisig, "Underwtaer acoustic communication channels: propagation models and statistical characterization," IEEE Commun. Mag. 47, 84-89 (2009). 10.1109/MCOM.2009.4752682

H. Lee and J. Chung, "Performance analysis of CDMA and OFDM on underwater acoustic environments," J. Korea Inst. Intell. Transp. Syst. 17, 135-142 (2018). 10.12815/kits.2018.17.5.135

T.-I. Kwon, K.-M. Kim, S. Kim, and J.-K. Ahn, "Near field acoustic source localization using beam space focused minimum variance beamforming" (in Korean), J. Acoust. Soc. Kr. 36, 100-107 (2017). 10.7776/ASK.2017.36.2.100

The Journal of the Acoustical Society of KoreaISSN:1225-4428(Print) 2287-3775(Online)한국음향학회

Preview

Covariance-based source localization performance improvement for underwater ultra-short baseline systems

ABSTRACT

MAIN

Fig. 1.

Array configuration.

(1)

(2)

(3)

(4)

Fig. 2.

Block diagram of the proposed method.

(5)

(6)

(7)

(8)

(9)

Table 1.

Simulation parameters.

Fig. 3.

Sound speed profile.

Fig. 4.

Channel impulse response.

Fig. 5.

(Color available online) RMSE curve for source localization.

Acknowledgements

References