A study on robust generalized cross correlation-phase transform based time delay estimation in impulsive noise environment using nonlinear preprocessing and frequency domain low-pass filter

Jun-Seok Lim; Keunwa Lee

doi:10.7776/ASK.2024.43.4.406

Preview

Research Article

The Journal of the Acoustical Society of Korea. 31 July 2024. 406-413
https://doi.org/10.7776/ASK.2024.43.4.406

A study on robust generalized cross correlation-phase transform based time delay estimation in impulsive noise environment using nonlinear preprocessing and frequency domain low-pass filter

비선형 전처리와 주파수 영역 저역 필터에 의한 임펄스성 잡음 환경에 강인한 위상 변환 일반 상호 상관 시간 지연 추정기 연구

Jun-Seok Lim¹^*

Keunwa Lee²

임 준석¹^*

이 근화²

¹세종대학교 전자정보통신공학과

²세종대학교 국방시스템공학과

^{*Corresponding Author}

License (open-access, http://creativecommons.org/licenses/by-nc/4.0/):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

The proposed method uses Generalized Cross Correlation – Phase Transform (GCC-PHAT) method with nonlinear preprocessing and a frequency domain low-pass filter. In this paper, by reinterpreting the calculation process of GCC-PHAT as DFT, we derive that there is an effective frequency band used for time delay estimation in GCC-PHAT, and by using only the effective band using a low-pass filter, the noise component is reduced and it improves the time delay performance in impulsive noise environments. By comparing the proposed method with the traditional GCC-PHAT in an impulsive noise environment, we show that the GCC-PHAT becomes more robust to the impulsive noise.

Keywords

Time-delay estimation

Generalized Cross Correlation – Phase Transform (GCC-PHAT)

Low-pass filter

Impulsive noise

본 논문은 임펄스성 잡음에 견실한 시간 지연을 추정 방법을 제안한다. 제안하는 방법은 Generalized Cross Correlation – Phase Transform(GCC-PHAT) 방법에 비선형 전처리와 주파수 영역 저역 통과 필터를 사용한다. 본 논문에서는 GCC-PHAT의 연산 과정을 DFT로 다시 해석함으로써 GCC-PHAT에서 시간 지연 추정에 실제 사용되는 유효한 주파수 대역이 있음을 파악하고, 저역 통과 필터 사용하여 유효 대역만을 사용하면 잡음 성분을 줄여서 시간 추정 성능을 향상시킬 수 있음을 보인다. 제안한 방법을 임펄스성 잡음 환경에서 전통적인 GCC-PHAT와 비교함으로써 추정 견실성이 향상됨을 보인다.

키워드

시간 지연 추정

상호 상관

저역 통과 필터

임펄스성 잡음

MAIN

I. 서 론
II. 비선형 전처리와 저역 통과 필터를 사용한 상호 상관 기반 시간 지연 신호 추정 기법
2.1 시간 지연 신호의 수치 모델링
2.2 임펄스성 잡음 환경에 강인함을 부가하기 위한 비선형 전처리
2.3 저역 통과 필터를 사용한 GCC-PHAT 기반 시간 지연 추정 방법
Ⅲ. 모의실험을 통한 성능 비교
3.1 임펄스 잡음 모델
3.2 모의 실험
IV. 결론 및 향후 과제

I. 서 론

두 개 이상의 센서 간의 시간 지연 차이 추정은 신호원의 수동적 위치 파악을 위한 중요한 방법이다. 이는 소나, 레이더, 실내 측위 또는 지진학 시스템 등 많은 분야에서 중요한 역할을 한다.^{[1,3,4,5,6,6]} 상호 상관 방법은 수신기가 수신한 신호 간의 상호 상관관계를 기반으로 하는 시간 지연 추정법으로 유용한 방법으로 여겨져 왔다. 또한 많은 연구자들이 상호 상관법을 수정한 방법들 제안하였다. 그중에 Carter 등에 의해서 제안되고 후속 연구로부터 성능이 향상된 일반화된 상호 상관(Generalized Cross Correlation, GCC)에 의한 시간 지연 추정법이 있다.^[1,7,8] GCC를 사용한 시간 지연 추정을 위해서 GCC-Maximum Likeli-hood (GCC-ML), GCC-Roth, GCC-Phase Transform(GCC-PHAT) 등과 같은 다양한 주파수 영역에서 가중치 함수를 설계하였고, 이 중에 GCC-PHAT가 여러 응용에 시간 지연 추정 방법으로 광범위하게 적용되고 있다.^[9,10,11] 그러나 GCC-PHAT을 비롯한 GCC 기반 추정법은 가우시안 잡음 환경하에서 최적의 성능을 보인다. 그러나 레이더나 소나 응용에서 접하는 주변 소음은 많은 경우 충격성이고 비가우시안적인 것으로 알려져 있다.^[12,13] 이런 형태의 임펄스성 잡음의 확률밀도함수는 평균에서 먼 쪽으로 갈수록 가우스 분포보다 더 두꺼워지는 형태를 보인다. 그리고 GCC-PHAT를 비롯한 GCC 기반 추정법들은 이런 잡음 환경에서 심각한 성능 저하를 보인다.^[12] 이런 임펄스성 잡음 상황에서 성능 저하를 줄이기 위해서 GCC-PHAT에 비선형 전처리를 도입하는 연구가 이뤄졌다.^[14] 그 결과 가우시안 환경 때만큼은 아니지만 전처리기 적용 전에 비해서 상당한 성능 향상을 보였다.^[14]

본 논문에서는 GCC-PHAT 연산 과정을 DFT로 다시 해석하는 과정에서 시간 지연 추정에 실제로 사용되는 유효 주파수 대역이 있음을 파악하고, 이 유효 대역을 저역 통과 필터를 통해서 분리한 후 GCC-PHAT의 최종 단계를 실시하게 함으로써 시간 지연 추정에 불필요한 잡음 성분이 개입되는 것을 배제할 수 있음을 확인한다. 그리고 비선형 전처리기와 저역 통과 필터를 함께 사용함으로써 비선형 전처리기만을 사용할 때보다 임펄스성 잡음하에서 추정 성능이 더 향상됨을 보인다.

제안한 방법에 의한 성능 향상 정도를 보이기 위해서 –5 dB ~ 15 dB 사이의 일반 신호 대 잡음 비에서 모의실험을 하고, 추정 결과를 히스토그램으로 보인다. 이때 다양한 차단 주파수를 갖는 저역 통과 필터를 적용한 결과들을 서로 비교한 결과를 도시한다. 도시된 결과를 통하여 저역 통과 필터를 적용하는 것이 임펄스성 잡음 환경에서 GCC-PHAT의 추정 성능을 향상시킬 수 있음을 보인다.

본 논문의 구성은 II장에서 GCC-PHAT의 기본 구조와 비선형 전처리를 설명하고, GCC-PHAT 구조에 저역 통과 필터를 사용하여 성능을 향상시킬 수 있음을 GCC-PHAT의 재해석을 통해 보인다. III장에서는 모의실험을 통해서 II장의 결과를 확인하고 IV장에서 결론을 맺는다.

II. 비선형 전처리와 저역 통과 필터를 사용한 상호 상관 기반 시간 지연 신호 추정 기법

2.1 시간 지연 신호의 수치 모델링

두 수신 채널에서 각각 수신된 신호를 x_i(n), I = 1,2,라 한다면, 그 신호의 시간 지연 추정 수치 모델은 다음과 같다.^[1]

(1)

x_{i} (n) = β_{i} s (n - τ_{i}) + n_{i} (n),

여기서 $β_{i}$ 는 원신호, s(n),가 i번째 수신기에 도착할 때의 신호 감쇠 계수이고, τ_i는 원신호와 i번째 수신기 사이의 전파 지연 시간이다. 또 n_i(k)는 i번째 수신기에 부가된 잡음이다. 이 모델에서 s(n), n_i(n)는 서로 상관관계가 없다. n_i(n)는 임펄스성 잡음이다. 두 수신기 사이의 상호 시간 지연은, $\hat{τ} = τ_{12} = τ_{1} - τ_{2}$ 이다.

2.2 임펄스성 잡음 환경에 강인함을 부가하기 위한 비선형 전처리

Pena et al.^[14]은 임펄스성 잡음에 강인한 GCC-PHAT를 위해서 비선형 전처리를 제안하였다. 이는 Eq. (1)과 같은 수신 신호가 시간 지연 추정을 위해서 GCC-PHAT에 입력되기 전에 Eq. (2)와 같은 비선형 전처리를 하면 GCC-PHAT가 임펄스성 잡음 환경에서 견실한 시간 지연 추정을 함을 보였다.^[14]

(2)

{\hat{x}}_{i} (n) = \tanh (x_{i} (n)) .

2.3 저역 통과 필터를 사용한 GCC-PHAT 기반 시간 지연 추정 방법

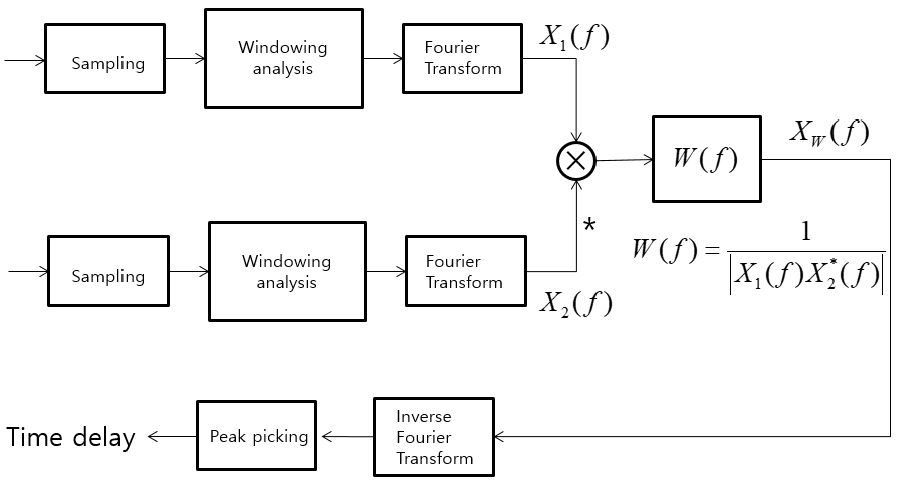
GCC-PHAT는 일종의 백색화 가중치를 사용하는 상호 상관 추정 기법이다. 주파수 영역에서 두 수신기 신호 간의 곱을 구한 후에 백색화 가중치 과정을 통과시켜서 위상만을 남김으로써 신호의 스펙트럼 크기의 영향을 배제한다. 전통적인 GCC-PHAT 기반의 시간 지연 추정 과정을 Fig. 1에 나타내었다. Fig. 1의 GCC-PHAT 방법을 간략히 기술하면 다음과 같다. $r_{s} \in R^{3}$ 에 위치한 신호원에서 $r_{1}, r_{2} \in R^{3}$ 에 위치한 두 수신기가 각각 도래하는 신호 간의 시간 지연을 GCC-PHAT 방법을 통해 구하기 위해서는 Eq. (3)과 같이 가중함수를 이용하여 위상만을 남기고 역 퓨리어 변환하여 상호 상관 함수를 구한다.^[1]

(3)

R (m) = \frac{1}{N} \sum_{k = 0}^{N - 1} ϕ (k) X_{1} (k) X_{2}^{*} (k) e^{\frac{j 2 π k m}{N}},

여기서 N은 DFT 샘플수이고, $X_{i} (k)$ 는 $x_{i} (n)$ 의 DFT 결과이며, $ϕ (k) = 1 / ∥ X_{1} (k) X_{2}^{*} (k) ∥$ 이다. 그리고 상호 상관 함수 중 최대치가 존재하는 위치가 구하려는 지연 값이 된다. 위의 역 퓨리어 변환은 순방향 퓨리어 변환으로도 생각할 수 있다. 즉, $ϕ (k) X_{1} (k) X_{2}^{*} (k) = e^{\frac{- j 2 π k p}{N}}$ 이라면 위 식은 다음 Eq. (4)와 같이 퓨리어 변환으로 바꿔 표현할 수 있다.

(4)

R (m) = {(\frac{1}{N} \sum_{k = 0}^{N - 1} ϕ (k) X_{1}^{*} (k) X_{2} (k) e^{\frac{- j 2 π k m}{N}})}^{*} = \frac{1}{N} {(\sum_{k = 0}^{N - 1} e^{\frac{j 2 π k p}{N}} e^{\frac{- j 2 π k m}{N}})}^{*} = \frac{1}{N} {(D F T (e^{\frac{j 2 π k p}{N}}))}^{*} .

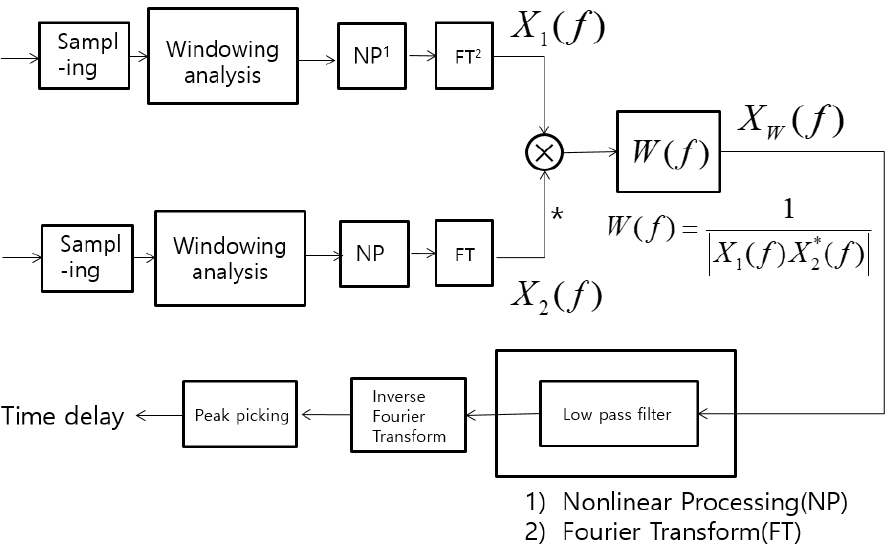
이때 DFT로 재해석한 결과는 p번째 빈에서 피크를 만들게 된다. 이때 p번째 빈은 DFT에 쓰인 데이터 길이 N을 2𝜋에 대응시킬 때 $2 π p / N$ 인 주파수 값에 대응시킬 수 있다. 그리고 두 수신 기간 최대 시간 지연이 $τ_{\max}$ 샘플 스텝이라고 할 때, 최대 지연 값 $τ_{\max}$ 에 해당하는 주파수는 $τ_{\max} / N$ 가 된다. 여기서 $τ_{\max} = ⌊ ∥ r_{1} - r_{2} ∥ F_{s} / c ⌋$ 이고 c는 전달속도이며, Fs는 샘플링 속도이다. 즉 DFT를 사용해서 시간 지연 추정을 할 때 모든 주파수가 필요한 것이 아니고, 주파수 $τ_{\max} / N$ 까지만 유효하게 필요하다는 뜻이 된다. 즉, 유효 주파수 폭이 있다는 의미이다. 따라서 푸리에 변환을 하기 전에 사용할 신호 데이터에 미리 유효 주파수 이상을 차단하는 저역 통과 필터를 통과시켜서 부가된 잡음 성분을 미리 제거하여 시간 지연 추정 성능을 향상할 수 있다는 것을 의미한다. Fig. 2는 일반 GCC-PHAT에 비선형 전처리와 저역 통과 필터를 적용하는 것을 보여주고 있다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-04/N0660430405/images/ASK_43_04_05_F1.jpg

Fig. 1.

Diagram of GCC-PHAT.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-04/N0660430405/images/ASK_43_04_05_F2.jpg

Fig. 2.

Diagram of GCC-PHAT using low-pass filter.

Ⅲ. 모의실험을 통한 성능 비교

3.1 임펄스 잡음 모델

대칭 α-안정 프로세스는 충격성 잡음을 모델링에 널리 사용된다.^[13] 본 논문의 실험에서도 임펄스 노이즈 모델로 대칭α안정(SymmetricαStable, $S α S$ ) 분포를 선택하였다. 이 모델의 특성 함수는 Eq. (5)와 같이 표현된다.^[12]

(5)

ϕ (ω) = \exp (- γ | ω |^{α}),

여기서 1 < α ≤ 2는 분포의 양쪽 끝 형태를 설명하는 특성 지수이다. 𝛾는 퍼짐 정도를 나타내는 상수이다. Eq. (5)에서 α = 2인 경우 대칭 α-안정 분포는 정규분포가 된다. α < 2인 경우 임펄스성 잡음 특성을 나타내어 대칭α안정 분포 잡음은 분포의 끝부분 즉 꼬리 부분이 정규분포보다 두껍게 된다. α가 1에 가까울수록 임펄스 발생 빈도가 높은 잡음이 된다. 또 α < 2인 경우 대칭α안정 분포의 2차 및 고차 모멘트는 무한대이므로 일반적으로 사용되는 신호 대 잡음비(Signal to Noise Ratio, SNR)는 의미가 없다. 따라서 본 실험에서는 신호와 잡음 사이의 상대적인 강도를 정량화하기 위해 Eq. (6)과 같이 정의되는 일반화된 신호 대 잡음비(Generalized Signal to Noise Ratio, GSNR)을 사용한다.^[12]

(6)

G S N R = 10 \log_{10} (E (x (n)^{2}) / γ^{α}) .

본 논문의 모의 실험에서는 임펄스성 잡음을 가우시안에 좀 더 가까운 α = 1.8인 경우와 이에 비해서 더 많은 임펄스성 잡음이 발생하는 α = 1.2인 경우를 각각 실험한다.

3.2 모의 실험

모의실험을 위해서 두 수신 채널을 위한 신호 열을 다음과 같이 발생시킨다. 비교실험을 위한 신호 발생을 위해서 첫 번째 채널 신호 x₁(n)은 백색 정규화 분포를 갖는 신호로 발생시켰다. 두 번째 채널 신호는 x₁(n)과 10 샘플 뒤진 신호로 모델 하였다. 즉, x₂(n) = x₁(n−10) 이다. 각 신호 x₁(n)과 x₂(n)에는 대칭α안정 분포 잡음, n₁(n)과 n₂(n)를 각각 부가했다. 그리고 Fig. 2에서와 같이 두 신호가 각각 푸리에 변환되기 전에 Eq. (2)의 tanh() 함수를 사용한 비선형 전처리를 하였다.

가상의 수신기 구성은 두 수신기간 거리는 10 m로 설정하고 수신기는 수중에 설치한 것으로 가정하였다. 그리고 표본화 주파수는 8000 sample/s로 가정하였다. 이 경우 수중 음파 전달속도를 1500 m/s로 가정한다면, 최대 지연에 해당하는 시간 스텝은 53.3 스텝이다. 그리고 II장에서 서술한 것과 같이 역 퓨리어 변환에 등가인 순방향 퓨리어 변환으로 해석할 때 최대 지연 스텝 수에 대응하는 등가 주파수는 약 0.12𝜋가 된다. 또 앞서 기술한 수신기 간 시간 지연을 10 샘플 스텝으로 할 때 이 시간 지연에 해당하는 등가 주파수는 약 0.03𝜋가 된다. 이를 토대로 저역 통과 필터를 계산 시간에 부담을 주지 않는 간단한 구조의 2차 버터워스 필터로 만들고, 그 차단 주파수를 각각 0.2𝜋, 0.12𝜋 및 0.05𝜋로 적용했을 때의 시간 지연 추정 성능을 저역 통과 필터를 사용하지 않는 일반 GCC-PHAT 방식으로 얻은 시간 지연 추정 성능과 비교하였다.

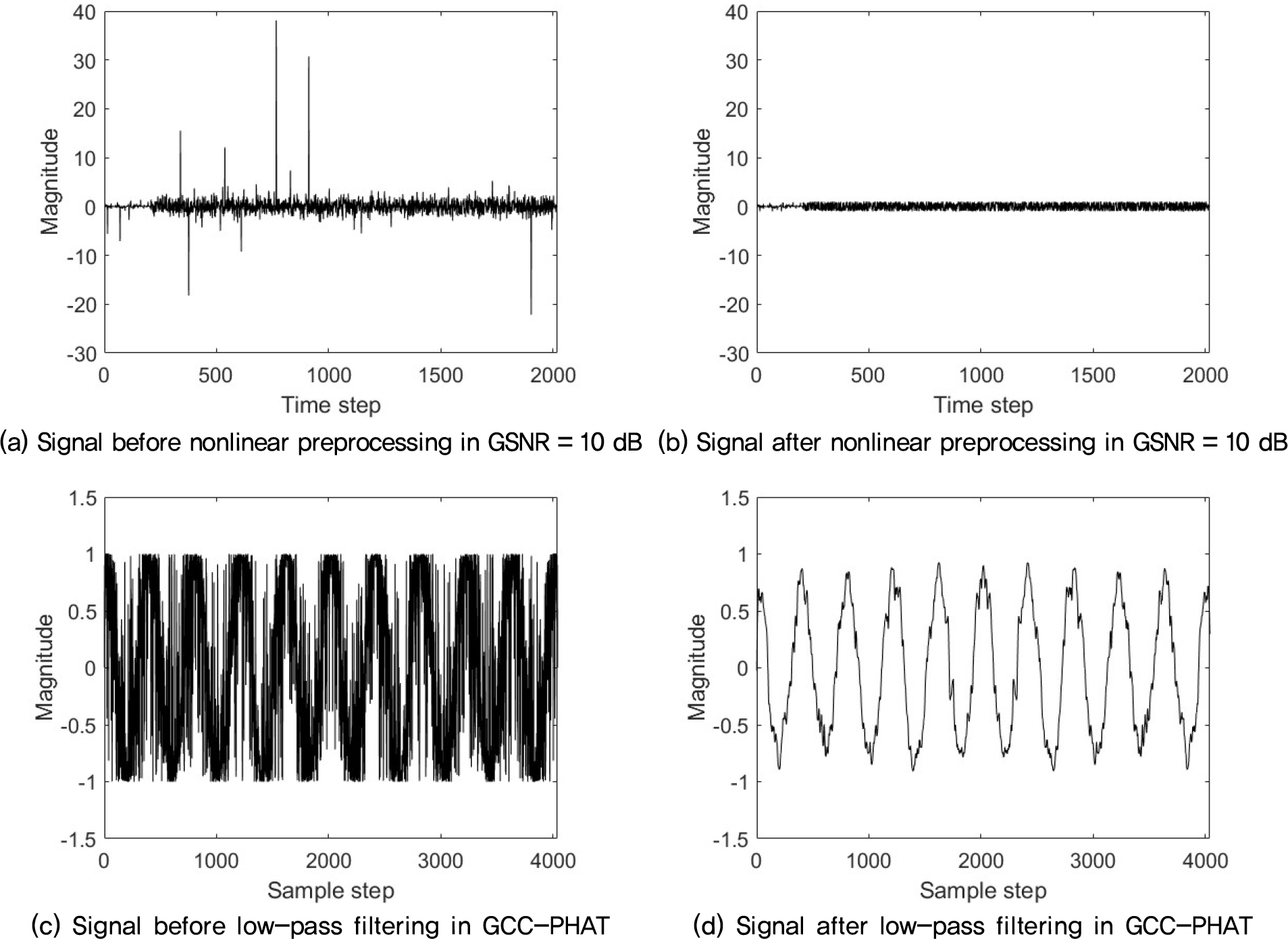
실험 결과를 보이기에 앞서 α = 1.2인 대칭 α 안정 분포의 잡음이 부가되는 경우에 대해서 일반화된 신호 대 잡음비 10 dB인 신호에 대해서 비선형 전처리기의 영향과 저역 통과 필터의 영향을 보이는 예를 Fig. 3에 도시하였다. Fig. 3(a)와 (b)는 전처리기를 사용하기 전과 후의 신호를 볼 수 있다. 전처리의 역할이 입력 신호의 임펄스 효과를 낮추고 있음을 알 수 있다. 이런 신호 크기의 억제 효과은 두 채널 신호 간 시간 지연량을 추정하는 본 논문과 같은 경우 영향을 미치지 않는다. Fig. 3(c)와 (d)는 GCC-PHAT 알고리즘 중에서 저역 통과 필터를 통과하기 전과 후를 비교하여 볼 수 있다. 두 그림에서 알 수 있는 것과 같이 저역 통과 필터 통과 후에 잡음 수준이 낮아진 것을 관찰할 수 있다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-04/N0660430405/images/ASK_43_04_05_F3.jpg

Fig. 3.

Illustration of effects of nonliear pre-processing and low-pass filtering (α = 1.2 and GSNR = 10 dB).

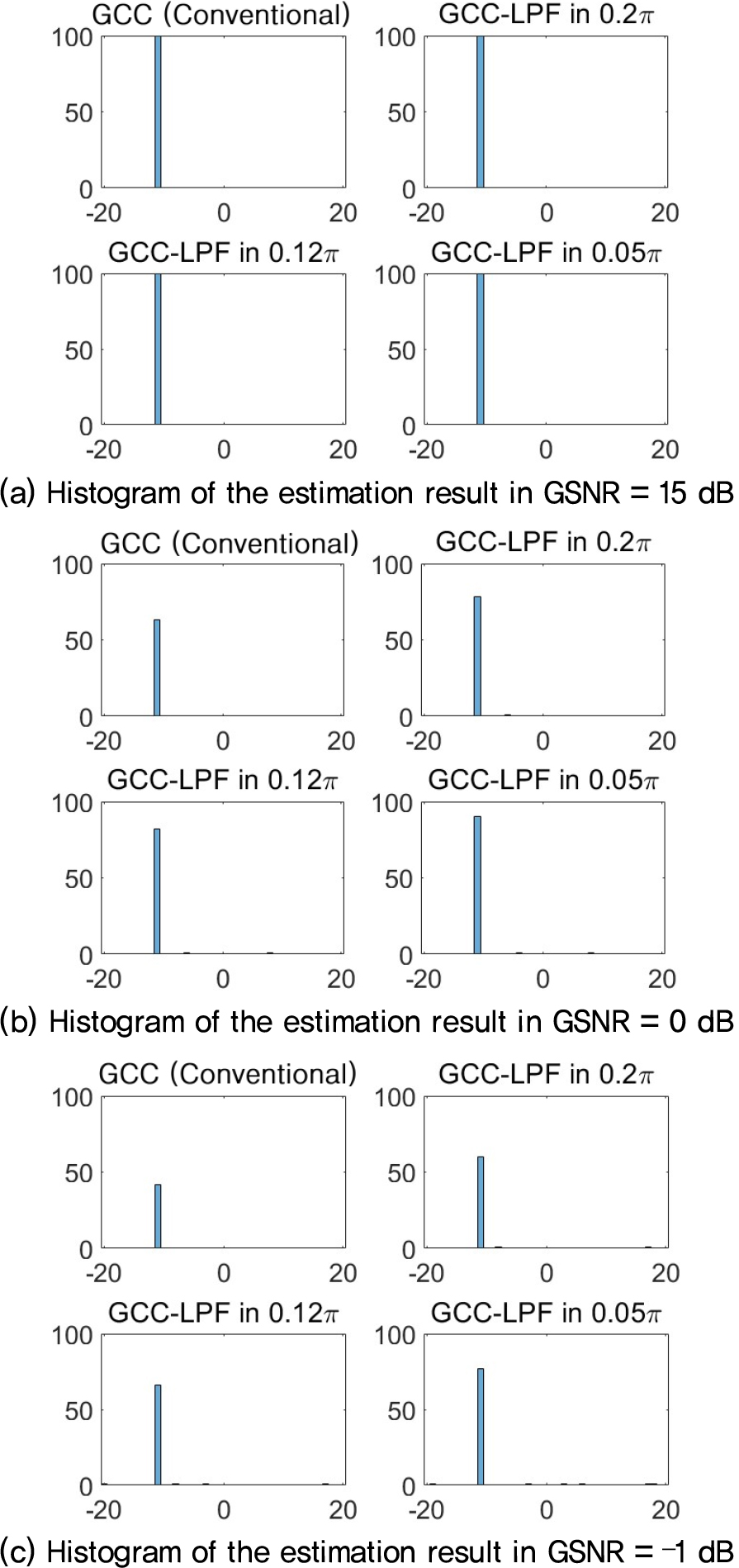
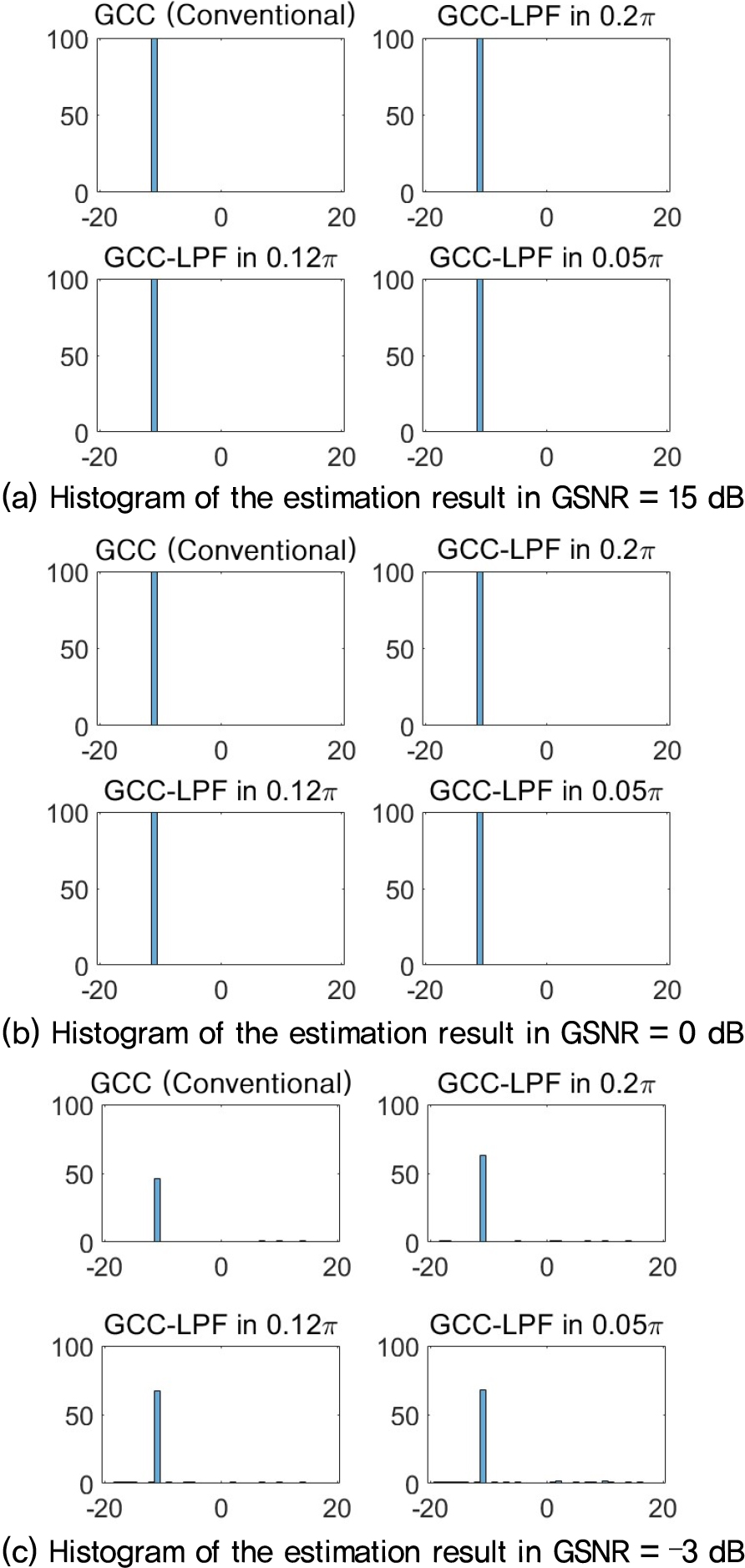
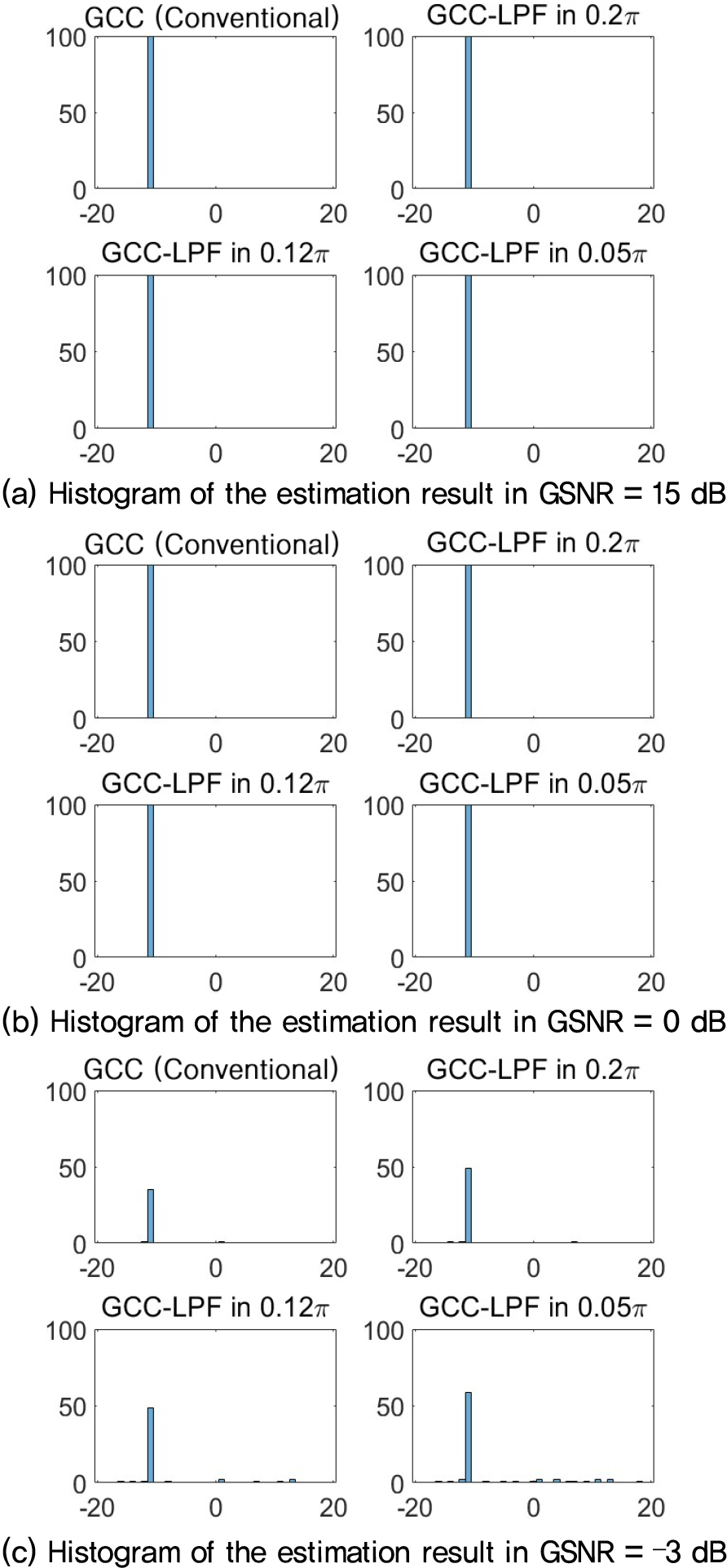
실험 결과는 Eq. (6)에 정의한 일반 신호 대 잡음 비를 사용하여 15 dB에서 –5 dB까지 조건에서 각각 100회씩 반복 시행하였고, 그 결과를 히스토그램으로 표시하였다. Fig. 4는 α = 1.8인 대칭α안정 분포의 잡음이 부가 되는 경우에 비선형 전처리를 사용하지 않은 전통적인 GCC-PHAT와 저역 통과 필터만을 적용한 GCC-PHAT에서의 시간 지연을 추정한 결과를 도시한 결과이다. Fig. 4(a)의 GSNR = 15 dB에서는 모든 알고리즘이 정확한 추정을 하였음을 보이고, Fig. 4(b)의 GSNR = 0 dB에서 전통적인 GCC-PHAT만 100회중 94회 정확한 추정을 하였고, 저역 통과 필터를 사용한 GCC-PHAT는 100회 모두 정확한 추정을 하는 결과를 보였다. 그리고 Fig. 4(c)의 GSNR = –1 dB에서는 일반 GCC-PHAT는 성공률이 50 % 이하로 떨어졌으나 저역 통과 필터를 사용한 GCC-PHAT는 필터의 차단 주파수가 0.2𝜋인 경우 60 %의 정확도를 보이고, 차단 주파수가 0.12𝜋인 경우 66 % 또 차단 주파수가 0.05𝜋인 경우 77 %의 정확도를 보였다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-04/N0660430405/images/ASK_43_04_05_F4.jpg

Fig. 4.

(Color available online) Estimation performance without nonlinear preprocessor (α = 1.8).

Fig. 5는 α = 1.8인 대칭α안정 분포의 잡음이 부가되는 경우에 비선형 전처리를 사용한 전통적인 GCC-PHAT와 비선형 전처리와 저역 통과 필터를 적용한 GCC-PHAT에서의 시간 지연을 추정한 결과를 도시한 결과이다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-04/N0660430405/images/ASK_43_04_05_F5.jpg

Fig. 5.

(Color available online) Estimation performance with nonlinear preprocessor (α = 1.8).

Fig. 5(a)의 GSNR = 15 dB에서는 모든 알고리즘이 정확한 추정을 하였음을 보이고, Fig. 5(b)의 GSNR = 0 dB에서 추정 결과인데 Fig. 4(b)와 달리 모든 알고리즘이 정확한 추정을 하였음을 보였다. 그리고 Fig. 5(c)의 GSNR = –3 dB에서 비선형 전처리를 사용한 일반 GCC-PHAT는 성공률이 50 % 이하로 떨어졌고(추정 성공률이 50 % 이하로 내려가는 것을 추정 임계치로 본다), 비선형 전처리와 저역 통과 필터를 사용한 GCC-PHAT는 필터의 차단 주파수가 0.2𝜋인 경우 63 %의 정확도를 보이고, 차단 주파수가 0.12𝜋인 경우 67 % 또 차단 주파수가 0.05𝜋인 경우 68 %의 정확도를 보였다.

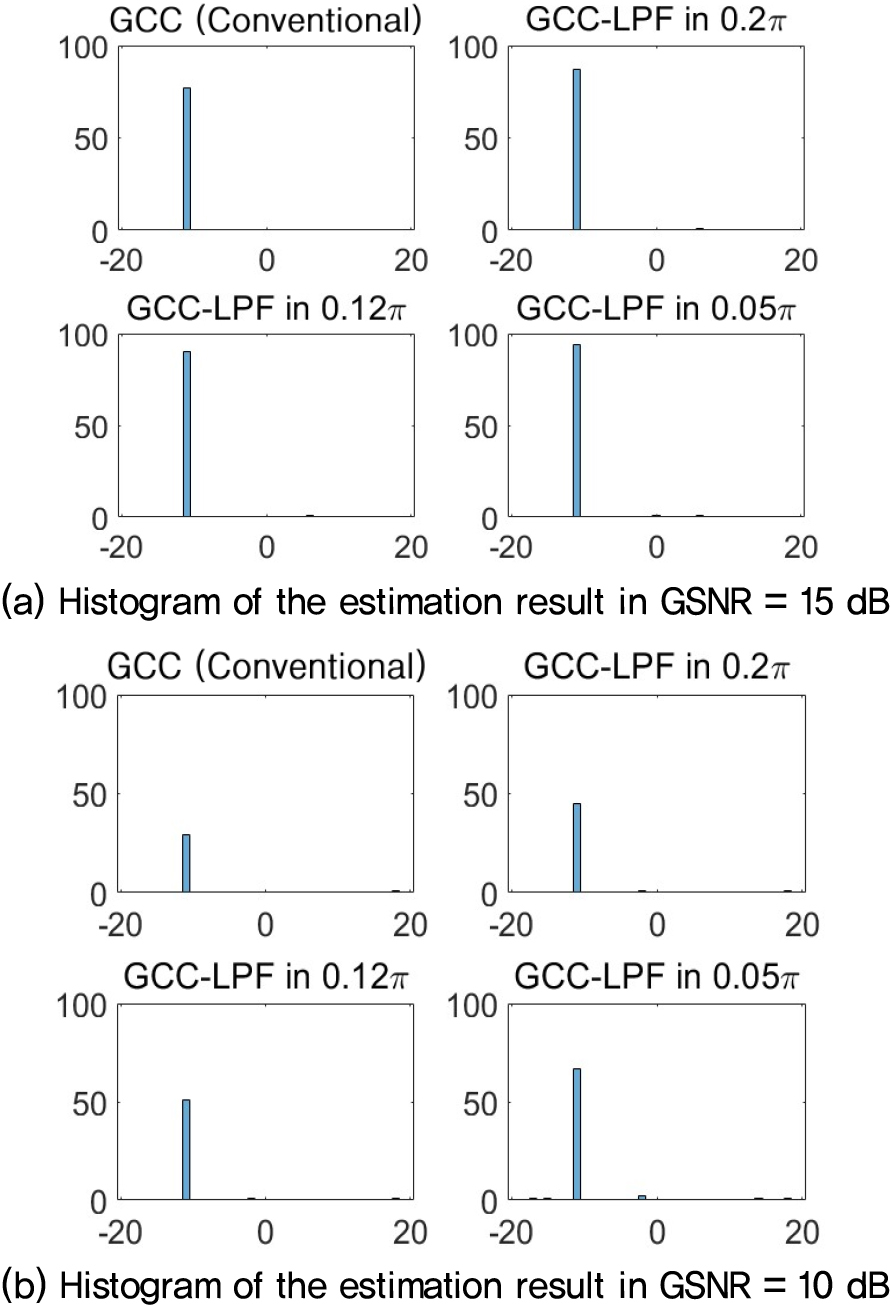
Fig. 6은 α = 1.2인 대칭α안정 분포의 잡음이 부가되는 경우에 비선형 전처리를 사용하지 않은 전통적인 GCC-PHAT와 저역 통과 필터만을 적용한 GCC-PHAT에서의 시간 지연을 추정한 결과를 도시한 결과이다. 이 경우 α = 1.8인 경우보다 임펄스성 잡음의 영향이 더 심한 경우를 모사하고 있다. Fig. 6(a)의 GSNR = 15 dB에서는 일반 GCC-PHAT는 성공률이 77 %이고, 저역 통과 필터를 사용한 GCC-PHAT는 필터의 차단 주파수가 0.2𝜋인 경우 87 %의 정확도를 보이고, 차단 주파수가 0.12𝜋인 경우 90 % 또 차단 주파수가 0.05𝜋인 경우 94 %의 정확도를 보였다. 그리고 Fig. 6(b)의 GSNR = 10 dB에서는 일반 GCC-PHAT는 성공률이 50 % 이하로 떨어졌음을 확인할 수 있다. 저역 통과 필터를 사용한 GCC-PHAT는 필터의 차단 주파수가 0.2𝜋인 경우 45 %의 정확도를 보이고, 차단 주파수가 0.12𝜋인 경우 51 % 또 차단 주파수가 0.05𝜋인 경우 67 %의 정확도를 보였다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-04/N0660430405/images/ASK_43_04_05_F6.jpg

Fig. 6.

(Color available online) Estimation performance without nonlinear preprocessor (α = 1.2).

Fig. 7은 α = 1.2인 대칭α안정 분포의 잡음이 부가되는 경우에 비선형 전처리를 사용한 전통적인 GCC-PHAT와 비선형 전처리와 저역 통과 필터를 적용한 GCC-PHAT에서의 시간 지연을 추정한 결과를 도시한 결과이다. Fig. 7(a)의 GSNR = 15 dB의 경우를 보면 같은 GSNR인 Fig. 6(a)와 달리 모든 알고리즘이 정확한 추정을 하였음을 보이고, Fig. 7(b)는 GSNR = 0 dB임에도 불구하고 여전히 모든 알고리즘이 정확한 추정을 하였음을 보이고 있음을 관찰할 수 있다. 그리고 Fig. 7(c)의 GSNR = –3 dB에서 비선형 전처리를 사용한 일반 GCC-PHAT는 성공률이 35 %로 성공률 50 % 이하로 떨어졌고, 비선형 전처리와 저역 통과 필터를 사용한 GCC-PHAT는 필터의 차단 주파수가 0.2𝜋인 경우 49 %의 정확도를 보이고, 차단 주파수가 0.12𝜋인 경우도 49 %였다. 그러나 차단 주파수가 0.05𝜋인 경우 59 %의 정확도를 보였다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-04/N0660430405/images/ASK_43_04_05_F7.jpg

Fig. 7.

(Color available online) Estimation performance with nonlinear preprocessor (α = 1.2).

Figs. 4, 5, 6, 7까지의 결과로부터 본 논문에서 제안한 비선형 전처리 후에 주파수 영역에서 저역 통과 필터를 사용하는 방법 GCC-PHAT 방법이 임펄스성 잡음 환경에서 시간 지연 추정하는 데에 견실성을 더할 수 있음을 확인하였다.

Tables 1과 2를 사용하여 저역 필터 없이 비선형 전처리기의 사용 효과와 저역 필터와 비선형 전처리기 사용 효과를 정리하였다. Table 1은 저역 필터 없이 비선형 전처리기를 사용했을 때와 사용하지 않았을 때 효과를 비교하기 위해서 추정 성공률 50 % 미만이 되는 GSNR을 비교하였다. 비선형 전처리기만을 사용했을 때 α = 1.8일 때 GSNR 개선 효과는 2 dB고, α = 1.2일 때 GSNR 개선 효과는 13 dB이다. Table 2는 저역 필터(차단 주파수 0.05𝜋)를 기본으로 사용하고, 비선형 전처리기를 사용했을 때와 사용하지 않았을 때 효과를 보이기 위해서 Table 1과 마찬가지로 추정 성공률 50 % 미만이 되는 GSNR을 비교하였다. α = 1.8일 때 GSNR 개선 효과는 1 dB고, α = 1.2일 때 GSNR 개선 효과는 12 dB이다.

Table 1.

Comparison of the effect of applying nonlinear preprocessing to GCC-PHAT without low-pass filter (GSNR comparison with the success rate of less than 50 %).

	Without nonlinear pre-processing	Nonlinear pre-processing
α = 1.8	–1 dB	–3 dB
α = 1.2	10 dB	–3 dB

Table 2.

Comparison of the effect of nonlinear preprocessing on GCC-PHAT with low-pass filter (GSNR comparison with the success rate of less than 50 %).

Cut-off frequency of low pass filter: 0.05𝜋	Low pass filter	Nonlinear pre-processing and low pass filter
α = 1.8	–3 dB	–4 dB
α = 1.2	8 dB	–4 dB

IV. 결론 및 향후 과제

임펄스성 잡음 환경에서 두 센서에 수신된 신호가 시간 지연을 추정하기 위한 비선형 전처리기를 사용하는 것 외에 GCC-PHAT 계산의 재해석을 통해서 주파수 영역에서 저역 통과 필터를 사용하면 잡음을 더 줄일 수 있음을 확인하였다. 그리고 모의실험을 통해서 비선형 전처리 후에 다양한 차단 주파수의 저역 통과 필터를 사용하는 GCC-PAHT의 시간 지연 추정 성능을 다양한 일반 신호 대 잡음 비에서 비교실험을 하였다. 그 결과 비선형 전처리와 주파수 영역 저역 통과 필터를 사용하는 GCC-PHAT가 임펄스성 잡음 환경하에서 시간 지연 추정 성능에 견실성이 있음을 보였다. 향후 본 결과를 임펄스성 잡음이 있는 실내 잔향 환경이나, 수중 환경에서 운영하는 배열 수신기를 사용한 소음원 위치 추정의 정확성 향상에 적용을 고려하고 있다.

Acknowledgements

이 논문은 2024년 정부(방위사업청)의 재원으로 국방기술진흥연구소의 지원을 받아 수행된 연구임(No.KRIT-CT-22-052, 물리데이터 기반 지능형 소나 신호 탐지 기술 연구).

References

G. Carter, "Time delay estimation for passive sonar signal processing," IEEE Trans. Acoust. Speech, Signal Process. 29, 463-470 (1981).

10.1109/TASSP.1981.1163560

H. Xin, X. Bai, J. Zhao, and B. Li, "On TDE techniques for the radar signal," J. Eng. 2019, 6554-6557 (2019).

10.1049/joe.2019.0151

L. Nguyen, J. V. Miro, and X. Qiu, "Multilevel B-splines-based learning approach for sound source localization," IEEE Sensors J. 19, 3871-3881 (2019).

10.1109/JSEN.2019.2895854

J. Wang, J. Wang, X. Jia, W. Shan, and J. Guan, "Research on imaging methods of single-beam mechanical scanning sonar," Proc. IEEE Int. Conf. Signal Process., Commun. Comput. 1-4 (2020).

10.1109/ICSPCC50002.2020.9259472

V. Faerman, K. Voevodin, and V. Avramchuk, "Frequency-domain generalized phase transform method in pipeline leaks locating," Proc. Int. Conf. High-Perform. Comput. Syst. Technol. Sci. Res. Automat. Control Prod. 22-38 (2023).

10.1007/978-3-031-23744-7_3

C. Du, S. Yu, H. Yin, and Z. Sun, "Microseismic time delay estimation method based on continuous wavelet," J. Sensors, 22, 1-11 (2022).

10.3390/s2208284535458829PMC9026944

J. S. Lim and K. Lee, "Time delay estimation algorithm using Elastic Net" (in Korean), J. Acoust. Soc. Kr. 42, 364-369 (2023).

J. Lim, "A study on improving time delay estimation performance of generalized cross correlation - phase transform using singular spectrum analysis" (in Korean), J. KIIT. 20, 99-106 (2022).

10.14801/jkiit.2022.20.8.99

C. S. Tan, R. M. Mokhtar, and M. R. Arshad, "Improved generalized cross correlation phase transform algorithm for time difference of arrival estimation," Proc. 10th Nat. Tech. Seminar Underwater Syst. Technol. 315-322 (2019).

10.1007/978-981-13-3708-6_26

J. M. Lorenzo, R. V. Abad, P. R. Lopez, F. Rivas, and J. Escolano, "Evaluation of generalized cross-correlation methods for direction of arrival estimation using two microphones in real environments," J. Appl. Acoust. 73, 698-712 (2012).

10.1016/j.apacoust.2012.02.002

T. Gustafsson, B. D. Rao, and M. Trivedi, "Source localization in reverberant environments: Modeling and statistical analysis," IEEE Trans. Speech Audio Process. 11, 791-803 (2003).

10.1109/TSA.2003.818027

P. G. Georgiou, P. Tsakalides, and C. Kyriakakis, "Alpha-stable modeling of noise and robust time-delay estimation in the presence of impulsive noise," IEEE Trans. Multimedia, 1, 291-301 (1999).

10.1109/6046.784467

P. Tsakalides, Array signal processing with alpha-stable distribution, (Ph.D. thesis, University of South California, 1995).

D. Pena, A. Lima, V. Junior, L. Silveira, and A. Medeiros, "Robust time delay estimation based on non-Gaussian impulsive acoustic channel," JCIS, 35, 86-89 (2020).

10.14209/jcis.2020.9

The Journal of the Acoustical Society of KoreaISSN:1225-4428(Print) 2287-3775(Online)한국음향학회

Preview

A study on robust generalized cross correlation-phase transform based time delay estimation in impulsive noise environment using nonlinear preprocessing and frequency domain low-pass filter

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

Fig. 1.

Diagram of GCC-PHAT.

Fig. 2.

Diagram of GCC-PHAT using low-pass filter.

(5)

(6)

Fig. 3.

Illustration of effects of nonliear pre-processing and low-pass filtering (α = 1.2 and GSNR = 10 dB).

Fig. 4.

(Color available online) Estimation performance without nonlinear preprocessor (α = 1.8).

Fig. 5.

(Color available online) Estimation performance with nonlinear preprocessor (α = 1.8).

Fig. 6.

(Color available online) Estimation performance without nonlinear preprocessor (α = 1.2).

Fig. 7.

(Color available online) Estimation performance with nonlinear preprocessor (α = 1.2).

Table 1.

Comparison of the effect of applying nonlinear preprocessing to GCC-PHAT without low-pass filter (GSNR comparison with the success rate of less than 50 %).

Table 2.

Comparison of the effect of nonlinear preprocessing on GCC-PHAT with low-pass filter (GSNR comparison with the success rate of less than 50 %).

Acknowledgements

References