I. 서 론
II. 대상 축류팬 시스템
III. 대상 팬 성능 평가를 위한 실험적 연구 기법
IV. 수치 해석을 통한 성능 비교
4.1 수치 해석 기법
4.2 수치 해석 영역
4.3 수치 해석 결과 비교를 통한 윙렛 효과 평가
V. 실험을 통한 성능 비교
VI. 결 론
I. 서 론
난방, 환기, 공조를 나타내는 HVAC 시스템은 기계 산업은 물론 건축 산업과 주거 환경에서 가장 핵심적인 부분을 차지한다. HVAC 시스템의 가장 대표적인 가전제품인 에어컨은 일반적으로 실외기와 실내기로 구성된다. 그 중 실외기는 외부에 장착되는 특징으로 인해 냉각 성능뿐만 아니라 소음 문제 또한 중요한 성능 지표로 작용한다. 따라서, 에어컨 실외기의 성능을 개선하기 위한 연구가 활발하게 진행되고 있다. 에어컨 실외기를 구성하는 여러 부품 중 축류팬은 실외기 내/외부로의 공기 순환을 유도하여 열교환기 냉각의 목적으로 사용되므로 이를 위한 충분한 유량 성능이 요구된다. 또한, 팬 회전으로 인해 발생하는 소음은 에어컨 실외기의 전체 소음에 지배적인 영향을 미치게 된다. 이에 대해 Ryu et al.[1]은 에어컨 실외기를 대상으로 수치적, 실험적 연구를 수행하여 부품별 주요 유동장을 평가하였다. 그 결과, 압축기를 제외한 축류팬, 오리피스, 방열판, 모터, 모터 마운트 중 축류팬과 오리피스로 구성된 축류팬 시스템이 전체 소음 및 유량 성능에 가장 지배적인 영향을 미침임을 확인하였다. 그에 따라 오리피스의 형상을 유동을 흡입, 발달, 토출 시키는 역할에 따라 구간화하여 형상 설계 변수에 대한 최적 설계를 수행하였으며, 최적 설계 오리피스에서 발생하는 소음과 유량 성능이 모두 기존과 비교하여 개선됨을 확인하였다. 이와 같이 축류팬과 축류팬의 유로를 포함하는 오리피스로 구성된 축류팬 시스템을 주로 튜브형 축류팬으로 표현하며, 본 논문에서는 튜브를 오리피스로 표현하였다.
축류팬과 오리피스 사이의 좁은 간극에서 발생하는 대표적인 유동 현상은 일반적으로 날개 끝 와류와 누설 와류로 알려져 있다. 이러한 와류는 축류팬 날개와 오리피스 간 간극의 압력 차로 인해 발생하여 고압 영역에서 저압 영역으로의 흐름이 형성된다. 이는 유동의 손실을 야기하고 소음원으로 작용하기 때문에 축류팬의 성능 개선을 위해서는 이러한 와류 구조에 관한 연구가 필수적이다. 날개 끝 와류 억제를 위한 가장 대표적인 설계로 윙렛형상을 들 수 있다. Whitcomb[2]는 항공기 날개 끝을 구부린 형상인 윙렛을 개발하여 유도 항력을 감소시켜 효율을 포함한 전체 성능을 개선하였다. 또한, Kappel et al.[3]은 윙렛 개념과 유사한 확장된 날개 끝 형상을 특징으로 하는 선박용 프로펠러를 개발하였다. 새로운 설계 접근을 통해 날개 끝 와류의 발생을 억제함으로써 에너지 손실을 최소화할 뿐만 아니라 선박 추진의 효율성과 성능을 향상시키는 것을 목표로 하였다. 이와 더불어 축류팬 날개 끝 와류와 누설 와류에 관한 연구가 활발하게 이루어졌다. Benedek et al.[4]는 오리피스형 축류팬의 입구인 벨마우스 크기를 다양하게 설계하고 이에 대한 noise map을 작성하여 주파수별 소음원을 규명하였다. Park et al.[5]는 축류팬 후단 근처의 오리피스에 펜스 형상을 추가하여 누설 와류에 미치는 영향을 평가하였다. Seyed et al.[6]은 축류팬과 오리피스 사이의 간극이 커질수록 간극에서 발생하는 누설 와류, 날개 끝 와류, 유동 박리 등의 현상이 증가하여 팬의 효율이 감소한다는 결과를 도출한 바 있다. 또한, Zhang et al.[7]은 축류팬 날개의 설계 요소 중 피치각에 관한 연구를 수행하여 임계값을 확인하고, 임계값 이하에서 피치각의 증가는 누설 와류를 유발하여 압력 손실과 효율 저하를 야기한다는 결과를 확인하였다.
이를 바탕으로 본 연구에서는 에어컨 실외기 내 축류팬 시스템을 대상으로 축류팬 날개 끝단에 윙렛을 적용하여 날개 끝 와류와 누설 와류의 변화를 관찰하고 성능에 미치는 영향을 수치적, 실험적으로 평가하고자 하였다.
II. 대상 축류팬 시스템
본 연구 대상인 축류팬 시스템은 Fig. 1에 나타낸 바와 같이 세 개의 날개로 구성된 축류팬과 이를 둘러싼 오리피스로 구성된다. 오리피스는 일반적으로 팬의 상류와 하류를 모두 포함하는 fully-ducted type의 오리피스가 아닌 partially-ducted type의 오리피스로 팬의 일부분만을 포함하는 형상이다. 이는 Fig. 2에 나타낸 바와 같이 오리피스의 입구단과 날개 끝과의 거리를 날개 코드에 따라 나타낸 그래프를 통해 정량적으로 확인할 수 있으며, 날개 끝의 코드 약 75 % 지점부터 뒷전까지의 구간만을 포함하여 둘러싼 시스템이다. 대상 팬 모델은 Fig. 3에 나타내었으며, 날개 끝 형상을 나타내기 위해 날개 코드의 약 10 %, 50 %, 90 % 지점에서 원주 방향의 단면을 나타내었다. Fig. 3(a)에 나타낸 모델 A는 윙렛 형상이 날개 끝에 고려되어 날개 끝의 앞전부터 뒷전까지 모두 동일한 곡률이 적용된 기존의 대상 팬 모델이다. 또한, 윙렛 형상에 따른 성능 변화를 비교하기 위해 Fig. 3(b)와 같이 날개 끝에 3차원 형상이 고려되지 않은 평평한 형상을 가진 모델 B를 추가로 설계하였다. 두 팬의 작동 회전 속도는 800 r/min으로 설정하였다.
III. 대상 팬 성능 평가를 위한 실험적 연구 기법
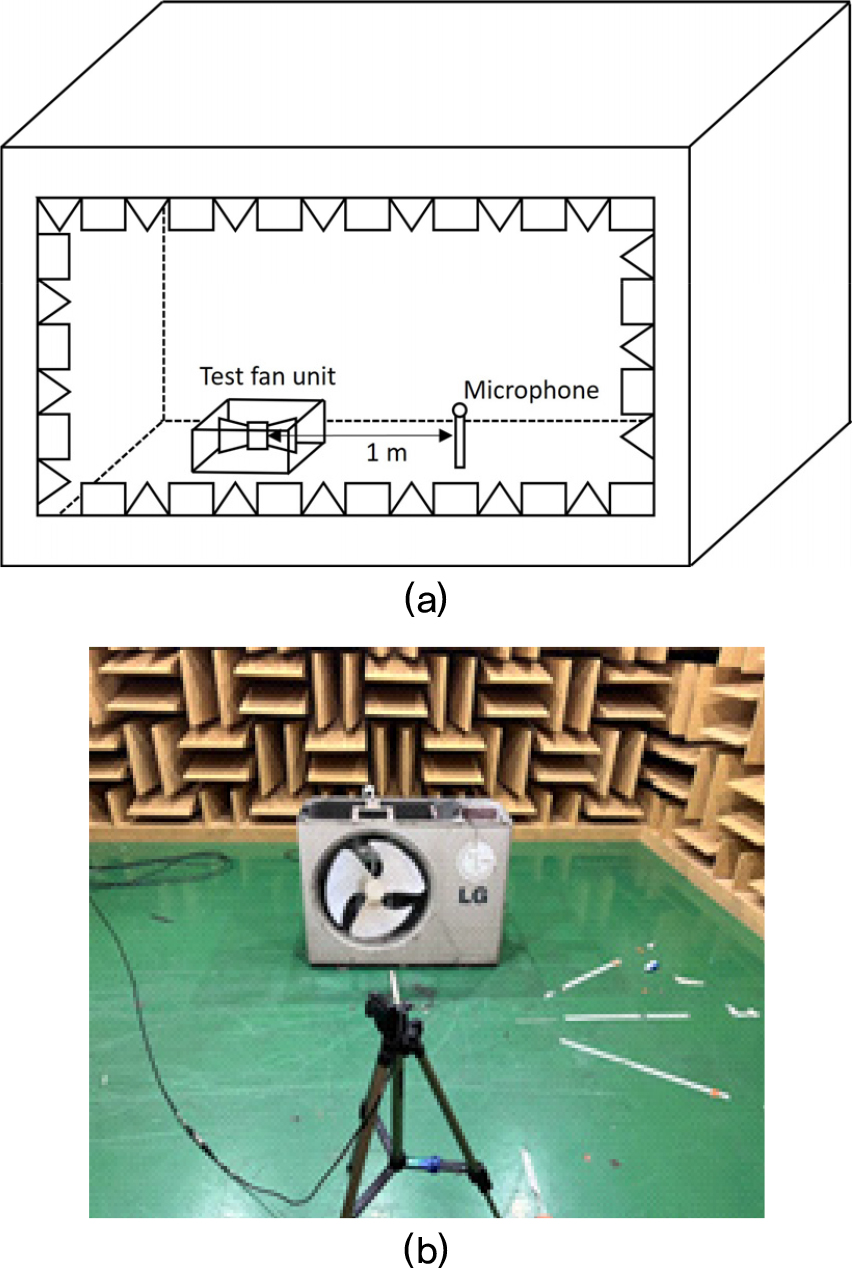
대상 축류팬 시스템의 성능을 평가하기 위한 실험을 실시하였다. 먼저, 대상 축류팬인 모델 A에 대해 소음 성능을 평가하기 위한 실험을 실시하였다. 소음 실험은 4 m × 4 m × 2.7 m 크기, 차단주파수 125 Hz, 배경 소음 18 dB 이하의 규격의 반무향실에서 수행하였다. 팬 회전에 따라 방사되는 가장 높은 음압을 측정하기 위해 팬 중심으로부터 전방 1 m 지점에 마이크로폰 1대를 설치하였다. 실험 개략도 및 환경은 Fig. 4에 나타낸 바와 같다. 소음의 측정은 국내 에어컨 실외기 소음 측정 표준 규격인 KS C 9306[8]에 의거하여 실시하였다. 측정을 통해 수집한 시간에 따른 음압 신호를 Fast Fourier Transform(FFT) 기법을 통해 주파수 신호로 변환하여 음압 레벨을 도출하였으며, 신호 처리에 관련된 정보는 Table 1에 나타내었다. 실험 결과는 대상 축류팬 시스템의 기존 성능을 평가하는 지표로 사용될 뿐만 아니라 본 연구에 사용된 수치 기법의 유효성을 검증하기 위한 비교 지표로 사용되었다. 그에 따라 모든 실험 결과는 4.2절의 기술한 수치 기법의 유효성 판단 결과에 나타내었다.
Table 1.
Information of signal processing used for FFT.
| Recording time [s] | 30 |
| Overlap [%] | 80 |
| Frequency resolution [Hz] | 1 |
| Sampling frequency [Hz] | 51,600 |
| Window function | Hanning |
소음 측정 실험과 더불어 팬 성능 시험기를 사용한 유량(Volume Flow Rate, VFR) 실험을 실시하였다. 팬 성능 시험기는 국제 규격인 Air Movement and Control Association(AMCA) 210-07[9]에 의거하여 Fig. 5에 나타난 실험 개략도와 같이 표현할 수 있다. 대상 팬이 일정한 속도로 회전할 때 보조 팬을 사용하여 팬에 가해지는 압력 저항을 발생시키고 이에 대한 정압차를 측정하는 장치이다. 측정된 정압차에 따라 유량이 계산되고 결과적으로 팬의 대표적인 성능 곡선인 P-Q 곡선을 얻을 수 있다. 일반적으로 팬이 특정 시스템에 장착될 때, 팬에 가해지는 저항 즉, 임피던스를 P-Q 곡선과 같이 2차 함수의 곡선으로 나타낼 수 있으며, 이를 저항 곡선으로 표현한다. 저항 곡선과 P-Q 곡선의 교차점이 팬의 실제 작동점이며, 본 연구에서는 작동 회전 속도 하에서 실제 작동점의 압력 조건을 대상으로 유량 성능을 평가하고 수치 해석의 경계 조건으로 설정하였다.
IV. 수치 해석을 통한 성능 비교
4.1 수치 해석 기법
본 연구에서는 윙렛 유무에 따라 두 팬에서 발생되는 유동장을 평가하고 유동 현상으로 인해 발생되는 공기역학적 성능과 유동 소음을 수치적으로 분석하기 위해 수치 해석을 수행하였다. 수치 해석은 유한 체적법 기반의 전산 유체 역학 기법을 사용하였다. 지배방정식으로 Eqs. (1), (2)의 Reynolds-Averaged Navier-Stokes(RANS) 방정식을 사용하였으며, 설정 회전 속도 내의 최대 유속인 날개 끝단 속도에 대한 마하수가 0.09라는 점을 근거로 해당 유동을 비압축성으로 가정하였다. 또한, Eq. (1)의 운동량 방정식의 레이놀즈 스트레스 항을 모델링 하기 위해 본 연구에서는 Re-Normalized Group(RNG) k-epsilon[10] 모델을 난류 모델로 선정하여 사용하였다. 해당 난류 모델은 난류의 소산 속도와 평균 전단 사이의 관계에 대한 모델링을 개선하기 위해 개발된 모델로 특히, 평균 전단이 난류 거동에 지배적인 영역에서 난류 특성을 모델링하는데 강점을 가진다. 이러한 특성으로 복잡한 3차원 유동, 강한 유선이 발생하는 회전 유동 등에 강점을 가진 난류 모델로 다양한 팬 대상 수치 해석에 사용되고 있다. 이와 더불어, 팬 회전 운동을 모사하기 위해 슬라이딩 메쉬 기법을 사용하였으며, 압력-속도 연성 기법으로 SIMPLE 기법을 사용하였다.
유동 해석 결과를 기반으로 음향장을 예측하기 위해 Hybrid Computational Aero-Acoustics(H-CAA) 기법을 이용한 음향 수치 해석을 수행하였다. H-CAA 기법은 계산된 유동 정보를 바탕으로 Lighthill의 음향상사법[4]에 기반한 Eq. (3)의 Ffowcs Williams-Hawkings (FW-H) 방정식을 지배방정식으로 하여 소음원을 모델링하고 그로 인해 전파되는 소음을 예측한다. FW-H에 대한 비투과성 적분면으로 본 연구의 대상인 축류팬의 강체 표면을 선정하였다.
4.2 수치 해석 영역
앞 절에서와 같이 정립한 수치 기법을 적용하기 위한 수치 해석 영역으로 본 연구에서는 Fig. 6와 같이 가상의 팬 성능 시험기 영역을 설계하였다. 해당 영역은 수치 해석의 정확도 및 신뢰도 향상을 위하여 실제 팬 성능 시험기의 환경을 모사하여 사각 덕트 형태로 구성하였다. 덕트의 양 끝단에 압력 경계 조건을 부여하여 팬의 작동 압력점의 저항 환경을 모사하였으며, 그 외 면은 모두 점착 벽면 조건을 부여하였다. 전체 영역의 총 크기는 대상 팬 직경에 비례하여 10 D ~ 15 D로 설정하였다. 해당 크기는 덕트 면으로 인한 폐쇄 효과를 방지하고 팬으로부터 토출되는 유동이 안정적으로 발달되고 소산될 수 있도록 충분한 크기로 설계하였다. 영역 내 모든 격자는 약 1,600만 개의 사면체 격자로 구성하였다.
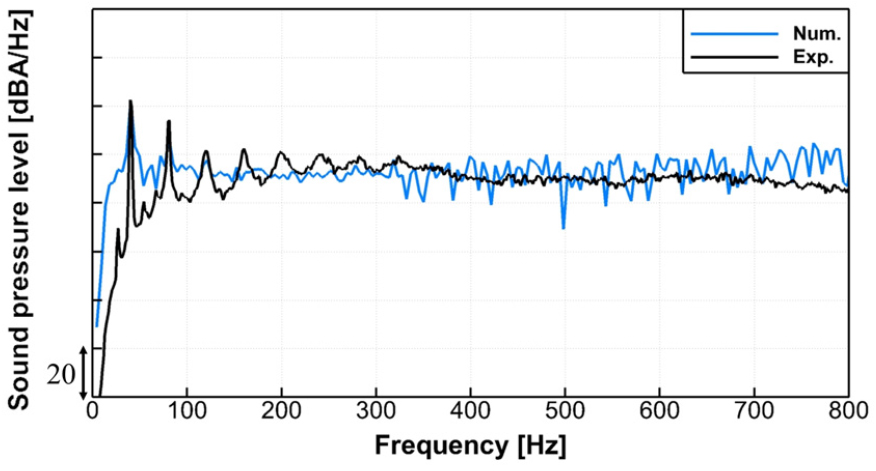
수치 기법과 수치 영역, 격자 구성에 대한 유효성을 검증하기 위해 수치 해석 결과와 실험 결과를 비교하여 오차를 확인하였다. 결과는 Figs. 7, 8에 나타내었다. 유동 해석의 경우, P-Q 곡선의 비교를 통해 작동점에서 약 0.5 %, 무부하 압력 조건에서 약 0.6 %의 오차를 확인하였다. 소음 성능은 음압 레벨(OverAll Sound Pressure Level, OASPL) 기준 약 1.9 dBA의 오차가 두 결과 간에서 발생하는 것을 확인하였다. 상당히 낮은 수준의 오차를 통해 본 연구의 수치 해석의 유효성 및 신뢰성을 확보한 것으로 판단하였다.
4.3 수치 해석 결과 비교를 통한 윙렛 효과 평가
본 연구의 대상인 두 개의 팬 모델에 대해 수치 해석한 결과 윙렛이 고려된 모델 A가 윙렛이 고려되지 않은 모델 B와 비교하여 약 10 % 적은 유량을 토출시키는 것을 정량적으로 확인하였다. 토출 유량 차이의 원인을 세부적으로 분석하고자 두 팬의 수치 유동장을 비교하여 나타내었다. 두 팬의 중심을 지나는 2차원 단면에서의 속도장 분포를 Figs. 9, 10에 비교하여 나타내었다. 두 팬 모두 팬의 상/하류의 압력 차에 따라 흡입되는 유동이 오리피스를 따라 발달되어 토출되는 동일한 유동 구조를 나타내며, 토출 유량 차이에 따라 속도장의 절대값에 차이가 나타남을 확인할 수 있다.
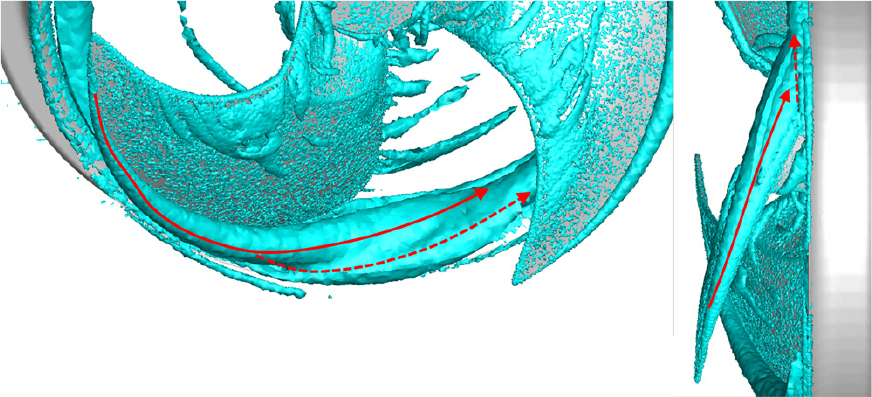
또한, 두 팬에서 발생하는 날개 끝 와류와 누설 와류의 분포를 세부적으로 식별하기 위해 Q-criterion[11]을 사용하여 결과를 Figs. 11, 12에 나타내었다.
Q 값은 Eq. (4)의 수식과 같이 와도 텐서(Ω)가 변형률 텐서(S)의 관계로 계산된다. 양의 Q 값은 전체 유동장 내에서 와류가 지배적인 영역을 나타내며 양의 Q 값을 통해 대상 와류를 수치적으로 가시화 할 수 있다. 두 팬 모두 공통적으로 날개 끝의 앞전에서 발생하여 날개 끝 코드를 따라 발달하는 날개 끝 와류(실선 표시)와 오리피스가 날개의 영역을 포함하기 시작하는 날개 끝 코드의 약 75 % 지점에서부터 누설 와류(점선 표시)가 발생하는 것을 확인할 수 있다. 날개 흡입면으로부터 날개 끝 와류의 거리가 상대적으로 모델 A에서 멀게 분포하는 유동이 식별되며, 이는 윙렛 형상이 와류에 대한 일종의 cavity 공간으로 작용하여 발생한 현상으로 확인할 수 있다. 또한, 날개 끝 와류가 코드를 따라 발달하여 누설 와류 생성지점에 도달한 후 모델 B의 날개 끝 와류와 누설 와류가 한 개의 큰 와류 구조로 결합된 것을 확인할 수 있다. 이는 날개 끝 와류가 발달되어 누설 와류 생성지점까지 도달한 후 두 와류가 상호 작용하는 과정에서 날개 흡입면과의 거리가 상대적으로 가까운 모델 B에서 더 강한 상호 작용 현상이 발생함을 의미한다.
이러한 와류의 강도를 정량적으로 평가하기 위해 각 팬 모델의 흡입면에서의 압력 분포를 Figs. 13, 14에 나타내었다. 이는 와류 중심부에서 유체의 구심력에 의한 압력 강하가 발생하고, 와류의 강도가 강할수록 구심력이 높아져 압력 강하가 더 크게 발생한다는 이론에 기반한다. 결과에서 확인할 수 있듯이, 가장 저압을 나타내는 구간이 날개 끝 주변에 분포한다. 또한, 날개 끝 와류와 날개 흡입면의 거리가 상대적으로 가까운 모델 B의 경우 저압 구간이 날개 끝 와류 구조를 따라 날개 끝 전체에 걸쳐 분포함을 확인할 수 있다. 모델 A의 전체적인 저압 영역에서의 압력값이 모델 B에서의 전체 저압 크기와 비교하여 상대적으로 높으며 이는 모델 A에서 발생하는 날개 끝 와류와 누설 와류의 강도가 상대적으로 약하다는 것을 의미한다. 모델 A에서 날개 끝 와류 영역과 비교하여 누설 와류 영역에서의 와류 강도가 강한 것을 확인할 수 있으며, 이는 윙렛 형상의 본 목적인 날개 끝 와류 저감에 효과적이지만 구조물과의 상호 작용으로 인한 누설 와류를 제어하는 측면에서 취약점을 가진다는 사실을 나타낸다. 또한, 3차원 와류로 인한 표면에서의 압력 강하는 결과적으로 활발한 압력 섭동을 초래하며 이는 결국 팬의 소음원으로 작용한다. 따라서, 본 결과를 통해 모델 B의 날개 끝 와류 구조가 난류 소음원으로 작용하여 광대역 소음 성분에 기여하고 더 큰 소음을 발생시킨다는 결과를 확인할 수 있다.
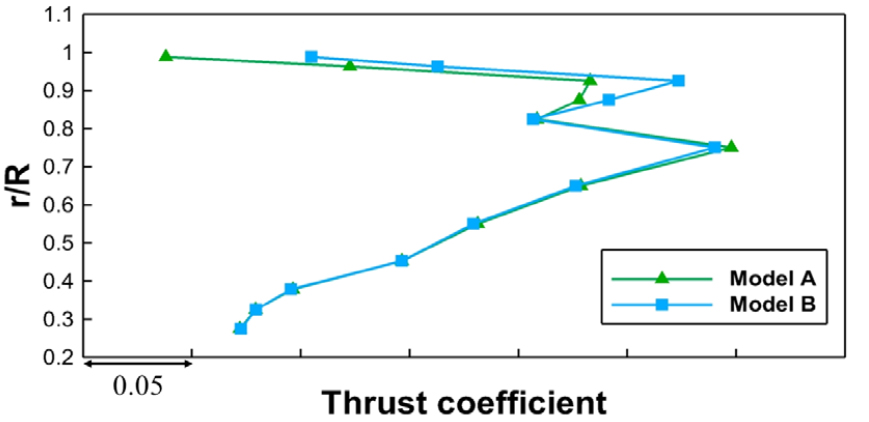
이러한 유동장 정보를 바탕으로 공기역학적 힘과 효율을 정량적으로 평가하였다. 팬을 반경별로 12개의 영역으로 나누어 영역별 면적에 따른 추력, 토크를 적분하여 계산하였다. 팬 표면에 발생하는 추력은 축류팬의 유동 흡입 및 토출 방향과 평행한 방향으로의 힘으로 토출 유량과 비례 관계로 해석할 수 있다. 또한, 토크는 팬이 회전함에 따라 발생하는 회전 방향으로의 저항력을 의미한다. 두 방향의 힘을 통해 팬의 효율을 Eq. (5)와 같이 계산할 수 있다.
여기서 A는 해당 날개 영역에 대한 면적, FT는 추력, va는 축 방향 속도, T는 토크를 나타낸다. 각 계산 결과는 Figs. 15, 16, 17에 나타내었으며, 그래프의 y축은 스팬 방향으로의 분포를, x축은 계산된 각 역학적 성능을 의미한다. 추력과 토크의 경우 두 팬 모델 모두 동일한 경향으로 날개 끝 근처에서 급격한 기울기 변화가 관찰된다. 또한, 모델 A는 모델 B에 비교하여 추력과 토크 모두 더 낮은 값을 나타내며 이는 모델 B의 흡입면에 분포하는 날개 끝 와류 중심부의 저압 영역과 압력면 간의 압력 차이로 인해 발생한 추력의 향상으로 인한 것이며 두 모델 간 유량 차이를 설명할 수 있는 결과이다. 날개 끝 와류의 영향으로 역학적 손실이 발생하여 토크의 증가로 나타난 것 또한 확인할 수 있다. 이러한 계산 결과를 바탕으로 Fig. 17에 나타낸 바와 같이 각 반경 지점에 대한 효율값을 계산하였다. 그 결과, 날개 끝을 제외한 반경 구간에서 두 모델이 동등 수준의 효율을 나타내며 날개 끝 부근에서 모델 B의 효율이 약 2 % 더 낮은 값을 가진다는 것을 알 수 있다. 이는 날개 끝의 윙렛 형상을 제외한 모든 설계 변수가 두 팬 모델에 동일하게 적용되었으며, 윙렛 형상이 적용되지 않은 모델 B가 효율 측면에서 불리하다는 것을 나타낸다.
두 팬의 소음 성능을 수치적으로 비교하기 위해 앞 절에서 서술한 바와 같이 계산된 유동장을 바탕으로 소음을 예측하고 그 결과를 Fig. 18의 소음 스펙트럼으로 나타내어 비교하였다. 수치 유동장 분석 결과와 같이 두 팬의 와류 구조 차이로 인해 광대역 성분의 소음 수준이 크게 차이 나고, 모델 B의 음압 레벨이 약 16 dBA 더 큰 것을 확인하였다.
V. 실험을 통한 성능 비교
수치적 분석 및 평가 결과를 바탕으로 두 팬의 시제품을 제작하여 소음 및 유량 실험을 실시하였다. 모든 실험 방법 및 환경은 앞 절에서 기술한 바와 동일하게 적용하였다. 결과는 Table 2에 정량화하여 나타내었으며, 모델 B가 더 큰 유량, 소음, 소비 전력을 나타냄을 확인할 수 있다. 소비 전력은 팬을 구동하는 데 필요한 입력 전력으로 팬의 효율과 반비례 관계를 가진다. 따라서, 모델 B의 더 큰 소비 전력은 더 낮은 팬 효율을 의미한다. 이러한 실험 결과는 앞서 계산된 수치 해석의 결과와 모두 동일한 경향을 나타내며, 이를 통해 실제 두 팬의 성능 차이를 실험적으로 확인할 수 있을 뿐만 아니라, 본 연구에서 사용된 수치 해석의 유효성 및 신뢰성을 재검증할 수 있는 결과로 사료된다.
VI. 결 론
본 연구는 에어컨 실외기용 축류팬 시스템을 대상으로 날개 끝의 윙렛 형상이 전체 축류팬 시스템의 유동 및 소음 성능에 미치는 영향을 수치적, 실험적으로 분석하였다. 연구 대상으로 윙렛 형상을 날개 끝단에 일정한 곡률로 적용한 모델과 3차원 곡률이 없는 평평한 날개 끝 형상을 가진 팬 모델을 설계하였다. 두 개의 대상 팬 모델에 대한 수치 해석을 수행하였으며, 수치 해석 기법 및 해석 모델의 유효성은 실험 결과와의 비교를 통해 검증하였다. 수치 해석 결과를 통해, 윙렛 형상이 적용되지 않을 경우 날개 끝 와류가 상대적으로 큰 강도로 발생하여 날개의 흡입면에 활발한 압력 섭동을 유도한다는 결과를 확인하였다. 또한, 윙렛 형상이 날개 끝 와류 저감에 효과적으로 작용할 수 있지만, 날개 끝과 주변 구조물과의 상호작용으로 인한 누설 와류에 대해 제어의 역할을 수행하지 못한다는 사실을 확인하였다. 더불어, 3차원 유동 구조 간의 차이로 인해 윙렛이 적용된 경우, 소음이 저감되고 효율이 향상하는 것을 수치적, 실험적으로 검증하였다. 본 연구를 통해 윙렛 형상이 코드를 따라 분포하는 다양한 유동 현상에 미치는 영향을 분석하였으며, 이를 바탕으로 추후 연구를 통해 윙렛 형상을 활용하여 날개 끝 와류와 누설 와류를 모두 억제할 수 있는 팬 모델을 개발할 예정이다.