Analysis of the distribution of the ultrasonic field transmitted into a solid cylinder from the outside

Misun Jo; Moojoon Kim

doi:10.7776/ASK.2025.44.2.126

Preview

Research Article

The Journal of the Acoustical Society of Korea. 31 March 2025. 126-131
https://doi.org/10.7776/ASK.2025.44.2.126

Analysis of the distribution of the ultrasonic field transmitted into a solid cylinder from the outside

원통 실린더 측면으로부터 내부로 전달되는 초음파 음장의 해석

Misun Jo¹

Moojoon Kim¹^*

조 미선¹

김 무준¹^*

¹Department of Physics, Pukyong National University

^{*Corresponding Author}

License (open-access, http://creativecommons.org/licenses/by-nc/4.0/):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

A mathematical model for analyzing the acousticfielddistribution formed inside a cylindrical container when a plane ultrasonic wave is incident on its lateral side is proposed. Predicting the distribution of the acoustic field inside a cylindrical container is critical for applications such as sonochemistry. This prediction becomes essential when high-intensity ultrasound is applied to a sample within the container. In this study, a relatively simple mathematical model was employed to propose a practical calculation method. The validity of the proposed method was verified by comparing experimental results with calculated results for glass cylindrical containers of varying thicknesses.

Keywords

Ultrasonic distribution

Cylindrical container

Luminescence images

Sonochemistry

Ultrasound

본 연구에서는 평면 초음파가 원통형 용기의 측면에 입사될 때, 용기 내부에 형성되는 음장 분포를 분석하기 위한 수학적 모델을 제안하였다. 원통형 용기 내부의 음장 분포를 예측하는 것은 음향화학(sonochemistry)과 같은 응용분야에서 매우 중요한 정보를 제공한다. 특히 용기 내부의 시료가 고강도 초음파에 노출될 때 음장 분포의 예측은 필수적이다. 본 연구에서는 비교적 간단한 수학적 모델을 사용하여 실용적인 계산 방법을 제시하였다. 다양한 두께를 가진 원통형 유리 용기를 대상으로 실험한 결과를 계산한 결과와 비교함으로써 제안된 방법의 타당성을 검증하였다.

키워드

초음파 음장 분포

원통 실린더

루미네센스 이미지

음향화학

초음파

MAIN

I. Introduction
II. Calculation model
III. Experiment method
IV. Results
V. Conclusion

I. Introduction

In the field of sonochemistry, which utilizes ultrasound to promote chemical reactions or induce changes in physical properties, it is common practice to avoid direct contact between the radiating surface of the ultrasonic transducer and the liquid sample to maintain sample purity.^[1,2] To achieve this, samples contained in glass vessels receive ultrasonic energy through an acoustic transmission medium, typically water.^[3,4] When high-intensity ultrasonic energy is required, it is customary for the ultrasonic energy to be transmitted through the side of the cylindrical container holding the sample in order to focus the energy.^[5,6] The plane waves emitted from the ultrasonic transducer reflect and transmit through the sides of the cylindrical container, creating an acoustic field inside the container. The distribution of this acoustic field depends on the thickness of the cylindrical container. Theoretical analyses of the transmission and scattering of plane ultrasonic waves by cylindrical containers have been widely reported.^[7,8,9] However, these studies often focus on cylindrical shells or employ highly complex mathematical expressions that consider transverse waves within the material of the cylindrical container, which are practically insignificant. In this study, a relatively simple mathematical analysis model was proposed for practical applications, and its validity was verified by comparing it with experimental results for cylindrical containers of varying thicknesses.

II. Calculation model

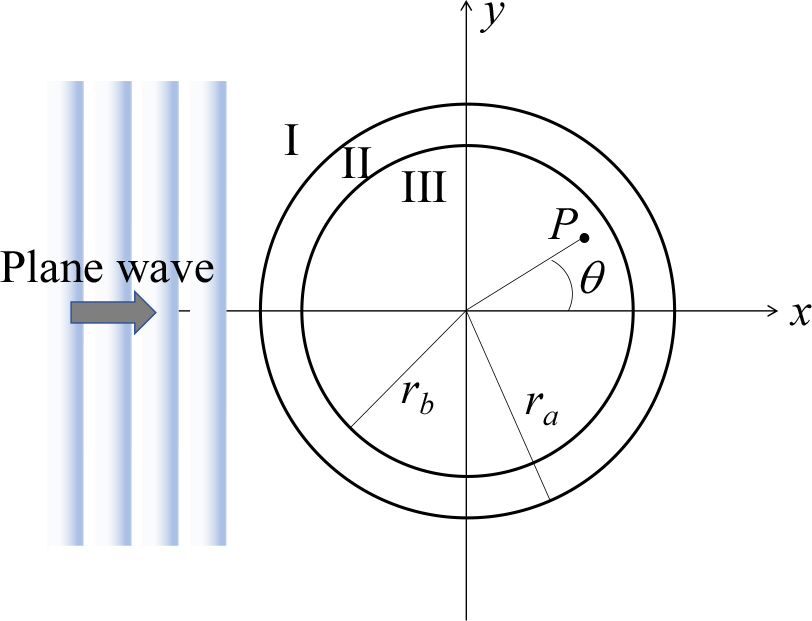
As shown in Fig. 1, the external and internal regions of the cylindrical container are denoted as I and III, respectively, while the medium constituting the cylindrical container is denoted as II. The sound speeds in each medium are denoted as $c_{1}$ , $c_{2}$ and $c_{3}$ , and the densities are denoted as $ρ_{1}$ , $ρ_{2}$ and $ρ_{3}$ , respectively.

https://cdn.apub.kr/journalsite/sites/ask/2025-044-02/N0660440205/images/ASK_44_02_05_F1.jpg

Fig. 1.

(Color available online) Coordinate system for sound field calculation formed by plane waves incident on a cylindrical container.

Assuming the length of the cylinder is infinite and that there is no variation in the incident sound pressure along the direction of the length, the wave equation in cylindrical coordinates for each region can be expressed as follows.

(1)

\frac{\partial^{2} p}{\partial r^{2}} + \frac{1}{r} \frac{\partial p}{\partial r} + \frac{1}{r^{2}} \frac{\partial^{2} p}{\partial θ^{2}} = \frac{1}{c_{i}^{2}} \frac{\partial^{2} p}{\partial t^{2}},

Here, $c_{i}$ is the sound speed in each region. The solutions for the incident sound pressure and scattered sound pressure in each region can be obtained as follows.

(2)

p_{1 i n} = - i ω ρ_{1} P_{0} [J_{0} (k_{1} r) + \sum_{n = 0}^{\infty} ϵ_{n} i^{n} J_{n} (k_{1} r) \cos (n θ)],

(3)

p_{1 s c} = - i ω ρ_{1} P_{0} \sum_{n = 0}^{\infty} i^{n} ϵ_{n} S_{n} H_{n} (k_{1} r) \cos (n θ),

(4)

p_{2 in} = - i ω ρ_{2} P_{0} \sum_{n = 0}^{\infty} i^{n} ϵ_{n} A_{n} J_{n} (k_{2} r) \cos (n θ),

(5)

p_{2 s c} = - i ω ρ_{2} P_{0} \sum_{n = 0}^{\infty} i^{n} ϵ_{n} B_{n} H_{n} (k_{2} r) \cos (n θ),

(6)

p_{3 i n} = - i ω ρ_{3} P_{0} \sum_{n = 0}^{\infty} i^{n} ϵ_{n} C_{n} J_{n} (k_{3} r) \cos (n θ),

(7)

p_{3 s c} = - i ω ρ_{3} P_{0} \sum_{n = 0}^{\infty} i^{n} ϵ_{n} D_{n} H_{n} (k_{3} r) \cos (n θ),

Here, the subscripts in and sc indicate the incident wave and scattered wave, respectively, while the subscripts 1, 2, and 3 represent each region. Additionally, $P_{0}$ , $ϵ_{n}$ , $r$ , $S_{n}$ , and $k_{i}$ represent the pressure amplitude of the incident wave, the Neumann coefficient ( $ϵ_{0}$ =1, $ϵ_{n}$ =2),^[10] the distance from the origin, the amplitude coefficient of the scattered wave, and the wave number in each region, respectively. The transverse wave that could occur in the solid cylindrical medium is neglected in this analysis. On the other hand, the particle velocity is defined as follows.

(8)

u = \frac{1}{i ρ ω} \frac{\partial p}{\partial r} .

The particle velocity in each region can be determined as follows.

(9)

u_{1 i n} = - P_{0} [- k_{1} J_{1} (k_{1} r) + \frac{k_{1}}{2} \sum_{n = 0}^{\infty} i^{n} ϵ_{n} \{J_{n - 1} (k_{1} r) - J_{n + 1} (k_{1} r)\} \cos (n θ)],

(10)

u_{1 s c} = P_{0} \sum_{n = 0}^{\infty} i^{n} ϵ_{n} S_{n} \frac{- k_{1}}{i ω ρ_{1}} \frac{\partial H_{n} (k_{1} r)}{\partial r} \cos (n θ),

(11)

u_{2 i n} = P_{0} \sum_{n = 0}^{\infty} i^{n} ϵ_{n} A_{n} \frac{- k_{2}}{i ω ρ_{2}} \frac{\partial J_{n} (k_{2} r)}{\partial r} \cos (n θ),

(12)

u_{2 s c} = P_{0} \sum_{n = 0}^{\infty} i^{n} ϵ_{n} B_{n} \frac{- k_{2}}{i ω ρ_{2}} \frac{\partial H_{n} (k_{2} r)}{\partial r} \cos (n θ),

(13)

u_{3 i n} = P_{0} \sum_{n = 0}^{\infty} i^{n} ϵ_{n} C_{n} \frac{- k_{3}}{i ω ρ_{3}} \frac{\partial J_{n} (k_{3} r)}{\partial r} \cos (n θ),

(14)

u_{3 s c} = P_{0} \sum_{n = 0}^{\infty} i^{n} ϵ_{n} D_{n} \frac{- k_{3}}{i ω ρ_{3}} \frac{\partial H_{n} (k_{3} r)}{\partial r} \cos (n θ) .

By applying the conditions of continuity for sound pressure and particle velocity at each boundary, the following results are obtained.

(15)

p_{1 i n} (r_{a}) + p_{1 s c} (r_{a}) = p_{2 i n} (r_{a}) + p_{2 s c} (r_{a}),

(16)

u_{1 i n} (r_{a}) + u_{1 s c} (r_{a}) = u_{2 i n} (r_{a}) + u_{2 s c} (r_{a}),

(17)

p_{2 i n} (r_{b}) + p_{2 s c} (r_{b}) = p_{3 i n} (r_{b}) + p_{3 s c} (r_{b}),

(18)

u_{2 i n} (r_{b}) + u_{2 s c} (r_{b}) = u_{3 i n} (r_{b}) + u_{3 s c} (r_{b}) .

At $r$ =0, the particle velocity must have a finite value. Therefore, the following expression must not diverge.

(19)

{C_{n} \frac{- k_{3}}{i ω ρ_{3}} \frac{\partial J_{n} (k_{3} r)}{\partial r}|}_{r = 0} + {D_{n} \frac{- k_{3}}{i ω ρ_{3}} \frac{\partial H_{n} (k_{3} r)}{\partial r}|}_{r = 0} = 0 .

By applying Eqs. (2) to (7) and (9) to (14) to Eqs. (15) to (18) and combining the results with Eq. (19), they can be expressed in matrix form as follows.

(20)

[\begin{array}{l} S_{n} \\ A_{n} \\ B_{n} \\ C_{n} \\ D_{n} \end{array}] = {[\begin{array}{l} m_{11} & m_{12} & m_{13} & m_{14} & m_{15} \\ m_{21} & m_{22} & m_{23} & m_{24} & m_{25} \\ m_{31} & m_{32} & m_{33} & m_{34} & m_{35} \\ m_{41} & m_{42} & m_{43} & m_{44} & m_{45} \\ m_{51} & m_{52} & m_{53} & m_{54} & m_{55} \end{array}]}^{- 1} [\begin{array}{l} q_{1} \\ q_{2} \\ q_{3} \\ q_{4} \\ q_{5} \end{array}],

Here, $m_{14} = m_{15} = m_{24} = m_{25} = m_{31} = 0,$

$m_{41} = m_{51} = m_{52} = m_{53} = q_{3} = q_{4} = q_{5} = 0$ ,

$m_{11} = H_{n} (k_{1} r_{a})$ , $m_{12} = - J_{n} (k_{2} r_{a})$ , $m_{13} = - H_{n} (k_{2} r_{a})$ , $m_{32} = J_{n} (k_{2} r_{b})$ , $m_{33} = H_{n} (k_{2} r_{b})$ , $m_{34} = - J_{n} (k_{3} r_{b})$ , $m_{35} = - H_{n} (k_{3} r_{b})$ , $q_{1} = - J_{n} (k_{1} r_{a})$ ,

$m_{21} = - {\frac{k_{1} S_{n}}{ρ_{1}} \frac{\partial H_{n} (k_{1} r)}{\partial r}|}_{r = r_{a}}$ , $m_{22} = {\frac{k_{2}}{ρ_{2}} \frac{\partial J_{n} (k_{2} r)}{\partial r}|}_{r = r_{a}}$ , $m_{23} = {\frac{k_{2}}{ρ_{2}} \frac{\partial H_{n} (k_{2} r)}{\partial r}|}_{r = r_{a}}$ ,

$m_{42} = - {\frac{k_{2}}{ρ_{2}} \frac{\partial J_{n} (k_{2} r)}{\partial r}|}_{r = r_{b}}$ , $m_{43} = - {\frac{k_{2}}{ρ_{2}} \frac{\partial H_{n} (k_{2} r)}{\partial r}|}_{r = r_{b}}$ , $m_{44} = {\frac{k_{3}}{ρ_{3}} \frac{\partial J_{n} (k_{3} r)}{\partial r}|}_{r = r_{b}}$ , $m_{45} = {\frac{k_{3}}{ρ_{3}} \frac{\partial H_{n} (k_{3} r)}{\partial r}|}_{r = r_{b}}$ ,

$m_{54} = - {\frac{k_{3}}{ρ_{3}} \frac{\partial J_{n} (k_{3} r)}{\partial r}|}_{r = 0}$ , $m_{55} = - {\frac{k_{3}}{ρ_{3}} \frac{\partial H_{n} (k_{3} r)}{\partial r}|}_{r = 0}$ , $q_{2} = {\frac{k_{1}}{ρ_{1}} \frac{\partial J_{n} (k_{1} r)}{\partial r}|}_{r = r_{n}}$ .

From Eqs. (6) and (7), the acoustic field distribution inside the solid cylindrical tube can be expressed as follows.

(21)

p_{3} = p_{3 i n} + p_{3 s c} = P_{0} \sum_{n = 0}^{\infty} i^{n} ϵ_{n} [\begin{array}{l} C_{n} J_{n} (k_{3} r) \\ + D_{n} H_{n} (k_{3} r) \end{array}] \cos (n θ) .

Therefore, by substituting the amplitude coefficients and obtained from Eq. (20) into (21), the acoustic field distribution inside the solid cylindrical tube can be determined.

III. Experiment method

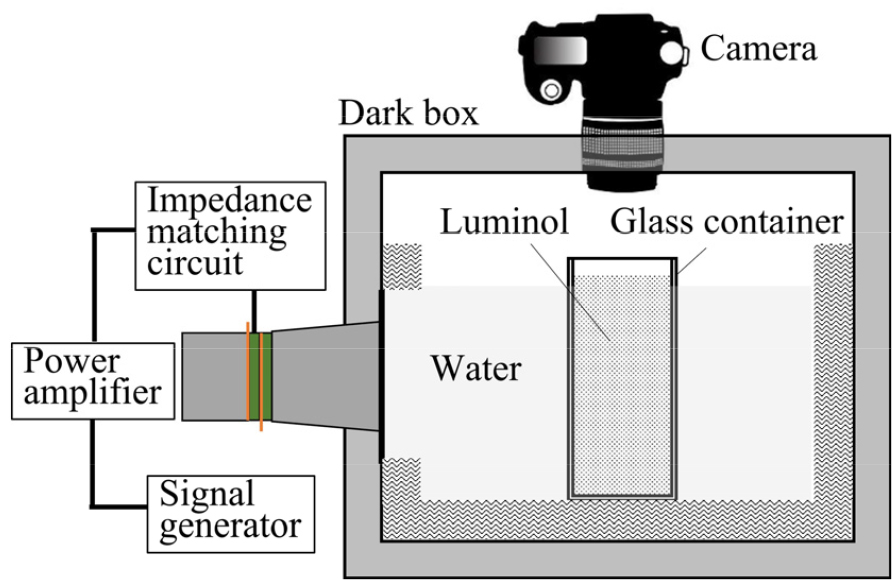
As shown in Fig. 2, the experiment used a 300 mm × 300 mm × 300 mm acrylic tank with a 10 mm thickness, lined with sound-absorbing material on the inner walls and bottom. A Langevin-type ultrasonic transducer with a resonance frequency of 40 kHz was fixed to one side of the tank to emit plane waves. A glass cylindrical container with an outer radius of 25 mm was used as the cylindrical container. It was positioned in front of the radiating surface of the transducer so that sound waves were incident on its side. The cylindrical container was filled with a luminol solution, while the rest of the tank, excluding the container, was filled with distilled water. All outer walls of the tank were covered with blackout material to block light transmission, except for the top surface, which had a hole to allow a camera to capture luminol luminescence images generated inside the cylindrical container. To investigate the distribution of the transmitted sound field with varying thicknesses of the cylindrical container, measurements were conducted by changing the thickness of the glass container to 1.2 mm, 1.8 mm, and 3.2 mm.

https://cdn.apub.kr/journalsite/sites/ask/2025-044-02/N0660440205/images/ASK_44_02_05_F2.jpg

Fig. 2.

(Color available online) Schematic of the experimental setup (side view).

IV. Results

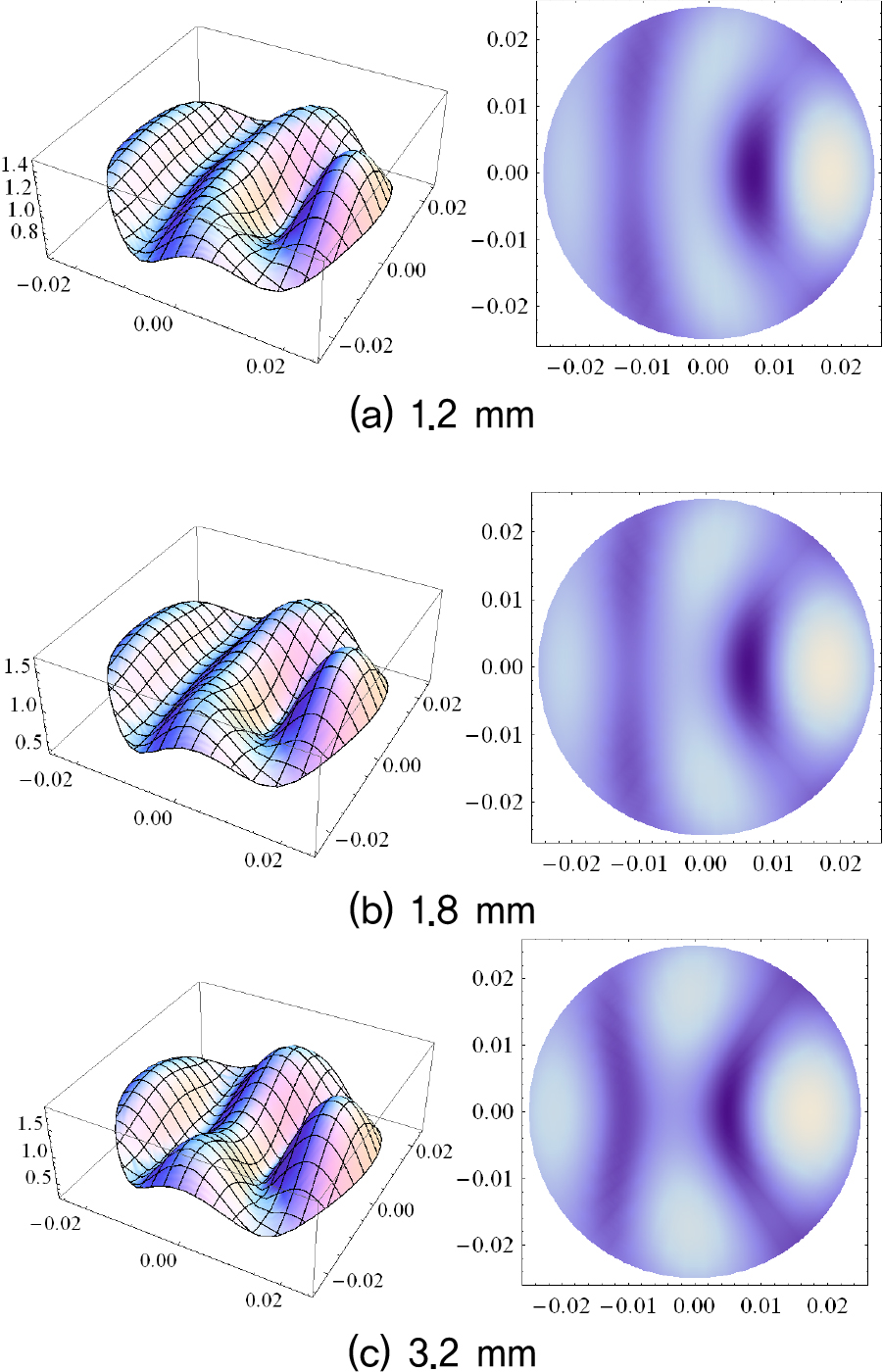
Fig. 3 shows the calculation results of acoustic pressure distribution in the cylindrical container with varying thicknesses. The results in Fig. 3, represented as a density plot, show the case where a plane wave is incident from the left to the right. In Fig. 3(a), the results correspond to the case where the cylindrical container has a thickness of 1.2 mm. The sound pressure distribution inside the cylinder exhibits a curved planar wave pattern, and it can be observed that the region opposite to the side of the incident plane wave exhibits a higher sound pressure level. In Fig. 3(b), which represents the results for a slightly thicker cylindrical container with a thickness of 1.8 mm, the sound pressure near the center of the cylinder appears slightly lower compared to that of Fig. 3(a). This is believed to be due to changes in the interference patterns of the scattered waves caused by the reduced inner diameter of the cylindrical container. Fig. 3(c) shows the results for a case where the thickness of the cylinder is further increased to 3.2 mm. Due to scattering and interference, the sound pressure near the center of the cylinder is observed to be even lower. The 3D graph on the left indicates that, for the thinnest case shown in Fig. 3(a), the sound pressure level is actually lower compared to the other cases. This suggests the existence of an optimal glass cylinder thickness where the transmission coefficient is maximized relative to the wavelength of the incident plane wave. Fig. 4 shows the experimental results.

https://cdn.apub.kr/journalsite/sites/ask/2025-044-02/N0660440205/images/ASK_44_02_05_F3.jpg

Fig. 3.

(Color available online) Results of simulation with different thicknesses of the glass container. (a) 1.2 mm, (b) 1.8 mm, (c) 3.2 mm.

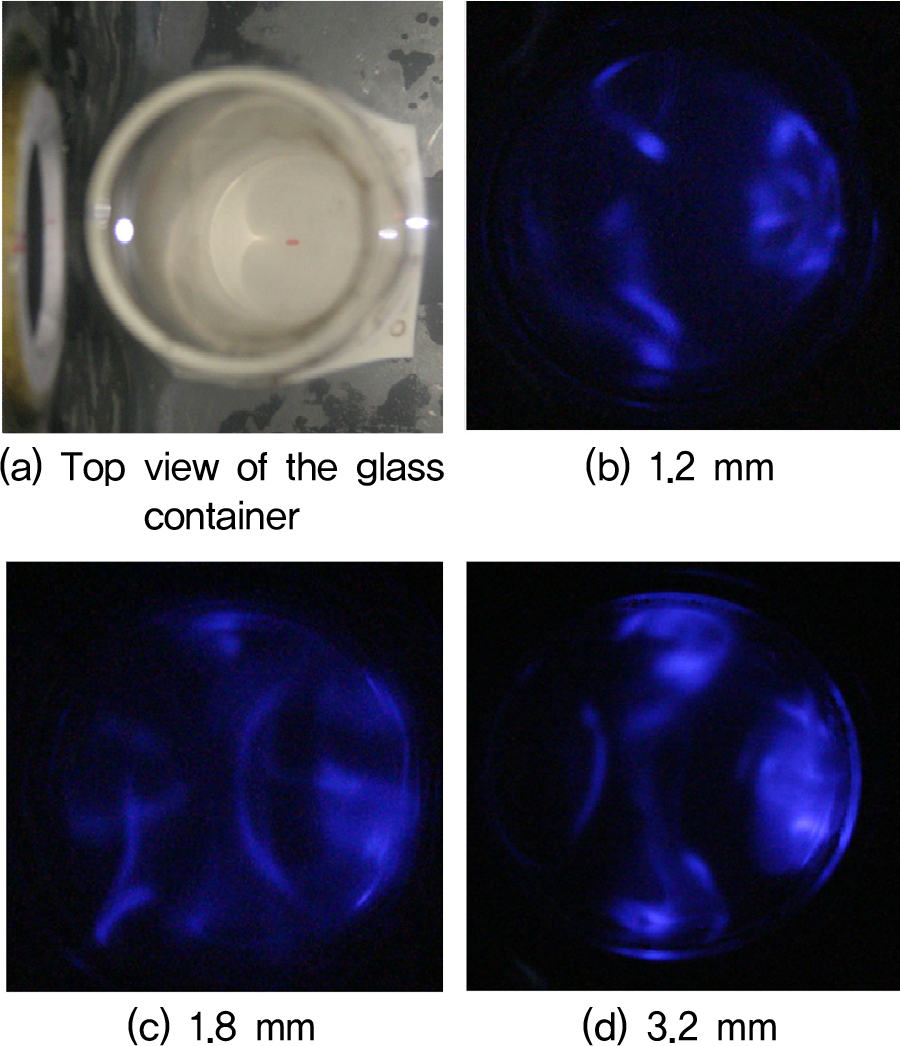
https://cdn.apub.kr/journalsite/sites/ask/2025-044-02/N0660440205/images/ASK_44_02_05_F4.jpg

Fig. 4.

(Color available online) Variation in luminol luminescence images with different thicknesses of the glass container.

Fig. 4(a) is a photograph depicting the glass cylindrical container fixed inside the water tank and the radiating surface of the transducer. The distance between the center of the glass cylinder and the radiating surface of the transducer was 30 mm. The luminescence images of the luminol solution filled inside the glass cylinder are shown in Fig. 4(b) ~ (d). Fig. 4(a) illustrates the luminescence pattern induced by the ultrasound transmitted through the glass cylinder with a thickness of 1.2 mm. This result closely resembles the theoretical calculation shown in Fig. 3(a), demonstrating the characteristic appearance of a plane wave. This is attributed to the relatively thin wall of the glass cylinder, which results in minimal internal scattering of the acoustic waves within the glass medium. The experimental result for the case where the glass cylinder has a thickness of 1.8 mm is shown in Fig. 4(b). Compared to the result in Fig. 4(a), the acoustic pressure distribution in this case appears more curved. Fig. 4(d) shows the luminescence pattern of luminol for the glass cylinder with a thickness of 3.2 mm. This result closely matches the theoretical calculation shown in Fig. 3(c). The ultrasound transmitted and scattered inside the glass cylinder exhibits a lower acoustic pressure at the center of the cylinder due to interference, while a higher acoustic pressure distribution is observed on the wall opposite the direction of incidence. This acoustic pressure distribution aligns well with the theoretical calculation results.

V. Conclusion

This study verified the theoretical model for predicting the distribution of acoustic fields inside a solid cylindrical vessel when ultrasound is transmitted from the outside, with a particular focus on the effect of material thickness on ultrasound transmission characteristics.

Experimentally, luminol luminescence patterns were used to compare theoretical predictions with observed phenomena, confirming that the cylinder thickness plays a crucial role in shaping the acoustic field distribution.

A thin cylinder (1.2 mm) exhibited a planar wave pattern with minimal internal scattering, closely matching theoretical calculations. As the cylinder thickness increased (1.8 mm and 3.2 mm), the acoustic pressure distribution became more curved, attributed to enhanced scattering and interference effects. For thicker cylinders, the ultrasound waves transmitted and scattered inside exhibited reduced acoustic pressure at the center and higher pressure along the walls opposite the incident direction, which aligned well with theoretical calculations.

These findings emphasize the critical role of scattering and interference in acoustic field formation and suggest the existence of an optimal cylinder thickness that maximizes ultrasound transmission efficiency relative to its wavelength.

By combining theoretical predictions with experimental validation, this study establishes a quantitative foundation for analyzing ultrasound transmission characteristics. The results provide valuable insights for applications such as sonochemistry, medical ultrasonics, and material processing, where precise control of ultrasound transmission is essential. Additionally, the practical calculation model proposed in this study serves as an accessible tool for researchers and engineers, bridging the gap between theoretical complexity and real-world implementation.

Future studies will investigate the distribution of internal acoustic fields in containers of various shapes and materials to evaluate the applicability of this theory. This will help assess the model’s validity and expand its potential use in ultrasonic applications.

Acknowledgements

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. 2022R1F1A1063797).

References

K. Sato, J.-G. Li, H. Kamiya, and T. Ishigaki, "Ultrasonic dispersion of TiO² nanoparticles in aqueous suspension," J. Am. Ceram. Soc. 91, 2481-2487 (2008).

10.1111/j.1551-2916.2008.02493.x

G. T. Caneba, C. Dutta, V. Agrawal, and M. Rao, "Novel ultrasonic dispersion of carbon nanotubes," J. Miner. Mater. Char. Eng. 9, 165-181 (2010).

10.4236/jmmce.2010.93015

S. J. Chung, J. P. Leonard, I. Nettleship, J. K. Lee, Y. Soong, D. V. Martello, and M. K. Chyu, "Characterization of ZnO nanoparticle suspension in water: Effectiveness of ultrasonic dispersion," Powder Technol. 194, 75-80 (2009).

10.1016/j.powtec.2009.03.025

T. Yamamoto, Y. Miyauchi, J. Motoyanagi, T. Fukushima, T. Aida, M. Kato, and S. Maruyama, "Improved bath sonication method for dispersion of individual single-walled carbon nanotubes using new triphenylene-based surfactant," Jpn. J. Appl. Phys. 47, 2000 (2008).

10.1143/JJAP.47.2000

M. Kim and J. Kim, "Nanoparticle dispersionizer by ultrasonic cavitation and streaming," Jpn. J. Appl. Phys. 57, 07LE03 (2018).

10.7567/JJAP.57.07LE03

J. Kim, M. Kim, and M. Chu, "Dispersion effect of nanoparticle according to ultrasound exposure using focused ultrasound field," Jpn. J. Appl. Phys. 50, 07HE19 (2011).

10.1143/JJAP.50.07HE19

R. P. Radlinski and M. M. Simon, "Acoustic and elastic wave scattering from elliptic‐cylindrical shells," J. Acoust. Soc. Am. 93, 2443-2453 (1993).

10.1121/1.405865

T. A. K. Pillai, V. K. Varadan, V. V. Varadan, and R. P. Radlinski, "Acoustic wave scattering by elastic cylindrical shells in water," J. Acoust. Soc. Am. 74, 619-624 (1983).

10.1121/1.389830

R. D. Dolittle, H. Überall, and P. Uginčius, "Sound scattering by elastic cylinders," J. Acoust. Soc. Am. 43, 1-14 (1968).

10.1121/1.1910757

Y.-H. He, J. H. Schwarz, M. Spradlin, and A. Volovich, "Explicit formulas for Neumann coefficients in the plane-wave geometry," Phys. Rev. D, 67, 086005 (2003).

10.1103/PhysRevD.67.086005

The Journal of the Acoustical Society of KoreaISSN:1225-4428(Print) 2287-3775(Online)한국음향학회

Preview

Analysis of the distribution of the ultrasonic field transmitted into a solid cylinder from the outside

ABSTRACT

MAIN

Fig. 1.

(Color available online) Coordinate system for sound field calculation formed by plane waves incident on a cylindrical container.

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

Fig. 2.

(Color available online) Schematic of the experimental setup (side view).

Fig. 3.

(Color available online) Results of simulation with different thicknesses of the glass container. (a) 1.2 mm, (b) 1.8 mm, (c) 3.2 mm.

Fig. 4.

(Color available online) Variation in luminol luminescence images with different thicknesses of the glass container.

Acknowledgements

References