Theoretical ground modelling for train-induced ground vibration and analysis on wave propagation along ground

Jungsoo Ryue; Jewon Yoon; Byungkuk Hong

doi:10.7776/ASK.2025.44.1.030

Preview

Review Article

The Journal of the Acoustical Society of Korea. 31 January 2025. 30-39
https://doi.org/10.7776/ASK.2025.44.1.030

Theoretical ground modelling for train-induced ground vibration and analysis on wave propagation along ground

철도기인 지반진동 해석을 위한 지반 이론모델링 및 지반의 파동 전파 특성 분석

Jungsoo Ryue¹^*

Jewon Yoon²

Byungkuk Hong³

유 정수¹^*

윤 제원²

홍 병국³

¹울산대학교 조선해양공학부

²팀버웨어(주)

³유니슨테크놀로지(주)

^{*Corresponding Author}

License (open-access, http://creativecommons.org/licenses/by-nc/4.0/):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

In recent years, ground-borne vibration produced by running trains has brought growing concerns as the demand for the comfortable living environments increases. To manage these problems, reliable analysis models are required, which can combine railway track and ground coupled. Unfortunately, however, domestic researches on developing theoretical track-ground models for train-induced ground vibration were little so far. In this paper, a theoretical ground model is reviewed for the purpose of producing a track-ground coupled model. The ground is treated as an elastic medium which consists of multiple layers above a bottom half-space. In this modelling, the ground is formulated by the flexibility matrix. As an analysis example, a ground which has a single upper layer on a bottom half-space is examined to figure out the features of wave propagation along ground. Also the effect of various loads (single or multiple, fixed or moving loads) onto the ground vibration is investigated.

Keywords

Railway ground vibration

Ground model

Flexibility matrix

Moving loads

최근 교통 환경에 대한 인식이 고조됨에 따라 철도로 인한 지반진동 문제가 꾸준히 제기되고 있다. 철도로 인한 지반진동 문제에 효과적으로 대응하기 위해서는 철도기인 지반진동을 신뢰성 있게 예측할 수 있는 이론적 궤도-지반 연성 모델의 개발이 필요하다. 그러나 그동안 국내에서는 이론적 궤도-지반 연성 해석에 대한 연구가 드물었다. 본 논문에서는 철도기인 지반진동 해석을 위한 이론적 궤도-지반 연성 모델 구축을 목적으로, 지반에 대한 이론 모델링을 수행하였다. 지반은 하부 반무한 지반 위에 여러 개의 지층이 놓인 다층 탄성체 지반으로 가정하였으며, 지표면에 작용하는 하중과 지표면 임의지점의 변위 응답의 관계를 지반 유연도행렬로 정식화하였다. 지반진동 해석 예로써, 하나의 상부 지층과 하부 반무한 지반으로 구성된 지반 모델에 대하여 지반의 파동 전파 특성을 검토하고, 지면에 고정 하중 또는 이동 하중이 작용할 때 발생하는 지반의 진동 응답을 해석하고 그 특성을 검토하였다.

키워드

철도 지반진동

지반 모델

유연도 행렬

이동 하중

MAIN

I. 서 론
II. 이론적 지반 모델링: 유연도행렬
2.1 지배방정식
2.2 지반의 변위와 응력-변형률
2.3 지반의 유연도 행렬
III. 지반의 진동 응답
3.1 분산 특성
3.2 지표면 강제진동응답
IV. 지반진동 해석 예
4.1 지반 모델
4.2 지반의 파동 전파 특성
4.3 고정 하중에 의한 지반진동
4.4 이동하중에 의한 지반진동
V. 결 론

I. 서 론

최근 친환경 교통에 대한 인식이 고조됨에 따라 철도 주행으로 인해 발생하는 환경 소음 및 환경 진동에 대한 규제 요구가 꾸준히 증가하고 있다. 특히 철도에 의해 유기되는 지반진동은 철로 주변 지역민들의 주거 환경에 직결되는 중요한 요소이다. 따라서 철도 시스템을 친환경 교통수단으로 지속 발전시키기 위해서는 철도기인 지반진동을 효과적이고 신뢰성 높게 예측할 수 있는 해석 기법의 개발 및 확보가 시급하다.

철도차량의 주행으로 인해 유기되는 지반진동을 예측하기 위해서는 철도 궤도 모델과 지반 모델이 결합 된 궤도–지반 연성모델이 구축되어야 한다. 철도 관련 연구가 활발한 유럽의 경우, 철도 기인 지반진동을 예측하기 위한 이론적 또는 수치적 궤도-지반 연성모델을 오랜 기간 개발해 오고 있다.^[1,2,3,4,5] 그러나 국내에서는 철도기인 지반진동의 발생 기구 및 전파 특성 등에 대한 체계적인 연구가 거의 이루어지지 못하였다. 이로 인해 아직 국내에서는 철도기인 지반진동을 신뢰성 있게 예측할 수 있는 해석 모델이 구축되지 못하였다. 다만, 유한요소법과 같은 수치 해석을 기반으로 한 소수의 연구가 수행되어 왔으나, 차량, 궤도, 지반 및 접촉하중을 통합한 이론 모델 개발 연구는 거의 수행되지 못하였다.

궤도-지반 연성 모델을 구축하기 위해서는 궤도와 지반에 대한 각각의 이론 모델이 필요하다. 철도 전동소음 해석에 이미 궤도 모델이 적용되고 있으므로 철도기인 지반진동 해석을 위한 궤도 모델 개발에 큰 어려움은 없다고 판단된다. 반면, 지반에 대한 이론적 모델링은 국내에서 수행된 바 없으므로, 본 연구에서는 지반진동 해석을 위한 이론적 지반 모델링을 수행하였다.

지반에 대한 이론모델링은 강성행렬^[6,7] 또는 유연도행렬^[2,3,8]을 이용하는 방법이 있다. 강성행렬 방법은 지층의 개수에 따라 행렬의 크기가 증가하며, 지반의 변위를 얻기 위해 강성행렬의 역행렬 계산이 필요하므로 수치적 안정성 문제를 갖는다. 반면, 유연도행렬 방법에서는 지층수에 상관없이 연산에 필요한 행렬의 크기가 [6×6]을 넘지 않으므로 연산이 단순하며 수치적 안정성이 높다. 또한 파수영역에서 해석을 수행하므로 궤도 모델과 연성하기가 용이하다.

본 연구에서는 Reference [8]을 참조하여 유연도행렬을 이용한 지반 모델링을 수행하였다. 그리고 구축된 지반 모델을 이용하여 지반을 통한 파동 전파 및 지반의 진동 응답 특성을 살펴보았다.

II. 이론적 지반 모델링: 유연도행렬

2.1 지배방정식

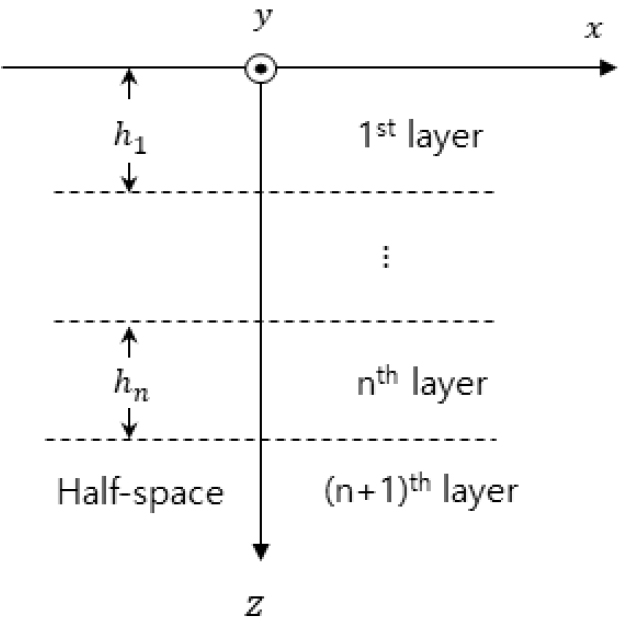
본 연구에서 지반은 Fig. 1에 나타낸 것과 같이 반무한 지반 위에 여러 개의 수평 지층이 놓인 다층 탄성체로 가정한다. $j$ 번째 지층에서 $x$ , $y$ , $z$ 방향(길이, 폭, 깊이 방향) 변위를 각각 $u_{j} (x, y, z, t)$ , $v_{j} (x, y, z, t)$ , $w_{j} (x, y, z, t)$ 라고 하자. 주파수 𝜔의 $x$ , $y$ , $z$ 방향 하중 $p_{x} (x, y) e^{i ω t}$ , $p_{y} (x, y) e^{i ω t}$ , $p_{z} (x, y) e^{i ω t}$ 이 지표면에 작용하는 경우 $x$ , $y$ 방향 파수(𝛽,𝛾)와 주파수(𝜔) 영역에서 표현한 $j$ 번째 지층의 Navier 방정식은 Eqs. (1), (2), (3)과 같다.

https://cdn.apub.kr/journalsite/sites/ask/2025-044-01/N0660440104/images/ASK_44_01_04_F1.jpg

Fig. 1.

Coordinate system for image construction using synthetic aperture sonar.

(1)

μ_{j} [\frac{d^{2} {\tilde{u}}_{j}}{d z^{2}} - (β^{2} + γ^{2} - \frac{ρ_{j} ω^{2}}{μ_{j}}) {\tilde{u}}_{j}] + (λ_{j} + μ_{j}) i β {\tilde{Δ}}_{j} = δ (z) {\tilde{p}}_{x} (β, γ),

(2)

μ_{j} [\frac{d^{2} {\tilde{v}}_{j}}{d z^{2}} - (β^{2} + γ^{2} - \frac{ρ_{j} ω^{2}}{μ_{j}}) {\tilde{v}}_{j}] + (λ_{j} + μ_{j}) i γ {\tilde{Δ}}_{j} = δ (z) {\tilde{p}}_{y} (β, γ),

(3)

μ_{j} [\frac{d^{2} {\tilde{w}}_{j}}{d z^{2}} - (β^{2} + γ^{2} - \frac{ρ_{j} ω^{2}}{μ_{j}}) {\tilde{w}}_{j}] + (λ_{j} + μ_{j}) (d {\tilde{Δ}}_{j} / d z) = δ (z) {\tilde{p}}_{z} (β, γ),

여기서 $\tilde{\cdot}$ 는 $x$ 와 $y$ 방향 파수영역에서 정의되는 변수이고, $δ (.)$ 는 Dirac 델타 함수를 의미하며, ${\tilde{Δ}}_{j} = i β {\tilde{u}}_{j} + i γ {\tilde{v}}_{j} + (d {\tilde{w}}_{j} / d z)$ 이다. $λ_{j}$ 와 $μ_{j}$ 는 $j$ 번째 지층의 Lamé 상수로서

(4)

λ_{j} = \frac{ν_{j} E_{j} (1 + i η_{j} sgn (ω))}{(1 + ν_{j}) (1 - 2 ν_{j})},

(5)

μ_{j} = \frac{E_{j} (1 + i η_{j} sgn (ω))}{2 (1 + ν_{j})},

$E_{j}$ , $ν_{j}$ , $η_{j}$ 는 각각 탄성계수, 프와송비, 감쇠손실계수를 의미한다. $j$ 번째 지층의 압축파와 전단파 전파 속도는 $c_{j 1} = \sqrt{(λ_{j} + 2 μ_{j}) / ρ_{j}}$ , $c_{j 2} = \sqrt{ρ_{j} / μ_{j}}$ 이며, 파수는 $k_{j 1} = ω / c_{j 1}$ , $k_{j 2} = ω / c_{j 2}$ 이다. Eq. (1)에 $i β$ 를, Eq. (2)에 $i γ$ 를 곱하고, Eq. (3)을 $z$ 에 관해 미분한 후 세 식을 합산하여 간략히 정리하면

(6)

\frac{d^{2} {\tilde{Δ}}_{j}}{d z^{2}} - (β^{2} + γ^{2} - k_{j 1}^{2}) {\tilde{Δ}}_{j} = 0

이다. Eq. (6)의 해는 ${\tilde{Δ}}_{j} = A_{j} e^{- α_{j 1} z_{j}} + B_{j} e^{α_{j 1} z_{j}}$ 이며, 여기서 $A_{j}$ 와 $B_{j}$ 는 $j$ 번째 지층이 갖는 $z$ 방향 변위의 크기, $\pm α_{j 1} = \pm \sqrt{β^{2} + γ^{2} - k_{j 1}^{2}}$ 이다.

하부 반무한 지반의 지배방정식은 하첨자 $j$ 만 $n$ +1로 대체하면 Eqs. (1), (2), (3)과 동일하다. 반무한 지반의 $z$ 범위는 $z_{n + 1} \geq 0$ 이므로 해는 양의 $z$ 방향으로 진행하는 파동만 갖는다. 따라서 반무한 지반의 해, ${\tilde{Δ}}_{n + 1}$ ,은 Eq. (7)과 같다.

(7)

{\tilde{Δ}}_{n + 1} = A_{n + 1} e^{- α_{n + 1, 1} z_{n + 1}} .

2.2 지반의 변위와 응력-변형률

Eqs. (1), (2), (3)에 Eq. (6)의 해 ${\tilde{Δ}}_{j}$ 를 대입하면

(8)

{\tilde{u}}_{j} (β, γ) = - (i β / k_{j 1}^{2}) A_{j} e^{- α_{j 1} z_{j}} - (i β / k_{j 1}^{2}) B_{j} e^{α_{j 1} z_{j}} + C_{j} e^{- α_{j 2} z_{j}} + D_{j} e^{α_{j 2} z_{j}},

(9)

{\tilde{v}}_{j} (β, γ) = - (i γ / k_{j 1}^{2}) A_{j} e^{- α_{j 1} z_{j}} - (i γ / k_{j 1}^{2}) B_{j} e^{α_{j 1} z_{j}} + G_{j} e^{- α_{j 2} z_{j}} + H_{j} e^{α_{j 2} z_{j}},

(10)

{\tilde{w}}_{j} (β, γ) = (α_{j 1} / k_{j 1}^{2}) A_{j} e^{- α_{j 1} z_{j}} - (α_{j 1} / k_{j 1}^{2}) B_{j} e^{α_{j 1} z_{j}} + [(i β / α_{j 2}) C_{j} + (i γ / α_{j 2}) G_{j}] e^{- α_{j 2} z_{j}} - [(i β / α_{j 2}) D_{j} + (i γ / α_{j 2}) H_{j}] e^{α_{j 2} z_{j}}

이다. 여기서 $α_{j 2} = \sqrt{β^{2} + γ^{2} - k_{j 2}^{2}}$ 이며, $A_{j}$ , $B_{j}$ , $C_{j}$ , $D_{j}$ , $G_{j}$ , $H_{j}$ , $L_{j}$ 그리고 $M_{j}$ 는 각 파동의 크기를 나타내는 미지 계수이다. 하부 반무한 지반의 경우에는 양의 $z$ 방향으로 진행하는 파동해만 존재하므로 변위해는 Eqs. (11), (12), (13)과 같다.

(11)

{\tilde{u}}_{n + 1} (β, γ) = - (i β / k_{n + 1, 1}^{2}) A_{n + 1} e^{- α_{n + 1, 1} z_{n + 1}} + C_{n + 1} e^{- α_{n + 1, 2} z_{n + 1}},

(12)

{\tilde{v}}_{n + 1} (β, γ) = - (i γ / k_{n + 1, 1}^{2}) A_{n + 1} e^{- α_{n + 1, 1} z_{n + 1}} + G_{n + 1} e^{- α_{n + 1, 2} z_{n + 1}},

(13)

{\tilde{w}}_{n + 1} (β, γ) = (α_{n + 1, 1} / k_{n + 1, 1}^{2}) A_{n + 1} e^{- α_{n + 1, 1} z_{n + 1}} + [i (β C_{n + 1} + γ G_{n + 1}) / α_{n + 1, 2}] e^{- α_{n + 1, 2} z_{n + 1}} .

한편, $j$ 번째 지층의 응력- 변형률 관계식을 2차원 Fourier 변환한 뒤 변위해를 대입해 정리하면

(14)

{\tilde{τ}}_{x y j} (β, γ) = 2 μ_{j} i β (α_{j 1} / k_{j 1}^{2}) (A_{j} e^{- α_{j 1} z_{j}} - B_{j} e^{α_{j 1} z_{j}}) - μ_{j} [(β^{2} / α_{j 2}) + α_{j 2}] (C_{j} e^{- α_{j 2} z_{j}} - D_{j} e^{α_{j 2} z_{j}}) - μ_{j} (β γ / α_{j 2}) (G_{j} e^{- α_{j 2} z_{j}} - H_{j} e^{α_{j 2} z_{j}}),

(15)

{\tilde{τ}}_{y z j} (β, γ) = 2 μ_{j} i γ (α_{j 1} / k_{j 1}^{2}) (A_{j} e^{- α_{j 1} z_{j}} - B_{j} e^{α_{j 1} z_{j}}) - μ_{j} [(γ^{2} / α_{j 2}) + α_{j 2}] (G_{j} e^{- α_{j 2} z_{j}} - H_{j} e^{α_{j 2} z_{j}}) - μ_{j} (β γ / α_{j 2}) (C_{j} e^{- α_{j 2} z_{j}} - D_{j} e^{α_{j 2} z_{j}}),

(16)

{\tilde{τ}}_{z z j} (β, γ) = - (μ_{j} / k_{j 1}^{2}) (k_{j 2}^{2} + 2 α_{j 2}^{2}) (A_{j} e^{- α_{j 1} z_{j}} + B_{j} e^{α_{j 1} z_{j}}) - 2 μ_{j} i β (C_{j} e^{- α_{j 2} z_{j}} + D_{j} e^{α_{j 2} z_{j}}) - 2 μ_{j} i γ (G_{j} e^{- α_{j 2} z_{j}} + H_{j} e^{α_{j 2} z_{j}})

이다. 하부 반무한 지반( $j = n + 1$ )에 대해서도 동일한 과정을 수행하면, Eqs. (14), (15), (16)에서 미지계수 $A_{n + 1}$ , $C_{n + 1}$ , $G_{n + 1}$ 로 구성된 응력식을 얻는다.

2.3 지반의 유연도 행렬

$j$ 번째 지층 상단( $z_{j}$ =0)과 하단( $z_{j} = h_{j}$ )의 파수영역 변위 벡터와 응력 벡터를 각각 ${\vec{u}}_{j 0}$ , ${\vec{τ}}_{j 0}$ 와 ${\vec{u}}_{j 1}$ , ${\vec{τ}}_{j 1}$ 라 하고, 지층 상단과 하단의 상태벡터를 각각 ${\vec{S}}_{j 0} = [{\vec{u}}_{j 0}; {\vec{τ}}_{j 0}]$ , ${\vec{S}}_{j 1} = [{\vec{u}}_{j 1}; {\vec{τ}}_{j 1}]$ 로 정의하자. 여기서 세미콜론은 행바꿈을 의미한다. 6개의 미지계수로 구성된 계수 벡터 $\vec{b_{j}} = {[\begin{array}{l} B_{j} & D_{j} H_{j} & A_{j} & C_{j} & G_{j} \end{array}]}^{T}$ 를 이용해 ${\vec{S}}_{j 0}$ 와 ${\vec{S}}_{j 1}$ 을 행렬로 표현하면

(17)

{\vec{S}}_{j 0} = A_{j 0} {\vec{b}}_{j}, {\vec{S}}_{j 1} = e^{α_{j} h_{1}} A_{j 1} {\vec{b}}_{j}

이며, Eq. (17)의 두 식에서 ${\vec{b}}_{j}$ 를 소거하면 지층 하단과 상단의 상태벡터는 Eq. (18)의 관계를 갖는다.

(18)

{\vec{S}}_{j 1} = e^{α_{1 j} h_{1}} A_{j 1} A_{j 0}^{- 1} {\vec{S}}_{j 0} .

반무한 지반의 변위 Eqs. (11), (12), (13)을 계수 벡터 ${\vec{b}}_{n + 1} = {[A_{n + 1} C_{n + 1} G_{n + 1}]}^{T}$ 를 이용해 벡터로 표현하면 ${\vec{u}}_{n + 1, 0} = R {\vec{b}}_{n + 1}$ 이다. 마찬가지로, 반무한 지반의 응력 벡터는 ${\vec{τ}}_{n + 1, 0} = S {\vec{b}}_{n + 1}$ 가 되므로 ${\vec{b}}_{n + 1}$ 를 소거하여 변위-응력 관계를 구하면

(19)

{\vec{u}}_{n + 1, 0} = {RS}^{- 1} {\vec{τ}}_{n + 1, 0}

이며, 여기서 R과 S는 [3×3]의 정방행렬이다.

지표면에 외력 $\vec{p} = {[{\tilde{p}}_{x}, {\tilde{p}}_{y}, {\tilde{p}}_{z}]}^{T}$ 가 작용하는 경우, 첫 번째 지층 상단의 상태 벡터( ${\vec{S}}_{10}^{p}$ )는 지층 상단변위와 외력을 분리하여 ${\vec{S}}_{10}^{p} = {\vec{S}}_{10} + {\vec{S}}^{p}$ 로 쓸 수 있으며, ${\vec{S}}_{10} = {[{\tilde{u}}_{10}, {\tilde{v}}_{10}, {\tilde{w}}_{10}, 0, 0, 0]}^{T}$ , $\vec{S^{p}} = {[0, 0, 0, - {\tilde{p}}_{x}, - {\tilde{p}}_{y}, - {\tilde{p}}_{z}]}^{T}$ 이다. 지반을 구성하는 모든 지층의 경계에서 변위 연속 조건과 힘의 평형 조건을 적용해 정리하면

(20)

{\vec{S}}_{n 1} = e^{\sum_{j = 1}^{n} α_{j 1} h_{j}} A_{n 1} A_{n 0}^{- 1} A_{n - 1, 1} A_{n - 1, 0}^{- 1} \dots A_{21} A_{20}^{- 1} A_{11} A_{10}^{- 1} {\vec{S}}_{10}^{p},

여기서 $T = A_{n 1} A_{n 0}^{- 1} A_{n - 1, 1} A_{n - 1, 0}^{- 1} \dots A_{11} A_{10}^{- 1}$ 라 하면 Eq. (20)은

(21)

{\vec{S}}_{n 1} = e^{\sum_{j = 1}^{n} α_{j 1} h_{j}} T {\vec{S}}_{10} + e^{\sum_{j = 1}^{n} α_{j 1} h_{j}} T {\vec{S}}^{p} = e^{\sum_{j = 1}^{n} α_{j 1} h_{j}} [\begin{matrix} T_{11} T_{12} \\ T_{21} T_{22} \end{matrix}] \{\begin{matrix} \vec{u_{10}} \\ \vec{0} \end{matrix}\} - e^{\sum_{j = 1}^{n} α_{j 1} h_{j}} [\begin{matrix} T_{11} T_{12} \\ T_{21} T_{22} \end{matrix}] \{\begin{array}{l} \vec{0} \\ \vec{p} \end{array}\}

로 쓸 수 있다. 여기서 $T_{11}$ 와 $T_{12}$ 는 $n$ 번째 지층 하단의 변위 ${\vec{u}}_{n 1}$ 를 만들어 내는 지표면 상단 변위 $\vec{u_{10}}$ 와 압력 $\vec{p}$ 의 기여도를 나타내며, $T_{21}$ 과 $T_{22}$ 는 지표면 하단 응력 ${\vec{τ}}_{n 1}$ 을 유발하는데 지표면 상단 변위와 압력 사이 관계를 나타낸다. ${\vec{S}}_{n 1} = [{\vec{u}}_{n 1}; {\vec{τ}}_{n 1}]$ 이므로, Eq. (21)을 변위에 관한 식과 응력에 관한 식으로 전개하고, 하부 반무한 지반의 상단에서 변위 연속 조건 및 응력 평형 조건을 적용하면

(22)

({RS}^{- 1} T_{21} - T_{11}) {\vec{u}}_{10} = ({RS}^{- 1} T_{22} - T_{12}) \vec{p}

이다. Eq. (22)의 좌변 행렬을 단위행렬로 만들면

(23)

{\vec{u}}_{10} = Q \vec{p}

이다. 여기서 Q는 [3×3]의 크기를 갖는 유연도행렬(또는 컴플라이언스 행렬)이다.

주파수 $Ω$ 의 $z$ 방향 조화 하중이 $x$ 축을 따라 일정속도 $c$ 로 이동하는 경우, 지표면에 작용하는 하중은 $p_{z} (x - c t, y) e^{i Ω t}$ 로 표현할 수 있다. 이 하중을 $x$ 와 $y$ 에 대해 2차원 Fourier 변환하면 ${\tilde{p}}_{z} (β, γ) e^{i (Ω - β c) t}$ 이 되며, 주파수를 $ω = Ω - β c$ 로 정의하면 이동하중 작용 시에도 지층의 지배 방정식은 Eqs. (1), (2), (3)과 동일하다. 즉, $ω = Ω - β c$ 의 관계를 적용하면 앞서 기술한 유연도행렬 $Q (β, γ, ω)$ 은 이동하중에 대해서도 동일하다.

III. 지반의 진동 응답

3.1 분산 특성

지반에서 발생하는 파동의 종류(진동 모드)와 전파 특성은 분산 관계를 통해 파악할 수 있다. 반무한 지반에서 전파되는 파동은 P-SV파와 SH파로 구분할 수 있으며, P-SV파와 SH파는 서로 독립적이므로 거동한다.

지반의 분산 관계는 지반의 자유진동 해석을 통해 얻을 수 있다. Eq. (22)의 우변에 $\vec{p} = \vec{0}$ 을 대입하면, 지반의 자유진동에 대한 지배방정식이 되다. 자유진동 지배방정식이 변위 해를 갖기 위해서는 Eq. (22)의 좌변에 있는 행렬은 역행렬이 존재하지 않아야 한다. 따라서 지반의 특성방정식은

(24)

det ({RS}^{- 1} T_{21} - T_{11}) = 0

이 되며, Eq. (24)를 풀어서 P-SV파와 SH파의 분산 선도를 얻을 수 있다.

3.2 지표면 강제진동응답

철도기인 지반진동은 궤도를 통해 지반으로 전달되는 하중에 의해 발생한다. 지반의 $x$ 축을 따라 놓인 궤도 하단 폭을 $2 b$ 라고 하면, 주파수 $Ω$ 인 수직방향 하중 $F_{0}$ 이 지표면에 가하는 압력은 파수영역에서 Eq. (25)로 표현된다(이후에는 고정 하중과 이동하중 모두 가진 주파수를 $Ω$ 로 표기한다. 고정 하중의 경우 $c$ =0이므로 $ω = Ω$ 이다).

(25)

{\tilde{p}}_{z} (β, γ; Ω) = {\tilde{F}}_{0} (β; Ω) \sin γ b / γ b .

수직방향 압력이 지표면에 작용할 때 지표면 변위를 Eq. (23)의 유연도행렬로 표현하면

(26)

\{\begin{array}{l} {\tilde{u}}_{10} \\ {\tilde{v}}_{10} \\ {\tilde{w}}_{10} \end{array}\} = [\begin{array}{l} Q_{11} & Q_{12} & Q_{13} \\ Q_{21} & Q_{22} & Q_{23} \\ Q_{31} & Q_{32} & Q_{33} \end{array}] \{\begin{matrix} 0 \\ 0 \\ {\tilde{p}}_{z} \end{matrix}\}

이므로, 지표면의 수직방향 변위는 Eq. (27)과 같다.

(27)

{\tilde{w}}_{10} (β, γ; Ω) = Q_{33} (β, γ; Ω) {\tilde{p}}_{z} (β, γ; Ω) .

Eq. (27)을 Fourier 역변환하면 공간영역 변위의 주파수 스펙트럼 $S_{w} (x, y; Ω)$ 를 얻는다.

(28)

S_{w} (x, y; Ω) = \frac{1}{4 π^{2}} \iint {\tilde{w}}_{10} (β, γ; Ω) e^{i β x} e^{i γ y} d β d γ .

한편, $x$ 축을 따라 이격된 M개의 수직방향 하중이 지면에 작용할 때는 Eqs. (1), (2), (3)의 우변을

(29)

{\tilde{P}}_{z} (β, γ; Ω) = δ (z) {\tilde{p}}_{z} (β, γ; Ω) \sum_{l = 1}^{M} e^{- i β a_{l}}

로 바꾸어 해석한다. 여기서 $a_{l}$ 은 $l$ 번째 하중 작용점의 $x$ 좌표를 의미한다. Eq. (29)에서, 하중 작용 지점간 거리차에 의해 위상 간섭이 발생함을 알 수 있다.

일정 속도 $c$ 로 움직이는 주파수 $Ω$ 의 이동하중에 의해 지면 위의 한 지점 ( $x, y$ )에서 발생하는 수직방향 변위 스펙트럼은 Eq. (30)과 같다.

(30)

S_{w} (x, y, ω; Ω) = \frac{1}{c} e^{i β x} (\frac{1}{2 π} \int {\tilde{w}}_{10} (β, γ; Ω) e^{i γ y} d γ) .

(이동하중에서는 $ω = Ω - β c$ 이므로 응답 주파수 𝜔가 𝛽에 따라 선형적으로 변화한다. 따라서 Eq. (30)의 좌변에 변수 𝜔를 표기하였다).

IV. 지반진동 해석 예

4.1 지반 모델

철도기인 지반진동해석에서는 일반적으로 지반은 하나 또는 두 개의 상부 지층과 하부의 반무한 지반으로 구성되었다고 가정한다.^[8] 본 연구에서는 하부 반무한 지반 위에 두께 2 m의 상부 지층이 놓인 지반 모델을 이용해 해석을 수행하였다. 상부 지층은 하부 지층보다 무른 물성을 가지도록 하였으며, 각 지층별 물성치는 Table 1에 나타내었다. 지반진동에서는 지표면은 따라 전파되는 표면파(Rayleigh 파)가 중요한 역할을 하므로 각 지층별 Rayleigh파 전파 속도도 Table 1에 함께 표기하였다.

Table 1.

Properties of a layered ground.

Properties	Upper Layer	Half-space
Thickness	2 m	semi-infinite
Density	1900 kg/m³	2000 kg/m³
Young’s modulus	35 MPa	290 MPa
Poisson’s ratio	0.35	0.49
Damping loss factor	0.1	0.1
Rayleigh wave speed	77 m/s	210 m/s

4.2 지반의 파동 전파 특성

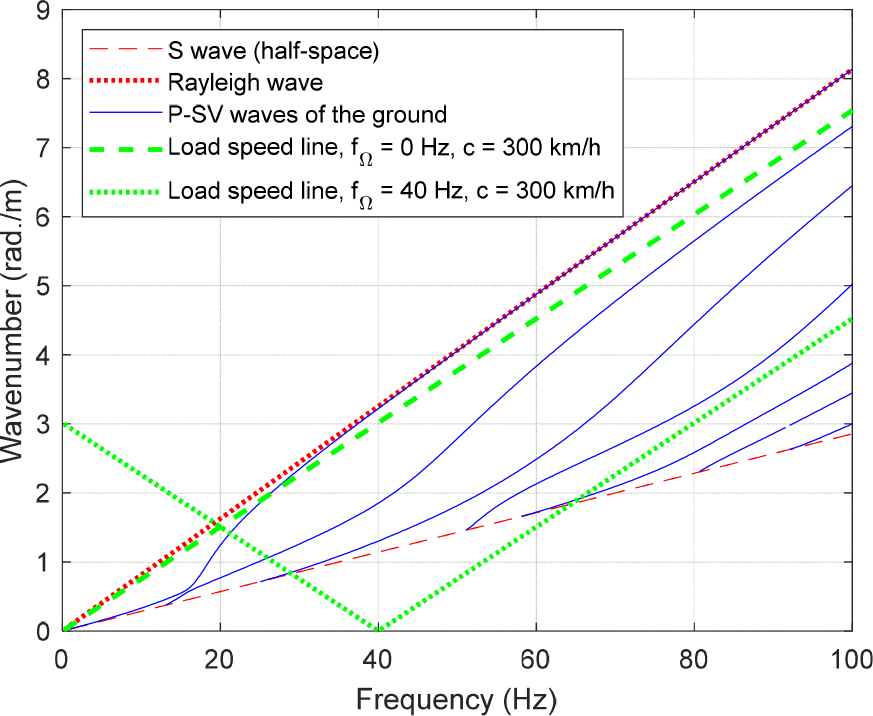
지반에서 발생하는 파동의 형태 및 전파 특성은 분산 선도를 통해 파악할 수 있다. 지반의 분산 선도는 Eq. (24)의 특성방정식으로부터 얻을 수 있으며, Fig. 2에는 Table 1에 제시된 지반의 분산 곡선을 나타내었다. 본 연구에서는 지반의 수직방향 변위를 구하고자 하므로 지반에서 발생하는 P-SV 파의 분산 곡선을 나타내었다.

https://cdn.apub.kr/journalsite/sites/ask/2025-044-01/N0660440104/images/ASK_44_01_04_F2.jpg

Fig. 2.

(Color available online) Dispersion curves of propagating waves in the ground listed in Table 1.

Fig. 2의 분산 곡선들은 상부 지층에서 $z$ 방향 모드를 형성해 전파되는 파동들이다. 이 파동들은 하부 반무한 지반의 전단파 분산선(얇은 빨간샌 점선)에서 시작(cut-on)된다. 즉, 하부 반무한 지반의 전단파보다 낮은 파수영역에서는 $z$ 방향 모드를 갖는 파동이 발생하지 않는다. 지반 상부 지층의 첫 번째 파동은 약 15 Hz 정도에서 발생하며 주파수가 증가함에 따라 표면파인 Rayleigh파 분산선에 접근하고 있다. [Fig. 2에 표시된 두 개의 하중속도선(굵은 초록 점선)에 대해서는 4.4절에서 설명한다].

하부 반무한 지반에서는 $z$ 방향 모드를 형성하는 파동이 존재하지 않으므로 Eq. (24)의 특성방정식에서는 하부 반무한 지반을 따라 전파되는 파동에 대한 정보가 나타나지 않는다. 하부 반무한 지반을 따라 전파되는 파동의 존재를 확인해 보기 위하여 𝛾=0일 때 단위하중에 의해 $x$ 방향을 따라 전파되는 지표면 변위, 즉, Eq. (27)의 ${\tilde{w}}_{1} 0 (β, 0; Ω)$ 를 주파수-파수영역 이미지로 Fig. 3에 나타내었다(선명한 이미지를 얻기 위하여 Fig. 3에서는 지반의 감쇠계수를 Table 1에 제시된 값보다 1/10로 줄여 해석하였다). Fig. 3에서 밝은 부분은 큰 변위를, 어두운 부분은 작은 변위를 의미한다. Fig. 3을 통해 하부 반무한 지반의 전단파 분산선(빨간색 점선) 아래에 변위가 크게 발생하는 파동들이 존재함을 알 수 있다. 이 파동들은 상부 지층에서 하부 반무한 지반으로 빠져나간 파동이라는 의미로 누설파(leaky wave)라 칭한다.^[7]

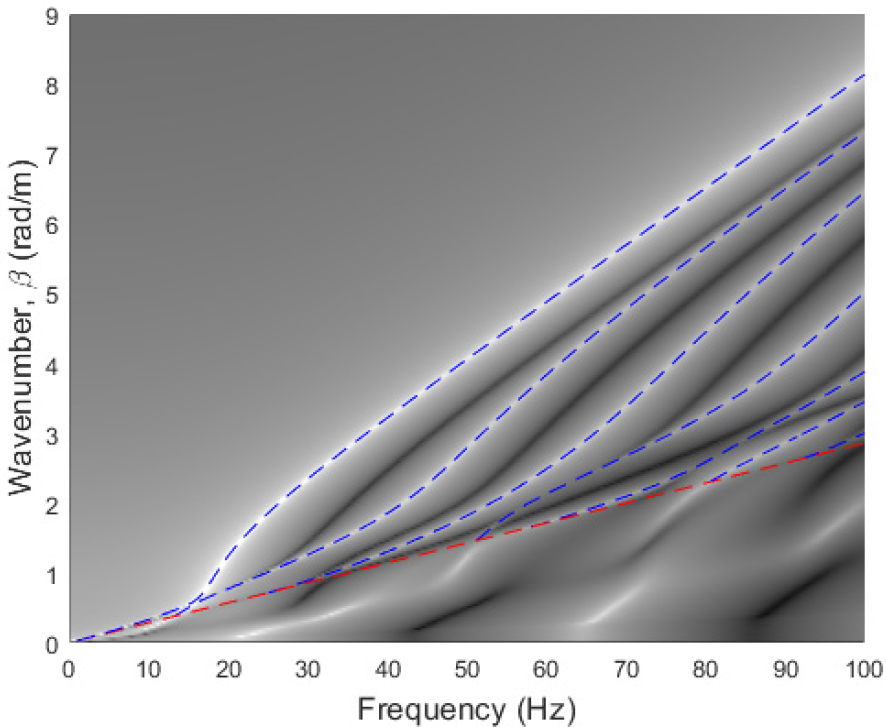
https://cdn.apub.kr/journalsite/sites/ask/2025-044-01/N0660440104/images/ASK_44_01_04_F3.jpg

Fig. 3.

(Color available online) Frequency-wavenumber domain image of vertical displacement at y=0 m on the ground surface. Dotted lines overlaid are dispersion curves of the ground shown in Fig. 2.

4.3 고정 하중에 의한 지반진동

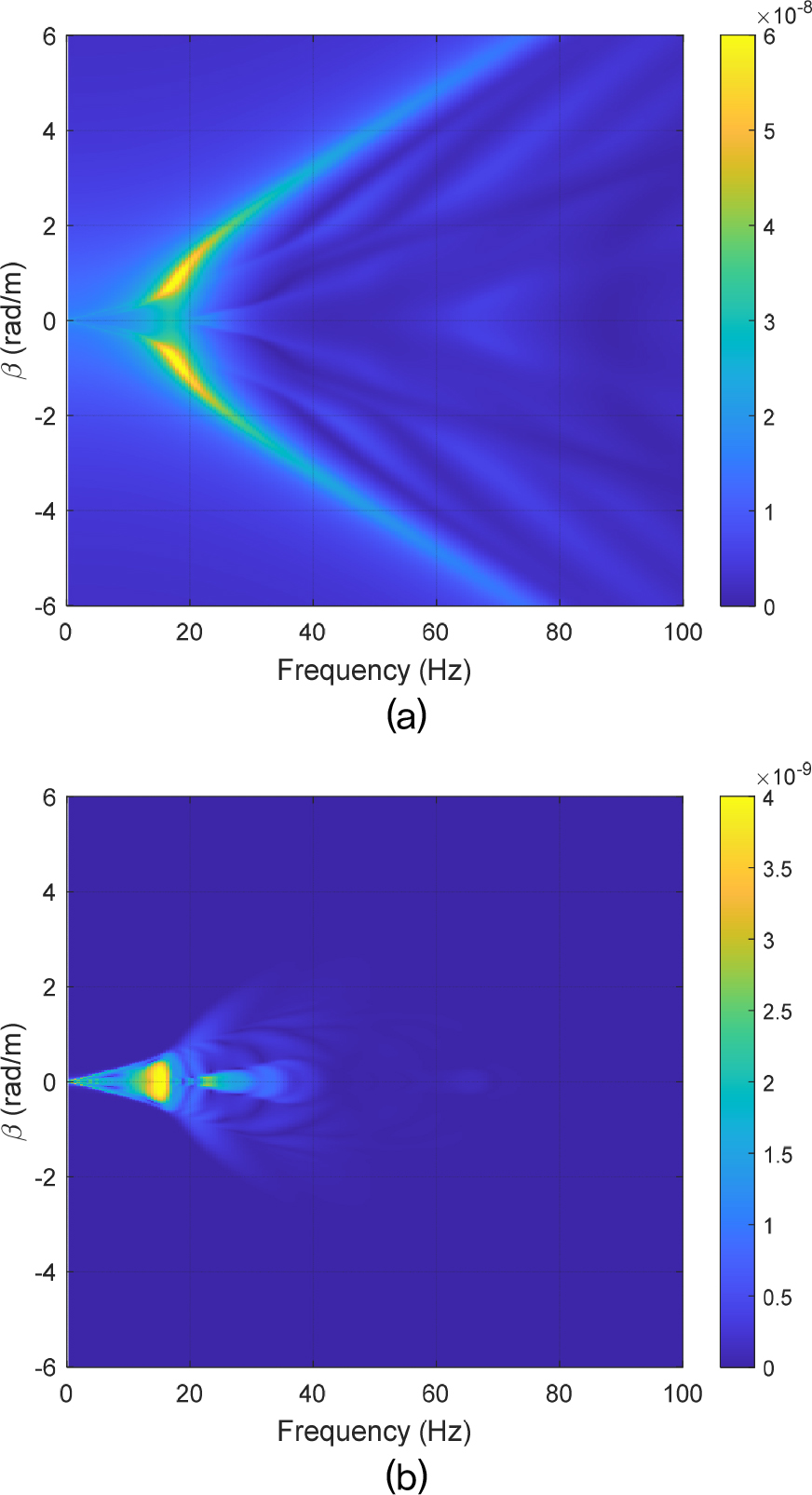
본 절에서는 Table 1의 물성을 갖는 지반에 대하여, 지표면 $x$ =0 m인 지점에 폭 2b인 단위 하중을 가했을 때 지표면 ( $x$ , $y$ ) 지점에 발생하는 수직방향 변위를 구하였다. 작용 하중의 폭은 2b = 3.2 m로 설정하였다. $x$ = 0, $| y | \leq b$ 인 영역에 Eq. (24)의 압력이 작용할 때, 지표면의 세 지점 $y$ = 0 m, 20 m에서 구한 주파수-파수영역의 수직방향 변위(전달 리셉턴스)를 Fig. 4에 나타내었다.

https://cdn.apub.kr/journalsite/sites/ask/2025-044-01/N0660440104/images/ASK_44_01_04_F4.jpg

Fig. 4.

(Color available online) Vertical displacements on the ground surface presented in frequency-wavenumber domain for a fixed load, c = 0 km/h. (a) y = 0 m, (b) y = 20 m.

Fig. 4(a)의 결과를 보면, Fig. 2에 나타낸 지반 상부 지층의 첫 번째 파동에 의해 큰 진동 응답이 발생한다는 것을 알 수 있다. 특히, 첫 번째 상부 지층 파동이 시작하는 주파수(약 15 Hz 부근)에서 지반진동이 가장 크게 발생한다. Fig. 4(a)와 (b)에서는 $y$ 방향 거리가 증가함에 따라 높은 주파수 및 높은 파수의 변위는 대부분 감쇄되어 사라진다. 반면, 낮은 주파수의 파동과 낮은 파수의 누설파는 원거리까지 전파되는 것을 볼 수 있다. 특히 상부 지층의 첫 번째 파동에 의해 발생한 15 Hz 대역 진동은 하부 반무한 지반을 타고 원거리까지 잘 전파되고 있다.

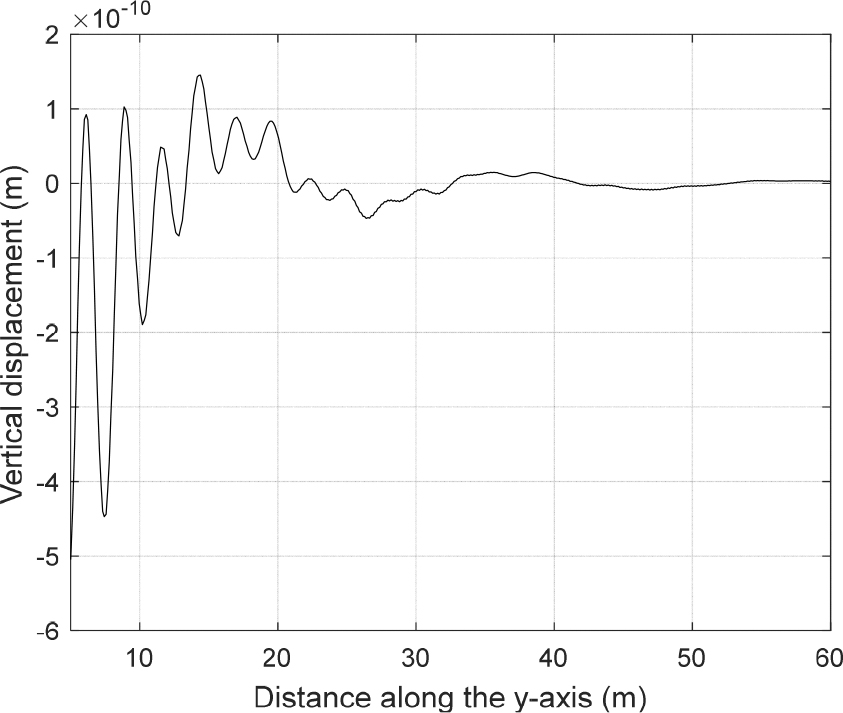
앞서 기술할 것과 같이, 누설파는 하부 반무한 지반을 통해 원거리까지 전파된다. 이를 확인하기 위해 $y$ 방향 거리를 증가시켜가면서 구한 30 Hz의 지표면 수직방향 변위를 Fig. 5에 나타내었다. Fig. 5의 결과를 보면, 상부 지층을 따라 전파되는 약 2.5 m 파장의 변위는 $y$ 가 멀어짐에 따라 급격히 감소하여 사라지며 원거리에서는 약 20 m 파장의 변위만 남는 것을 볼 수 있다. Fig. 3에서, 30 Hz 누설파의 파수는 약 0.3 rad/m이며 파장으로는 약 20 m이다. 따라서 Fig. 5의 원거리 지표면 변위는 하부 반무한 지반을 따라 전파된 누설파에 의한 것임을 알 수 있다.

https://cdn.apub.kr/journalsite/sites/ask/2025-044-01/N0660440104/images/ASK_44_01_04_F5.jpg

Fig. 5.

Vertical displacement along y on the ground surface for a fixed excitation at 30 Hz.

4.4 이동하중에 의한 지반진동

앞 4.3절에서는 주파수 $Ω$ 의 하중이 지반에 고정되어 작용할 때 발생하는 지반 응답을 해석하였다. 한편, 철도기인 지반진동을 해석하기 위해서는, 궤도를 따라 움직이는 이동하중이 고려되어야 한다. 본 절에서는 $x$ 축을 따라 이동하는 하중에 의해 발생하는 지반진동을 해석하고 응답 특성을 살펴본다.

가진 주파수 $Ω$ 의 하중이 $x$ 축을 따라 일정한 속도 $c$ 로 이동하는 경우, 지표면에 고정된 관찰자에게 관측되는 응답 주파수는 Doppler 효과로 인해 $ω = Ω - β c$ 이다. 여기서 𝛽는 $x$ 방향으로 진행하는 파동의 파수로서, 𝛽<0은 양의 $x$ 방향으로 진행하는 파동, 𝛽>0는 음의 $x$ 방향으로 진행하는 파동으로 정의된다.

주파수 $Ω$ 의 하중이 속도 $c$ 로 이동할 때 관찰되는 응답 주파수 𝜔는 파수 𝛽와 선형(linear) 관계를 갖는다. 즉, 응답 주파수는 분산 선도에서 직선으로 표현되는데, 이를 하중속도선(load speed line)이라고 칭한다. Fig. 2의 분산 선도에는 $f_{Ω}$ = 0 Hz의 정하중과 $f_{Ω}$ = 40 Hz의 동하중이 $c$ = 300 km/h의 속도로 이동하는 경우에 대한 하중속도선을 굵은 초록색 점선으로 나타내었다(Fig. 2에서는 하중속도선의 절대값을 도시하였다).

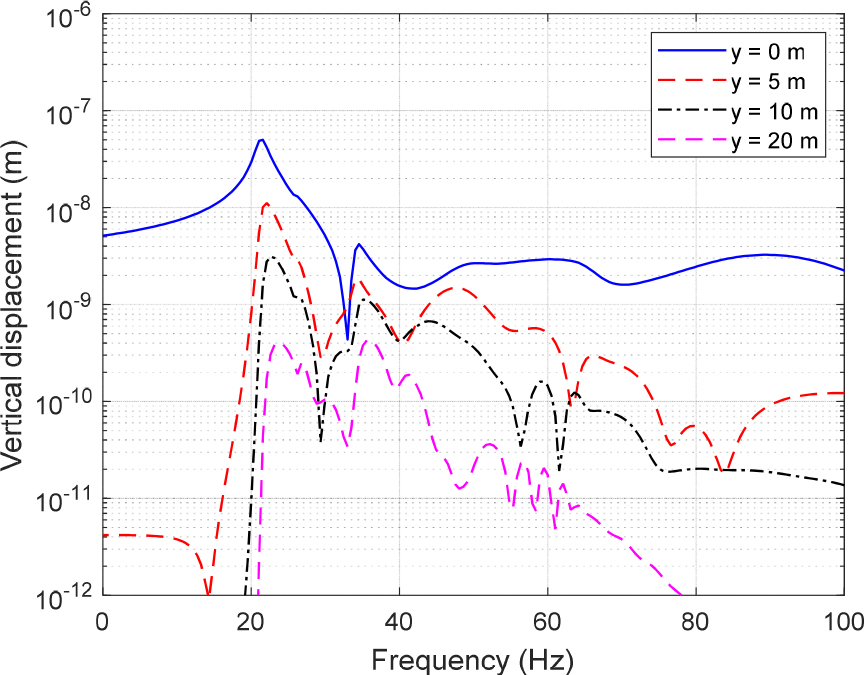
Fig. 2에서 정하중 및 동하중의 하중속도선과 지반 파동의 분산선이 교차하는 지점은 높은 지반 변위가 발생할 것으로 예상할 수 있다. Fig. 6에는 가진 주파수 $f_{Ω}$ = 40 Hz의 하중이 $c$ = 300 km/h 속도로 이동할 때 $y$ 축 위의 네 지점에서 발생하는 지표면 수직방향 변위를 나타내었다. Fig. 6을 보면 지반의 첫 번째 분산 곡선과 40 Hz 하중속도선이 교차하는 약 21 Hz에서 최대 변위가 발생하며, 교차점이 집중된 20 Hz ~ 30 Hz 대역에서 높은 진동 응답이 나타난다. 또한 하중속도선과 누설파가 교차하는 약 34 Hz 부근에서도 큰 변위가 발생하며, 누설파에 의한 진동 응답은 거리 감쇠가 적다는 것을 Fig. 6의 결과로부터 다시 한번 확인할 수 있다. 한편 Fig. 2에서 𝛽>0인 구간은 음의 $x$ 방향으로 진행하는 파동을 의미하므로, 하중 작용점을 기준으로 하중 진행 방향의 뒤편에서 발생하는 지표면 변위가 하중 진행 방향 앞쪽에서 발생하는 변위보다 더 크다는 것을 알 수 있다.

https://cdn.apub.kr/journalsite/sites/ask/2025-044-01/N0660440104/images/ASK_44_01_04_F6.jpg

Fig. 6.

(Color available online) Vertical displacement on the ground surface at various locations of y induced by a moving load of c = 300 km/h with $f_{Ω}$ = 40 Hz.

철도기인 지반진동 해석에서 정하중은 차량 중량이 차륜을 통해 레일에 가해지는 윤축하중이다. 정하중(윤축하중)이 속도 $c$ 로 주행하는 경우에도 Doppler 효과에 의해 주파수 𝜔의 동적응답이 발생하므로, 이동하는 정하중을 준정적 하중이라 부른다.

$c$ = 300 km/h에 대한 준정적 하중의 하중속도선은 Fig. 2에 나타내었으며, 이동속도 $c$ 는 하중속도선의 기울기를 결정한다. 즉, 이동속도가 빨라지면 하중속도선은 수평축에 가까워지며 속도가 느려지면 하중속도선은 수직축에 가까워진다. 준정적 하중에 의한 지표면 변위는 하중속도선을 따라가도록 Eq. (30)에 $Ω$ =0와 $β = ω / c$ 를 적용해 얻을 수 있다.

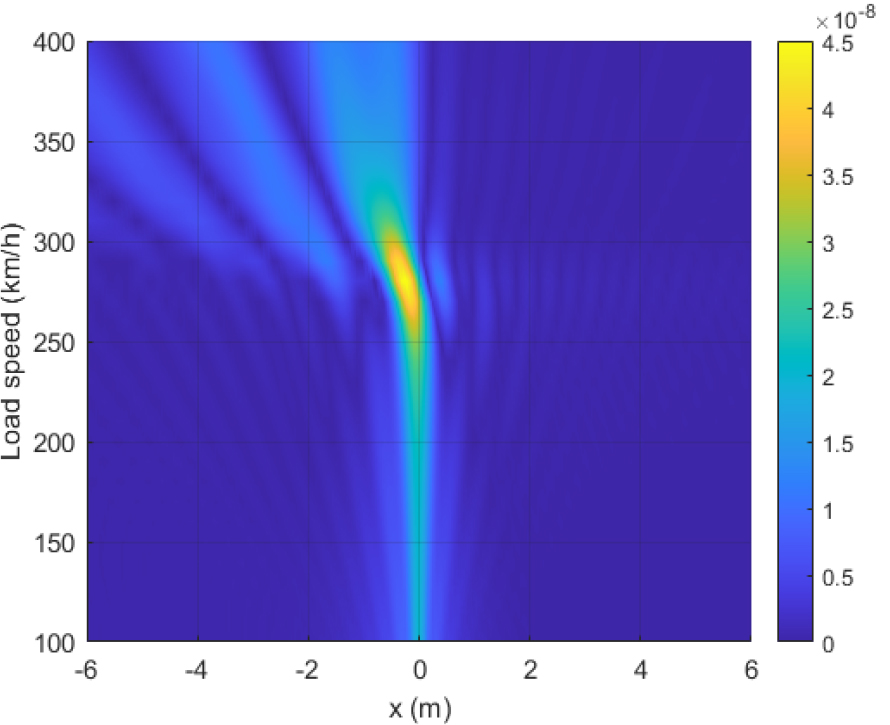
Fig. 7에는 준정적 하중에 의해 발생하는 지표면 $x$ 축( $y$ = 0 m)의 수직방향 변위를 나타내었다. Fig. 7에서 $x$ 축은 하중과 함께 움직이는 이동 좌표계이며, $x$ = 0 지점은 이동하중의 작용점을 의미한다. Fig. 7의 해석 결과로부터 최대 변위가 발생하는 하중 이동속도는 $c$ = 280 km/h 부근으로 나타났다. 이 속도는 Fig. 2의 분산선도에 표시한 Rayleigh 파의 전파속도 (77 m/s)에 해당한다. 즉, 준정적 하중에 의한 지반 변위는 하중 이동속도가 지반 표면파인 Rayleigh 파 전파 속도와 같아질 때 최대가 된다. 또한 Fig. 7로부터 하중 진행 방향의 뒤편(하중 작용점의 뒤편)에서 최대 변위가 발생함을 알 수 있다.

https://cdn.apub.kr/journalsite/sites/ask/2025-044-01/N0660440104/images/ASK_44_01_04_F7.jpg

Fig. 7.

(Color available online) Vertical displacement along x on the ground surface for various loading speeds.

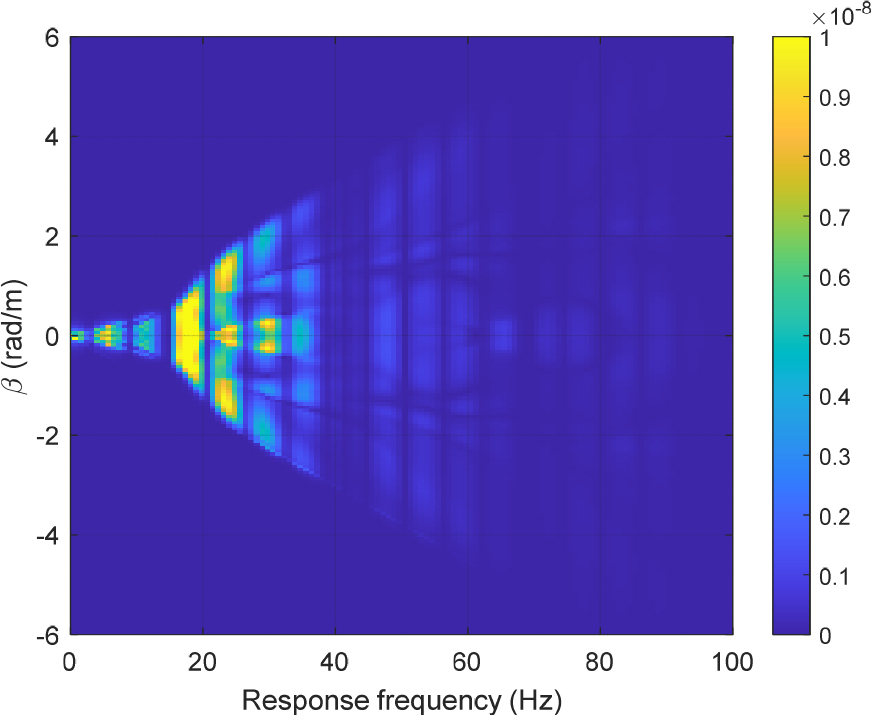
철도기인 지반진동은 차륜-레일 접촉 하중에 의해 발생하므로 복수 개의 하중이 궤도를 통해 지반에 작용한다. Eq. (29)와 같이, M개의 수직방향 단위 하중이 지반에 작용할 때 발생하는 $y$ = 10 m 지점의 지반 변위를 Fig. 8에 나타내었다. 하중의 개수는 M = 4, 하중 작용점의 위치는 $x$ = 8.5 m, 5.5 m, -5.5 m, -8.5 m로 설정하였다. 속도 $c$ 로 이동하는 M개 하중은 지면에 고정된 관측자가 볼 때 시간 지연을 가지고 관측되는 M개의 하중과 같다. 하중 또는 응답의 시간 지연은 주파수영역에서 위상 간섭(상쇄 또는 보강 간섭)으로 나타난다. Fig. 8에서는 시간 지연에 따른 위상 간섭으로 인해 특정 주파수 대역에서 변위가 증대 또는 감소되는 현상을 확인할 수 있다. 실제 열차는 많은 수의 객차로 편성되므로 Fig. 8보다 훨씬 복잡한 위상 간섭이 발생할 것으로 예상할 수 있다.

https://cdn.apub.kr/journalsite/sites/ask/2025-044-01/N0660440104/images/ASK_44_01_04_F8.jpg

Fig. 8.

(Color available online) Vertical displacements on the ground surface at y = 10 m presented in frequency-wavenumber domain induced by four unit loads moving with c = 300 km/h.

V. 결 론

본 연구에서는 유연도행렬 방법을 이용해 철도기인 지반진동 해석에 필요한 지반을 모델링하였다. 구축된 지반 모델을 이용해 두께 2 m의 상부 지층과 하부 반무한 지반으로 구성된 예제 지반에 대한 해석을 수행하였다.

본 해석을 상부 지층의 첫 번째 파동이 발생하는 주파수 부근에서 동하중에 의한 지반 변위가 가장 크게 발생함을 알았다. 또한, 하부의 반무한 지반을 통해 전파되는 파동들이 발생하며, 이들은 상부 지층의 파동에 비해 원거리까지 전파하는 특성을 갖는다.

지반에 이동하중이 작용하는 경우에는, 하중속도선과 지반의 파동 분산선이 교차하는 지점에서 높은 진동응답이 발생하였다. 한편, 준정적 하중은 이동속도가 지반의 Rayleigh파와 같아질 때 최대 변위가 발생시키는 것으로 나타났다. 한편 길이 방향을 따라 배열된 복수개의 하중이 작용하면 하중의 거리 간격에 의한 위상간섭으로 인해 특정 주파수 대역에서 지반진동이 증가하거나 감소함을 확인하였다. 다만, 본 연구에서 관찰된 지반진동의 특성은 지층의 물성이나 지반 구성 등에 의해 큰 영향을 받을 것으로 판단된다.

본 연구에서 확보한 지반 모델은 추후 궤도 모델과 결합시켜 궤도-지반 연성 이론 모델을 구축할 계획이다. 궤도-지반 연성 모델이 확보되면 철도차량 모델 및 차륜-레일 접촉하중 모델을 이용해 궤도에 가해지는 동하중을 산출할 수 있으므로 이론해석을 통한 철도기인 지반진동 예측이 가능하다. 후속 연구에서는 철도기인 지반진동을 해석하고 문헌 자료 또는 지반진동 측정치와 비교함으로써 구축한 궤도-지반 연성 모델의 신뢰성을 검증하고자 한다.

References

D. V. Jones, D. Le Houedec, and M. Petyt, "Ground vibration due to a rectangular harmonic load," J. Sound Vib. 212, 61-74 (1998).

10.1006/jsvi.1997.1367

X. Sheng, C. J. C. Jones, and M. Petyt, "Ground vibration generated by a load moving along a railway track," J. Sound Vib. 228, 129-156 (1999).

10.1006/jsvi.1999.2406

X. Sheng, C. J. C. Jones, and D. J. Thompson, "A theoretical model for ground vibration from trains generated by vertical track irregularities," J. Sound Vib. 272, 937-965 (2004).

10.1016/S0022-460X(03)00782-X

G. Lombaert, G. Degrande, and D. Clouteau, "Numerical modelling of free field traffic induced vibrations," Soil Dyn. Earthq. Eng. 19, 473-488 (2000).

10.1016/S0267-7261(00)00024-5

E. Kausel and J. M. Roësset, "Stiffness matrices for layered soils," Bull. Seismol. Soc. Am. 71, 1743-1761 (1981).

10.1785/BSSA0710061743

E. Kausel, "Generalized stiffness matrix method for layered soils," Soil Dyn. Earthq. Eng. 115, 663-672 (2018).

10.1016/j.soildyn.2018.09.003

X. Sheng, Ground vibrations generated from trains, (Ph.D. thesis, University of Southampton, 2001).

E. Ntotsios, D. J. Thompson, and M. F. M. Hussein, "A comparison of ground vibration due to ballasted and slab tracks," Transp. Geotech. 21, 100256 (2019).

10.1016/j.trgeo.2019.100256

The Journal of the Acoustical Society of KoreaISSN:1225-4428(Print) 2287-3775(Online)한국음향학회

Preview

Theoretical ground modelling for train-induced ground vibration and analysis on wave propagation along ground

ABSTRACT

MAIN

Fig. 1.

Coordinate system for image construction using synthetic aperture sonar.

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

Table 1.

Properties of a layered ground.

Fig. 2.

(Color available online) Dispersion curves of propagating waves in the ground listed in Table 1.

Fig. 3.

(Color available online) Frequency-wavenumber domain image of vertical displacement at y=0 m on the ground surface. Dotted lines overlaid are dispersion curves of the ground shown in Fig. 2.

Fig. 4.

(Color available online) Vertical displacements on the ground surface presented in frequency-wavenumber domain for a fixed load, c = 0 km/h. (a) y = 0 m, (b) y = 20 m.

Fig. 5.

Vertical displacement along y on the ground surface for a fixed excitation at 30 Hz.

Fig. 6.

(Color available online) Vertical displacement on the ground surface at various locations of y induced by a moving load of c = 300 km/h with fΩ = 40 Hz.

Fig. 7.

(Color available online) Vertical displacement along x on the ground surface for various loading speeds.

Fig. 8.

(Color available online) Vertical displacements on the ground surface at y = 10 m presented in frequency-wavenumber domain induced by four unit loads moving with c = 300 km/h.

References

(Color available online) Vertical displacement on the ground surface at various locations of y induced by a moving load of c = 300 km/h with $f_{Ω}$ = 40 Hz.