Optimal deployment of sonobuoy for unmanned aerial vehicles using reinforcement learning considering the target movement

Geunyoung Bae; Juhwan Kang; Jungpyo Hong

doi:10.7776/ASK.2024.43.2.214

Preview

Research Article

The Journal of the Acoustical Society of Korea. 31 March 2024. 214-224
https://doi.org/10.7776/ASK.2024.43.2.214

Optimal deployment of sonobuoy for unmanned aerial vehicles using reinforcement learning considering the target movement

표적의 이동을 고려한 강화학습 기반 무인항공기의 소노부이 최적 배치

Geunyoung Bae¹

Juhwan Kang²

Jungpyo Hong¹^*

배 근영¹

강 주환²

홍 정표¹^*

¹창원대학교 정보통신공학과

²국방기술품질원

^{*Corresponding Author}

ABSTRACT

Sonobuoys are disposable devices that utilize sound waves for information gathering, detecting engine noises, and capturing various acoustic characteristics. They play a crucial role in accurately detecting underwater targets, making them effective detection systems in anti-submarine warfare. Existing sonobuoy deployment methods in multistatic systems often rely on fixed patterns or heuristic-based rules, lacking efficiency in terms of the number of sonobuoys deployed and operational time due to the unpredictable mobility of the underwater targets. Thus, this paper proposes an optimal sonobuoy placement strategy for Unmanned Aerial Vehicles (UAVs) to overcome the limitations of conventional sonobuoy deployment methods. The proposed approach utilizes reinforcement learning in a simulation-based experimental environment that considers the movements of the underwater targets. The Unity ML-Agents framework is employed, and the Proximal Policy Optimization (PPO) algorithm is utilized for UAV learning in a virtual operational environment with real-time interactions. The reward function is designed to consider the number of sonobuoys deployed and the cost associated with sound sources and receivers, enabling effective learning. The proposed reinforcement learning-based deployment strategy compared to the conventional sonobuoy deployment methods in the same experimental environment demonstrates superior performance in terms of detection success rate, deployed sonobuoy count, and operational time.

Keywords

Reinforcement Learning

Sonobuoy

Optimal Deployment

Unmanned Aerial Vehicles (UAVs)

소노부이는 수중에서 음파를 활용하여 정보 수집을 수행하는 장치로, 엔진 소음이나 다양한 음향 특성을 감지하여 수중 표적을 정확하게 탐지하는 대잠전에 효과적인 탐지체계이다. 다중상태 시스템에서의 기존 소노부이 배치 방식은 고정된 패턴이나 휴리스틱 기반의 규칙에 의존하므로, 예측하기 힘든 수중 표적의 기동으로 인해 소노부이 투하 개수 및 작전 소요 시간 측면에서 효율적인 배치를 보장하지는 못한다. 본 논문에서는 기존 소노부이 배치 방식의 한계를 극복하기 위해, 수중 표적의 이동을 고려한 시뮬레이션 기반의 실험 환경에서 강화학습을 이용한 무인항공기의 소노부이 최적 배치를 제안한다. 제안한 방법은 Unity ML-Agents를 통해 Proximal Policy Optimization(PPO) 알고리즘을 이용하여 가상 작전환경과 실시간 상호작용하며 무인항공기를 학습한다. 소노부이 투하 개수 및 음원 및 수신기 간의 비용을 고려한 보상 함수를 설계하여 효과적인 학습이 가능하게 한다. 동일한 실험 환경에서 강화학습을 적용한 배치 방식과 기존 소노부이 배치 방식을 비교한 결과, 탐지 성공률, 투하된 소노부이 개수, 작전 소요 시간 측면에서 강화학습을 적용한 배치 방식이 가장 우수한 성능을 보였다.

키워드

강화학습

소노부이

최적 배치

무인항공기

MAIN

I. 서 론
II. 관련 연구
2.1 격자구조 소노부이 배치 방식
2.2 유전 알고리즘을 이용한 소노부이 최적 배치
2.3 강화학습을 이용한 소노부이 최적 배치
III. 제안한 방법
3.1 보상 함수 설계
3.2 학습 에피소드 진행
IV. 실험 환경 및 결과
4.1 실험 개요
4.2 실험 가정
4.3 학습
4.4 실험 결과
V. 결 론

I. 서 론

해양 안보를 위해 수중 표적을 효과적으로 탐지하는 것은 군사 작전 및 해양 안전에 있어서 핵심 과제 중 하나로 꼽힌다. 대잠전(Anti-Submarine Warfare, ASW)은 이러한 문제에 대응하기 위한 필수적인 작전 중 하나로, 수중 표적의 기동성과 은밀성으로 인해 어려움이 따른다. 이러한 환경에서 소노부이는 소나를 탑재한 부표 형태의 센서로, 다양한 음향 정보를 수집하여 수중에서 수중 표적의 존재를 감지하고 위치를 파악하여 대잠전을 효과적으로 수행할 수 있게 한다.^[1] 소노부이는 음원을 방사하는 능동형과 표적의 방사소음을 수신하는 수동형으로 나뉘는데, 다수의 능·수동 소노부이로 운용되는 탐지체계를 다중상태 소노부이 시스템이라고 한다. 이러한 다수의 센서 간 협력적인 구조로 인해, 신호 대 잡음비가 낮은 상황에서도 대상에 대한 탐지 성능이 크게 향상된다.^[2]

다중상태 소노부이는 음원과 수신기가 각각 어떻게 배치되느냐에 따라 대잠전의 성공에 직접적인 영향을 미친다.^[3] 기존 소노부이 배치 방식들은 고정된 패턴이나 휴리스틱 기반의 규칙에 의존하는 경우가 많다.^[4] 이러한 방식들은 매번 최적의 결과를 도출하기 어렵다. 특히, 복잡한 환경 조건과 적의 다양한 전략에 대응하기 어려운 한계가 존재한다. 이러한 한계를 극복하기 위한 방법으로 다양한 선행 연구가 수행되어 왔다.^[5,6,7] 대표적인 최적 배치 연구로 유전 알고리즘을 적용한 방식이 있다. 유전 알고리즘은 생물의 진화 원리를 모방하여 최적화 문제에 적용되며, 소노부이 배치 문제에 대한 적응력을 향상시키는 데 기여할 수 있다. 하지만 이러한 휴리스틱 기반의 정적 알고리즘은 최적 배치에 대한 근사적인 해결책을 찾게 되어, 지역 해에 빠질 가능성이 크다.

최근에는 보다 정확하고 동적인 소노부이 배치 방식을 찾기 위해 강화학습이 주목받고 있다.^[8,9] 강화학습은 에이전트가 환경과 상호작용하며 행동에 대한 보상을 최대화하는 전략을 학습하는 기법으로 적응성과 학습 능력에서 강점을 가지고 있으며, 유전 알고리즘보다 지역 해에 빠지는 문제의 개선이 가능하다. 특히, 예측할 수 없는 대잠전 상황에서 유연하게 대응할 수 있는 특성이 강화학습을 소노부이 최적 배치 문제에 적용하는 데에 대한 새로운 가능성을 열고 있다. 더불어, 유전 알고리즘과 강화학습을 결합한 방법의 연구 또한 수행되었다.^[10] 유전 알고리즘의 탐색 다양성 및 강화학습의 동적인 학습 능력을 조합함으로써 최적 배치 문제에 대한 효과적인 접근 가능성을 제시하였다. 하지만, 선행된 연구에서는 수중 표적의 기동이 고려되지 않은 실험 환경에서, 탐지 확률 및 탐지 영역의 최대화를 위한 소노부이 최적 배치 패턴을 생성한다. 이는 실제 대잠전 상황에 적용되기에 다소 어려움이 존재하며, 항상 효과적인 결과를 보장하지는 못한다.

따라서, 본 논문에서는 수중 표적의 기동을 고려한 시뮬레이션 기반의 실험 환경에서 강화학습을 이용한 무인항공기의 소노부이 최적 배치를 제안한다. 학습된 모델에 따라 무인항공기(Unmanned Aerial Vehicle, UAVs)가 가상의 작전 해역에서 소노부이를 투하하며 예측 불가능하게 기동하는 수중 표적을 탐지한다. 또한, 대잠전에서는 수중 표적을 신속하고 정확하게 탐지하고 추적할 수 있는 능력을 갖추어야 한다. 그러므로 고가의 소노부이를 효과적으로 활용하기 위해서는 한정된 수량으로 최대한의 성능을 발휘하는 것이 중요하다. 이는 자원의 효율적인 사용을 의미하며, 이는 예산 및 운용 비용을 절감할 수 있다. 이에 따라 본 논문에서는 소노부이 최적 배치의 요건을 최소 소노부이 사용, 최단 시간 탐지로 설정한다. 최적 배치를 달성하기 위한 보상 함수를 제안하였으며, 시뮬레이션을 통해 제안된 방법과 기존 방법의 탐지 성능 및 효율성을 비교함으로써 제안된 방법의 유효성을 입증한다.

II. 관련 연구

2.1 격자구조 소노부이 배치 방식

기존 소노부이 배치 방식에서 주로 사용되는 고정된 패턴에는 Fig. 1과 같이 특정한 해역에 격자 형태로 음원과 수신기를 일정한 간격으로 배치하는 방식이 있다. 이는 전체 해역에 대한 균일한 감시를 가능케 하여 탐지 누락을 최소화한다는 장점이 있다. 격자 패턴으로 배치하는 것에도 삼각형, 사각형, 육각형 등 다양한 방법이 있으며, 이는 소노부이 종류와 배치 간격에 따라 성능에 영향을 미친다. 관련된 연구로, Reference [5]에서는 다양한 배치 패턴에 대해서 음원과 수신기 비용의 비에 따라 실험한다. 다중상태 시스템에서 음원과 수신기의 비용이 동일한 경우, 정사각형 방식이 투하된 소노부이 개수 대비 가장 뛰어난 탐지 범위를 가진다.

https://static.apub.kr/journalsite/sites/ask/2024-043-02/N0660430209/images/ASK_43_02_09_F1.jpg

Fig. 1.

Placement form of square grid (Sources: ●, receivers: ○).

2.2 유전 알고리즘을 이용한 소노부이 최적 배치

유전 알고리즘을 이용한 소노부이 최적 배치에서는 개체 평가를 위해 사용되는 목적함수의 설정이 곧 최적 배치의 요건이 된다. 일반적으로 목적함수로 가장 많이 사용되는 것이 탐지 확률 혹은 탐지 범위이다. Reference [6]에서는 고정익 항공기의 기동 특성을 고려하여 정해진 규칙에 따라 음원과 수신기의 투하 지점을 지정하여 초기 개체를 생성하고, Cassini Oval의 개념을 적용하여 Exponential 방식에 따라 탐지 확률을 산출한다. 탐지 확률 필드를 바탕으로 탐지 영역을 구하고, 이를 통해 개체를 평가하고 선택, 교차, 변이를 여러 세대에 거쳐 반복하여 가장 우수한 개체를 생성한다. 실험에 사용되는 소노부이의 수를 설정 후, 해당 개수로 최대의 탐지 영역을 가지는 배치 패턴을 얻을 수 있다.

2.3 강화학습을 이용한 소노부이 최적 배치

Reference [7]은 강화학습 알고리즘인 Deep Deterministic Policy Gradient(DDPG) 알고리즘을 이용한 소노부이 최적 배치를 제안하고, 최적 배치 요건을 최단 시간, 최대 탐지 영역으로 설정하였다. 본 논문과 동일하게 Unity ML-Agents를 활용하여 가상의 작전 해역에서 실험을 진행한다. 음향 탐지 성능 분포도를 활용하여 사전에 지정된 소노부이 투하 가능 지점을 설정한 후, 최적 배치 요건에 맞게 설계된 보상 함수로 에피소드 진행 방식에 따라 학습한다. 단상태 시스템을 적용하여, 소노부이 간 탐지 영역이 겹치지 않도록 하였다. 사전에 설정된 투하 가능 지점들 중 가장 가깝되, 탐지 영역이 겹치지 않는 투하 지점을 선택한다. 매 스텝마다 선택된 투하 지점과의 거리를 계산하여 이전 거리와 현재 거리의 차로 보상을 부여한다. 목표 지점에 도달할 시에는 일정한 큰 보상을 부여하도록 설계하여 최적 배치를 달성한다.

이외에도 유전 알고리즘과 강화학습을 결합한 방법으로 연구가 수행되었다.^[10]Reference [10]에서는 최단 시간 및 최소 불확실성을 목표로 한 소노부이 최적 배치 연구를 수행한다. 두 가지 목표를 달성하기 위해 파레토 최적(Pareto Optimal)의 개념을 적용하여 유전 알고리즘을 통해 다양한 배치 패턴을 생성하고, 초기 Pareto non-dominated 솔루션을 찾아 아카이브를 구축한다. 구축된 아카이브에서 강화학습 단계에서 전통적인 강화학습 알고리즘인 Q-Learning을 통해 업데이트된 정보를 사용하여 개선된 솔루션을 찾는다. 이 방법 또한 유전 알고리즘을 이용한 소노부이 최적 배치 연구와 같이 소노부이를 개수 별로 실험하여, 격자 패턴과의 비교를 통해 성능이 향상됨을 확인하였다.

III. 제안한 방법

선행된 연구의 공통점은 수중 표적의 기동을 고려하지 않는다는 것이다. 해당 연구의 최적 배치 요건에 대해서는 충분한 의의를 가지지만, 예측 불가능한 실제 대잠전 상황에서는 적합하지 않을 수 있다. 작전 해역에 수중 표적이 존재한다고 가정했을 때, 수중 표적의 속력이 소노부이를 투하하는 비행체의 속력에 비해 현저히 느리다 할지라도 수중 표적이 소노부이의 존재를 의식하고 회피 기동하여 전체 탐지 영역이 형성되기 전에 탐지 영역을 이탈할 수도 있다. 또한 자원 효율성을 고려하는 데에도 어려움이 있다. 소노부이는 운용 가능한 시간이 제한적이기 때문에 넓은 해역에서 생성된 배치 패턴에 따라 소노부이를 투하할 시, 수중 표적과 거리가 먼 지점의 소노부이는 사실상 필요가 없는 것이나 다름 없다. 이러한 불필요한 구역에 배치되는 소노부이로 인해 수중 표적을 탐지하기까지 작전에 소요되는 시간 또한 오래 걸리게 된다.

따라서, 본 연구에서는 수중 표적의 기동을 고려한 실험 환경을 통해 실제 대잠전 상황에 적용 가능한 연구를 수행한다. 또한 대잠전의 신속성과 효율성을 위해, 최적 배치의 요건을 최소 소노부이 개수 및 최소 탐지 시간으로 정의한다는 점에서 선행 연구와의 차별성이 있다. 무인항공기의 소노부이 최적 배치를 달성하기 위해 강화학습을 적용한다. 강화학습은 기계학습의 한 분야로, 에이전트가 환경과 상호 작용을 하며 보상을 최대화하기 위한 학습 방법이다. 에이전트는 주어진 환경에서 특정한 상태에서 행동을 선택하고 이에 대한 보상(Reward)을 받으며 최적의 정책을 학습한다. 본 연구에서 에이전트는 무인항공기이며, 상태와 행동 벡터는 Table 1에서와 같이 정의한다. 강화학습 알고리즘으로는 전통적인 강화학습 알고리즘이 아닌, 심층 강화학습 알고리즘 중 하나인 Proximal Policy Optimization(PPO)를 적용하여 보다 안정적이고 효과적인 학습을 가능하게 한다.^[11] Fig. 2는 본 연구의 간략적인 개념도이다.

Table 1.

State and action vectors of UAVs.

State	Axis	Description
Location	x	longitudinal location
Location	z	lateral location
Speed	x	longitudinal location
	y	vertical location
	z	lateral location
Submarine location	x	longitudinal location
Submarine location	z	lateral location
Action	Axis	Description
UAV	x	longitudinal move
	z	lateral move
	scalar	distance to move

https://static.apub.kr/journalsite/sites/ask/2024-043-02/N0660430209/images/ASK_43_02_09_F2.jpg

Fig. 2.

(Color available online) Conceptual diagram of proposed system.

투하된 다중상태 소노부이의 탐지 범위를 나타내기 위해 Cassini Oval의 개념을 활용한다. 이는 두 개의 고정된 점, 즉 음원 및 수신기와 수중 표적에 대한 일정한 거리의 합이 상수인 점들의 집합으로, Fig. 3과 같이 나타난다. Cassini Oval 방정식은 Eq. (1)로 정의되며, 방정식을 만족하는 평면 상의 좌표가 타원을 이루게 된다. 타원의 형태를 제어하는 매개 변수 a와 타원의 크기를 결정하는 매개 변수 b에 따라 변형된다. 여기서 b는 아래의 Eq. (2)로 소나 방정식을 통해 계산된다.^[12] Cassini Oval은 음원에서 수중 표적까지의 거리와 수중 표적에서 수신기까지 거리의 기하 평균이 일정하다는 특성을 가진다. 이를 통해 Eq. (3)에서 $R_{e q u}$ 를 계산하여 Eq. (4)와 같이 소노부이의 평균 탐지거리 $R_{0}$ 만을 가지고 계산하는 Exponential 방식을 적용하여 탐지 확률을 산출한다.^[13]

(1)

(x^{2} + y^{2})^{2} - 2 a^{2} (x^{2} - y^{2}) + a^{4} = b^{4} .

(2)

D_{1} D_{2} ≦ 10^{(\frac{S L - N L + T S + D I - D T}{20})} \equiv b^{2} .

(3)

R_{e q u} = \sqrt{R_{S T} R_{T R}} .

(4)

p_{d (R_{e q u})} = 10^{- 0.30103 R_{e q u} / R_{0}} .

https://static.apub.kr/journalsite/sites/ask/2024-043-02/N0660430209/images/ASK_43_02_09_F3.jpg

Fig. 3.

(Color available online) Cassini oval conceptual plot.

3.1 보상 함수 설계

강화학습에서 보상 함수는 에이전트가 특정 행동을 취한 결과에 대한 피드백을 제공하는 핵심적인 역할을 한다. 보상 함수의 설계는 학습 알고리즘이 원하는 목표를 달성하도록 도와주며, 에이전트가 바람직한 행동을 학습하고 최적의 전략을 개발하는 데 결정적인 영향을 미친다. 소노부이 최적 배치 요건은 최소한의 소노부이로 최단 시간 내에 수중 표적을 탐지하는 것이다. 따라서 다음과 같이 최적화 공식을 정의하면,

Minimize

(5)

c (r), t (r) .

subject to

(6)

0 \leq d \leq d_{\max}, 0 \leq D_{k} \leq D_{\max} .

(7)

r \geq r_{\min} .

여기서 r은 투하된 소노부이 개수이고 $c (r)$ 은 소노부이의 비용함수로

(8)

c (r) = λ_{1} r_{s o u r c e} + λ_{2} r_{r e c e i v e r}

와 같이 표현된다, Eq. (8)은 음원과 수신기의 비용에 대한 가중치를 각각 $λ_{1}$ 과 $λ_{2}$ 로 달리 설정하여 각각의 투하된 소노부이 개수만큼의 곱의 합으로 정의된다. 또한, $t (r)$ 은 무인항공기가 작전 상공에 배치됨으로부터 수중 표적을 탐지하기까지 작전에 소요되는 시간으로

(9)

t (r) = a + \sum_{k = 0}^{r - 1} (D_{k} + l)

과 같이 정의된다. 여기서 a는 초기 투하 지점까지의 이동 거리에 대한 시간이다. 투하된 r개의 소노부이만큼 매 투하 지점까지의 이동 거리에 대한 시간인 $D_{k}$ 와 투하에 소요되는 시간 $l$ 을 합산한 값으로 나타낸다.

최적화 공식의 제약 조건을 Eqs. (6)과 (7)으로 정의한다. 현재 소노부이 투하 지점에서 다음 투하 지점을 지정하기 위해 본 연구에서는 무인항공기의 최대 이동 범위의 $d_{\max}$ 만큼의 제한을 둔다. 탐지에 성공하기 위한 최소 소노부이 투하 개수 또한 $r_{\min}$ 이상이 되도록 제한하여 실험한다.

무인항공기가 최소한의 소노부이로 최단 시간 내에 수중 표적을 탐지할 수 있도록 Fig. 4와 같이 보상 함수를 설계한다. 수중 표적 탐지 시에 1만큼의 양의 보상을 부여한다. 수중 표적과 더 가까운 곳에 투하하는 것이 탐지 확률이 높으므로, 탐지 시에 소노부이가 수중 표적과 200 m 이내에 존재한다면 1만큼의 추가적인 보상을 부여한다. 만약 소노부이 투하 시에 탐지에 실패하였다면 –0.5만큼의 음의 보상을 부여하고, 음원과 수신기에 대해 각각 –0.6, –0.5만큼의 음의 보상을 부여한다. 이를 통해 소노부이의 비용을 고려하여 보다 효율적인 배치를 가능하게 한다. 수중 표적 또는 무인항공기가 작전 해역을 이탈한다면 –5만큼의 보상을 부여하여 무인항공기가 작전 해역을 벗어나지 않도록 학습하고, 수중 표적이 작전 해역을 이탈하기 전까지 탐지하도록 한다.

https://static.apub.kr/journalsite/sites/ask/2024-043-02/N0660430209/images/ASK_43_02_09_F4.jpg

Fig. 4.

Flowchart of designed reward function.

3.2 학습 에피소드 진행

강화학습은 에이전트가 설계된 보상 함수에 따라 여러 번의 에피소드를 반복하며 학습하게 된다. 따라서 무인항공기가 학습하기 위한 에피소드의 진행 방법은 Fig. 5와 같다.

https://static.apub.kr/journalsite/sites/ask/2024-043-02/N0660430209/images/ASK_43_02_09_F5.jpg

Fig. 5.

Method of the episode procedure for learning UAV.

먼저 특정 지점에서 첫 접촉되었다는 가정하에 에피소드를 시작한다. 에피소드 초기에 무인항공기는 작전 해역 외부에서 생성되어 내부로 진입하게 되고, 수중 표적은 작전해역 가운데에 랜덤한 방향으로 생성된다. 수중 표적은 에피소드 초기에는 랜덤한 주기에 따라 랜덤한 방향으로 기동하게 된다. 이후 소노부이가 수중 표적의 근방에 투하될 시에는, 투하로 인한 진동 및 소음을 인지하여 회피 기동을 실시하게 된다. 첫 접촉 지점에 무인항공기가 도달하게 되면 소노부이를 투하하고, 그 이후는 학습에 따른 액션을 통해 다음 소노부이 투하 지점을 설정하고 이동한다. 그 사이 수중 표적은 예측 불가능한 지점에서 기동을 하고 있으며, 수중 표적이 작전 해역을 이탈하게 된다면 실패로 간주하고 에피소드는 종료된다. 무인항공기가 작전 해역을 이탈하게 되어도, 이 또한 실패로 간주하고 에피소드는 종료된다. 소노부이 투하 시 수중 표적 탐지 여부를 확인하여 3번 이상 수중 표적이 탐지된다면, 이는 성공으로 간주하고 에피소드는 종료된다. 에피소드가 종료되면 또다시 새로운 에피소드 시작되고, 에피소드 반복을 통해 무인항공기는 소노부이 최적 배치를 달성하기 위해 학습된다.

IV. 실험 환경 및 결과

4.1 실험 개요

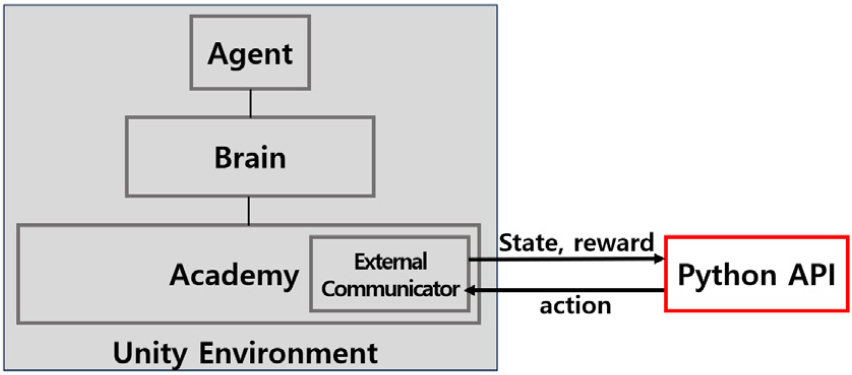
실험 환경 제작을 위해 유니티 게임 엔진을 활용한다. 이를 통해 실제 지형 및 해양 정보를 고려한 가상의 작전 환경 구축이 가능하다. 본 실험에서는 특정하는 해역이 없으므로 지름 1.2 km의 원형의 간단한 작전 환경을 구축하였다. Fig. 6과 같이 우측 상단의 미니맵을 통해 무인기 및 수중 표적의 이동을 한 눈에 파악할 수 있다. 음원은 빨간색, 수신기는 파란색 점으로 표시하여 투하된 소노부이의 위치 및 생성된 탐지 범위를 확인할 수 있다. Fig. 7은 Unity ML-Agents의 시스템 구동 방식이다. Unity ML-Agents는 Academy 클래스를 통해 에이전트들의 상호 작용 환경을 설정하고 관리하며, Brain 클래스는 각 에이전트가 사용하는 학습 알고리즘을 나타낸다. External Communicator를 통해 Unity 환경과 Python API 간의 통신이 이루어지며 에이전트를 훈련하고 테스트할 수 있는 강화학습 시스템을 제공한다.

https://static.apub.kr/journalsite/sites/ask/2024-043-02/N0660430209/images/ASK_43_02_09_F6.jpg

Fig. 6.

(Color available online) Virtual experimental environments built by Unity.

https://static.apub.kr/journalsite/sites/ask/2024-043-02/N0660430209/images/ASK_43_02_09_F7.jpg

Fig. 7.

(Color available online) Operation principles of Unity ML-Agents.

4.2 실험 가정

보다 현실적인 실험을 위해선 소노부이의 탐지 성능 및 다양한 해양 환경 등을 고려해야 한다. 그러나 이는 많은 변수들과 불확실성을 고려해야 하므로 매우 복잡한 일이다. 이에 따라 본 실험에서는 단순한 가정을 통하여 실험을 진행하였다.

무인항공기 및 수중 표적은 2차원으로의 이동만 고려한다. 앞·뒤, 좌·우로의 이동은 가능하나, 상·하 이동은 배제하였다. 수중 표적의 경우, Fig. 6에서 수상으로 떠오른 것으로 나타나지만 실제 실험에서는 잠항했을 때의 경우만 존재하며, 수심에 대한 정보는 고려하지 않는다. 본 연구에서는 Cassini Oval을 적용하여 탐지 범위를 나타낸다. Eq. (1)에서 타원형의 형태를 조절하는 파라미터 b는 소나 방정식에 따라 결정되는데, 적용되는 소나 방정식 내 성능지수는 Table 2와 같이 정의하였다. 신호와 수중 표적 간의 각도에 따라 표적 강도가 달라지므로, Reference [12]에서와 같이 선수와 선미, 선포, 그리고 그 사이 중간 각도에 따라 표적 강도를 달리하고, 그 외 성능지수는 고정한 값으로 두어 실험하였다. 소노부이의 탐지 확률 및 탐지 범위 또한 2차원으로만 고려되며, Exponential 탐지 확률 계산 방식을 통해 단순화하였다. Eq. (4)에서 산출된 탐지 확률이 0.5 이상인 지점을 탐지가 가능한 영역으로 간주하고, 해당 영역에 수중 표적이 존재할 시 수중 표적은 탐지되었다고 간주한다.^[6]

Table 2.

Sonar equation parameters.

Parameters	Values
SL (dB)	156
NL (dB)	65
TS (dB)	Bow/Stern	5
	Intermediate	8
	Beam	10
DI (dB)	3
DT (dB)	0

이동 속력은 무인항공기는 100 kts로 일정하게 설정한다. 수중 표적의 경우 평상시에는 7 kts로 순항하다, 표적의 200 m 내에 소노부이 투하 시에는 회피 기동하여 일정 시간 동안 22 kts로 기동하도록 하였다. 또한 수중 표적의 일정 방위각 내에 소노부이가 투하되었다면 반대 방향으로 침로를 변경하도록 하였다.

다중상태 시스템에서 주로 운용되는 AN/SSQ-125 (source) 모델과 AN/SSQ-101(receiver) 모델의 경우 음원의 비용이 약 20 % 가량 더 비싸다는 것을 고려하여, Eq. (8)의 소노부이 비용에 대한 가중치를 $λ_{1}$ = 0.6, $λ_{2}$ = 0.5로 설정하였다.^[14] 또한 Eq. (6)에서 무인항공기의 최대 이동 범위 $d_{\max}$ 를 600 m로 설정한다. 무인항공기의 속력을 약 100 kts로 가정하고, 이를 통해 다음 투하 지점까지의 이동 시간인 $D_{k}$ 는 0 ~ 12 사이의 값을 가지게 된다. 또한 탐지 성공의 기준을 소노부이 투하 시마다 탐지 여부를 측정하여, 3번 이상 수중 표적이 탐지될 시 성공으로 간주한다. Multi-Static 시스템의 경우 음원과 수신기가 각각 한 개씩은 있어야 탐지가 가능하므로, Eq. (7)에서 최소 소노부이 투하 개수 $r_{\min}$ 은 4가 된다.

4.3 학습

본 실험에서는 PPO 알고리즘을 사용한다. PPO는 정책 최적화 기반의 강화학습 알고리즘으로, Eq. (10)과 같이 나타낼 수 있다. 최적의 정책 𝜃를 구하기 위해 새로운 정책과 이전 정책 간의 비율 $r_{t (θ)}$ 을 사용하여 정책 업데이트를 수행하며, 이를 통해 안정적인 학습을 추구한다. 클리핑 파라미터 𝜖를 통해 이 비율을 특정 범위 내로 제한하여 너무 큰 변화를 방지하고, 안정적이면서도 적절한 정책의 업데이트를 수행한다. 클리핑 이전과 이후의 비율을 어드밴티지 ${\hat{A}}_{t}$ 와 곱하여, 두 값 중 작은 것을 선택하여 클리핑이 적용된 PPO의 손실함수를 정의한다. 학습에 사용된 PPO 알고리즘의 하이퍼 파라미터는 Table 3과 같다.

(10)

L^{C L I P} (θ) = \min (r_{t} (θ) \hat{A_{t}}, c l i p (r_{t} (θ), 1 - ϵ, 1 + ϵ) \hat{A_{t}}) .

Table 3.

State and action vectors of UAVs.

Parameter	Description	Value
Epsilon	Clipping parameter	0.2
Lambda	Depreciation rate	0.95
Beta	Coefficient of entropy bonus	0.01
Batch size	Batch size of sample	64
Buffer size	Size of replay buffer	2048
Num epoch	Number of updates performed for each batch	3
Hidden units	The hidden layer size of the policy neural network	256
Max steps	Maximum number of steps in a learning episode	2000000

3.1장에서 설명한 보상 함수로 3.2장에서의 에피소드의 진행 방식에 따라 학습을 진행하였다. 총 200만 step만큼 학습하였으며, Fig. 8(a)은 에피소드 평균 보상 그래프이다. 보이는 바와 같이 학습 초기에서는 많은 실패로 및 무분별한 소노부이 투하로 인해 낮은 보상 값을 띄고 있다. 그러나 이후 급격히 평균 보상이 상승하고, 점차 증가하여 약 3 정도에서 수렴한다. Fig. 8(b)의 에피소드 평균 step 수 또한 학습 초반에 비해 크게 감소하여 점차 수렴하게 되므로 에피소드 소요 시간이 단축되었음을 알 수 있다. 따라서 무인항공기가 최적 배치 요건에 따라 학습이 성공적으로 이루어졌음을 알 수 있다.

https://static.apub.kr/journalsite/sites/ask/2024-043-02/N0660430209/images/ASK_43_02_09_F8.jpg

Fig. 8.

(Color available online) Results of learning.

4.4 실험 결과

본 실험에서는 강화학습을 적용한 소노부이 배치 방식의 우수성을 검증하기 위해, 격자 패턴과 유전 알고리즘을 적용한 방법과의 실험 결과에 대한 비교를 진행한다.

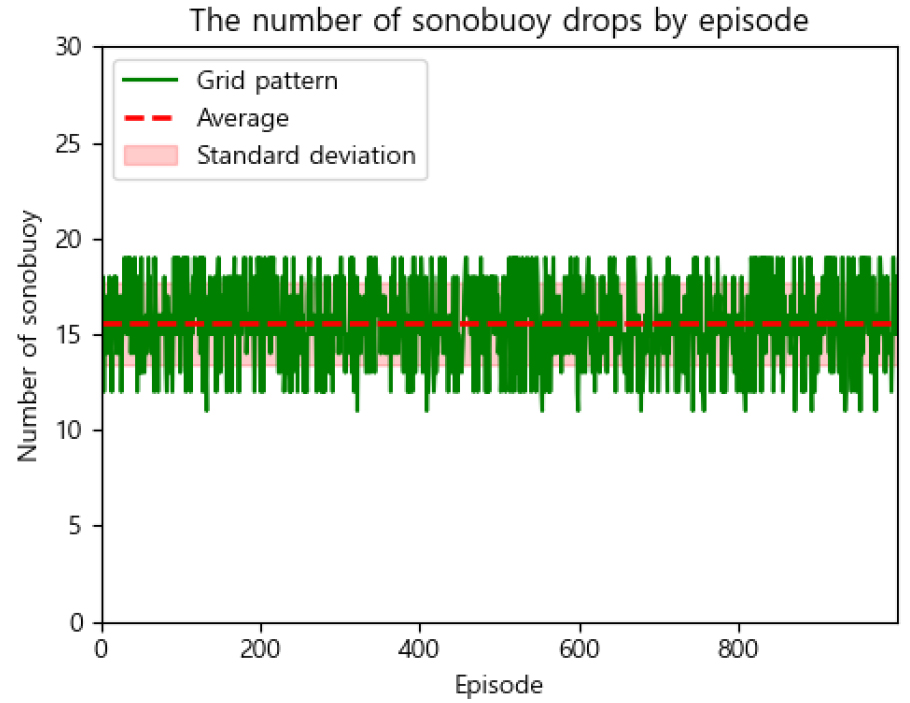
먼저 격자 패턴은 2장에서 설명한 이전 연구에서의 square grid 패턴을 사용하여 본 실험의 작전 해역에 투하되도록 적용하였다. 이는 특정 지점에서 첫 접촉되어, 에피소드 초기 해당 지점으로 이동하는 강화학습의 에피소드 진행 방식과 달리, 정해진 배치 패턴을 순차적으로 투하하도록 하여 에피소드가 진행된다. 그 외 실험 조건에 있어서는 강화학습을 적용한 방식과 동일하며, 1,000번의 에피소드를 진행하여 에피소드마다 소노부이 투하 개수 및 소요 시간, 탐지 성공 여부를 측정한다. Figs. 9와 10은 실험 결과이다. 성공률은 61 %를 기록했으며, 평균 소노부이 투하 개수는 15.5개, 평균 소요 시간은 125.3 s였다.

https://static.apub.kr/journalsite/sites/ask/2024-043-02/N0660430209/images/ASK_43_02_09_F9.jpg

Fig. 9.

(Color available online) Number of sonobuoy drops for each episode of deployment with grid pattern.

https://static.apub.kr/journalsite/sites/ask/2024-043-02/N0660430209/images/ASK_43_02_09_F10.jpg

Fig. 10.

(Color available online) Time required for each episode of deployment with grid pattern.

유전 알고리즘은 2장에서 설명한 관련 연구와 동일한 방법으로, 한 세대 당 30개의 개체로 100세대에 걸쳐 수행하였다. 이를 통해 생성된 배치 패턴을 본 실험의 작전 해역에 투하되도록 적용하였다. 이 또한 격자 패턴을 적용한 방법과 같은 조건으로 실험하고, 1,000번의 에피소드를 진행한다. Figs. 11과 12는 실험 결과이다. 성공률은 69.9 %를 기록했으며, 평균 소노부이 투하 개수는 10.2개, 평균 소요 시간은 78.1 s였다.

https://static.apub.kr/journalsite/sites/ask/2024-043-02/N0660430209/images/ASK_43_02_09_F11.jpg

Fig. 11.

(Color available online) Number of sonobuoy drops for each episode of deployment with genetic algorithm.

https://static.apub.kr/journalsite/sites/ask/2024-043-02/N0660430209/images/ASK_43_02_09_F12.jpg

Fig. 12.

(Color available online) Time required for each episode of deployment with genetic algorithm.

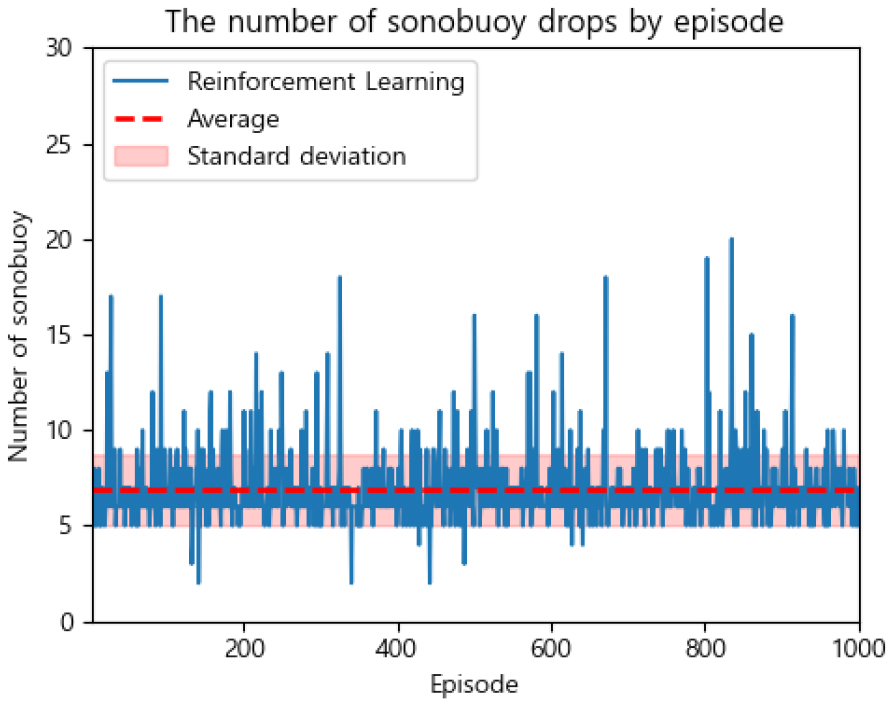
마지막으로, 본 논문에서 제안하는 강화학습을 적용한 배치 방식에서는 학습이 완료된 모델을 통해 학습과 동일한 에피소드 진행 방식에 따라 실험을 진행하였다. 1,000번의 에피소드를 진행한다. Figs. 13과 14는 실험 결과이다. 성공률은 94.8 %를 기록했으며, 평균 소노부이 투하 개수는 6.9개, 평균 소요 시간은 52.3 s였다.

https://static.apub.kr/journalsite/sites/ask/2024-043-02/N0660430209/images/ASK_43_02_09_F13.jpg

Fig. 13.

(Color available online) Number of sonobuoy drops for each episode of deployment with reinforcement learning.

https://static.apub.kr/journalsite/sites/ask/2024-043-02/N0660430209/images/ASK_43_02_09_F14.jpg

Fig. 14.

(Color available online) Time required for each episode of deployment with reinforcement learning.

위 실험의 결과를 아래 Table 4로 정리하였다. 탐지 성공률, 평균 소노부이 투하 개수, 에피소드 평균 소요 시간에 대해 강화학습을 적용한 배치 방식이 타 배치 방식과 비교하여, 가장 우수한 성능을 보였다. 그다음으로는 유전 알고리즘이 우수했다.

Table 4.

Summary of the experimental results.

	Grid^[5]	GA^[6]	RL
Success rate (%)	61.0	69.9	94.8
Average number of drops	15.5	10.2	6.9
Average time required (s)	125.3	78.1	52.3

V. 결 론

본 논문에서는 최소한의 소노부이로 최단 시간 내에 수중 표적을 탐지하는 것을 최적 배치의 요건으로 하였다. 이를 위해 수중 표적의 기동을 고려한 시뮬레이션 환경에서 강화학습을 도입하고, 최적 배치를 위한 보상 함수를 제안하였다. 제안한 방법이 타 배치 방식과 비교했을 때 월등히 우수한 성능을 보였다. 이는 예측 불가능한 수중 표적의 기동에 대해서도 높은 탐지 성공률 및 효율적인 운용이 가능하므로, 강화학습을 적용한 소노부이 배치에 대한 충분한 활용 가능성을 확인할 수 있었다.

그러나 무인항공기 및 수중 표적의 이동을 2차원 상에서만 고려하였으며, 실험 환경에서는 소노부이의 탐지 성능 및 다양한 해양 환경 등의 객관적 정보를 반영하지 않았다. 비록 실험에서 많은 고려 사항을 단순화하였으나, 본 논문에서 얻은 결과를 더 현실적이고 복잡한 실험 환경에서 검증하고 확장하기 위한 연구를 진행할 예정이다. 무인항공기 및 수중 표적의 3차원 이동과 함께 객관적인 정보를 고려한 실험을 수행함으로써, 다양한 상황과 조건에서 최적의 배치를 달성하는 데 있어 높은 성과를 낼 것으로 기대된다.

Acknowledgements

이 논문은 2024년도 국방기술품질원의 재원으로 방산혁신클러스터의 지원을 받아 수행된 연구 일부임(DCL2020L, 2020년 방산혁신클러스터 방산 소재 부품연구실 사업).

References

K. Iqbal, M. Zhang, S. Piao, and H. Ge, "Evolution of sonobuoy through history & its applications: A survey," Proc. IEEE IBCAST, 543-554 (2020). 10.1109/IBCAST47879.2020.9044549

C. Gilliam, B. Ristic, D. Angley, S. Suvorova, B. Moran, F. Fletcher, H. Gaetjens, and S. Simakov, "Scheduling of multistatic sonobuoy fields using multi- objective optimization," Proc. IEEE ICASSP, 3206-3210 (2018). 10.1109/ICASSP.2018.8462152

S. Simakov, "Localization in airborne multistatic sonars," IEEE J. Ocean. Eng. 33, 278-288 (2008). 10.1109/JOE.2008.927916

U. G. Kim and E. J. Kim, "The optimal sonobuoy deployment method using ASW tactics of US Navy" (in Korean), Proc. International Smart Navy Conference, 1-3 (2019).

S. Ozols and M. P. Fewell, "On the design of multistatic sonobuoy fields for area search," DSTO-TR-2563, Defence Science and Technology Organisation, Tec. Rep., 2011.

E. J. Yun, Optimal deployment of multi-static sonobuoys in fixed-wing aircraft using genetic algorithm (in Korean), (Master. thesis, Hanyang University, 2022).

J. I. Kim and M. S. Han, "Research on optimal deployment for autonomous aerial vehicles using virtual environment and DDPG algorithm" (in Korean), JKIIECT 22-4, 15, 152-163 (2022).

L. P. Kaelbling, M. L. Littman, and A. W. Moore, "Reinforcement learning: A survey," JAIR. 4, 237-285 (1996). 10.1613/jair.301

C. M. Taylor, S. Maskell, A. Narykov, and J. F. Ralph, "Joint optimization of sonar waveform selection and sonobuoy placement," Proc. IEEE SSPD, 1-5 (2023). 10.1109/SSPD57945.2023.10256991

C. M. Taylor, S. Maskell, and J. F. Ralph, "Using hybrid multiobjective machine learning to optimise sonobuoy placement patterns," IET Radar, Sonar & Navigation, 17, 374-387 (2023). 10.1049/rsn2.12347

J. Schulman, F. Wolski, P. Dhariwal, A. Radford, and O. Klimov, "Proximal policy optimization algorithms," arXiv preprint arXiv:1707.06347 (2017).

A. Avcioglu, A. Bereketli, and O. F. Bay, "Three dimensional volume coverage in multistatic sonar sensor networks," IEEE Access, 10, 123560-123578 (2022). 10.1109/ACCESS.2022.3223714

M. P. Fewell and S. Ozols, "Simple detection-performance analysis of multistatic sonar for anti-submarine warfare," Australian Government Department of Defence, Tech. Rep., 2011.

US Navy, "Department of defense Fiscal Year (FY) 2019 budget estimates", Defense-Wide Justification Book Vol. 3 of 5, Tech. Rep., 2018.

The Journal of the Acoustical Society of Korea ISSN:1225-4428(Print) 2287-3775(Online) 한국음향학회지

Preview

Optimal deployment of sonobuoy for unmanned aerial vehicles using reinforcement learning considering the target movement

ABSTRACT

MAIN

Fig. 1.

Placement form of square grid (Sources: ●, receivers: ○).

Table 1.

State and action vectors of UAVs.

Fig. 2.

(Color available online) Conceptual diagram of proposed system.

(1)

(2)

(3)

(4)

Fig. 3.

(Color available online) Cassini oval conceptual plot.

(5)

(6)

(7)

(8)

(9)

Fig. 4.

Flowchart of designed reward function.

Fig. 5.

Method of the episode procedure for learning UAV.

Fig. 6.

(Color available online) Virtual experimental environments built by Unity.

Fig. 7.

(Color available online) Operation principles of Unity ML-Agents.

Table 2.

Sonar equation parameters.

(10)

Table 3.

State and action vectors of UAVs.

Fig. 8.

(Color available online) Results of learning.

Fig. 9.

(Color available online) Number of sonobuoy drops for each episode of deployment with grid pattern.

Fig. 10.

(Color available online) Time required for each episode of deployment with grid pattern.

Fig. 11.

(Color available online) Number of sonobuoy drops for each episode of deployment with genetic algorithm.

Fig. 12.

(Color available online) Time required for each episode of deployment with genetic algorithm.

Fig. 13.

(Color available online) Number of sonobuoy drops for each episode of deployment with reinforcement learning.

Fig. 14.

(Color available online) Time required for each episode of deployment with reinforcement learning.

Table 4.

Summary of the experimental results.

Acknowledgements

References