Enhancing the output of ultrasonic sensors for automobiles using acoustic metamaterial

Jeonghun Ahn; KyungJun Song

doi:10.7776/ASK.2025.44.1.022

Preview

Research Article

The Journal of the Acoustical Society of Korea. 31 January 2025. 22-29
https://doi.org/10.7776/ASK.2025.44.1.022

Enhancing the output of ultrasonic sensors for automobiles using acoustic metamaterial

음향 메타물질을 활용한 자동차용 초음파 센서 출력 향상

Jeonghun Ahn¹

KyungJun Song¹^*

안 정훈¹

송 경준¹^*

¹부산대학교 기계공학부

^{*Corresponding Author}

License (open-access, http://creativecommons.org/licenses/by-nc/4.0/):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

본 논문에서는 차량용 초음파 센서에 음향 메타물질을 결합하여 초음파 신호의 음압 레벨(Sound Pressure Level, SPL)을 증가시키는 효과를 연구하였다. 본 연구에서는 초음파 센서에 탈부착이 가능한 형태로 매우 얇은 음향 메타물질을 부착하여, 센서와 메타물질 사이에 형성된 슬릿(slit)과 갭(gap) 구조를 통해 공진 현상을 유도하였다. 이를 통해 초음파 센서의 발진 시 발생하는 음파와 메타물질 구조가 공진 형상을 이루며, 임피던스 매칭 조건에 의해 음압 레벨이 증가하는 원리를 이론적으로 규명하였다. 더불어, 유한요소 해석(Finite Element Analysis, FEA)과 실험 결과를 통해 음향 메타물질을 적용한 경우 초음파 센서의 음압 레벨이 58 kHz 주파수 대역에서 약 10 dB 증가함을 확인하였다. 이러한 신호 강도의 증가로 인해 초음파 센서의 감지 거리가 기존 대비 3배 이상 향상되는 결과를 얻었다. 본 연구는 음향 메타물질을 활용하여 기존 초음파 센서의 성능을 획기적으로 향상시킬 수 있는 가능성을 제시한다.

Keywords

Metamaterial

Ultrasonic sensor

Impedance matching

Signal amplification

키워드

메타물질

초음파 센서

임피던스 일치

신호 증폭

MAIN

I. 서 론
II. 초음파 센서 및 메타물질 적용 해석
III. 메타물질 기반 초음파 센서 성능 유한요소 해석 및 실험 비교
IV. 거리별 초음파 신호 측정 실험
V. 결 론

I. 서 론

초음파 센서는 거리를 측정하기 위한 중요한 도구로, 다양한 산업 분야에서 널리 활용되고 있다. 이 센서는 초음파를 송신한 후, 물체에 반사되어 돌아오는 시간을 측정하여 거리를 계산하는 방식으로 작동한다. 이러한 기술은 특히 자동차 분야에서 많이 사용되며, 주행 중에는 측･후방과 전방의 차량 및 장애물을 감지하고, 주차 시에는 충돌을 방지하는 데 도움을 준다.^[1,2]

하지만 초음파 센서는 공기와의 임피던스 불일치로 인해 초음파 신호가 공기 중에서 전파될 수 있는 거리가 제한적이다. 이로 인해 초음파 센서의 탐지 범위가 짧아지는 문제가 발생하며, 이를 극복하기 위해 다양한 방법이 연구되고 있다.

대중적인 방법으로는 혼을 통해 증폭하는 경우이다. 그러나 혼의 경우 부피가 크고 내구성이 취약하다는 단점이 있다.^[3] 그래서 그 대안 중 하나가 음향 메타물질을 이용해 임피던스를 일치시키는 방법이다.^[4,5,6,7] 음향 메타물질은 인위적으로 설계된 구조로, 초음파 신호가 공기 중에서 더 멀리 전파될 수 있도록 임피던스 차이를 줄여준다. 이를 통해 초음파 신호의 진폭이 크게 증가하고, 결과적으로 기존보다 더 먼 거리까지 초음파가 도달할 수 있다는 장점이 있다.

음향 메타물질을 이용하는 또 다른 큰 장점은 그 소형성과 내구성에 있다. 이 메타물질은 매우 얇은 두께로 설계될 수 있으며, 지름도 초음파 센서와 거의 일치시킬 수 있다. 또한 내구성이 뛰어나기 때문에 차량에 장착하기에 적합하다. 이로 인해 공간 탐지 및 다양한 응용 분야에서 효과적으로 활용될 수 있다.

음향 메타물질을 초음파 센서와 결합하여 초음파 신호의 특성이 어떻게 변화하는지를 분석하고자 한다. 설계된 메타물질의 성능을 유한요소 해석(Finite Element Analysis, FEA)을 통해 이론적으로 검토하였고, 실험을 통해 그 결과를 검증하였다. 이를 통해 메타물질을 적용한 초음파 센서가 신호의 진폭을 크게 증가시켜 탐지 거리를 확장시킬 수 있음을 확인한다.

II. 초음파 센서 및 메타물질 적용 해석

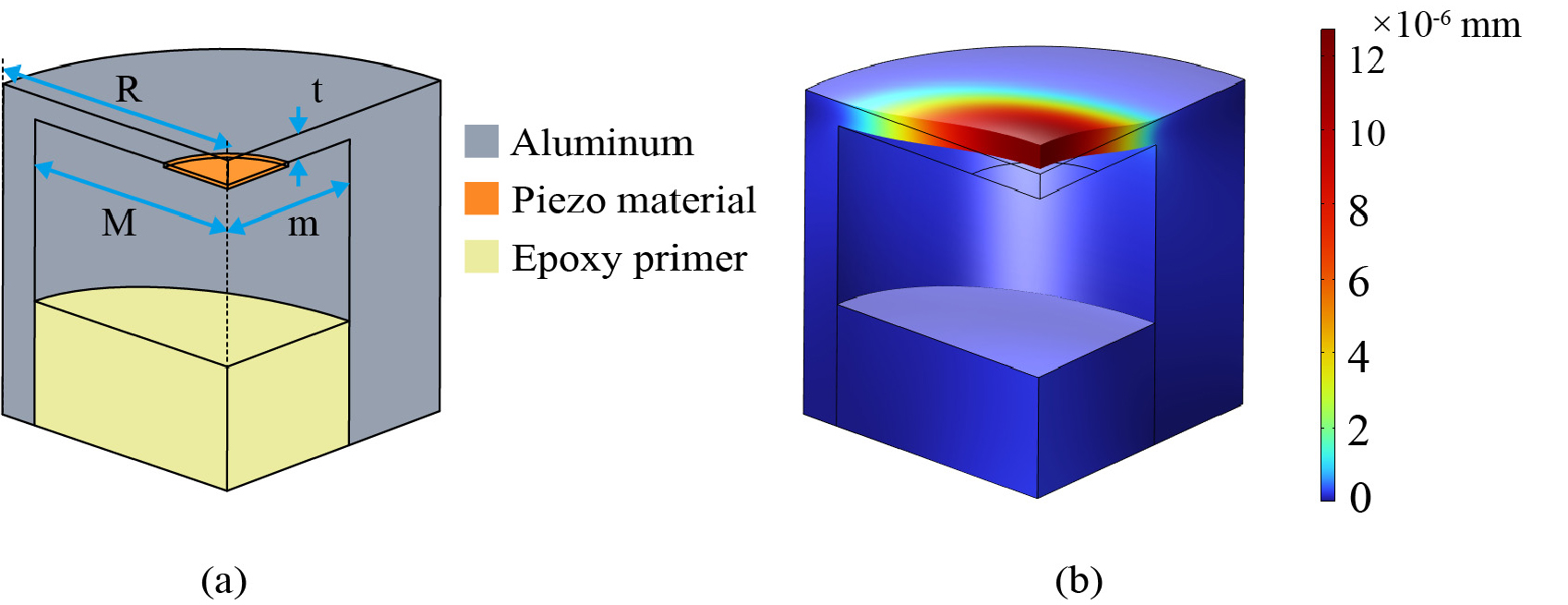
메타물질을 이용하여 자동차용 초음파 센서에 대한 성능을 비교하기 위해서 먼저 기존에 사용되고 있는 58 kHz용 자동차용 초음파 센서에 대한 성능 해석을 수행하였다. Fig. 1(a)는 기존 초음파 센서에 대한 기본적인 도면이고 진동하는 원판부의 외부반경은 R = 7 mm이며 원판의 정합층은 타원형으로 되어있으며 장반경과 단반경의 길이는 M = 6 mm, m = 4 mm이다. 정합층의 두께는 t = 0.6 mm이다. 소재는 알루미늄이며 정합층 내부에는 압전소자가 붙어 있다. 내부 비어 있는 공간의 후면부는 초음파가 전면으로만 진행할 수 있도록 에폭시 프라이머로 채워져 있다.^[1]

https://cdn.apub.kr/journalsite/sites/ask/2025-044-01/N0660440103/images/ASK_44_01_03_F1.jpg

Fig. 1.

(Color available online) (a) 1/4 model of ultrasonic sensor (b) modal analysis result and displacement of ultrasonic sensor at 58 kHz which is the first mode.

Fig. 1(b)에서 볼 수 있듯이 모드 해석 결과 정합층의 고유주파수는 1차 모드에서 약 58 kHz이고 중심 부분에서 진폭이 가장 큰 것을 확인할 수 있다. 알루미늄에 대한 물성치는 Table 1에 첨부하였다. 실제 초음파 센서와 비교했을 때 초음파 센서의 형상 내부 치수를 정확히 알기 어려운 점 등의 이유로 실제 초음파 센서의 형상과는 차이가 있을 수 있다.

Table 1.

Material properties of aluminum.

Property	Value
Density	2700 kg/m³
Young’s modulus	70 GPa
Poisson’s ratio	0.33

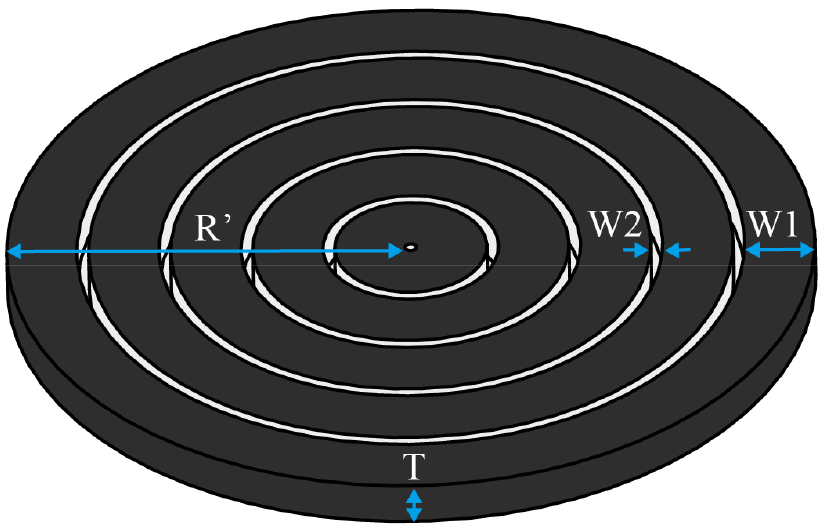
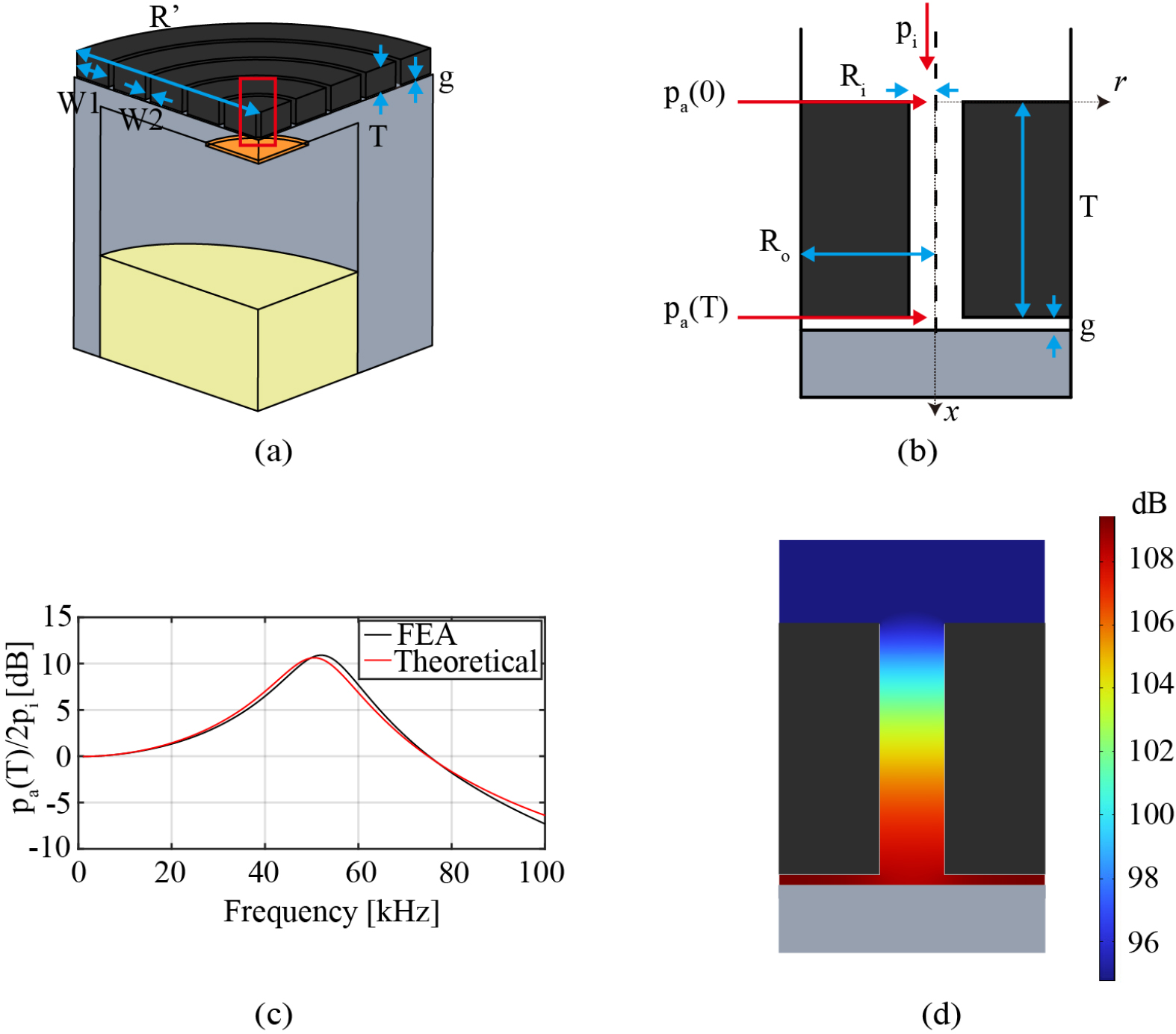
Fig. 2는 메타물질의 형상을 나타낸 것이다. Fig. 3(a)는 메타물질과 Fig. 1(a)의 초음파 센서에 결합된 형태를 나타낸 것이다. 메타물질은 초음파 센서와 갭을 벌린 채 결합된다. 보이는 바와 같이 메타물질은 일정한 패턴을 가지고 반복하는 모양을 가지고 있다. 메타물질의 반경은 R′ = 6.9 mm이고 고리의 폭은 W1 = 1.2 mm이며, 슬릿의 폭은 W2 = 0.2 mm이다. 두께는 T = 0.75 mm이다. 메타물질과 초음파 센서 사이의 갭은 g = 50 µm이다. 이와 같은 패턴 구조를 사용하는 이유는, 초음파 센서가 구동될 때 슬릿과 갭에 의해 형성된 공간이 음향학적 공진 구조를 형성하기 때문이다. 특히, 메타물질의 공진 주파수를 초음파 센서의 진동 공진 주파수와 일치시키면 최대 음향 신호 증폭이 일어나도록 설계되었다. 메타물질이 작동 주파수 58 kHz에 해당하는 파장과 비교하였을 때, 센서 크기에 비해 훨씬 큰 증폭이 일어나기 때문에 매우 얇은 두께를 가지고 설계가 가능하다.

https://cdn.apub.kr/journalsite/sites/ask/2025-044-01/N0660440103/images/ASK_44_01_03_F2.jpg

Fig. 2.

(Color available online) Shape of metamaterial.

https://cdn.apub.kr/journalsite/sites/ask/2025-044-01/N0660440103/images/ASK_44_01_03_F3.jpg

Fig. 3.

(Color available online) (a) Ultrasonic sensor with metamaterial (b) unit cell of metamaterial (c) FEA and theoretical value of sound pressure ratio in the frequency domain (d) SPL distribution of unit cell at 58 kHz.

Fig. 3(b)는 (a)의 붉은 사각형 부분을 확대한 것에 대한 단면도이다. 이를 임피던스 일치 구조라고 한다. 메타물질은 다공성 물질로 간주하여 일정 부분에 대하여 해석을 할 수 있다.^[8,9] $p_{i}$ [Pa]는 입력된 음압이고, $p_{a} (T)$ [Pa]은 슬릿을 통과한 슬릿 내부의 음압이다. R_o= 0.4 mm는 메타물질 임피던스 일치 구조에 대한 반지름, R_i = 0.1 mm는 기존 슬릿인 원형 튜브의 반지름이다. 이러한 일부를 나타낸 이유는 음향 신호 증폭을 해석하기 위함이다. 이 신호 증폭은 음압비인 $p_{a} (T) / 2 p_{i}$ 로 계산된다.^[4]

음압이 들어오는 튜브의 임피던스를 계산하기 위해 특성 음향 임피던스 개념을 이용한다.^[10] Fig. 3(b)에서 제일 윗부분은 단면의 반지름이 $R_{o}$ 인 튜브로 가정한다. 동시에 $R_{o}$ 는 일정 부분에 대한 반지름이다. 이 구간에서의 임피던스를 구하면 $Z_{R} = ρ_{0} c_{0} / π R_{o}^{2}$ 이다. $ρ_{0}$ 는 공기의 밀도이고 $c_{0}$ 는 공기의 음속이다.

슬릿은 반지름이 $R_{i}$ 이고 길이가 $T$ 인 튜브로 고려될 수 있다. $x$ 축 방향으로 $x$ =0인 지점에서의 음압과 체적 속도를 각각 $p_{a} (0)$ , $u_{a} (0)$ 라고 하고 $x = T$ 인 지점에서의 음압과 체적 속도를 $p_{a} (T)$ , $u_{a} (T)$ 라고 정한다. 여기서 $u_{a} (T)$ 의 방향은 $- x$ 방향이다. 각 튜브의 내부에서는 $ρ_{s}$ 는 공기의 밀도, $c_{s}$ 는 공기의 음속이고 $k_{s}$ 는 파수이다.

음압과 체적 속도에 대한 관계식은 임피던스 행렬로 나타낼 수 있다.

(1)

[\begin{array}{l} p_{a} (0) \\ p_{a} (T) \end{array}] = [\begin{array}{l} Z_{11} & Z_{12} \\ Z_{21} & Z_{22} \end{array}] [\begin{matrix} u_{a} (0) \\ u_{a} (T) \end{matrix}],

(2)

Z_{11} = Z_{22} = \frac{ρ_{s} c_{s}}{π R_{i}^{2}} \frac{\cos (k_{s} T)}{j \sin (k_{s} T)},

(3)

Z_{12} = Z_{21} = \frac{ρ_{s} c_{s}}{π R_{i}^{2}} \frac{1}{j \sin (k_{s} T)} .

다음으로 갭에서의 임피던스를 구하기 위해 원통좌표계에서의 파동 방정식을 이용한다.^[11]

(4)

\frac{d^{2} R}{d r^{2}} + \frac{1}{R} \frac{d R}{d r} + k^{2} R = 0 .

이 방정식은 축대칭이므로 $m$ =0인 베셀 방정식이 된다. 시간항을 생략하면, 일반해를 통해 갭에서의 음압은 아래와 같이 주어진다.

(5)

p_{g} (r) = A [J_{0} (k_{g} r) - α N_{0} (k_{g} r)] .

입자 속도는 식 $p = - ρ ϕ_{t}$ 와 $u = \nabla ϕ$ 를 연립하여 $u = \frac{\partial}{\partial r} (- \frac{1}{ρ} \int p d t)$ 로 아래와 같이 주어진다.

(6)

u_{g} (r) = \frac{1}{j ρ_{g} c_{g}} A [J_{1} (k_{g} r) - α N_{1} (k_{g} r)] .

$A$ 와 𝛼는 상수이다. $J_{n}$ 과 $N_{n}$ 은 각각 1, 2종 베셀 함수이고 $j = \sqrt{- 1}$ 이다. $ρ_{g}$ 는 갭에서의 공기의 밀도이고 $c_{s}$ 는 공기에서의 음속이고 $k_{g}$ 는 파수이다. 여기서 가장자리의 경계조건으로 $u_{g} (R_{o}) = 0$ 이므로 $α = \frac{J_{1} (k_{g} R_{o})}{N_{1} (k_{g} R_{o})}$ 이다.

정의에 의해 $Z_{g} = \frac{p_{g}}{S u_{g}}$ 로 주어진다. $S$ 는 단면적이다.

(7)

Z_{g} = \frac{j ρ_{g} c_{g}}{2 π R_{i} g} \frac{J_{0} (k_{g} R_{i}) - α N_{0} (k_{g} R_{i})}{J_{1} (k_{g} R_{i}) - α N_{1} (k_{g} R_{i})} .

임피던스를 계산할 때에는 모든 경계를 hard wall boundary로 고려한다.

$u_{a} (0) = \frac{2 p_{i} - p_{a} (0)}{Z_{R}}$ , $u_{a} (T) = - \frac{p (T)}{Z_{g}}$ 를 Eq. (1)에 대입하여, $p_{a} (0)$ 를 소거하면 아래와 같다.

(8)

\frac{p_{a} (T)}{2 p_{i}} = \frac{Z_{21} Z_{g}}{(Z_{R} + Z_{11}) (Z_{g} + Z_{22}) - Z_{12} Z_{21}} .

파장에 비해 좁은 메타물질의 슬릿과 메타물질과 초음파 센서 사이의 갭 때문에 열점성 효과를 고려해야 한다.^[12] 좁은 갭과 슬릿에서 밀도 𝜌나 체적탄성계수 $K$ 같은 주파수에 의존적인 변수들에 의해 열점성 효과가 계산된다.

(9)

ρ = ρ_{0} {[1 - \frac{\tanh (\frac{h}{2} G_{ρ})}{\frac{h}{2} G_{ρ}}]}^{- 1},

(10)

K = K_{0} {[1 + (γ - 1) \frac{\tanh (\frac{h}{2} G_{K})}{\frac{h}{2} G_{K}}]}^{- 1} .

$ρ_{0}$ 는 공기의 밀도, $K_{0}$ 는 공기의 체적탄성계수이며 $h$ 는 좁은 도파관의 두께이다.

$G_{ρ} = \sqrt{\frac{j ω ρ_{0}}{η}}$ , $G_{K =} \sqrt{\frac{j ω \Pr ρ_{0}}{η}}$ 로 주어진다. $P_{0}$ 는 대기압이다. $K_{0} = γ P_{0}$ 는 자유 공간에서의 공기의 체적탄성계수이다. 공기의 기본적인 특성을 고려해 밀도 $ρ_{0} = 1.23 k g / m^{3}$ , 비열비 𝛾=1.4, 동점성계수 $η = 1.95 \times 10^{- 5} k g m ∙ s^{- 1}$ , 프란틀 수 Pr=0.7로 한다. 공기의 음속은 $c = \sqrt{\frac{K}{ρ}}$ 로 주어진다. 이를 각각 슬릿과 갭의 밀도와 음속에 대해서 대입한다.

Fig. 3(c)는 유한요소 해석 결과값과 매트랩으로 계산한 이론값을 비교한 그래프이다. 그래프에서 $x$ 축 변수는 주파수, $y$ 축 변수는 $20 \log_{10} [p_{a} (T) / 2 p_{i}]$ 이다. 50 kHz 대역에서 가장 큰 값을 나타내고 있다.

Fig. 3(d)는 유한요소 해석에서 58 kHz에서 일정 부분에 대한 각 지점에 대한 음압레벨(Sound Pressure Level, SPL)을 나타냈다. $p_{i}$ 는 최솟값을 가지고 $p_{a} (x)$ 는 $x$ 가 증가할 때마다 증가하는 것을 시뮬레이션 결과를 통해 확인할 수 있다. $p_{a} (T)$ 일 때 최댓값을 나타낸다. 음압레벨은 아래의 식으로 정의된다.^[4]

(11)

S P L = 20 \log_{10} \frac{p_{r m s}}{p_{r e f}} .

위 식에서 $p_{r e f} = 20 μ P a$ 이다.

Fig. 4(a)는 58 kHz에서 메타물질의 기존 형상을 유지한 채, 두께 변화에 따른 음압비를 그래프로 나타낸 것이다. 이 그래프를 통해 0.7 mm와 0.8 mm 사이에서 음압비가 최대값을 보임을 확인할 수 있다. Fig. 4(b)는 58 kHz에서 메타물질과 초음파 센서 사이의 기존 형상을 유지한 상태에서 갭 변화에 따른 음압비를 그래프로 나타낸 것이다. 이 그래프에서는 50 μm에서 음압비가 가장 큰 값을 보였다. 이를 통해 메타물질의 최적 설계를 통해 가장 효과적인 파라미터를 도출할 수 있음을 제시하였다.

https://cdn.apub.kr/journalsite/sites/ask/2025-044-01/N0660440103/images/ASK_44_01_03_F4.jpg

Fig. 4.

(Color available online) (a) FEA and theoretical value of sound pressure ratio in the thickness at 58 kHz (b) FEA and theoretical value of sound pressure ratio in the gap at 58 kHz.

III. 메타물질 기반 초음파 센서 성능 유한요소 해석 및 실험 비교

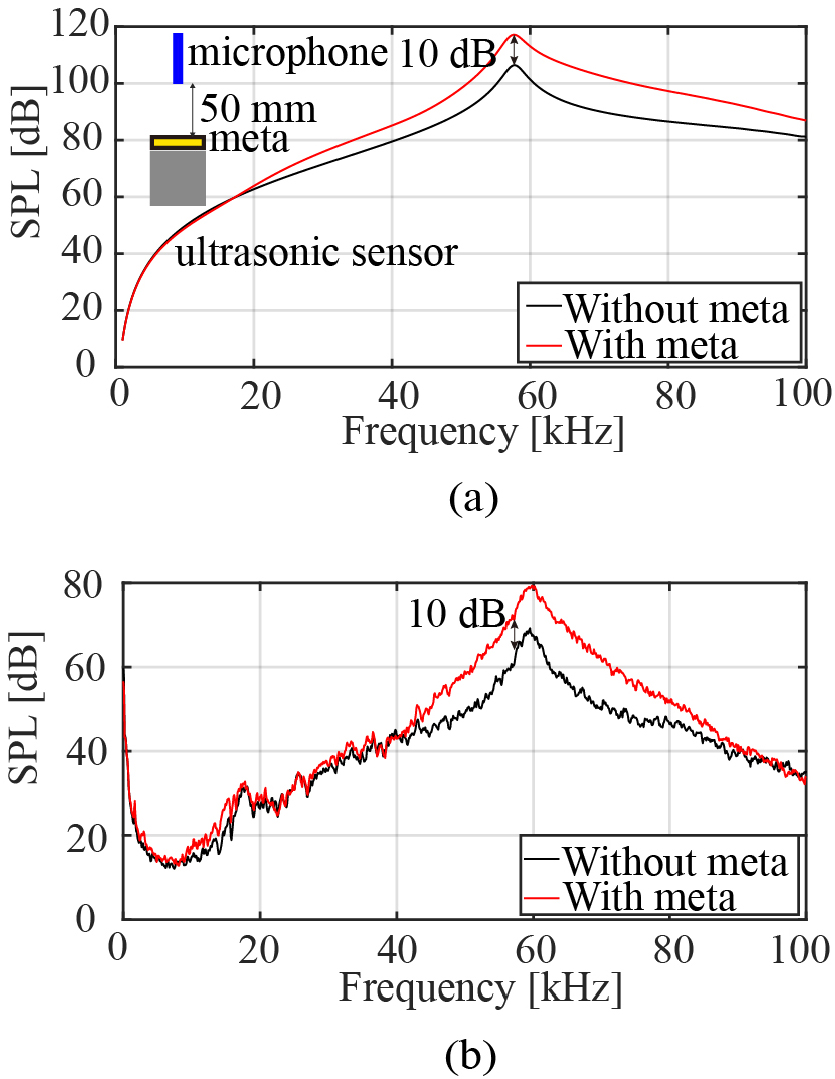
주파수 영역에서의 메타물질 유무에 따른 결과를 보기 위해 메타물질을 적용하여 유한요소 해석을 통해 음향해석을 수행하였다. 적용한 초음파 센서와 메타물질 형상은 Fig. 1(a)와 Fig. 3(a)에서 제시된 구조와 동일하다. 음향해석은 1 kHz부터 100 kHz까지 0.1 kHz 간격으로 조화 해석으로 수행하고 초음파 센서 원판부로부터 50 mm의 반구의 공기 영역을 형성하였다. 알루미늄에는 물성치의 구조감쇠를 활성화하였다. 원판 내부를 1 N으로 가진하여 원판부 중앙으로부터 50 mm 떨어진 지점에서 주파수 영역에 대한 음압레벨을 구하였다. 그리고 메타물질 적용 전후로 해석을 수행하였다. Fig. 5(a)과 같이 음압레벨이 증가한 것을 확인할 수 있다. 그리고 초음파 센서의 고유주파수인 58 kHz에서 가장 높은 SPL이 측정되었다. 메타물질을 적용했을 때 그 증가량은 58 kHz에서 10 dB로 가장 큰 음압레벨을 나타내고 있다. 유한요소 해석 도메인은 Fig. 6와 같이 구성하였다.

https://cdn.apub.kr/journalsite/sites/ask/2025-044-01/N0660440103/images/ASK_44_01_03_F5.jpg

Fig. 5.

(Color available online) (a) Comparison of SPL in frequency domain without and with metamaterial by FEM (b) comparison of SPL without and with metamaterial by experiments.

https://cdn.apub.kr/journalsite/sites/ask/2025-044-01/N0660440103/images/ASK_44_01_03_F6.jpg

Fig. 6.

(Color available online) Schematic of ultrasonic sensor with metamaterial harmonic simulation.

실험은 함수발생기(Keysight 33600A Waveform Generator)로 대역폭이 100 kHz이고 진폭이 10 Vpp인 백색 소음을 연결된 초음파 센서(Multicomp PRO MCUSD 14A58S9RS-30C)에 인가하였다. 그리고 데이터 수집 장비(Siemens Scadas Mobile, SSM)를 마이크로폰(GRAS 46BE 1/4” CCP Free-field Stnadard Microphone Set)에 연결하여 신호를 받아 그래프로 나타내었다. 측정 전, 캘리브레이터(Acoustic Calibrator Type 4231)를 이용해 SPL을 조정하였고 신호 평균화를 1,000회 실시하여 그 데이터를 얻었다. Fig. 7는 실험에서 사용된 초음파 센서와 메타물질이 결합된 초음파 센서다. 실험에서는 메타물질과 초음파 센서 사이의 갭을 만들기 위해 초음파 센서에 얇은 테이프를 진동하지 않는 가장자리에 붙였다. 실험 환경은 실제 자동차가 운용되는 환경을 고려하여 흠음 처리가 안되고 외부 소음이 있는 장소를 선정했다. 실험 신호가 초음파임을 고려하여, 소음에 대한 직접적인 영향은 없는 것을 확인했다. Fig. 5(b)에서 초음파 영역 내, 59 kHz에서 가장 높은 음압레벨을 나타내고 있다. 이는 센서의 설계오차로 추정된다. 메타물질을 적용하면 시뮬레이션과 같이 58 kHz에서 10 dB 증가한 것을 확인할 수 있다. 실험의 경우 시뮬레이션에 비해 SPL값이 낮게 측정된 것을 볼 수 있는데 이는 유한요소 해석에서 모델링한 초음파 센서와 실제 초음파 센서의 형상과 스펙이 다르기 때문이다.

https://cdn.apub.kr/journalsite/sites/ask/2025-044-01/N0660440103/images/ASK_44_01_03_F7.jpg

Fig. 7.

(Color available online) Ultrasonic sensors without and with metamaterial.

IV. 거리별 초음파 신호 측정 실험

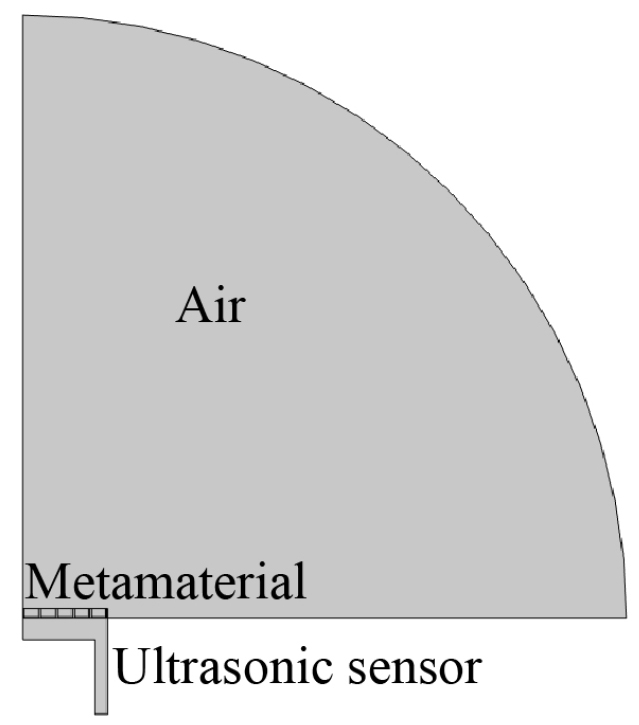
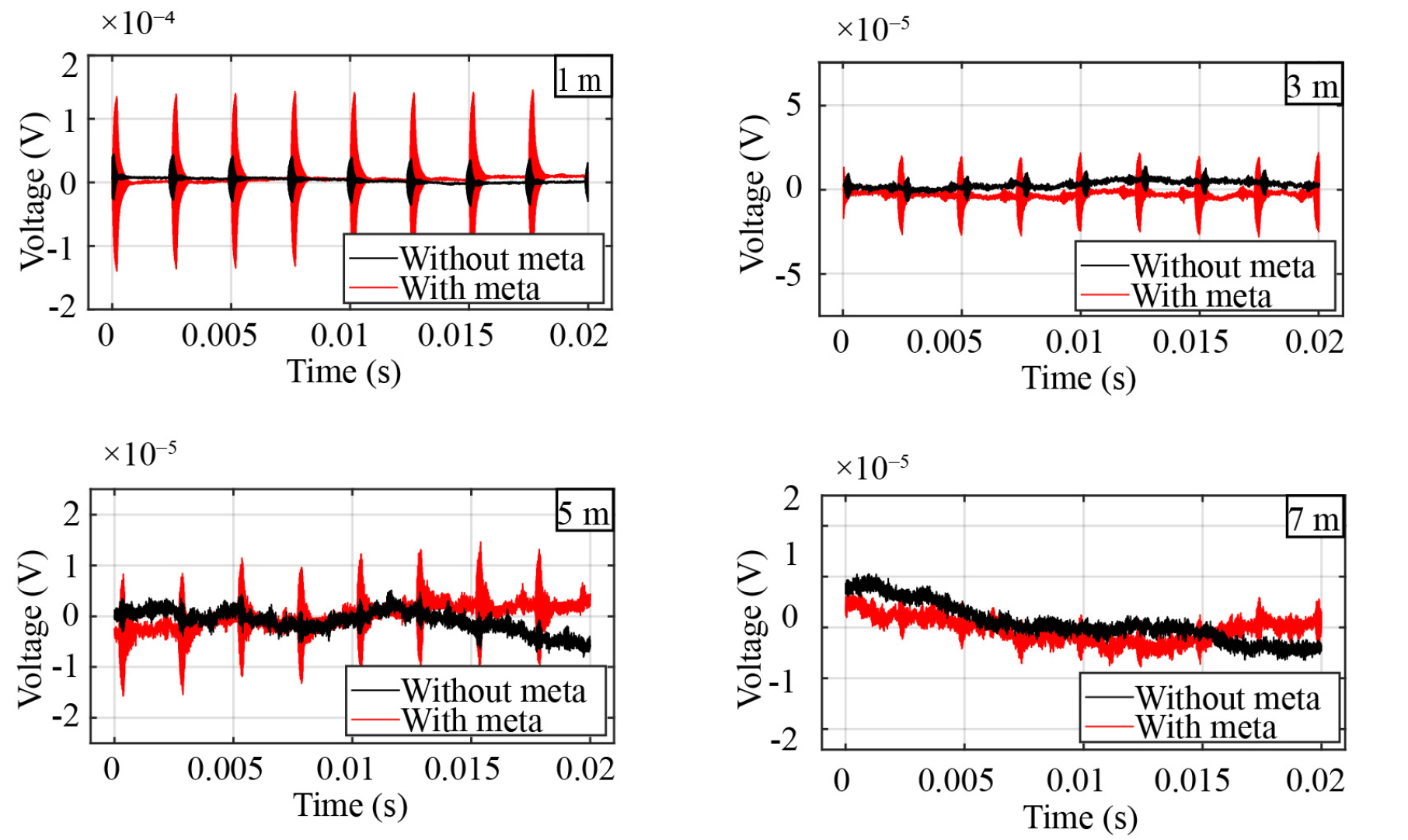
거리에 대한 신호 크기를 확인하기 위해 초음파 센서에서 발생된 신호를 1 m에서 8 m까지 1 m 간격으로 마이크로폰을 통해 측정하였다. 초음파 센서는 함수발생기로 2.5 ms 간격으로 58 kHz 사각파형이 12회 발생하도록 하여 초음파 센서에 인가했다. 진폭은 10 Vpp이다. Fig. 8에서 각각 초음파 센서와 마이크 사이의 거리가 1 m, 3 m, 5 m, 7 m일 때 신호 파형을 앰프(Brüel & Kjær 1704)를 통해 10배 증폭하고 오실로스코프(Teledyne LeCroy HDO4034A)로 나타냈다. 1 m에서 메타물질이 있는 경우 신호 파형이 3.8배 큰 것을 확인할 수 있다. 이를 dB로 환산하면 11.7 dB 정도 증가한 것으로 볼 수 있다. 그리고 3 m, 5 m에서도 3배 이상 증가한 것을 확인할 수 있다. 그리고 7 m에서는 메타물질이 없는 경우 그 신호를 잡음 때문에 확인할 수 없지만 있으면 그 신호를 확인할 수 있다. 메타물질을 적용한다면 측정 거리가 늘어나는 것을 확인할 수 있다.

https://cdn.apub.kr/journalsite/sites/ask/2025-044-01/N0660440103/images/ASK_44_01_03_F8.jpg

Fig. 8.

(Color available online) Comparison of ultrasonic signal in time domain without and with metamaterial by distance each 1 m, 3 m, 5 m, 7 m in experiments.

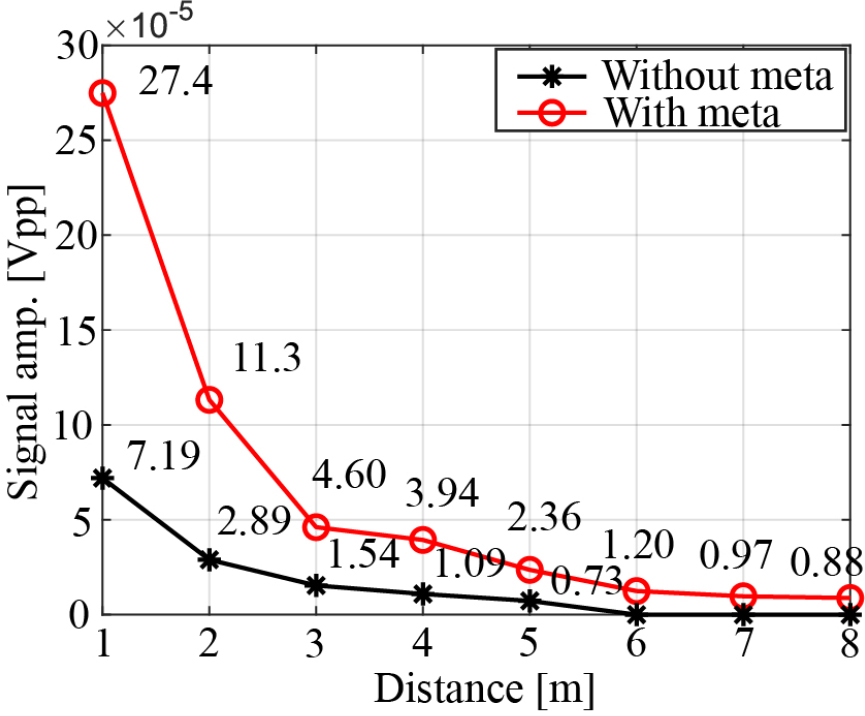
거리에 대한 신호 크기를 Fig. 9에서 그래프로 나타냈다. 신호 대 잡음비는 아래와 같이 주어진다.^[13]

https://cdn.apub.kr/journalsite/sites/ask/2025-044-01/N0660440103/images/ASK_44_01_03_F9.jpg

Fig. 9.

(Color available online) Signal amplitude for distance 1 m to 8 m.

(12)

S N R_{d B} = 20 \log_{10} \frac{V_{S i g n a l}}{V_{N o i s e}} .

메타물질의 유무에 상관없이 거리가 멀어질수록 진폭이 작아지는 것을 확인할 수 있다. 메타물질이 있는 경우에 진폭이 최소 3배 이상 큰 것도 확인할 수 있다. 그래프를 통해 5 m 이상 거리에서도 메타물질이 있으면 거리를 측정할 수 있다는 것을 실험을 통해 확인했다. 메타물질 적용 시 초음파 센서를 이용한 거리 측정 방법이 향상된다고 할 수 있다. 거리에 대한 신호 대 잡음비는 Table 2에 첨부하였다. 실제 운용되는 차량용 초음파 센서의 경우 초음파가 장애물에 반사되어 돌아온다. 그 경우에도 신호가 커진 만큼 회신할 수 있다.

Table 2.

SNR for the distance without and with metamaterial.

Distance (m)	SNR_dB (dB)
Distance (m)	Without meta	With meta
1	23.9	35.6
2	16	27.9
3	10.5	20.1
4	7.55	18.7
5	4.07	14.3
6	0	8.67
7	0	6.54
8	0	5.69

V. 결 론

본 논문에서 메타물질을 초음파 센서에 적용하여 초음파 신호가 증폭하는 것을 확인하였다. 메타물질을 적용하였을 때 음압은 3배 정도 증가하고 음압레벨은 10 dB 증가하는 것을 보였다. 이에 대한 이론적으로 설명하였고 유한요소 해석과 실험에서 이를 입증하였다. 그리고 거리에 대한 실험을 통해 메타물질을 적용한 경우에 최종적으로 더 먼 거리까지 초음파 신호를 송·수신 가능한 것을 보였다.

Acknowledgements

이 논문은 2024년도 산업통상자원부 및 산업기술평가관리원(KEIT) 연구비 지원에 의한 연구임(0014 4500).

References

S. Dixon, L. Kang, M. Ginestier, C. Wells, G. Rowlands, and A. Feeney, "The electro-mechanical behaviour of flexural ultrasonic transducers," Appl. Phys. Lett. 110, 223502 (2017).

10.1063/1.4984239

D. E. Chimenti, "Review of air-coupled ultrasonic materials characterization," Ultrasonics, 54, 1804-1816 (2014).

10.1016/j.ultras.2014.02.00624650685

S. O. Seon and J. O. Kim, "Acousic reception characteristics using horn guide of ultrasonic sensor" (in Korean), Trans. Korean Soc. Noise Vib. Eng. 28, 664-669 (2018).

10.5050/KSNVE.2018.28.6.664

K. Song, J.-H. Kwak, J. J. Park, and S. Hur, "Acoustic metasurfaces for efficient matching of non-contact ultrasonic transducers," Smart Mater. Struct, 30, 085011 (2021).

10.1088/1361-665X/ac085a

K. Song, J. Kim, S. Hur, J.-H. Kwak, S.-H. Lee, and T. Kim, "Directional reflective surface formed via gradient-impeding acoustic meta-surfaces," Sci. Rep. 6, 32300 (2016).

10.1038/srep3230027562634PMC4999803

Z. Li, D.-Q. Yang, S.-L. Liu, S.-Y. Yu, M.-H. Lu, J. Zhu, S.-T. Zhang, M.-W. Zhu, X.-S. Guo, H.-D. Wu, X.-L. Wang, and Y.-F. Chen, "Broadband gradient impedance matching using an acoustic metamaterial for ultrasonic transducers," Sci. Rep. 7, 42863 (2017).

10.1038/srep4286328211510PMC5314352

G. Ma, M. Yang, S. Xiao, Z. Yang, and P. Sheng, "Acoustic metasurface with hybrid resonances," Nat. Mater. 13, 873-878 (2014).

10.1038/nmat399424880731

X. Wang, "Acoustical mechanism for the extraordinary sound transmission through subwavelength apertures," Appl. Phys. Lett. 96, 134104 (2010).

10.1063/1.3378268

X. Liu, X. Zeng, J. Wang, and D. Gao, "Characteristics and applications of acoustic metasurfaces with subwavelength apertures," J. Phys D: Appl. Phys. 50, 405108 (2017).

10.1088/1361-6463/aa81b2

D. T. Blackstock, Fundamental of Physical Acoustics (Wiley, New York, 2000), pp. 46-48.

M. W. Cho, S. H. Hwang, J.-Y. Jang, S.-k. Hwang, K. J. Cha, D. Y. Park, K. Song, and S. M. Park, "Beyond the limits of parametric design: Latent space exploration strategy enabling ultra-broadband acoustic metamaterials," Eng Appl. Artif. Intell. 133, 108595 (2024).

10.1016/j.engappai.2024.108595

N. Jiménez, V. Romero-García, V. Pagneux, and J.-P. Groby, "Quasiperfect absorption by subwavelength acoustic panels in transmission using accumulation of resonances due to slow sound," Phys. Rev. B, 95, 14205 (2017).

10.1103/PhysRevB.95.014205

S. William, Data and Computer Communications (PEARSON, Boston, 2014), pp. 99-101.

The Journal of the Acoustical Society of KoreaISSN:1225-4428(Print) 2287-3775(Online)한국음향학회

Preview

Enhancing the output of ultrasonic sensors for automobiles using acoustic metamaterial

ABSTRACT

MAIN

Fig. 1.

(Color available online) (a) 1/4 model of ultrasonic sensor (b) modal analysis result and displacement of ultrasonic sensor at 58 kHz which is the first mode.

Table 1.

Material properties of aluminum.

Fig. 2.

(Color available online) Shape of metamaterial.

Fig. 3.

(Color available online) (a) Ultrasonic sensor with metamaterial (b) unit cell of metamaterial (c) FEA and theoretical value of sound pressure ratio in the frequency domain (d) SPL distribution of unit cell at 58 kHz.

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

Fig. 4.

(Color available online) (a) FEA and theoretical value of sound pressure ratio in the thickness at 58 kHz (b) FEA and theoretical value of sound pressure ratio in the gap at 58 kHz.

Fig. 5.

(Color available online) (a) Comparison of SPL in frequency domain without and with metamaterial by FEM (b) comparison of SPL without and with metamaterial by experiments.

Fig. 6.

(Color available online) Schematic of ultrasonic sensor with metamaterial harmonic simulation.

Fig. 7.

(Color available online) Ultrasonic sensors without and with metamaterial.

Fig. 8.

(Color available online) Comparison of ultrasonic signal in time domain without and with metamaterial by distance each 1 m, 3 m, 5 m, 7 m in experiments.

Fig. 9.

(Color available online) Signal amplitude for distance 1 m to 8 m.

(12)

Table 2.

SNR for the distance without and with metamaterial.

Acknowledgements

References