I. 서 론

최근 수중음향통신은 해양 환경 모니터링, 해양 탐사 및 군사적 임무 등에서 많은 관심을 받고 있다.^[1,2] 그러나 수중 음향 채널은 낮은 전파 속도, 다중경로 전달, 주파수 선택적 페이딩, 좁은 대역폭, 빠른 시변동성 등의 문제를 갖고 있다. 이러한 통신 장애 요인들을 극복하는 것이 수중음향통신 분야에서의 도전적인 과제이지만 이와 함께 전송 거리 증대에 대한 관심도 꾸준하게 이어져 왔다. 수중음향통신에서 전송 거리가 100 km를 넘으면 초장거리 전송으로 분류되며,^[3] 이러한 경우에는 수신부에서의 신호대잡음비(Signal-to-Noise Ratio, SNR)이 크게 낮아지므로 이를 보완하기 위한 방법들이 적용되기도 한다. 이 가운데 몇몇 대역확산 기술은 원래 은밀한 통신^[4]을 목적으로 하지만 신호 설계를 적절하게 한다면 낮은 SNR을 갖는 환경에서 유용한 기술^[5]이며, 직접 수열 대역확산 방식과 처프 대역확산 방식 등이 포함된다. 또한 수신부를 배열 센서로 구성하여 시역전 처리나 빔 형성 기법을 적용하여 추가적인 처리 이득을 얻기도 한다.

장거리 수중음향통신에 대한 대표적인 연구를 살펴보면 Liu et al.^[6]은 Double Differentially coded Spread Spectrum(DD-SS) 방식으로 태평양에서 550 km의 초장거리 수중음향통신 실험을 수행하였다. 수신기는 64개의 수평 배열을 이루고 있었으며, 빔 형성 기법을 적용하여 전송률이 6.4 bit per second(bps)일 때 비트 오류율 0.04의 결과를 발표하였다. Shimura et al.^[7]은 일본의 오가사와라 섬 인근 해역에서 400 bps의 전송율로 16-Quadrature Amplitude Modulation(QAM) 신호를 최대 600 km까지 보내는 초장거리 수중음향통신 실험을 진행하였다. 이 때 18개의 수직 선배열 수신기와 수동 시역전 처리 등의 방법이 적용되었다. Zhao et al.^[8]은 남중국 해역의 80 km 거리에서 66.7 bps로 전송 실험을 수행하였으며, 12개의 수직 선배열로 구성된 수신단에서는 시역전 처리 방식의 변형인 Composite Channel Virtual Time Reversal Mirror (CCVTRM) 방식을 적용하였다. 최근에는 이스라엘 북부 연안 지중해에서 적응형 변조 기법을 이용하여 최대 100 km의 전송 실험을 한 결과가 발표되었다.^[9] 국내에서는 동해의 23 km 송수신 거리에서 16-QAM 방식과 시역전 처리 방법 등을 적용하여 최대 2,731 bps의 전송 속도로 해상실험을 수행한 결과가 보고되었으며,^[10] 같은 실험에서 24 bps의 중첩된 직접 수열 대역확산 방식으로 전송한 실험 결과가 발표되었다.^[11] 장거리 수중 네트워크 구현과 관련하여 노드 사이의 거리가 30 km인 경우 100 bps 통신이 가능한 수중통신 모뎀이 소개되기도 하였다.^[12] 또한 동해의 90 km 거리에서 Frequency Shift Keying(FSK) 및 처프 대역확산 방식으로 전송 실험을 수행한 결과^[13]가 발표되었지만 국내의 경우 소요 비용이나 장비 등의 문제로 인해 100 km 이상의 초장거리에서 대역확산 방식의 수중음향통신 실험 결과를 보고한 사례는 아직 없다.

본 논문에서는 동해에서 8개의 수직 배열 센서를 이용하여 160 km 거리에서 변형된 직접 수열 대역확산 방식 가운데 하나인 다중 코드 대역 확산(Multi-Code Spread Spectrum, MCSS) 방식과 처프 대역확산 방식을 이용하여 통신을 수행한 해상실험 결과를 제시하고, 수신부에서의 낮은 신호대잡음비 문제를 보완하기 위해 각 수신 센서의 출력 신호들을 조합하여 다이버시티 처리한 결과를 제시한다.

본 논문의 구성은 다음과 같다. 제 2장에서 해상실험 구성과 적용된 통신 방식에 대해서 설명하고, 제 3장에서는 해상실험 결과를 비부호화된 비트 오류율 관점에서 제시한다. 이 때 각 수신 채널 별 결과뿐만 아니라 다이버시티 기법을 적용한 결과도 함께 제시한다. 마지막으로 결론은 제4장에서 서술한다.

II. 해상실험 설계

2.1 실험 구성 및 환경

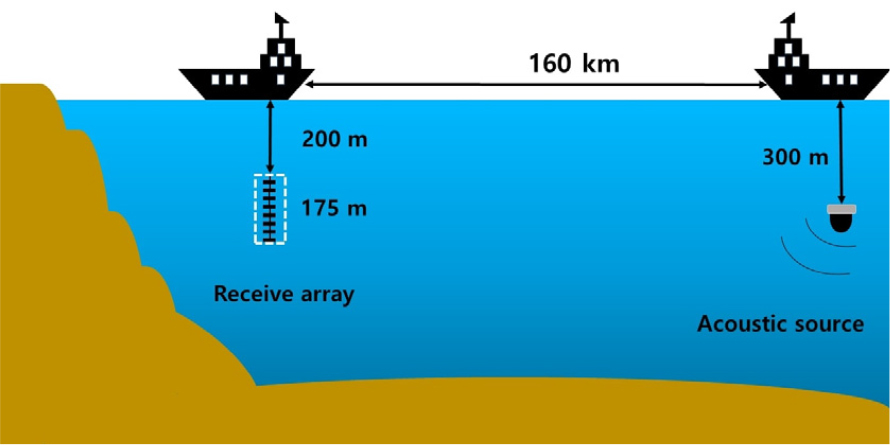
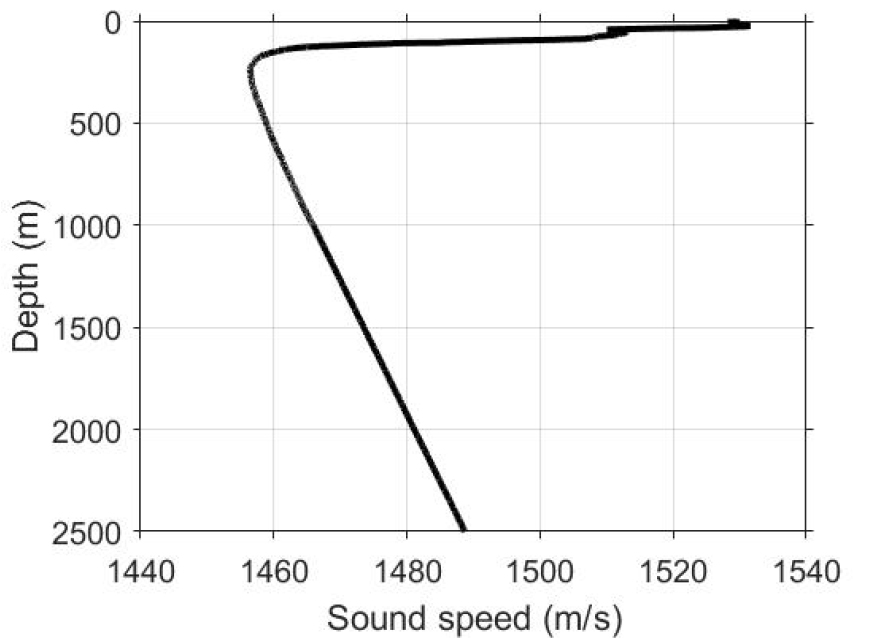
해상실험은 2021년 9월말 동해(포항 동방 해역 ~ 울릉도 인근 해역)에서 수행되었다. 실험에는 한국해양과학기술원의 이어도호와 국방과학연구소의 연구시험선이 활용되었다. 이어도호에서는 송신장치를 운용하였고, 연구시험선에서는 수신 장치를 운용하였다. Fig. 1은 해상실험의 개략도로서 음원과 수직 배열 센서의 깊이, 음원과 수신기 사이의 거리를 표현한 것이다. 송신기인 음원과 수신 배열 사이의 거리는 약 160 km이었고, 수신기 수심은 약 200 m ~ 375 m이었다. 전송되는 신호는 음향축의 깊이, 음원 깊이 및 수신 배열의 설치 범위에 따라 전달 손실의 정도가 다양해진다. 전달 손실이 증가한다는 것은 곧 SNR의 감소로 이어지며, 이는 통신 성능에 영향을 미친다. 따라서 전달 손실을 최소화하기 위해 음향 채널을 사용하는 것이 필요하다. 이를 위해 먼저 음속 분포를 측정하였는데 Fig. 2에 나타낸 것과 같이 수신 배열이 있는 위치에서 측정한 음속 분포에서는 수심 약 300 m 주변에서 음향축이 형성되었다. 이에 따라 해상실험에서는 음원의 깊이를 약 300 m로 유지하였다.

Fig. 1.

(Color available online) Schematic of sea trial.

Fig. 2.

Measured sound speed profile.

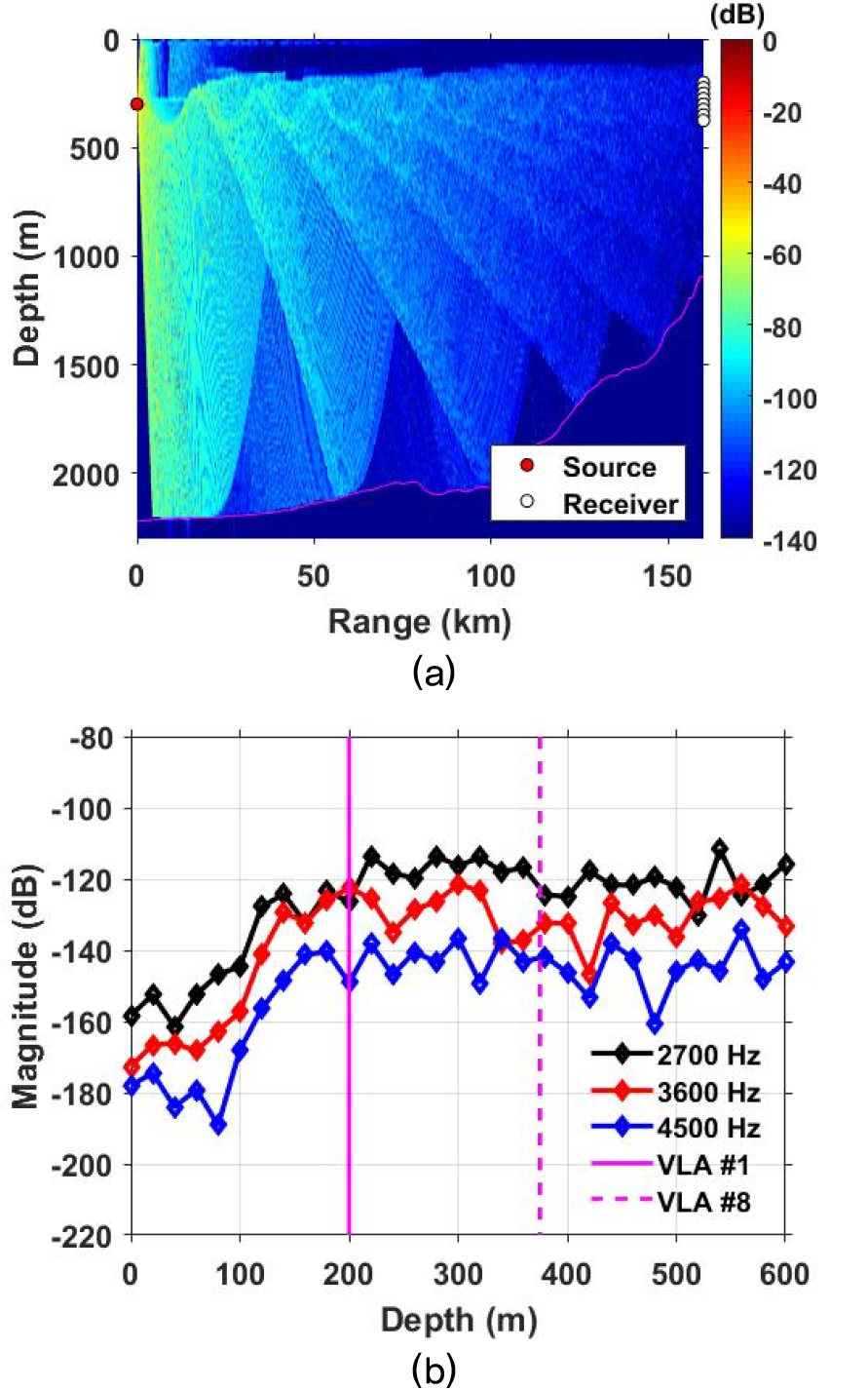
Fig. 3은 측정된 음속 분포와 수중 음파 전파 모델을 이용하여 전달 손실을 계산한 결과이다. Fig. 3(a)는 3,600 Hz에서의 전달 손실을 나타낸 것이며, Fig. 3(b)는 160 km에서 2.7 kHz, 3.6 kHz 및 4.5 kHz의 전달 손실을 수심에 따라 나타낸 그림이다. 왼쪽의 세로 실선과 오른쪽의 세로 점선 사이의 구간이 8개의 수신기가 배치된 영역이다. 전체적으로 수신기들이 위치한 수심에서의 전달 손실은 약 –115 dB에서 약 –150 dB 사이에 분포하여 그 편차가 30 dB 이상이었다. 또한 3.6 kHz에서는 세로 점선과 가까운 약 330 m 보다 깊은 수심에서 값이 약 18 dB 정도 급격하게 감소하는 것을 보이고 있다. 이처럼 수신 배열이 설치된 위치에서는 음원으로부터의 거리가 너무 멀어서 큰 전달 손실이 나타났으며, 160 km 이내의 중간 영역에서는 음영지역과 수렴지역이 확인되었다.

Fig. 3.

(Color available online) (a) Transmission loss at 3,600 Hz, (b) transmission loss at 160 km.

신호의 송신을 위한 프로젝터로는 상용 음원을 사용하였고, 중심 주파수가 3,600 Hz이다. 실험 당시 음원의 준위는 190 dB 이상으로 하였다. 수신기는 8개의 수직 배열 센서들을 사용하였으며, 8개의 센서가 25 m 간격으로 배열을 이루었다. 이 수신 배열은 부이에 달려 해상에 투하되었으며, 수신 신호는 100 kHz의 샘플링 주파수로 저장되었다.

2.2 전송 신호 설계

실험에 적용된 2가지 대역확산 방식은 변형된 직접수열 대역확산 방식 가운데 하나인 다중 코드 대역 확산 방식과 처프 대역확산 방식이다. 일반적인 직접수열 대역확산 방식에서는 정보 비트에 Pseudo Noise(PN) 시퀀스를 곱하여 확산 이득을 얻는데 확산된 신호에 Phase Shift Keying(PSK) 변조 등을 사용한다. 여기서 PN 시퀀스 안의 하나의 펄스를 칩이라 한다. 만약 이진 PSK 변조를 사용한다면 비트와 심볼은 동일하고, 결국 이는 하나의 비트에 여러 개의 칩을 곱하는 형태가 된다. 이 칩의 속도를 칩율이라고 하고, 그 단위는 보통 chip per second(cps)로 표기한다. 다중 코드 대역 확산 방식은 M-ary Spread Spectrum(MSS) 방식이라고도 하며, 대역확산을 위해 하나가 아닌 다수의 직교 PN 시퀀스를 할당하여 변조하는 방식으로 각 PN 시퀀스들은 하나의 심볼을 표현한다.^[14,15] 예를 들어 하나의 심볼이 3-bit로 구성된 경우 8가지의 직교 PN 시퀀스를 사용한다. 다중 코드 대역 확산은 동일한 대역폭에서 기존의 직접수열 대역확산 방식보다 높은 전송율을 얻을 수 있다. 다중 코드 대역 확산 방식은 다수의 PN 시퀀스를 사용하기 때문에 직접수열 대역확산 방식보다 더 강한 가로채기 저항성을 갖는다. 수신기는 복조할 정합 필터와 동일한 파형들의 세트로 구성된다.

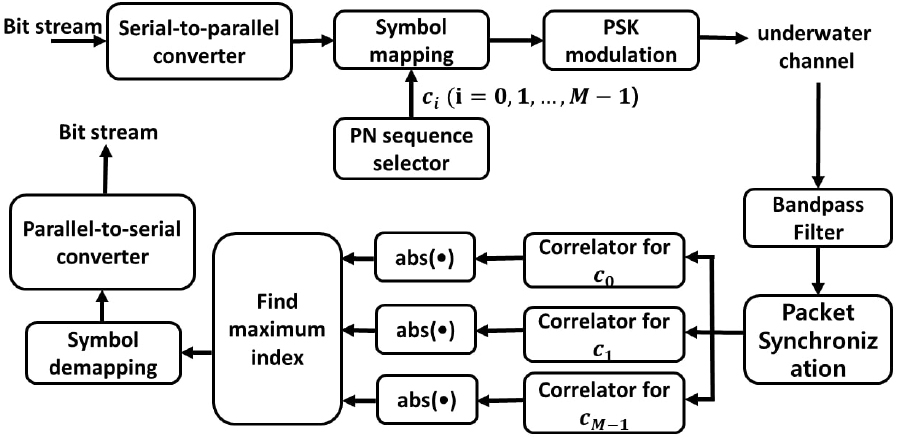
Fig. 4에 나타낸 다중 코드 대역 확산 방식의 송신부에서는 먼저 전송 비트 열에 대해 직렬-병렬 변환을 수행한 다음 입력 비트 세트에 따라 PN 시퀀스 선택기가 적절한 PN 시퀀스를 선택한다. 이후 PN 시퀀스에 대해 PSK 변조가 수행되어 전송 신호를 생성한다. 다중 코드 대역 확산 방식에서 사용하는 확산 PN 시퀀스를 c0,c1,⋯cM-1이라고 가정하고, 이들 각각 N개의 칩으로 구성되어 있다고 가정하자. 다중 코드 대역 확산 방식에서는 하나의 심볼마다 각각에 해당하는 PN 시퀀스 값을 할당한 뒤 변조된다.

Fig. 4.

Block diagram of MCSS transmission.

수신부에서는 먼저 대역 통과 필터링을 수행한 다음 프레임 및 주파수 동기화를 수행한다. 이후 심볼 단위로 적용된 직교 PN 시퀀스의 수만큼의 다수의 상관기로 전달되며, 원래의 이진 정보는 이들 상관기 가운데 최대 출력을 갖는 인덱스를 찾아 획득한다. 다중 코드 대역 확산 방식은 동일한 길이의 M개의 직교 PN 시퀀스를 사용하기 때문에 이산 상관기들의 뱅크로 설정된다.

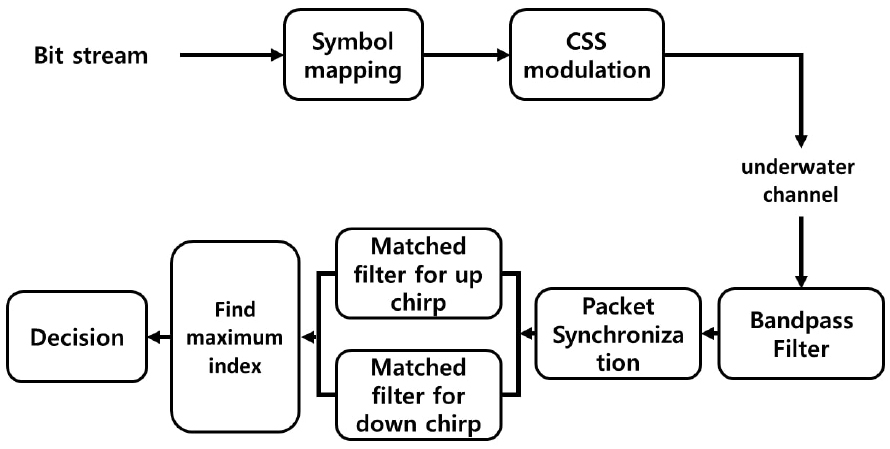
처프 대역확산 방식의 신호는 Fig. 5의 블록도와 같은 과정으로 처리되었다. 처프 대역확산 방식에서는 다음의 식들로 표현되는 처프 신호를 이용한다.

Fig. 5.

Block diagram of CSS transmission.

Eqs. (1)과 (2)에서 fmin는 최소 주파수, fmax는 최대 주파수를 의미한다. Eq. (1)은 초기 주파수 fmin을 시작으로 fmax까지의 상향 주파수 변화를 가지는 신호를 표현하고, Eq. (2)는 초기 주파수 fmax을 시작으로 fmin까지의 하향 주파수 변화를 갖는 신호를 표현한다. 즉, 처프 대역확산 방식에서는 처프 신호에서 변화하는 주파수의 기울기 부호에 정보를 담는 방식이다. 예를 들어, 이진 값 “0”은 상향 주파수 변화를 갖는 처프 신호, 이진 값 “1”은 하향 주파수 변화를 갖는 처프 신호로 각각 할당할 수 있다.^[13,16]

실험에 사용된 패킷의 구성을 Fig. 6에 나타내었다. 신호를 확인하고 대략적인 시작점을 찾기 위해 프로브 신호의 역할을 하는 처프 신호를 0.5 s 길이로 전송하였고, 상관 함수를 이용하여 데이터 프레임의 정확한 시작점을 찾기 위해 프리앰블은 255 비트의 m-sequence를 연속적으로 2회 반복하여 510 비트를 전송하였다. 프로브와 프리앰블 사이에는 0.5 s의 보호 구간을 두었다. 이후 데이터 구간이 이어지고, 마지막으로 포스트앰블로써 255 비트의 m-sequence를 삽입하였다. 프리앰블과 포스트앰블은 모두 데이터 구간과는 별도로 설계되어 전송률이 1,000 bps인 이진 PSK의 방식으로 변조되었으며, 대역확산이 적용되지 않았다.

Fig. 6.

Packet structure.

데이터 구간에서 다중 코드 대역 확산 방식과 CSS 방식 모두 336 비트를 전송하였다. 다중 코드 대역 확산 방식의 신호는 3개의 비트를 하나의 심볼로 구성하여 심볼 전송율은 10 symbol per second(sps), 비트 전송율은 30 bps로 하였다. 3개의 비트를 하나의 심볼로 구성하였기 때문에 8개의 직교 PN 시퀀스가 적용되었으며, 실험에서는 127 비트 길이의 Walsh 코드를 사용하였다. 심볼들은 이진 PSK 변조 되었는데 이 과정에서 펄스 성형을 위하여 기본적인 raised cosine 필터를 사용하였으며, 이에 적용된 roll-off 계수는 0.5로 하였다. 그러므로 다중 코드 대역 확산 방식의 전체 패킷 길이는 약 13 s 정도가 되었다.

처프 대역확산 신호의 경우 전송율은 100 bps로 하였고, 중심 주파수는 3,600 Hz로 설정하였다. 처프 신호의 최소 주파수 fmin은 2,700 Hz, 최대 주파수 fmax는 4,500 Hz로 하였다. 따라서 CSS 방식에서의 전체 패킷의 길이는 5 s 정도가 되었다.

III. 실험 결과

3.1 채널 임펄스 응답

해상실험 기간 중 날씨는 대체로 양호하였으나 실험 기간 직전 나쁜 해상 상태의 여파로 초반에 비교적 높은 파고를 나타내었으며, 수신 배열 인근에 돌고래 군집과 항행 선박 등의 다수의 소음원이 불규칙적으로 존재하였다. 특히, 원인을 알 수 없는 주기적인 클릭음은 임펄스 형태의 광대역 신호로써 수집된 데이터의 분석을 어렵게 하였다. 또한 전달 손실이 커서 각 수신 채널에서의 신호대잡음비는 시점에 따라 편차는 있으나 평균 약 –11.55 dB로 계산되었다.

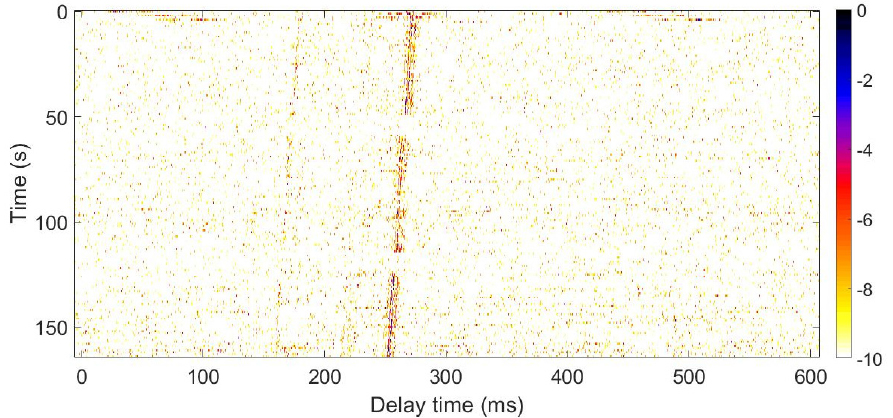
통신 신호 전송에 앞서 채널의 전달 특성을 측정하였는데 이를 위해서 선형 주파수 변조된 신호를 일정한 시간 간격으로 반복 송신하였다. 신호의 반송파 주파수는 3,600 Hz, 대역폭은 1,800 Hz, 핑과 핑 사이의 간격은 1 s, 각각의 핑 길이는 0.128 s로 하였다. 수신단에서의 채널 임펄스 응답 특성은 Fig. 7과 같이 측정되었다. 그림은 매우 낮은 신호대잡음비 환경으로 인하여 전체적으로 선명하지는 않으나 대체적인 전달 경로는 확인할 수 있다. 음원이 의도적으로 이동하지는 않았지만 조류에 따른 느린 이동으로 인하여 시간에 따른 기울기의 변화가 있으며, 이는 그림이 150 s 이상의 구간에서 표현한다는 점을 감안하면 매우 작은 도플러 주파수 천이 값이다. 또한 다중경로 전달이 나타나고 있음을 확인할 수 있다.

Fig. 7.

(Color available online) Channel impulse response as a function of the delay time.

3.2 다이버시티 기법을 포함한 통신실험 결과

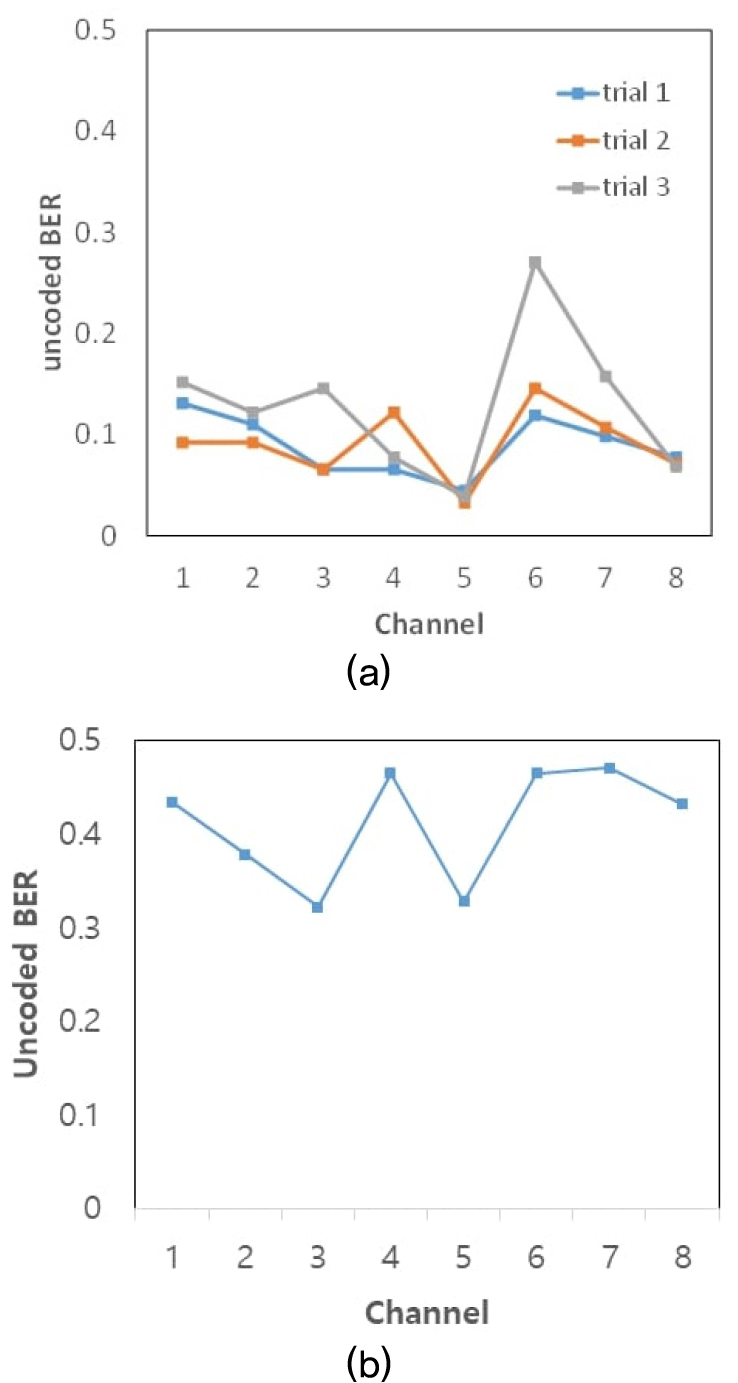
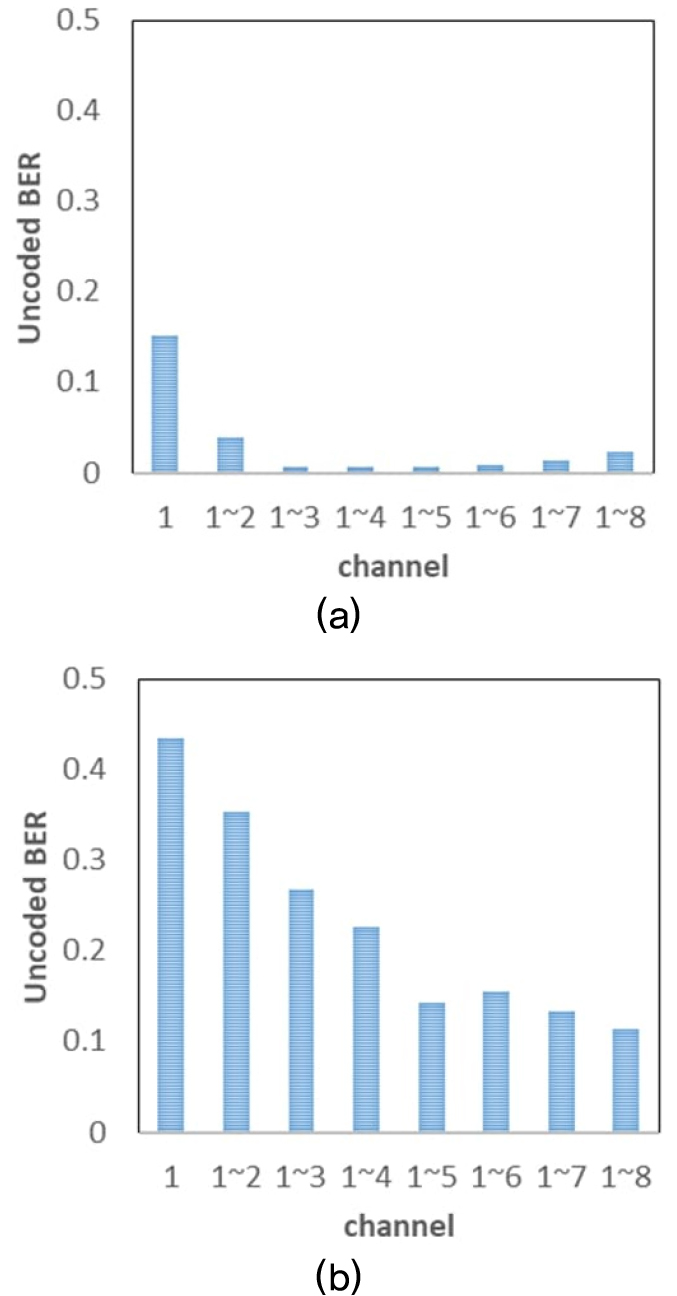
8개 모든 채널마다 채널 부호화 기법을 고려하지 않은 비부호화된 비트 오류율에 대한 결과를 Fig. 8에 나타내었다. Fig. 8(a)는 수신 채널 별로 다중 코드 대역 확산 방식에 대한 결과이며, Fig. 8(b)는 처프 대역확산 방식의 결과이다. 1번 채널이 해수면과 가장 가까이 위치한 채널이며, 8번 채널이 가장 깊은 수심에 위치한 채널이다. 다중 코드 대역 확산 방식은 3회의 반복 실험이 진행되었으나 처프 대역확산 방식은 실험 시점에 해양 생물과 같은 외부 소음원에 의하여 수신 신호가 강하게 오염되어 오직 1회 실험 분량만 분석이 가능하였다. 결과에서 비부호화된 비트 오류율은 다중 코드 대역 확산 방식의 경우 최소 0.0387부터 최대 0.2708까지 나타났으며, 처프 대역확산 방식은 최대 0.47까지 나타났다. 결과적으로 2가지 방식 모두 높은 비트 오류율을 나타내었으며, 이는 기본적으로 긴 전송 거리에 따른 전달 손실 증가 및 신호대잡음비 저하에 기인한다. 따라서 단일 채널만으로는 대부분 정보 전송이 적절하지 못하였다.

Fig. 8.

(Color available online) Uncoded BER, (a) MCSS, (b) CSS.

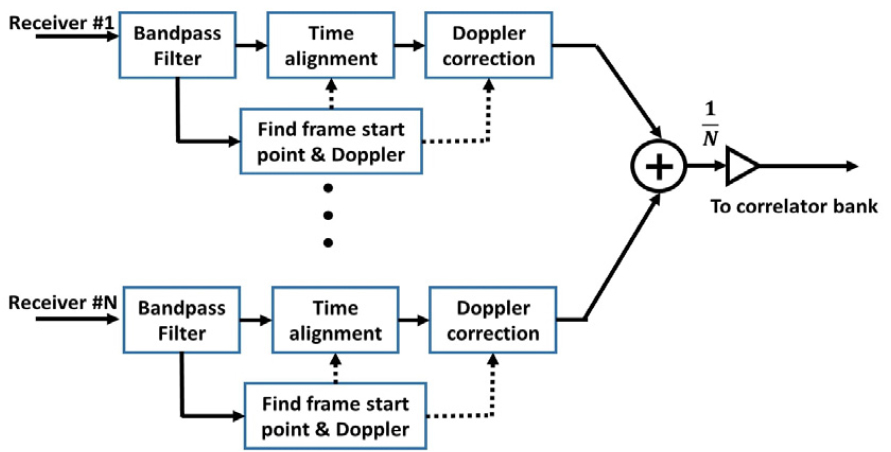
위의 결과에서 비부호화된 비트 오류율 대부분 순방향 오류 정정(Forward Error Correction, FEC) 한계^[17]인 10^-1 이상으로 나타나 이를 개선하기 위해 다수의 채널 출력 신호를 조합하는 다이버시티 기법을 적용하였다. 여러 다이버시티 기법 가운데 본 논문에서는 등이득 조합(Equal Gain Combining, EGC) 다이버시티 기법을 적용하였는데 이 기법은 Additive White Gaussian Noise(AWGN) 채널에서 단순하지만 성능 개선 효과를 나타낸다는 것이 입증되어 있다.^[18] Fig. 9는 N개의 수신기 배열로 구성된 경우에 다중 코드 대역 확산 방식의 신호 처리를 위한 등이득 조합 다이버시티 과정의 전체적인 흐름을 보인다.

Fig. 9.

(Color available online) Block diagram of EGC diversity.

위의 블록도처럼 각 채널 출력 신호에서 프레임의 시작점을 찾아 동기화 하고 도플러 주파수 보정을 수행한다. 이후 등이득 조합 다이버시티 기법을 적용하였는데 Fig. 10은 그 결과를 보여준다. Fig. 10(a)는 다중 코드 대역 확산 방식에 대해 1번 채널을 기준으로 순차적으로 채널을 하나씩 추가하면서 등이득 조합 다이버시티 기법을 적용하였을 때 비부호화된 비트 오류율을 보인 것이다. 예를 들어 그림의 가로축에서 “1 ~ 3”은 1번부터 3번 채널까지 3개의 채널에 대해 등이득 조합 다이버시티 기법을 적용하였다는 의미이다. 8개 채널을 모두 적용한 경우 기존의 문헌^[19]에 나타난 방식에 따라서 패킷 내의 보호 구간과 데이터 구간의 값들을 이용하여 계산된 신호대잡음비는 약 1.2 dB로 나타나 단일 채널의 경우 계산된 신호대잡음비인 약 –10.6 dB 보다 신호대잡음비가 증가하였다. 이러한 영향으로 인하여 그림에서는 단일 채널의 비트 오류율 보다 등이득 조합 다이버시티 기법을 적용하였을 때 대부분 낮은 비트 오류율 결과가 나타나는 것을 볼 수 있다. 하지만 마지막 6, 7, 8번 채널을 순차적으로 등이득 조합 다이버시티 기법에 적용할 경우 성능이 약간 저하되는 현상을 볼 수 있는데 이러한 원인으로 우선 Fig. 3(b)에 나타낸 160 km 거리에서의 전송 손실을 나타낸 그림을 보면 중심주파수인 3.6 kHz를 기준으로 세로 점선(8번 채널이 위치한 수심)과 인접한 약 330 m 아래의 수심 영역에서 전송 손실이 증가하여 8번 채널이 위치한 지점과 약 18 dB 정도의 비교적 큰 차이를 보이고 있다. 또한 수중 채널은 단순한 AWGN 채널이라고 볼 수는 없으며, 채널마다 다른 지연 확산 및 해양 생물에 의한 잡음 등과 같은 기타 요인들이 모두 포함되어 있는 상황이라는 점도 원인으로 볼 수 있다. 특히, 채널마다 다른 지연 확산과 도플러 확산의 경우 별도의 심볼 단위의 위상 동기화 과정을 적용하지 않은 상태에서 성능에 영향을 미칠 수 있다. 또 다른 시각으로써 공간 필터 관점에서 본다면 실험에 사용된 수신기 사이의 간격과 주파수 대역 사이의 관계를 고려하면 공간 앨리어싱이 발생한다. 일반적으로 공간 필터 관점에서 이상적인 수신기 배치는 신호의 반파장 간격이지만 이 실험에 적용된 수신 배열은 이보다 길어서 공간 앨리어싱이 주파수 성분마다 다르게 나타나며 결국 주파수마다 다른 이득을 갖고 조합된다. 따라서 이러한 여러 요인들이 복합되면서 단순히 등이득 조합 다이버시티 과정에서 채널 수를 증가시킨다고 하여 성능이 비례하여 개선되지는 않은 것으로 판단된다.

Fig. 10.

(Color available online) Uncoded BER by EGC diversity, (a) MCSS, (b) CSS.

Fig. 10(b)는 CSS 방식에 대해 1번 채널을 기준으로 채널 순서대로 등이득 조합 다이버시티를 적용한 결과이다. 전반적인 양상은 앞선 다중 코드 대역 확산 방식과 유사하지만 각 심볼의 길이가 상대적으로 긴 다중 코드 대역 확산 방식의 성능이 좋게 나타났으며, 등이득 조합 다이버시티를 적용한 후에도 그 차이는 줄어들었지만 여전히 다중 코드 대역 확산 방식의 결과가 CSS 방식보다 좋게 나타난 것으로 보인다. 하지만 두 종류의 신호는 심볼 길이도 다르고 실험 시점에 따라 채널에 의한 영향도 차이가 있기 때문에 직접적으로 이 둘을 직접적으로 비교할 수는 없다. 결과적으로 8개 채널 모두를 이용하여 등이득 조합 다이버시티 기법을 적용하였을 때 다중 코드 대역 확산 방식의 경우 비부호화된 비트 오류율은 약 0.02 정도까지 낮아졌으며, 처프 대역확산 방식의 경우에도 약 0.1 정도로 나타나 이는 전송 신뢰도 향상을 위한 채널 부호화 기법이 적용되는 경우 순방향 오류 정정 한계 아래의 값^[17]으로써 이런 정도의 오류는 대부분 복호될 가능성이 크다고 판단된다.

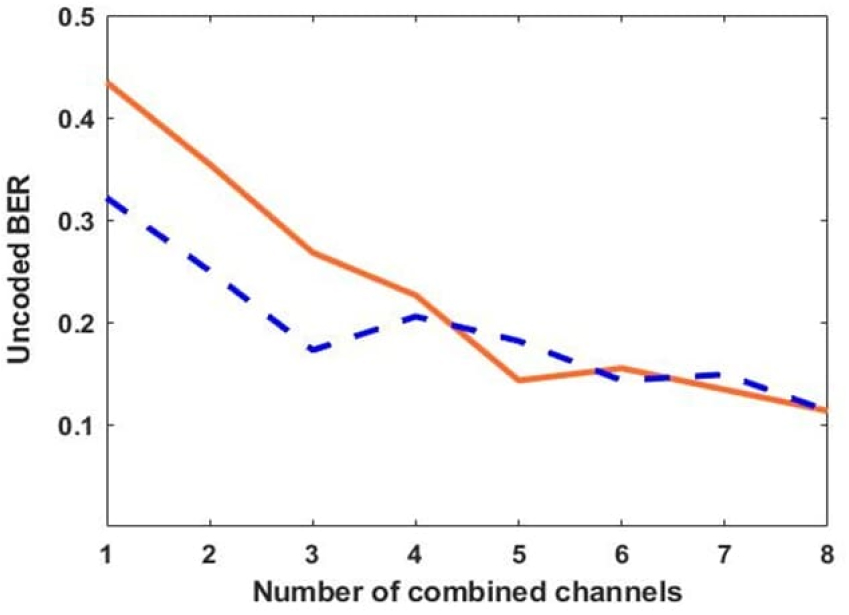
Fig. 11은 CSS 방식에 대해 각 단일 채널의 비트 오류 성능에 따라 순차적으로 등이득 조합 다이버시티 기법을 적용한 결과와 Fig. 10(b)의 결과를 함께 표시한 것이다. 점선으로 표기한 단일 채널 성능이 더 우수한 순서로 등이득 조합 다이버시티를 적용한 결과가 더 나은 값으로 보이기는 하나 궁극적으로는 같은 값으로 수렴함을 알 수 있고, 이러한 선택적인 조합이 가능하려면 사전에 각 채널의 상태를 예측하여야 한다.

Fig. 11.

(Color available online) Uncoded BER by selective EGC diversity (solid line : diversity according to adjacent channel, dotted line : diversity according to BER performance).

IV. 결 론

본 논문에서는 2021년 9월말 동해에서 수행된 160 km 초장거리 수중음향통신 해상실험에 대한 결과를 제시하였다. 이 때 각 심볼마다 직교하는 PN 시퀀스로 확산하는 30 bps의 다중 코드 대역 확산 방식과 100 bps의 처프 대역확산 방식을 적용하였다. 전송 거리 약 160 km에서 각 채널 별로 비부호화된 비트 오류율은 다중 코드 대역 확산 방식의 경우 최대 0.2708, 처프 대역확산 방식은 최대 0.47의 결과가 나타났다. 이는 전달 손실이 크고, 그에 따라 낮은 신호대잡음비를 나타낸 것이 주요 원인이다. 이러한 성능을 개선하기 위해 등이득 조합 다이버시티 기법을 추가로 적용하였으며, 그 결과 다중 코드 대역 확산 방식의 비부호화된 비트 오류율은 평균적으로 0.02, 처프 대역확산 방식은 0.1의 결과가 나타났다. 이 정도의 오류율은 채널 부호화 기법이 적용된다면 대부분의 오류가 복구될 수 있는 범위이다. 또한 등이득 조합 다이버시티 적용 확대 순서에 따라 반드시 성능이 향상되지는 않았으며, 이는 수중 채널이 지연 확산 및 도플러 확산을 갖고 이러한 확산은 채널마다 다르며 실험 시점에 따라 외부 요인에 의한 잡음이 포함되어 있기 때문으로 판단된다. 이는 앞으로 수신 신호 처리에 위상 동기화 과정 등이 포함된다면 향상된 결과를 얻을 수 있을 것으로 기대된다.

향후 100 km 이상의 초장거리 수중음향통신에 있어서 더 높은 신뢰성과 효율성을 갖는 전송방식에 대한 연구와 함께 심해가 아닌 천해에서 장거리 전송에 대한 연구가 필요할 것으로 보인다.