Speech extraction based on AuxIVA with weighted source variance and noise dependence for robust speech recognition

Ui-Hyeop Shin; Hyung-Min Park

doi:10.7776/ASK.2022.41.3.326

Preview

Research Article

The Journal of the Acoustical Society of Korea. 31 May 2022. 326-334
https://doi.org/10.7776/ASK.2022.41.3.326

Speech extraction based on AuxIVA with weighted source variance and noise dependence for robust speech recognition

강인 음성 인식을 위한 가중화된 음원 분산 및 잡음 의존성을 활용한 보조함수 독립 벡터 분석 기반 음성 추출

Ui-Hyeop Shin¹

Hyung-Min Park¹^*

신 의협¹

박 형민¹^*

¹서강대학교 전자공학과

^{*Corresponding Author}

ABSTRACT

In this paper, we propose speech enhancement algorithm as a pre-processing for robust speech recognition in noisy environments. Auxiliary-function-based Independent Vector Analysis (AuxIVA) is performed with weighted covariance matrix using time-varying variances with scaling factor from target masks representing time-frequency contributions of target speech. The mask estimates can be obtained using Neural Network (NN) pre-trained for speech extraction or diffuseness using Coherence-to-Diffuse power Ratio (CDR) to find the direct sounds component of a target speech. In addition, outputs for omni-directional noise are closely chained by sharing the time-varying variances similarly to independent subspace analysis or IVA. The speech extraction method based on AuxIVA is also performed in Independent Low-Rank Matrix Analysis (ILRMA) framework by extending the Non-negative Matrix Factorization (NMF) for noise outputs to Non-negative Tensor Factorization (NTF) to maintain the inter-channel dependency in noise output channels. Experimental results on the CHiME-4 datasets demonstrate the effectiveness of the presented algorithms.

Keywords

Independent vector analysis

Variance

Adaptive filtering

Robust speech recognition

Speech extraction

이 논문에서는 배경 잡음이 포함되는 환경에서 강인한 음성 인식을 하기 위한 전처리 단계로서 쓰이는 목표 음성 향상 방법을 제안한다. 보조 함수 기반의 독립 벡터 분석(Auxiliary-function-based Independent Vector Analysis, AuxIVA) 기법을 기반으로 가중 공분산 행렬에서 시간에 따라 변하는 분산에 의해서 가중치가 결정된다. 목표 음성에 대한 시간-주파수별 기여도를 나타내는 마스크를 통해 분산의 크기를 조절한다. 이러한 마스크는 음성 향상을 위해서 학습된 신경망 혹은 목표 화자로부터의 직선 성분의 기여도를 찾기 위한 확산성으로부터 추정할 수 있다. 이에 더하여 둘러싼 잡음에 대한 출력들은 서로 다차원 독립 성분 분석을 도입하여 의존성을 주어 안정적으로 노이즈 성분을 추출할 수 있다. 이 AuxIVA 기반의 목표 음성 추출 알고리즘은 또한 노이즈에 대해서 비음수 행렬 분해(Non- negative Matrix Factorization, NMF)를 비음수 텐서 분해(Non-negative Tensor Factorization, NTF)로 확장하여 독립 단순 행렬 분석(Independent Low-Rank Matrix Analysis, ILRMA)의 틀에서도 수행될 수 있다. 이러한 확장을 통해서 여전히 잡음 출력 채널에서의 채널간 의존성을 유지할 수 있다. CHiME-4데이터셋에 대한 실험 결과는 소개된 알고리즘에 대한 효과를 보여준다.

키워드

독립 벡터 분석

분산

적응 필터

강인 음성 인식

음성 추출

MAIN

I. 서 론
II. 제안 알고리즘
2.1 노이즈 출력 간의 의존성과 목표 마스크 기반의 AuxIVA를 사용한 목표 음원 추출
2.2 ILRMA로의 확장
III. 실험 결과
IV. 결 론

I. 서 론

잡음 강인성은 음성 인식 분야에서 중요한 문제로 남아있는데, 이는 학습 환경과 시험 환경의 차이로 인해 음성 인식 시스템의 성능이 크게 떨어질 수 있기 때문이다. 이러한 차이를 보완하기 위해서 다양한 접근법들이 개발되어왔다.^[1,2,3] 기존 방법들은 특정 상황에 대해서는 인식 성능을 향상시켰지만, 불규칙한 간섭이 포함되는 다양한 실제 환경에서도 인식 성능을 강인하게 유지하지는 못했다.^[4] 다채널 마이크 신호가 있을 때, 잡음에 강인한 음성 인식을 위한 전처리로서 독립 성분 분석(Independent Component Analysis, ICA)에 기반한 다양한 방식들이 사용되고 있다. 이는 독립 성분 분석이 암묵 음원 분리(Blind Source Separation, BSS) 상황에서 좋은 성능을 내기 때문이다.^{[4,5,6,7,8,9,10]} 반향을 포함한 혼합 신호는 주파수 축에서 독립 성분 분석(ICA)을 통해 통계적으로 독립인 음원들을 찾으며 분리할 수 있다. 하지만 이러한 ICA는 주파수축에서 출력 순서가 무작위로 뒤섞이는 문제가 있다. 이에 대한 해결책으로 제안된 독립 벡터 분석(Independent Vector Analysis, IVA)는 주파수 축에서 균일한 의존성을 주거나^[11,12,13] 군집 단위로 의존성을 줌(Clique model)^[14,15]으로써 사전 음원 정보를 모델링하여 효과적으로 음원 뒤섞임을 방지할 수 있다.

최적화 관점에서, 기대값-최대화 알고리즘의 확장으로서 빠르고 안정적인 업데이트가 가능한 보조 함수 기반 독립 벡터 분석(Auxiliary function-based IVA, AuxIVA) 기술이 발전하였다.^[16,17] 게다가, 독립 단순 행렬 분석(Independent low-rank matrix analysis, ILRMA)은 각 음원별 스펙트로그램을 단순 행렬로 근사하여 주파수의 뒤섞임을 해결하는 동시에 좀 더 정확한 음원 모델을 학습할 수 있다. 이는 비음수 행렬 분해(Non-negative Matrix Factorization, NMF)^[18,19]와 음원 간의 독립성^[20,21]을 동시에 이용하여 이뤄진다. 최근에는 군집 분산 추정과 함께 inter-clique 의존 모델을 사용한 AuxIVA 또한 연구되었다. 이는 시간에 따라 다른 군집 분산을 사용하고, 합쳐진 군집의 지수를 달리하여 대부분의 기존 모델을 일반화하였다.^[22]

하지만 어떤 채널의 출력 신호가 음성 인식에 사용돼야 하는지는 불분명한데, 일반적인 ICA에서 모든 채널에 대해 동일한 음원 모델이 사용되기 때문이다. 동일하게 음원이 모델링 되는 기존의 ICA/IVA에서 음성과 잡음 간의 음원 특성의 차이가 다뤄질 수 없기 때문에, 단일 채널 음원 분리에 의해 추정된 시간-주파수 분산을 기반으로 한 가우시안 모델이 사용되었다.^[23] 반면에, 음성 인식 기술의 전처리는 잡음 분리와 관계없이 목표 음성만 강화하면 된다. 이에 따라 목표 음원 추출 기술이 목표 화자에 방향적 널 게인을 형성하도록 잡음 채널을 제한하여 잡음 분리 필터를 계산할 필요없이 목표 음성 신호를 얻어낼 수 있는 출력 필터를 추정함으로써 발전하였다. 특히 독립 성분 추출(Independent Component Extraction, ICE) 및 독립 벡터 추출(Independent Vector Extraction, IVE)은 분리 신호들이 직교성을 갖도록 제한을 두며 목표 음원을 추출한다. 이는 파일럿 신호를 사용해 채널의 모호성을 해결하여 목표 음원을 안정적으로 추출한다.^[24,25]

둘러싼 잡음이 존재하는 실제 환경에서 잡음에 강인한 음성인식을 하기 위한 전처리 단계로서, 본 논문은 보조 함수 기반의 독립 벡터 분석 기법(AuxIVA)을 기반으로 가중 공분산 행렬에서 가중치를 목표 음성에 대한 마스크를 활용해 크기를 조절하는 목표 음성 추출 방법을 제안한다. 마스크는 음성 향상을 위해 학습된 신경망으로부터 추정할 수 있다. 미리 학습된 신경망 대신에, 본 논문은 마스크를 목표 화자로부터의 직선 성분의 기여도를 찾기 위한 확산성으로부터 추정하는 방식을 소개한다. 이때, 확산성은 마이크 쌍 간의 공간적 일관성을 기반으로 한 직진성 대 확산성 파워 비율(Coherent-to-Diffuse Ratio, CDR)로부터 추정된다. 출력 중 목표 음원을 제외하고, 다차원 독립 성분 분석(Multi-dimensional ICA)을 통해 둘러싼 잡음에 대한 출력들은 서로 연관성을 가지도록 모델링 한다.^[26] 또한, 각 음원들의 시간-주파수 구조에서 단순 행렬 근사의 장점을 얻기 위해 다차원 잡음 출력에 대한 비음수 행렬 분해(Non-negative Matrix Factorization, NMF)를 비음수 텐서 분해(Non-negative Tensor Factorization, NTF)로 변경하여 ILRMA 구조로 확장한다.^[27]

II. 제안 알고리즘

2.1 노이즈 출력 간의 의존성과 목표 마스크 기반의 AuxIVA를 사용한 목표 음원 추출

둘러싼 배경 잡음이 있는 실세계 환경에서, $k$ 번째 주파수 빈과 $τ$ 번째 프레임에서 $M$ 개의 혼합 음성 관측 $x (k, τ) = [X_{1} (k, τ), \dots, X_{M} (k, τ)]^{T}$ 는

(1)

x (k, τ) = a (k) S (k, τ) + n (k, τ)

로 표현될 수 있으며 여기서 $S (k, τ)$ 와 $a (k)$ 는 각각 대응되는 시간-주파수 음성 성분 및 목표 화자에서 관측으로의 $k$ 번째 주파수 빈에서의 전달 함수를 가리킨다. $n (k, τ)$ 는 $x (k, τ)$ 에서 노이즈 성분을 나타낸다. AuxIVA를 적용하기 위해서 분리 모델

(2)

y (k, τ) = W (k) x (k, τ)

를 고려한다. 이때 $y (k, τ) = [Y_{1} (k, τ), \dots, Y_{M} (k, τ)]^{T}$ 는 분리된 시간-주파수 출력 성분으로 구성되는 벡터이고 $W (k)$ 는 $k$ 번째 주파수 빈에서의 분리 행렬이다. $Y_{1} (k, τ)$ 는 목표 음성 추정 값이며 다른 성분은 노이즈 추정 값을 나타낸다.

음원의 변화하는 특성을 잡아내기 위해 음원 모델로 아래와 같이 시간에 따라 변화하는 가우시안 분포를 고려할 수 있다.^[17,23]

(3)

q (Y_{m} (k, τ)) \propto \frac{1}{λ_{m} (k, τ)} \exp \{- \frac{{|Y_{m} (k, τ)|}^{2}}{λ_{m} (k, τ)}\},

여기서 $λ_{m} (k, τ)$ 는 $m$ 번째 음원, $k$ 번째 주파수 빈, $τ$ 번째 프레임에서 시간에 따라 변하는 분산을 의미한다. 이때, $k$ 번째 주파수 빈에 대한 보조 함수 [16]는

(4)

Q_{k} = \sum_{m = 1}^{M} w_{m}^{H} (k) V_{m} (k) w_{m} (k) - \log | detW (k) |

로 주어질 수 있다. 이때 $w_{m}^{H} (k)$ 는 $W (k)$ 의 $m$ 번째 행 벡터이고 $V_{m} (k)$ 는

(5)

V_{m} (k) = \frac{1}{T} \sum_{τ = 1}^{T} \frac{x (k, τ) x^{H} (k, τ)}{\max (r_{m} (k, τ) λ_{m} (k, τ), ϵ)}

로 계산되는 가중 분산 행렬이다. 여기서 $T$ 와 $ϵ$ 는 각각 프레임의 개수와 안정적인 $V_{m} (k)$ 의 추정을 위한 작은 바닥 양수 값이다. $r_{m} (k, τ)$ 는 0과 1사이의 값을 가지는 $λ_{m} (k, τ)$ 에 대한 신뢰 가중치를 나타낸다. 기존의 AuxIVA달리, Eq. (5)는 이러한 신뢰 가중치 $r_{m} (k, τ)$ 를 포함하도록 설계하였다. $W (k)$ 는 일반적으로 단위 행렬로 초기화되기 때문에, $y (k, τ)$ 는 초기 수렴과정에서 $x (k, τ)$ 와 유사하다고 볼 수 있다. 더불어 최대 우도 기반 추정에 따라서 References [17],[22]와 비슷하게 $λ_{m} (k, τ) = | Y_{m} (k, τ) |^{2}$ 로 주어진다. 이 경우에, 본 논문에서는 초기의 수렴단계에서 $Y_{1} (k, τ)$ 에 목표 음성을 얻고자 $r_{1} (k, τ)$ 와 $λ_{1} (k, τ)$ 에 대해서 각각 $M (k, τ)$ 와 $λ^{(s)} (k, τ) = | Y_{1} (k, τ) |^{2}$ 을 사용하기를 제안한다. 여기서 $M (k, τ)$ 는 관측 신호에서 왜곡되지 않은 목표 음성 성분의 상대적인 평균 파워의 기여도를 나타내는 마스크를 의미한다. 마스크는 음성 향상을 위해서 학습된 별도의 신경망으로의 출력 값을 제곱하여 얻을 수 있다.^[28] 미리 학습이 된 신경망을 활용하는 대신, $M (k, τ)$ 는

(6)

M (k, τ) = \frac{1}{1 + \exp (- κ (D (k, τ) - β))}

로도 얻을 수 있다. 𝜅와 𝛽는 각각 기울기와 치우침 정도를 나타내는 파라미터이다. 여기서 $D (k, τ)$ 는 목표 화자로부터 완전한 직진 소리 성분의 기여 정도를 찾고자 추정한 모든 마이크 쌍 $X_{m} (k, τ), X_{n} (k, τ), 1 \leq m, n \leq M$ 에 대한 확산성 수치 $D_{m n} (k, τ)$ 들의 중간값을 나타내며,^[29,30] 이는 같이 재귀적으로 계산되는 마이크 쌍의 correlation,

(7)

C_{m n} (k, τ) = γ_{C} C_{m n} (k, τ - 1) + (1 - γ_{C}) X_{m} (k, τ) X_{n}^{*} (k, τ)

에 의해서 추정된다. 이때 $γ_{C}$ 는 0과 1사이의 값으로 설정하는 스무딩 팩터를 나타낸다. 이러한 correlation $C_{m n} (k, τ)$ 로부터 coherence,

(8)

Γ_{m n} (k, τ) = \frac{C_{m n} (k, τ)}{\sqrt{C_{m m} (k, τ) C_{n n} (k, τ)}}

를 추정하여 이로부터 Reference [30]과 동일하게 $D_{m n} (k, τ)$ 를 추정할 수 있다.

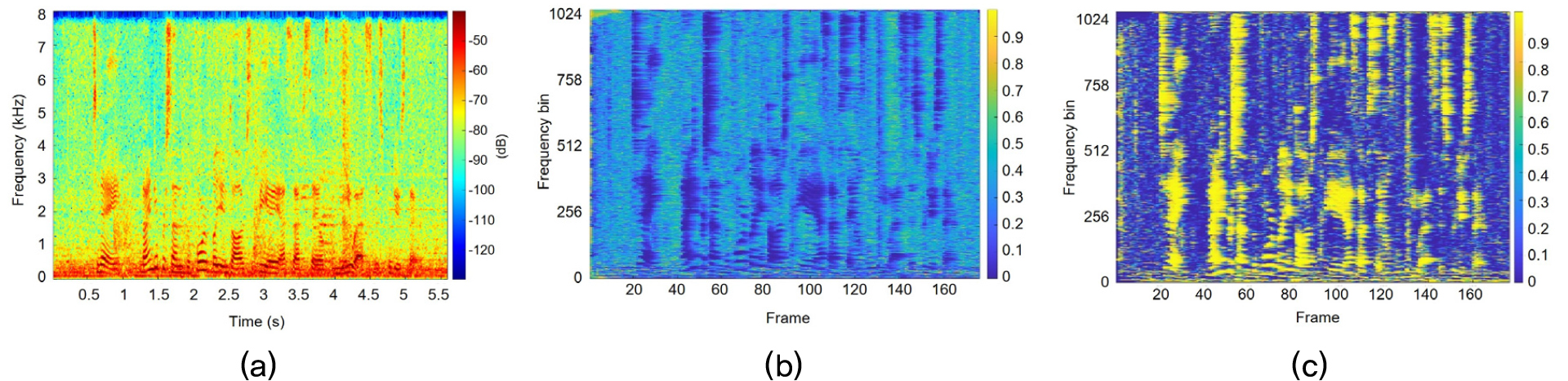
Fig. 1은 주어진 입력 신호에 대한 확산성 수치 추정 값과 이를 Eq. (6)을 거쳐서 얻어낸 목표 마스크를 나타낸 것이다. 이 확산성 기반의 목표 마스크는 입력 신호의 음성 성분을 효과적으로 추정하였음을 확인할 수 있다. 비록 목표 음성 분산의 추정은 위와 같이 이루어질 수 있으나, 각각의 개별적인 잡음들에 대한 분산 추정은 매우 까다롭다. 사실, 강인한 음성인식을 위한 전처리로서 유도하고자 하는 알고리즘은 개별적인 잡음원에 대한 분리를 필요로 하지 않는다. 본 논문에서는 둘러싼 배경 잡음 환경을 고려하기 때문에, 잡음 출력 $Y_{m} (k, τ), m = 2, \dots, M$ 은 서로 간에 의존성을 가질 수 있도록 하여도 무방하다. 그리고 이 분산들은 똑같다고 가정할 수 있고 이는 초기 수렴에서의 Eq. (3)의 음원 모델을 가지는 AuxIVA에 대해서 잡음에 대한 가중치는 아래와 같이 역 마스크 값으로 설정하고,

(9)

r_{m} (k, τ) = 1 - M (k, τ),

채널 별 분산 값은 잡음간 공유된 하나의 분산으로 가정하여 추정할 수 있다.

(10)

λ_{m} (k, τ) = λ^{(n)} (k, τ) = \frac{1}{M - 1} \sum_{m' = 2}^{M} | Y_{m'} (k, τ) |^{2} .

이러한 수식은 마치 IVA에서 주파수 성분 간에 그러하듯 잡음 출력 간의 의존성을 준다. 기존의 AuxIVA와 달리 Eq. (5)는 $r_{m} (k, τ)$ 를 포함하기 때문에, $\frac{1}{T} \sum_{τ = 1}^{T} r_{m} (k, τ)$ 로 $r_{m} (k, τ)$ 를 정규화 하여 이로 인해서 발생할 수 있는 $V_{m} (k)$ 의 과추정을 방지해줄 수 있다. 초기 수렴후에는, $r_{m} (k, τ)$ 는 더 나은 수렴을 위해 1로 바꿀 수 있다.

https://static.apub.kr/journalsite/sites/ask/2022-041-03/N0660410308/images/ASK_41_03_08_F1.jpg

Fig. 1.

(Color available online) Spectrograms of input and its diffuseness estimator. (a) Input spectrogram, (b) diffuseness estimator, and (c) target masks obtained by its diffuseness estimator (b).

References [31],[32]에서, $λ_{m} (k, τ)$ 는 각 주파수 빈 별로 인접 프레임의 출력 파워 간의 이동평균을 도입하여 음원 신호의 시간적 연속성을 향상시켜 추정의 정확도를 개선할 수 있다.

(11)

λ_{1} (k, τ) = λ^{(s)} (k, τ) = \frac{1}{2 τ_{0} + 1} \sum_{t = τ - τ_{0}^{}}^{τ + τ_{0}} | Y_{1} (k, t) |^{2},

(12)

λ_{m} (k, τ) = λ^{(n)} (k, τ) = \frac{1}{(2 τ_{0} + 1) (M - 1)} \sum_{t = τ - τ_{0}^{}}^{τ + τ_{0}} \sum_{m' = 2}^{M} | Y_{m'} (k, t) |^{2}, m = 2, \dots, M,

여기서 $2 τ_{0 + 1}$ 는 평균을 내고자 하는 프레임의 개수를 말한다. 한번 $V_{m} (k)$ 가 계산되면, $W (k)$ 는 다른 벡터 $w_{n} (k), n \neq m$ 를 고정한 채 순차적으로 $w_{m} (k)$ 를 아래와 같은 방식을 통해서 업데이트 된다. 업데이트 방식은 아래와 같다(References [16],[17],[22]와 유사함).

(13)

w_{m} (k) = (W (k) V_{m} (k) + δ I)^{- 1} e_{m},

(14)

w_{m} (k) = \frac{w_{m} (k)}{\sqrt{w_{m}^{H} (k) V_{m} (k) w_{m} (k)}},

여기서 𝛿와 $e_{m}$ 는 대각 성분 로딩을 위한 작은 양수 값과 $m$ 번째 성분이 1에 해당에는 단위 벡터를 말한다.

2.2 ILRMA로의 확장

Eq. (3)의 음원 모델에 상호 주파수 의존성을 부과하기 위해 개별 음원의 스펙트로그램은 ILRMA에서 NMF를 사용해 주파수에 대한 기저 함수와 시간에 대한 활성 함수의 단순 행렬 분해로 모델링 될 수 있다.^[20,21] 주파수에 대한 $l$ 번째 기저함수 $b^{(s)} (k, l)$ 는 기본적인 구성 음성 성분을 의미하는 주파수 축으로의 벡터를 나타내며, 시간에 대한 활성함수 $v^{(s)} (l, τ)$ 는 이러한 기저함수의 음성 성분이 언제 발생할지를 나타내는 벡터이다. 총 $L$ 개의 기저함수가 음성을 구성한다고 가정할 때, $λ_{1} (k, τ) = λ^{(s)} (k, τ) = \sum_{l = 1}^{L} b^{(s)} (k, l) v^{(s)} (l, τ)$ 의 수식을 사용하여 $λ_{1} (k, τ)$ 의 업데이트를 $b^{(s)} (k, l)$ 와 $v^{(s)} (l, τ)$ 의 업데이트로 대체할 수 있다. 이때 Eq. (3)에 대입하여 얻어지는 로그-우도 함수는 아래와 같다.

(15)

Q_{N M F}^{(s)} = \sum_{k = 1}^{K} \sum_{τ = 1}^{T} \frac{| Y_{1} (k, τ) |^{2}}{\sum_{l = 1}^{L} b^{(s)} (k, l) v^{(s)} (l, τ)} + \log \sum_{l = 1}^{L} b^{(s)} (k, l) v^{(s)} (l, τ) .

해당 함수를 각각 $b^{(s)} (k, l)$ 와 $v^{(s)} (l, τ)$ 의 편미분을 통해 아래와 같은 방정식을 얻는다.

(16)

\frac{\partial Q_{N M F}^{(s)}}{\partial b^{(s)} (k, l)} = \sum_{τ = 1}^{T} (\frac{v^{(s)} (l, τ)}{\sum_{l = 1}^{L} b^{(s)} (k, l) v^{(s)} (l, τ)} - \frac{| Y_{1} (k, τ) |^{2} v^{(s)} (l, τ)}{\sum_{l = 1}^{L} b^{(s)} (k, l) v^{(s)} (l, τ)^{2}}) = 0 .

(17)

\frac{\partial Q_{N M F}^{(s)}}{\partial v^{(s)} (l, τ)} = \sum_{k = 1}^{K} (\frac{b^{(s)} (k, l)}{\sum_{l = 1}^{L} b^{(s)} (k, l) v^{(s)} (l, τ)} - \frac{| Y_{1} (k, τ) |^{2} b^{(s)} (k, l)}{\sum_{l = 1}^{L} b^{(s)} (k, l) v^{(s)} (l, τ)^{2}}) = 0 .

이에 따라서 목표 음성에 대한 기저 함수 $b^{(s)} (k, l)$ 와 활성 함수 $v^{(s)} (l, τ)$ 의 곱셈 기반의 업데이트 식을 아래와 같이 얻을 수 있다.

(18)

b^{(s)} (k, l) \leftarrow b^{(s)} (k, l) \sqrt{\frac{\sum_{τ} | Y_{1} (k, τ) |^{2} v^{(s)} (l, τ) λ_{1}^{- 2} (k, τ)}{\sum_{τ} v^{(s)} (l, τ) λ_{1}^{- 1} (k, τ)}} .

(19)

v^{(s)} (l, τ) \leftarrow v^{(s)} (l, τ) \sqrt{\frac{\sum_{k} | Y_{1} (k, τ) |^{2} b^{(s)} (k, l) λ_{1}^{- 2} (k, τ)}{(\sum_{k} b^{(s)} (k, l) λ_{1}^{- 1} (k, τ)}} .

이때, $λ_{1} (k, τ) = \sum_{l = 1}^{L} b^{(s)} (k, l) v^{(s)} (l, τ)$ 로 Eq. (18)와 Eq. (19)의 $λ_{1} (k, τ)$ 를 구할 수 있다.

한편, 이전의 개별 잡음에 대한 분산이 모두 똑같이 $λ^{(n)} (k, τ)$ 로 주어진다는 가정은 이상적인 등방성 확산 잡음을 기반으로 하였다. 이러한 과도하게 엄밀한 가정을 완화하기 위해, 본 논문에서는 출력 성분들의 공통의 기저 함수 $b^{(s)} (k, l)$ 와 활성 함수 $v^{(s)} (l, τ)$ 가 이득 함수 $g_{m} (l)$ 에 의해서 아래와 같이 가중치가 설정되도록 분해하여 잡음 출력 간의 의존성을 유지한다.

(20)

λ_{m} (k, τ) = \sum_{l}^{} g_{m} (l) b^{(n)} (k, l) v^{(n)} (l, τ), m = 2, \dots, M

Eq. (15)과 유사하게 잡음 소스 모델에 대한 로그-우도 함수를 얻어 동일한 방식으로 잡음의 분산을 나타내는 NTF^[27] 매개변수에 대해서

(21)

b^{(n)} (k, l) \leftarrow b^{(n)} (k, l) \cdot \sqrt{\frac{\sum_{τ} \sum_{m = 2}^{M} | Y_{m} (k, τ) |^{2} g_{m} (l) v^{(n)} (l, τ) λ_{m}^{- 2} (k, τ)}{\sum_{τ} \sum_{m = 2}^{M} g_{m} (l) v^{(n)} (l, τ) λ_{m}^{- 1} (k, τ)}},

(22)

v^{(n)} (l, τ) \leftarrow v^{(n)} (l, τ) \cdot \sqrt{\frac{\sum_{k} \sum_{m = 2}^{M} | Y_{m} (k, τ) |^{2} g_{m} (l) b^{(n)} (k, l) λ_{m}^{- 2} (k, τ)}{\sum_{k} \sum_{m = 2}^{M} g_{m} (l) b^{(n)} (k, l) λ_{m}^{- 1} (k, τ)}},

(23)

g_{m} (k, l) \leftarrow g_{m} (k, l) \cdot \sqrt{\frac{\sum_{τ} \sum_{k}^{} | Y_{m} (k, τ) |^{2} b^{(n)} (l, τ) λ_{m}^{- 2} (k, τ)}{\sum_{τ} \sum_{k}^{} b^{(n)} (k, l) v^{(n)} λ_{m}^{- 1} (k, τ)}},

로 표현되는 업데이트 식을 가질 수 있다.

III. 실험 결과

제안 알고리즘의 음성 인식 성능은 CHiME-4 데이터셋을 기반으로 평가를 하였다.^[33,34] 이는 6개의 마이크가 부착된 태블릿 PC를 통해서 실제 잡음 환경에서 녹음된 음성 데이터로, 총 4가지의 환경(café, street, bus, pedestrian)에서 네 명의 화자가 330개의 발화를 녹음하여 총 2640개의 실제 발화 데이터로 구성되어 있다. 추가적으로 무향실에서 녹음한 410개의 발화를 네 명의 화자가 발화하여 동일 환경에서 별도로 취득한 잡음 데이터를 더하여 시뮬레이션 데이터 6560개가 추가적으로 포함되어 있다. 구성한 음성 인식 시스템은 Reference [32]과 같다. Reference [32]에서와 같이, 마이크 입력 신호의 샘플링 주파수를 16 kHz로 설정하고, 1024 샘플 길이의 Hanning 윈도우를 256 샘플 간격으로 이동하여 국소 푸리에 변환(Short-Time Fourier Transform, STFT)을 수행했다.

Table 1에서, AuxIVA에 기반한 제안 알고리즘(Prop. AuxIVA)과 ILRMA에 기반한 제안 알고리즘(Prop. ILRMA)은 모델에 기반한 IVA(Model IVA)와 비교하였다. 평가 지표로는 단어 오류율(Word Error Rate, WER)을 사용했고, 목표 음원에 대한 마스크로는 Reference [28]을 따라 학습된 인공 신경망 기반 마스크 또는 CDR로 추정된 확산성 기반의 마스크를 사용하였다^[29,30]. Reference [24]의 직교 제한(Orthogonal Constraint, OC)은 인식 성능을 향상시키기 위해 모델 기반 IVA에 적용했다(Model IVA + OC). 추가적으로 마스크를 쓰지 않고 기존에 효과적인 성능을 보여주었던 빔포밍 알고리즘인 복소 가우시안 혼합 모델(Complex Gaussian mixture model, CGMM)^[35] 및 최소 파워 왜곡 방지 응답(Minimum-Power Distortionless Response, MPDR) 방법^[36] 또한 비교하였다.

Table 1.

WERs (%) on the CHiME-4 dataset for the no processing for input data acquired at the fifth microphone and enhancement with batch processing by CGMM + MPDR, Model IVA, Model IVA + OC, Prop. AuxIVA, and Prop. ILRMA.

Mask	Method	Dev.		Test
Mask	Method	Simu.	Real	Simu.	Real
-	No processing	5.57	6.47	6.85	11.98
-	CGMM^[35] + MPDR^[36]	3.86	3.24	6.09	5.66
CDR^[29]	Model IVA^[23]	4.49	5.91	6.50	9.78
	Model IVA^[23] + OC^[24]	3.53	4.54	4.38	7.46
	Prop. AuxIVA	2.55	3.23	3.73	4.83
	Prop. ILRMA	2.61	3.15	3.71	4.65
NN^[28]	Model IVA^[23]	3.59	5.03	4.72	9.15
	Model IVA^[23] + OC^[24]	2.86	4.22	3.54	6.96
	Prop. AuxIVA	2.51	2.99	3.27	4.65
	Prop. ILRMA	2.62	3.08	3.24	4.51

제안 알고리즘의 일괄 처리에서, 𝜀, 𝜅, 𝛽, 𝜏₀와 𝛿는 각각 10^-6, 20, 0.2, 1, 와 10^-10으로 설정했다. 100회 전체 반복을 수행하되, ${\bar{M}}_{m} (k, τ)$ 가 30회 반복 후 1로 변경 되었다. 마스크가 수렴에 도움이 되기 때문에, ILRMA에서 목표 음원과 잡음을 위한 기저의 개수를 50개로 설정했다. 이는 기존 ILRMA보다 훨씬 많이 설정한 값이다. CGMM 방법의 경우 총 10회의 수렴 반복을 수행하였다.

사용된 마스크에 상관없이, 그리고 Model IVA이 직교 제한이 있든 없든 간에 제안 알고리즘들이 더 좋은 음성 인식 성능을 보였다. 이는 Model IVA^[23]에서 분산을 수정하여 모든 개별 채널에 고정된 분산을 쓰는 방식과 달리, 초반 수렴에서 마스크 정보를 활용하여 목표 음원을 목표 채널로 유도하고 동시에 잡음 출력 채널 간에는 의존도를 줄 수 있기 때문이다. 한편, 제안 알고리즘 중 Prop. ILRMA는 Prop. AuxIVA보다 약간 더 개선된 WERs를 보이는데, 이는 충분한 반복을 거치며 추정 변수가 많은 NMF 변수가 충분히 수렴하기 때문이다. 한편 신경망 기반의 마스크를 활용하였을 때에는 Prop. AuxIVA 방법이 비교적 좀 더 향상된 결과를 보였는데, 이는 더 정확한 마스크가 주어지면서 NMF를 통한 근사가 성능 향상에 크게 도움이 되지 않은 것으로 이해할 수 있다.

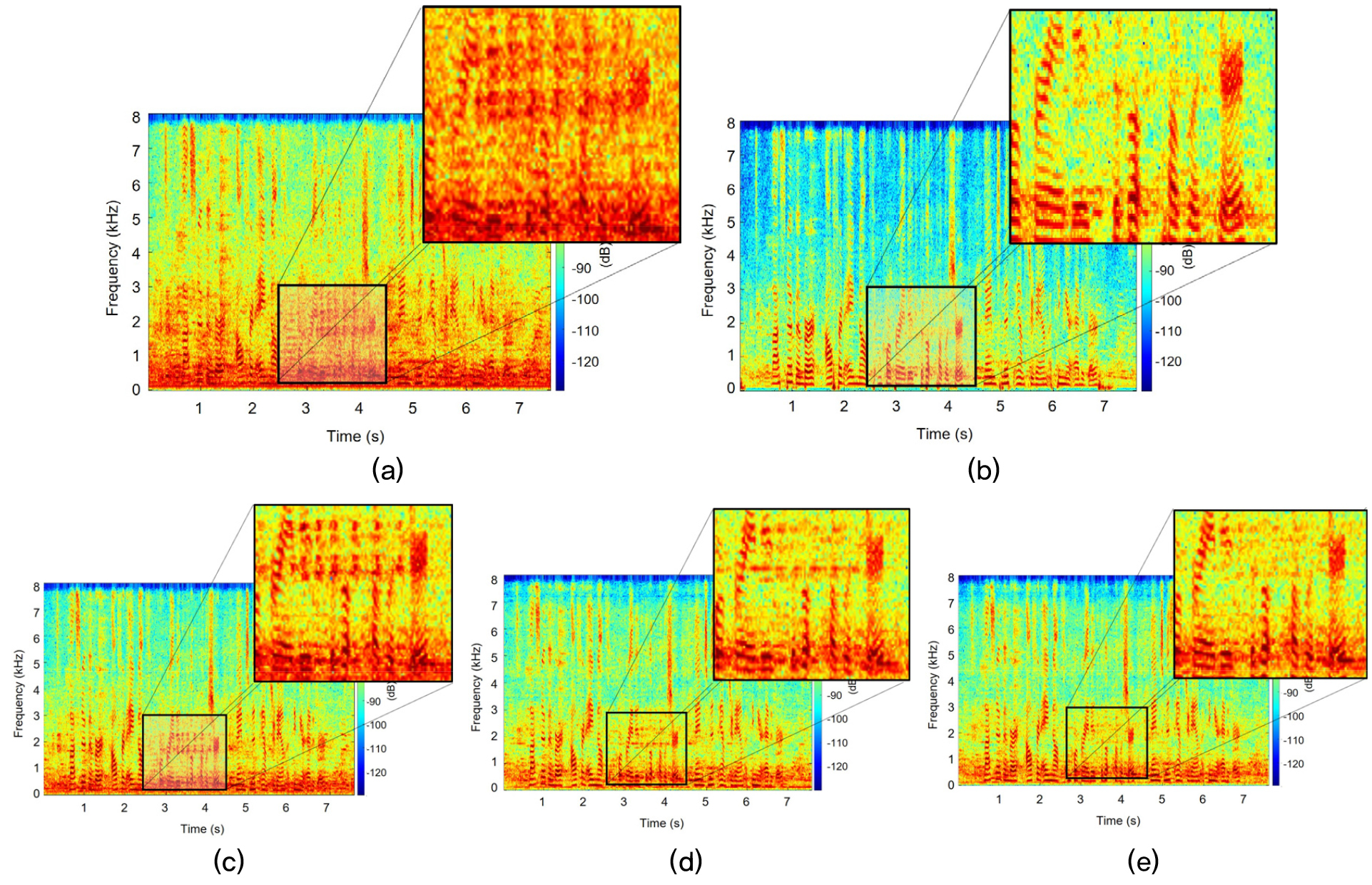
Fig. 2는 샘플 입력 스펙트로그램과 근거리 레퍼런스 신호, 그리고 입력 신호에 대해서 각각 CGMM + MPDR방법 및 CDR 마스크를 활용하여 제안 방법(Prop. AuxIVA, Prop. ILRMA)으로 향상시킨 출력 스펙트로그램을 표시한 것이다. Fig. 2(b)의 근거리 레퍼런스 신호와 비교하여 기존 Fig. 2(c)의 MPDR 빔포밍 방법과 비교하여 CDR 마스크를 활용한 제안 방법이 좀 더 효과적으로 잡음 성분을 억제하는 것을 확인할 수 있다.

https://static.apub.kr/journalsite/sites/ask/2022-041-03/N0660410308/images/ASK_41_03_08_F2.jpg

Fig. 2.

(Color available online) Spectrograms of an example of (a) input, (b) close-talk microphone input as a reference signal, and outputs of (c) MPDR, (d) Prop. AuxIVA, (e) Prop. ILRMA.

IV. 결 론

본 논문은 둘러싼 잡음이 있는 환경에서 강인한 음성 인식이 가능하도록 하는 전처리 단계로 AuxIVA와 ILRMA를 기반으로 한 목표 음원 추출 알고리즘을 제안했다. 제안 알고리즘은 잡음 출력 간의 의존성과 목표 음원의 마스크를 통해 가중 공분산 행렬을 활용한 AuxIVA/ILRMA 기반의 알고리즘이다. 실험 결과는 제안 알고리즘이 출력의 모호성이 없는 강인한 음성 인식을 위한 목표 음원 분리를 성공적으로 했음을 보여준다.

Acknowledgements

이 논문은 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(NRF- 2020R1A2B5B01002398).

References

T. Virtanen, R. Singh, and B. Raj, Techniques for Noise Robustness in Automatic Speech Recognition (John Wiley & Sons, New York, 2012), pp. 109-154. 10.1002/9781118392683

M. Ẅolfel and J. McDonoug, Distant Speech Recognition (John Wiley & Sons, New York, 2009), pp. 387-491.

J. Droppo and A. Acero. Environmental Robustness (Springer, Heidelberg, 2008), pp. 653-680. 10.1007/978-3-540-49127-9_33

M. Kim and H.-M. Park, "Efficient online target speech extraction using DOA-constrained independent component analysis of stereo data for robust speech recognition," Signal Processing, 117, 126-137 (2015). 10.1016/j.sigpro.2015.04.022

L. Albera, "Independent component analysis and applications," Handbook of Blind Source Separation: Independent Component Analysis and Applications, edited by P. Comon and C. Jutten (Academic press, Kidlington, 2010).

S. Haykin, Unsupervised Adaptive Filtering, volume 1: Blind Source Separation (John Wiley & Sons, New York, 2000), pp. 238-258.

A. Hyv̈arinen, J. Karhunen, and E. Oja, Independent Component Analysis and Blind Source Separation (John Wiley & Son, New York, 2001), pp. 4-42. 10.1002/0471221317

Y. Takahashi, T. Takatani, K. Osako, H. Saruwatari, and K. Shikano, "Blind spatial subtraction array for speech enhancement in noisy environment," IEEE Transactions on Audio, Speech, and Language Processing, 17, 650-664 (2009). 10.1109/TASL.2008.2011517

F. Nesta and M. Matassoni, "Blind source extraction for robust speech recognition in multisource noisy environments," Computer Speech and Language, 27, 703-725 (2013). 10.1016/j.csl.2012.08.001

M. El Rhabi, H. Fenniri, A. Keziou, and E. Moreau, "A robust algorithm for convolutive blind source separation in presence of noise," Signal Processing, 93, 818-827 (2013). 10.1016/j.sigpro.2012.09.026

T. Kim, H. T. Attias, S.-Y. Lee, and T.-W. Lee, "Blind source separation exploiting higher-order frequency dependencies," IEEE Transactions on Audio, Speech, and Language Processing, 15, 70-79 (2007). 10.1109/TASL.2006.872618

T. Kim, "Real-time independent vector analysis for convolutive blind source separation," IEEE Transactions on Circuits and Systems I: Regular Papers, 57, 1431-1438 (2010). 10.1109/TCSI.2010.2048777

M. Oh and H.-M. Park, "Blind source separation based on independent vector analysis using feed-forward network," Neurocomputing, 74, 3713-3715 (2011). 10.1016/j.neucom.2011.06.008

I. Lee, G.-J. Jang, and T.-W. Lee, "Independent vector analysis using densities represented by chain-like overlapped cliques in graphical models for separation of convolutedly mixed signals," Electronics Letters, 45, 710-711 (2009). 10.1049/el.2009.0945

C.-H. Choi, W. Chang, and S.-Y. Lee, "Blind source separation of speech and music signals using harmonic frequency dependent independent vector analysis," Electronics Letters, 48, 124-125 (2012). 10.1049/el.2011.3215

N. Ono, "Stable and fast update rules for independent vector analysis based on auxiliary function technique," Proc. IEEE WASPAA, 189-192 (2011). 10.1109/ASPAA.2011.6082320

N. Ono, "Auxiliary-function-based independent vector analysis with power of vector-norm type weighting functions," Proc. APSIPA, 1-4 (2012).

D. D. Lee and H. S. Seung, "Learning the parts of objects by non-negative matrix factorization," Nature, 401, 788 (1999). 10.1038/4456510548103

D. D. Lee and H. S. Seung, "Algorithms for non- negative matrix factorization," Advances in Neural Information Processing Systems, 13, 556-562 (2001).

D. Kitamura, N. Ono, H. Sawada, H. Kameoka, and H. Saruwatari, "Efficient multichannel nonnegative matrix factorization exploiting rank-1 spatial model," Proc. IEEE ICASSP, 276-280 (2015). 10.1109/ICASSP.2015.7177975

D. Kitamura, N. Ono, H. Sawada, H. Kameoka, and H. Saruwatari, "Determined blind source separation unifying independent vector analysis and nonnegative matrix factorization," IEEE/ACM TASLP, 24, 1622- 1637 (2016). 10.1109/TASLP.2016.2577880

U.-H. Shin and H.-M. Park, "Auxiliary-function-based independent vector analysis using generalized inter- clique dependence source models with clique variance estimation," IEEE Access, 8, 68103-68113 (2020). 10.1109/ACCESS.2020.2985842

A. R. Ĺopez, N. Ono, U. Remes, K. Palom̈aki, and M. Kurimo, "Designing multichannel source separation based on single-channel source separation," Proc. IEEE ICASSP, 469-473 (2015).

Z. Koldovsḱy, P. Tichavsḱy, and V. Kautsk, "Orthogonally constrained independent component extraction: Blind MPDR beamforming," Proc. EUSIPCO, 1155- 1159 (2017). 10.23919/EUSIPCO.2017.8081389

T. Kounovsḱy, Z. Koldovsky, and J. Cmejla, "Recursive and partially supervised algorithms for speech enhancement on the basis of independent vector extraction," Proc. IWAENC, 401-405 (2018). 10.1109/IWAENC.2018.8521399

J.-F. Cardoso, "Multidimensional independent component analysis," Proc. IEEE ICASSP, 4, 1941-1944 (1998).

D. FitzGerald, M. Cranitch, and E. Coyle, "Non- negative tensor factorisation for sound source separation," Proc. Irish Signals and Systems Conf. 8-12 (2005). 10.1049/cp:20050279

J. Heymann, L. Drude, and R. Haeb-Umbach, "Neural network based spectral mask estimation for acoustic beamforming," Proc. IEEE ICASSP, 196-200 (2016). 10.1109/ICASSP.2016.7471664

A. Schwarz and W. Kellermann, "Coherent-to-diffuse power ratio estimation for dereverberation," IEEE/ ACM Transactions on Audio, Speech, and Language Processing, 23, 1006-1018 (2015). 10.1109/TASLP.2015.2418571

R. Lee, M.-S. Kang, B.-H. Kim, K.-H. Park, S. Q. Lee, and H.-M. Park, "Sound source localization based on gcc-phat with diffuseness mask in noisy and reverberant environments," IEEE Access, 8, 7373-7382 (2020). 10.1109/ACCESS.2019.2963768

J. Caroselli, I. Shafran, A. Narayanan, and R. Rose, "Adaptive multichannel dereverberation for automatic speech recognition," Proc. Interspeech, 3877-3881 (2017). 10.21437/Interspeech.2017-1791

B. J. Cho, J.-M. Lee, and H.-M. Park, "A beamforming algorithm based on maximum likelihood of a complex gaussian distribution with time-varying variances for robust speech recognition," IEEE Signal Processing Letters, 26, 1398-1402 (2019). 10.1109/LSP.2019.2932848

E. Vincent, S. Watanabe, A. A. Nugraha, J. Barker, and R. Marxer, "An analysis of environment, microphone and data simulation mismatches in robust speech recognition," Computer Speech & Language, 46, 535-557 (2017). 10.1016/j.csl.2016.11.005

J. Barker, R. Marxer, E. Vincent, and S. Watanabe, "The third "CHiME" speech separation and recognition challenge: Dataset, task and baselines," Proc. IEEE Workshop on ASRU, 504-511 (2015). 10.1109/ASRU.2015.740483726035872

T. Higuchi, N. Ito, T. Yoshioka, and T. Nakatani, "Robust MVDR beamforming using time-frequency masks for online/offline ASR in noise," Proc. IEEE ICASSP, 5210-5214 (2016). 10.1109/ICASSP.2016.7472671

O. L. Frost, "An algorithm for linearly constrained adaptive array processing," Proceedings of the IEEE, 60, 926-935 (1972). 10.1109/PROC.1972.8817

The Journal of the Acoustical Society of Korea ISSN:1225-4428(Print) 2287-3775(Online) 한국음향학회지

Preview

Speech extraction based on AuxIVA with weighted source variance and noise dependence for robust speech recognition

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

Fig. 1.

(Color available online) Spectrograms of input and its diffuseness estimator. (a) Input spectrogram, (b) diffuseness estimator, and (c) target masks obtained by its diffuseness estimator (b).

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

Table 1.

WERs (%) on the CHiME-4 dataset for the no processing for input data acquired at the fifth microphone and enhancement with batch processing by CGMM + MPDR, Model IVA, Model IVA + OC, Prop. AuxIVA, and Prop. ILRMA.

Fig. 2.

(Color available online) Spectrograms of an example of (a) input, (b) close-talk microphone input as a reference signal, and outputs of (c) MPDR, (d) Prop. AuxIVA, (e) Prop. ILRMA.

Acknowledgements

References