I. 서 론

최근 함정의 고성능화로 탑재 장비들은 대형화가 되었고, 그로 인해 함정 내 배관설비들이 다수 필요하게 되었다. 특히 함정의 공조와 관련된 관내 소음은 좁은 공간적 상황으로 인해 다른 함내 소음에 비해 승조원의 생활에 큰 영향을 미친다. 이런 배관소음을 저감 방안으로 배관 구조 설계 변경, 소음기 사용 등 다양한 방법이 있지만, 전체적인 구조 변경 없이 소음기를 부착하는 방법이 주로 사용되고 있다. 이렇게 사용되는 소음기는 크게 반사형 소음기와 흡음형 소음기로 분류된다. 일반적으로 반사형 소음기는 저주파수 대역에서, 흡음형 소음기는 중고주파수 대역에서 성능이 우수하게 나타난다.^[1] 소음기의 성능을 향상시키기 위해 소음기 자체의 크기를 키우는 방법이 있지만, 함정 경량화 및 협소한 공간문제로 크기 대비 성능이 우수한 흡음형 소음기를 사용하는 것이 유용하다. 흡음형 소음기의 원리는 음파가 전파되면서 소음기 내부에 부착된 흡음물질로 인해 음향에너지가 열로 전환되어 소음기 통과 후의 음향에너지를 줄여 소음을 저감시키는 것이다.^[2] Craggs^[3]는 유한요소법을 사용하여 흡음물질이 라이닝된 단순확장형 챔버의 음향학적 행동에 대해 연구하였고, 그 결과 흡음물질에 따라 투과손실 그래프 개형이 변하였고, 흡음물질 두께를 증가시키면 투과손실 최대값에 해당되는 주파수가 변하는 것을 확인하였다. Munjal^[4]은 단순확장형 챔버형태 외에 다양한 형태의 소음기의 음향성능에 대한 연구를 수행하였고, 소음기 형태 변화에 따른 음향성능에의 영향을 이론적으로 분석하였다. Peat^[5]는 부피반응성 흡음형 소음기에 대한 전달행렬을 개발하여 음향성능을 계산하는데 더 편리한 방법을 제시하였다. Tao와Seybert^[6]는 소음기 투과손실 측정법 중 가장 일반적인 방법인 decomposition method, two-source method, two-load method에 대해 각각 설명하였고, 각 방법을 통해 도출한 결과를 비교하였다. 또한 측정 시 two-load method는 음원을 움직이지 않아도 되기 때문에 다른 방법들에 비해 편리한 방법임을 알렸다. Xu et al.^[1]은 단순확장형 흡음형 소음기에 대해 흡음재 두께, 유동저항 등 흡음재 특성이 음향성능에 미치는 영향에 대해 이론 결과와 수치해석 결과를 비교·분석하였다. Selamet et al.^[7]은 서로 다른 유동저항을 갖는 두 흡음재가 층을 이루는 소음기의 음향성능을 확인하였고, 확장 및 수축되는 소음기 전·후에서 압력·속도의 연속성을 적용한 이론식 결과와 수치해석 결과를 비교·분석하였다. Selamet et al.^[8]는 흡음재 안쪽 면에 다공성 판을 놓은 상태에서 소음기 음향성능을 이론식을 통해 확인하였고, 이론 결과와 실험결과를 비교하였다. Veerababu와 Venkatesham^[9]는 다층으로 흡음재가 부착되고 각 흡음재 사이에 다공성 판이 있는 원통형 소음기의 투과손실을 그린함수를 사용하여 예측하는 이론식을 개발하였고, 해당 식을 통해 다층으로 구성된 흡음재가 음향성능에 미치는 영향을 분석하였다.

본 논문에서는 유동이 없는 배관 소음기 중 원통형의 단순확장형인 흡음형 소음기에서 흡음재 물성치 변화에 따라 음향성능에 미치는 영향에 대해 연구를 진행하였다. 지금까지 다양한 소음기에 대한 연구가 진행되었지만, 각각의 매개변수가 음향성능에 미치는 영향만을 고려하였고, 이를 종합적으로 분석하지는 않았다. 하여 본 연구에서는 소음기의 음향성능을 실험 및 시뮬레이션을 통해 산출하고, 그 결과를 비교하였다. 특히 흡음재 물성치에 따른 음향성능 변화를 시뮬레이션을 통해 예측하였으며, 각 물성치가 음향성능에 어떤 영향을 미치는 지에 대해 종합적으로 비교·분석하였다.

II. 소음기 음향성능 계측실험

2.1 투과손실 측정기법

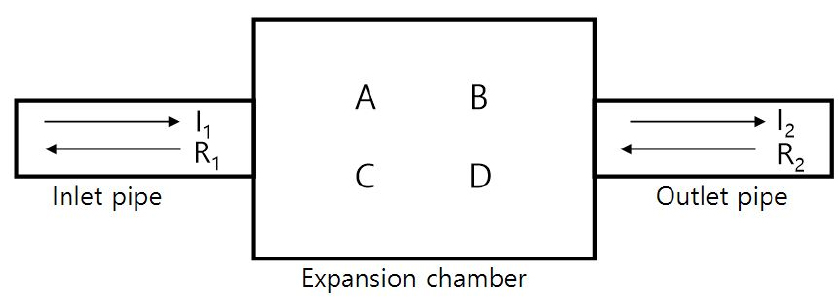
일반적으로 소음기가 탑재된 배관계통은 Fig. 1과 같이 입력단, 소음기, 출력단으로 구성되어 있다. 음원에서 발생한 음파가 입력단, 소음기 그리고 출력단으로 전파되며, 여기서 음파의 전파는 강체배관 내 평면파 전파로 가정하였다. decomposition method 와는 달리 two-load method는 끝단을 완전한 무반향 조건을 만들지 않아도 되고, two-source method처럼 음원을 이동시키지 않아도 되므로, two-load method를 사용한다. two-load method는 두 load의 임피던스 값이 비슷할 경우 측정이 제대로 이루어지지 않아 결과값이 불안정하게 나오게 된다.^[6] two-load method는 소음기의 전체 전달행렬의 계산에 기반을 둔다. 투과손실은 4개의 마이크로폰이 있는 임피던스 튜브를 사용하여 측정한다. 음원으로부터의 입사파와 반사파 및 소음기를 통과한 후의 입사파와 반사파 사이의 관계를 전달행렬로 표현하면 Eq. (1)와 같이 된다.

여기서 I1과 R1은 각각 임피던스 튜브 입력단에서의 입사파와 반사파를 의미한다. 이와 유사하게 I2와 R2는 임피던스 튜브 출력단에서의 입사파와 반사파를 의미한다. Eq. (1)에서 각 입사파 간의 비를 통해 투과손실을 구할 수 있으며, Eq. (2)와 같이 나타낼 수 있다.

Fig. 1.

Transfer matrix between incident wave and reflected wave.

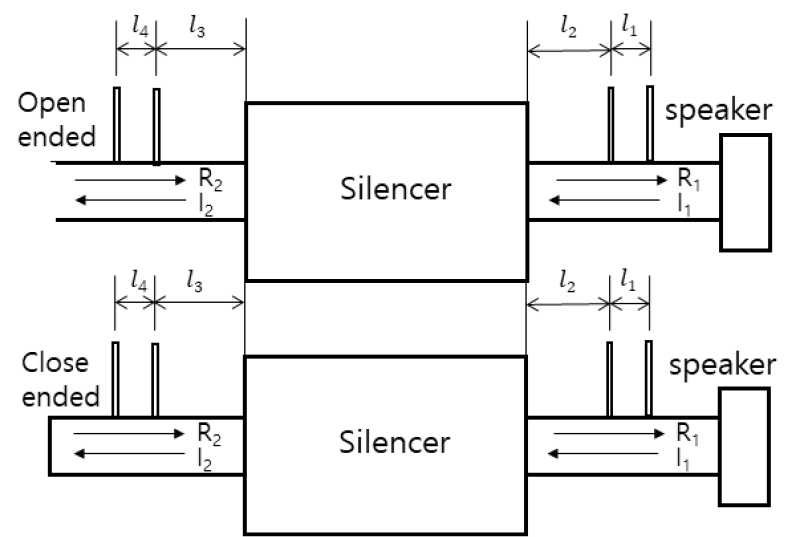
하지만 two-load method에서는 끝단 임피던스를 바꿔주기 때문에 크게 open ended와 close ended 총 두 경우로 나눠서 생각해야 하며, 각각을 전달행렬로 나타내면 Eqs. (3)과 (4)와 같다.

여기서 아래첨자 “O” 와 “C” 는 각각 open ended와 close ended 를 의미한다. Eqs. (3)과 (4)를 이용하여 A에 대해 나타내면 Eq. (5) 와 같이 된다.

음압의 측정위치는 Fig. 2와 같으며, 각 측정위치에서 계측된 음압은 평면파 이론에 따라Eqs. (6), (7), (8), (9)와 같이 표현된다.

Fig. 2.

Schematic diagram of measurement setup of two-load method.

Eqs. (6), (7), (8), (9)를 I1,R1,I2,R2에 대한 식으로 나타내면 Eqs. (10), (11), (12), (13)과 같다.

Eqs. (10), (11), (12), (13)에서의 입사파와 반사파를 P1*를 이용하여 자기스펙트럼 및 상호스펙트럼으로 표현하면 Eqs. (14), (15), (16), (17)과 같이 나타난다.

여기서 S11은 첫 번째 마이크로폰에서 측정된 데이터의 자기스펙트럼을 나타내고, S12,S13,S14는 각각 첫 번째와 2 ~ 4번째 마이크로폰에서 측정된 데이터의 상호스펙트럼을 나타낸 것이다. Eqs. (14), (15), (16), (17)을 이용하여 Eq. (2)를 다시 쓰면 Eq. (18)과 같이 투과손실이 표현된다.^[10]

2.2 실험 방법

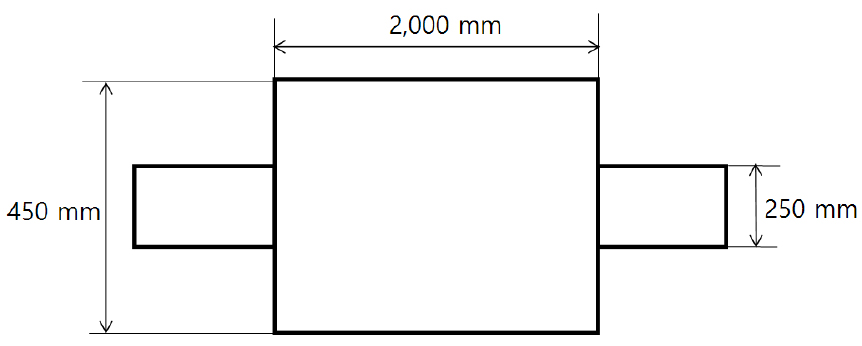
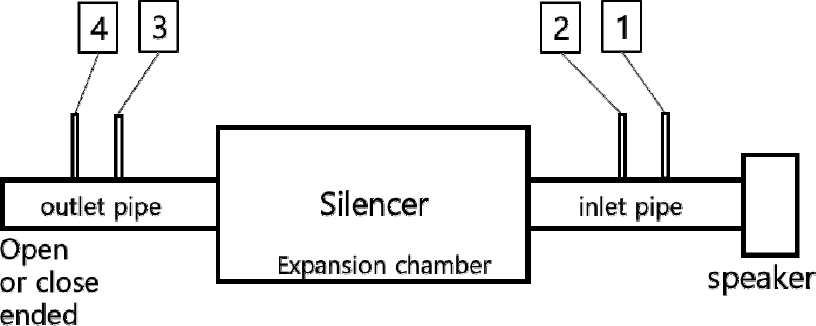
선박용 공조 소음기의 경우 일반적으로 1 m 이하의 길이를 갖지만, 폐기관 소음기의 경우 1 m ~ 8 m 길이로 다양한 길이 및 직경을 갖는다. 본 실험은 길이 2,000 mm, 직경 450 mm인 단순확장형 소음기를 사용하여 실시하였다. 단순확장형 소음기에 대한 개략도는 Fig. 3, 테스트 설정 개략도는 Fig. 4와 같다.

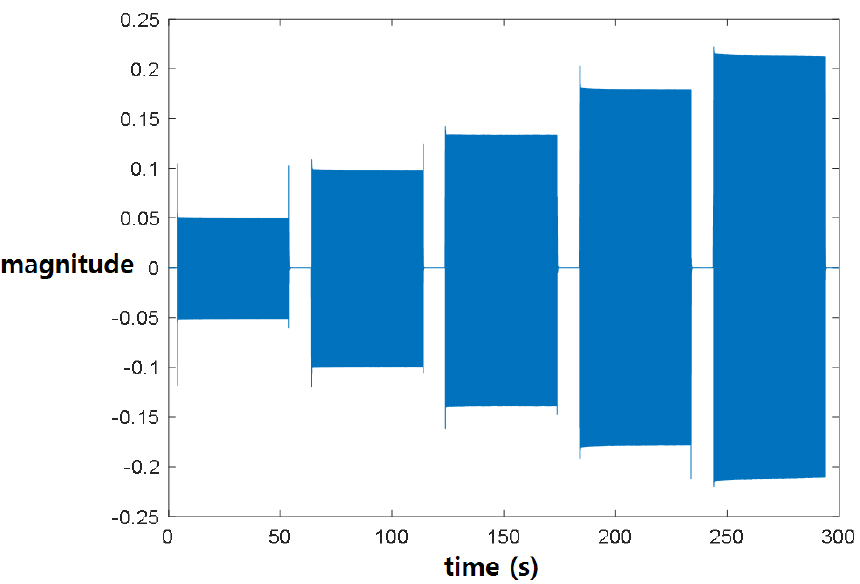
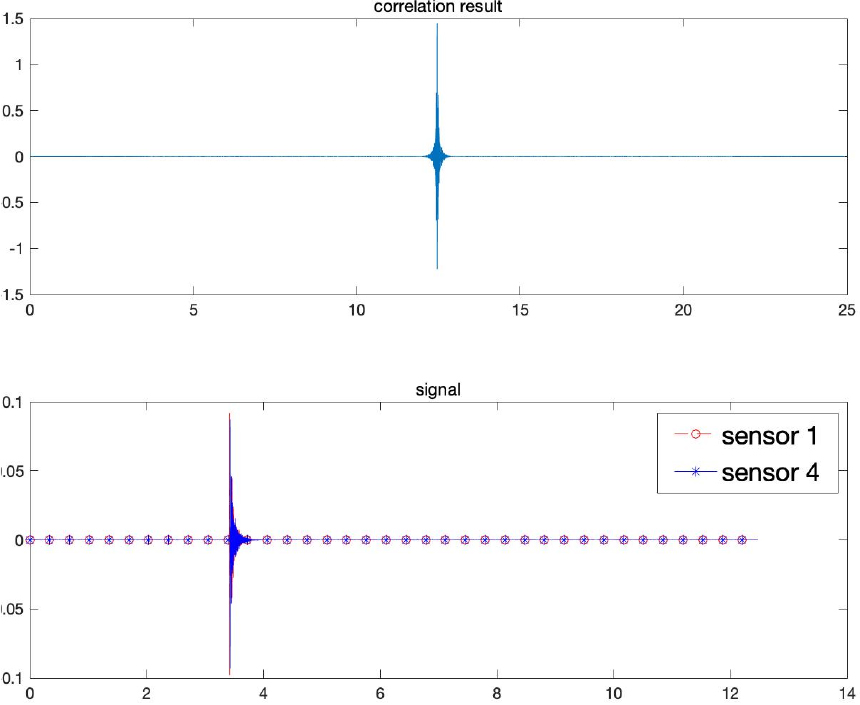
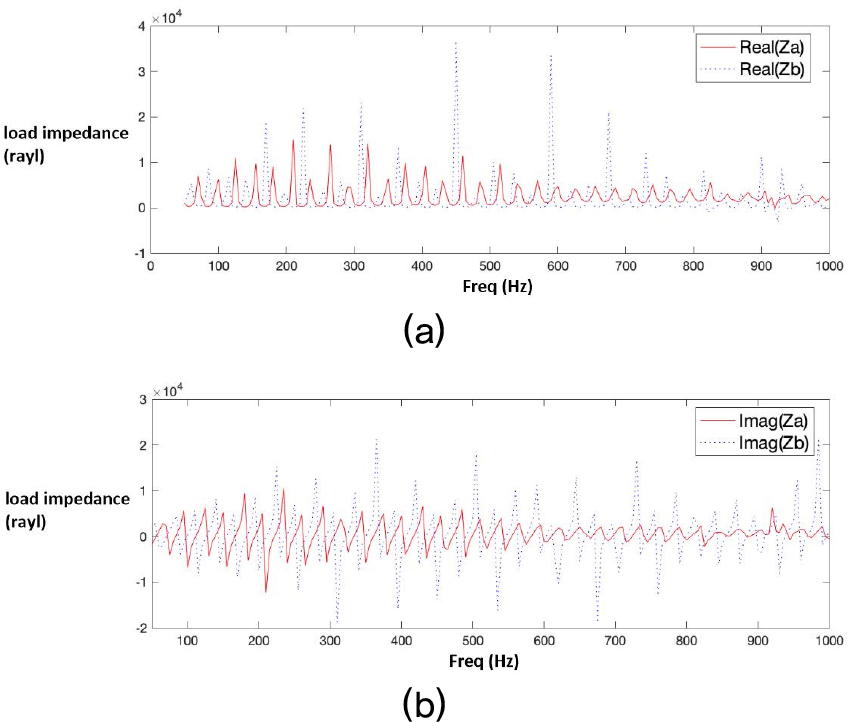
실험에 사용된 스피커는 B&K 4224 지향성 스피커이고, 마이크로폰은 378B02 1/2’’ 자유 음장 마이크로폰이다. 신호는 45 Hz ~ 1,000 Hz까지 주파수를 5 Hz 간격으로 50 s 가진, 10 s 휴식하는 형태의 Continuous Wave(CW) 신호로 사용하였고 시간영역에서 보면 Fig. 5와 같다. 단순확장형 소음기의 투과손실을 Eq. (18)을 사용하여 구하기 위해 실험환경에서의 음속산출을 실시하였다. 음속은 핑 신호가 두 센서에 들어오면 그 신호를 상호상관 관계함수를 이용하여 Fig. 6과 같이 시간지연을 확인하고 센서사이의 거리와의 관계식을 통해 산출하였다. 산출된 음속은 351.3677 m/s이다. 또한 two-load method를 사용하여 투과손실을 측정할 때, load의 임피던스를 다르게 해야하므로 각 load의 임피던스 값을 다르게하여 실험을 실시하였다. 결과는 Fig. 7과 같으며 open-ended 일 때와 close-ended 일 때 load의 임피던스가 다르게 나타나는 것을 확인할 수 있다.

Fig. 3.

Schematic diagram of single expansion silencer used in experiment.

Fig. 4.

Schematic diagram of experimental test setting.

Fig. 5.

(Color available online) Time domain CW signal (45 Hz ~ 1,000 Hz, 5 Hz interval, 50 s excitation and 10 s rest).

Fig. 6.

(Color available online) Time delay of the ping signal from sensor 1 and 4.

Fig. 7.

(Color available online) Load impedance results, (a) real part, (b) imaginary part.

2.3 실험 결과

Eq. (19)는 소음기 투과손실에 대한 이론식을 나타내며, L은 소음기의 길이, m은 소음기와 임피던스 튜브의 단면적 넓이의 비를 의미한다.^[4]

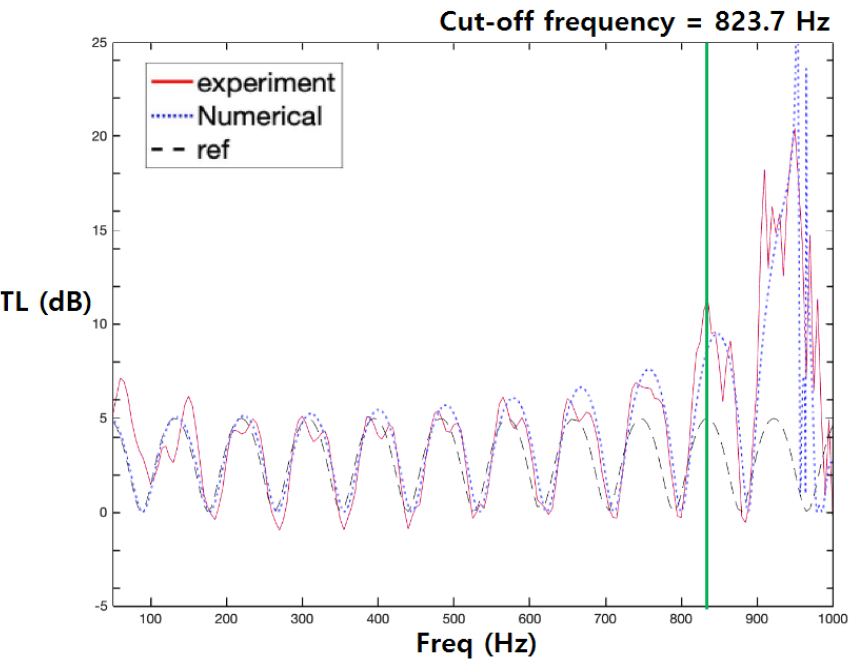
Fig. 8은 소음기 투과손실 결과를 나타내며, 이론식 결과와 비교해볼 때 마루와 골이 위치한 주파수가 일치하며, 투과손실 값 또한 잘 맞는 것을 확인할 수 있다. 주파수가 증가할수록 투과손실 값의 차이가 커지는 것은 기존에 평면파 전파 가정을 하였지만, 평면파 전파에 해당되는 모드뿐만 아니라 고차 모드가 짧게나마 나오게 되고, 소음기를 통과하면서 고차 모드가 모두 사라져 투과손실 값이 높게 산출되기 때문이다.^[11] 추가로 약 820 Hz 이후 투과손실 값의 차이는 실험에서 설정된 차단주파수가 823.7 Hz이므로 차단주파수 이하의 주파수에서의 측정결과만 유효하게 생각할 수 있다.

Fig. 8.

(Color available online) Transmission loss result of single expansion silencer experiment.

III. 소음기 음향성능 시뮬레이션

3.1 배경이론

흡음형 소음기의 경우 단순확장형 소음기와는 달리 흡음재가 내장되어 있다. 흡음재를 통해 음향에너지가 흡수되어 소음기를 통과한 음에너지가 감소하기 때문에 소음이 감소된다. 흡음재의 음향특성은 특성 음향 임피던스와 파수로 나타낼 수 있다. 흡음재는 복잡한 구조로 이루어져 있기 때문에 음향특성은 실험적인 방법을 통해 결정된다.^[12] 이 음향특성을 표현하는 모델은 유동저항을 각 음향특성의 주 변수로 사용하는 Delany-Bazley-Miki 모델,^[12] 공극을 실린더 형태로 가정하고 공극의 직경과 공극률을 주 변수로 하는 Zwikker-Kosten 모델,^[13] Zwikker-Kosten 모델의 확장형으로 전파 방향에 대한 공극의 상대적 방향을 나타내는 굴곡률을 추가 변수로 사용하는 Attenborough 모델^[14] 등 다양한 모델이 있다. 여러 모델 중 음향특성을 유동저항에 대한 식으로 표현할 수 있는 모델은 Delany-Bazley-Miki 모델이다.^[15]

Delany-Bazley-Miki 모델은 다수의 실험 데이터를 통해 특성 음향 임피던스와 파수에 대해 간단한 멱급수 관계를 제시한 모델로 특성 음향 임피던스와 파수는 각각 Eqs. (20) 및 (21)과 같이 표현된다.

여기서 Zc는 특성 음향 임피던스, k는 파수, σ는 유동저항, f는 주파수, w는 각주파수 그리고 ρ0와 c0는 각각 공기의 밀도와 속도를 의미한다. 위의 식은 많은 다양한 흡음재들을 대상으로 실험적 방법을 통해 구한 경험식이다. 흡음재는 미네랄울(또는 암면, 스톤울), 글라스울(또는 유리섬유), 폴리우레탄 등 다양한 종류가 있지만 본 연구에서 다루는 흡음재는 기체배관에 탑재되는 소음기에서 주로 사용하는 미네랄울과 글라스울로 한정한다.

Delany-Bazley-Miki 모델은 유동저항을 입력 매개변수로 한다. 유동저항은 흡음재의 흡음특성을 결정하는 매우 중요한 매개변수 중 하나로,^[16] 유체속도에 대한 샘플의 단위길이에 따른 압력 차이의 비율로 정의된다.^[17] 정의된 식은 Eq. (22) 와 같다.

d는 흡음물질 두께, U는 평균유속, ∆p는 흡음물질 통과 전·후의 압력차를 의미한다. 유동저항의 단위는 N/m⁴ 또는 rayl/m로 나타낸다.

3.2 시뮬레이션 방법

소음기에 대한 시뮬레이션은 유한요소법 기반 범용 해석프로그램을 사용하여 실시하였다. 해석에 있어 지배방정식은 파동방정식을 사용하였고, 계측한 351.3677 m/s를 음속으로, 실험 환경 온도 기준 1.293 kg/m³를 공기밀도로 하였다. 또한 다공성물질의 물성치는 유동저항을 입력하였으며, 음향해석을 위해서 Delany-Bazley-Miki 모델을 적용하였다. 음파가 전파되는 배관은 강체로 가정하였으며, 내부 음파의 전파는 평면파 전파를 가정하였다. 평면파 전파를 가정함으로써 차단주파수 설정이 필요하고, Eq. (23) 과 같이 나타낼 수 있다.

D는 임피던스 튜브의 직경이고, c0는 튜브 내 음속을 의미한다. 실험에 사용된 튜브에서의 평면파 전파에 따른 차단주파수는 823.7 Hz가 된다.

시뮬레이션은 실험결과와 비교하는 1가지 경우와 흡음형 소음기에 대한 5가지 상황까지 총 6가지 상황으로 분류하여 실시하였다. 흡음형 소음기에 대한 실험은 실시하지 않았으므로, Xu et al.의 실험에서 사용된 소음기에 대해 시뮬레이션을 실시하였고, 앞으로의 시뮬레이션 결과에 대한 신뢰성을 얻었다. 나머지 4가지 경우는 흡음재 두께, 유동저항, 소음기 직경 변화 및 흡음재 층 구분에 따른 소음기 분류이며, 각 경우에 대해 시뮬레이션을 실시하였고, 이를 통해 소음기 음향성능의 변화를 확인하였다.

3.3 시뮬레이션 결과

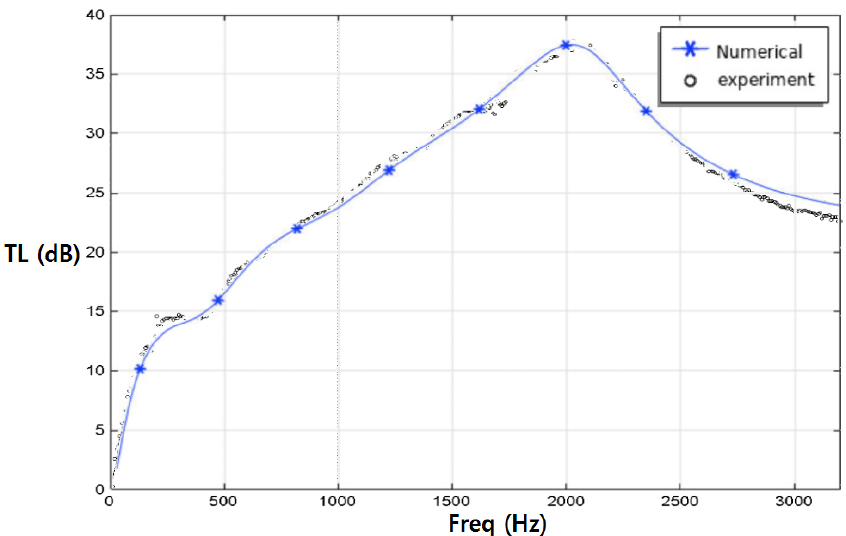
Fig. 9는 Fig. 3형태의 단순확장형 소음기의 실험결과 및 시뮬레이션 결과를 투과손실로 비교한 그래프다. 차단주파수까지 실험결과와 시뮬레이션 결과가 잘 일치하는 것을 확인할 수 있고, 그 이상의 주파수에서는 음파가 전달되지 못하고 오히려 감쇠하여 투과손실이 비정상적으로 증가하는 경향을 보인다. 따라서 차단주파수까지의 결과에 대해서만 유효하게 해석할 수 있다.^[18]

Fig. 9.

(Color available online) Transmission loss results of experimental, theoretical and numerical analysis according to frequency.

Fig. 10은 Xu et al.의 실험에서 사용된 소음기를 시뮬레이션한 결과와 비교한 그래프이다. 시뮬레이션 결과와 실험결과가 잘 일치하는 것을 확인할 수 있으며, 결과를 통해 앞으로 흡음형 소음기 시뮬레이션에 대한 신뢰성을 얻을 수 있다.

Fig. 10.

(Color available online) Transmission loss of experiment and analysis resutls: ∘,experimental; *,numerical.

Fig. 11은 흡음형 소음기에 내장된 흡음재의 두께 변화에 따른 음향성능을 확인하기 위한 개략도이다. 흡음재 두께는 10 mm ~ 100 mm 까지 10 mm 간격으로 구분하였고, 유동저항은 Table 1에서와 같이 많이 사용되는 글라스울과 미네랄울의 유동저항 범위에서 10,000 rayl/m와 20,000 rayl/m를 선정하였다.

Fig. 11.

(Color available online) Schematic diagram of dissipative silencer according to the thickness change of sound absorbing material.

Fig. 12는 흡음형 소음기 내부에 부착된 흡음재의 두께 변화에 따른 음향성능을 시뮬레이션한 결과다. (a)는 유동저항이 10,000 rayl/m, (b)는 20,000 rayl/m의 결과이며, (a)에서는 10 mm 두께 변화당 10 dB 정도의 차이를 보이지만, (b)에서는 5 dB ~ 10 dB 정도로 증가폭이 작아지게된다. 증가폭은 작아지지만 전반적으로 흡음재의 두께가 두꺼워질수록 투과손실이 크게 나타난다.

Fig. 12.

(Color available online) Transmission loss results according to the thickness change of sound absorbing material, (a) flow resistivity : 10,000 rayl/m, (b) flow resistivity : 20,000 rayl/m.

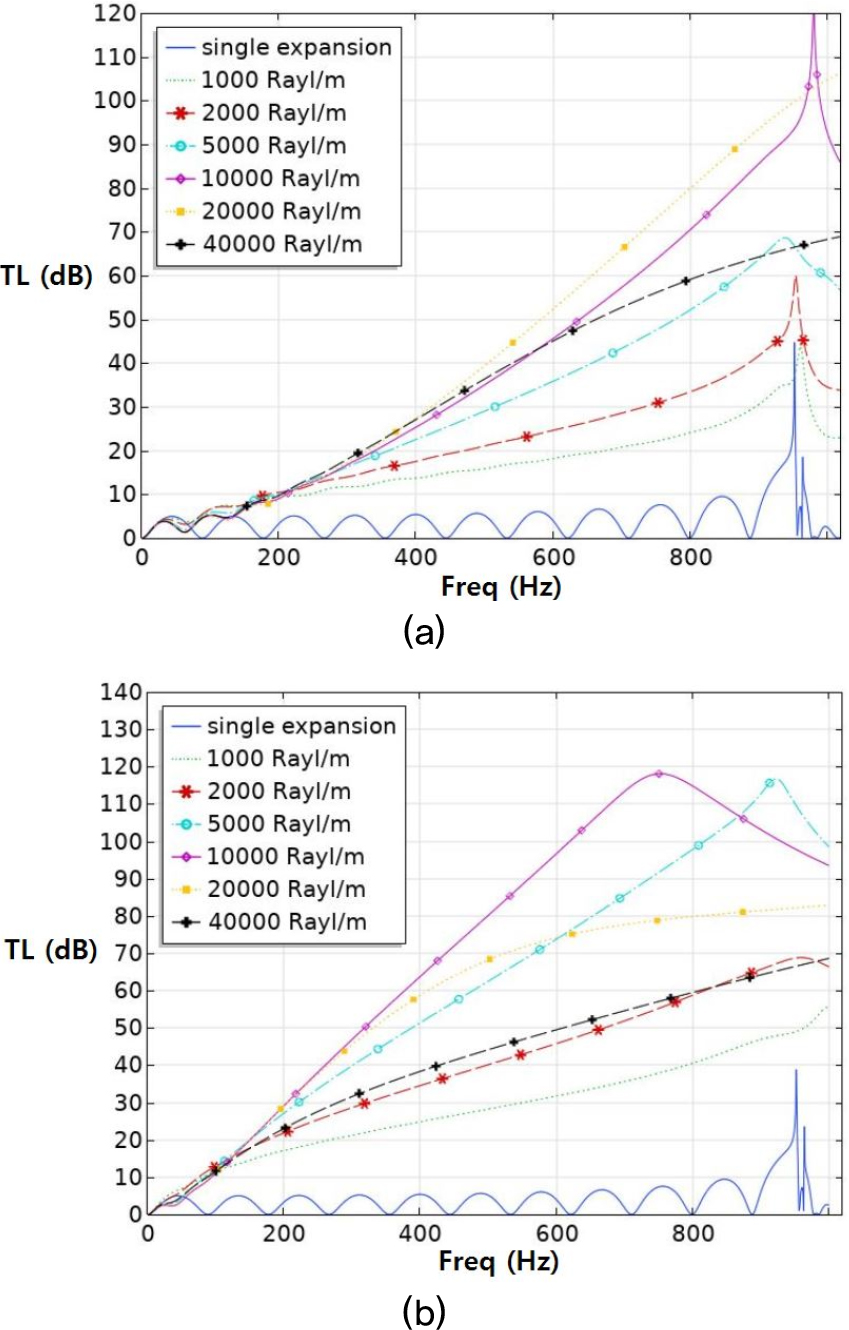
Fig. 13은 흡음재의 유동저항 변화에 따른 소음기 음향성능을 확인하기 위한 개략도이다. 두께에 따른 음향성능 변화와는 달리 흡음재의 유동저항 변화에 따른 음향성능 변화를 확인하기 위해 10,000 rayl/m과 20,000 rayl/m의 앞 뒤로 유동저항 값을 추가하여 해석하였고, 1,000 rayl/m, 2,000 rayl/m, 5,000 rayl/m, 10,000 rayl/m, 20,000 rayl/m, 40,000rayl/m으로 구분하였다.

Fig. 13.

Schematic diagram of dissipative silencer according to the flow resistivity change of sound absorbing material.

Fig. 14는 흡음형 소음기 내부에 부착된 흡음재의 유동저항 변화에 따른 음향성능의 시뮬레이션 결과이다. (a)는 두께가 50 mm, (b)는 100 mm일 때의 결과이며, 전반적으로 유동저항이 증가할수록 투과손실이 증가하지만, (b)에서 보면 20,000 rayl/m부터는 오히려 감소하는 것을 알 수 있다. 또한 유동저항이 일정수준 이상으로 높아지게 되면 임피던스가 증가하게 되고, 음이 흡음재에서 반사되는 양이 커져 투과손실이 감소하게 된다. 즉, 흡음효과가 떨어지게 된다.

Fig. 14.

(Color available online) Transmission loss results according to the flow resistivity change of sound absorbing material, (a) thickness : 50 mm, (b) thickness : 100 mm.

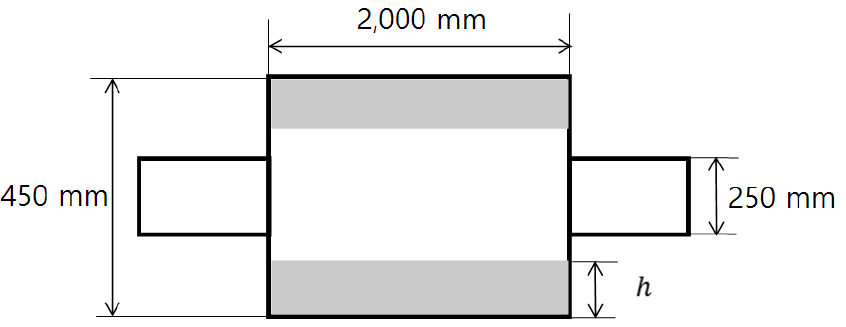
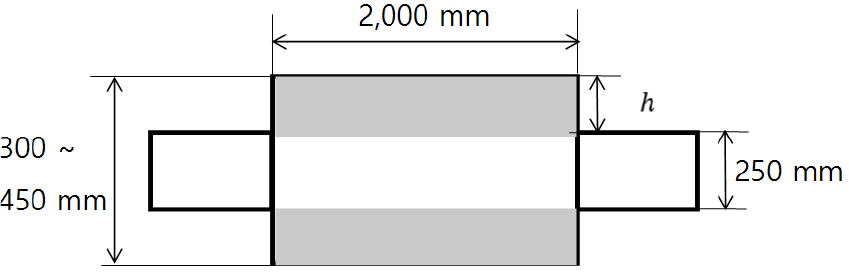
Fig. 15는 입구단에서 흡음형 소음기로 확장될 때 확장된 부분이 모두 흡음재로 채워진 상태로, 흡음재의 두께가 변하면 소음기 직경도 같이 변하는 소음기에 대한 개략도이다. 흡음재 두께는 25 mm ~ 100 mm 까지 25 mm 간격으로 구분하였다.

Fig. 15.

Schematic diagram of dissipative silencer according to the thickness change of sound absorbing material with no empty space in expansion part.

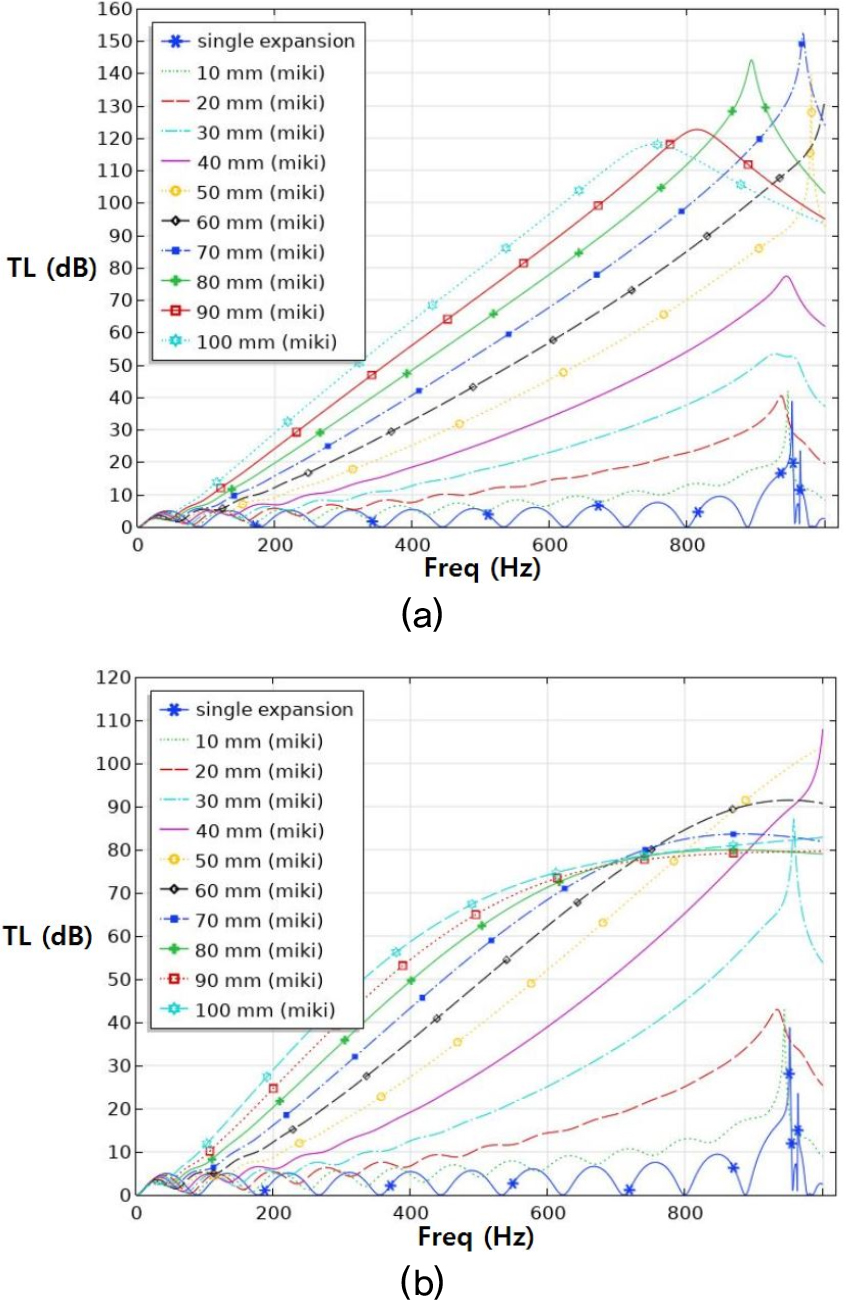
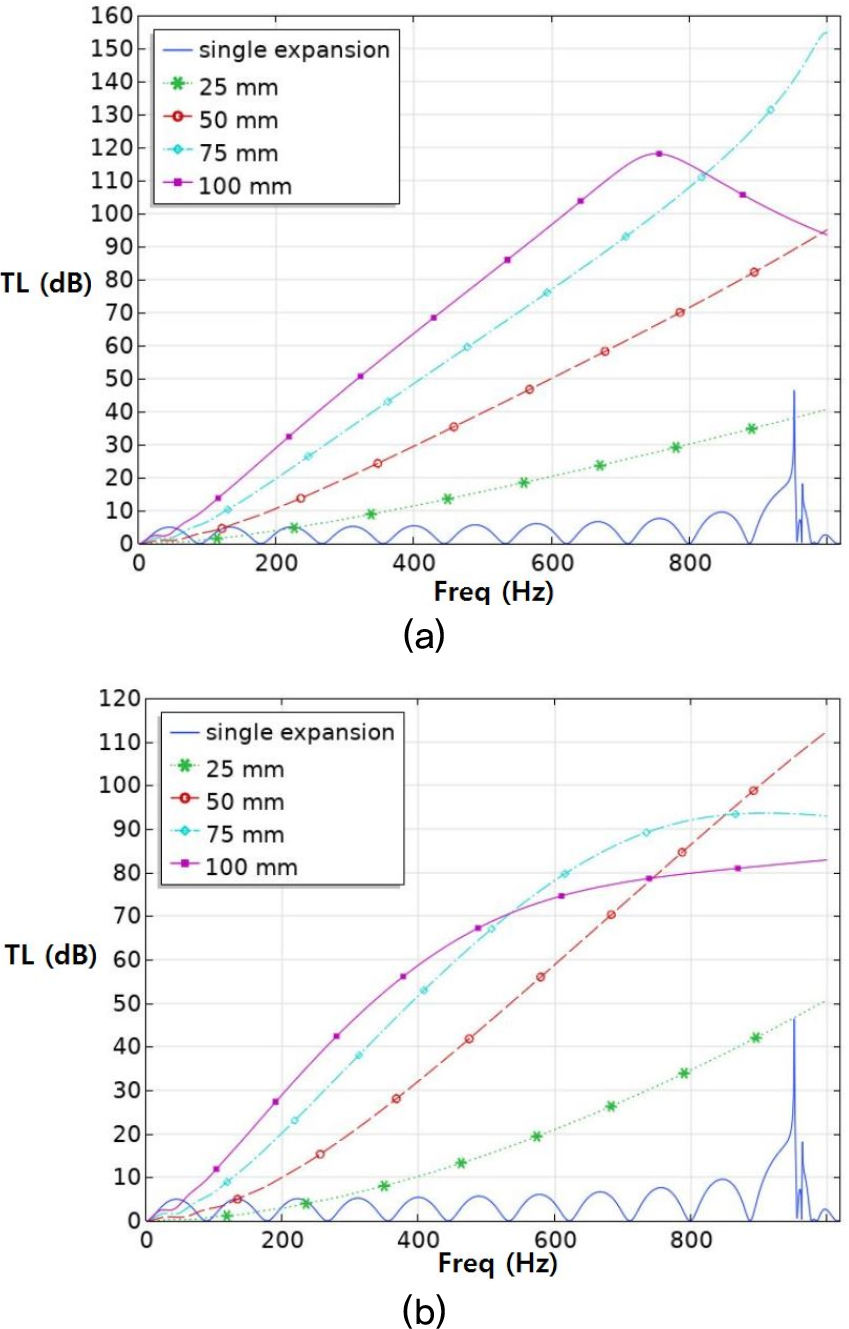
Fig. 16은 흡음형 소음기 내부에 부착된 흡음재의 유동저항 변화에 따른 음향성능의 시뮬레이션 결과이다. (a)는 유동저항이 10,000 rayl/m, (b)는 20,000 rayl/m의 결과이며, (a)와 (b)를 비교해보면 0 Hz ~ 300 Hz의 저주파수 대역에서는 흡음재의 유동저항 변화에 따른 투과손실은 약 3 dB 정도 차이나지만, 소음기 직경을 변경하면서 나타나는 투과손실 변화는 동일한 주파수 범위에서 10 dB 이상의 차이를 보인다. 즉, 소음기의 크기 변화에 따른 흡음효과가 흡음재의 유동저항 변화에 따른 효과보다 더 큰 것을 확인할 수 있다.

Fig. 16.

(Color available online) Transmission loss results according to the thickness change of sound absorbing material with no empty space in expansion part, (a) flow resistivity : 10,000 rayl/m, (b) flow resistivity : 20,000 rayl/m.

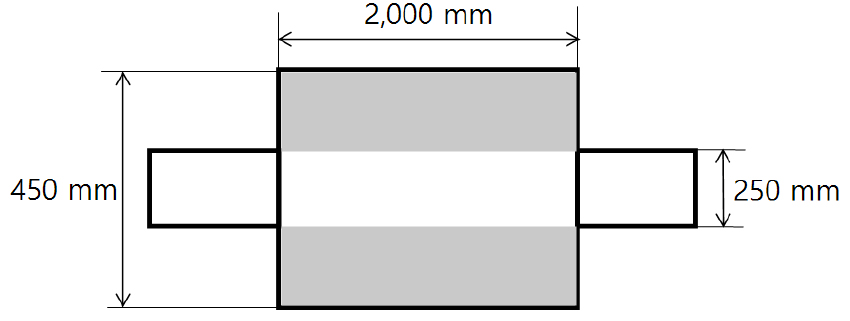
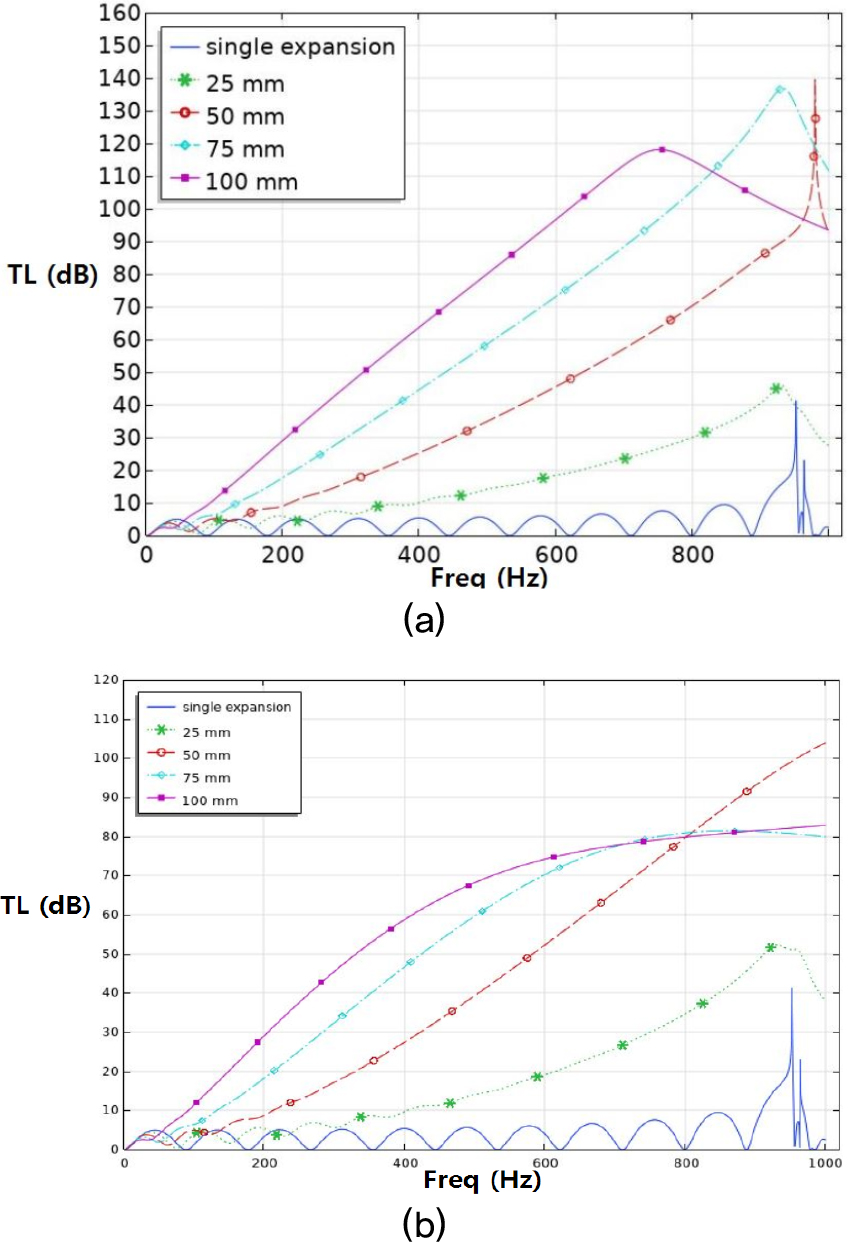
Fig. 17은 소음기 확장부분에 흡음재가 모두 채워지지 않은 상태로 나머지 조건은 Fig. 16과 동일한 소음기에 대한 음향성능 결과이다. Figs. 16과 17의 (a)를 비교해보면 모두 흡음재 두께가 증가할수록 투과손실이 증가하였고, (b)에서는 소음기 직경이 변하는 경우가 그렇지 않은 경우보다 적게는 2 dB에서 크게는 10 dB 이상 흡음효과가 크게 나타난다. 같은 흡음재 두께여도 팽창부분이 모두 채워져 직경이 변한 경우에 흡음효과가 더 크게 나타났다.

Fig. 17.

(Color available online) Transmission loss results according to the thickness change of sound absorbing material, (a) flow resistivity : 10,000 rayl/m, (b) flow resistivity : 20,000 rayl/m.

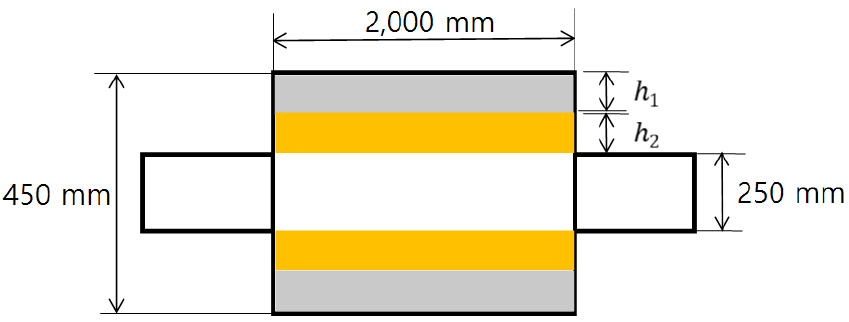
Fig. 18은 두 층의 흡음재로 이루어진 흡음형 소음기의 개략도를 나타낸다. 각 흡음재의 두께 h1,h2는 25/75 mm, 50/50 mm, 75/25 mm 로 구분하였다. 또한 각 흡음재의 유동저항은 10,000 rayl/m, 20,000 rayl/m, 40,000 rayl/m로 구분하였다.

Fig. 18.

(Color available online) Schematic diagram of two-layer dissipative silencer.

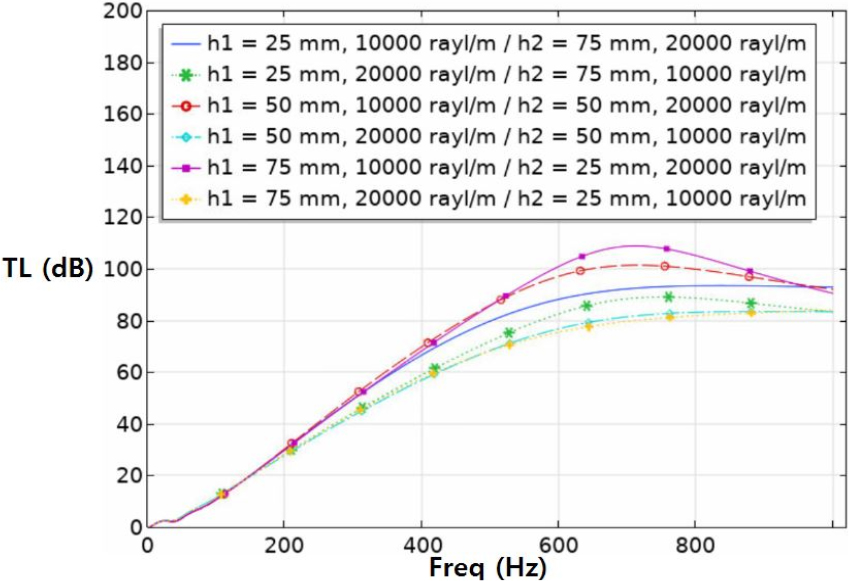
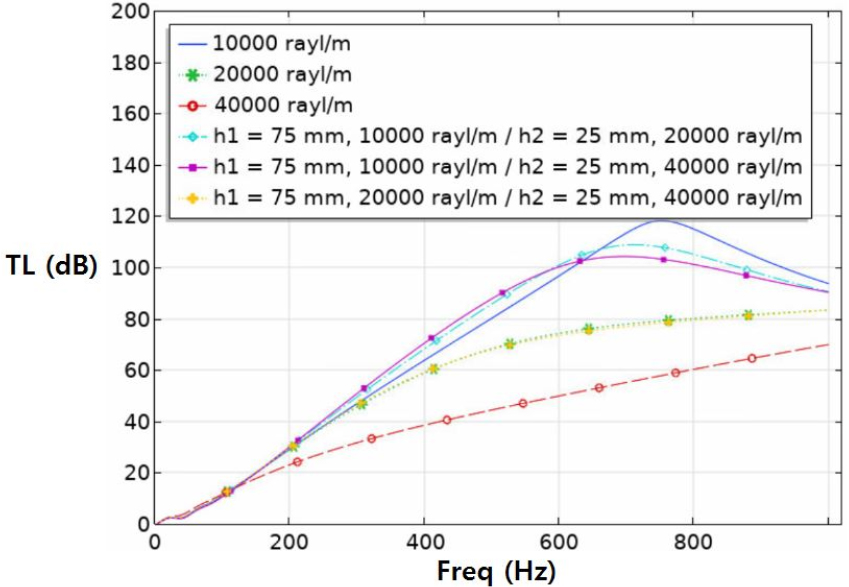
Figs. 19 , 20, 21은 흡음재 층을 구분한 소음기의 시뮬레이션 결과이다. Fig. 19에서는 각 흡음재의 유동저항이 10,000 rayl/m, 20,000 rayl/m인 소음기의 음향성능을 흡음재 두께 구분에 따라 예측한 결과이다. 결과적으로 내측흡음재의 유동저항이 작은 경우가 큰 경우보다 투과손실이 더 크게 나타나므로 Figs. 20과 21에서는 내측흡음재의 유동저항이 더 작은 경우에 대해서만 결과를 확인한다.

Fig. 19.

(Color available online) Transmission loss results of two layer dissipative silencer with each flow resistivity of 10,000 rayl/m and 20,000 rayl/m.

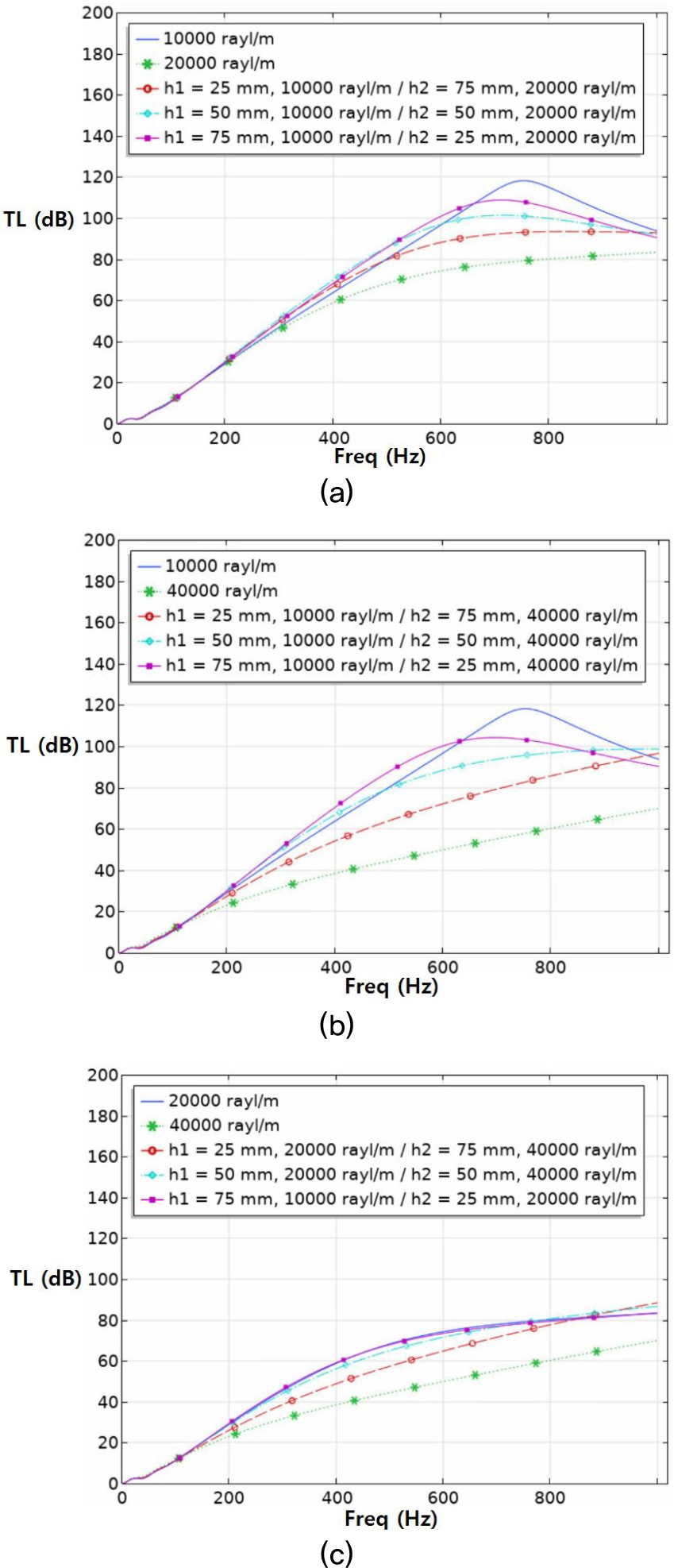
Fig. 20.

(Color available online) Transmission loss results of two layer dissipative silencer according to the thickness change of sound absorbing material, (a) flow resistivity : 10,000 rayl/m, 20,000 rayl/m, (b) flow resistivity : 10,000 rayl/m, 40,000 rayl/m, (c) flow resistivity : 20,000 rayl/m, 40,000 rayl/m.

Fig. 20은 3가지의 유동저항을 2개씩 묶어 3가지 경우에 대해 흡음재 두께 구분에 따른 투과손실 결과와 단일흡음재에 대한 결과를 동시에 나타낸다. (a)에서는 약 660 Hz 이상에서 최대 10 dB 정도 단일흡음재의 경우 흡음효과가 더 크게 나타나고 그 이하의 주파수에서는 두 층의 흡음재가 있는 경우가 약 6 ~ 7 dB 정도 더 크게 나타나는 것을 확인할 수 있다. (b)에서도 약 630 Hz의 주파수에서 (a)와 같은 경향을 보인다. (c)에서는 앞선 두 경우와는 달리 큰 차이를 보이지 않는다. 또한 (a), (b), (c) 모두 내측 두께가 75 mm인 경우 투과손실이 가장 크게 나왔다. 따라서 Fig. 21은 Fig. 20에서 내측 두께가 75 mm인 결과를 선정하여 비교한다. 여기서는 내측흡음재의 유동저항이 10,000 rayl/m, 외측흡음재가 20,000 rayl/m일 때 가장 투과손실이 크게 나타났다. 결론적으로 두 층의 흡음재를 사용하는 소음기의 경우 내측흡음재의 유동저항이 외측흡음재보다 작을 때 소음기의 음향성능이 좋게 나타나고, 약 600 Hz 이하의 저주파수 대역에서는 단일흡음재를 사용하는 경우보다 두 층의 흡음재를 사용하는 경우가 성능이 더 좋게 나타나는 것을 확인할 수 있다.

Fig. 21.

(Color available online) Transmission loss results of two layer dissipative silencer with each thickness of 75 mm and 25 mm.

위의 경우에 대해 모두 비교해보면, 흡음효과가 가장 큰 경우는 약 660 Hz 이하에서 내측흡음재 유동저항이 10,000 rayl/m, 외측흡음재가 20,000 rayl/m인 경우였고, 660 Hz 이상에서는 흡음재가 확장부분에 모두 채워진 상태에서 두께 100 mm, 유동저항 10,000 rayl/m인 경우이다. 결론적으로 전 주파수 대역에서 흡음효과를 높이기 위해서는 소음기의 크기 및 흡음재의 유동저항을 증가시켜야 하지만, 설치 환경 및 흡음재의 유동저항의 영향을 고려하여 최적값을 찾아야 한다.

IV. 결 론

본 논문에서는 흡음재 물성치에 따른 소음기의 음향성능을 수치해석 방법을 이용하여 예측 및 분석하였고, 이를 위해 단순확장형 소음기의 음향성능 결과를 실험 및 수치해석 방법을 통해 비교·검증하였다. 유동이 없는 환경에서 흡음재의 두께, 유동저항 및 흡음재 층 구분 등 4가지 경우로 분류하여 각 경우에 대한 소음기 음향성능을 확인하였다. 그 결과 흡음재 두께가 증가할수록, 유동저항이 커질수록 소음기 음향성능이 증가하였다. 다만, 유동저항이 일정 수준 이상이 될 경우 임피던스의 증가로 인한 음파의 반사로 흡음효과가 감소하였다. 또한 저주파수 대역에서 유동저항보다 소음기 형상의 변화가 음향성능에 더 큰 영향을 미치는 것이 확인되었고, 흡음재를 두 층으로 나눌 경우 내측흡음재의 유동저항이 더 작을 때 성능이 좋게 나타나는 것을 확인하였다. 하지만 흡음재의 물성치를 두께, 유동저항 변화 및 층을 구분하는 정도로 한정하였기 때문에, 추가적인 흡음재의 특성 변화가 음향성능에 미치는 영향을 확인할 수 없는 한계점이 있다. 또한 저주파수 대역에서 음향성능에 더 많은 영향을 미치는 소음기의 형상에 있어 원통형 1가지에 대해서만 실험 및 시뮬레이션을 진행하였기 때문에, 다른 형상의 소음기가 음향성능에 미치는 영향을 확인하는데 한계가 있다. 따라서 전주파수 대역에서 흡음효과를 높이기 위해서는 다양한 형상의 소음기에 대한 실험 및 시뮬레이션을 통해 음향성능에 미치는 영향을 확인할 필요가 있고, 추가적인 물성치를 반영하여 흡음재가 음향성능에 미치는 영향 또한 분석할 필요가 있다. 이를 토대로 형상 및 흡음재 물성치가 소음기 음향성능에 미치는 영향의 정도에 대해 최적화를 통해 최적의 소음기를 선정할 필요가 있다.