A study on the application of residual vector quantization for vector quantized-variational autoencoder-based foley sound generation model

Seokjin Lee

doi:10.7776/ASK.2024.43.2.243

Preview

Research Article

The Journal of the Acoustical Society of Korea. 31 March 2024. 243-252
https://doi.org/10.7776/ASK.2024.43.2.243

A study on the application of residual vector quantization for vector quantized-variational autoencoder-based foley sound generation model

벡터 양자화 변분 오토인코더 기반의 폴리 음향 생성 모델을 위한 잔여 벡터 양자화 적용 연구

Seokjin Lee¹^*

이 석진¹^*

¹경북대학교 전자공학부, 전자전기공학부

^{*Corresponding Author}

ABSTRACT

Among the Foley sound generation models that have recently begun to be studied, a sound generation technique using the Vector Quantized-Variational AutoEncoder (VQ-VAE) structure and generation model such as Pixelsnail are one of the important research subjects. On the other hand, in the field of deep learning-based acoustic signal compression, residual vector quantization technology is reported to be more suitable than the conventional VQ-VAE structure. Therefore, in this paper, we aim to study whether residual vector quantization technology can be effectively applied to the Foley sound generation. In order to tackle the problem, this paper applies the residual vector quantization technique to the conventional VQ-VAE-based Foley sound generation model, and in particular, derives a model that is compatible with the existing models such as Pixelsnail and does not increase computational resource consumption. In order to evaluate the model, an experiment was conducted using DCASE2023 Task7 data. The results show that the proposed model enhances about 0.3 of the Fréchet audio distance. Unfortunately, the performance enhancement was limited, which is believed to be due to the decrease in the resolution of time-frequency domains in order to do not increase consumption of the computational resources.

Keywords

Foley sound generation model

Vector Quantized-Variational AutoEncoder (VQ-VAE)

Residual vector quantization

Generative Model

최근에 연구되기 시작한 폴리(Foley) 음향 생성 모델 중 벡터 양자화 변분 오토인코더(Vector Quantized-Variational AutoEncoder, VQ-VAE) 구조와 Pixelsnail 등 생성모델을 활용한 생성 기법은 중요한 연구대상 중 하나이다. 한편, 딥러닝 기반의 음향 신호의 압축/복원 분야에서는 기존의 VQ-VAE 구조에 비해 잔여 벡터 양자화 기술이 더 적합한 것으로 보고되고 있으며, 따라서 본 논문에서는 폴리 음향 생성 분야에서도 잔여 벡터 양자화 기술이 효과적으로 적용될 수 있을지 연구하고자 한다. 이를 위하여 본 논문에서는 기존의 VQ-VAE 기반의 폴리 음향 생성 모델에 잔여 벡터 양자화 기술을 적용하되, Pixelsnail 등 기존의 다른 모델과 호환이 가능하고 연산 자원의 소모를 늘리지 않는 모델을 고안하여 그 효과를 확인하고자 하였다. 효과를 검증하기 위하여 DCASE2023 Task7의 데이터를 활용하여 실험을 진행하였으며, 그 결과 평균적으로 0.3 가량의 Fréchet audio distance 의 향상을 보이는 것을 확인하였다. 다만 그 성능 향상의 정도가 제한적이었으며, 이는 연산 자원의 소모를 유지하기 위하여 시간-주파수축의 분해능이 저하된 영향으로 판단된다.

키워드

폴리 음향 생성 모델

벡터 양자화 변분 오토인코더 (Vector Quantized-Variational AutoEncoder, VQ-VAE)

잔여 벡터 양자화

생성 모델

MAIN

I. 서 론
II. 벡터 양자화 변분 오토인코더
2.1 변분 오토인코더
2.2 벡터양자화 변분 오토인코더와 잔여 벡터 양자화 기법
III. 잔여 벡터 양자화를 활용한 폴리 음향 생성 모델
3.1 인코더 및 디코더 구조
3.2 잔여 벡터 양자화
3.3 입력 특징 벡터 및 음향 신호 합성
IV. 실험 결과
4.1 실험 및 학습 설정
4.2 실험 결과
V. 결 론

I. 서 론

최근 딥러닝을 기반으로 하는 다양한 모델이 크게 발전함에 따라, 이를 활용하여 영상, 음향 등 미디어 신호를 처리하는 다양한 분야에도 많은 변화가 일어나고 있다. 특히, 주로 원하는 신호를 복원 및 보강하거나 원하지 않는 신호를 제거하는 등의 연구에 집중하던 과거와 달리, 딥러닝 기술을 활용하여 신호의 의미를 파악하거나 원하는 신호를 생성하는 등 다양한 분야에 걸쳐 놀라운 연구 성과들이 얻어지고 있는 추세이다.

특히, 최근 생성모델에 대한 연구가 활발히 이루어지면서 영상,^[1] 텍스트,^[2] 음악,^[3] 음향^[4] 등의 신호를 만들어낼 수 있는 생성 모델들이 개발되고 있다. 그 중에서도 음향 신호를 만들어내기 위한 생성 모델들은 특정 목적을 위한 모델에 대한 여러 방면의 연구가 지속되고 있다. 예를 들어, HiFi-GAN^[5]과 같이 멜-스펙트럼 데이터를 음향 신호로 생성해 준다던가, Diffentiable Digital Signal Processing(DDSP)^[6] 등 기본 음향을 바탕으로 음향 특징을 바꾼 신호를 생성하는 등, 특정 목적에 부합하는 생성 모델을 연구하는 것을 목표로 하는 연구가 진행되고 있는 추세이다.

이러한 목적의 일환으로, 최근에는 폴리(Foley) 음향 생성을 위한 연구가 제안된 바 있다.^[7] 폴리 음향이란 동영상 혹은 영화 제작의 포스트-프로덕션 단계에서 사용될 수 있는 음향 효과음을 뜻하는 것으로, 발자국 소리, 개 짖는 소리, 빗소리 등과 같은 음향 신호를 의미한다. 이러한 음향 신호의 경우 실제 녹음을 통해 얻어질 수도 있지만, 많은 경우 그럴 듯한 소리를 만들어 내기 위해 다양한 트릭을 사용하여 제작되며, 이를 전문적으로 제작하는 ‘폴리 아티스트’에 의해 만들어지기도 한다.

폴리 음향 생성 연구는 이와 같은 폴리 아티스트의 작업에 도움을 주거나, 혹은 일반인들이 영상 제작에 손쉽게 활용할 수 있도록 접근성을 높이는 것을 목표로 한다. 최근 다방면의 음향 생성 모델이 연구되면서 폴리 음향 생성 모델도 함께 연구가 시작되는 단계이며, GAN 모델 혹은 Diffusion 모델과 같은 다양한 생성 모델을 기반으로 시도되고 있다.^[8,9] 본 연구에서는 이 중에서 벡터 양자화 변분 오토인코더(Vector Quantized Variational Autoencoder, VQ-VAE)를 기반으로 하는 연구에 주목하였으며, 이는 폴리 음향 생성을 위한 주요 기법 중 하나로, 저명 경연대회 중 하나인 Detection and Classification of Acoustic Scenes and Events(DCASE) 2023 Task 7 의 기본 모델로도 제시된 바 있다.^[7]

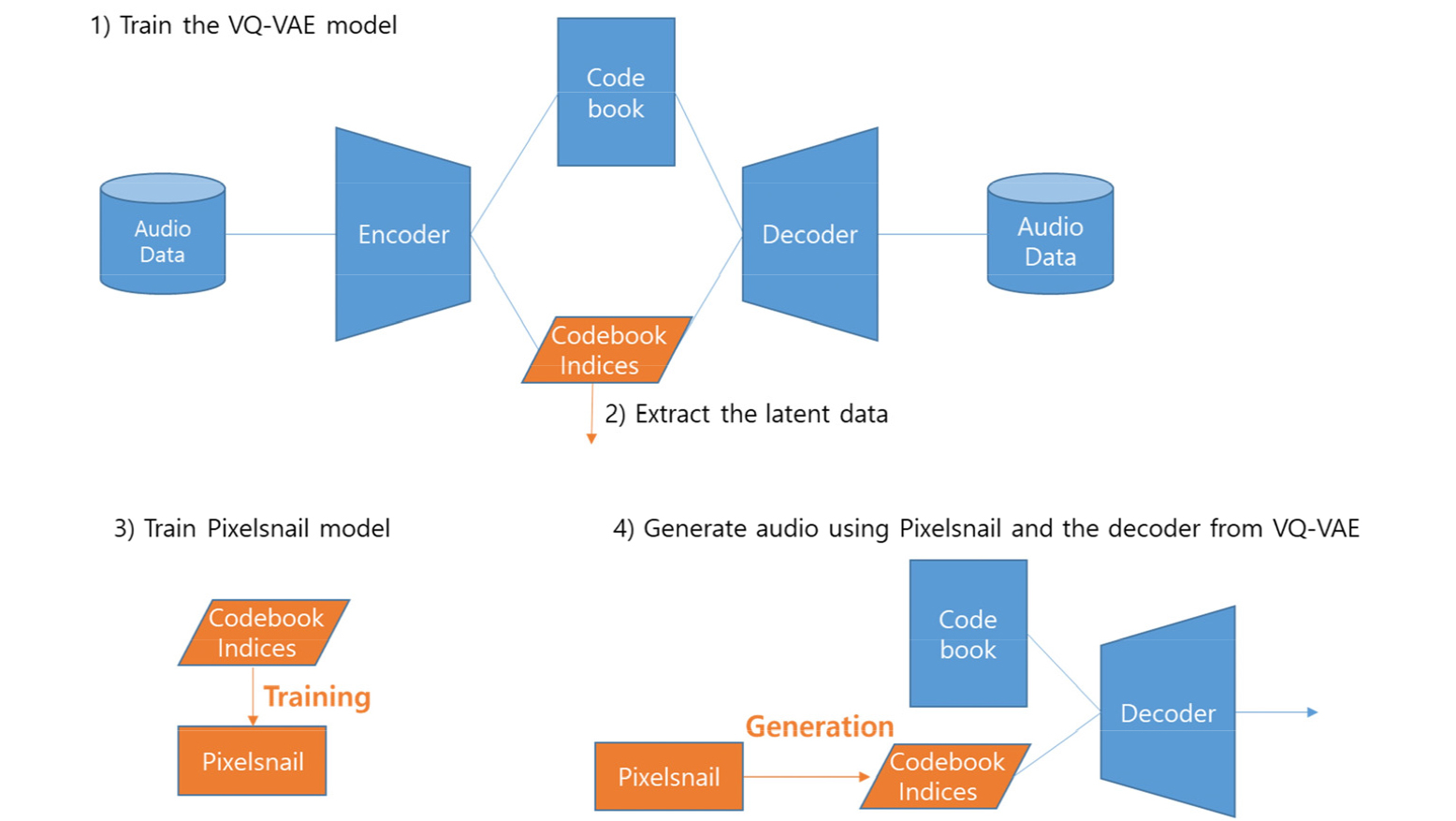
VQ-VAE 기반의 폴리 음향 생성 모델의 학습 및 활용 과정은 Fig. 1과 같다. 1) 폴리 음향 신호들을 벡터 양자화된 잠재 벡터 공간으로 인코딩하는 VQ-VAE를 학습하고, 2) 학습된 VQ-VAE 로 클래스 별 인코딩 결과물을 추출한 후, 3) 추출된 벡터 양자화 코드와 클래스 정보를 활용하여 코드 생성 모델을 학습시키고, 4) 생성된 코드를 VQ-VAE 의 디코더를 활용하여 음향 신호로 변환하면 된다. 이 과정에서 양자화된 코드를 생성하는 코드 생성 모델이 필요한데, 본 연구에서는 DCASE 2023 Task 7 과 동일하게 PixelSnail^[10] 모델을 활용하여 벡터 양자화 코드를 생성하는 모델을 구성하였다.

https://static.apub.kr/journalsite/sites/ask/2024-043-02/N0660430212/images/ASK_43_02_12_F1.jpg

Fig. 1.

(Color available online) Structure and process of deep learning-based Foley sound generation method.

VQ-VAE 모델은 폴리 음향 생성 외에도 음향 신호처리의 여러 분야에 걸쳐 연구되고 있다. VQ-VAE 는 벡터 양자화를 활용하기 때문에 벡터 코드북의 크기와 같은 파라미터에 의해 성능이 영향을 받는다. 최근 연구들에 따르면, 음향 신호의 스펙트럼을 충분히 표현하기 위해서는 코드북의 크기가 매우 커야 하지만, 크기가 큰 코드북은 효율적으로 학습시키기가 어렵고 메모리 등의 자원 소모가 커서 실질적으로 활용하기가 어렵다는 문제가 있다.^[11] VQ-VAE를 주로 활용하는 음향 신호 압축 분야에서는 이러한 문제를 해결하기 위하여 잔여 벡터 양자화(Residual Vector Quantization, RVQ)를 활용하고 있으며, 이를 활용한 모델들이 현재 가장 좋은 성능을 보여주고 있다.^[11,12]

본 논문에서는, RVQ-VAE 기술이 음향 압축 모델이 아닌 폴리 음향 생성 모델에서도 효과적으로 적용될 수 있을지 연구해보고자 한다. 이를 위하여 VQ-VAE 와 PixelSnail 기반의 폴리 음향 생성 모델을 구축하고, VQ-VAE를 RVQ-VAE 로 변형하여 효과를 살펴보고자 한다. 또한, VQ-VAE를 단순히 RVQ-VAE 로 대치하면 잠재 벡터 공간의 크기가 커져서 PixelSnail 모델의 크기가 매우 커지는 문제가 있으므로, 잠재 벡터 공간의 크기를 동일하게 유지하면서 RVQ-VAE를 활용하는 방안을 고안하고, 이 경우에 성능을 향상시킬 수 있는지 살펴보고자 한다.

II. 벡터 양자화 변분 오토인코더

2.1 변분 오토인코더

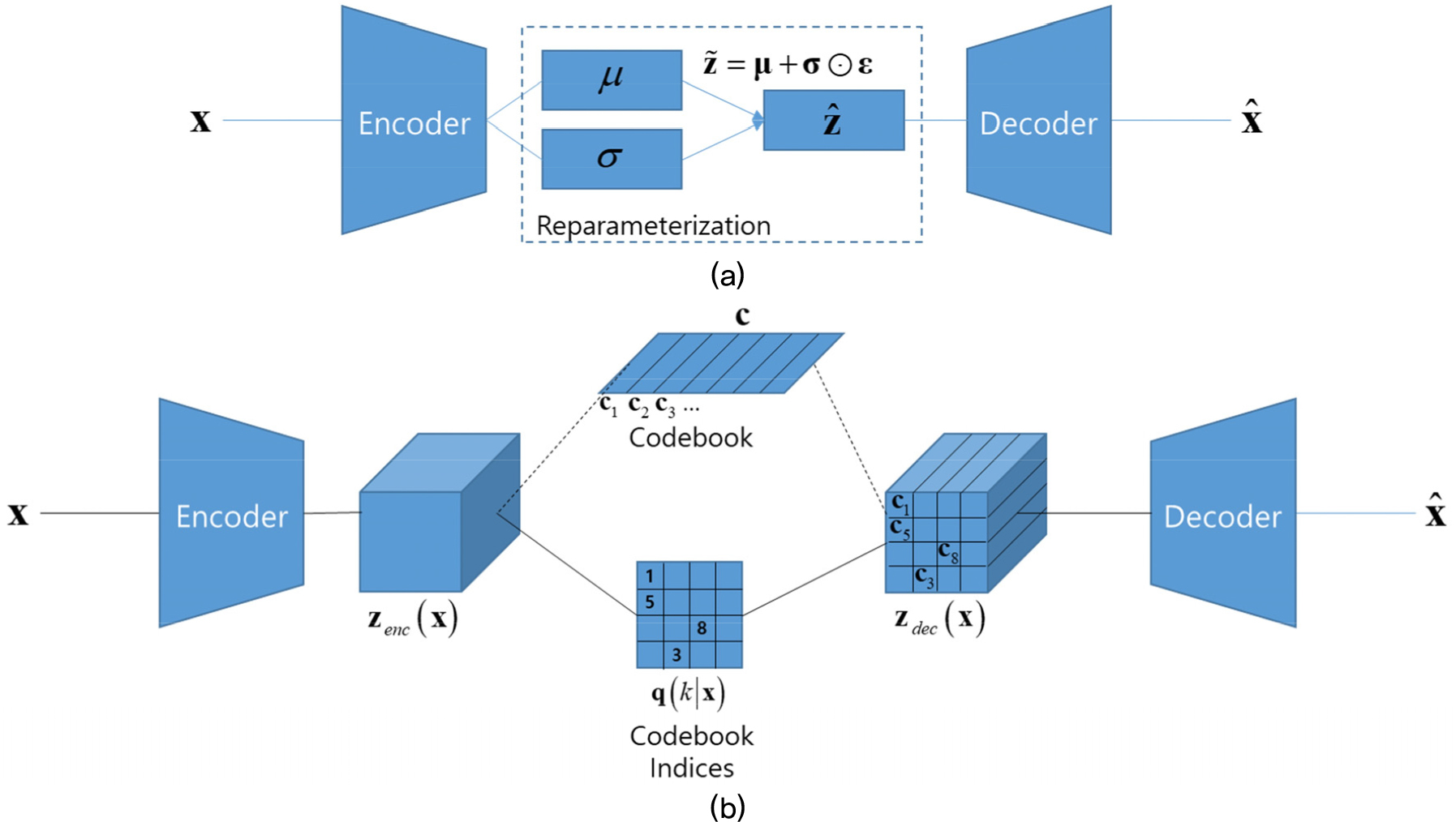
VQ-VAE를 이해하기 위해서는 먼저 변분 오토인코더(Variational Autoencoder, VAE)를 살펴볼 필요가 있다. 변분 오토인코더는 Fig. 2(a)와 같이 인코더와 디코더로 이루어진 오토인코더와 유사한 형태를 가지고 있다. 다만, 일반적으로 데이터를 잠재 벡터 공간으로 변환하는 특징 추출 역할을 수행하는 오토인코더와 달리, 변분 오토인코더는 생성 모델을 목표로 하여 고안된 모델이다.

https://static.apub.kr/journalsite/sites/ask/2024-043-02/N0660430212/images/ASK_43_02_12_F2.jpg

Fig. 2.

(Color available online) Structures of (a) variational autoencoder and (b) vector quantized-variational autoencoder.

랜덤 변수인 관측 가능한 데이터 x가 있고, 이 데이터는 관측 불가능한 랜덤 변수 z로부터 생성된다고 가정하자. 즉, 이 과정은 다음과 같은 두 단계로 생성된다고 가정할 수 있다: 1) 사전 확률 분포 $p_{θ} (z)$ 에 의해 z 생성, 2) 조건부 확률 분포 $p_{θ} (x z)$ 에 의한 x 생성.^[13] 최적 생성 파라미터 𝜃를 찾기 위해 다음과 같은 수식을 통해 최대 우도 추정법(maximum likelihood estimation)을 활용할 수 있다.^[13]

(1)

\log p_{θ} (x^{(i)}) = D_{K L} (q_{ϕ} (z | x^{(i)}) ∥ p_{θ} (z | x^{(i)})) + L (θ, ϕ; x^{(i)}),

여기서 $q_{ϕ} (z | x^{(i)})$ 은 문제를 풀기위해 도입된 인지 모델로, 알기 어려운 사후 확률 분포 $q_{θ} (z | x^{(i)})$ 의 추정값을 의미하며, $D_{K L} (A ∥ B)$ 은 $A$ 와 $B$ 의 Kullback-Leibler 발산을 의미한다. Kullback-Leibler 발산은 항상 0보다 큰 값이기 때문에, 우도는 항상 $L (θ, ϕ; x^{(i)})$ 보다 크게 된다. 따라서 이를 variational lowerbound 혹은 evidence of lowerbound(ELBO)라 하며, 다음과 같은 값을 가진다.^[13]

(2)

L (θ, ϕ; x^{(i)}) = E_{q_{ϕ} (z | x^{(i)})} [\log p_{θ} (x^{(i)} | z)] - D_{K L} (q_{ϕ} (z | x^{(i)}) ∥ p_{θ} (z)),

여기서 E[ ]는 랜덤 변수의 기댓값을 의미한다. 우변의 첫 번째 항은 알고리즘 대상 신호의 잠재 벡터에 대한 생성 신호의 기댓값으로, 복원 오차와 관련된 항으로 생각할 수 있으며, 두 번째 항은 두 확률 분포의 Kullback-Leibler 발산으로 정규화 항으로 해석할 수 있다.^[14]

위에서 언급한 바와 같이 최대 우도 추정법을 활용하기 위해서는 우도의 하한값인 $L (θ, ϕ; x^{(i)})$ 을 최대화하면 된다. 다만, 해당 하한값에 대한 미분값을 얻기가 어려운 문제가 있기 때문에 이를 해결하기 위한 트릭이 필요하다.

VAE를 고안한 Kingma와 Welling은 위와 같은 문제를 재매개화를 통한 몬테 카를로 추정을 활용하여 해결하였다. 미분가능한 변환 $g_{ϕ} (ϵ, x)$ 을 활용하여 재매개화된 랜덤 변수 $\tilde{z} = g_{ϕ} (ϵ, x)$ 를 생성한 후 다음과 같이 통계적 기댓값을 계산한다.^[13]

(3)

E_{q_{ϕ} (z | x^{(i)})} [f (z)] = E_{p (ϵ)} [f (g_{ϕ} (ϵ, x^{(i)}))] ≃ \frac{1}{M} \sum_{m = 1}^{M} f (g_{ϕ} (ϵ^{(m)}, x^{(i)})),

여기서 $ϵ^{(m)}$ 은 특정 확률 분포 $p (ϵ)$ 에 따라 샘플링된 잡음값을 나타낸다. Kimgma 와 Welling 은 위의 미분 가능한 변환 $g_{ϕ} (ϵ, x)$ 으로 딥러닝 네트워크를 활용하는 방안을 제시하고 있다. 먼저 인코더 네트워크를 활용하여 입력신호 $x^{(i)}$ 에 대한 평균 $μ^{(i)}$ 와 표준편차 $σ^{(i)}$ 를 얻는다. 그리고 이를 활용하여 $M$ 개의 샘플링된 잠재 벡터 ${\tilde{z}}^{(i, m)} = μ^{(i)} + σ^{(i)} ⊙ ϵ^{(m)}$ 을 얻는다. 여기서 ⊙은 원소끼리의 곱셈을 의미하며, $ϵ^{(m)} ~ N (0, I)$ 은 정규분포를 따르는 난수값이다. 마지막으로 디코더를 활용하여 샘플링된 잠재 벡터에서 생성 신호를 얻는다. 이 경우 Eq. (2)의 우변 두 번째 항인 정규화 값은 다음과 같이 얻어진다.^[13]

(4)

- D_{K L} (q_{ϕ} (z | x^{(i)}) ∥ p_{θ} (z)) = \frac{1}{2} \sum_{j = 1}^{J} (1 + \log ((σ_{j})^{2}) - (μ_{j})^{2} - (σ_{j})^{2}) .

음향 신호를 대상으로 하는 VAE 에서는 위의 이론을 다음과 같이 구현한다. Fig. 2(a)와 같이 인코더, 재매개화, 디코더로 구성된 딥러닝 구조를 구성한다. 인코더를 활용하여 입력 신호 x를 바탕으로 확률 분포의 𝜇와 𝜎를 얻어 내고, 가우시안 분포를 활용하여 잠재 벡터 $\tilde{z}$ 를 생성, 이를 바탕으로 디코더를 활용하여 생성 신호 $\hat{x}$ 을 얻는다. 이 때 딥러닝 네트워크를 학습하기 위한 손실 함수는 Eq. (2)에 기반하여 다음과 같이 설정한다.^[14]

(5)

L (x, \hat{x}) = D (x, \hat{x}) + \frac{1}{2} \sum_{j = 1}^{J} (1 + \log ((σ_{j})^{2}) - (μ_{j})^{2} - (σ_{j})^{2}),

여기서 $D (x, \hat{x})$ 는 입력 신호와 생성 신호의 거리 함수로, 입력 신호와 생성 신호가 모두 시간-주파수 영역의 데이터인 경우에는 평균 제곱 오차를 활용하기도 하고,^[7] 시간 영역의 파형을 활용하는 경우에는 단시간 푸리에 변환을 수행한 데이터(혹은 그 데이터의 로그함수값)의 평균 제곱 오차를 활용하기도 한다.^[11,14]

2.2 벡터양자화 변분 오토인코더와 잔여 벡터 양자화 기법

벡터양자화 변분 오토인코더, 즉 VQ-VAE 는 VAE 모델의 구조를 활용하되 잠재 벡터 공간을 벡터양자화 기술을 통해 양자화하는 딥러닝 모델이다. Fig. 2(b)에서 보는 바와 같이 VQ-VAE 구조는 기본적으로 VAE 구조와 유사하지만, 가우시안 분포에서 샘플링을 수행하는 VAE의 재매개화 대신 벡터 양자화 구조가 적용되어 있다는 것이 가장 큰 차이점이다.

VQ-VAE 에서는 인코더의 출력 $z_{e n c} (x)$ 를 Fig. 2(b) 의 벡터 양자화 블록을 활용하여 양자화된 디코더 입력 $z_{d e c} (x)$ 를 만든다. 먼저, 인코더 출력 $z_{e n c} (x)$ 과 코드북 $c = \{c_{1}, c_{2}, \dots, c_{N}\}$ 를 비교하여 다음과 같이 원-핫 인코딩된 코드 인덱스 $q^{(i, j)} (k | x)$ 를 만든다.^[15]

(6)

q^{(i, j)} (k | x) = \{\begin{cases} 1 if k = {argmin}_{n} ∥ z_{enc}^{(i, j)} (x) - c_{n} ∥_{2} \\ 0 otherwise \end{cases} .

원-핫 인코딩된 코드 인덱스는 Fig. 2(b) 와 같이 원-핫 인코딩의 역변환을 적용하여 하나의 값으로 나타내기도 한다(데이터 압축이 목적인 경우는 당연히 이쪽이 더 유리하다). 이 후 코드북을 이용하여 양자화된 디코더 입력 $z_{d e c} (x)$ 를 다음과 같이 얻는다.^[15]

(7)

z_{dec}^{(i, j)} (x) = c_{k}, if k = {argmin}_{n} ∥ z_{enc}^{(i, j)} (x) - c_{n} ∥_{2} .

VQ-VAE 의 파라미터를 얻기 위한 손실 함수는 다음과 같이 구성한다.^[15]

(8)

\begin{aligned} L = & \log p (x ∣ Z_{dec} (x)) + {∥ sg [Z_{enc} (x)] - c ∥}_{2}^{2}, \\ + β {∥ Z_{enc} (x) - sg [c] ∥}_{2}^{2} \end{aligned}

여기서 $s g [R I G H T]$ 은 stop gradient 연산자, 즉 기울기 연산을 수행하지 않는 것을 의미한다. Eq. (8)의 첫 번째 항은 인코더와 디코더 파라미터를 학습하기 위한 복원 손실을 나타내고, 두 번째 항은 벡터 양자화 손실, 그리고 세 번째 항은 기여(commitment) 손실을 나타낸다.^[15] 수식에서 볼 수 있듯이 벡터 양자화 손실은 코드북을 학습하는 데에만 사용되는데, VQ-VAE를 활용하는 일부 응용에서는 벡터 양자화 손실을 사용하지 않고 코드북을 $z_{e n c} (x)$ 의 이동 평균으로 갱신하기도 한다.^[16] Soundstream 과 같은 최근의 음향 신호처리 모델에서는 이동 평균을 활용하는 경우가 더욱 많이 발견된다.^[11]

최근 영상 혹은 음향 신호의 압축에 VQ-VAE를 적용하는 연구가 진행된 바 있는데, 특히 음향 신호의 압축 및 복원에 VQ-VAE 가 적용되는 경우 충분한 성능을 내기 위해서는 비현실적인 수준의 코드북 크기가 필요하다는 문제가 제기된 바 있다. Zeghidour et al.은 벡터 양자화를 다음과 같이 여러 단계로 수행하는 잔여 벡터 양자화(Residual Vector Quantization, RVQ)를 적용하는 방안을 제안하였다.^[11]

1. ${\hat{y}}^{(0)} = 0$ , $r^{(0)} = z_{enc} (x)$ 로 초기화한다.

2. $i$ 번째 벡터 코드북을 활용하여 벡터 양자화 결과 $y^{(i)} = y^{(i - 1)} + Q_{i} (r^{(i - 1)})$ 를 얻는다. 여기서 $Q_{i} ()$ 는 양자화 함수를 의미한다.

3. 잔여(residual) 벡터 $r^{(i)} = r^{(i - 1)} - Q_{i} (r^{(i - 1)})$ 를 얻는다.

4. $i = 1, \dots, N_{q}$ 까지 2번 및 3번 작업을 반복한다. 여기서 $N_{q}$ 는 벡터 코드북의 개수를 의미한다.

5. $y^{(N_{q})}$ 를 출력값으로 반환한다. 즉, $z_{dec} (x) = y^{(N_{q})}$ 가 된다.

앞서 언급한 바와 같이, 최근의 연구를 통해 음향 신호의 압축 및 복원에 있어서 VQ-VAE에 비해 RVQ-VAE 구조가 훨씬 유리한 것을 확인할 수 있다. 다만, 아직 폴리 음향 생성 모델과 같이 다른 분야의 VQ-VAE 응용 구조에서도 RVQ-VAE 구조가 유리한지에 대해 연구가 더 필요한 상황이다. 따라서, 서론에서 언급한 바와 같이, 본 논문에서는 RVQ-VAE 구조를 활용한 폴리 음향 생성 모델을 구축하고 그 성능을 살펴보고자 한다.

III. 잔여 벡터 양자화를 활용한 폴리 음향 생성 모델

본 논문에서는 Fig. 1과 같이 VQ-VAE를 활용하여 음향 신호를 잠재 벡터로 변환하고 Pixelsnail 모델을 활용하여 클래스에 맞는 잠재 벡터를 생성하는 모델을 baseline으로 활용하여, RVQ를 적용하여 성능을 개선할 수 있을지 여부를 확인하고자 한다. 기존의 VQ를 RVQ 로 바꾸면 코드북의 개수만큼 코드북 인덱스, 즉 $q (k | x)$ 의 개수도 늘어나게 되는데, 이 경우 Pixelsnail 의 구조도 크게 바뀌어야 하는 문제가 있다. 특히, Pixelsnail은 선형레이어를 포함하고 있기 때문에 출력 데이터의 크기가 커지는 경우 파라미터의 개수도 크게 바뀌는 문제가 있다. 따라서, 본 논문에서는 기존의 Pixelsnail의 구조를 크게 바꾸지 않도록 $q (k | x)$ 의 형태를 최대한 유지한 채로 RVQ를 적용할 수 있는 방안을 고안하였다.

본 논문에서 제안하는 구조에서는 baseline과 마찬가지로 Pixelsnail 모델을 활용하여 클래스 별 코드북 인덱스 데이터를 생성한다. 본 연구에 사용한 Pixelsnail은 범용적인 2차원 데이터를 생성하는 모델이고, baseline 모델과 동일한 구조를 활용하였기 때문에 본 논문에서 상세히 언급하지는 않겠다. 구체적인 구조는 Reference [7]에서 확인할 수 있다. 본 논문에서 고안한 RVQ-VAE의 구조는 Fig. 3에서 살펴볼 수 있다.

https://static.apub.kr/journalsite/sites/ask/2024-043-02/N0660430212/images/ASK_43_02_12_F3.jpg

Fig. 3.

(Color available online) Structures of (a) baseline model, (b) proposed model, and (c) proposed residual vector quantization.

3.1 인코더 및 디코더 구조

본 논문에서는 DCASE2023 Task7에서 활용된 오토인코더 구조를 참고하여 인코더와 디코더 구조를 구축하였다. Fig. 3에서 보는 바와 같이 인코더는 서로 다른 커널 크기를 가지는 4 개의 인코더 블록이 병렬로 구성되어 있으며, 각 인코더 블록은 3개의 2차원 콘볼루션 레이어와 1개의 잔여블록(residual block)으로 이루어져 있다.

후술할 바와 같이, 제안하는 RVQ-VAE 모델은 양자화 인덱스 행렬, 즉 $q (k | x)$ 의 개수가 늘어나게 되는데, 이 데이터는 Pixelsnail 이 생성해야 하는 값이기 때문에 양자화 인덱스 행렬의 전체 크기가 커지면 Pixelsnail이 거대해지는 문제가 있다. 수 시간 내로 학습이 끝나는 VQ-VAE 모델과 달리 Pixelsnail 모델은 학습에 수 일이 걸릴 정도로 파라미터의 개수가 많기 때문에, 생성할 데이터의 크기가 커지는 것은 학습 과정에 있어서 심각한 부담이 된다.

따라서, 본 논문에서 고안한 RVQ-VAE 구조의 인코더 및 디코더에서는 stride의 크기를 늘려서 시간-주파수 축의 분해능을 크게 만들었으며, 오토인코더 구조 부분에서는 이것이 baseline과의 차이점이다.

3.2 잔여 벡터 양자화

제안된 RVQ-VAE 모델 중 기존 baseline과 가장 큰 차이점을 가지는 부분은 잔여 벡터 양자화 모듈이다. Fig. 3(a)에서 보는 바와 같이 baseline 모델에서는 하나의 코드북으로 한 번의 벡터 양자화 작업이 수행되는 반면, 제안하는 RVQ-VAE 모델은 Fig. 3(b)에서 보는 바와 같이 4개의 코드북으로 4 번의 벡터 양자화 작업을 수행하게 된다. 그 과정에서 생성된 4개의 코드북 인덱스, 즉 $q (k | x)$ 데이터는 Pixelsnail에서 생성이 가능하도록 주파수 축 방향으로 2차원 행렬 형태로 연결한다. 즉, Fig. 3(b)에서 보는 바와 같이 (10×43) 크기의 행렬 4개가 모여 (40×43) 크기의 행렬이 된다.

Eq. (8)에서 보는 바와 같이 VQ-VAE를 학습시키기 위한 손실 함수는 복원 손실, 벡터 양자화 손실, 기여 손실의 3개의 항으로 이루어져 있다. Soundstream 등 음향 신호를 다루는 최근의 VQ-VAE 기반 모델에서는 벡터 양자화 손실을 활용하여 코드북을 학습하는 대신 이동 평균 함수를 이용하여 코드북을 학습하는 경우가 많다.^[11,12] 본 연구에서도 이동 평균 함수를 활용하여 코드북을 학습하였으며, 따라서 벡터 양자화 손실을 제외한 복원 손실과 기여 손실만을 사용하여 모델을 학습하였다.

3.3 입력 특징 벡터 및 음향 신호 합성

Baseline 모델과 마찬가지로, 제안하는 RVQ-VAE 모델의 입력으로는 멜-스펙트럼이 사용되었다. 따라서, Pixelsnail 로 생성된 코드북 인덱스 데이터를 RVQ-VAE 의 디코더로 변환하게 되면 음향 신호의 파형 데이터가 아닌 멜-스펙트럼 데이터가 생성된다. 따라서, 멜-스펙트럼 데이터로부터 음향 신호를 합성해 낼 필요가 있는데, 본 연구에서는 Baseline 과 동일하게 사전에 학습된 HiFi-GAN^[5]을 활용하여 음향 신호를 합성하였다. HiFi-GAN 의 사전 학습 모델은 DCASE2023 Task7을 통해 제공된 모델을 별도의 학습 과정 없이 그대로 활용하였다.

IV. 실험 결과

4.1 실험 및 학습 설정

폴리 음향 생성 모델에서의 RVQ 의 적용 효과를 살펴보기 위하여, PC를 활용한 폴리 음향 생성 실험을 다음과 같이 수행하였다.

본 연구에서는 DCASE2023 Task7에서 제공된 데이터셋을 활용하였다.^[7] 본 데이터셋은 UrbanSound8K, FSD50K, BBC Sound Effects 등에서 추출된 데이터로, 7개의 클래스에 대해 총 4,850개의 데이터로 구성되어 있다. 각 데이터는 4 s 길이의 16 비트 양자화 및 22050 Hz 샘플링 주파수로 가공되어 있으며, 각 클래스 별 데이터 구성은 Table 1과 같다. 각 음향 데이터는 75 % 중첩된 1024 길이의 창함수를 사용하여 80개의 멜-주파수 빈으로 변환되었다.

Table 1.

Composition of training dataset (from References [7]).

Class ID	Category	Number of Files
0	DogBark	617
1	Footstep	703
2	GunShot	777
3	Keyboard	800
4	MovingMotorVehicle	581
5	Rain	741
6	Sneeze/Cough	631

RVQ-VAE 구조는 Adam^[17] 최적화 기법을 사용하여 0.0003의 학습률로 학습되었다. 학습에 사용된 데이터의 배치 크기는 16으로 설정되었고, 600 에포크 동안 학습이 진행되었다.

Pixelsnail 모델은 DCASE2023 Task7서 제공되는 모델과 동일한 모델 구조를 사용하되, 생성되는 데이터의 크기만 기존 (20×86)에서 (40×43)으로 변경되었다. 학습은 Adam^[17] 최적화 기법을 사용하여 0.004의 학습률로 수행되었고, 데이터의 배치 크기는 16으로, 1500 에포크 동안 학습이 진행되었다.

생성된 데이터로 성능을 평가하기 위해서는 Fréchet Audio Distance(FAD)^[18]를 사용하였다. 해당 지표는 두 확률 분포의 거리를 측정하는 Fréchet Distance에 음향 신호로 학습된 범용 모델인 VGGish^[19]를 적용하여 개발된 지표로, DCASE2023 Task 7에서 폴리 음향 생성 모델에 대한 표준 성능 지표로 사용된 바 있다. 본 연구에서는 해당 경연대회에서 제공하는 도구를 활용하여 모델의 성능을 평가하였다.

4.2 실험 결과

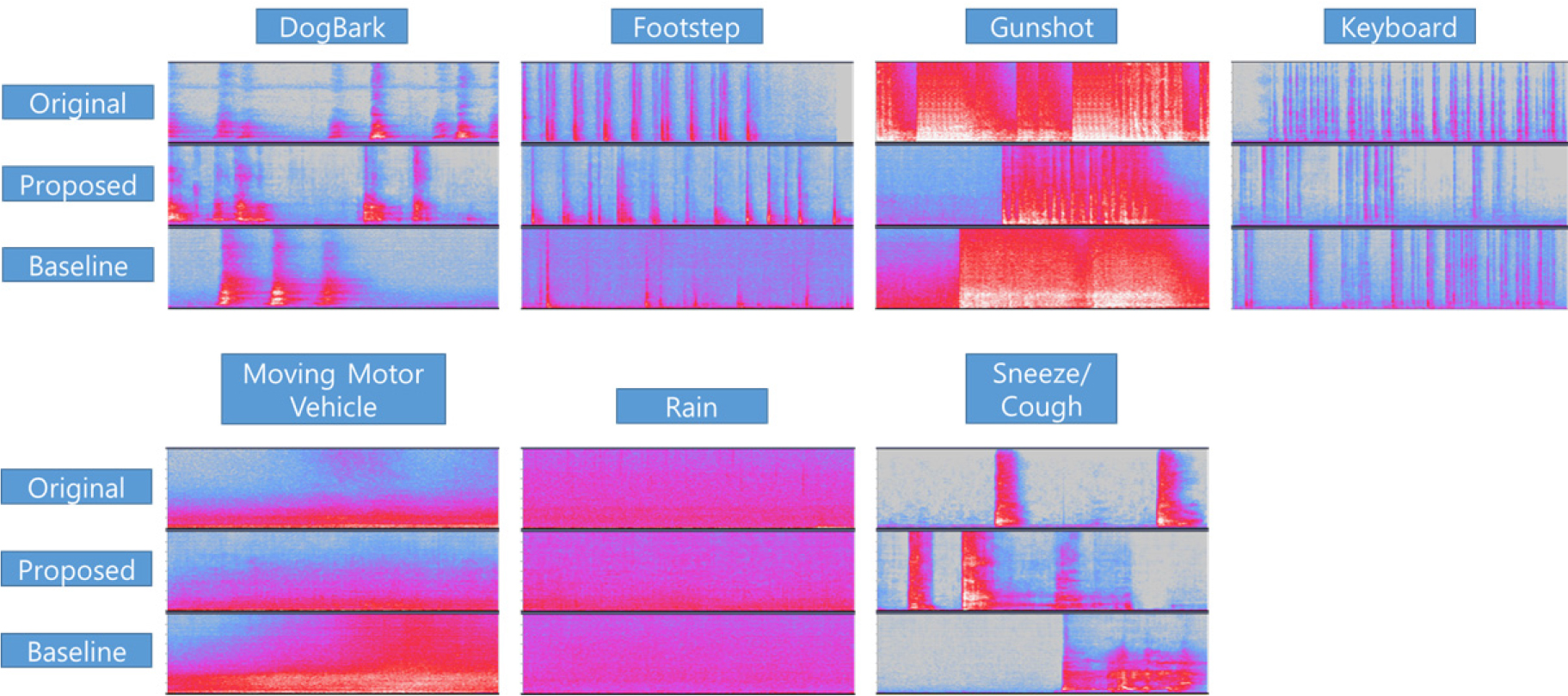
Fig. 4 는 클래스 별 생성된 데이터의 예시를 보여주고 있다. 해당 데이터가 전체 데이터의 성능을 대표할 수는 없으나, 적어도 입력 클래스와 유사한 형태의 데이터를 생성하고 있음을 보여주고 있다.

https://static.apub.kr/journalsite/sites/ask/2024-043-02/N0660430212/images/ASK_43_02_12_F4.jpg

Fig. 4.

(Color available online) Examples of spectrograms of generated Foley sound signals (using linear axis for frequency).

Table 2는 VQ-VAE를 활용한 baseline 모델과, RVQ-VAE를 활용한 제안 모델의 FAD 성능 결과를 보여주고 있다. FAD는 확률분포 상의 거리를 나타내므로, 해당 수치가 작을수록 더 적합한 생성 결과를 나타낸다. Table 2의 두번째 열(RVQ-VAE)이 제안하는 모델의 성능을 나타내고 있다. Baseline 과 비교하였을 때 강아지 짖는 소리(Class 0)와 키보드 소리(Class 3), 그리고 자동차 소리(Class 4)에서 baseline 모델이 더 좋은 성능을 보이지만, 이 중 Class 0과 3의 경우에는 그 차이가 매우 작은 것을 확인할 수 있다. 그 외의 Class에서는 RVQ-VAE 가 더 좋은 성능을 보이는 것을 확인할 수 있으며, 평균적인 수치도 향상된 것을 확인할 수 있다.

Table 2.

Performance comparisons with FAD.

Class ID	Baseline (VQ-VAE)	RVQ-VAE	RVQ-VAE (stride = (4,2))	RVQ-VAE (stride = (2,4))
0	10.21	10.31	14.73	12.78
1	7.50	7.22	11.99	7.23
2	9.62	8.81	11.22	9.97
3	3.69	3.73	5.09	4.11
4	12.81	13.71	24.91	15.41
5	13.13	11.40	17.70	11.05
6	3.55	3.05	3.97	2.39
Avg.	8.64	8.32	12.80	8.99

전술한 바와 같이 제안하는 모델에서 학습 비용의 증가 없이 RVQ-VAE를 적용하기 위해서 오토인코더의 stride를 늘려서 분해능을 크게 만든 바 있는데, 이에 대한 부작용을 확인하기 위하여 stride 의 구조를 바꾼 모델의 성능을 함께 확인하였다. Table 3의 세 번째 열(RVQ-VAE with stride = (4, 2))은 오토인코더 구조 중 stride가 적용되는 2개의 컨볼루션 레이어를 모두 (4, 2)로 설정한 모델로, baseline 모델 대비 시간축의 분해능을 그대로 유지하고 주파수 분해능을 4배로 크게 한 모델이다[제안하는 모델은 2개의 컨볼루션 레이어에 각각 (2, 2)와 (4, 4)의 stride를 활용한다]. 또한, Table 3의 네 번째 열[RVQ-VAE with stride = (2, 4)]는 역시 2개의 stride를 모두 (2, 4)로 설정한 모델로, 주파수 분해능을 유지하고 시간축 분해능을 4배로 크게 한 모델이다. Table 3의 결과를 보았을 때 주파수축 분해능을 크게 한 모델(세 번째 열)은 성능이 매우 저하된 것을 확인할 수 있고, 시간축 분해능을 크게한 모델(네 번째 열)의 경우 빗소리(Class 5) 및 코골이(Class 6) 소리의 성능이 향상된 반면 나머지 성능이 저하된 것을 확인할 수 있다. 이는 생성되는 소리의 시간-주파수 축 특성에 대한 차이일 것으로 판단되는데, 강아지 짖는 소리나 총소리 등에 비해 빗소리 등의 시간 축 변화가 더 적기 때문이다.

Table 2의 결과를 종합해보면, 잠재벡터의 크기를 크게 하지 않는 조건 하에서 기존의 VQ-VAE 대비 RVQ-VAE 모델이 다소 향상된 성능을 보이는 것으로 판단된다. 하지만 그 성능 향상의 정도가 두드러지게 큰 것은 아닌 것으로 보이는데, 이는 잠재벡터의 크기를 유지하기 위해 시간-주파수 축의 분해능을 저하시킨 것이 성능에 부정적인 영향을 주기 때문으로 추측된다.

V. 결 론

본 논문에서는 폴리 음향 생성 모델에 적용되는 VQ-VAE 모델을 대상으로, 최근 음향 신호의 압축/복원 모델에 활용되는 잔여 벡터 양자화 기술을 적용하여 성능을 향상시킬 수 있는지를 연구하고자 하였다. 잔여 벡터 양자화 기술에서는 코드북의 개수가 늘어나기 때문에 생성 모델에서 생성해야 할 잠재벡터의 데이터 또한 늘어나는데, 이 경우 성능은 향상될 수 있지만 실제로 사용하기가 어려운 문제가 있다. 따라서, 본 논문에서는 잠재벡터의 크기와 형태를 유지한 채로 잔여 벡터 양자화 기술을 적용하는 구조를 고안하여 실험을 진행하였다.

본 연구에서는 DCASE2023 Task7의 데이터를 활용하여 폴리 음향 생성 실험을 진행하였으며, 그 결과 제안하는 모델이 기존 대비 평균적으로 향상된 성능을 보이는 것을 확인하였다. 다만 그 성능 향상 정도가 다소 제한적이었으며, 이는 잠재 벡터의 크기를 그대로 유지하기 위하여 시간-주파수 축 분해능이 저하된 영향으로 판단된다.

Acknowledgements

이 논문은 2023학년도 경북대학교 연구년 교수 연구비에 의하여 연구되었음

References

A. Ramesh, M. Pavlov, G. Goh, S. Gray, C. Voss, A. Radford, M. Chen, and I. Sutskever, "Zero-shot text-to-image generation," Proc. ICML, 8821-8831 (2021).

OpenAI, "GPT-4 technical report," arXiv preprint, arXiv:2303.08774 (2023).

M. Pasini and J. Schluter, "Musika! fast infinite waveform music generation," arXiv preprint, arXiv: 2208.08706 (2022).

Z. Borsos, R. Marninier, D. Vincent, E. Kharitonov, O. Pietquin, M. Sharifi, D. Roblek, O. Teboul, D. Grangier, M. Tagliasacchi, and N. Zeghidour, "Audiolm: a language modrlling approach to audio generation," IEEE/ACM Trans. on Audio, Speech, and Lang. Process. 31, 2523-2533 (2023). 10.1109/TASLP.2023.3288409

J. Kong, J. Kim, and J. Bae, "Hifi-gan: generative adversarial networks for efficient and high fidelity speech synthesis," Proc. NeurIPS. 33, 17022-17033 (2020).

J. Engel, L. Hantrakul, C. Gu, and A. Roberts, "DDSP: differentiable digital signal processing," arXiv preprint, arXiv:2001.04643 (2020).

K. Choi, J. Im, L. M. Heller, B. McFee, K. Imoto, Y. Okamoto, M. Lagrange, and S. Takamichi, "Foley sound synthesis at the dcase 2023 challenge," arXiv preprint, arXiv:2304.12521 (2023).

H. C. Chung, "Foley sound synthesis based on GAN using contrastive learning without label information," DCASE2023, Tech. Rep., 2023.

Y. Yuan, H. Liu, X. Liu, X Kang, M. D. Plumbley, and W. Wang, "Latent diffusion model based Foley sound generation system for DCASE challenge 2023 task 7," arXiv preprint, arXiv:2305.15905 (2023).

X. Chen, N. Mishra, M. Rohaninejad, and P. Abbeel, "Pixelsnail: an improved autoregressive generative model," Proc. International Conference on Machine Learning, 864-872 (2018).

N. Zeghidour, A. Luebs, A. Omran, J. Skoguld, and M. Tagliasacchi, "Sonudstream: an end-to-end neural audio codec," IEEE/ACM Trans. on Audio, Speech, and Lang. Process. 30, 495-507 (2021). 10.1109/TASLP.2021.3129994

A. Déffossez, J. Copet, G. Synnaeve, and Y. Adi, "High fidelity neural audio compression," arXiv preprint, arXiv:2210.13438 (2022).

D. P. Kingma and M. Welling, "Auto-encoding variational bayes," arXiv preprint, arXiv:1312.6114 (2013).

A. Caillon and P. Esling, "RAVE: a variational autoencoder for fast and high-quality neural audio synthesis," arXiv preprint, arXiv:2111.05011 (2021).

A. van den Oord and O. Vinyals, "Neural discrete representation learning," Proc. NeurIPS. 1-10 (2017).

A. Razavi, A. van den Oord, and O. Vinyals, "Generating diverse high-fidelity images with VQ-VAE-2," Proc. NeurIPS, 1-11 (2019).

D. P. Kingma and J. Ba, "Adam: a method for stochastic optimization," arXiv preprint, arXiv:1412.6980 (2014).

K. Kilgour, M. Zuluaga, D. Roblek, and M. Sharifi, "Fréchet audio distance: a metric for evaluating music enhancement algorithms," arXiv preprint, arXiv:1812.08466 (2018). 10.21437/Interspeech.2019-2219

S. Hershey, S. Chaudhuri, D. P. W. Ellis, J. F. Gemmeke, A. Jansen, R. C. Moore, M. Plakal, D. Platt, R. A. Saurous, B. Seybold, M. Slaney, R. J. Weiss, and K. Wilson, "CNN architectures for large-scale audio classification," Proc. IEEE ICASSP, 131-135 (2017). 10.1109/ICASSP.2017.7952132

The Journal of the Acoustical Society of Korea ISSN:1225-4428(Print) 2287-3775(Online) 한국음향학회지

Preview

A study on the application of residual vector quantization for vector quantized-variational autoencoder-based foley sound generation model

ABSTRACT

MAIN

Fig. 1.

(Color available online) Structure and process of deep learning-based Foley sound generation method.

Fig. 2.

(Color available online) Structures of (a) variational autoencoder and (b) vector quantized-variational autoencoder.

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

Fig. 3.

(Color available online) Structures of (a) baseline model, (b) proposed model, and (c) proposed residual vector quantization.

Table 1.

Composition of training dataset (from References [7]).

Fig. 4.

(Color available online) Examples of spectrograms of generated Foley sound signals (using linear axis for frequency).

Table 2.

Performance comparisons with FAD.

Acknowledgements

References