I. 서 론
Ⅱ. 음선 이론 기반 음장 차분 기법
Ⅲ. 해상 실험 데이터
IV. 음장 차분 기법 신호 처리 파라미터 설정
4.1 윈도우 길이
4.2 교차 상관 시간 간격(∆t)
Ⅴ. 결 론
I. 서 론
수중 환경에서 음원의 위치를 탐지하고 환경정보를 얻기 위한 소나 시스템은 매우 중요한 분야이며, 오랜 연구가 진행되고 있다. 최근 국내외에서 해양 안보 및 해양 생태계 보호 등의 목적으로 수동 소나 시스템을 이용하여 해양환경을 모니터링하는 활동이 활발하게 이루어지고 있으며, 이에 따른 기술 개발 또한 활발하게 이루어지고 있다. 수동 소나 시스템은 일반적으로 수직선 배열 또는 수평선 배열 등의 음향 배열 센서를 이용하여 음원의 위치를 추정한다. 배열을 이용하여 음원의 거리를 추정하는 기법으로 가장 널리 알려진 정합장 처리 기법(Matched Field Processing, MFP)[1]은 음파 전달 모델을 통해 생성된 복제 음장과 수신 배열 센서를 통해 수신된 데이터 간 상관관계를 통해 음원의 위치를 추정할 수 있는 기법이다. 하지만 MFP는 음원이 존재할 수 있는 모든 영역에 대하여 복제 음장을 사전에 계산해야 하며, 이는 상당한 연산량이 요구된다. 또한, 해양 환경 정보(음속 구조, 지 음향 매개변수 등)가 충분하지 않을 경우 오정합 문제가 일어나기 때문에 정확한 해양환경에 대한 정보가 필요로 한다. 또 다른 기법으로 거리와 주파수의 변화량으로 계산되는 도파관 불변량(Waveguide Invariant, WI)[2]이론을 통해 음원의 거리를 추정할 수 있다. 그러나 도파관 불변량을 이용하는 기존 기법들도 MFP와 마찬가지로 배열 센서를 사용하는 경우가 많아 저전력 소모 조건의 감시 체계에서는 적절하지 않은 단점이 있다.
이러한 문제점을 해결하기 위해 본 연구에서는 단일 수신기를 이용하여 음원의 거리를 추정하는 기법에 관한 연구 결과를 제시하고자 한다. 단일 수신기를 이용하여 음원의 거리를 추정하는 방법으로 알려진 음장 차분 기법(Field differencing method)[3]은 음원에서 방사된 신호로부터 서로 다른 범위에서 수신된 압력을 상호 상관시키며, 생성된 교차 상관 음장으로부터 음원의 속도를 추정하여 거리를 추정하는 기법이다. 해당 기법은 전파 모델이 필요 없으며, 단일 수신기만으로도 음원의 거리를 추정할 수 있어 연산량이 적다는 장점이 있다. 이러한 특성으로 인해 Autonomous Underwater Vehicle(AUV)와 같은 수중 로봇에도 적용되고 있다.[4]
본 연구는 선행 연구[3,5]의 결과를 토대로, 음장 차분 기법을 이용하여 음원의 이동 속도를 추정할 때 사용하는 여러 신호 처리 매개변수에 대하여 적절한 선정 기준과 매개변수에 따른 속도 추정 성능 변화를 분석한 결과를 제시한다. 기존 연구에서는 매개변수 선정 기준에 관한 내용을 제시하지 않거나[3,4] 혹은 제한적으로만 다룬[6] 한계가 있었다. 이에 음장 차분 기법 사용 시 오류가 발생하는 조건들을 검토하고 정확한 해를 구할 수 있는 매개변수 선정 조건과 성능을 향상하기 위한 매개변수 선정 기준을 제시한 것이 본 연구의 의의라 할 수 있다.
본 논문의 구성은 다음과 같다. II장에서는 음선 이론을 바탕으로 하여 음장 차분 기법을 통해 이동하는 음원의 속도 추정 방법을 설명하고, III장에서는 해상 실험 데이터에 대한 설명과 신호 처리 절차, 기존 Reference [3] 신호 처리 매개변수에 대한 성능 검증을 보여준다. IV장에서는 여러 매개변수에 의한 영향을 분석하며, 마지막으로 V장에서 결론을 맺는다.
Ⅱ. 음선 이론 기반 음장 차분 기법
음장 차분 기법은 교차 상관 음장(Cross-correlated field) 을 이용하며, 다음과 같이 정의된다.[3,6,7]
여기서 은 음장에서 수신기로부터의 수평 방향 거리 에서의 압력을 의미한다. 음선 이론에 따라 음선의 경로는 직접 경로(D)와 해수면-반사 경로(SR)로 음원이 전파된다고 가정한다. 이외의 다른 반사 경로가 추가되는 경우에 대한 분석은 해당 장의 후속 부분에 설명한다. 이에 거리 의 음압은 아래와 같이 나타낼 수 있다.
여기서 와 는 i번째 음원 거리에서의 진폭, 는 i번째 음원 거리에 대한 D와 SR 경로 시간 사이의 시간 차이를 의미하며, i는 수평 방향 거리 를 나타낸다. 그리고 음원의 거리 따라 는 내에서 거의 차이가 없다고 한다면,로 가정할 수 있다. Eq. (1)에 Eqs. (2), (3)을 대입하여 교차 상관 음장을 얻을 수 있다.[3,6]
Fig. 1은 음원과 수신기 사이의 기하학적 구조를 나타낸 것이다. 간단한 유도를 위하여 음속은 일정하고 거리에 따라 수심이 변하지 않는 도파관을 가정한다. 여기서 은 음원과 수신기 사이의 경사 거리를 나타낸다. 과 사이의 차이는 로 나타낼 수 있다. Eq. (4)에서 , 로 나타낼 수 있다. Eq. (4)에서 첫 번째 코사인 항은 ∆r에 의해 변화하는 반면, 두 번째 코사인 항은 ∆r에 의한 변화가 매우 작은 항이므로 속도 추정 시 첫 번째 코사인 항을 이용하여 음원의 시선 속도를 추정한다.[7] 그러면 Eq. (4)의 첫 번째 코사인 항으로부터 다음과 같이 표현할 수 있다.
여기서 는 수신기에서 획득한 시간에 대한 시선 속도를 나타낸다. , 은 일정 거리 간격, 는 해당 거리 이동에 소요된 시간 간격을 의미하며, 는 음원의 이동 속도이며 해당 구간 내에서는 일정하다고 가정한다. Eq. (5)이 최대일 때 협대역 주파수 음원의 시선 속도는 다음과 같이 나타낸다.
여기서 dt는 (∆t, t) 평면에서의 의 정점 간격을 의미한다. 이때, 는 도파관의 평균 음속을 나타낸다. Eq. (4)를 통해 음선 이론 기반 교차 상관 음장의 간섭패턴은 코사인 항의 조합으로 만들어지며, 음원과 수신기 사이의 직접 경로만 고려됨을 알 수 있다.[6] 음원의 시선 속도는 을 다음과 같이 푸리에 변환하여 얻을 수 있다.
추가하여, 본 논문에서는 다른 경로에 의한 영향을 확인하기 위해 해저면-반사 경로(BR), 해저면-해수면 반사 경로(BSR)를 포함하여 경로의 증가에 따른 영향을 확인하였다. Eqs. (2), (3)에 해저면 반사 경로, 해저면-해수면 반사 경로를 포함한 음압은 다음과 같다.
여기서와 는 거리 과 에서의 고려하는 각각 경로의 진폭과 직접 경로와 j 경로의 경로 간 시간 차이를 의미하며, j는 음선의 경로 을 나타낸다. 음원 이동에 따른 음선 경로 간의 시간 차이의 변화가 무시할 정도로 작다고 가정하면, 교차 상관 음장은 다음과 같이 최종적으로 유도 된다.
Reference [6]의 교차 상관 음장 유도와 마찬가지로 음원의 이동에 따른 음선 경로 차이의 변화가 크지 않는 경우, 음선의 다른 경로를 포함한 Eq. (10)도 음원의 속도는 첫 번째 코사인 항으로부터 유도가 됨을 알 수 있다. 첫 번째 코사인 항은 두 거리 사이의 직접 경로 시간 차이만으로 음원의 속도를 추정하고 있으므로, 다른 반사 경로가 고려되어도 직접 경로만으로 음원의 속도를 추정할 수 있다.
요약하면, 음선 이론 기반 음장 차분 기법을 이용하여 협대역 신호의 음원의 이동 속도는 음원과 수신기 사이의 직접 경로만 고려가 되며, 음장의 간섭패턴은 코사인 항의 조합으로 만들어짐을 알 수 있다.
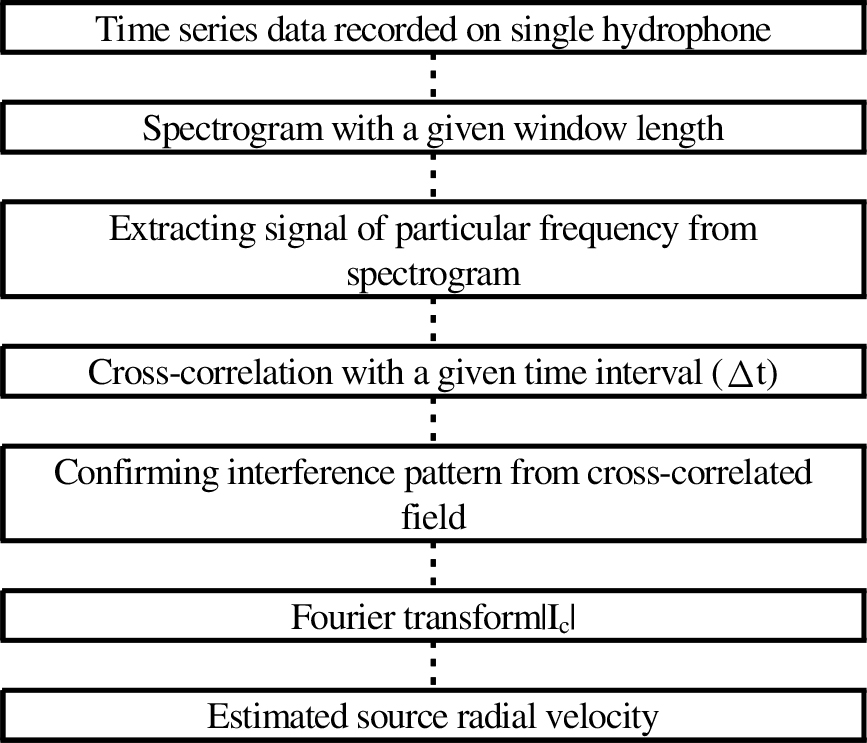
음장 차분 기법을 이용하여 음원의 이동 속도를 추정하는 신호 처리 절차는 총 4단계의 과정을 거쳐 이동 음원의 속도를 추정한다. 먼저 단일 수신기를 이용하여 움직이는 음원의 신호를 수신한 후, 해당 신호를 단시간 푸리에 변환을 이용하여 스펙트로그램으로 변환한다. 스펙트로그램에서 특정 주파수의 신호를 추출하고, 일정한 시간 간격으로 교차 상관을 하여 신호 간의 간섭패턴을 확인한 후, 푸리에 변환을 통해 음원의 이동 속도를 추정한다. 여기서 스펙트로그램으로 변환할 때, 사용되는 윈도우 길이와 교차 상관을 할 때의 시간 간격이 신호 처리 시 사용되는 파라미터이다. 신호 처리 절차 흐름도는 아래의 Fig. 2에 나타내었다.
Ⅲ. 해상 실험 데이터
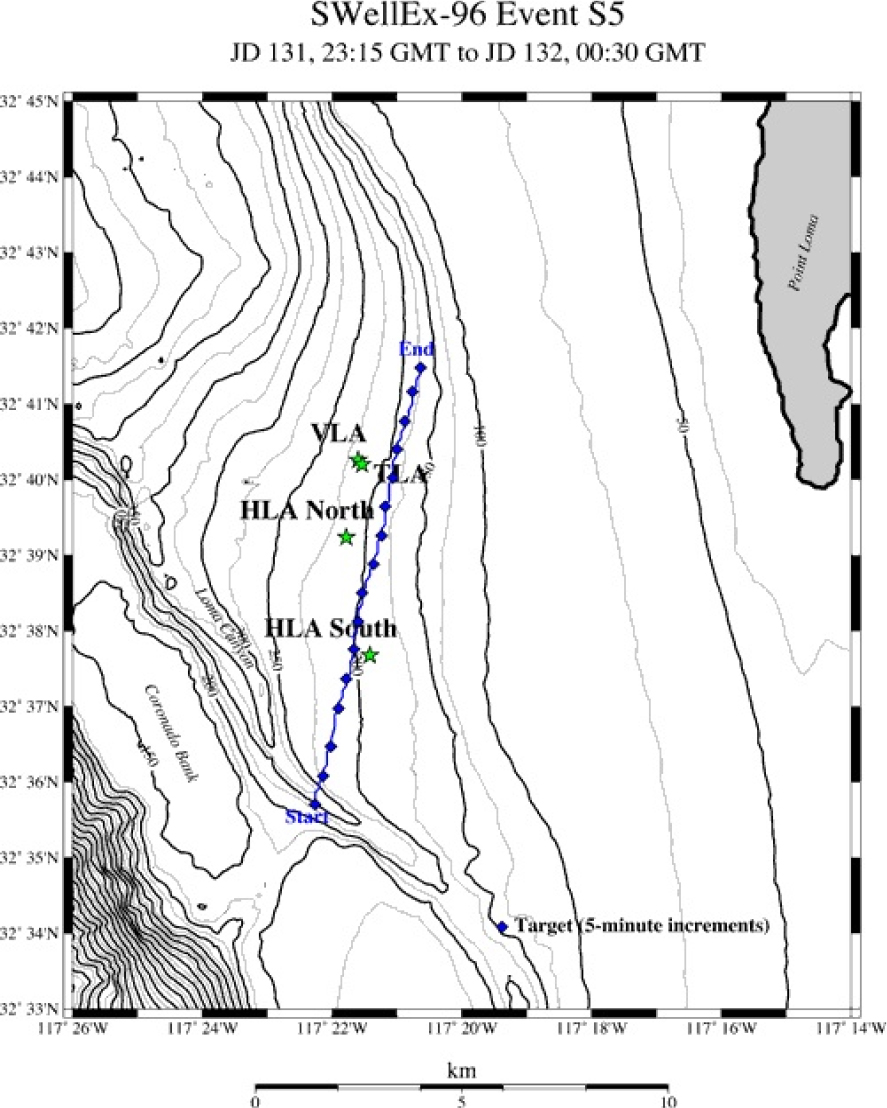
본 논문에는 1996년 미국 Scripps 해양연구소에서 시행한 SWellEx-96,[8] S5 실험 데이터를 사용하여 연구를 진행하였다. SWellEX-96 데이터 중에서 S5 데이터 세트를 사용하였는데, S5는 아래의 Fig. 3에 표시된 바와 같이 선형 경로를 따라 수심 54 m에서 약 2.5 m/s의 일정한 속도로 견인된 음원에서 방사된 신호를 기록한 것이다. 실험 환경의 수심은 180 m에서 220 m이며, 경로 중반 이후 약 180 m로 수심이 일정하게 유지된다. 음원은 다양한 주파수와 신호 대 잡음비(Signal-to-Noise Ratio, SNR)로 Continuous Wave(CW) 음원을 송신하였다. 실험은 약 75분간 진행되었으며, 64개의 센서로 구성된 수직선 배열 센서를 통해 기록되었다. SWellEx-96, S5 실험 데이터 중 본 연구에 사용된 데이터는 약 190 m에 있는 13번 수신기에 기록된 신호를 사용하였다.
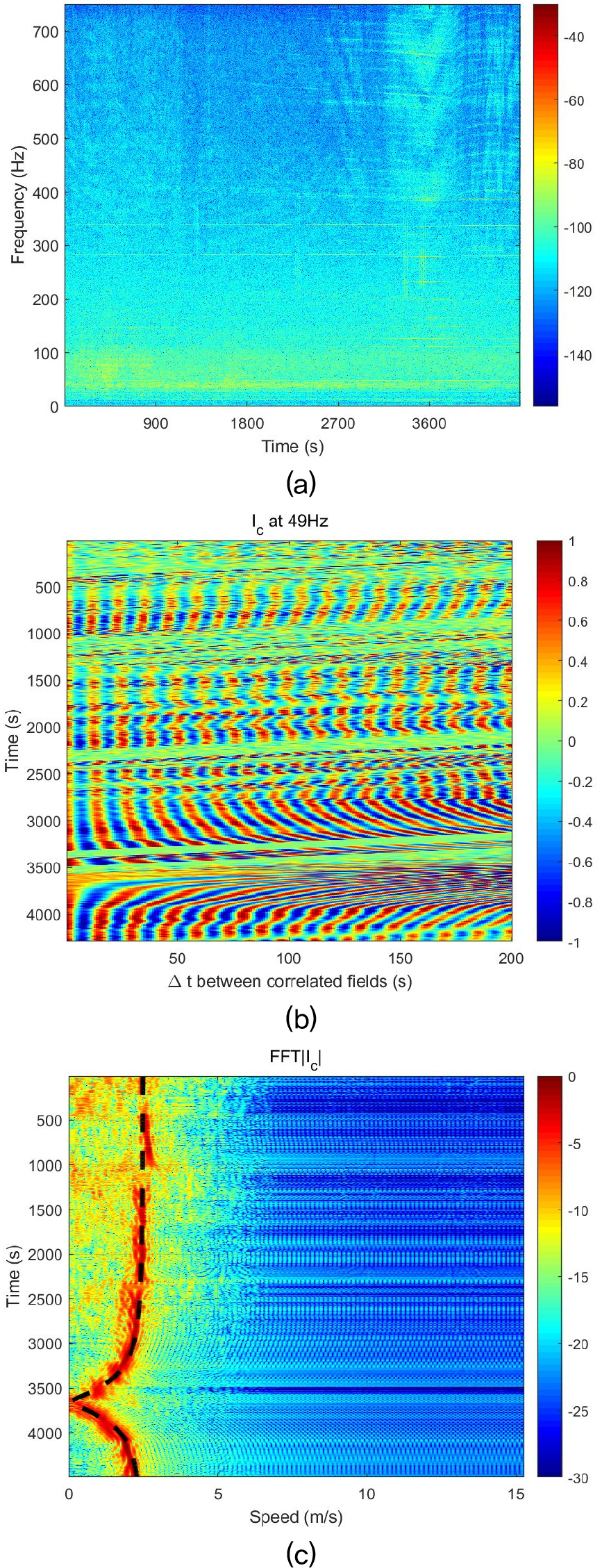
Fig. 4는 최초로 음장 차분 기법을 제안한 참고문헌[3]에서 사용한 신호 처리 파라미터(Table 1)를 사용하여 음장을 추출하고, 추출된 음장으로부터 음원의 시선 속도를 추정한 결과를 나타낸 것이다. Fig. 4(a)는 신호의 스펙트로그램을 나타낸 것으로 II장에서 설명한 바와 같이 특정 주파수 신호의 음장을 추출하는 데에 사용된다. Fig. 4(b)는 Eq. (1)에서 정의된 교차 상관 음장을 나타낸 것이고, 이를 푸리에 변환하면 Fig. 4(c)와 같이 시선 속도 추정 결과를 얻게 된다. Fig. 4(c)의 검은색 점선은 음원의 이동에 따른 음원의 시선 속도를 나타낸 것이다. Fig. 4에서 사용한 신호의 주파수는 49 Hz이며, 그림에서 나타난 바와 같이 속도 추정 결과가 실제 음원 이동 속도(2.5 m/s)와 유사하게 나타나는 것을 확인할 수 있다. 단, 최근 접점(Closest Point of Approach, CPA) 근처에서는 시선 속도가 0에 가까워지게 되므로 속도 추정 결과도 0으로 수렴하는 현상이 나타났다. S5 데이터는 전체 길이의 4/5 정도 되는 위치에서 CPA가 존재하므로(Fig. 3), 속도 추정 결과에서도 CPA의 영향이 약 3,600 s 근처에서 나타나는 것을 관찰할 수 있다.
Table 1.
Information of signal processing parameters.
| Signal processing parameter | |
| Sampling frequnecy | 1500 Hz |
| Window | Hamming |
| Window length | 8 s |
| Overlap | 50 % |
| Time interval (∆t) | 1 s |
이와 같은 과정을 통해 추정한 음원의 시선 속도를 이용해 음원까지의 거리를 계산할 수 있다. 즉, 음원이 일정한 속력으로 이동하는 것을 가정하였을 때, 가능한 음원 거리와 속력 후보값에 대해 나타날 수 있는 시선 속도를 계산하고, 이것과 실제 데이터에서 관찰된 시선 속도 측정값을 서로 비교하여 가장 오차가 적은 음원 거리 및 속력을 선정하는 방법으로 이루어진다. 따라서 음장 차분 기법에 따른 음원 거리의 추정은 기본적으로 정확한 음원 시선 속도 추정으로 결정됨을 알 수 있다. 본 연구에서는 이동 음원 시선 속도 추정을 위해 음장 차분 기법을 적용할 때 사용되는 신호 처리 파라미터의 구속 조건과 효과를 분석하였으며, 다음 장에서 그 결과를 제시하고자 한다.
IV. 음장 차분 기법 신호 처리 파라미터 설정
음장 차분 기법을 이용하여 음원의 속도를 추정하는 과정에서는 측정된 음향신호로부터 스펙트로그램으로 변환하기 위한 파라미터인 윈도우 길이를 설정하며, 스펙트로그램으로부터 추출한 신호를 이용해 교차 상관을 할 때 교차 상관 시간 간격(∆t)을 설정해야 한다. 본 장에서는 속도 추정 시 이러한 신호 처리 파라미터들이 성능에 미치는 영향을 차례로 분석하고자 한다. III장에서 소개한 SWellEX-96, S5 실험 데이터를 사용하여 분석을 진행하였으며, 분석에 사용한 신호는 음원 준위가 가장 높은 톤 신호 세트를 사용하였다.
4.1 윈도우 길이
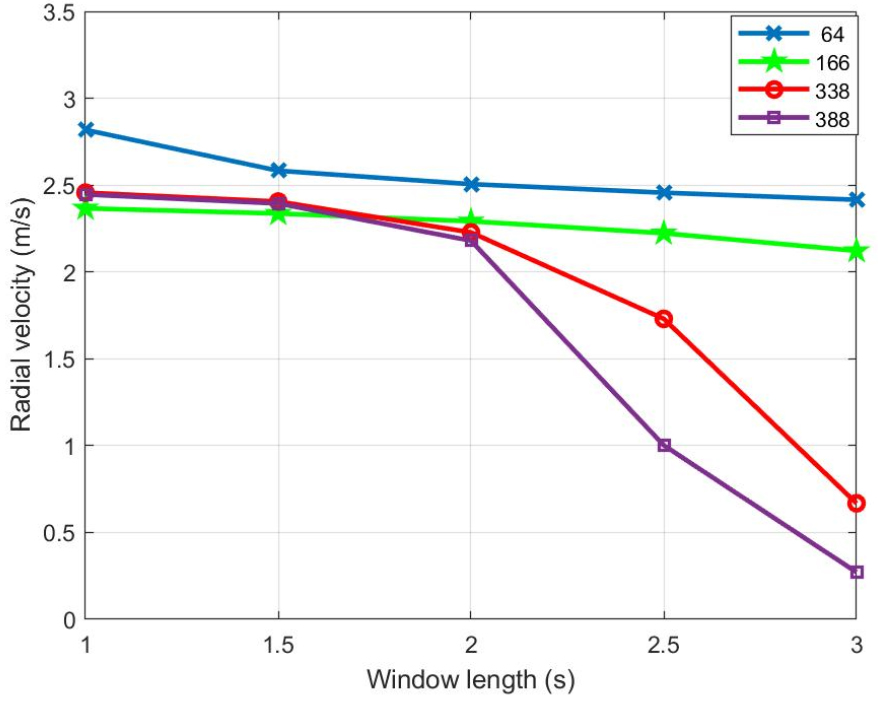
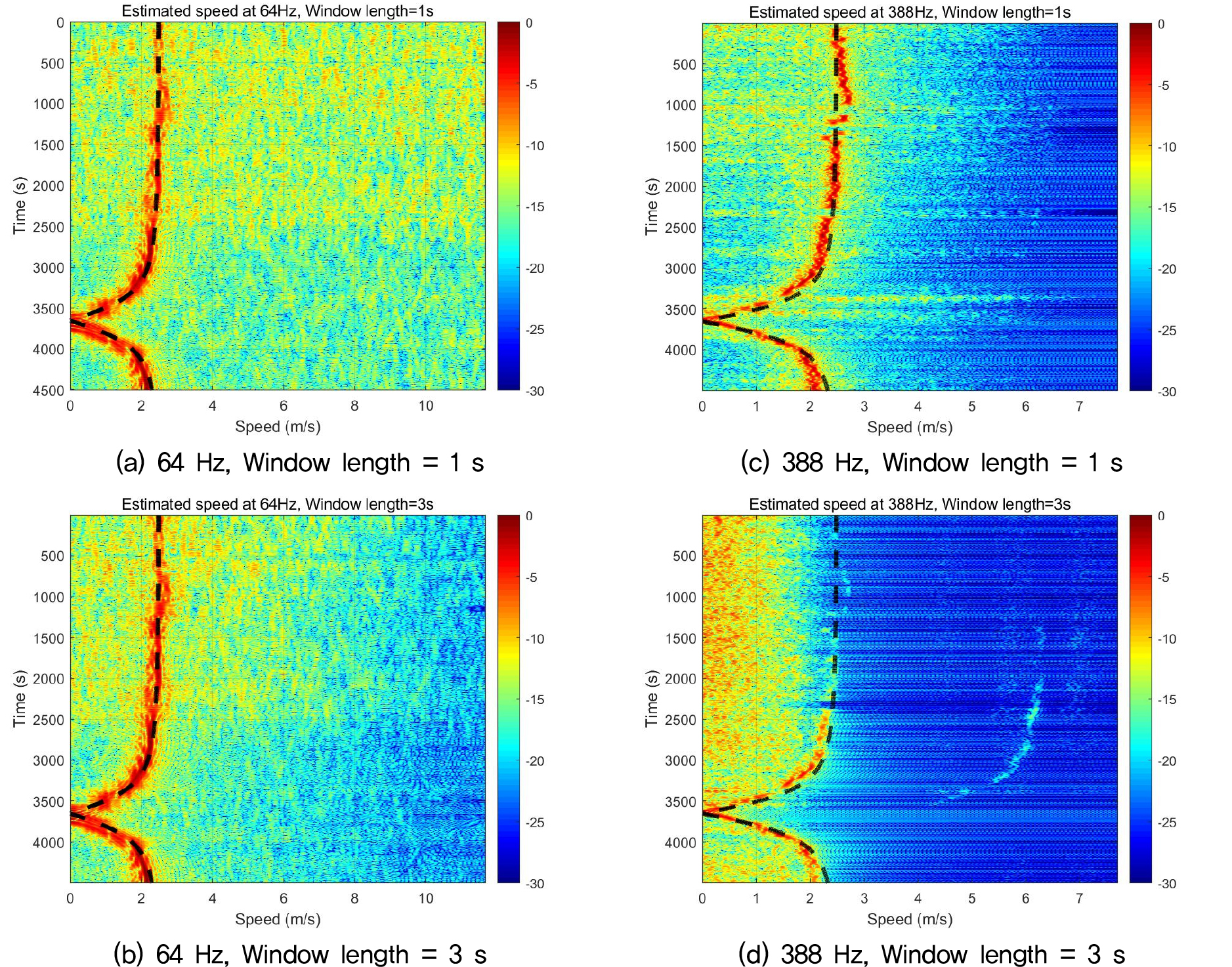
윈도우 길이는 설정 주파수의 음장을 얻기 위해 사용되는 단시간 푸리에 변환의 길이이다. 윈도우 길이의 효과는 신호의 주파수에 따라 다르게 나타났다. 긴 윈도우 길이 사용이 속력이 일정한 음원의 속도 추정 분산을 줄이는 데 도움이 되지만, 고주파 신호의 경우 성능이 저하될 수 있다. Fig. 5는 64 Hz, 166 Hz, 338 Hz, 388 Hz 신호에 대해 음원이 0 s에서 2,400 s 사이에 있을 때, 윈도우 길이를 변화시켜 가며 평균 시선 속도를 추정한 결과를 나타낸 것이다. 0 s에서 2,400 s 사이에서는 음원이 수신기로부터 상당히 거리가 떨어져 있는 상태이므로, 측정된 시선 속도가 실제 음원의 속도(2.5 m/s)와 유사하게 측정된다. 따라서 해당 범위의 데이터를 속도 추정 정확도를 평가하는 데에 활용할 수 있다. Fig. 6에서 나타난 바와 같이, 저주파 신호의 경우 윈도우 길이가 길어질 때 평균 추정값이 실제 속도 값에 더 근접하여 성능이 약간 향상되는 것을 볼 수 있다. 특히 64 Hz에서 윈도우 길이가 증가할수록 바이어스 오차가 감소하는 것을 볼 수 있다. 반면, 고주파 신호에서는 속도 추정 결과가 2 s 이상의 윈도우 길이에서 급격하게 나빠지는 현상이 관찰된다. 이는 Fig. 6(d)에 나타난 것처럼 속도가 제대로 추정되지 않는 구간이 포함되어 큰 오차가 발생한 것으로 판단된다.
4.2 교차 상관 시간 간격(∆t)
교차 상관 시간 간격(∆t)는 가 푸리에 변환을 하여 속도를 추정할 때 중요한 역할을 한다. 이때 ∆t는 두 신호 간의 샘플 간격을 나타내며 샘플링 주기를 나타내게 된다. 따라서 음원의 최대 시선 속도와 시간 간격(∆t)은 다음의 관계를 가진다.
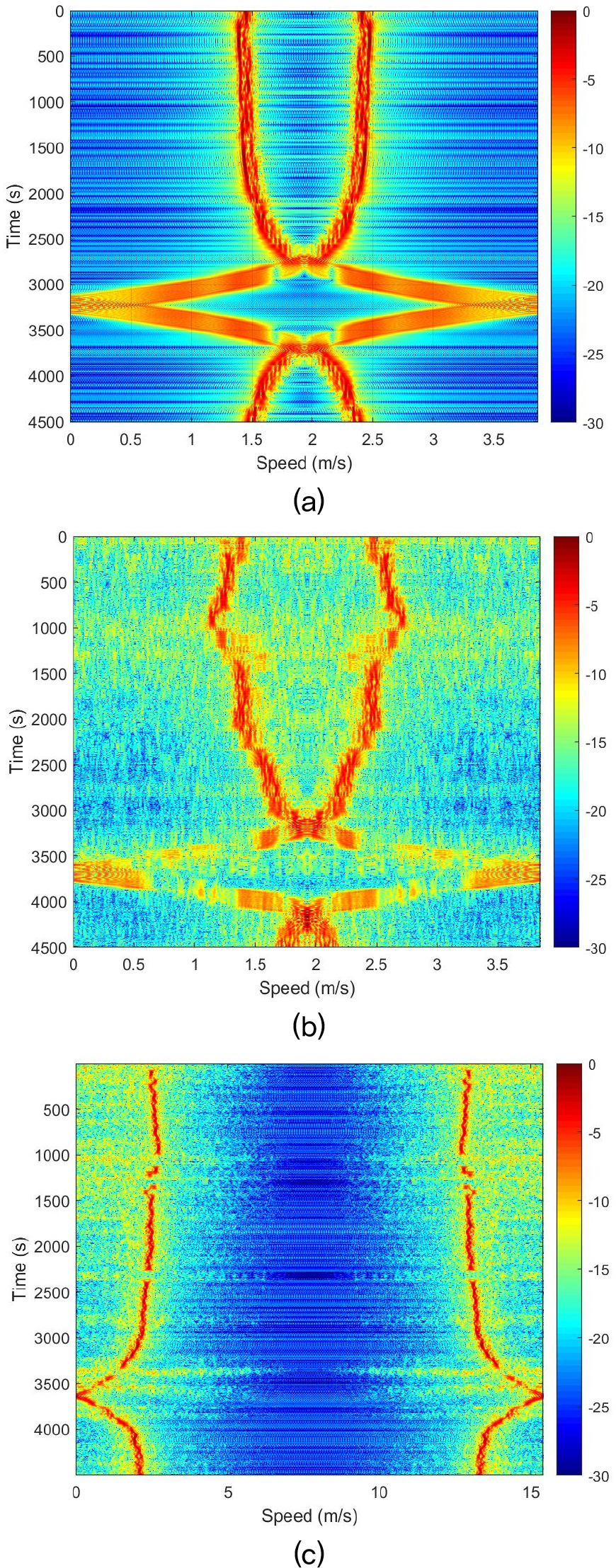
Fig. 7은 388 Hz 신호에 대해 윈도우 길이가 1 s일 때, 교차 상관 시간 간격에 따른 시뮬레이션 결과와 실 해역 데이터 분석 결과를 보여준다. 시뮬레이션 환경은 수심이 200 m이며, 수심에 따른 음속이 일정한 도파관을 고려하였다. 음원은 수신기로부터 8,000 m 거리에서 출발하여 2.5 m/s의 일정한 속도로 움직인다고 가정한다. 약 3,200 s 후 CPA 지점을 지나며 수신기와 CPA 지점까지는 900 m로 설정하였다. Fig. 7(a)는 ∆t = 1 s일 때 시뮬레이션 결과이며, Fig. 7(b)와 7(c)는 ∆t = 1 s, ∆t = 0.25 s일 때의 실 해역 데이터 분석 결과를 나타낸다. Fig. 7에서 주목할 점은 주파수 축에서 나타나는 앨리어싱 효과이다. 이 그림은 양의 주파수(속도)와 음의 주파수(속도)를 동시에 나타내어 앨리어싱 효과를 명확히 시각화하고 있다. 특히, 음의 주파수(속도)의 축 값은 실제 값이 아니며, 샘플링 왜곡에 의한 결과임을 주의해야 한다. Fig. 7(a)에서 시뮬레이션 결과를 통해 샘플링 왜곡이 발생하여 속도 추정에 오류가 나타나는 것을 확인할 수 있다. 이러한 결과는 가정된 음원의 최대 이동 속도와 신호 주파수를 고려하여 교차 상관 시간 간격(∆t)을 적절히 설정해야 함을 알 수 있다.
협대역 주파수 신호를 사용하여 음원의 시선 속도를 추정할 때, 교차 상관 시간 간격(∆t)은 신호주기의 정수배 이어야 한다. ∆t가 신호주기의 정수배가 아니면, 각 지점에서 교차 상관을 수행하는 데 사용되는 음압 값들이 서로 위상이 맞지 않게 되어, 추정된 속도에 오프셋이 발생할 수 있다. 식의 간단한 유도를 위해 음선의 직접 경로만 고려하고 ∆t가 신호주기의 정수배가 아닌 경우, 거리 r과 r + ∆r에서의 음압은 다음과 같이 표현 할 수 있다.
여기서 은 진폭, 는 음원이 거리 에 있을 때 시간을 나타낸다. Eq. (13)의 에서 는 신호의 주기를 의미하며, 가 신호 주기의 정수배가 아니면 로 위상 차이가 생기게 되며, 교차 상관 음장을 구성하는 음압의 값이 서로 다른 시간의 음압 값을 사용하게 되므로, 실제 음원의 시선 속도 추정에 오프셋이 발생한다. 위상 오프셋을 포함한 교차 상관 음장은 다음과 같이 나타낼 수 있다.
이처럼 ∆t가 신호주기의 정수배가 아니면 교차 상관 음장은 Eq. (14)와 같이 위상차이가 포함 된 식으로 표현 되며, 이를 푸리에 변환하여 음원의 속도 추정시 속도 오프셋을 야기한다.
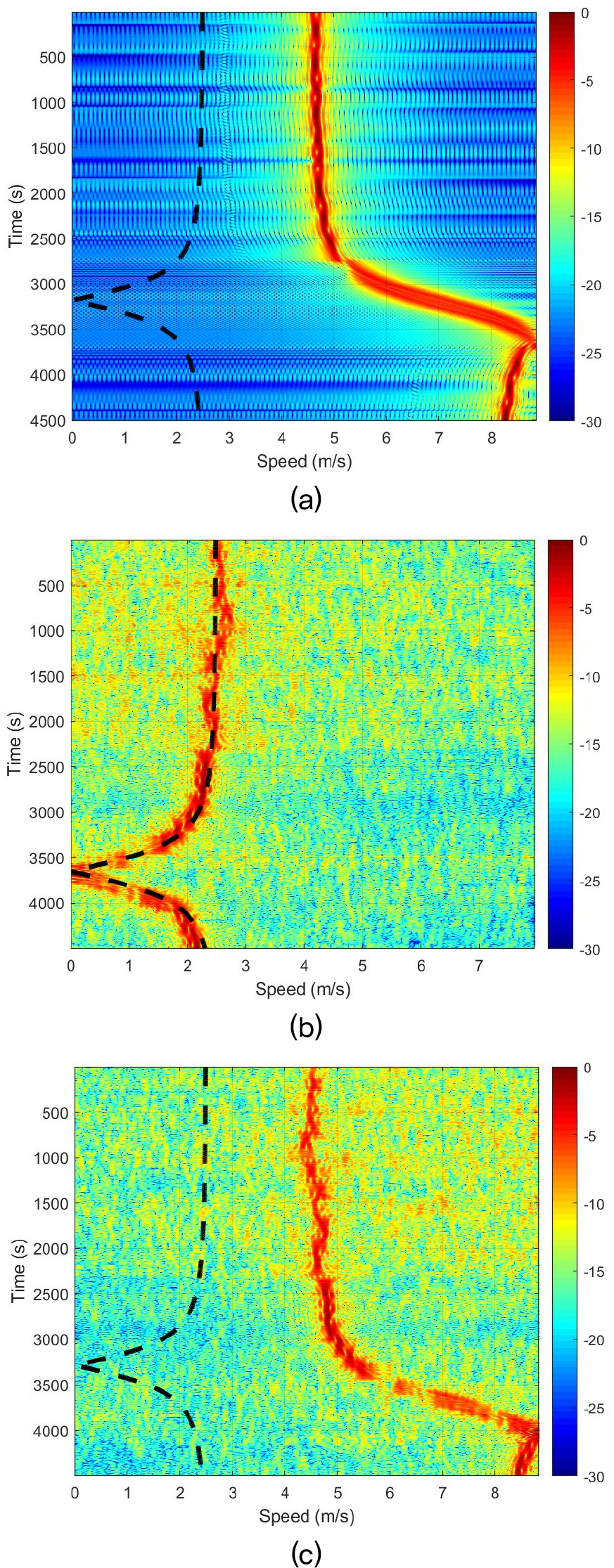
Fig. 8은 94 Hz 신호에 대해 윈도우 길이가 2 s일 때, 교차 상관 시간 간격과 협대역 신호 주파수 간의 관계를 Fig. 7(a)의 환경의 시뮬레이션 결과와 실제 해역 데이터 분석 결과를 통해 보여준다. Fig. 8(a)에서 보이는 것처럼, 시뮬레이션 결과에서도 ∆t가 신호주기의 정수배를 만족하지 않을 경우 정확한 속도 추정이 어려워지는 것을 확인할 수 있다. Fig. 8(b)와 8(c)는 실제 해역 데이터 분석 결과를 나타내며, Fig. 8(b)에서는 ∆t가 1 s로 설정되어 신호주기의 정수배를 만족하므로 정확한 속도 추정 결과를 도출한다. 반면, Fig. 8(c)에서는 ∆t가 0.9 s로 설정되어 84.6 사이클이 발생한다. 이 경우, 교차 상관 시간 간격을 200 s까지 설정하면 216°의 위상 오프셋이 발생하며, 이에 따라 음원의 속도 추정 결과가 실제 음원의 이동 속도와 차이를 보이게 된다.[9]
Ⅴ. 결 론
본 연구에서는 단일 수신기를 사용하여 음원의 속도를 추정하는 음장 차분 기법에 관한 연구 결과를 제시하였다. 음장 차분 기법은 비교적 단순한 알고리즘 구조로 되어 있어 저전력 음원 거리 추정 방법으로서 장점을 지니고 있지만, 알고리즘 사용 시 파라미터를 잘못 설정하면 큰 오류가 나타낼 수 있어 주의가 필요하다. 본 연구에서는 SWellEx-96, S5 실험 데이터를 이용하여 음장 차분 기법의 윈도우 길이와 교차 상관 시간 간격에 따른 속도 추정 결과의 변화를 관찰하였다. 음원의 주파수가 저주파일 경우, 윈도우 길이가 길수록 추정 결과의 분산을 줄일 수 있지만, 고주파 신호의 경우 반대로 성능이 저하될 수 있음을 확인하였다. 또, 음원의 이동 속도와 신호 주파수에 따라 교차 상관 시간 ∆t가 샘플링 이론의 구속 조건을 가지게 됨을 설명하고 이에 따른 오차 발생 사례를 나타내었다. 이에 따르면 음원의 이동 속도가 증가할 때, 교차 상관 시간도 감소 적용되어야 함을 보여주며, 위상 오프셋이 발생하지 않도록 ∆t가 사용하는 톤 신호주기의 배수로 설정되어야 함을 아울러 확인하였다. 이러한 결과들은 향후 음장 차분 기법 적용 시 준수해야 하는 가이드라인으로 참고 될 수 있을 것이다.