Insertion loss by bubble layer surrounding a spherical elastic shell submerged in water

Keunhwa Lee; Cheolwon Lee; Cheolsoo Park

doi:10.7776/ASK.2022.41.2.174

Preview

Research Article

The Journal of the Acoustical Society of Korea. 31 March 2022. 174-183
https://doi.org/10.7776/ASK.2022.41.2.174

Insertion loss by bubble layer surrounding a spherical elastic shell submerged in water

수중의 구형 탄성 몰수체를 둘러싼 기포층에 의한 삽입손실

Keunhwa Lee¹^*

Cheolwon Lee²

Cheolsoo Park³

이 근화¹^*

이 철원²

박 철수³

¹세종대학교 국방시스템공학과

²㈜에이엘

³선박해양플랜트연구소

^{*Corresponding Author}

ABSTRACT

Acoustic radiation from a submerged elastic shell with an internal fluid surrounded by the bubble layer is studied with the modal theory. An omni-directional point source located on the center of the internal fluid is used as acoustic noise source. The unknown coefficients of modal solutions are solved using the interface conditions between media. To preserve the stability of the modal solution over wide frequency ranges, the scaled technique of modal solution is used. The bubble layer is modeled with four kinds of bubble distribution; uni-modal distribution, uniform distribution, normal distribution, and power-law distribution, based on the effective medium theory of Commander and Prosperetti. For each bubble distribution, the insertion losses are mainly calculated for the frequency. In addition, the numerical simulations are performed depending in the bubble void fraction, the material property of elastic shell, and the gap between the bubble layer and the elastic shell.

Keywords

Acoustic radiation

Spherical shell

Bubble layer

Insertion loss

본 논문에서는 내부 유체를 갖는 수중에 몰수된 탄성 쉘이 기포층으로 둘러싸여 있을 때의 음향 방사를 모드 이론을 이용해 연구했다. 전 방향성의 점음원이 내부 유체의 중심에 위치해 있고 음향 소음원으로서 사용되었다. 모드 해의 미지수는 매질 사이의 경계조건으로부터 계산된다. 넓은 주파수 대역에서 모드 해의 안정성을 유지하기 위해, 모드 해의 규격 기법이 사용되었다. 기포 층은 Commander와 Prosperetti의 유효 매질 이론에 기반하여, 단일 모드 분포, 균일 분포, 정규 분포, 멱함수 분포를 이용해 각각 모의되었다. 각각의 기포 분포에 대해 삽입손실이 주파수에 대해 계산되었다. 추가적으로 공극비, 탄성 쉘의 매질 특성, 탄성 쉘과 기포층의 간극의 영향에 대한 수치해석을 수행했다.

키워드

음향 방사

구형 쉘

기포 층

삽입 손실

MAIN

I. 서 론
II. 기포 분포를 고려한 유효 매질 이론
III. 모드 해 기반 삽입손실 모델
IV. 삽입손실
V. 결 론

I. 서 론

최근 선박이나 해양 파일링 작업에서 발생하는 수중소음을 감소시키기 위해 기포층이 활용되고 있다.^[1] 인위적으로 기포층을 발생시켜서 수중 소음원을 둘러싸거나^[2] 또는 공기가 가득 찬 풍선과 같은 연성의 탄성 쉘로 구성된 감쇠막을 수중에 설치하여 수중소음을 차단한다.^[3]

선박의 에어마스커시스템^[1,4]은 선체의 주요 소음원이 위치한 선박의 후미와 추진기를 기포층으로 덮어서 소음을 감소시키는 시스템이다. 에어마스커 시스템은 필요할 때마다 기포층을 직접 생성하므로 사용하기 매우 편리하다. 하지만 발생하는 기포의 세세한 설계 변수를 사용자의 요구에 맞춰서 제어하는 것은 현재 기술로는 매우 어려우며, 기포 발생이 제어되더라도 선체 주변의 복잡한 유동과 부력 때문에 기포층의 물성이 교란되는 문제점이 추가적으로 발생한다. 이러한 교란의 영향을 반영하기 위해서는 완고한 설계 관점에서 기포층의 설계 변수가 삽입손실에 미치는 영향에 대한 다양한 분석이 필요하다.

2021년 Park et al.^[1]은 2차원 환경(평면 좌표 및 축대칭 좌표)에서 ‘유체-기포층-유체’ 모델과 ‘진공-평판-유체-기포층-유체’ 모델에서 삽입손실에 대한 해석해를 유도하고 수치모의를 통해서 기포층의 설계 변수의 영향을 관찰했다. 기포층은 단일 기포 분포 및 정규 분포에 대해 Commander와 Prosperetti의 유효매질 이론^[5]을 이용하여 모의했다. 또한 평판은 Kirchhoff-Love 이론으로 불리는 얇은 판 이론^[6]으로 모의했다.

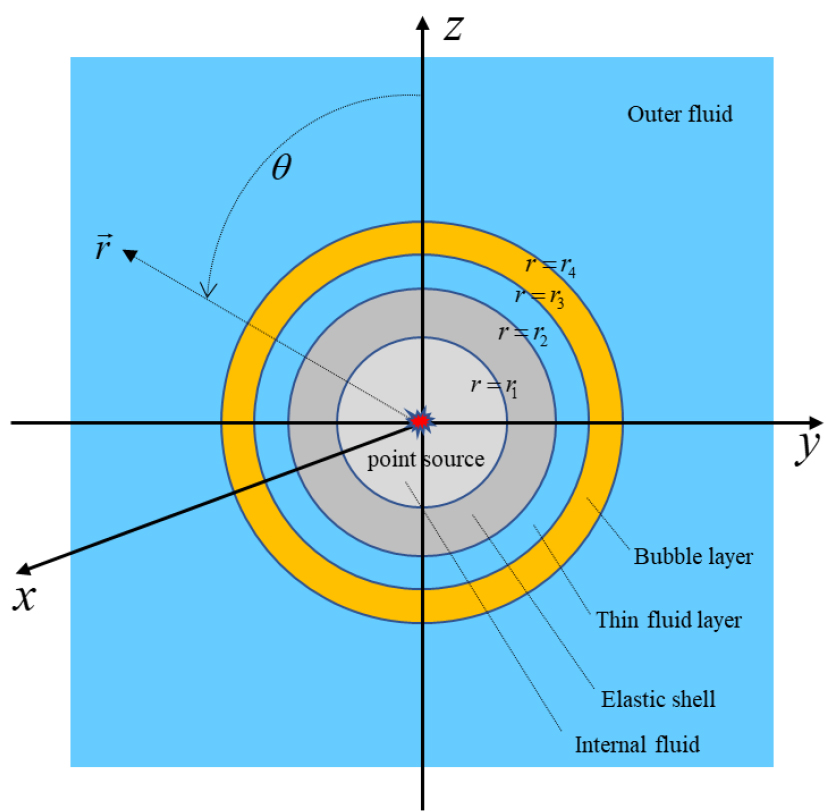
본 연구에서는 3차원 구형 좌표계 환경에서 기포층에 의한 삽입 손실을 생각했다. 모의 환경은 내부 유체를 가진 구형의 탄성 쉘을 가정했다. 탄성 쉘의 중심에 전 방향성의 점 음원을 놓고 삽입손실을 구하기 위한 소음원으로 사용했다. 또한 탄성 쉘은 등방성의 3차원 탄성파 이론을 이용하여 모의했다. 탄성 쉘은 Fig. 1과 같이 순서대로 ‘간극유체층, 기포층, 외부유체층’으로 둘러싸여 있다고 생각했다. 기포층은 박철수 등의 연구와 동일하게 Commander와 Prosperetti의 유효매질 이론을 이용해 모의했으나, 추가적으로 기포의 분포가 균일하지 않은 일반적인 경우를 고려했다. 본 연구에서는 단일 기포 분포외에 균일 분포, 정규 분포, 멱함수 분포가 가정되었으며 이들 분포에 의한 기포층의 음향학적 특성을 보였다.

https://static.apub.kr/journalsite/sites/ask/2022-041-02/N0660410208/images/ASK_41_02_08_F1.jpg

Fig. 1.

(Color available online) Spherical coordinate and multi-layered spherical shell system.

참고로 기포 분포 특성에 대한 연구는 모델링보다는 주로 음향 역산 분야에서 많이 다뤄졌다. 모델링 분야에서는 Commander와 Prosperetti^[5]는 기포 분포가 정규 분포일 때 기포층의 음속과 감쇠계수의 모의결과를 제시했다. 역산 분야에서는 1996년에 Choi와 Yoon^[7]이 기포가 각각 단일 기포, 정규 분포, 멱함수 분포를 가질 때, 상관 및 비상관 기포분포 추정기법의 정확도를 분석했다. 또한 1999년 Caruthers et al.^[8]은 기포층의 감쇠계수 데이터를 이용하여 기포 분포를 추정하는 반복적 역산기법을 제안했다. Choi와 Yoon^[9]은 기포층의 음속을 이용한 반복적 기포분포 추정기법을 제안하고 단일 기포, 정규 분포, 역함수 분포의 경우에 대한 역산 결과를 보였다. Stanic et al.^[10]은 선박의 후류에서 얻어진 기포 분포 역산 결과를 1차 및 2차의 멱함수 분포와 적합도 분석을 통해 후류의 기포 분포가 멱함수 분포와 유사하다는 것을 보였다. 그 외 많은 분야에서 기포분포 역산 연구가 수행되고 있다.^[11,12]

3차원 구형 좌표계 환경에서 삽입 손실 모델은 각 층의 해석적인 모드 해를 이용해 공식화했으며, 모드 해의 미지수는 경계조건을 이용하여 계산했다.

특별히 수 Hz에서 수백 kHz까지의 삽입손실을 계산하기 위해, 규격화 기법을 이용해 매질의 파수와 쉘의 반지름의 곱으로 표현되는 Rayleigh 수에 안정적인 모드 해를 제시했다. II장은 기포 분포를 고려한 유효 매질 이론에 대한 소개, III장은 모드 해를 이용한 삽입손실 모델을 기술했으며, IV장은 기포층의 설계변수에 따른 삽입손실의 변화를 보였다. V장은 결론이다.

II. 기포 분포를 고려한 유효 매질 이론

유체에 다양한 크기의 기포가 존재할 때 유체는 이상 매질로 볼 수 있다. 이때 공극비는 단위 이상 매질의 부피(1 m³)에 대한 기포의 부피의 비로 정의된다. 기포의 반지름을 $a$ 라고 하고, $[a, a + d a]$ 의 구간에 존재하는 ‘단위 부피 당 기포의 개수’를 $f (a) d a$ 로 정의할 때, 이상 매질의 공극비 $β$ 는 아래와 같이 공식화할 수 있다.^[5]

(1)

β = \frac{4 π}{3} \int_{a_{m i n}}^{a_{m a x}} a^{3} f (a) d a,

여기서 $f (a)$ 는 ‘단위 부피 및 단위 기포 반지름 당 기포의 개수’가 되며, 차원은 $m^{- 4}$ 이 된다. 본 연구에서는 $f (a)$ 를 기포분포함수로 부를 것이다.

Commander와 Prosperetti의 유효매질이론에 의하면, 기포가 포함된 이상 매질의 복소 파수 $k_{m}$ 은 기포분포함수를 이용해 아래와 같이 정의된다.

(2)

k_{m}^{2} = k_{0}^{2} + 4 π \int_{a_{m i n}}^{a_{m a x}} \frac{a ω^{2} f (a) d a}{ω_{0}^{2} - ω^{2} + 2 j b ω},

여기서 $k_{0} = ω / c_{0}$ 로 정의되는 유체의 파수이고 $w$ 는 각주파수로 주파수 $f$ 와 $ω = 2 π f$ 의 관계가 있다. $c_{0}$ 는 유체매질의 음속이다. $w_{0}$ 와 $b$ 는 고유주파수와 감쇠 계수이다. 이 두 개의 양은 기포의 반지름에 의존적이다. Eq. (2)는 기포에 작용하는 점성력, 표면장력, 관성력, 압축력, 열역학적 에너지 보존을 선형 근사 관점에서 모두 고려하여 얻어진 식이다. Commander와 Prosperetti 모델은 근사적 모델이기 때문에 기포의 모든 음향현상을 설명하는 통일이론은 아니다. 본 연구 범위에 대해서는 위 모델의 적합성에 대해 주파수 및 물성에 대해 COMSOL physics와 교차검증 수행했다.

또한, Eq. (2)는 Commander와 Prosperetti가 $e^{j ω t}$ 의 가정에서 유도한 식임을 밝힌다. 참고로 본 논문의 삽입손실은 $e^{- j ω t}$ 의 가정에 따라 유도가 되었으므로, Eq. (2)로 계산된 복소 파수의 켤레를 계산에 사용해야 한다. 그리고 Commander와 Prosperetti 모델은 송수신기와 기포층의 위치좌표에 독립적인 임의의 혼합물의 음향학적 물성을 표현하는 ‘유효이론’이라는 것을 강조한다.

본 연구에서는 네 종류의 기포분포 함수를 가정했다. 단일 기포분포함수는 아래와 같이 정의된다.

(3)

f (a) = α δ (a - a_{0}),

여기서 $α$ 는 기포분포함수의 크기를 좌우하는 파라미터이다. Eq. (3)을 Eq. (1)에 넣으면, $α = β / (4 π a_{0}^{3} / 3)$ 이 되며, $α$ 는 단위 부피에서 단일 기포의 총 개수에 해당하는 양임을 알 수 있다.

균일 기포분포함수는 기포의 반지름이 $[a_{\min}, a_{\max}]$ 에 존재할 때 아래와 같이 표현된다.

(4)

f (a) = α .

유사하게 정규 기포분포함수는 아래와 같이 정의된다.

(5)

f (a) = α e^{- \frac{(a - a_{0})^{2}}{2 σ^{2}}},

여기서 $a_{0}$ 와 $σ$ 는 분포의 모수로써 기포 반지름의 평균과 표준편차와 관련이 있다.

멱함수 기포분포함수는 아래와 같이 정의된다.

(6)

f (a) = α a^{- k},

여기서 $k$ 는 $k$ >0인 실수로 모수이다. 위의 Eqs. (4), (5), (6)에서 $α$ 의 값은 Eq. (1)을 이용해 계산된다.

본 연구에서는 Table 1과 같은 기포의 범위와 모수들을 생각했다. Table 1의 값에 대해 기포분포 함수를 그려보면 Fig. 2 (a)와 같다.

Table 1.

Hyper-parameters for bubble distribution functions (BDF).

Hyper-parameters	Values	BDF
Bounds of bubble radius	[300 μm, 3000 μm]	All
Mean radius	1500 μm	Eqs. (3), (5)
Variance	3002 μm2	Eq. (5)
k	2.5	Eq. (6)

https://static.apub.kr/journalsite/sites/ask/2022-041-02/N0660410208/images/ASK_41_02_08_F2.jpg

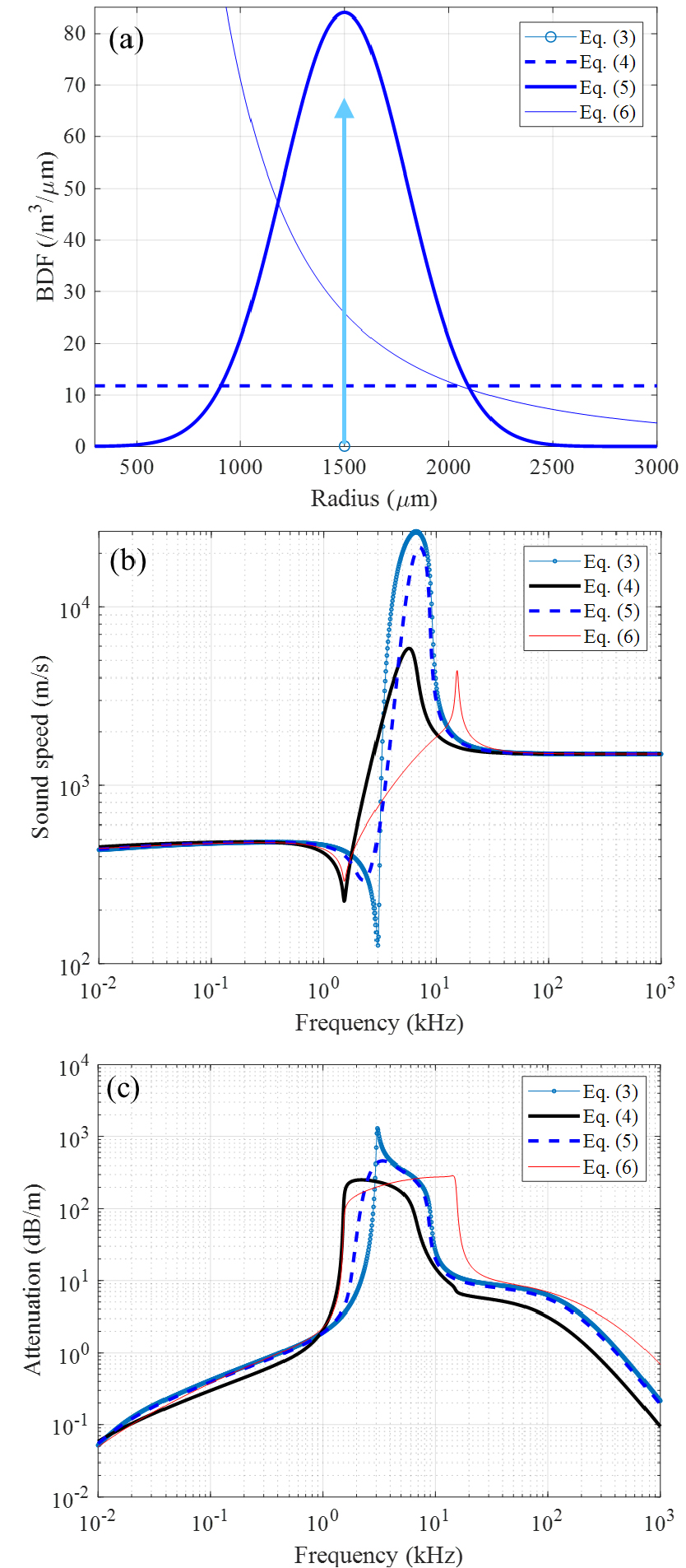
Fig. 2.

(Color available online) (a) Four kinds of bubble distribution functions (BDFs); (b) sound speed and (c) sound attenuation in the bubbly fluid for each BDF as a function of frequency (Note that Fig. 2 in Ref. 1 was to plot $R e (w / k_{m})$ . It is an error and different from the sound speed of $w / R e (k_{m})$ shown in Fig. 2(b) of this paper.).

각각의 기포분포함수에 대한 유효매질의 음속과 감쇠계수는 Fig. 2(b)와 Fig. 2(c)에 도시했다. 음향학적 계산에 사용된 기포와 유체의 물성은 상온에서의 가스와 해수의 물성을 이용했다. 공극비는 0.001을 사용했다. 또한 Commander와 Prosperetti 모델에서 열확산계수의 값은 기포 크기에 독립적인 상수 값을 사용했다.

Fig. 2(b)와 2(c)를 보면, 발생하는 기포의 범위와 공극비가 같더라도, 기포 분포에 따라 유효매질의 음향학적 물성이 크게 달라지는 것을 확인할 수 있다. 단일 기포 분포와 정규 기포분포는 비교적 유사하게 나타났다. 이것은 정규 기포분포가 단일 기포분포처럼 우세종의 기포분포로 표현되기 때문이다. 하지만, 나머지 분포들은 단일 기포분포와는 차이가 컸다. 균일 기포분포와 멱함수 기포 분포의 공진주파수는 보다 저주파 영역에서 발생했고, 다소 명확하게 나타나지 않았다. 양 분포에서 음속과 감쇠계수의 변동폭이 줄어드는 것을 볼 수 있다. 멱함수 기포분포는 공진영역에서 절대적인 크기는 줄어들었지만 고주파수 영역에서 감쇠계수의 값이 전체적으로 크게 증가한다. 이것은 기포의 크기가 작을수록 해당 기포의 개수가 크게 늘어나기 때문으로 판단한다. 그리고 기포분포에 따라, $f \to 0$ 영역에서 음속과 감쇠계수의 값이 10 % 이내로 차이가 나는 것을 확인할 수 있었다.

III. 모드 해 기반 삽입손실 모델

Fig. 1과 같은 구형 좌표계에서 구 형상의 다층 구조를 생각한다. 생성되는 음장은 z축에 대해 축대칭으로 발생한다고 가정한다. 이때 각 매질의 해석해는 구형 좌표계에 대한 모드 함수를 이용하여 표현할 수 있다. 공식화를 수행하기 전에 구형 Hankel 함수가 복소수의 입력 값에서 지수적으로 증가하거나 감소하는 문제를 해결하기 위해 임의의 제 1종 및 제 2종 구형 Hankel 함수와 일차, 이차 미분항을 아래와 같이 규격화했다.

(7)

h_{n}^{(1)} (x) = {\hat{h}}_{n}^{(1)} (x) e^{j x}, h_{n}^{(2)} (x) = {\hat{h}}_{n}^{(2)} (x) e^{- j x} h_{n}^{(1)'} (x) = {\hat{h}}_{n}^{(1)'} (x) e^{j x}, h_{n}^{(2)'} (x) = {\hat{h}}_{n}^{(2)'} (x) e^{- j x} h_{n}^{(1)''} (x) = {\hat{h}}_{n}^{(1)''} (x) e^{j x}, h_{n}^{(2)''} (x) = {\hat{h}}_{n}^{(2)''} (x) e^{- j x} .

위 식에서 $'$ 와 $''$ 는 $x$ 에 대한 일차 및 이차 미분을 나타낸다. $^$ 는 규격화된 함수를 나타낸다. 규격화는 도함수, 일차, 이차 미분에 대해 모두 동일하게 수행하였으며, $^$ 이 붙은 규격화된 함수는 원래의 Hankel 함수와 다르다는 것에 유의해야 한다.

Eq. (7) 및 다층 구조에서의 해석해의 수치적인 안정성을 고려하여 각각의 매질에서 해석해는 아래와 같이 표현했다. 소음원으로 구형 좌표계의 원점에 놓인 전방향성 음원을 사용하기 때문에 해석해는 0차 모드 해로 정확하게 표현 가능하다. 그렇지만 일반화를 위해 임의의 n차의 모드해로 기술하겠다. 미지 계수를 $[f_{n}, b_{n}, c_{n}, d_{n}, e_{n}, p_{n}, q_{n}, g_{n}, h_{n}, a_{n}]$ 이라고 할 때 각 매질에서 해석해는 아래와 같이 기술된다.^[13,14,15]

(1) 내부 유체

(8)

p_{I} = e^{- j ω t} \sum_{n = 0}^{\infty} j^{n} (2 n + 1) f_{n} P_{n} (\cos θ) j_{n} (k_{I} r) .

(9)

p_{s} = e^{- j ω t} \sum_{n = 0}^{\infty} s_{n} j^{n} (2 n + 1) P_{n} (\cos θ) a_{n} {\hat{h}}_{n}^{(1)} (k_{I} r) e^{j k_{I} r},

여기서 $k_{I}$ 는 내부 유체의 파수이다. 전방향성 음원을 사용하므로 $s_{0}$ =1이고, $s_{n} (n \neq 0)$ 은 0이다. $j_{n} ()$ 은 1종 구형 베셀함수이다.

(2) 탄성 쉘

탄성 쉘의 길이 및 응력항은 Helmholtz 분해의 발산 항에 대한 길이 포텐셜 $ϕ_{1}$ 과 회전 항에 대한 벡터 포텐셜 중 방위각 방향 요소인 $ψ_{χ}$ 를 이용해 표현할 수 있다. 각각의 포텐셜은 아래와 같은 해석해로 주어진다.

(10)

ϕ_{1} = \frac{e^{- j ω t}}{ρ_{s} ω^{2}} \sum_{n = 0}^{\infty} j^{n} (2 n + 1) P_{n} (\cos θ) \times [b_{n} {\hat{h}}_{n}^{(1)} (k_{L} r) e^{j k_{L} (r - a)} + c_{n} {\hat{h}}_{n}^{(2)} (k_{L} r) e^{- j k_{L} (r - b)}],

(11)

ψ_{χ} = \frac{e^{- j ω t}}{ρ_{s} ω^{2}} \sum_{n = 0}^{\infty} j^{n} (2 n + 1) \frac{d P_{n} (\cos θ)}{d θ} \times [d_{n} {\hat{h}}_{n}^{(1)} (k_{T} r) e^{j k_{T} (r - a)} + e_{n} {\hat{h}}_{n}^{(2)} (k_{T} r) e^{- j k_{T} (r - b)}],

여기서 $k_{L}$ 은 p파의 파수이며, $k_{T}$ 는 s파의 파수`이다. $ρ_{s}$ 는 탄성 쉘의 밀도이다. 0차 모드에서 Eq. (11)은 0이 되므로 전단 성분에 의한 영향은 존재하지 않는다.

(3) 간극 유체

(12)

p_{F} = e^{- j ω t} \sum_{n = 0}^{\infty} j^{n} (2 n + 1) P_{n} (\cos θ) \times [p_{n} {\hat{h}}_{n}^{(1)} (k_{F} r) e^{j k_{F} (r - b)} + q_{n} {\hat{h}}_{n}^{(2)} (k_{F} r) e^{- j k_{F} (r - c)}],

여기서 $k_{F}$ 는 간극 유체의 파수이다.

(4) 기포 층

(13)

p_{B} = e^{- j ω t} \sum_{n = 0}^{\infty} j^{n} (2 n + 1) P_{n} (\cos θ) \times [g_{n} {\hat{h}}_{n}^{(1)} (k_{B} r) e^{j k_{B} (r - c)} + h_{n} {\hat{h}}_{n}^{(2)} (k_{B} r) e^{- j k_{B} (r - d)}],

여기서 $k_{B}$ 는 기포 층의 파수이다.

(5) 외부 유체

(14)

p_{0} = e^{- j ω t} \sum_{n = 0}^{\infty} j^{n} (2 n + 1) P_{n} (\cos θ) a_{n} {\hat{h}}_{n}^{(1)} (k_{0} r) e^{j k_{0} (r - d)},

여기서 $k_{0}$ 는 외부 유체의 파수이다.

위의 Eqs. (8), (9), (10), (11), (12), (13), (14)는 매질의 각 경계면에서 경계조건을 만족시켜야 한다.

유체/유체 경계면에서는 압력 연속, 경계면에 수직 변위의 연속 조건이 성립해야하며, 유체/탄성체의 경계면에서는 전단응력이 사라지는 조건이 추가위에서 기술한 해석해와 COMSOL Multi-physics를 된다. 0차 모드에서는 전단응력 소실 조건이 필요없다. 이를 이용하면 위 식에 나타나는 미지 계수의 값을 계산할 수 있다.

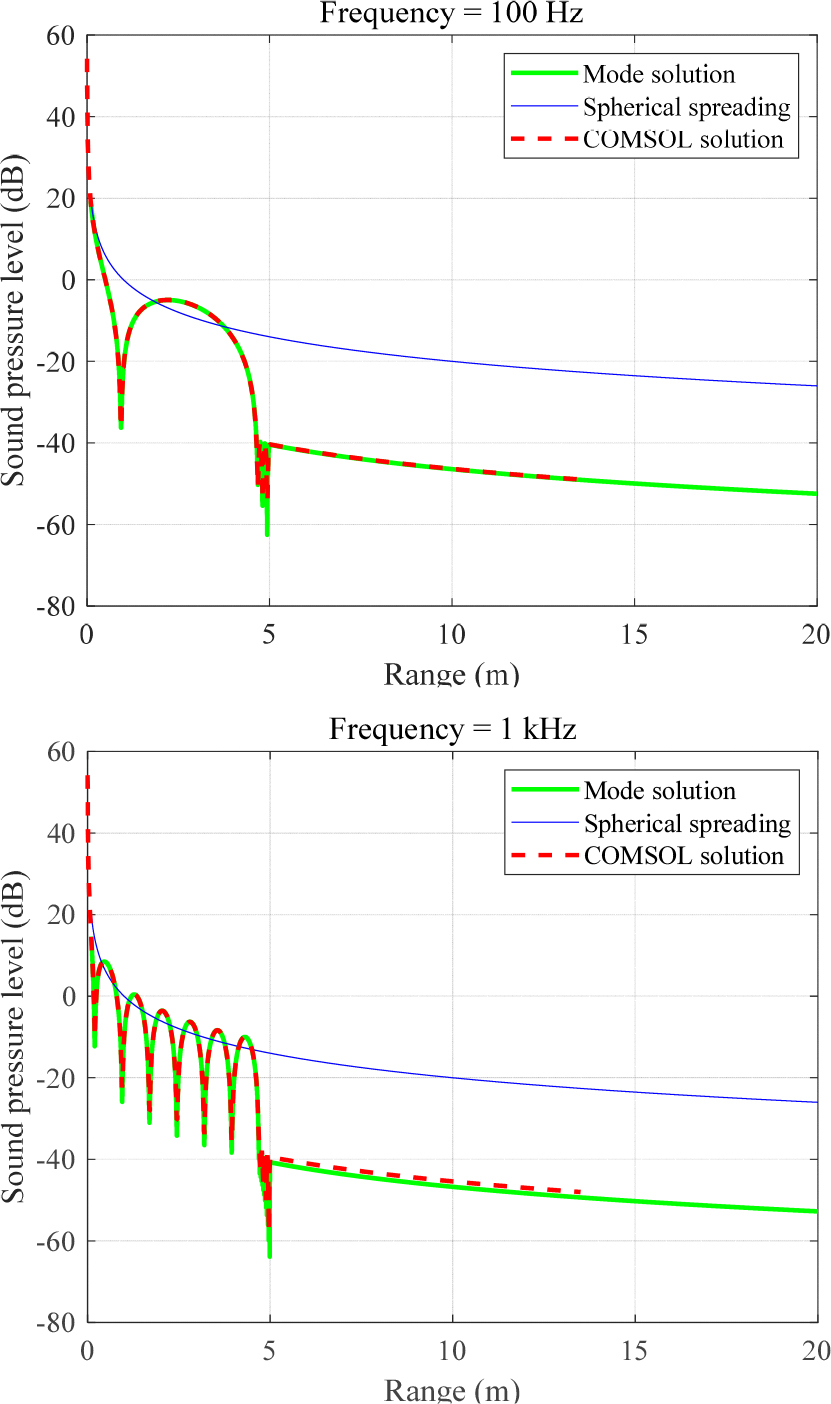
Fig. 3은 ‘내부 유체/기포층/외부 유체’의 경우에 이용해 계산한 유한요소법 수치해를 비교한 것이다. 소음원의 주파수는 200 Hz와 1 kHz이며, x축은 소음원에서부터 떨어진 거리, y축은 음압레벨로 r = 1 m에서 0 dB로 정규화하였다. 내부유체와 외부유체는 1500 m/s와 1000 kg/m³의 해수를 사용했으며, 기포층은 0.1의 공극비를 가지며 200 Hz에서 51.27 m/s, 900.1 kg/m³, 6.31 dB/m, 1 kHz에서 49.33 m/s, 900.1 kg/m³, 18.73 dB/m의 물성을 사용했다. 내부 유체 구의 반지름은 4.7 m이며, 기포층의 두께는 0.3 m를 사용했다.

https://static.apub.kr/journalsite/sites/ask/2022-041-02/N0660410208/images/ASK_41_02_08_F3.jpg

Fig. 3.

(Color available online) Comparison of mode solution and COMSOL solution for 200 Hz and 1 kHz frequencies.

Fig. 3에서 모드 해와 COMSOL 해는 서로 잘 일치하는 것을 볼 수 있다. 먼 거리에서 약간의 오차는 COMSOL 해의 mesh를 성기게 나누어서 발생하는 것이다. 수 kHz 대역을 해석할 때, 일반 워크스테이션에서 COMSOL은 축대칭 모듈로 수 시간이 걸리는데, 해석해는 5초 이내로 계산 가능하다.

IV. 삽입손실

기포층에 의한 삽입손실은 기포 층이 있을때의 압력( $p$ )과 기포층이 없을때의 압력( $p_{r e f}$ )의 비로 아래와 같이 정의한다.

(15)

I L = - 20 \log_{10} |\frac{p}{p_{r e f}}| .

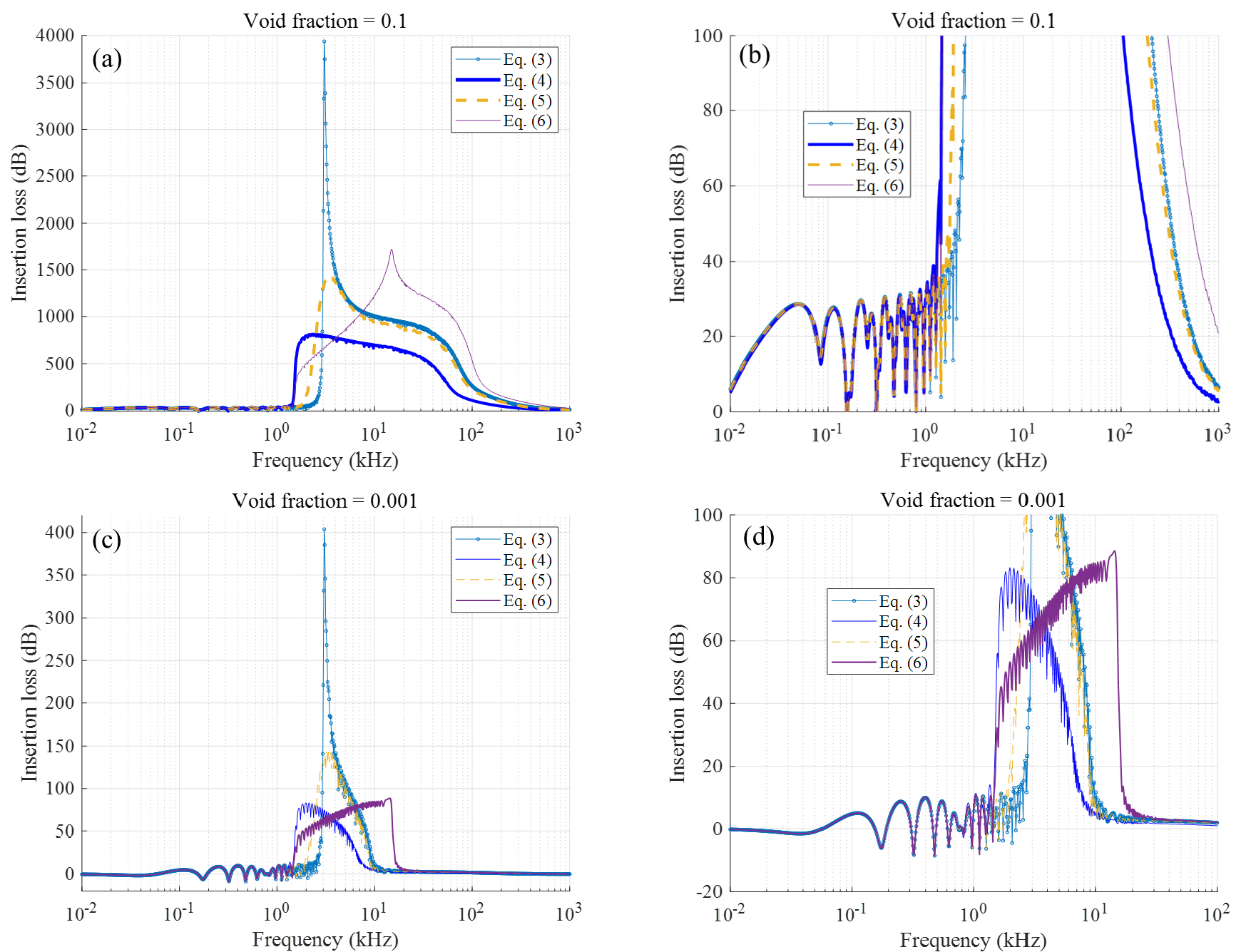
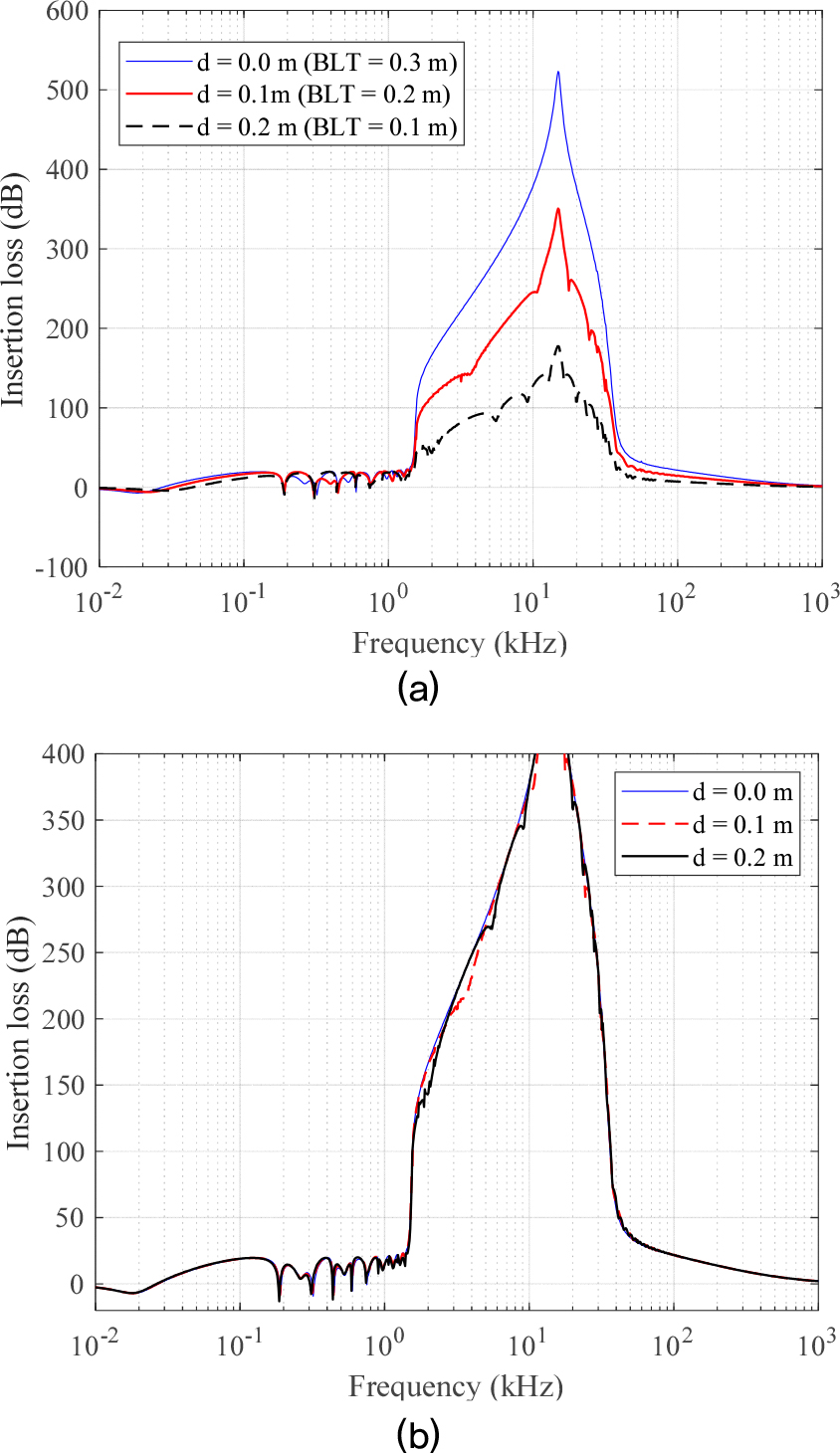
우선, 삽입손실에 미치는 기포 분포가 미치는 영향을 알아보기 위해 수치 모의를 수행하였다. 수치 환경은 ‘내부유체/기포층/외부유체’로 생각했다. 기포의 분포는 Table 1의 값을 사용했으며, 공극비는 각각 0.1과 0.001을 생각했다. 내부 유체 쉘의 반지름은 4.7 m이며, 기포층의 두께는 0.3 m로 가정했다. 결과는 Fig. 4에 도시했다.

https://static.apub.kr/journalsite/sites/ask/2022-041-02/N0660410208/images/ASK_41_02_08_F4.jpg

Fig. 4.

(Color available online) Insertion loss as a function of frequency for four bubble size distributions. (a) void fraction of 0.1, (b) enlarged figure of Fig. 4(a), (c) void fraction of 0.001, and (d) enlarged figure of Fig. 4(c).

Fig. 4는 주파수에 따른 삽입손실을 도시한 것이다. Fig. 4(a)와 4(c)를 보면, 단일기포에 비해 여러 크기의 기포가 분포할 때, 삽입손실 곡선이 보다 부드러워지는 것을 볼 수 있다. 이것은 단일기포에서 하나의 주파수로 나타나는 공진주파수의 효과가 여러 크기의 기포가 존재할 때는 넓은 대역에 걸쳐서 분산되어 나타나기 때문이다. 단일 기포의 공진 주파수와 기포크기의 관계는 아래의 Minnaert 주파수 식으로 간단히 표시할 수 있다.^[16]

(16)

ω_{0} = \frac{1}{a} \sqrt{\frac{3 γ P_{0}}{ρ_{w}}},

여기서 $γ$ 는 유체의 비열 계수, $P_{0}$ 는 주변 유체의 압력, $ρ_{w}$ 는 유체의 밀도이다. Minnaert 주파수는 Eq. (2)의 Commander와 Prosperetti 모델의 공진주파수에서 기포의 표면장력을 무시하고 저주파 근사를 취할 때 얻어지는 주파수와 동일하다. 이 식은 공진주파수와 기포 크기의 관계를 간단하게 파악할 때 유용하다. Fig. 4에서 단일 기포분포의 공진주파수는 Eq. (16)과 유사하게 산출되는 것을 볼 수 있다. 또한 공진주파수 근처에서 삽입손실이 가장 큰 것을 확인할 수 있다.

위 그림에서 정규분포의 결과가 단일기포분포의 삽입손실과 가장 유사했다. 이것은 정규분포도 단일분포처럼 특정 우세종의 기포를 가정하기 때문이다. 이에 비해 균일분포는 큰 기포부터 작은 기포까지 균등하게 포함되므로 삽입손실의 절대적인 크기는 작아지지만 폭이 보다 넓어지는 것을 볼 수 있다. 정규분포에 비해 삽입손실 곡선이 저주파쪽으로 약간 이동한 것은 본 예제어 사용한 정규분포에서 기포의 평균보다 균등분포에서 기포의 평균이 더 낮기 떄문이다. 멱함수 분포의 삽입손실이 균등분포처럼 낮고 넓게 퍼지는 것은 유사하나, 저주파 영역보다 고주파 영역에서 삽입손실이 높은 것을 볼 수 있다. 이것은 멱함수 분포 자체가 작은 기포에 대해 더 가중치를 주는 방식이기 때문에, 고주파 영역의 감쇠가 더 큰 것으로 추론할 수 있다. 위 결과를 종합하면, 다양한 기포 분포를 가진 기포층을 사용하는 경우 단일기포분포에 비해 최대 삽입손실을 줄어들지만, 공진주파수 주변(또는 기포분포의 평균크기에 해당하는 주파수 주변)에서 유효한 삽입손실의 폭은 커지는 것을 알 수 있다. 그렇기 때문에 단일 기포보다는 기포분포를 사용하는 것이 유리한 것을 알 수 있다. 또한, 정규분포 같은 우세종이 있는 분포보다는 기포 분산이 큰 균일분포나 멱함수분포가 실제 소음저감에 유리한 것을 알 수 있다.

한편, Fig. 4(a)와 4(c)를 보면 공극비가 클수록 기포층의 고유 감쇠계수가 크기 떄문에, 공극비 0.1의 삽입손실이 0.001의 삽입손실보다 큰 것을 볼 수 있다. 결국 전체적인 삽입손실을 높이기 위해서는 공극비를 높이는 것이 유리한 것을 알 수 있다.

Fig. 4(b)와 4(d)는 저주파 영역을 각각 확대한 그림이다. 우선, 저주파 영역에서는 음속과 감쇠계수에 기포분포의 영향이 매우 적은 것을 알 수 있다. 이것은 Commandar와 Prosperetti의 기포모델의 저주파 근사를 통해서도 쉽게 확인할 수 있다. 기포분포의 영향은 존재하나 그 차이가 미미하다는 의미이다. 또한, 이 그림에서 닫힌 공간안에 소음원이 존재할 때, 기포 쉘 시스템의 공진이 발생하는 것을 확인할 수 있다. 공진 주파수에서 삽입손실은 0에 가까워진다. 심지어 저주파 영역에서 기포층의 고유 감쇠계수가 작은 0.001의 공극비에서는 음수의 삽입손실도 발생하는 것을 확인할 수 있다. 결국 앞 문단의 결론과 마찬가지로 저주파 영역에서 삽입손실을 높이기 위해서는 높은 공극비를 사용하는 것이 유리하다는 것을 추론할 수 있다.

두 번째 수치예제로 탄성 쉘의 영향을 관찰했다. 수치 환경은 ‘내부유체/탄성 쉘/기포층/외부유체’로 구성했다. 각각의 반지름은 내부 유체층은 4.6 m, 탄성 쉘은 4.7 m, 기포층은 5.0 m로 가정했다. 즉, 탄성 쉘의 두께는 0.1 m이고, 기포층의 두께는 0.3 m이다. 소음 관측거리는 원점에서 20 m 떨어져있다. 탄성 쉘의 물성은 Table 2에 도시했다.

Table 2.

Elastic property of steel and FRP used in the numerical examples.

Property	Steel	CFRP
P-wave speed (m/s)	5600	8300
S-wave speed (m/s)	3100	2600
P-wave attenuation (dB/λ_p)	0	0
S-wave attenuation (dB/λ_s)	0	0
Density (kg/m³)	7700	1410

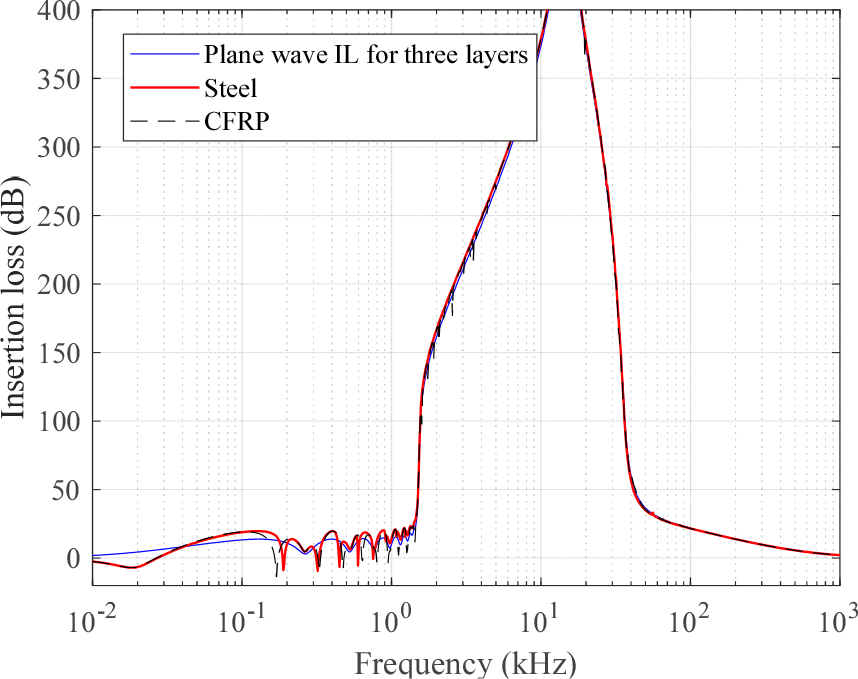
입손실만을 관찰하는 것이 목적이므로 소음원은 단순히 원점에 위치한 음향소음원을 사용했다. 멱함수 분포의 기포층을 이용했고 공극비는 0.01을 적용했다. Fig. 5는 그 결과를 보여준다. 탄성 쉘에 따라 저주파 영역에서 나타나는 쉘 시스템의 공진 모드가 달라지는 것을 볼 수 있다. 이 차이는 고주파 영역으로 갈수록 작아지는 것이 관찰되었다.

https://static.apub.kr/journalsite/sites/ask/2022-041-02/N0660410208/images/ASK_41_02_08_F5.jpg

Fig. 5.

(Color available online) Effect of the material property of elastic shell on the insertion loss.

또한 탄성 쉘에서 얻어진 삽입손실은 Reference [1]의 평면파에서 얻어진 삽입손실과 비교했다. 평면파에서 얻어진 삽입손실은 2차원 직각좌표계의 3층 구조(반무한영역/기포층/반무한영역)에서 얻어진 삽입손실이다. Fig. 5에서 보면 탄성 쉘에서 얻어진 삽입손실과 평면파 삽입손실은 저주파 영역을 제외하고 거의 비슷한 것을 볼 수 있다. 그렇기 때문에 기포층을 공학적으로 설계할 때 간단한 평면파 삽입손실을 이용해도 무방할 것이다.

세 번째 수치예제는 탄성 쉘과 기포층 사이에 간극 유체 층이 존재하는 경우이다(내부유체/탄성 쉘/간극유체/기포층/외부유체). 실제 환경에서 선박 표면을 타고 흐르는 유동에 의해 기포층이 선체 표면과 접하지 못하고 이격되어 둘러싸는 경우도 발생할 수 있을 것이다. 외부유체층이 발달하는 시나리오는 크게 두 가지로 가정했다. 첫 번째는 간극유체와 기포층의 두께를 일정하게 놓고, 간극유체의 두께만 변화되는 경우이다. 두 번째는 기포층의 두께를 일정하게 놓고, 외부유체의 두께만 변화하는 경우다.

수치 결과는 Fig. 6에 도시했다. 공극비는 0.01을 사용했고 탄성 쉘은 철을 사용했다. Fig. 6( a)는 첫 번째 시나리오의 결과를 도시했다. ‘간극유체와 기포층’의 두께는 0.3 m로 고정했다. 간극유체의 두께가 두꺼워질수록 기포층이 얇아지면서 삽입손실이 줄어드는 것을 관찰할 수 있다. 또한 공진 모드의 위치도 달라지는 것을 볼 수 있다.

Fig. 6(b)는 두 번째 시나리오에 해당하며 기포층의 두께를 0.3 m로 고정을 시켰다. 간극유체의 두께가 늘어날수록 전체 쉘 시스템의 반지름도 커진다. 그림에서 보듯이 기포층의 두께가 일정하고,간극유체 의 두께가 기포층의 두께보다 작은 경우에는, 간극유체의 영향은 제한적인 것을 알 수 있다.

https://static.apub.kr/journalsite/sites/ask/2022-041-02/N0660410208/images/ASK_41_02_08_F6.jpg

Fig. 6.

(Color available online) Insertion loss for the thickness of outer fluid 1. (a) the case that the thickness of ‘outer fluid 1 and bubble layer’ is fixed as 0.3 m, and (b) the case that the thickness of bubble layer is set to be 0.3 m. BLT means bubble layer thickness.

V. 결 론

본 연구에서는 음향 소음원이 구형의 탄성 쉘과 다양한 기포 분포를 가지는 기포 쉘로 둘러싸여 있을 때 삽입손실에 대해 연구했다. 기포 분포는 단일기포분포, 균일기포분포, 정규기포분포, 멱함수기포분포를 가정했다. 구형 좌표계에 대한 모드 해를 이용해 삽입손실을 계산하였고 COMSOL multi-physics의 수치해를 이용해 검증했다.

우세종의 기포를 갖는 단일기포분포나 정규기포분포에서는 기포 층의 음속과 감쇠계수에서 공진주파수가 뚜렷하게 나타났지만, 균일분포나 멱함수분포에서는 공진주파수가 뚜렷하지 않았다. 또한 기포 분포의 분산이 클수록 음속과 감쇠계수의 분산곡선이 주파수에 대해 부드러워지고 넓어지는 경향을 보였다.

삽입손실도 유사한 결과를 얻었다. 기포분포의 분산이 클수록 삽입손실의 최대값은 줄어들었지만, 주파수에 대해 삽입손실곡선이 넓어지는 경향을 보였다. 주파수 별 정량적인 삽입손실의 크기는 기포크기 별 기포분포함수의 크기와 상관성을 보였다. 이는 기포분포함수를 조절하면 삽입손실곡선의 형상도 인위적으로 설계할 수 있다는 것을 의미한다. 또한 음향 소음원의 구형 쉘에서의 삽입손실은 3층 구조의 평면파에서 얻어진 삽입손실과 저주파 영역의 일부 공진 특성을 제외하고는 매우 유사했다.

마지막으로 간극유체층은 그 두께가 기포층보다 두께가 작은 경우에는 삽입손실에 미치는 영향이 제한적이었다. 다만 간극 유체층의 존재가 기포층의 두께를 얇게 하는 경우에는 삽입 손실이 줄어드는 것을 확인하였다.

Acknowledgements

본 논문은 한국해양플랜트연구소의 “다중산란 기포층 해석모델 및 마스킹 연구용역”과 해양수산부의 “인공지능을 이용한 하이브리드 음전달 모델 선박 수중방사소음 분석 프로그램 개발”의 연구 결과 중 일부이다.

References

C. Park, W. Jeong, G. Kim, I. Moon, and G. Yim, "Acoustic insertion loss by a bubble layer for the application to air bubble curtain and air masker," J. Acoust. Soc. Kr. 39, 227-236 (2020).

B. Wüsig, C. R. Greene, and T. A. Jefferson, "Development of an air bubble curtain to reduce underwater noise of percussive piling," Marine Environmental Research, 49, 79-93 (2000). 10.1016/S0141-1136(99)00050-1

A. Tsouvalas, "Underwater noise emission due to offshore pile installation: A review," Energies, 13, 3037 (2020). 10.3390/en13123037

IMO, "Ship underwater radiated noise technical report and matrix," IMO MEPC 74/INF.28, 2019.

K. W. Commander and A. Prosperetti, "Linear pressure waves in bubbly liquids: Comparison between theory and exeriments," J. Acoust. Soc. Am. 85, 732-746 (1989). 10.1121/1.397599

F. Fahy, Sound and Vibration (Academic Press, San Diego, 1985). Chap. 4.

B.-K. Choi and S-.W. Yoon, "Theoretical study of coherent acoustic inverse method for bubble sizing in bubbly water," J. Acoust. Soc. Kr. 15, 3-8 (1996).

J. W. Caruthers, P. A. Elmore, J. C. Novarini, and R. R. Goodman, "An interative approach for approximating bubble distributons from attenuation measurements," J. Acoust. Soc. Am. 106, 185-189 (1999). 10.1121/1.427047

B.-K. Choi and S-.W. Yoon, "Acoustic bubble couting technoque using sound speed extracted from sound attenuation," IEEE J. Ocean. Eng. 26, 125-130 (2001). 10.1109/48.917945

S. Stanic, J. W. Caruthers, R. R. Goodman, E. Kennedy, and R. A. Brown, "Attenuation measurements across surface-ship wakes and computed bubble distributions and void fractions," IEEE J. Ocean. Eng. 84, 83-92 (2009). 10.1109/JOE.2008.2008411

E. J. Terrill and W. K. Melville, "A broadband acoustic technique for measuring bubble size distributions: Laboratory and shallow water measurements," J. Atmos. Oceanic Technol. 17, 220-239 (2000) 10.1175/1520-0426(2000)017<0220:ABATFM>2.0.CO;2

X.-j. Wu and G. L. Chahine, "Development of an acoustic instrument for bubble size distribution measurement," Proc. 9^th International Conference on Hydrodynamics, 11-15 (2010).

R. R. Goodman and R. Stern, "Reflection and transmission of sound by elastic spherical shell," J. Acoust. Soc. Am. 34, 338-344 (1962). 10.1121/1.1928120

A. P. Poddubnyak, V. V. Porokhovskii, V. A. Pozdeev, and V. V. Dykhta, "Radiation of an acoustic signal generated by an internal source from a spherical elastic shell," Soviet Applied Mechanics, 21, 509-513 (1985). 10.1007/BF00887049

E. J. Avital, N. D. Bholah, G. C. Giovanelli, and T. Miloh, "Sound scattering by an elastic spherical shell and its cancellation using a multi-pole approach," Archives of Acoustics, 42, 697-705 (2017). 10.1515/aoa-2017-0072

M. A. Ainslie and T. G. Leighton, "Review of scattering and extinction cross-sections, damping factos, and resonance frequencies of a spherical gas bubble," J. Acoust. Soc. Am. 130, 3184-3208 (2011). 10.1121/1.362832122087992

The Journal of the Acoustical Society of Korea ISSN:1225-4428(Print) 2287-3775(Online) 한국음향학회지

Preview

Insertion loss by bubble layer surrounding a spherical elastic shell submerged in water

ABSTRACT

MAIN

Fig. 1.

(Color available online) Spherical coordinate and multi-layered spherical shell system.

(1)

(2)

(3)

(4)

(5)

(6)

Table 1.

Hyper-parameters for bubble distribution functions (BDF).

Fig. 2.

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

Fig. 3.

(Color available online) Comparison of mode solution and COMSOL solution for 200 Hz and 1 kHz frequencies.

(15)

Fig. 4.

(Color available online) Insertion loss as a function of frequency for four bubble size distributions. (a) void fraction of 0.1, (b) enlarged figure of Fig. 4(a), (c) void fraction of 0.001, and (d) enlarged figure of Fig. 4(c).

(16)

Table 2.

Elastic property of steel and FRP used in the numerical examples.

Fig. 5.

(Color available online) Effect of the material property of elastic shell on the insertion loss.

Fig. 6.

(Color available online) Insertion loss for the thickness of outer fluid 1. (a) the case that the thickness of ‘outer fluid 1 and bubble layer’ is fixed as 0.3 m, and (b) the case that the thickness of bubble layer is set to be 0.3 m. BLT means bubble layer thickness.

Acknowledgements

References