Analysis of noise generation mechanism for two-phase flow of refrigerant in evaporator inlet pipe of refrigerator

Jooyoung Lee; Sangheon Lee; Cheolung Cheong; Taehun Kim; Junhyo Koo

doi:10.7776/ASK.2024.43.6.593

Preview

Research Article

The Journal of the Acoustical Society of Korea. 30 November 2024. 593-604
https://doi.org/10.7776/ASK.2024.43.6.593

Analysis of noise generation mechanism for two-phase flow of refrigerant in evaporator inlet pipe of refrigerator

냉장고 증발기 입구 배관의 냉매 이상유동에 의한 소음 발생 메커니즘 분석

Jooyoung Lee¹

Sangheon Lee¹

Cheolung Cheong¹²^*

Taehun Kim³

Junhyo Koo³

이 주영¹

이 상헌¹

정 철웅¹²^*

김 태훈³

구 준효³

¹부산대학교 기계공학부

²부산대학교 첨단냉동공조에너지센터

³LG 전자

^{*Corresponding Author}

License (open-access, http://creativecommons.org/licenses/by-nc/4.0/):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

In this paper, numerical flow and acoustic analysis were conducted on the inlet piping of refrigerator evaporator, taking actual operating conditions to investigate the mechanism of refrigerant induced noise generation. Four operating conditions were selected as boundary conditions, considering the expansion process of the refrigeration cycle. Two-phase flow analysis was performed, considering temperature changes and phase transitions of the R600a refrigerant in the region from the condenser outlet to the evaporator inlet. Acoustic analysis results confirmed that the area near the evaporator inlet has a higher noise contribution compared to the capillary tube. By comparing the instantaneous sound pressure of bubbles and acoustic analysis result, pipe area for reducing refrigerant induced noise was proposed.

Keywords

Two-phase flow

Refrigerant induced noise

Numerical analysis

Vapor volume fraction

Bubble dynamics model

본 논문에서는 실제 작동 조건을 고려하여 냉장고 증발기 입구 배관에 대해 수치적으로 유동해석 및 소음해석을 진행하여 냉매음의 발생메커니즘을 분석했다. 냉장사이클의 팽창과정을 고려하여 4개의 작동조건을 선정 후 경계조건으로 부여했다. 응축기 출구부터 증발기 입구까지 영역에 대해 R600a냉매의 온도 변화 및 상변화를 고려하여 이상유동해석을 진행했다. 소음해석 결과 증발기 입구 근처 영역이 모세관 대비 높은 소음기여도를 가지는 것을 확인했다. 소음해석 결과를 기포 순간 음압과 비교하여 냉매소음 개선을 위한 배관영역을 제시했다.

키워드

이상유동

냉매소음

수치해석

기체부피분율

기포동역학

MAIN

I. 서 론
II. 수치해석 기법
2.1 유동해석 기법
2.2 질량 전달 모델
III. 해석 모델 정의
3.1 해석 영역 정의 및 경계조건
3.2 유동해석 격자 구성
3.3 진동 및 소음해석 격자 구성
IV. 해석결과 및 분석
V. 결 론

I. 서 론

현대의 주거 공간은 단순한 휴식의 장소를 넘어, 취미 활동과 업무를 수행하는 다기능적인 공간의 의미를 가진다. 또한, 1인 가구의 증가와 함께 가전제품의 판매량이 증가하고 있으며, 실외에 위치하던 많은 가전제품이 실내에 배치되는 추세다. 이로 인해 가전제품에서 발생하는 소음은 구매자의 휴식과 일상 활동을 방해하는 요소로 인식되며, 가전제품의 주요한 구매지표로 급부상했다. 가전제품 중에서도 냉장고는 24 h 가동된다는 특성으로 인해 저소음에 대한 요구가 높으며, 이에 따라 개발사들은 냉장고의 소음 저감에 많은 노력을 기울이고 있다. 냉장고의 압축기의 성능은 지속적으로 개선되고 있어 압축기의 소음은 감소하는 추세이며, 상대적으로 전체 소음에서 냉매소음이 차지하는 비율이 커지고 있다.

압력 및 온도 강하를 목적으로 증발기 입구에 널리 설치되는 모세관 및 전자팽창밸브에서 발생하는 냉매소음은 액체 상태의 냉매가 기체 상태로 상변화를 겪는 이상유동에 기인한다. 이러한 이상유동으로 인해 큰 소음이 발생한다.^[1,2] 일반적으로 소음은 완전하게 제거하기 어렵기 때문에, 구조적 개선을 통한 냉매소음 저감을 목표로 한 연구가 활발하게 진행되고 있다.

Umeda et al.^[3]는 전자팽창밸브의 입구가 수직으로 배치되었을 때 강한 소음이 발생하며, 밸브의 입구를 수평으로 놓았을 때 냉매소음이 감소하는 것을 실험을 통해 확인했다. Hirakuni et al.^[4]는 팽창밸브의 입구와 출구에 다공성 금속을 설치하면 냉매소음이 감소하는 것을 보였다. 또한 Han et al.^[5]은 응축기 출구 배관의 직경을 33 % 줄이고 다공성 금속을 설치하면 냉매소음을 감소시킬 수 있다는 것을 실험을 통해 검증했다.

이러한 연구들은 에이컨 냉동 사이클에 사용되는 전자팽창밸브를 대상으로 실험을 진행했다. 에어컨 실내기 및 실외기 주위의 온도 변화가 작기 때문에 팽창밸브로 유입되는 유체의 온도 및 압력이 일정하게 유지되며, 실험을 통하여 확인된 유동 현상이 실제 냉동 사이클에서도 재현이 된다. 하지만, 냉장고의 경우 열교환기가 위치하는 냉장실 및 기계실의 체적이 작기 때문에 냉매의 온도와 압력의 변동이 크게 발생한다. 이로 인해 실험에서 확인된 유동 현상과 실제 냉장고에서 발생한 유동 현상이 다르게 발생한다. 또한, 모세관은 전자팽창밸브에 비해 유로가 길기 때문에, 다양한 이상유동 구조가 발생제 냉장고에서 발생하는 유동 현상을 예측하고 설계 단계에서 냉매 소음의 발생 메커니즘을 파악할 필요가 있다. 이상유동 현상을 예측하기 위해서는 정밀한 수치해석 기법이 요구되며, 이를 목표로 한 연구 역시 다양하게 진행되고 있다.

Alnaimat et al.^[6]는 수치해석을 통해 냉매의 질량유속과 입구단의 증기 건도를 바꿔가며 모세관에서의 유동현상을 분석하는 연구를 수행했다. Alok와 Sahu^[7] 는 수치해석을 통해 코일형 모세관을 통과하는 R134a 및 R600a 냉매의 유동특성을 관찰하고 질량유량과 냉각부하 간의 비례관계를 도출했다. Zhang et al.^[8]는 모세관 출구 영역을 대상으로 수치해석을 수행하였고, 모세관 출구에 대해 공기주입모듈을 설치하면 압력 섭동을 억제하여 냉매소음을 줄일 수 있음을 보였다. 대부분의 연구는 상변화가 일어나는 모세관에 대하여 입출구 온도와 압력을 제어하기 위하여 단순화된 형상에 대하여 수치해석을 수행하였다. 하지만, 앞서 설명한바와 같이 실제 냉장고에선 형상이 변화함에 따라 실험과 다른 이상유동 구조가 발생할 수 있으며, 실제 냉장사이클의 팽창과정을 수치적으로 해석한 연구는 아직 부족한 실정이다. 따라서 본 연구에서는 냉장고 증발기 입구 배관의 냉매 이상유동에 의한 냉매소음 발생 메커니즘 규명을 진행하였으며, 이를 위해 냉장고 증발기 입구 배관 전체를 대상으로 수치해석을 진행했다. 유동 해석 단계에서 열역학적 냉장사이클을 고려하여 해석 영역 및 조건을 선정하고, 온도에 따른 R600a 냉매의 동작을 고려하여 유동해석을 수행했다. 이후 배관의 실제 결합 상태를 고려한 진동 및 소음해석을 진행했다. 이후, 기포순간음압을 계산하여 냉장고 증발기 입구 배관의 냉매소음 개선을 위한 영역을 특정했다.

II. 수치해석 기법

2.1 유동해석 기법

본 연구에서는 유동해석의 지배 방정식으로 비정상 나비에 스톡스 방정식(Unsteady Reynolds-Averaged Navier-Stokes, URANS)을 선정했다. 또한, 증발기 입구 배관에서의 이상유동을 수치적으로 모사하기 위해 균질 다상유동 모델(Homogeneous multiphase model)기반의 Volume of Fluid(VoF)모델을 적용했다. 균질 다상유동 모델은 여러 상의 물성치와 부피분율을 바탕으로 혼합물 상태의 Pseudo-material을 생성하고, Pseudo-material의 물성치를 각각의 방정식에 대입하여 해를 구한다. VoF모델은 각 유체의 부피분율(Volume fraction)을 추적하여 두 개 이상의 비혼합성 유체를 모델링하며, 각 상의 경계면을 명확히 표현할 수 있다는 장점이 있다. VoF모델에서 사용하는 부피분율 방정식, 연속방정식, 운동량 방정식 및 에너지 방정식은 다음과 같다.

(1)

\frac{\partial α_{l}}{\partial t} + \nabla ∙ (α_{l} \vec{u}) = \frac{1}{ρ_{l}} ({\dot{m}}_{v \to l} - {\dot{m}}_{l \to v}) .

(2)

\frac{\partial ρ_{m}}{\partial t} + \nabla ∙ (ρ_{m} \vec{u}) = 0 .

(3)

\frac{\partial (ρ_{m} \vec{u})}{\partial t} + \nabla ∙ (ρ_{m} \vec{u} \vec{u}) = - \nabla p + \nabla ∙ [(μ + μ_{t}) (\nabla \vec{u} + \nabla {\vec{u}}^{T})] + ρ_{m} \vec{g} + \vec{F} .

(4)

\frac{\partial (ρ_{m} E)}{\partial t} + \nabla ∙ [\vec{u} (ρ_{m} E + p)] = \nabla ∙ [(k + k_{t}) \nabla T] + S_{h},

여기서

(5)

α_{l} + α_{v} = 1 .

(6)

ρ_{m} = ρ_{l} α_{l} + ρ_{v} α_{v} .

(7)

E = \frac{(α_{l} ρ_{l} E_{l} + α_{v} ρ_{v} E_{v})}{(α_{l} ρ_{l} + α_{v} ρ_{v})} .

(8)

T = \frac{(α_{l} ρ_{l} T_{l} + α_{v} ρ_{v} T_{v})}{(α_{l} ρ_{l} + α_{v} ρ_{v})} .

$ρ_{m}$ 은 혼합물의 밀도, $ρ_{l}$ 은 액체상의 밀도, $ρ_{v}$ 은 기체상의 밀도, $α_{l}$ 은 액체상의 부피분율, $α_{v}$ 은 기체상의 부피분율, $E$ 와 $T$ 는 각각 질량 평균 에너지와 질량 평균 온도를 의미한다.

난류모델로는 Mentor^[9]에 의해 제안된 SST $k - ω$ 모델을 채택했다. SST $k - ω$ 모델은 혼합함수를 도입하여 여러 유동상황에서 벽면 근처와 자유유동 영역의 유동을 정밀하게 예측한다고 알려져 있다.^[9]

SST $k - ω$ 모델의 난류 점성계수, 난류운동에너지 및 소산율에 대한 식은 다음과 같다.

(9)

μ_{t} = \frac{a_{1} ρ k}{\max (a_{1} ω, \bar{S} F_{2})} .

(10)

\frac{\partial k}{\partial t} + u_{j} \frac{\partial k}{\partial x_{j}} = \frac{\partial}{\partial x_{j}} \{(ν + σ_{k} ν_{t}) \frac{\partial k}{\partial x_{j}}\} + P_{k} - β * k ω .

(11)

\frac{\partial ω}{\partial t} + u_{j} \frac{\partial ω}{\partial x_{j}} = \frac{\partial}{\partial x_{j}} \{(ν + σ_{ω} ν_{t}) \frac{\partial ω}{\partial x_{j}}\} + α S^{2} - β ω^{2} + 2 (1 - F_{1}) σ_{ω^{2}} \frac{1}{ω} \frac{\partial k}{\partial x_{i}} \frac{\partial ω}{\partial x_{i}},

여기서

(12)

S_{i j} = \frac{1}{2} \{\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}}\} .

$k$ ,𝜔는 각각 난류운동에너지와 소산율이다. $F_{1}, F_{2}$ 는 혼합함수이며, 계수 $σ_{k}$ , $σ_{ω}$ , 𝛽, $a$ , 𝛼는 다음의 식을 통해 계산된다.

(13)

ϕ = F_{1} ϕ_{1} + (1 - F_{1}) ϕ_{2} .

본 연구에서는 각각의 계수에 대해 Mentor가 제시한 값을 사용했다.

유동해석을 위해 상용프로그램인 Fluent 2023 R2를 사용했다. 압력-속도 연성 기법으로는 SIMPLE 기법을 선택했다. 이상 유동해석은 기체와 액체사이의 질량 및 운동량의 교환이 발생하기 때문에, 안정성 높은 수치해석 기법이 필요하다. 또한, 높은 속도로 흐르는 냉매에 대해 수치해의 정밀도를 높이기 위해 밀도, 운동량, 에너지 및 난류운동에너지에 대해 2차 풍상차분법(Second order upwind scheme)을 적용했다. 목표 주파수가 1,000 Hz이지만 해석의 안정성과 정밀도를 높이기 위하여 해석의 시간 간격을 0.0001(1/10,000 s)로 설정하였다.

2.2 질량 전달 모델

기포 생성으로 인한 액체상과 기체상 간의 질량 전달을 고려하기 위해 캐비테이션 모델 중 Schenrr와 Sauer^[10]에 의해 제안된 Schenrr-Sauer모델을 적용했다.

지배방정식은 다음과 같다.

(14)

\frac{\partial (ρ_{v} α_{v})}{\partial t} + \nabla ∙ (ρ_{v} α_{v} \vec{u}) = {\dot{m}}^{+} - {\dot{m}}^{-},

여기서

(15)

{\dot{m}}^{+} = \frac{3 α (1 - α)}{R_{b}} \frac{ρ_{v} ρ_{l}}{ρ_{m}} \sqrt{\frac{2}{3} \frac{(p_{v} - p)}{ρ_{l}}} .

(16)

{\dot{m}}^{-} = \frac{3 α (1 - α)}{R_{b}} \frac{ρ_{v} ρ_{l}}{ρ_{m}} \sqrt{\frac{2}{3} \frac{(p - p_{v)}}{ρ_{l}}} .

(17)

R_{b} = (\frac{α}{(1 - α)} \frac{3}{4 π} \frac{1}{n})^{\frac{1}{3}} .

${\dot{m}}^{+}$ 과 ${\dot{m}}^{-}$ 는 각각 기화, 액화에 의한 단위 부피당 상간 질량 전달율이며, $R_{b}$ 는 기포의 지름, $n$ 은 액체의 단위부피당 기포 수, $p_{v}$ 는 기체의 포화압력, $p$ 는 기포의 압력을 의미한다.

Schenrr-Sauer모델은 단순화된 Rayleigh-Plesset 방정식을 기반으로 액체 내부 단일 기포의 성장을 가정하고 있기에, 기화 및 액화 항은 기체압력과 포화압력 차이의 제곱근에 비례하게 된다.

III. 해석 모델 정의

3.1 해석 영역 정의 및 경계조건

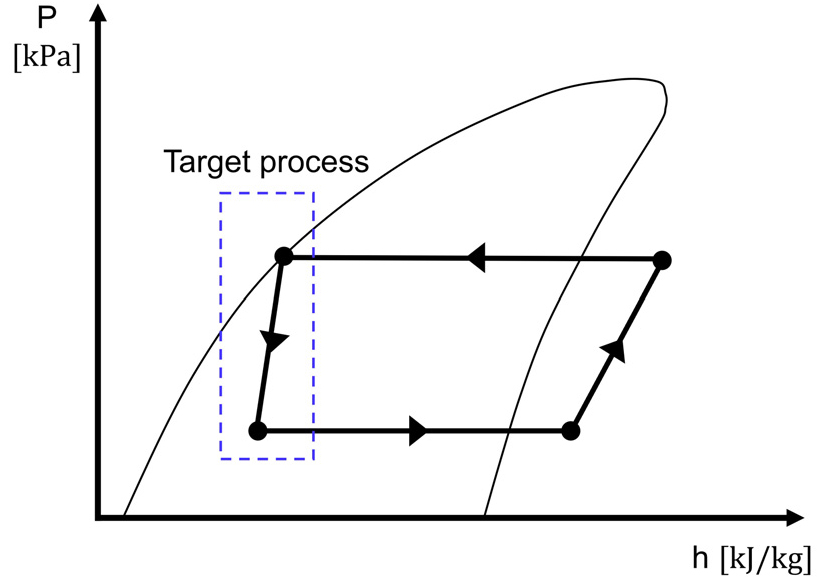
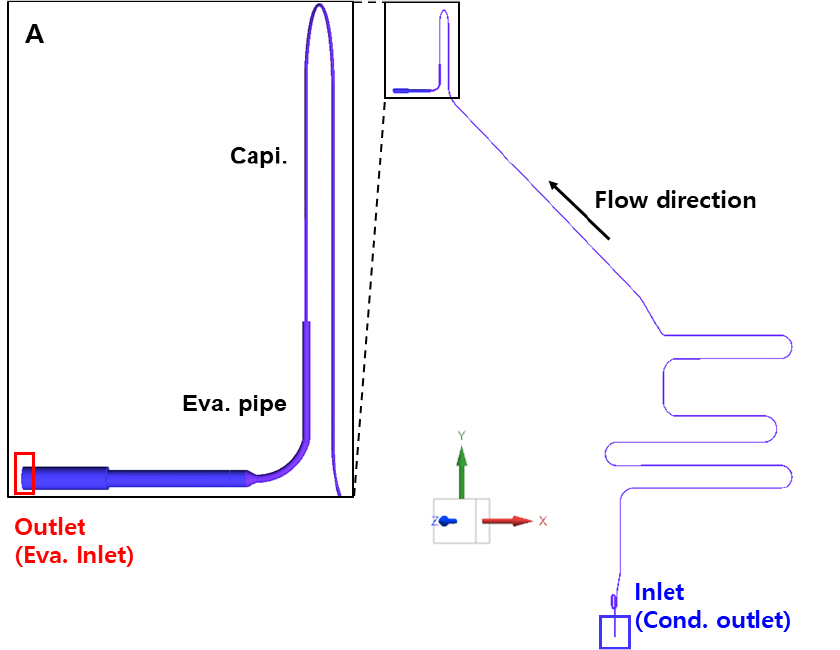
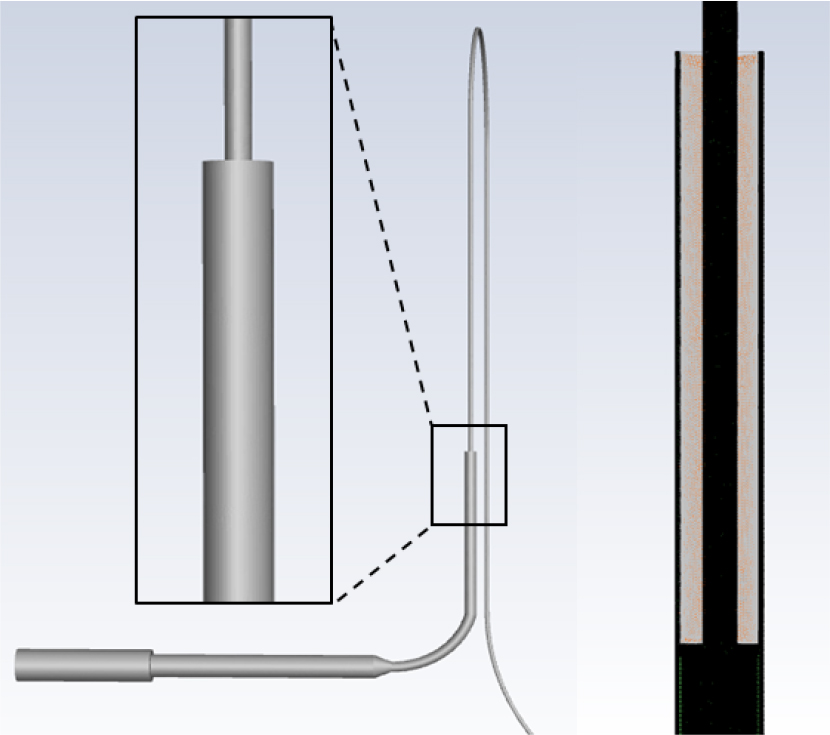
Fig. 1은 P-h 선도 상에서 냉동사이클을 나타내었다. Fig. 1의 냉동사이클에서 고압의 가로선은 응축기에서의 응축과정이며, 저압의 가로선은 증발기에서의 증발과정이다. 또한, 파란색 사각형으로 표시한 영역은 모세관의 팽창 과정을 나타낸다. 마지막으로 팽창 과정의 반대편의 수직선은 압축기의 압축과정을 나타낸다. Fig. 1의 화살표로 확인할 수 있듯이, 냉매는 압축기, 응축기, 모세관, 증발기를 거쳐 다시 압축기로 돌아간다. 본 논문의 해석 대상으로서 팽창과정에 해당하며 이상 유동이 활발하게 발생하는 모세관을 선정하였으며, 본 시스템에서 모세관은 응축기 출구부터 시작하여 증발기 입구 배관까지 연결되어 있다. 해석영역은 모세관 전체와 증발기 입구의 배관을 선정하였으며, Fig. 2에 나타내었다. Fig. 2의 Eva. Inlet, Eva. pipe, Capi., Cond. outlet은 각각 증발기 입구, 증발기 배관, 모세관 및 응축기 출구를 의미한다. 응축기와 모세관의 연결부를 입구단으로 구성하였으며, 모세관을 지나 증발기로 유입되는 영역을 출구단으로 구성하였다. Fig. 3은 Fig. 2의 A영역의 실제사진을 나타내었으며, 냉장실로 배관이 들어오는 영역을 나타내었다. 해당 영역은 배관이 온도가 낮은 냉장실로 들어오는 영역으로서 냉매소음이 크게 발생하는 영역으로 알려져 있다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430601/images/ASK_43_06_01_F1.jpg

Fig. 1.

(Color available online) Expansion process of refrigeration cycle in the simulation.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430601/images/ASK_43_06_01_F2.jpg

Fig. 2.

(Color available online) Schematic diagram of computational geometry.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430601/images/ASK_43_06_01_F3.jpg

Fig. 3.

(Color available online) Evaporator pipe of refrigerator.

실제 냉장고는 냉장실의 온도에 따라 압축기의 작동속도가 제어된다. 이로인해 냉매의 온도와 압력이 고정되지 않고 계속해서 변동하게 된다. 본 논문에서는 이러한 냉장고의 작동 조건을 고려하여 4개의 온도조건을 선정하였다. Table 1에 각 조건 별 부여한 경계조건을 정리했으며, $P_{s}$ ( $T_{1}$ )는 $T_{1}$ °C에서의 포화압력을 의미한다.

Table 1.

Boundary condition of each case.

		Case1	Case2	Case3	Case4
Inlet	Temp. [°C]	$T_{1}$	$T_{1}$	$T_{1}$ +8	$T_{1}$ +8
	Pressure [Pa]	$P_{s}$ ( $T_{1}$ )	$P_{s}$ ( $T_{1}$ )	$P_{s}$ ( $T_{1}$ +8)	$P_{s}$ ( $T_{1}$ +8)
	Vapor volume fraction	0
Outlet	Pressure [Pa]	$P_{s}$ ( $T_{2}$ )	$P_{s}$ ( $T_{2}$ +8)	$P_{s}$ ( $T_{2}$ )	$P_{s}$ ( $T_{2}$ +8)

입구단은 압력조건으로 설정하고 압력, 온도, 기체부피분율 값을 부여했다. 명확한 경계조건 설정을 위해 각 Case의 입구단은 포화액체로 가정했다. 출구단은 압력조건으로 설정하고 압력 값을 부여했다. 포화액체와 포화기체 사이의 혼합물 상태에서는 엔탈피 변화가 일어나면 기체부피분율이 변화하지만, 상변화에 필요한 에너지인 잠열에 의하여 압력과 온도는 일정하게 유지된다. 따라서, 출구단의 압력값은 증발기로 유입되는 냉매의 온도조건에서의 포화 압력 값으로 선정했다.

3.2 유동해석 격자 구성

모세관과 증발기 배관의 직경이 다르기 때문에 영역을 구분하고 배관 벽면에는 프리즘격자, 배관 내부에는 사면체 격자를 생성했다. 프리즘 격자에 대한 정보는 Table 2에 정리했다. 벽면에서의 경계층 유동을 정밀하게 예측하기 위하여 프리즘 격자를 구성했다. 프리즘 격자의 첫 번째 층 높이는 0.000986 mm로 설정하여 Y+는 1 이하를 유지하도록 구성하였으며, 8개 층의 프리즘 격자를 구성했다. 성장률은 모세관에 대해서는 1.3, 증발기 배관에 대해서는 1.5의 값을 적용했다. 체적 격자는 사면체 격자를 선정하였으며, 격자의 크기는 유동을 정밀하게 해석할 수 있도록 음속을 고려하여 배관 직경의 1/20수준을 유지했다. 이를 위해 격자의 길이가 모세관에 대해 0.04 mm, 증발기 배관에 대해 0.1 mm를 초과하지 않도록 구성했다.

Table 2.

Prism mesh information.

Property	Capillary tude	Evaporator inlet pipe
Pipe diameter	0.85 mm	2.2 mm
First layer height	0.000986 mm	0.003 mm
Mesh size (Growth rate)	0.1 mm (1.3)	0.25 mm (1.5)
Number of layers	8
Total prism thickness	0.024 mm	0.148 mm
Target Y+	< 1

모세관이 증발기 배관에 일부 삽입되는 형태로 배관이 구성되어 있기 때문에, 해당 구조를 모사하기 위해 Fig. 4과 같이 배관의 두께를 고려하여 격자를 생성했다. 배관의 총 격자수는 약 7400만 개다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430601/images/ASK_43_06_01_F4.jpg

Fig. 4.

(Color available online) Capillary tube inserted to evaporator inlet pipe.

작동유체는 R600a이며, 냉매의 온도에 따른 특성을 적절히 반영하기 위해 미국 국립 표준 기술연구소(National Institute of Standards and Technology, NIST)^[11]에서 제공하는 냉매의 물성치를 온도에 대해 보간하여 적용했다. 기체의 밀도는 이상기체로 가정했다. 보간한 기법과 물성치는 Table 3에 정리했다.

Table 3.

R600a property interpolation technique.

Case	R600a Liquid	R600a Vapor
Density	4^thorder-polynomial	Ideal gas
$C_{p}$ (Specific heat)	2^nd order-polynomial
Thermal conductivity	2^nd order-polynomial
Viscosity	2^nd order-polynomial
Surface tension	2^nd order-polynomial

3.3 진동 및 소음해석 격자 구성

진동 및 소음해석을 위해 상용프로그램인 Simcenter 3D을 사용했으며, 구조 및 소음해석 지배방정식은 다음과 같다.

(18)

[- w^{2} [M] + i w [B] + [K]] {X (w)} = {X (w)},

여기서

(19)

[M] = [\begin{matrix} M_{s} & 0 \\ - A^{T} & M_{a} \end{matrix}] .

(20)

[B] = [\begin{matrix} B_{s} & 0 \\ 0 & B_{a} \end{matrix}] .

(21)

[K] = [\begin{matrix} K_{s} & A \\ 0 & K_{a} \end{matrix}] .

[M]은 질량 행렬, [B]는 감쇠 행렬, [K]는 강성 행렬을 의미한다. Eq. (19)와 Eq. (21)의 A값은 음향 및 소음 격자의 연성 벡터를 의미하며 [A]행렬은 다음과 같이 정의된다.

(22)

[A] = \int_{S} N_{s}^{T} N_{f} {n_{s}} d S .

Eq. (22)의 N은 형상 벡터를 의미하며, 아래 첨자 s와 f는 각각 구조 및 음향 격자 영역을 나타낸다. 소음이 방사되는 영역의 매질이 공기이며, 공기와 배관의 밀도가 약 7,400배 차이나기 때문에 공기의 진동이 배관의 진동에 미치는 영향을 무시할 수 있다고 판단하여 단방향 연성기법을 적용했다.

배관 진동해석을 위한 구조 격자는 실제 배관의 형상을 고려하여 구성했다. 유동해석 격자를 기반으로 1 mm 크기로 2D Shell 격자를 생성했으며, 0.5 mm 두께를 부여했다. 배관에는 구리(C10100)의 물성치를 적용했다.

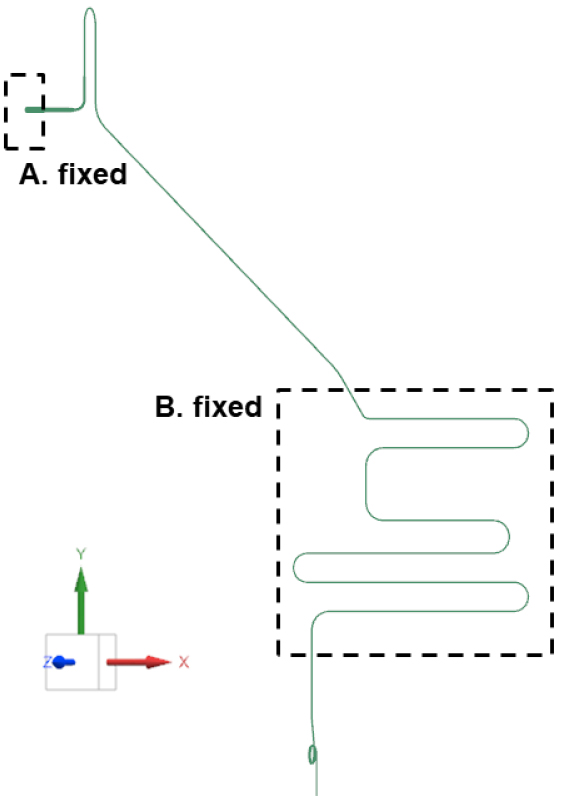
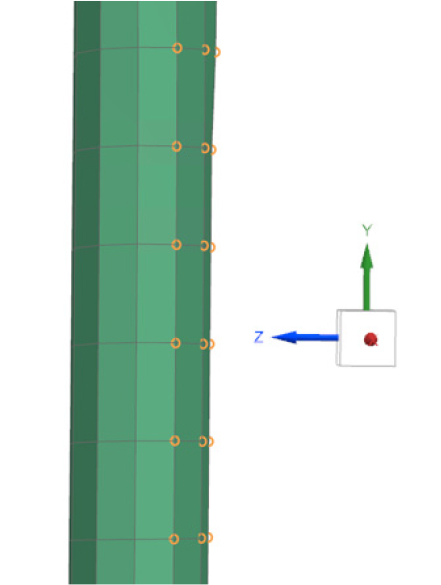
진동해석의 구속조건을 부여한 영역은 Fig. 5과 같다. Fig. 5의 영역 A와 영역 B에 구속조건을 부여했다. 영역 A는 증발기와 연결되는 부분이며, 고정 구속조건을 부여했다. 영역 B는 모세관이 직경이 10배 큰 배관과 결합된 영역으로, 실제 배관의 결합 상태를 고려하여 영역 B 전체에 고정구속조건을 부여했다. 이때, 배관의 절반에 대해서만 구속조건을 부여하여 Fig. 6과 같이 –Z방향에 대해서 고정된 것을 모사했다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430601/images/ASK_43_06_01_F5.jpg

Fig. 5.

(Color available online) Schematic diagram of constraint condition.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430601/images/ASK_43_06_01_F6.jpg

Fig. 6.

(Color available online) Constraint applying point of B.

진동해석의 가진력으로 유동해석을 통해 계산된 벽면의 압력신호를 적용했다. 유동해석 격자와 진동해석격자 사이의 압력 데이터 전달을 위해 역거리가중법을 이용하여 보간했다. 샘플링 주파수와 해석의 효율성을 고려하여 500개의 압력 데이터를 추출하였으며, 푸리에 변환을 통하여 노드 별로 20 Hz의 주파수 분해능을 가지는 압력 스펙트럼으로 변환했다.

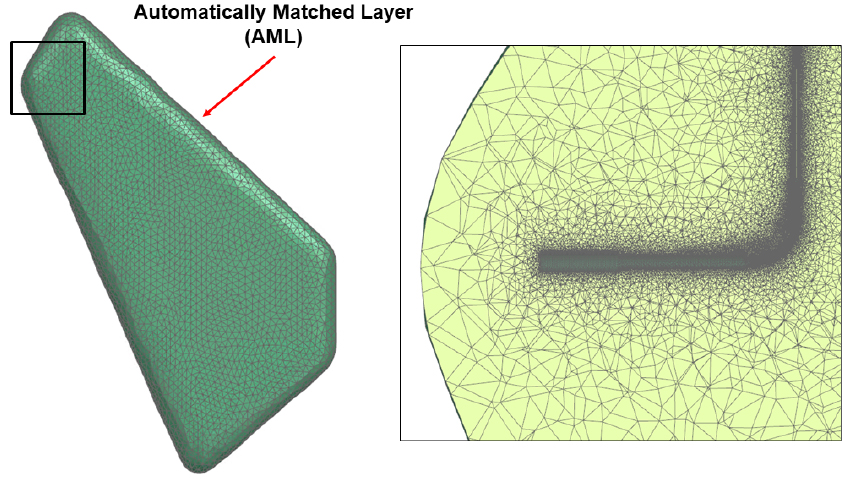
소음해석을 위해 배관 외부 영역에 사면체 격자를 생성하고 공기 물성치를 부여했다. 격자의 크기는 음속을 고려하여 한 파장에 10개의 격자가 구성될 수 있도록 최대 격자크기를 15 mm로 설정하였으며, Fig. 7에 나타냈다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430601/images/ASK_43_06_01_F7.jpg

Fig. 7.

(Color available online) Tetrahedral mesh for acoustic analysis and internal acoustic mesh.

음파가 격자표면에서 반사되는 비물리적인 현상을 피하기 위해 소음해석 격자의 표면에 Automatically Matched Layer(AML) 경계조건을 적용하였다. AML 경계조건은 음파를 흡수하는 가상의 감쇠층을 만들어 음파가 반사되지 않도록 조머펠트(Sommerfeld) 경계조건을 계산한다. 조머펠트 방정식은 다음과 같이 정의된다.

(23)

\lim_{r \to \infty} [r (\frac{\partial p}{\partial r} + \frac{1}{c} \frac{\partial p}{\partial t})] = 0 .

구조 및 음향 해석은 20 Hz부터 1,000 Hz까지 20 Hz 간격으로 진행했다.

IV. 해석결과 및 분석

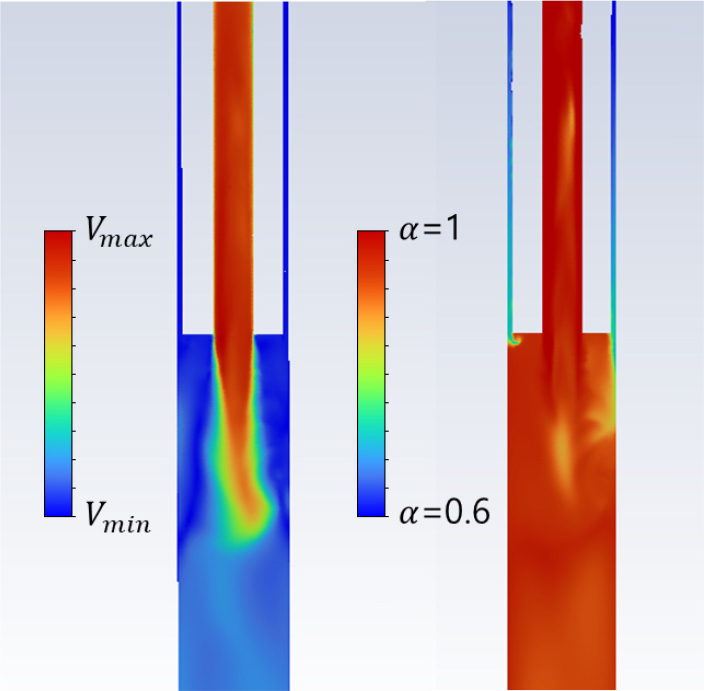
Table 1에서 정의한 경계조건에 대해 유동해석을 수행하였다. 4개의 조건에서 모세관 출구의 유동장을 확인하였을 때, 유사한 유동구조를 가지고 있었으며 그 중 Case3의 유동장을 Fig. 8에 나타내었다. 유동해석의 유효성을 검증하기 위해 출구의 기체부피분율을 이론값과 비교했다. 실제 사이클에서 기체부피분율을 측정하는 것은 어렵기 때문에, 이상적인 상황을 가정하여 입출구 온도 및 압력을 바탕으로 건도를 계산했다. 이후 건도와 기체부피분율의 상관식을 이용하여 실제 배관에서의 기체부피분율을 추정하였으며, 다음의 방정식을 활용했다.^[12]

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430601/images/ASK_43_06_01_F8.jpg

Fig. 8.

(Color available online) Mixture velocity contour (case3, left) and vapor volume fraction contour (case3, right).

(24)

α = {[1 + (\frac{1 - x}{x}) (\frac{ρ_{g}}{ρ_{l}}) \sqrt{1 - x (1 - \frac{ρ_{l}}{ρ_{g}})}]}^{- 1} .

Table 4에는 실제 조건에서의 수치해석 결과를 통해 계산된 기체부피분율 값과 이론값을 비교하여 나타내었다. 등엔탈피 과정으로 가정하여 이론값과 비교했을 때 최대 6.9 %의 오차가 발생했다. Lee와 Su^[13]의 실험에 따르면, R600a냉매의 팽창과정은 등엔탈피 과정으로 근사할 수 있기에 수치해석이 냉매의 이상 유동 현상을 재현하고 있다고 판단된다. Table 4의 오차에서 음의 값은 수치해석이 과대 예측을 하고 있다는 의미를 나타낸다.

Table 4.

Calculated outlet vapor volume fraction compared to ideal process.

Case	Calculated outlet vapor volume fraction	Percentage error with ideal process
Case1	0.984	-5.1 %
Case2	0.981	-6.9 %
Case3	0.978	-3.6 %
Case4	0.979	-5.4 %

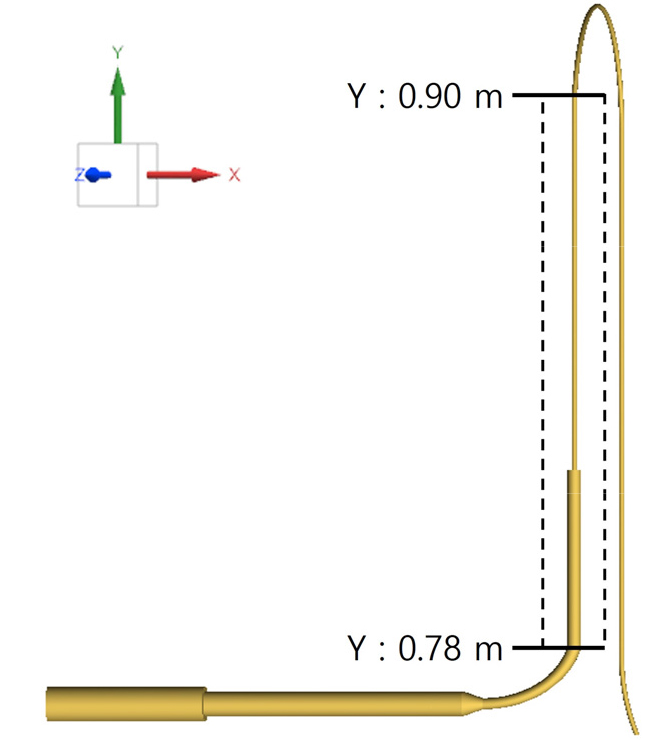
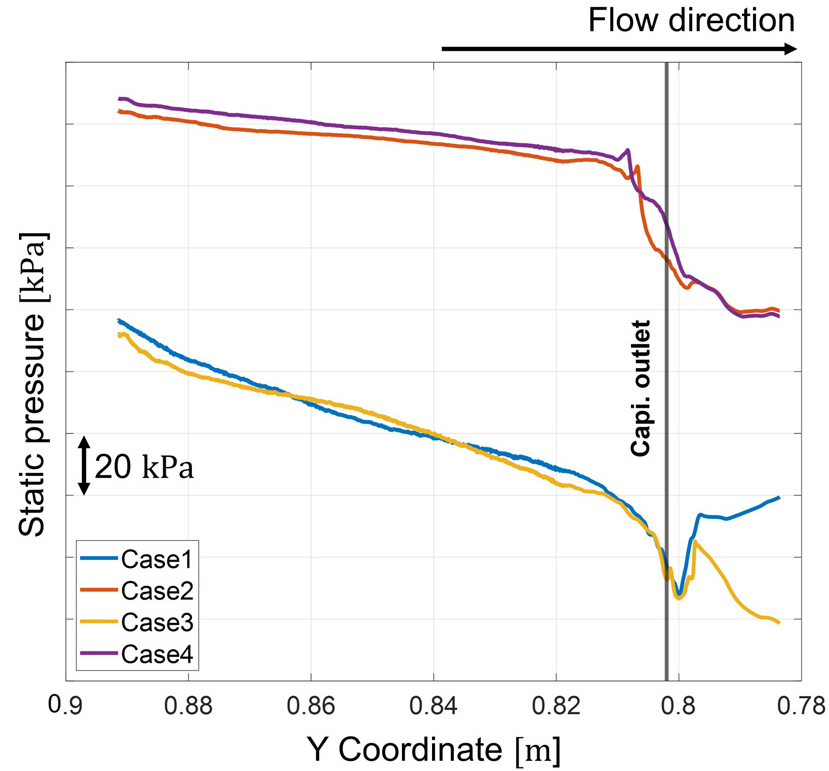
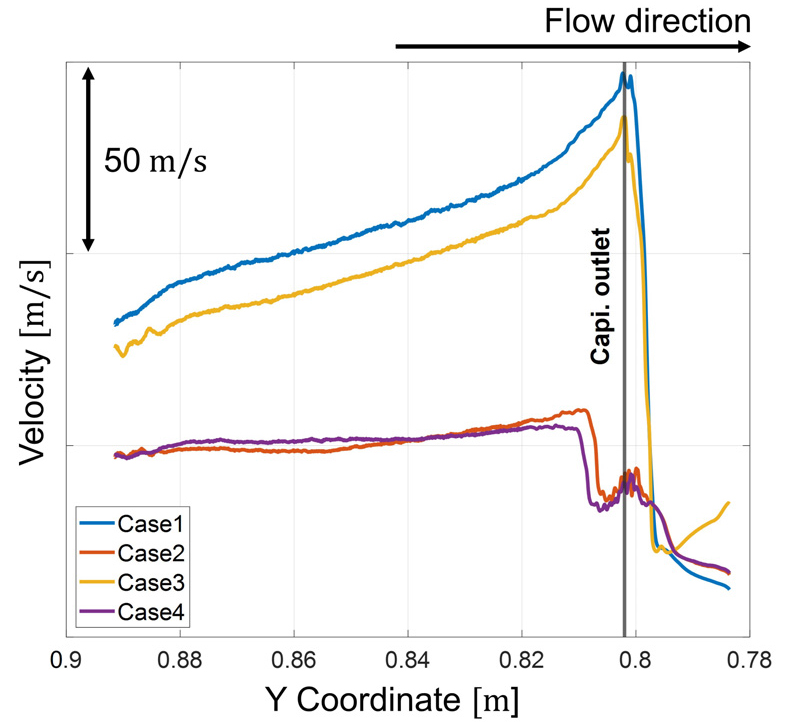
실제 모세관 출구에서는 압력 변화가 매우 크고, 면적이 넓어짐에도 유체의 관성력에 의해 높은 속도가 유지된다고 알려져 있다. 이에 유동해석 결과가 급격한 압력구배와 높은 속도를 보이는지 파악하기 위해 Fig. 9과 같이 Y좌표가 0.78 ~ 0.90인 수직배관의 중심 지점에 대해 압력과 속도 데이터를 추출하였으며, Figs. 10과 11에 압력 및 속도 값을 각각 나타내었다. Figs. 10과 11의 가로축은 배관의 Y 좌표를 의미하며, 편의를 위해 좌우를 반전했다. 따라서, 유동방향이 Y 좌표가 작아지는 방향인 왼쪽에서 오른쪽이 되도록 했다. 또한 모세관 출구에서의 유동현상 변화를 파악하기 위해 Figs. 10과 11에 모세관 출구의 위치를 표시했다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430601/images/ASK_43_06_01_F9.jpg

Fig. 9.

(Color available online) Pressure and velocity data extraction area.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430601/images/ASK_43_06_01_F10.jpg

Fig. 10.

(Color available online) Static pressure drop in vertical pipe.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430601/images/ASK_43_06_01_F11.jpg

Fig. 11.

(Color available online) Velocity change in vertical pipe.

Cases 1과 3은 모세관 출구에서의 유동현상을 잘 보여주고 있다. 단면적이 급격히 확장되며 압력 기울기가 매우 커지게 되고, 높은 유속이 관찰되고 있다. Cases 2와 4는 앞선 두 Case와 같이 모세관 출구의 유동현상을 명확하게 보여주고 있지는 않지만 급격한 압력 강하 곡선이 관찰된다.

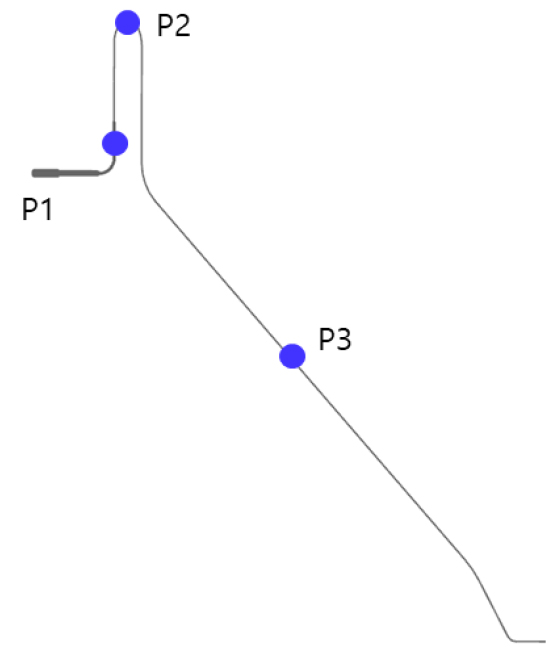
진동해석 결과를 확인하기 위해 Fig. 12와 같이 각 배관 요소를 대표할 수 있는 3개의 지점을 선정했다. P1지점은 모세관과 증발기 배관이 만나는 지점, P2지점은 U자 곡관의 최상단 지점, P3지점은 모세관에서 구속조건이 부여되지 않은 영역의 중앙지점이다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430601/images/ASK_43_06_01_F12.jpg

Fig. 12.

(Color available online) Data extraction points.

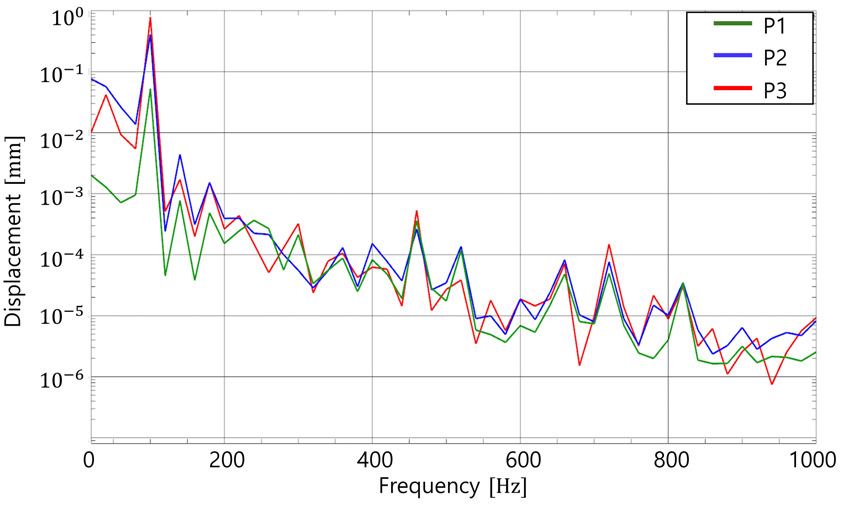
선정한 3개 지점에서 추출한 3축 진동의 크기를 Fig. 13에 나타냈으며, 100 Hz에서 큰 진동 변위가 확인된다. 유동해석 결과가 실제 R600a 냉매의 유동과 큰 오차를 보이지 않았으므로 가진력으로 입력한 유동의 벽면 압력데이터 역시 유효하며, 실제 배관의 물성치 및 고정조건을 부여했기에 진동해석 격자도 적절히 실제 배관을 모사하고 있으므로 진동해석 결과를 신뢰 할 수 있다고 판단했다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430601/images/ASK_43_06_01_F13.jpg

Fig. 13.

(Color available online) Direct frequency response analysis result (Case1, df = 20 Hz).

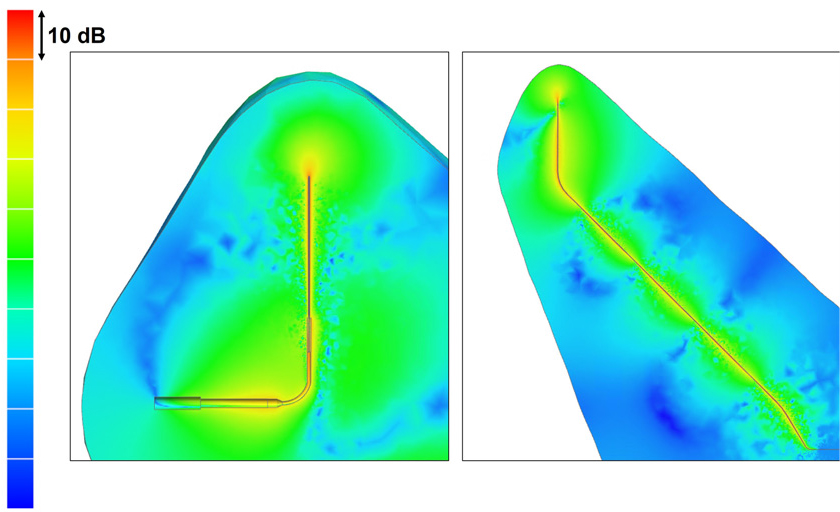
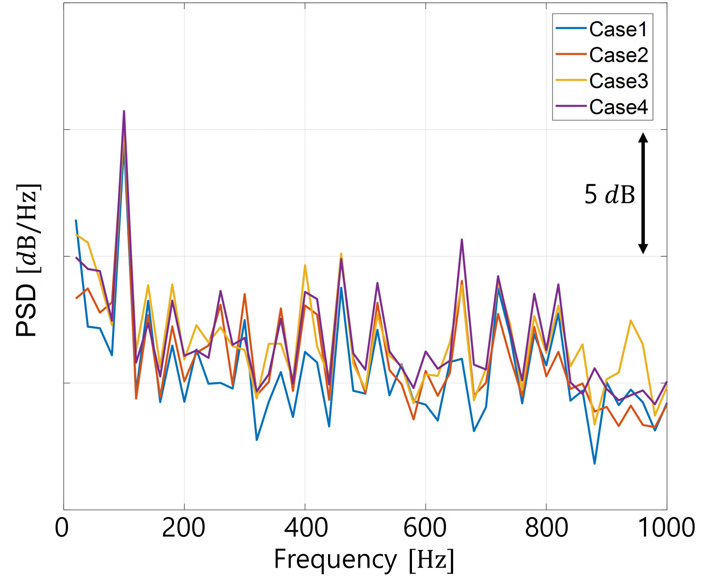
이후 소음해석을 진행했으며, 소음방사패턴을 확인하고자 Fig. 14과 같이 음압을 Sound Pressure Level (SPL)로 변환했다. Fig. 14의 좌측과 우측은 각각 증발기 배관 영역과 모세관 영역의 소음방사패턴이다. 각 Case의 방사패턴을 분석하였을 때 SPL의 최댓값이 곡관 및 배관 면적이 급격히 변하는 배관요소에서 주로 방사하고 있다. 상세히 소음해석 결과를 분석하기 위해 소음해석 결과 데이터를 Power Spectral density(PSD)로 변환하여 Fig. 15에 나타냈다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430601/images/ASK_43_06_01_F14.jpg

Fig. 14.

(Color available online) Acoustic pressure contour (Case1, 100 Hz, dB scale, ref. 2e-5 pa).

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430601/images/ASK_43_06_01_F15.jpg

Fig. 15.

(Color available online) Power spectral density of each case.

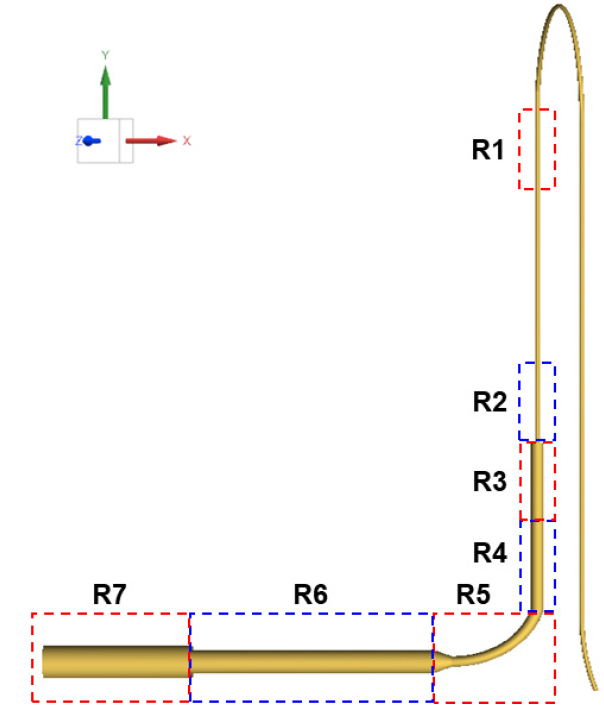
Fig. 15의 100 Hz에서 4개 Case가 모두 높은 값을 가지고 있었으며, 각 배관 요소별 냉매소음의 기여도를 파악하기 위해 100 Hz에서 PWL값이 큰 배관영역을 추적했다. 그 결과, 모세관보다는 증발기 입구 배관에서 냉매소음의 기여도가 큰 것을 확인했다. 따라서 분석 영역을 증발기 배관으로 한정하고, 배관 요소에 따라 증발기 배관을 7개의 영역으로 분할했다. 100 Hz에서의 PSD 차이는 Table 5에 나타냈으며, 분할 영역은 Fig. 16와 같다.

Table 5.

PSD of each case at 100 Hz.

Case	PSD
Case1	X
Case2	X + 0.7
Case3	X + 0.7
Case4	X + 1.2

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430601/images/ASK_43_06_01_F16.jpg

Fig. 16.

(Color available online) Segmentation of evaporator inlet pipe.

Strasberg^[14]는 기포의 부피가 맥동할 때 소음이 크게 발생한다고 언급하였으며, 기포순간음압을 기포순간부피를 이용하여 표현했다. 기포순간부피를 이용하여 기포순간음압을 계산하는 방법은 기포의 형태에 독립적이라는 장점이 있기 때문에, 기포류와 슬러그류 등 이상유동패턴에 관계없이 적용할 수 있다. 따라서, 기포순간음압을 계산하기 위해 기체부피분율을 이용하여 기포순간부피의 2차 시간 미분값을 계산했다. 기포순간음압 계산을 위해 사용한 식은 다음과 같다.

(25)

p_{a} = \frac{\ddot{V_{b}} ρ}{4 π R} .

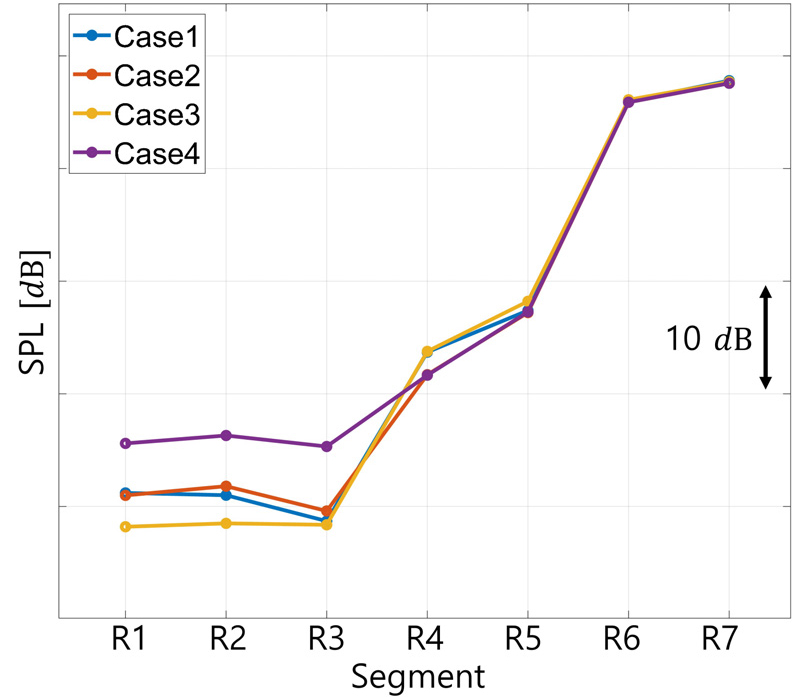
$V_{b}$ 는 기포의 부피, $R$ 은 수음점까지의 거리를 의미하며, 사용자가 냉장고 문을 여는 상황을 가정하여 Fig. 16를 기준으로 +Z방향 1 m로 지정했다. 𝜌는 매질의 밀도를 나타내며 각 영역에 포함된 액체상의 부피평균밀도를 추출하여 적용했다. 이를 SPL로 변환하여 각각의 분할영역에 대해 나타낸 결과는 Fig. 17과 같다.

https://cdn.apub.kr/journalsite/sites/ask/2024-043-06/N0660430601/images/ASK_43_06_01_F17.jpg

Fig. 17.

(Color available online) SPL conversion result (dB scale, ref. 2e-5 pa).

기포순간음압과 냉매소음의 상관성을 파악하기 위해 Fig. 15의 소음해석 결과 데이터를 바탕으로 Overall Sound Power Level(OAPWL)을 계산하여 Table 6에 나타냈다.

Table 6.

OAPWL of each case.

Case	OAPWL (dB, ~1,000 Hz)
Case1	Y
Case2	Y + 3.5
Case3	Y + 3.5
Case4	Y + 6.2

출구단에 가까운 영역에서는 상변화가 거의 완료되었기 때문에, 매질의 밀도는 크게 변하지 않는다. 따라서 기포순간음압은 기포순간부피의 2차 시간 미분값에 큰 영향을 받게 되며, 값이 클수록 기포가 급격하게 성장하고 있음을 의미하게 된다.

Fig. 17은 Eq. (25)을 이용하여 기포에 의한 소음을 영역별로 계산한 결과이다. R5, R6, R7 영역 순서대로 배관의 직경이 커지며, 면적 변화는 압력의 변화를 유발한다. 이로 인해 해당영역에서 기포의 크기가 급격하게 변화하여 소음을 유발한다. R5, R6와 R7영역 SPL값이 이러한 물리적 현상을 잘 나타내고 있다. 급격하게 성장하는 기포는 Strasburg가 제시한 주요 소음원에 해당하며, 따라서 해당영역이 OAPWL에 대한 기여도가 커지게 된다.

Fig. 10과 Fig. 11에서 출구단 경계조건이 유동패턴에 영향을 준다고 판단했다. 따라서 같은 출구단 경계조건으로 4개의 Case를 구분하였고, R1-R4영역에서 Cases 2와 4의 평균 SPL은 다른 두 Case의 평균 SPL보다 높은 것을 확인했다. 방사되는 에너지 역시 비례하여 Table 6에서도 Cases 2와 4의 평균 OAPWL이 더 높으며, 이에 따라 R1-R4영역이 R5-R7영역보다 냉매소음 경향성의 기여도가 큰 것으로 분석된다. 따라서 R1-R4영역을 개선하는 것이 냉매소음을 저감하는데 효과적일 것으로 판단한다.

V. 결 론

본 연구에서는 냉장고 증발기 입구 배관을 대상으로 수치해석을 통하여 냉매음의 발생 메커니즘을 파악하고, 소음과 유동현상 사이의 관계를 분석하였다. 이를 위해 R600a 냉매의 온도변화와 상변화를 고려하여 유동해석을 진행하였고, 모세관 출구에서의 이상유동 특성을 확인했다. 이상유동에 의해 벽면에 형성되는 압력장을 가진력으로 구조진동 및 방사소음해석을 진행하였으며 온도 및 압력 조건별 소음값을 계산하였다.

또한, 이상 유동에서 발생하는 기포의 체적을 이용하여 소음원을 계산하였으며, 소음원과 방사되는 소음의 상관성을 분석하였다.

이를 통하여 배관 직경의 변동에 의해 발생하는 유속 변화 및 압력 변화가 기포의 체적변화를 유발함을 확인하였으며, 기포의 체적 변화로 인해 발생하는 소음이 모세관 및 증발기 입구단에서의 주요 소음원임을 확인하였다.

본 논문에서는 RANS기반의 난류 유동해석을 진행함에 따라 출구에서의 지속적인 유동을 예측하였지만, 실제 광대역의 가진이 되는 난류 성분 및 기포의 특성을 예측하는데는 미흡했다고 판단된다. 따라서, 추후 연구로서 Large Eddy Simulation(LES) 또는 Detached Eddy Simulation(DES)와 같이 고정밀한 해석 기법을 통하여 기체와 액체 상태의 냉매를 명확하게 구분하여 Fig. 11과 같이 소음의 경향의 차이를 유발하는 인자에 대하여 평가 할 예정이다.

References

H. S. Han, W. B. Jeong, M. S. Kim, S. Y. Lee, and M. Y. Seo, "Reduction of the refrigerant-induced noise from the evaporator-inlet pipe in a refrigerator," Int. J. Refrig. 33, 1478-1488 (2010).

10.1016/j.ijrefrig.2010.05.014

G. J. Kim and S. M. Song, "Noise reduction of refrigerant two-phase flow using flow conditioners near the electric expansion valve," J. Mech. Sci. Technol. 34, 719-725 (2020).

10.1007/s12206-020-0118-3

T. Umeda, T. Fukushima, S. Nakamura, and T. Fukano, "Reduction of intermittent noise caused by gas-liquid two-phase refrigerant flow through an expansion valve," Proc. KSME-JSME Fluids Eng. Conf. 39-43 (1994).

S. Hirakuni, M. Nakayama, H. Makino, A. Mochizuki, and Y. Sumida, "Noise reduction technology with porous metal for refrigerant two-phase flow through the expansion valve," Int. Refrig. Air Cond. Conf. paper no. 713 (2004).

H. S. Han, W. B. Jeong, S. Aoyama, and J. Y. Mo, "Experimental analysis for reducing refrigerant-induced noise of 4-way cassette type air conditioner," J. Mech. Sci. Technol. 23, 1456-1467 (2009).

10.1007/s12206-008-1128-8

F. Alnaimat, K. E. Kadi, and B. Mathew, "CFD investigation of R134a and propane condensation in square microchannel using VOF model: Parametric study using steady state solution," Therm. Sci. Eng. Prog. 38, 101662 (2023).

10.1016/j.tsep.2023.101662

P. Alok and D. Sahu, "Flow analysis of isobutane (R-600a) inside an adiabatic capillary tube," IOP Conf. Ser. Mater. Sci. Eng. 310, 012148 (2018).

10.1088/1757-899X/310/1/012148

Y. Zhang, Y. Liu, S. Liu, Z. Gong, and L. Wu, "Transient analysis of a noise suppression method with aerating techniques in capillary tubes," Therm. Sci. 27, 4637-4649 (2023).

10.2298/TSCI221127093Z

F. R. Menter, "Two-equation eddy-viscosity turbulence models for engineering applications," AIAA J. 32, 1598-1605 (1994).

10.2514/3.12149

G. H. Schnerr and J. Sauer, "Physical and numerical modeling of unsteady cavitation dynamics," Proc. 4th Int. Conf. Multiphase Flow, 1-12 (2001).

Thermophysical Properties of Fluid Systems, https://webbook.nist.gov/chemistry/fluid/, (Last viewed September 4, 2024).

X. Yu and F. Xiande, "Correlations of void fraction for two-phase refrigerant flow in pipes," Appl. Therm. Eng. 64, 242-251 (2014).

10.1016/j.applthermaleng.2013.12.032

Y. S. Lee and C. C. Su, "Experimental studies of isobutane (R600a) as the refrigerant in domestic refrigeration system," Appl. Therm. Eng. 22, 507-519 (2002).

10.1016/S1359-4311(01)00106-5

M. Strasberg, "Gas bubbles as source of sound in liquids," J. Acoust. Soc. Am. 28, 20-27 (1956).

10.1121/1.1908212

The Journal of the Acoustical Society of KoreaISSN:1225-4428(Print) 2287-3775(Online)한국음향학회

Preview

Analysis of noise generation mechanism for two-phase flow of refrigerant in evaporator inlet pipe of refrigerator

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

Fig. 1.

(Color available online) Expansion process of refrigeration cycle in the simulation.

Fig. 2.

(Color available online) Schematic diagram of computational geometry.

Fig. 3.

(Color available online) Evaporator pipe of refrigerator.

Table 1.

Boundary condition of each case.

Table 2.

Prism mesh information.

Fig. 4.

(Color available online) Capillary tube inserted to evaporator inlet pipe.

Table 3.

R600a property interpolation technique.

(18)

(19)

(20)

(21)

(22)

Fig. 5.

(Color available online) Schematic diagram of constraint condition.

Fig. 6.

(Color available online) Constraint applying point of B.

Fig. 7.

(Color available online) Tetrahedral mesh for acoustic analysis and internal acoustic mesh.

(23)

Fig. 8.

(Color available online) Mixture velocity contour (case3, left) and vapor volume fraction contour (case3, right).

(24)

Table 4.

Calculated outlet vapor volume fraction compared to ideal process.

Fig. 9.

(Color available online) Pressure and velocity data extraction area.

Fig. 10.

(Color available online) Static pressure drop in vertical pipe.

Fig. 11.

(Color available online) Velocity change in vertical pipe.

Fig. 12.

(Color available online) Data extraction points.

Fig. 13.

(Color available online) Direct frequency response analysis result (Case1, df = 20 Hz).

Fig. 14.

(Color available online) Acoustic pressure contour (Case1, 100 Hz, dB scale, ref. 2e-5 pa).

Fig. 15.

(Color available online) Power spectral density of each case.

Table 5.

PSD of each case at 100 Hz.

Fig. 16.

(Color available online) Segmentation of evaporator inlet pipe.

(25)

Fig. 17.

(Color available online) SPL conversion result (dB scale, ref. 2e-5 pa).

Table 6.

OAPWL of each case.

References