A study on training DenseNet-Recurrent Neural Network for sound event detection

Hyeonjin Cha; Sangwook Park

doi:10.7776/ASK.2023.42.5.395

Preview

Research Article

The Journal of the Acoustical Society of Korea. 30 September 2023. 395-401
https://doi.org/10.7776/ASK.2023.42.5.395

A study on training DenseNet-Recurrent Neural Network for sound event detection

음향 이벤트 검출을 위한 DenseNet-Recurrent Neural Network 학습 방법에 관한 연구

Hyeonjin Cha¹

Sangwook Park¹^*

차 현진¹

박 상욱¹^*

¹국립강릉원주대학교 전자공학과

^{*Corresponding Author}

ABSTRACT

Sound Event Detection (SED) aims to identify not only sound category but also time interval for target sounds in an audio waveform. It is a critical technique in field of acoustic surveillance system and monitoring system. Recently, various models have introduced through Detection and Classification of Acoustic Scenes and Events (DCASE) Task 4. This paper explored how to design optimal parameters of DenseNet based model, which has led to outstanding performance in other recognition system. In experiment, DenseRNN as an SED model consists of DensNet-BC and bi-directional Gated Recurrent Units (GRU). This model is trained with Mean teacher model. With an event-based f-score, evaluation is performed depending on parameters, related to model architecture as well as model training, under the assessment protocol of DCASE task4. Experimental result shows that the performance goes up and has been saturated to near the best. Also, DenseRNN would be trained more effectively without dropout technique.

Keywords

Sound event detection

Network architecture

Mean-teacher model

Dense connection

Skip connection

음향 이벤트 검출(Sound Event Detection, SED)은 음향 신호에서 관심 있는 음향의 종류와 발생 구간을 검출하는 기술로, 음향 감시 시스템 및 모니터링 시스템 등 다양한 분야에서 활용되고 있다. 최근 음향 신호 분석에 관한 국제 경연 대회(Detection and Classification of Acoustic Scenes and Events, DCASE) Task 4를 통해 다양한 방법이 소개되고 있다. 본 연구는 다양한 영역에서 성능 향상을 이끌고 있는 Dense Convolutional Networks(DenseNet)을 음향 이벤트 검출에 적용하기 위해 설계 변수에 따른 성능 변화를 비교 및 분석한다. 실험에서는 DenseNet with Bottleneck and Compression(DenseNet-BC)와 순환신경망(Recurrent Neural Network, RNN)의 한 종류인 양방향 게이트 순환 유닛(Bidirectional Gated Recurrent Unit, Bi-GRU)을 결합한 DenseRNN 모델을 설계하고, 평균 교사 모델(Mean Teacher Model)을 통해 모델을 학습한다. DCASE task4의 성능 평가 기준에 따라 이벤트 기반 f-score를 바탕으로 설계 변수에 따른 DenseRNN의 성능 변화를 분석한다. 실험 결과에서 DenseRNN의 복잡도가 높을수록 성능이 향상되지만 일정 수준에 도달하면 유사한 성능을 보임을 확인할 수 있다. 또한, 학습과정에서 중도탈락을 적용하지 않는 경우, 모델이 효과적으로 학습됨을 확인할 수 있다.

키워드

음향 이벤트 인식

네트워크 구조

평균 교사 모델

밀집 연결

스킵 연결

MAIN

I. 서 론
II. 본 론
2.1 DenseRNN
2.2 준지도학습: 평균-교사 모델
2.3 학습 변수 최적화
III. 실험 결과
3.1 실험데이터
3.2 실험 설정
3.3 실험 결과
IV. 결 론

I. 서 론

음향 이벤트 검출(Sound Event Detection)은 오디오 신호에 포함된 관심 음향을 탐지하는 기술로, 환경 모니터링, 음악 정보 검색, 음성 인식, 자동 음향 분류 등 여러 응용 분야에서 활용된다. 음향 신호 분석에 관한 국제 경연 대회(Detection and Classification of Acoustic Scenes and Events, DCASE)를 통해, 심층 신경망을 활용한 방법이 소개되고 있다.

음향 이벤트 검출에 관한 DCASE의 기본 방법(baseline)에서는 Convolutional Neural Network(CNN)과 Gated Recurrent Units(GRUs)로 구성된 음향 이벤트 검출 모델^[1]을 사용하여, 음향 이벤트 종류를 식별하기 위한 특징을 추출하고 음향 이벤트의 발생 시점과 종료 시점을 검출한다. 모델 학습을 위해서는 각각의 음향 신호에 포함된 이벤트 종류와 구간이 명시된 라벨이 필요하다. 반면, 준지도 학습 방법에서는 라벨이 없는 데이터를 학습에 활용할 수 있다. DCASE의 기본 방법에서는 학습 데이터 수집에 필요한 비용을 줄이기 위해, 음향 종류와 구간에 따라 합성된 데이터와 음향 종류만 명시된 실제 데이터, 아무런 라벨이 없는 실제 데이터를 바탕으로 평균-교사 모델(Mean Teacher Model)^[2]에 기반하여 음향 검출 모델을 학습한다.

음향 이벤트 검출 성능 향상을 위해서는 음향 특징을 효과적으로 표현할 수 있는 음향 모델이 필요하다. 음향 특징을 효과적으로 추출하기 위해, 다양한 Convolutional Neural Networks(CNN) 모델이 소개되었다. 학습 과정에서 발생하는 기울기 소멸 문제를 해결하기 위해 스킵연결을 활용한 ResNet 모델이 소개됐다.^[3,4,5] 이후 각 계층에서는 모든 이전 계층의 특징 맵이 입력으로 사용되고, 그 계층의 특징 맵은 모든 후속 계층으로 입력되는 밀집연결이 적용된 Dense Convolutional Networks(DenseNet)이 소개되어 여러 분야에서 인식 성능 향상을 이끌고 있다.^[6,7,8]

반면, DenseNet 설계에는 수많은 매개변수가 존재하고 학습시간 또한 오래 걸리기 때문에, 매개변수를 최적화하는데 어려움이 있다. 본 논문은 음향 이벤트 검출을 위한 DenseNet 활용 방안을 고찰한다. 실험에서는 DCASE 2020 기본방법을 활용하여, DenseNet with Bottleneck and Compression(DenseNet-BC)^[6]와 순환신경망(Recurrent Neural Network, RNN)의 한 종류인 양방향 게이트 순환 유닛 Bidirectional Gated Recurrent Unit(Bi-GRU)^[9]로 구성된 음향 이벤트 검출 모델(DenseRNN)을 평균-교사 모델을 통해 학습한 후, 음향 이벤트 검출 성능을 비교/분석한다. 실험 결과는 DenseNet의 모델 복잡도가 높고 학습과정에서 중도탈락을 적용하지 않는 경우에 높은 성능을 보임을 보여준다.

본론에서는 DenseRNN과 평균 교사 모델과 관련된 하이퍼 파라미터를 설명한다. 이어서, 실험 데이터와 실험 조건, 결과를 보여준다. 끝으로 주요 실험 결과를 요약한다.

II. 본 론

음향 이벤트 검출을 위해, 음향 신호는 로그 멜-스펙트로그램으로 변환되어 DenseRNN에 입력된다. DenseRNN은 DenseNet-BC와 Bi-GRU로 구성되고 평균 교사 모델에 기반하여 학습된다.

2.1 DenseRNN

2.1.1 DenseNet-BC

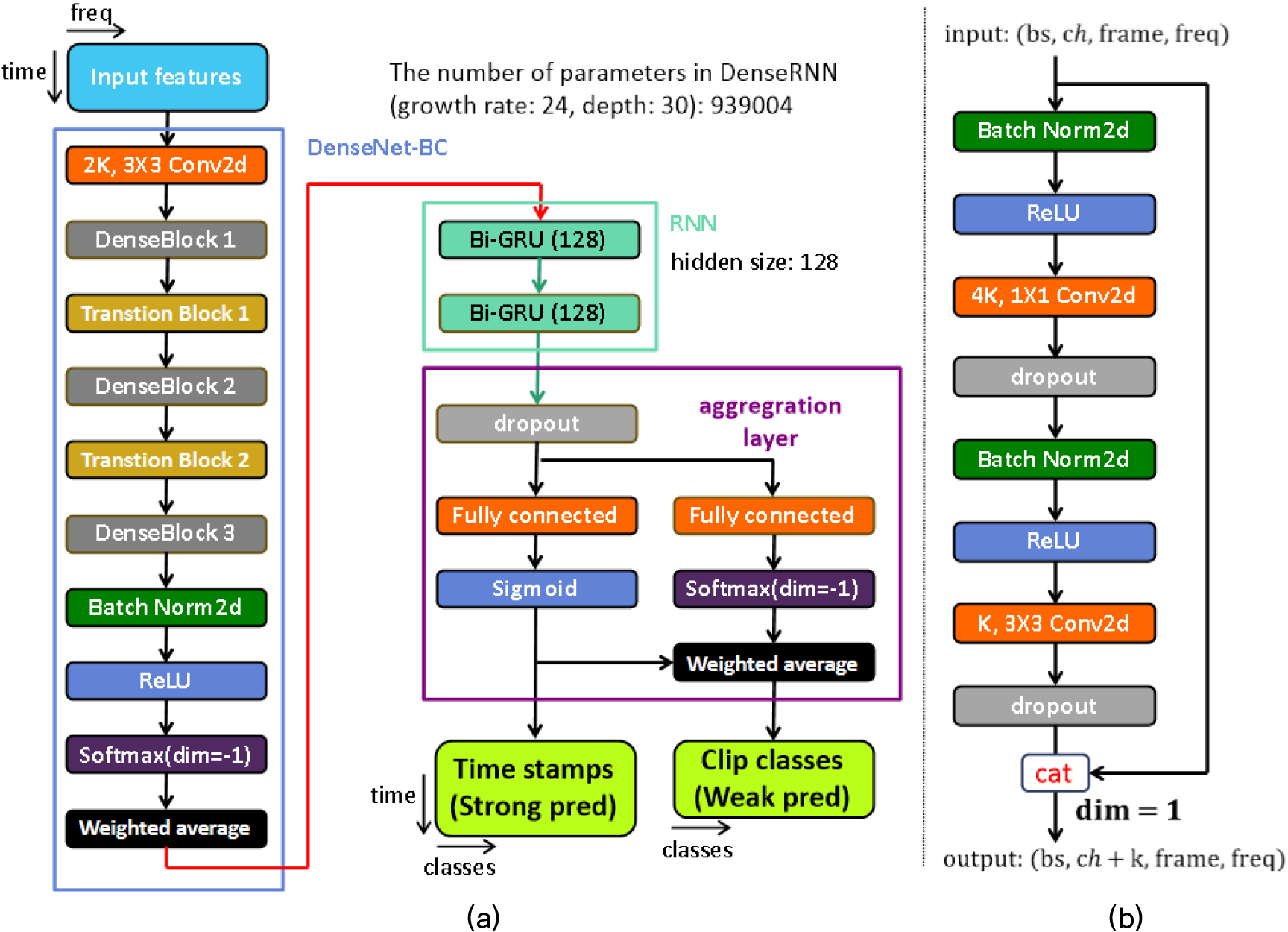
Fig. 1(a)는 DenseNet-BC 기반 음향 검출 모델을 보여준다.^[10] 첫 합성곱 계층에서는 복수의 합성곱 필터를 적용하여 로그 멜 스펙트로그램의 채널을 확장하여 다차원의 채널을 생성한다.

https://cdn.apub.kr/journalsite/sites/ask/2023-042-05/N0660420503/images/ASK_42_05_03_F1.jpg

Fig. 1.

(Color available online) (a) Proposed DenseRNN structure for sound event detection and (b) bottleneck block.

이어서 다수의 밀집 블록과 전환 블록이 이어진다. 밀집 블록은 복수의 병목 블록으로 구성된다. 병목 블록은 1x1 컨볼루션 레이어와 3 × 3 컨볼루션 레이어를 결합하여 구성된다[Fig. 1(b)]. 입력의 특징 맵은 1 × 1 컨볼루션에서 차원 수가 줄어들며, 3 × 3 컨볼루션에서 지역적 특징이 효과적으로 추출된다. 출력은 차원 수는 줄었지만 높은 수준의 특징을 포함한 정보와, 입력을 채널 차원에서 연결하여 구성된다. 병목 블록을 통과한 정보와 입력이 연결될 때마다 추가되는 채널 수를 성장률로 정의한다.

전환 블록은 인접한 두 밀집 블록 사이에서 압축 요인, θ를 사용하여 특징 맵을 압축하여 채널 수를 줄인다. 압축된 특징 맵은 다음 밀집 블록으로 입력된다(예: θ = 0.5일 경우, 입력 크기 1/2배). 세 단계의 밀집블록 이후에는 안정적인 학습을 위해, Batch Norm과 Rectified Linear Unit(ReLU)이 적용된다.^[11,12] 이때, DenseNet-BC의 깊이는 사용된 전체 컨볼루션 레이어 수로 정의된다. 음향 신호에 포함된 정보를 효과적으로 추출하기 위해, DenseNet-BC에서 성장률과 깊이의 최적화가 필요하다.

기존 DenseNet-BC^[10]는 ReLU 이후 전역 평균 풀링과 완전 연결 계층을 사용한다. 하지만, 음향 신호는 음향 이벤트 종류에 따라 주파수에 따른 에너지 분포가 다르기 때문에, 전역 평균 풀링을 적용할 경우, 평균 연산에 의해 정보가 희석될 수 있다. 이러한 점을 방지하기 위해, 전역 평균 풀링 대신 가중 평균을 사용한다. 이때 가중치는 모델 학습을 통해 최적화된다.

심층 신경망 모델을 학습할 때, 과학습을 방지하기 위해 중도탈락을 사용한다.^[13] 하지만, DenseNet-BC에서 스킵연결이 끊어져 정보가 손실될 수 있다. 이러한 trade-off 관계에서 DenseNet-BC의 병목블록과 전환블록^[10]에 적용되는 중도탈락을 고찰할 필요가 있다.

2.1.2 Bi-GRU 및 종합 계층

Bi-GRU는 시간에 따른 음향 특징의 변화를 학습하여 음향 이벤트의 발생 구간을 검출한다.^[14,15] Bi-GRU 이후에는 종합 계층을 통해, 음향 이벤트 종류와 발생 구간에 대한 예측값(강한 예측: strong pred)과 음향 이벤트 종류에 대한 예측값(약한 예측: weak pred)을 도출한다[Fig. 1(a)]. DenseRNN에서 Bi-GRU와 종합 계층은 DCASE 2020 기본방법 모델과 동일하게 설계된다.^[14]

2.2 준지도학습: 평균-교사 모델

평균-교사 모델은 학생 모델과 교사 모델로 구성된다. 매 학습 단계에서, 학생 모델은 경사하강법으로 학습되고, 교사 모델은 학생 모델의 단계별 평균값으로 모델 변수가 결정된다. 음향 이벤트 검출 모델 학습을 위한 평균 교사 모델에서 손실 함수는 분류 손실, $L^{c l s}$ 과 일관성 손실, $L^{c o n}$ 로 구성된다[Eq. (1)].

(1)

L = L^{c l s} (p, y) + λ L^{c o n} (p, \hat{p}) . L^{c l s} (p, y) = B C E_{x \in S} (p_{x}, y_{x}^{s}) + B C E_{x \in W} (E_{m} [p_{x}], y_{x}^{w}) . L^{c o n} (p, y) = M S E_{x \in S, W, U} (p_{x}, \hat{p_{x}}) .

이때, 첨자 $S, W, U$ 는 각각 음향 종류와 구간에 따라 합성된 데이터와 음향 종류만 명시된 실제 데이터, 아무런 라벨이 없는 실제 데이터 셋을 나타낸다. BCE와 MSE는 각각 Binary Cross Entropy와 Mean Squared Error를 나타낸다. $y_{x}^{s}$ 와 $y_{x}^{w}$ 는 각각 입력 $x$ 에 대한 strongly label, weakly label을 의미하고, $p_{x}$ 와 ${\hat{p}}_{x}$ 는 각각 학생 모델과 교사 모델의 예측값을 나타낸다. $E_{m}$ 은 시간에 대한 기대 연산자를 나타낸다.^[16] 𝜆는 일관성 손실에 대한 가중치를 나타낸다. 음향 이벤트 검출 모델은 $L$ 을 최소화하도록 학습된다. 학습 초기에는 교사 모델이 충분히 학습되지 않았기 때문에, 𝜆가 작은 값이지만, 학습이 진행되면서 그 값이 점차 증가한다. 만일 𝜆가 0인 경우, 라벨이 있는 데이터만 학습에 사용된다.

2.3 학습 변수 최적화

경사하강법에 기반한 모델학습에서 학습 변수는 학습 속도뿐만 아니라 학습 성패에도 영향을 준다. 특히, 지역 최적점 문제로 인해, 학습 변수에 따라 큰 성능 차이를 보인다. 이러한 점을 고려하여 DenseRNN 학습에 가장 효과적인 학습 변수를 설정해야 한다. DenseRNN을 학습하기 위해 사용되는 손실 함수 Eq. (1)에서 일관성 가중치 𝜆는 최대 일관성 가중치까지 증가하는 지수 증가 함수로 설계된다. 이때, 최대 일관성 가중치가 클수록 준지도 학습의 효과를 기대할 수 있지만, 분류 손실의 기여도가 상대적으로 낮아져 최적의 값으로 수렴하는 것을 방해할 수 있다.

이외에, 본 연구는 학습 비율, 최적화 방법(Adam, RAdam, SGD), 그리고 가중치 초기화 방법(Xavier Glorot,^[17] He^[18])에 따른 모델 성능 변화를 살펴본다. 학습 비율은 모델의 학습 속도를 결정하는 동시에 안정적으로 수렴하는 데 영향을 준다. 또한 지역 최적점 문제를 완화하기 위해, 최적화 방법과 초기화 방법을 고려할 수 있다. 이때, 각 방법은 상황에 따라 장단점이 있기 때문에 최적의 방법을 찾을 필요가 있다.

III. 실험 결과

3.1 실험데이터

모델 학습과 성능 평가를 위해 DCASE2020 Task 4에서 사용하는 DESED 데이터 셋을 사용한다.^[19] 학습 데이터는 음향 이벤트 종류와 발생 구간이 모두 명시된 synthetic strongly labeled set(2,584개 오디오), 음향 이벤트 종류만 명시된 weakly labeled set(1,578개 오디오), 그리고 두 정보가 모두 명시되지 않은 unlabeled set(14,412개 오디오)으로 구성된다. 이때, 학습 데이터 준비에 필요한 비용을 줄이기 위해, synthetic strongly labeled set은 음향 이벤트 종류와 발생 구간에 따라 합성된 오디오로 구성된다. 반면, 나머지 두 셋은 모두 실제 환경에서 녹음된 오디오로 구성된다. 음향 신호는 16,000 Hz로 다시 샘플링되고 단일 채널 신호로 변환된다. 또한 테스트 셋은 검증 데이터 셋(1,168개 오디오)으로 구성된다.

3.2 실험 설정

성능 평가를 위해, 이벤트 기반 클래스별 F1 점수들의 평균(Event-based Class averaging f-score), Eb f-score(class-avg)를 성능 지표로 사용한다. F1 점수는 정확도와 호출의 조화평균으로 정의되고, 예측값과 라벨(실제 값)이 음향 이벤트 종류와 발생 구간에서 모두 일치할 때, 참 양성으로 정의한다. 이때, 200 ms 또는 음향 이벤트 길이의 20 % 만큼의 오차는 참으로 허용한다.^[20] 매 epoch마다 F1점수를 계산하여, 15 epoch 이내에 성능개선이 없으면 학습을 조기 중단하고 모델의 성능을 평가한다.^[14]

학습 변수는 다음과 같이 설정한다: (1) batch size: 18, (2) early stopping patience: 15 epoch, (3) DenseNet-BC dropout rate: 0.0, (4) max learning rate: 1e-3, (5) optimizer: Adam, (6) weight decay: 0.0, (7) 가중치 초기화: Xavier Glort 초기화. 이외 변수는 DCASE2020 task4에서 제공하는 기본 방법과 동일한 변수를 사용한다.^[14] 모델 학습과 테스트에는 메모리가 24 GB인 그래픽 연산 유닛(Graphics Processing Unit, GPU)이 사용됐다.

3.3 실험 결과

3.3.1 성장률과 깊이에 따른 성능 분석

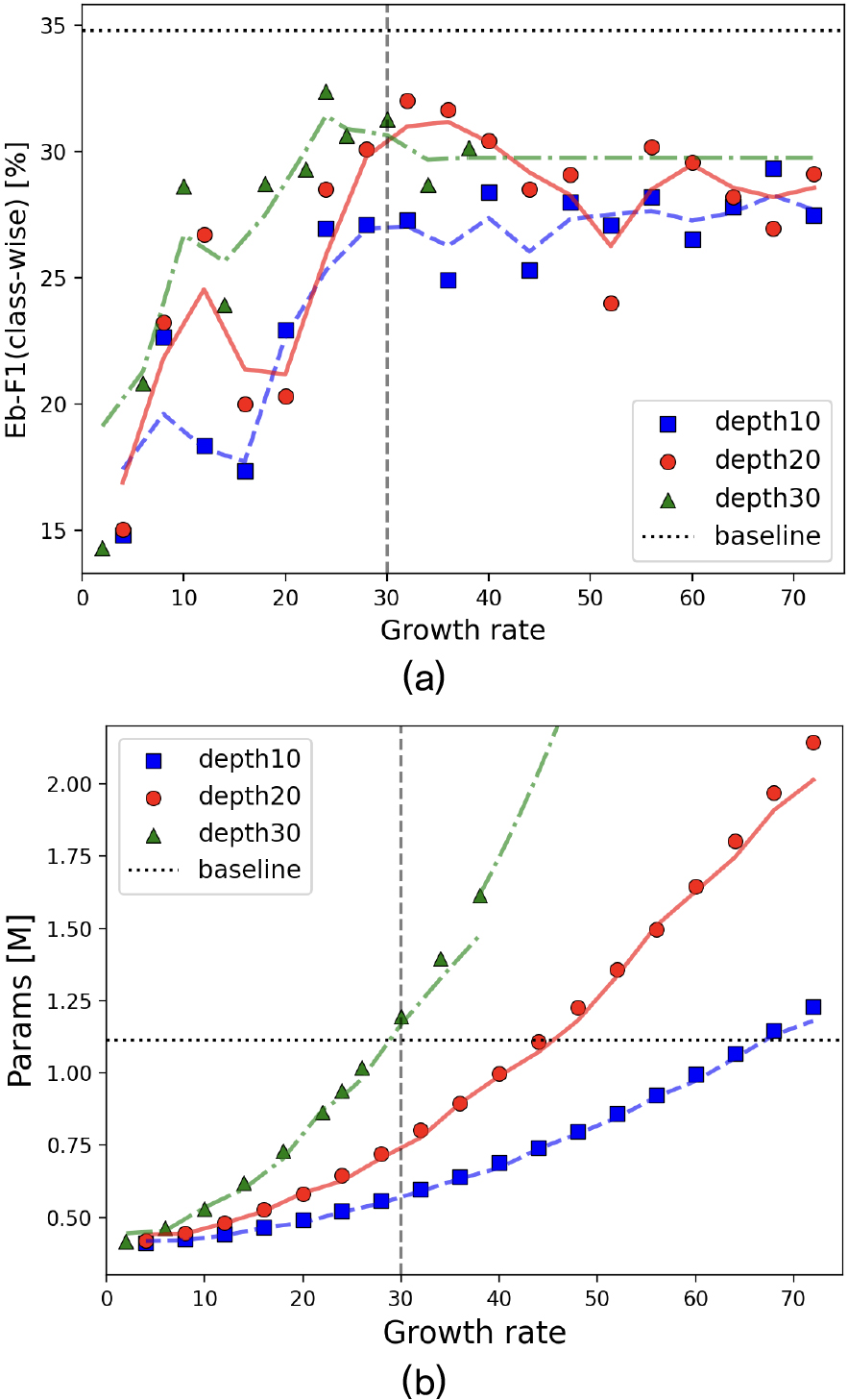
Fig. 2는 DenseRNN 설계를 위한 성장률과 깊이에 따른 모델의 성능과 파라미터 수를 보여준다. 이때, 최대 일관성 가중치는 2.0으로 설정하고 실험 장치의 메모리 용량을 고려하여, 학습이 가능한 최대 성장률까지 성능 평가를 수행한다.

https://cdn.apub.kr/journalsite/sites/ask/2023-042-05/N0660420503/images/ASK_42_05_03_F2.jpg

Fig. 2.

(Color available online) (a) The event-based class-averaging f-score and (b) the total number of parameters in DenseRNN, both as functions of growth rate and depth.

Fig. 2(a)에서 성장률이 30 이하인 경우, 대체로 깊이와 성장률이 클수록 성능이 향상된다. 반면, 성장률이 30 보다 큰 경우, 모델이 복잡하더라도 더 이상 성능이 향상되지 않는다. 이는 모델의 복잡도가 일정 수준을 넘어서면 성능이 포화 상태에 도달한 것으로 해석할 수 있다.

Fig. 2(b)에서 성장률에 따라 모델 복잡도가 지수적으로 증가하는 것을 확인할 수 있다. 이때, 성장률이 같은 경우, 깊이가 깊을수록 전체 모델 복잡도가 더욱더 커지는 것을 확인할 수 있다.

다양한 설정으로 실험한 결과 성장률이 24이고, 깊이가 30일 때, 가장 높은 성능(32.38 %)을 확인할 수 있다. 향후 실험은 이때 변수로 설계된 모델을 사용한다.

3.3.2 중도탈락률(Dropout rate)에 따른 성능 분석

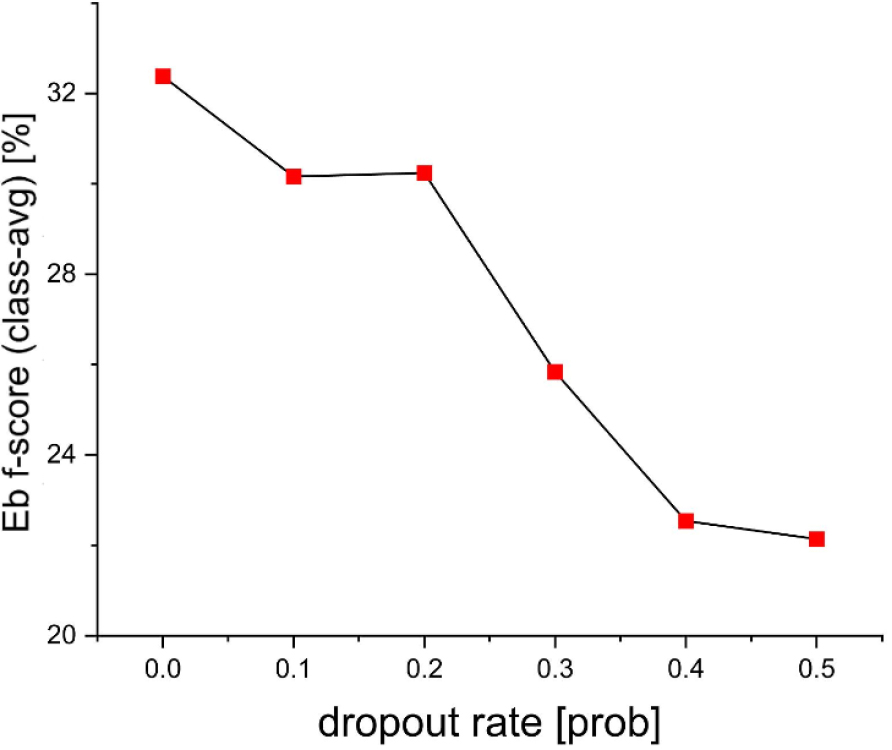
중도탈락이 밀집연결에 미치는 영향을 확인하기 위해 중도탈락률에 따라 학습된 모델의 성능을 비교한다(Fig. 3). 이때, 최대 일관성 가중치는 2.0으로 설정한다. DenseRNN에 중도탈락을 적용할 경우, 스킵연결이 끊어져 정보 손실이 발생하고 경사도 흐름이 방해받을 수 있다. 이러한 문제점은 중도탈락률이 높을수록 성능이 하락하는 결과로부터 확인할 수 있다.

https://cdn.apub.kr/journalsite/sites/ask/2023-042-05/N0660420503/images/ASK_42_05_03_F3.jpg

Fig. 3.

(Color available online) The Event-based class averaging f-score as a function of dropout rate.

3.3.3 학습 변수에 따른 성능 변화

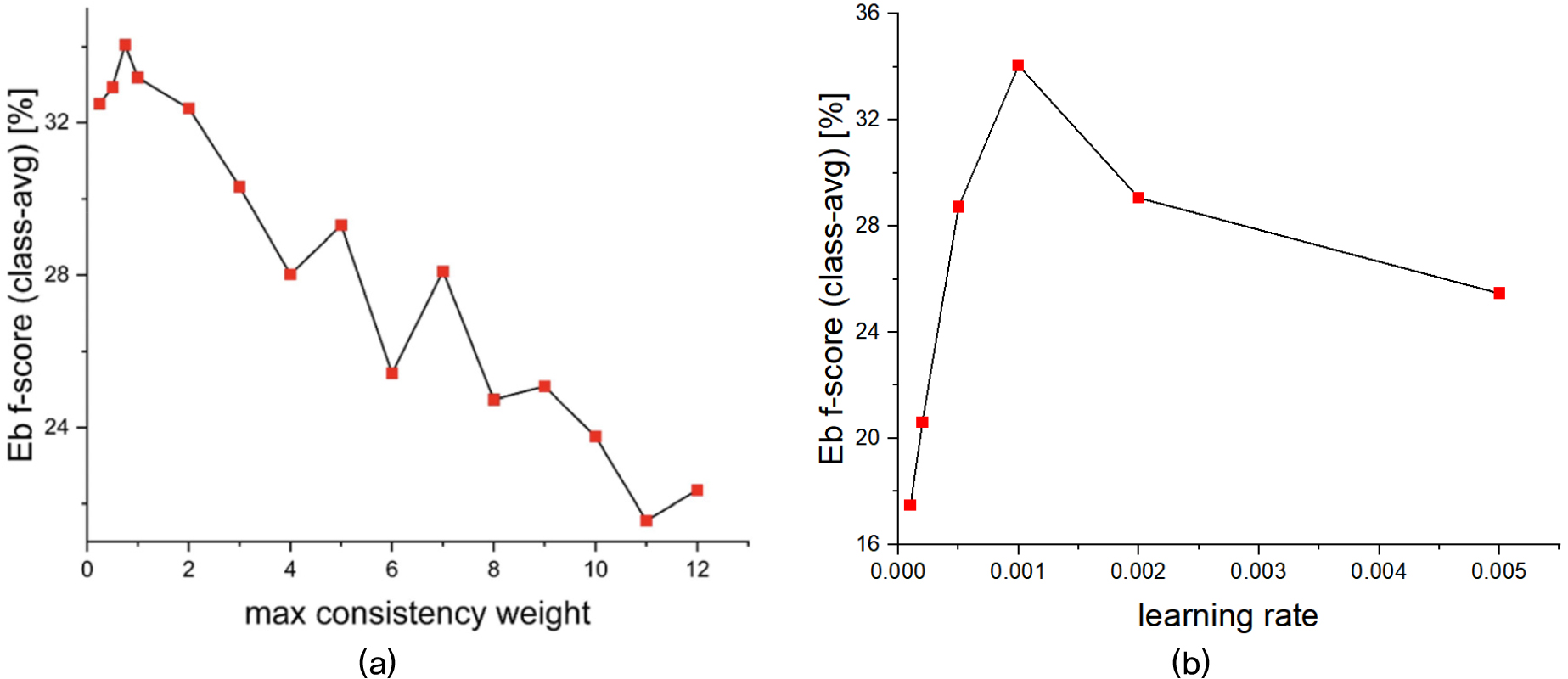
Fig. 4는 DenseRNN의 최적화를 위해 수행한 학습 변수에 따른 검출 성능을 보여준다. 이때, 분석 대상 변수 이외에 나머지 변수는 실험 설정에 요약된 값이 적용됐다. 평균 교사 모델 학습에 적용된 손실 함수 Eq. (1)에서 일관성 손실의 비율을 결정하는 최대 가중치 별 실험에서, 최대 가중치가 0.25, 0.5, 0.75, 1, 2인 경우 유사한 성능을 확인할 수 있다(0.25: 32.5 %, 0.5: 32.94 %, 0.75: 34.05 %, 1.0: 33.19 %, 2.0: 32.38 %) [Fig. 4(a)]. 만일, 최대 가중치가 0인 경우, 레이블링 된 데이터만 사용하여 모델이 학습된다. 최대 가중치가 증가하면, Eq. (1)에서 학생 모델과 교사 모델의 일관성이 더욱 큰 기여도를 갖기 때문에, 검출 결과에 상관없이 두 모델이 일치된 결과를 도출하기 위해 학습된다. 이 경우, 학생 모델과 교사 모델 모두 라벨(실제 값)을 알 수 없기 때문에, 올바른 방향으로 학습되는 데 한계가 있다.

https://cdn.apub.kr/journalsite/sites/ask/2023-042-05/N0660420503/images/ASK_42_05_03_F4.jpg

Fig. 4.

(Color available online) The Event-based class averaging f-score as a function of (a) max consistency weight and (b) max learning rate.

최대 학습 비율에 따른 실험 결과는 10^-3에서 가장 높은 성능을 보여준다[Fig. 4(b)]. 이때, 최대 일관성 가중치는 0.75으로 설정한다. Tables 1과 2는 각각 최적화 방법과 모델 변수 초기화 방법에 따른 검출 성능을 보여준다.

Table 1.

The Event-based class averaging f-score as a function of optimizers.

Optimizer	Eb f-score (class-avg)
Adam	34.05 %
RAdam	33.35 %
SGD	9.62 %

Table 2.

The Event-based class averaging f-score as a function of weight initialization methods.

Weight init	Eb f-score (class-avg)
Xavier	34.05 %
He	27.67 %

Table 1에서 Stochastic Gradient Descent(SGD)의 경우, 검출 성능이 큰 폭으로 하락한 결과를 확인할 수 있다. SGD는 모든 파라미터에 대해 동일한 학습률을 사용하여 업데이트하는 반면, Adam과 RAdam 같은 알고리즘은 ‘적응적 학습률’을 적용하여 각 파라미터를 독립적으로 조정한다. 이로 인해, Adam과 RAdam은 넓고 평평한 영역이나 안장점과 같은 복잡한 최적화 문제에서 SGD보다 더 효과적으로 탈출할 수 있다.^[21]

Table 2에서 두 가지 초기화 방법은 서로 유사한 성능을 보임을 확인할 수 있다.

IV. 결 론

본 논문은 DenseNet을 음향 이벤트 검출에 활용하기 위해, 모델 구조와 학습에 관한 변수에 따른 검출 성능을 비교했다. 실험에서는 DenseNet-BC와 Bi-GRU(RNN)으로 구성된 DenseRNN 모델을 사용했고, 이 모델은 평균 교사 모델에 기반하여 준지도 학습으로 학습된다. 다양한 변수에 따른 실험 결과에서, DenseRNN의 복잡도가 높을수록 성능이 향상되지만 일정 수준 이상의 복잡도에서는 유사한 성능을 기대할 수 있다. 또한 밀집연결에 중도탈락이 적용되지 않은 경우, 효과적인 음향 이벤트 검출이 가능함을 확인할 수 있다. DenseRNN의 최적 성능은 34.05 %로 DCASE2020의 기본방법(34.8 %)과 유사한 성능을 보이는 반면, 모델변수 수(모델 복잡도)는 기본모델과 비교하여 약 20 % 적다. 향후 DenseRNN의 성능 개선을 위한 연구를 수행할 계획이다.

Acknowledgements

본 논문은 2022년도 강릉원주대학교 신임교원 연구비 지원과 2023년도 교육부의 재원으로 한국연구 재단의 지원을 받아 수행된 지자체-대학 협력 기반 지 역 혁신 사업의 결과입니다(2022RIS-005).

References

L. Delphin-Poulat and C. Plapous, "Mean teacher with data augmentation for dcase 2019 task 4," Orange Labs Lannion, Tech. Rep., 2019.

A. Tarvainen and H. Valpola, "Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results," Proc. NIPS, 1-10 (2017).

K. He, X. Zhang, S. Ren, and J. Sun, "Deep residual learning for image recognition," Proc. IEEE Conf. on CVPR, 770-778 (2016). 10.1109/CVPR.2016.9026180094

K. He, X. Zhang, S. Ren, and J. Sun, "Identity mappings in deep residual networks," Proc. Computer Vision-ECCV, 1-15 (2016). 10.1007/978-3-319-46493-0_38

S. Zagoruyko and N. Komodakis, "Wide residual networks," arXiv preprint arXiv:1605.07146 (2016). 10.5244/C.30.87

G. Huang, Z. Liu, L. Van Der Maaten, and K. Q. Weinberger, "Densely connected convolutional networks," Proc. Computer Vision-ECCV, 1-9 (2017). 10.1109/CVPR.2017.243PMC5598342

B. McMahan and D. Rao, "Listening to the world improves speech command recognition," Proc. AAAI Conf. on Artificial Intelligence, 378-385 (2018). 10.1609/aaai.v32i1.11284

K. Palanisamy, D. Singhania, and A. Yao, "Rethinking CNN models for audio classification," arXiv preprint arXiv:2007.11154 (2020).

PyTorch Torch.nn.GRU, https://pytorch.org/docs/stable/generated/torch.nn.GRU.html, (Last viewed February 12, 2023).

A PyTorch Implementation for Densely Connected Convolutional Networks (DenseNets), https://githubcom/andreasveit/densenet-pytorch, (Last viewed February 12, 2023).

S. Ioffe and C. Szegedy, "Batch normalization: Accelerating deep network training by reducing internal covariate shift," arXiv preprint arXiv:1502.03167 (2015).

X. Glorot, A. Bordes, and Y. Bengio, "Deep sparse rectifier neural networks," Proc. of the 14^th International Conf. on Artificial Intelligence and Statistics, 315-323 (2011).

N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever, and R. Salakhutdinov, "Dropout: a simple way to prevent neural networks from overfitting," J. Mach. Learn. Res. 15, (2014).

DCASE 2020 Task 4 GitHub, https://github.com/turpaultn/dcase20_task4, (Last viewed February 12, 2023).

N. Turpault, R. Serizel, A. Shah, and J. Salamon, "Sound event detection in domestic environments with weakly labeled data and soundscape synthesis," Proc. DCASE Workshop, 253-257 (2019). 10.33682/006b-jx26

S. Park and M. Elhilali, "Time-balanced focal loss for audio event detection," Proc. ICASSP, 311-315 (2022). 10.1109/ICASSP43922.2022.9747736

X. Glorot and Y. Bengio, "Understanding the difficulty of training deep feedforward neural networks," Proc. 13^th International Conf. on Artificial Intelligence and Statistics, 249-256 (2010).

K. He, X. Zhang, S. Ren, and J. Sun, "Delving deep into rectifiers: Surpassing human-level performance on imagenet classification," Proc. IEEE ICCV, 1026-1032 (2015). 10.1109/ICCV.2015.123

DCASE 2020 Task 4: Sound Event Detection and Separation in Domestic Environments, https://dcase.community/challenge2020/task-sound-event-detection-and-separation-in-domestic-environments, (Last viewed July 25, 2023).

A. Mesaros, T. Heittola, T. Virtanen, and M. D. Plumbley, "Sound event detection: A tutorial," IEEE Signal Process. Mag. 38, 67-83 (2021). 10.1109/MSP.2021.3090678

D. P. Kingma and J. Ba, "Adam: A method for stochastic optimization," arXiv preprint arXiv:1412.6980 (2014).

The Journal of the Acoustical Society of KoreaISSN:1225-4428(Print) 2287-3775(Online)한국음향학회

Preview

A study on training DenseNet-Recurrent Neural Network for sound event detection

ABSTRACT

MAIN

Fig. 1.

(Color available online) (a) Proposed DenseRNN structure for sound event detection and (b) bottleneck block.

(1)

Fig. 2.

(Color available online) (a) The event-based class-averaging f-score and (b) the total number of parameters in DenseRNN, both as functions of growth rate and depth.

Fig. 3.

(Color available online) The Event-based class averaging f-score as a function of dropout rate.

Fig. 4.

(Color available online) The Event-based class averaging f-score as a function of (a) max consistency weight and (b) max learning rate.

Table 1.

The Event-based class averaging f-score as a function of optimizers.

Table 2.

The Event-based class averaging f-score as a function of weight initialization methods.

Acknowledgements

References