I. 서 론
II. 새로운 단일 pMUT의 집중 변수 모델
2.1 새로운 단일 pMUT 소자의 설계 개념
2.2 박막 파트의 집중 변수 모델
2.3 방사 파트의 집중 변수 모델
2.4 방사 파트의 체적 속도 증폭 효과
2.5 패키징 파트의 집중 변수 모델
2.6 전체 단일 pMUT 소자의 집중 변수 모델
III. 광대역 단일 pMUT 소자 설계
3.1 박막 파트 설계
3.2 방사 파트 설계
3.3 패키징 파트 설계
3.4 최종 설계된 광대역 단일 pMUT 소자
IV. 유한요소해석을 이용한 새로운 단일 pMUT 소자의 설계
V. 공정 개념도
VI. 결 론
I. 서 론
광대역 트랜스듀서는 다양한 분야에서 장점을 갖는다. 예를 들어 수중통신 분야에서 광대역 수중 트랜스듀서는 넓은 대역폭으로 인해 한번에 더 많은 정보 전달이 가능하다.[1] 의료용 초음파 분야에서도 광대역 트랜스 듀서는 더 많은 종류의 영상을 획득할 수 있다.[2] 그리고 일반적인 라우드 스피커 유닛의 경우, 10 kHz정도의 가청 주파수 대역을 갖는다.[3]
광대역 트랜스듀서를 제작하는 대표적인 방법은 다공진을 이용하는 것이다. 다공진을 이용한 트랜스듀서들에는 다공진 스텝 플레이트, Free Flooded Ring (FFR), piezoelectric Micro-machined Ultrasonic Transducer (pMUT) 어레이 등이 있다.[4], [5], [6] 다공진 스텝 플레이트의 경우, 드라이버, 방사 파트, 혼(Horn) 파트의 3 자유도 시스템으로 설계하여 광대역을 달성하였다.[4] FFR의 경우, 압전 링의 공진과 링 안에 존재하는 매질의 공진(Helmholtz resonance frequency)을 이용하여 광대역을 달성하였다.[5] 그리고 pMUT 배열의 경우, 서로 다른 공진을 갖는 2개의 pMUT을 배열하고, 이를 역위상으로 구동함으로써 광대역을 달성하였다.[6] 하지만, 서로 다른 공진을 갖는 pMUT 배열의 경우 출력이 나누어지며, 역위상 구동을 위한 별도의 전극 분리와 복잡한 신호처리과정을 위한 추가적인 회로가 필요하다는 단점이 있다.
본 논문에서는 하나의 pMUT의 앞뒤에 적절한 음향 구조를 추가하여 공기 중 적용을 위한 광대역 초소형 초음파 트랜스듀서를 설계하였다.
설계된 트랜스듀서는 박막 파트, 방사파트, 패키징 파트로 구성된 3 자유도 시스템으로 설계되었으며, 최종적으로 유한요소해석을 통해 검증되었다.
II. 새로운 단일 pMUT의 집중 변수 모델
2.1 새로운 단일 pMUT 소자의 설계 개념
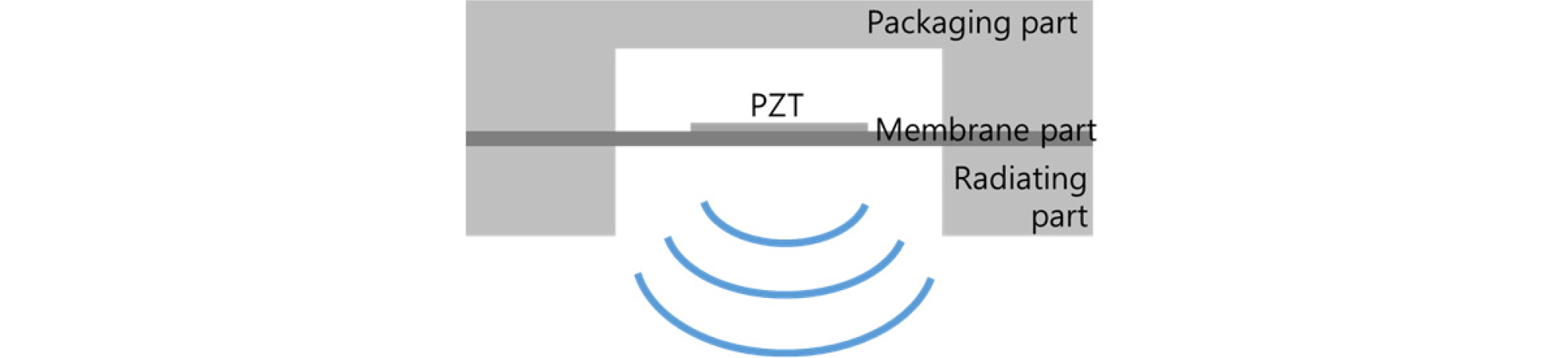
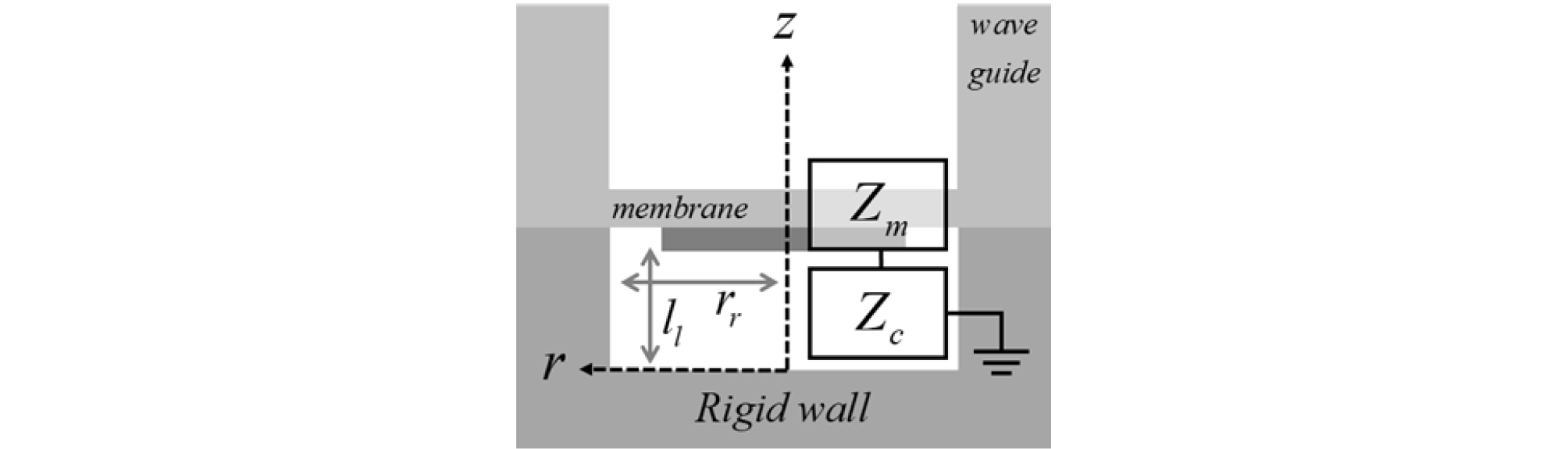
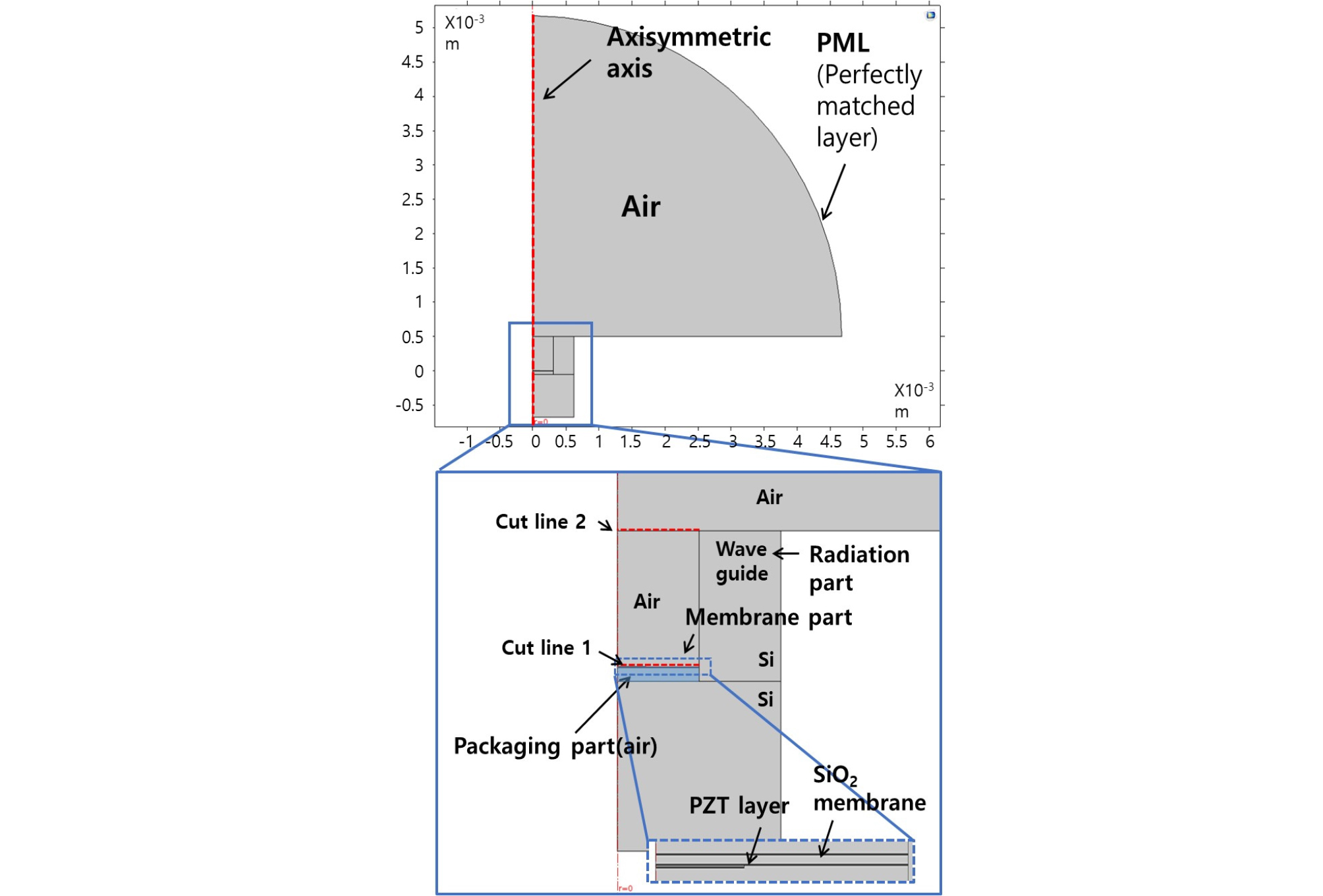
새로운 pMUT 소자는 축대칭의 원형 박막 기반으로 가장 일반적인 pMUT의 형태이다.[6], [7] 기존의 단일 pMUT 소자는 직접적인 박막 파트의 공기 중 방사만 고려하였으며, 그 외의 음향학적 구조를 고려하지 않았다.[6], [7] 하지만 패키징 된 하나의 pMUT 모듈은 Fig. 1과 같이 두 개의 음향학적 구조를 포함하고 있다. 하나는 박막의 앞에 위치한 도파관 구조로 모델링된 방사 파트이며, 다른 하나는 박막의 뒤에 위치한 음향 공동(closed caity)으로 모델링된 패키징 파트이다. 본 논문에서는 새로운 pMUT의 정확한 설계를 위해 방사 파트모델과 패키징 파트 모델을 고려하였으며, 이를 이용하여 광대역 설계에 이용하였다.
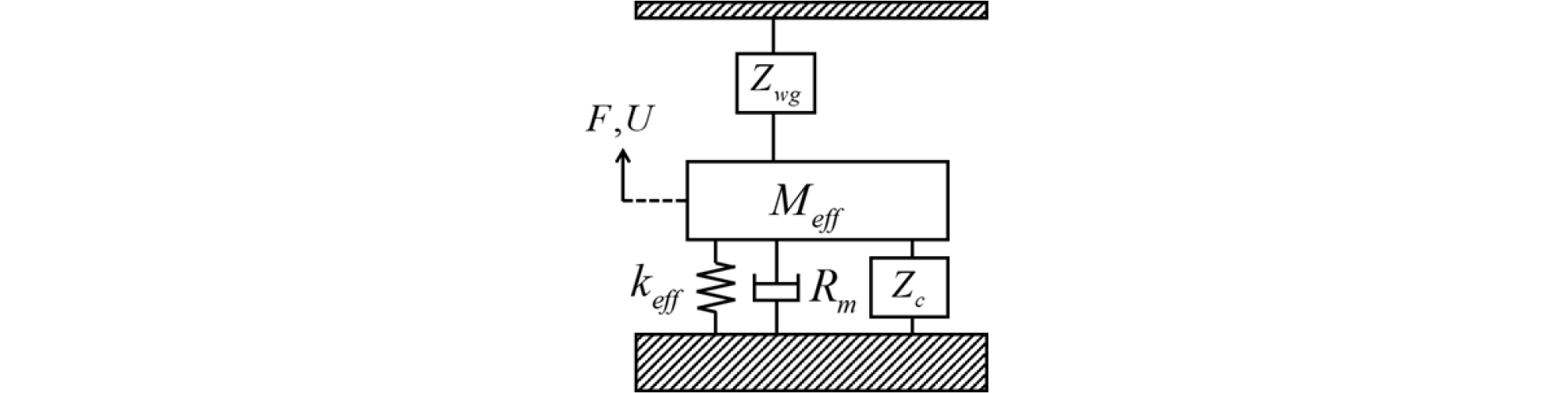
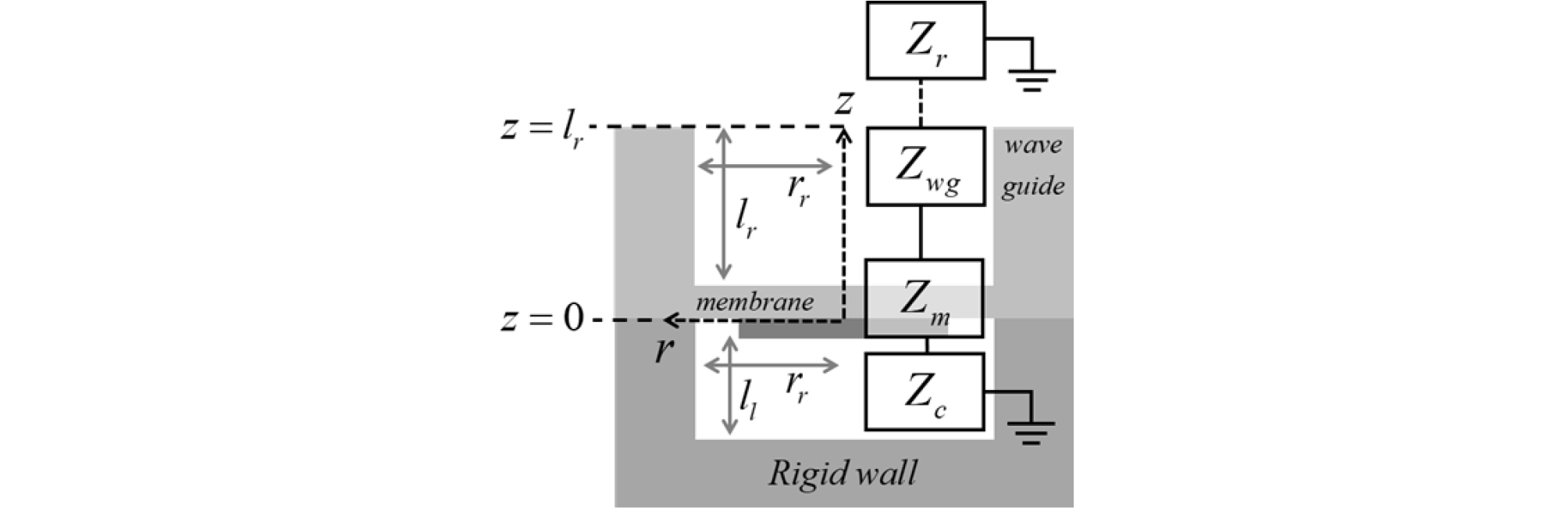
새로운 pMUT은 Fig. 2와 같이 박막 파트, 방사 파트, 패키징 파트를 포함한 3 자유도 시스템으로 모델링 되었다. 새롭게 설계된 pMUT은 다공진 시스템으로 공진 주파수와 그 사이에서 광대역을 달성할 수 있다.
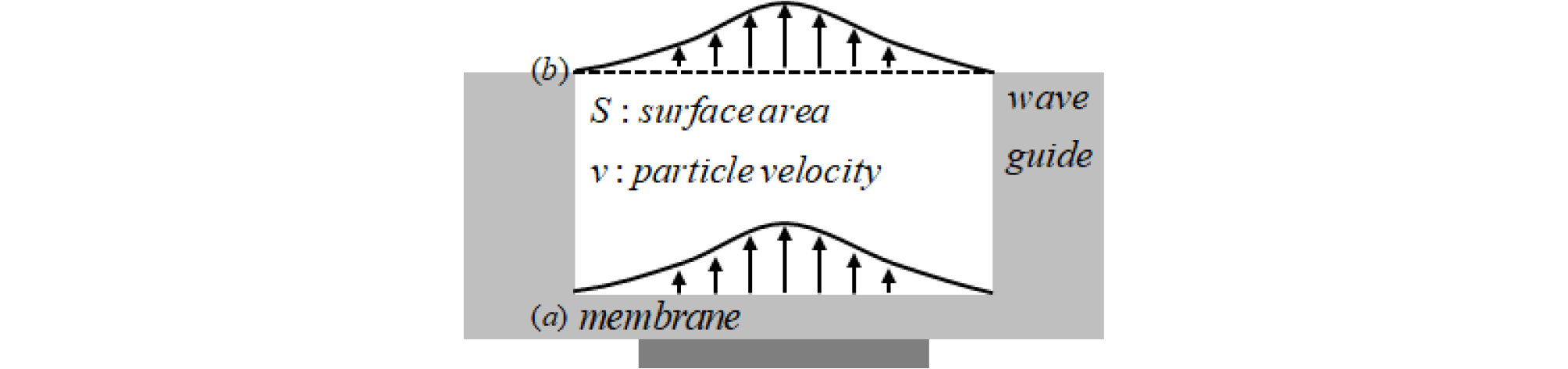
Fig. 3는 박막 근처 (a)와 방사면 (b)에서 음향 체적 속도를 보여준다. 체적 속도(vS)는 입자속도 v와 표면적 S의 곱으로 나타낼 수 있다. 박막에서 발생된 음파는 도파관 구조의 방사 파트를 지나 최종적으로 방사 파트의 끝단에서 방사가 이루어진다. 따라서 설계의 핵심은 체적 속도의 주파수 응답특성이 가능한 평탄하고 넓은 대역을 갖도록 설계하는 것이다.
본 논문에서 설계될 pMUT은 비선형성을 이용하여 두 개의 고주파수 음파로 지향성이 높은 차주파수를 발생시키는 PA 라우드 스피커의 적용을 위해서 100 kHz의 공진 주파수와, 최소 20 kHz의 주파수 대역을 갖도록 선정하였다.[6]
2.2 박막 파트의 집중 변수 모델
가장 먼저 박막 파트의 집중 변수 모델이 설계되었다. Fig. 1과 같이 박막 위에는 pMUT의 구동을 위한 압전 물질이 증착된다. 압전 물질은 박막파트에 비해 상대적으로 얇은 두께를 가지므로 집중 변수 모델에서는 모델의 단순화를 위해 고려되지 않았으며, 좀 더 정확한 해석을 위한 유한요소 모델에서 고려되었다. Fig. 4는 박막파트의 집중변수 모델이다. 일반적으로 pMUT의 박막 파트는 가장자리가 고정된 조건으로 가정되기 때문에, Fig. 5와 같이 박막은 휨 모드 플레이트로 모델링될 수 있다.[8] 이때, 박막의 수직 변형 곡선은 Eq. (1)처럼 나타낼 수 있다.[8]
Eq. (1)에서 q는 표면에 가해지는 균일한 분포 압력이며, a는 박막의 반지름, D는 굽힘 강성(flexural rigidity)이며, 로 계산된다.
| $$U(r)=\frac q{64D}(a^2-r^2{)^2,}$$ | (1) |
이 때, 로 표현하면, Eq. (1)을 Eq. (2)와 같이 간략화 할 수 있다.
| $$U(r)=U_0(1-(r/a)^2)^2,$$ | (2) |
수직방향의 유효강성 keff은 Eq. (3a), (3b)와 같이 박막이 받는 총 힘 F(= q×πa2)을 평균 수직 변형 Uavg로 나누어 얻어질 수 있다.
| $$\begin{array}{l}U_{avg}=\frac{\int_0^a{U(r)dA}}{\pi a^2}=\frac{\int_0^a{{\displaystyle\frac q{64D}}(a^2-r^2)2\pi rdr}}{\pi a^2}=\frac{qa^4}{192D}=\frac{q(1-\nu^2)}{16Et^3}a^4,\end{array}$$ | (3a) |
| $$k_{eff}=\frac F{U_{avg}}=\frac{16\pi Et^3}{a^2(1-\nu^2)},$$ | (3b) |
자연 주파수 및 모드 형태에 대한 공식을 활용하면, 고정된 원형 플레이트의 첫 번째 공진주파수는 Eq. (4)와 같이 계산될 수 있다.[9]
| $$f=\frac{\Lambda_0t}{2\pi a^2}\sqrt{\frac E{12\rho(1-\nu^2)}},\;where\;\Lambda_0=10.22,$$ | (4) |
여기서 E는 박막의 영률이다. Eq. (4)의 공진주파수 식과 Eq. (3b)의 유효 강성을 이용하여, 고정된 원형 플레이트의 유효 질량을 Eq. (5)처럼 계산할 수 있다.
| $$M_{eff}=\frac{k_{eff}}{4\pi^2f^2}=\frac{k_{eff}}{\Lambda_0^2\frac{t^2}{a^4}\left(\frac E{12\rho(1-\nu^2)}\right)}=\frac{192}{\Lambda_0^2}\rho(\pi a^2t),$$ | (5) |
박막의 기계 Q 인자를 통해, 고정된 원형 플레이트의 기계 저항 Rm은 Eq. (6)처럼 계산될 수 있다.[7] 최종 기계적 임피던스 Zm는 Eq. (7)과 같이 표현할 수 있다.
| $$R _{m} = \frac {\sqrt {M _{eff} k _{eff}}}{Q _{m}},$$ | (6) |
| $$Z _{m} =R _{m} +j(M _{eff} \omega -k _{eff} / \omega ),$$ | (7) |
2.3 방사 파트의 집중 변수 모델
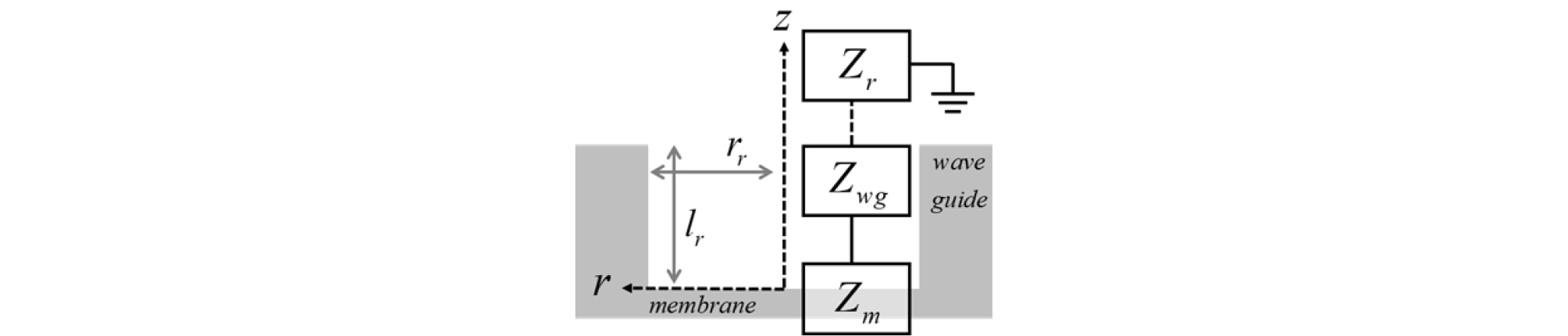
두 번째로 방사 파트의 집중 변수 모델이 설계되었다. Fig. 6은 방사 파트의 집중 변수 모델이다. 방사 파트의 기계적 임피던스를 정량화 하기 위해서는 원형 구멍을 적절한 음향학적 구조로 모델링하는 것이 필요하다. 본 논문에서는 Fig. 6과 같이 베플이 있는 원형 형태의 도파관으로 모델링 되었다.
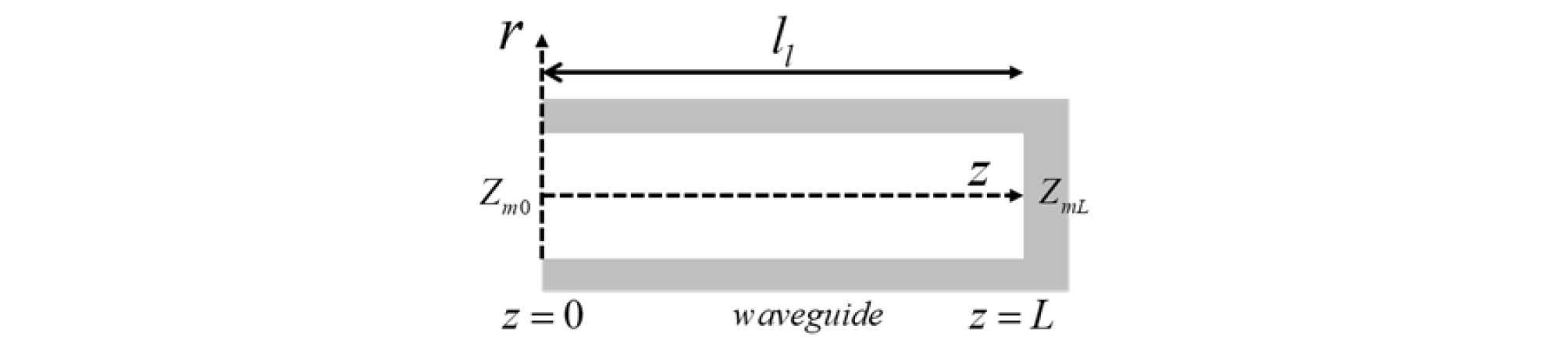
Fig. 7은 개방된 도파관의 임피던스이다. 원형 피스톤 음원은 z = 0에 위치해 있고, 이때의 기계적 임피던스는 Zm0이라하고, 음향이 방사되는 열린 영역인 z = L에서의 기계적 임피던스는 ZmL이라 하자. 오직 평면파만 진행된다 가정할 때, 도파관내에서의 음압은 Eq. (8)과 같이 나타낼 수 있다.[10], [11]
| $$p=Ae^{j(\omega t+k(L-z))}+Be^{j(\omega t-k(L-z))},$$ | (8) |
여기서 k는 wavenumber이다. Eq. (8)의 음압과 음향 입자 속도 의 관계로부터, 음원이 위치한(z = 0) 도파관의 임피던스 Zm0는 Eq. (9a)와 같이, 도파관 끝단(z = L)에서의 임피던스 ZmL는 Eq. (9b)와 같이 얻어질 수 있다.
| $$Z_{m0}=\rho_0cS\frac{Ae^{jkL}+Be^{-jkL}}{Ae^{jkL}-Be^{-jkL}},$$ | (9a) |
| $$Z_{mL}=\rho_0cS\frac{A+B}{A-B},$$ | (9b) |
Eqs. (9a)와 (9b)에서 S는 도파관의 면적이다. Eqs. (9a)와 (9b)를 통해, 도파관의 입력 기계 임피던스는 Eq. (10)와 같이 표현할 수 있다.
| $$\frac{Z_{m0}}{\rho_0cS}=\frac{(Z_{mL}/\rho_0cS)+j\tan kL}{1+j(Z_{mL}/\rho_0cS)\tan kL},$$ | (10) |
방사 임피던스 Zrad는 Eq. (11)과 같이 계산될 수 있다.[11]
| $$\begin{array}{l}Z_{rad}=R_{rad}+jX_{rad}\\R_{rad}=\rho_0cS\bullet\frac12(ka)^2\;,\\X_{rad}=\rho_0cS\bullet\frac8{3\pi}ka\end{array}$$ | (11) |
따라서, 방사파트의 입력 기계적 임피던스는 Eqs. (10)과 (11)을 이용하여, Eq. (12)처럼 표현할 수 있다.
| $$\frac{Z_{wg}}{\rho_0cS}=\frac{(Z_{rad}/\rho_0cS)+j\tan kL}{1+j(Z_{rad}/\rho_0cS)\tan kL},$$ | (12) |
Eqs. (10)과 (12)에서 ρ0는 음향 매질의 밀도이고, c는 매질에서의 음파 속도이다.
2.4 방사 파트의 체적 속도 증폭 효과
방사 파트는 도파관의 공진에 의해 체적 속도를 증폭해주는 역할을 해준다. 체적 속도 비는 도파관 길이 lr에 의한 도파관의 식을 통해 계산될 수 있다.
압력 및 속도의 연속성과 Eqs. (9b)와 (10)을 이용하면, 음향 입자 속도는 Eq. (13)과 같이 계산될 수 있다.[11]
| $$u(z,t)=u_0\frac{\cos(k(l_r-z))+j(\frac{Z_{rad}}{\rho_0cS})\sin(k(l_r-z))}{\cos(kl_r)+j(\frac{Z_{rad}}{\rho_0cS})\sin(kl_r)}\times e^{j\omega t},$$ | (13) |
Eq. (13)에서 u0는 z = 0에서의 음향 입자 속도이다. Eq. (13)을 이용하여, 도파관 끝단에서의 음향 입자속도는 Eq. (14)와 같이 계산 될 수 있다.
| $$u(l_r,\;t)=u_0\frac1{\cos(kl_r)+j(\frac{Z_{rad}}{\rho_0cS})\sin(kl_r)}e^{j\omega t},$$ | (14) |
최종적으로 평면파가 진행한다고 가정했을 때, 음원의 위치와 도파관 끝단의 음향 체적 속도 비, V는 Eq. (15)과 같이 계산 될 수 있다.
| $$V=\frac{u(l_r,t)}{u(0,t)}=\frac1{\cos(kl_r)+j(\frac{Z_{rad}}{\rho_0cS})\sin(kl_r)},$$ | (15) |
2.5 패키징 파트의 집중 변수 모델
마지막으로 패키징 파트의 집중 변수 모델이 설계되었다. Fig. 8은 패키징 파트의 집중 변수 모델이다. 닫힌 공동으로 모델링된 패키징 파트의 임피던스 Zc는 닫힌 도파관의 식을 이용하여 계산 될 수 있다. Fig. 9는 닫힌 도파관의 임피던스를 나타낸다. 닫힌 도파관의 임피던스는 Eq. (10)에 를 대입하여 Eq. (16)와 같이 계산할 수 있다. Fig. 9는 패키징 파트의 집중 변수 모델을 나타낸다. 본 논문에서 공동의 반지름은 박막의 반지름과 동일하게 가정하였으므로, Zc는 오직 공동의 길이 ll에만 의존한다.
| $$\frac{Z_c}{\rho_0cS}=-\cot kl_l,$$ | (16) |
2.6 전체 단일 pMUT 소자의 집중 변수 모델
박막 파트, 방사 파트, 패키징 파트를 모두 포함한 전체 단일 pMUT소자의 최종 집중 변수 모델은 Fig. 10와 같다. 박막에 가해지는 힘 F = 1로 간단히 할 때, z = 0에서의 최종 pMUT 단일 소자의 체적 속도 U(z = 0,t)은 Eq. (17)와 같이 면적과 전체 임피던스의 비로 표현할 수 있다. Eq. (17)에 음향 체적 속도 비 V를 곱하면, Eq. (18)과 같이 pMUT에서 도파관을 지나 최종 방사되는 체적 속도 U(z = lr,t)를 계산할 수 있다.
| $$U(z=0,t)=\frac S{Z_{tot}}=\frac S{Z_{eff}+Z_{wg}+Z_c},$$ | (17) |
| $$U(z=l_r,\;t)=V\times\frac S{Z_{tot}}=\frac1{\cos(kl_r)+j(Z_{rad}/\rho_0cS)\sin(kl_r)}\times\frac S{Z_{eff}+Z_{wg}+Z_c},$$ | (18) |
III. 광대역 단일 pMUT 소자 설계
3.1 박막 파트 설계
본 논문의 pMUT은 PA 라우드스피커 적용을 위해 100 kHz ~ 120 kHz의 주파수 대역을 갖도록 설계 목표를 정하였다.[6] 먼저 박막 파트가 설계되었다. 본 논문에서 설계된 pMUT의 재질은 SiO2가 선택되었다. SiO2박막은 막질의 밀도가 높고, 압전을 구동할 때 절연 역할도 수행하기 때문에 일반적으로 pMUT의 재질로 많이 선택되는 물질이다.[6], [7] 박막에 증착되는 압전은 박막에 비해 상대적으로 얇은 두께로 집중 변수 모델을 이용한 설계에서는 고려되지 않았으며, 추후 유한요소해석을 이용한 정밀 설계단계에서 고려되었다. 음향 매질은 공기에서의 사용을 목적으로 하므로, 공기가 선택되었다. Tables 1과 2는 설계에 사용된 SiO2 와 공기의 물성치이다.
Table 1. Properties of SiO2.
| The properties | Values |
| Density, ρ | 2300 [kg/m3] |
| Young's modulus, Ε | 70 [GPa] |
| Poisson ratio, ν | 0.17 |
| Mechanical quality factor | 50 |
Table 2. Properties of air.
| The properties | Values |
| Density, ρ | 1.21 [kg/m3] |
| Sound speed, c | 343 [m/s] |
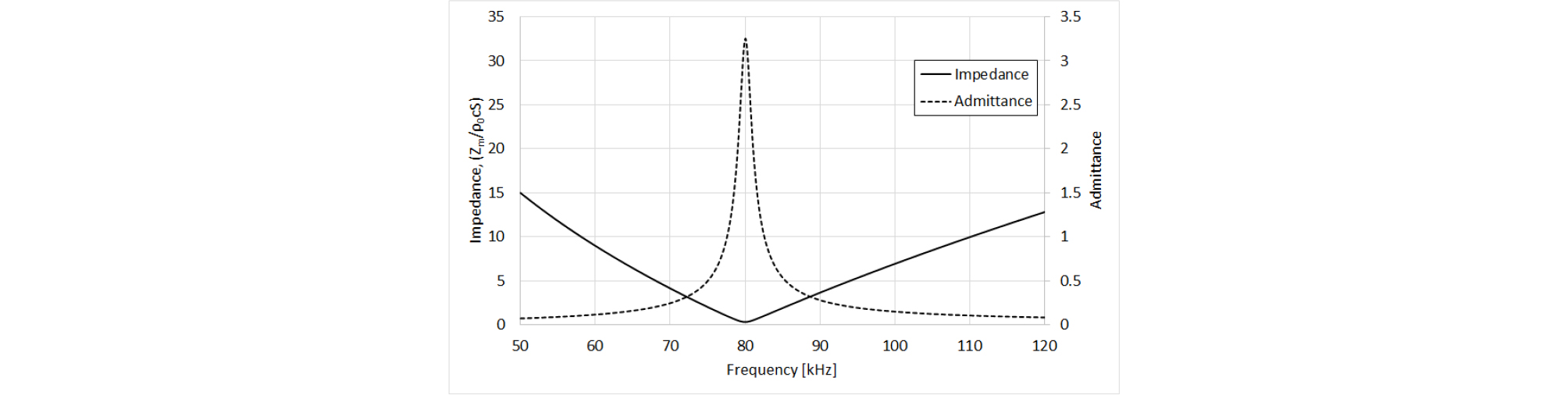
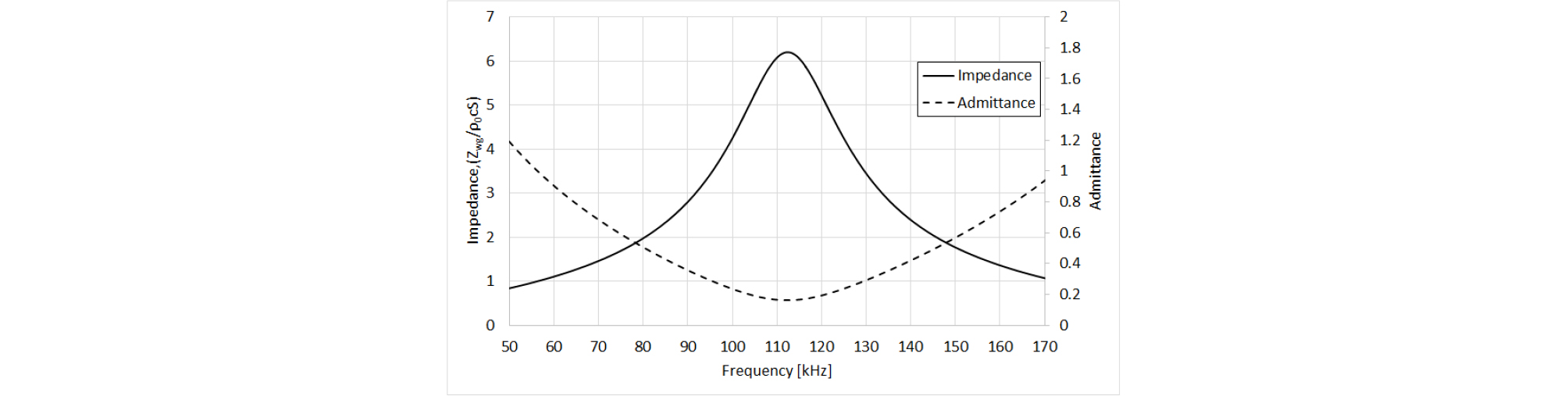
일반적으로 열산화 공정으로 형성 가능한 SiO2의 두께는 1 μm정도이며, 추가로 LP-CVD로 증착 가능한 SiO2의 두께는 최대 약 2 μm정도이다. 따라서, SiO2 박막의 두께는 최대 3 μm로 제한 되었다. 설계된 박막의 공진 주파수 fr는 80 kHz로 선정되었고, 이 때, 두께는 3 μm로 반지름은 Eq. (19)를 통해 313 um로 결정되었다. 이 때, 계산된 유효강성과 유효질량은 각각 1005 N/m와 305.6 mg였다. Fig. 11은 80 kHz에서 공진을 갖는 박막의 임피던스와 어드미턴스 곡선이다.
| $$a^2=\sqrt{\frac E{12\rho\left(1-\nu^2\right)}}\bullet\left(\frac{\Lambda_0^2}{2\pi f_r}\right),$$ | (19) |
3.2 방사 파트 설계
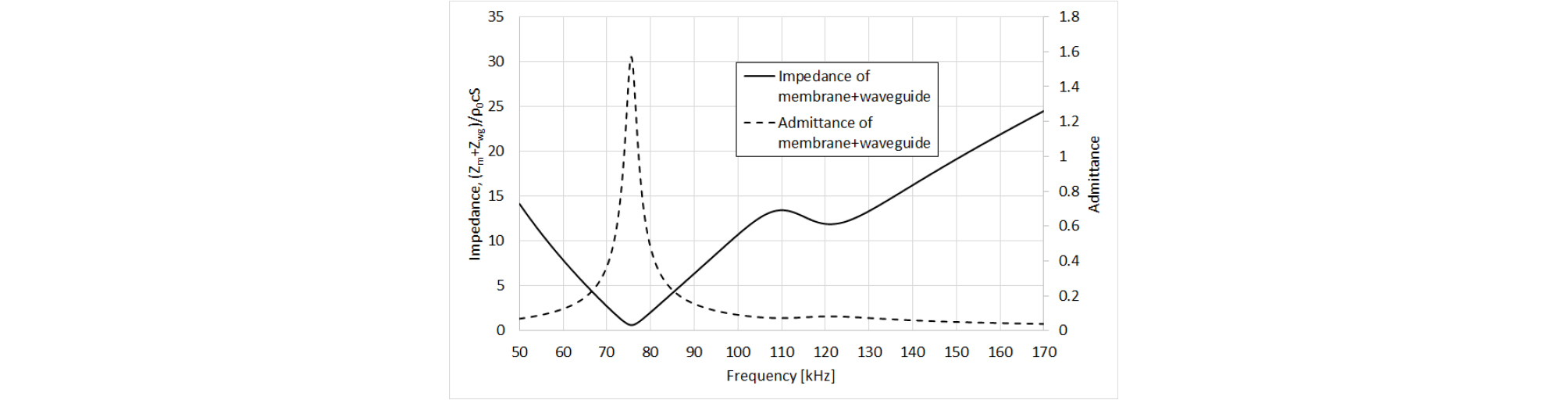
다음으로는 방사 파트의 설계이다. 박막 파트에 방사 파트를 추가함으로써 광대역에 가까운 주파수 곡선을 갖도록 설계할 수 있다. 방사 파트를 이루는 도파관의 반지름은 박막의 지름과 동일하므로, 본 설계 단계에서는 오직 도파관의 길이 lr만 결정된다. 도파관의 길이는 구조상 웨이퍼의 두께와 동일하므로, 일반적인 웨이퍼 두께인 350 μm ~ 650 μm 정도의 제약 조건을 갖는다. 설계된 lr은 목표로 하는 주파수 대역인 100 kHz ~ 120 kHz의 중심부인 약 110 kHz에서 최대의 임피던스를 갖도록 하는 500 μm으로 선정되었다. Fig. 12는 설계된 방사파트의 임피던스와 어드미턴스의 그래프이며, 임피던스는 약 112 kHz에서 최대 값을 갖는 것을 확인할 수 있다. Fig. 13은 박막 파트와 방사 파트가 합쳐진 임피던스와 어드미턴스 그래프이다. 112 kHz를 기준으로 이전과 이후에 두 개의 국부적인 임피던스 최소 값을 갖는다.
3.3 패키징 파트 설계
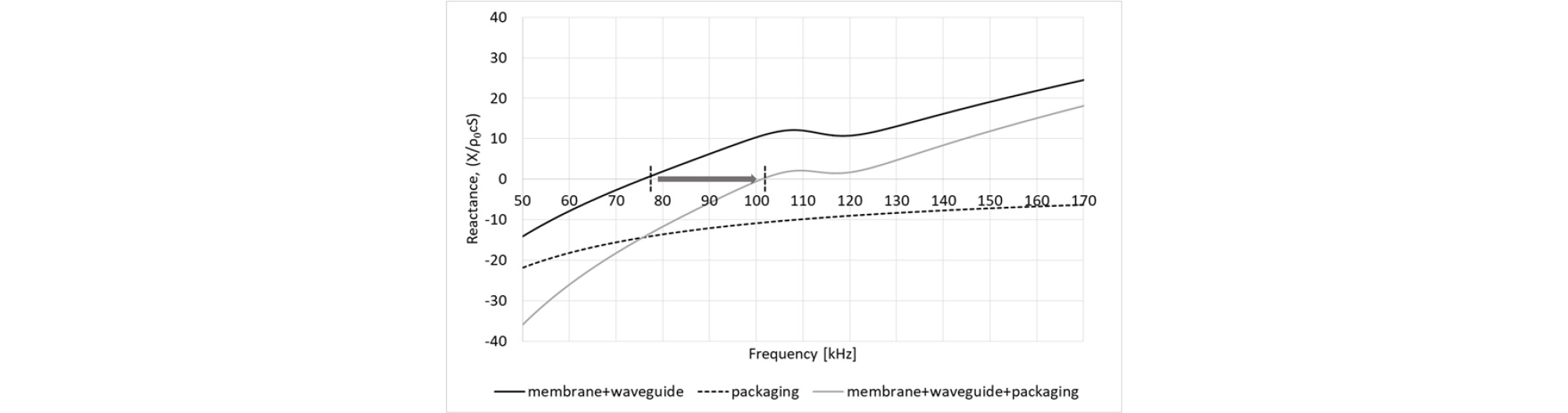
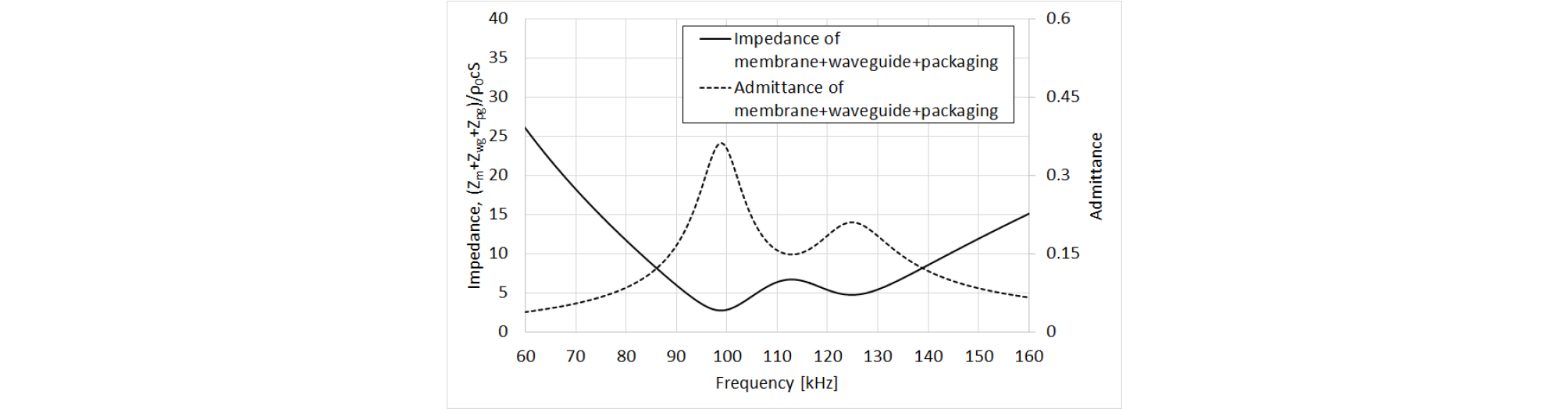
마지막으로 패키징 파트가 설계되었다. 닫힌 공동으로 모델링되는 패키징 파트의 임피던스는 Eq. (16)과 같이 리액턴스의 성분만 존재한다. 일반적으로 리액턴스가 0이 될 때가 그 시스템의 공진을 의미한다. Fig. 14는 패키징 파트와 박막, 방사 파트의 리액턴스 그래프이다. 기존에 설계되었던 박막과 방사 파트의 리액턴스의 합은 약 76 kHz에서 0의 값을 갖는다. 패키징 파트의 음의 리액턴스 값의 크기와 기울기를 조절하면, 공진의 위치를 이동시키고, 좀 더 평탄한 어드미턴스 곡선을 설계할 수 있다. 닫힌 공동 구조 또한 반지름은 박막과 동일하게 제한되었으며, 오직 닫힌 공동의 길이만 설계되었다. 닫힌 공동의 길이를 조절하여, 모든 리액턴스의 합이 100 kHz에서 0을 갖도록 하여, 공진의 위치를 기존의 76 kHz에서 100 kHz로 이동하도록 설계하였다. 최종 설계된 닫힌 공동의 길이는 50 μm이다. Fig. 15는 모든 파트가 결합된 최종 pMUT 소자의 임피던스와 어드미턴스 그래프를 보여준다. 어드미턴스 곡선에서 첫 번째 피크는 약 100 kHz에 존재하며, 두 번째 피크는 약 125 kHz에 존재한다.
3.4 최종 설계된 광대역 단일 pMUT 소자
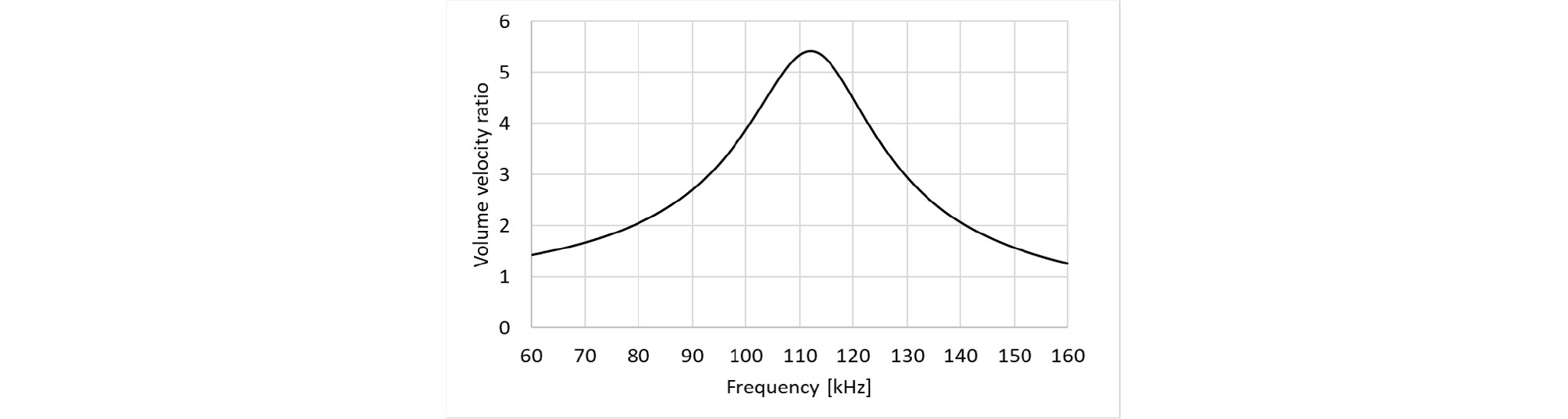
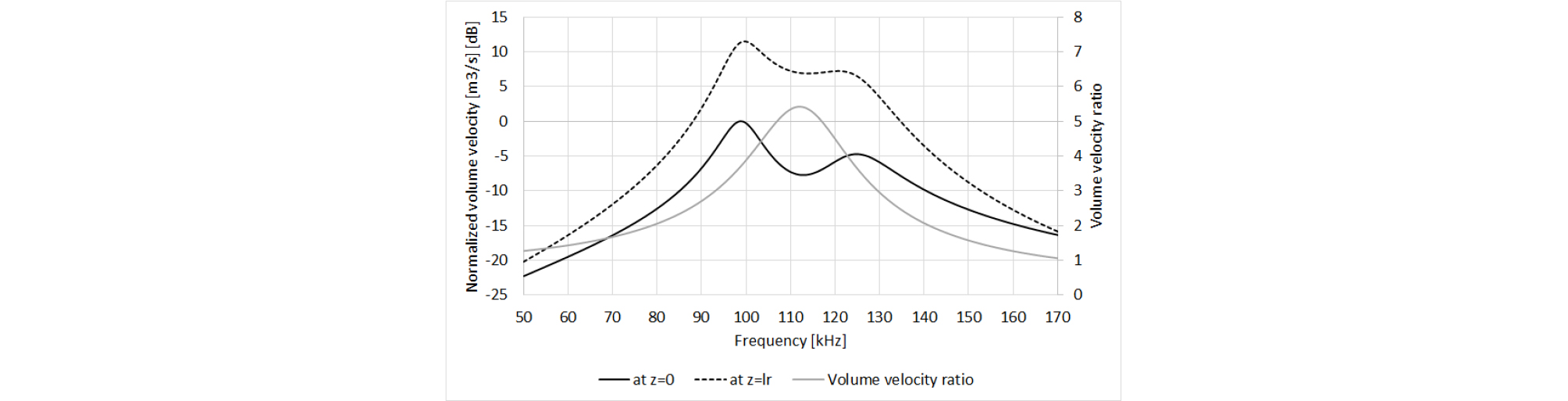
최종 방사되는 음압은 체적 속도에 비례한다. Eq. (15)로 계산된 설계된 도파관의 체적 속도 비는 Fig. 16과 같다. 112 kHz 구간에서 최대 피크를 가지며, 최대 5.4배의 부피 체적 증폭 효과가 있다. Fig. 17은 최종 설계된 pMUT 소자의 정규화된 체적 속도 곡선을 보여준다. 체적 속도 곡선은 박막이 위치한 z = 0에서 첫 번째 피크의 최대 값으로 정규화되었다. 최종적으로 도파관 끝단(z = lr)에서 방사되는 체적 속도는 박막 위치의(z = 0) 체적 속도에 체적 속도 비 V가 곱해진 형태로 나오게 된다. 두 개 피크 값의 중앙에 위치한 도파관의 공진이 대역의 중간 영역을 증폭시켜준다.
IV. 유한요소해석을 이용한 새로운 단일 pMUT 소자의 설계
집중 변수 모델로 설계된 새로운 단일 pMUT 소자를 기반으로 유한요소 해석을 통해 상세 설계가 진행되었다. 집중 변수 모델은 모델이 간단하고, 설계의 경향성을 파악하기 쉽다는 장점이 있지만, 다양한 근사화된 조건이 포함된 모델이므로 좀 더 신뢰성 있는 설계를 위해 유한요소 해석을 통해 설계가 보정되었다. Fig. 18은 상용 유한요소해석 프로그램인 COMSOL Multiphysis의 압전을 포함한 박막의 모델이다. pMUT에 구동을 위해 박막위에 증착되는 PZT는 일반적으로 압전 구동기에 널리 사용되는 PZT-5H로 선택되었다.[12] 이때 사용된 PZT-5H의 물성치는 Table 3과 같다.
Table 3. Properties of PZT-5H.
| The properties | Values |
| Density, ρ | 7500 [kg/m3] |
| Poisson ratio, ν | 0.31 |
| Permittivity, ε33 | 3400ε0 |
| Loss tangent, tanδ | 0.02 |
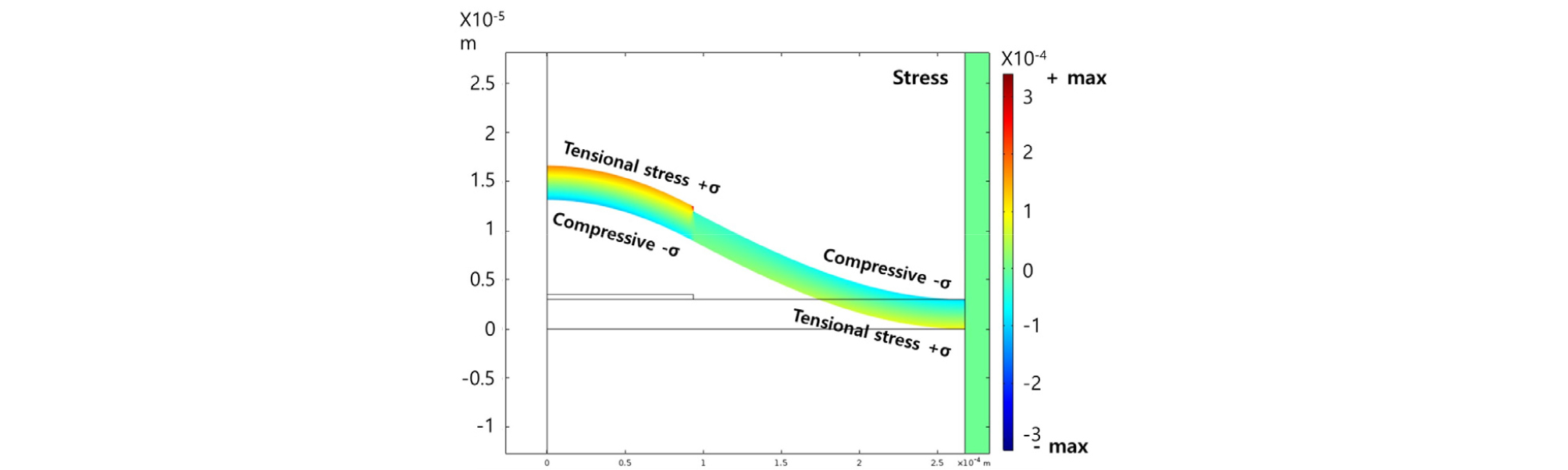
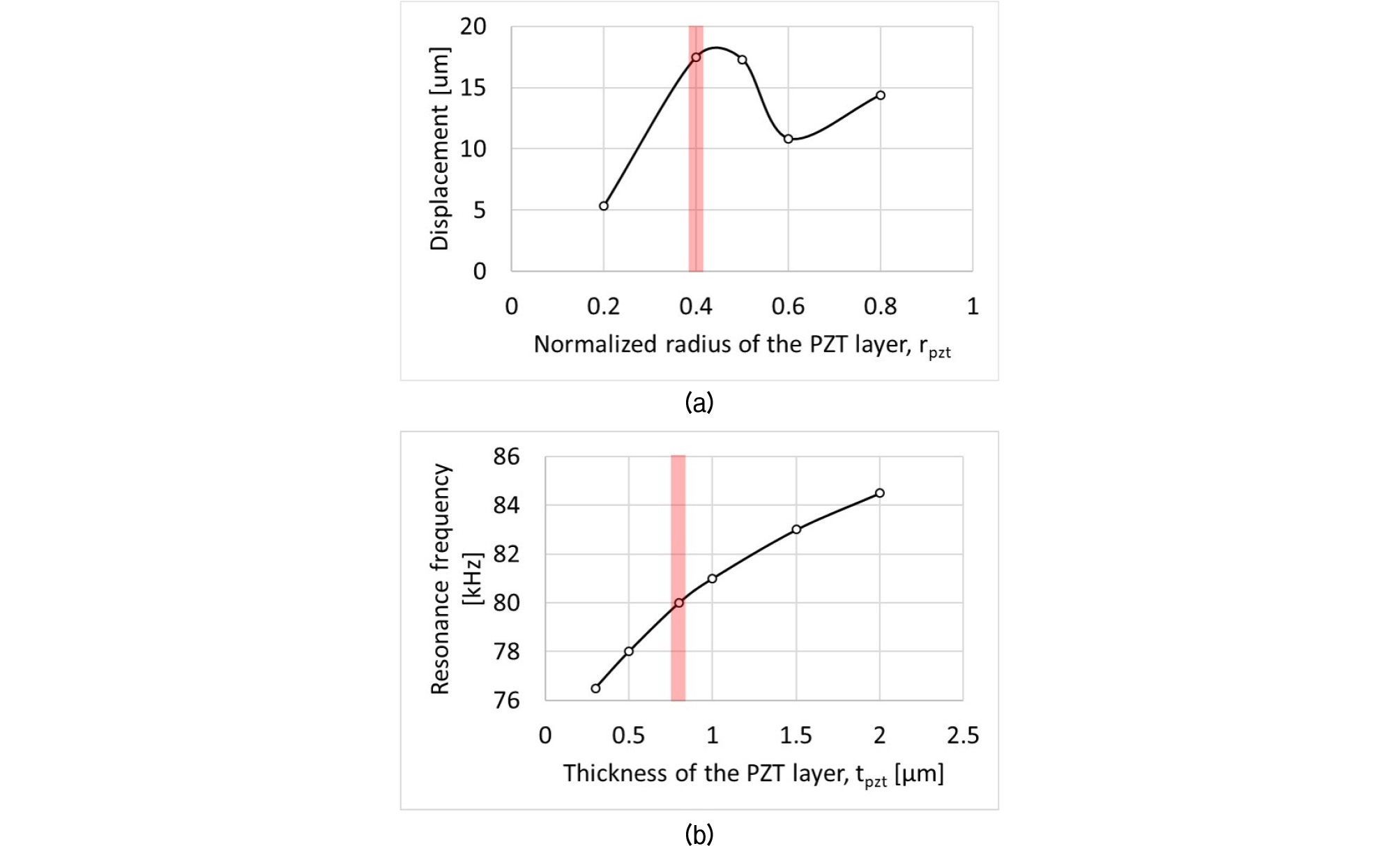
먼저, 증착된 압전의 지름과 두께가 설계되었다. 일반적으로 박막이 거동할 때, 박막의 내부응력은 Fig. 18과 같이 박막의 위치에 따라 압축응력과 인장 응력을 갖는다. 이때, Fig. 19(a)에서 보는 바와 같이 압전의 반지름이 박막의 반지름의 0.4배일 때, 박막이 가장 큰 변위를 갖는다. 그리고, Fig. 19(b)에서 보는 바와 같이 압전의 두께가 0.8 um일 때, 앞서 집중 변수 모델로 설계한 박막의 공진인 80 kHz에 가장 근접한다.
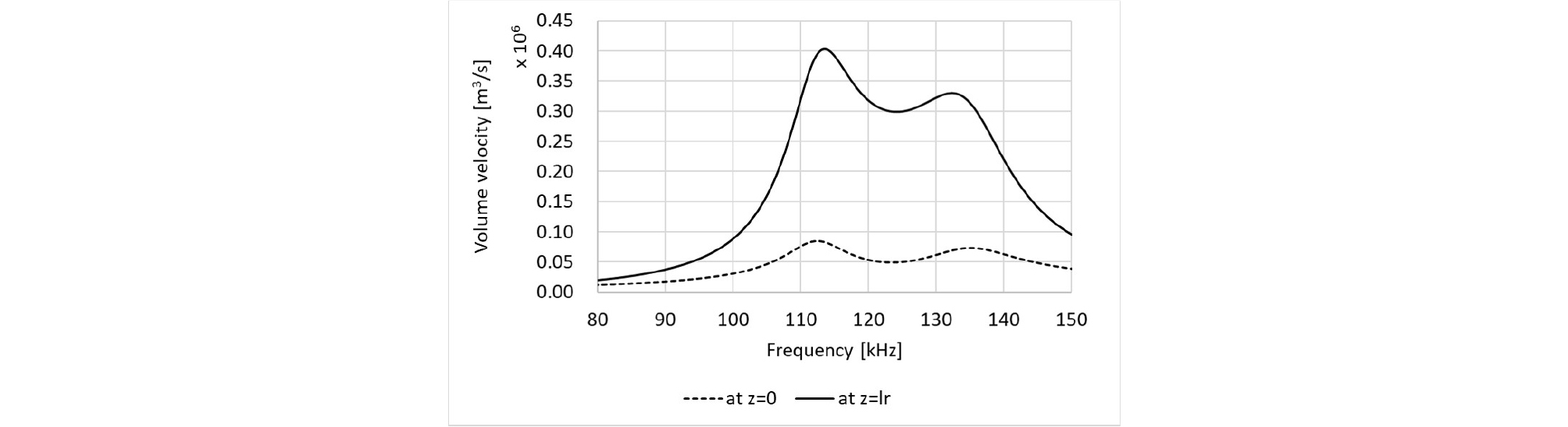
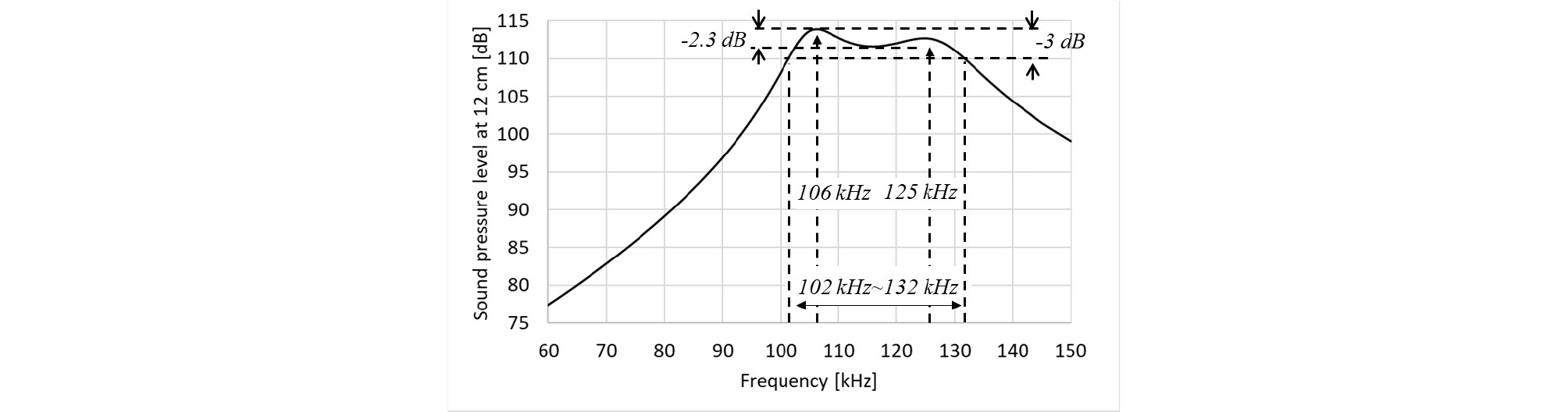
Fig. 20은 전체 pMUT의 유한요소 모델이다. 축대칭 모델이며, 박막 파트, 방사 파트, 패키징 파트를 모두 포함하고 있으며, 매질은 공기이다. 박막의 반지름을 조금씩 변경해가면서 cut line 1(z = 0)과 cut line 2 (z = lr)에서 발생하는 체적 속도가 평탄한지 확인하였으며, 레일리 길이보다 충분히 먼 12 cm 거리에서 발생한 음압 곡선을 확인하였다. 유한요소해석을 이용하여 최종 설계된 pMUT의 설계 변수는 Table 4과 같다. Fig. 21은 유한요소해석을 통해 최종 설계된 pMUT소자의 체적 속도를 보여준다. cut line 1에서의 체적 속도보다 cut line 2에서 발생한 체적 속도가 약 5배 정도 더 큰 것을 확인할 수 있었다. Fig. 22은 레일리 길이보다 충분히 큰 약 12 cm 거리에서 압전에 1 V를 가해줬을 때, 유한요소해석으로 계산된 음압 곡선이다. 첫 번째 피크인 106 kHz에서 약 113.87 dB, 두 번째 피크인 125 kHz에서 약 112.76 dB가 계산되었으며, 최대 피크 값과 최소 피크 값 차이는 –2.3 dB가 발생하였으며, Half-Power Band Width(HPBW)를 기준으로 하는 약 –3 dB 내에서는 102 kHz ~ 132 kHz의 30 kHz의 대역을 달성함을 확인할 수 있었다.
Table 4. Tuned design parameters.
V. 공정 개념도
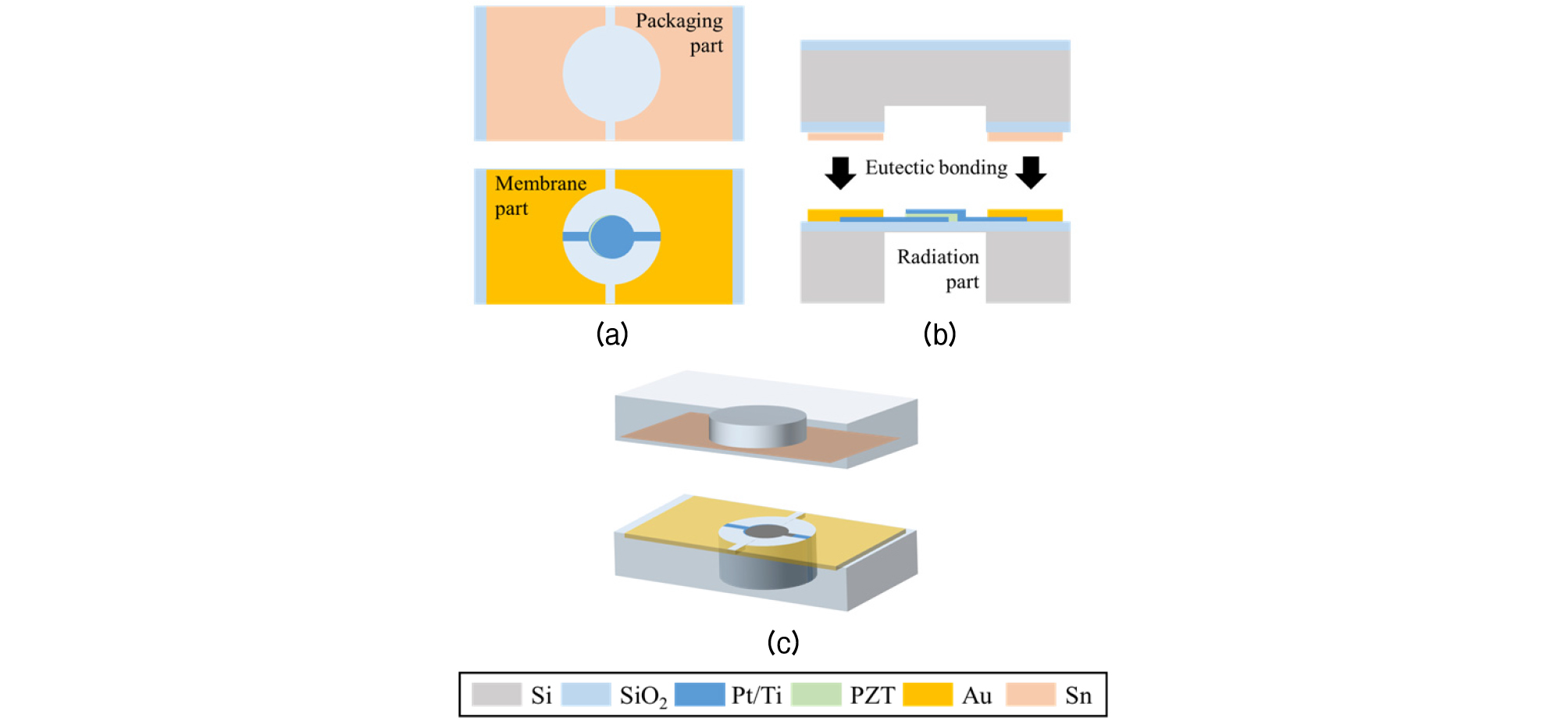
본 논문에서 설계된 pMUT은 미세가공 공정 기술을 이용하여 제작할 수 있다. Fig. 23은 본 논문에서 설계된 pMUT의 간략한 공정 개념도이다. 먼저, Fig. 23(a)와 같이 패키징 파트의 Si 웨이퍼와 박막 파트와 방사 파트의 Si 웨이퍼가 각각 제작된다. 박막파트는 Si 웨이퍼 위에 SiO2 막을 thermal oxidation을 통해 형성한 후, 하부전극(Pt/Ti), PZT, 상부전극(Pt/Ti)를 패터닝한 다음, Au 본딩 패드를 패터닝한다. 마지막으로 DRIE를 통해 박막을 형성한다. 패키징 파트는 Si 웨이퍼에 Sn 본딩 패드를 패터닝한 뒤, DRIE를 통해 닫힌 공동을 형성한다. 마지막으로 제작된 두 개의 웨이퍼를 Fig. 23(b)와 같이 웨이퍼 수준에서 Au-Sn eutectic bonding을 이용하여 접합시켜 완성한다. Fig. 23(c)는 최종적으로 본딩이 이루어질 pMUT의 3차원 도식도이다.
VI. 결 론
본 논문에서는 공기 중 파라메트릭 어레이 라우드 스피커에 적용하기 위한 광대역 초음파 방사용 압전 박막 기반 초소형 초음파 트랜스듀서(pMUT)에 대한 설계 연구가 진행되고, 이것의 공정 개념도를 제시하였다. 새로운 pMUT은 박막 구조의 앞면과 뒷면에 방사 파트와 패키징 파트를 추가한 다공진 시스템으로 모델링 되었으며, 3자유도의 집중 변수 모델로 설계되었다. 설계된 단일 pMUT 소자는 최종적으로 유한요소해석을 통해 보정되었으며, 최종 설계된 pMUT소자의 –3 dB 대역은 102 kHz ~ 132 kHz로 약 30 kHz의 대역폭을 달성하였다. 기존 연구는 서로 다른 공진을 갖는 두 개의 pMUT소자를 배열하여, 역 위상 구동을 통해 광대역을 확보하였으나, 본 논문의 소자는 단일 pMUT소자로 광대역을 확보할 수 있었다. 따라서 out-of-phase 구동을 위한 별도의 신호처리와 그를 위한 회로 및 별도의 전극 분리를 생략할 수 있으며, 이를 위한 공간도 절약할 수 있다. 따라서 이는 휴대용 파라메트릭 어레이 라우드 스피커의 적용 분야에 유리할 뿐만 아니라 광대역을 요구로 하는 다양한 분야의 적용에도 유리할 것으로 기대된다.